Multi-Modal Alignment of Visual Question Answering Based on Multi-Hop Attention Mechanism
Abstract
:1. Introduction
2. Materials and Methods
2.1. Classical Attention Mechanisms
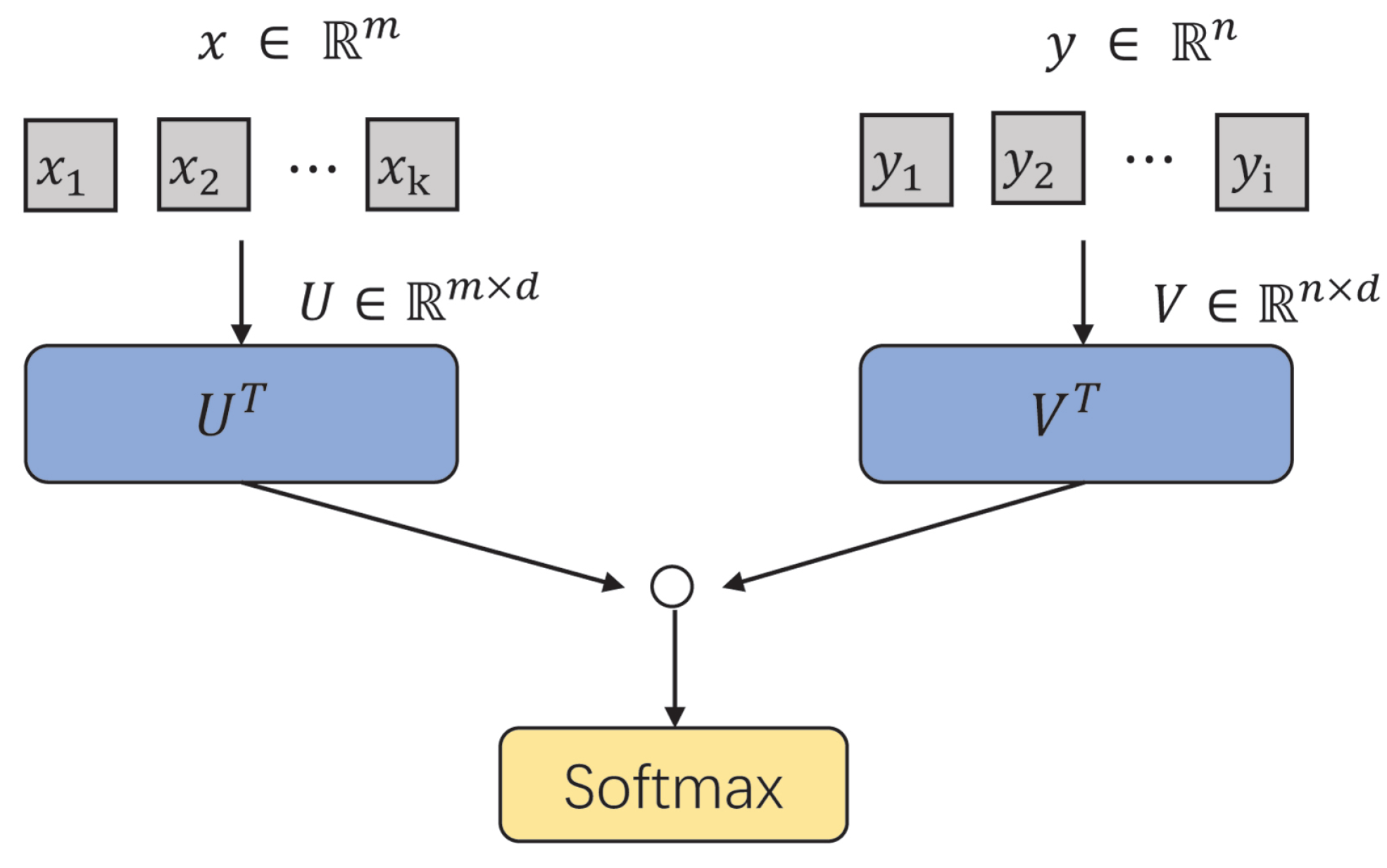
2.1.1. Dot Product Attention
2.1.2. Multi-Head Attention
2.1.3. Multi-Modal Factorized Bilinear Pooling
2.1.4. Top-Down Attention for VQA
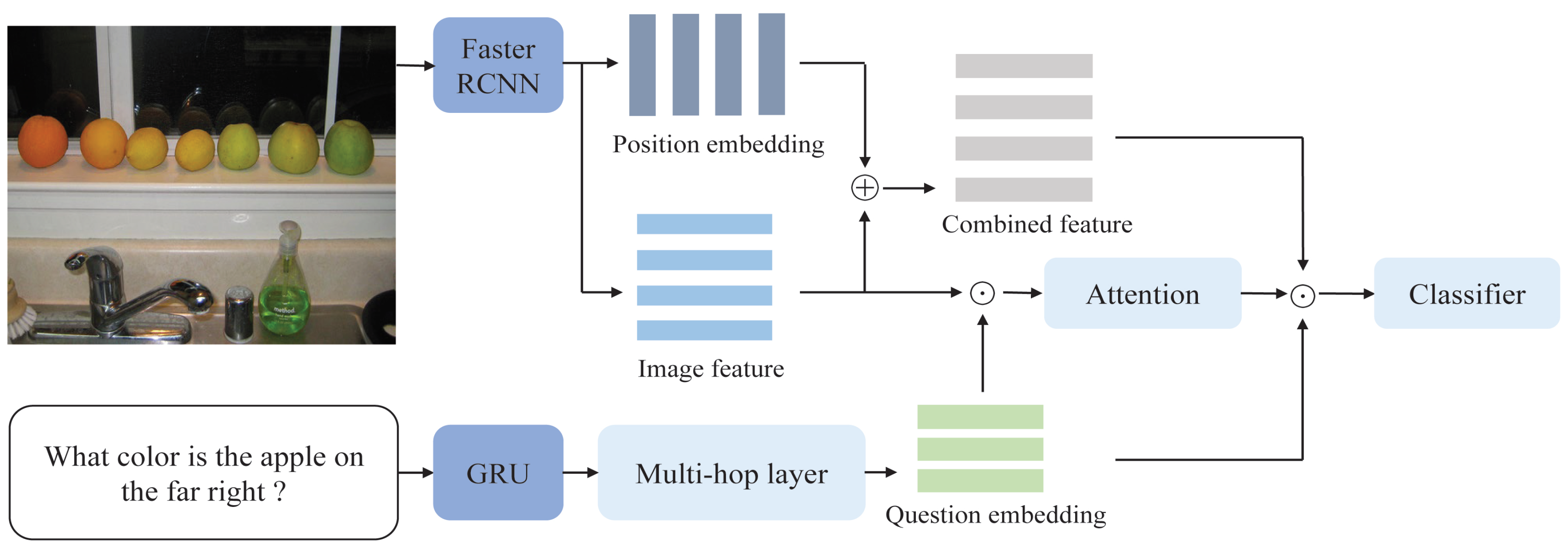
2.2. Model Input Preprocessing
2.2.1. Question Word Embedding
2.2.2. Image Feature Extraction
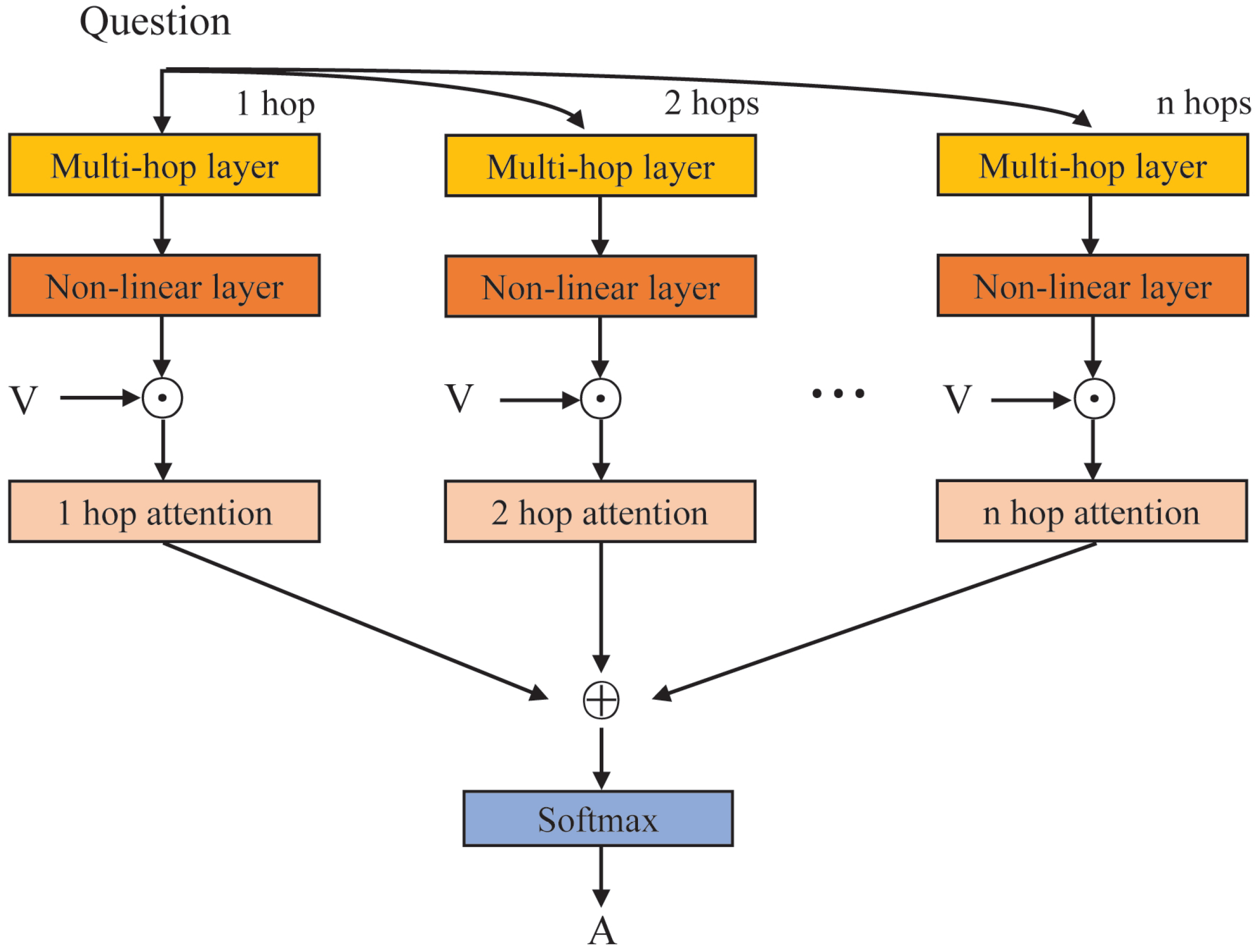
2.3. Multi-Hop Attention Layer
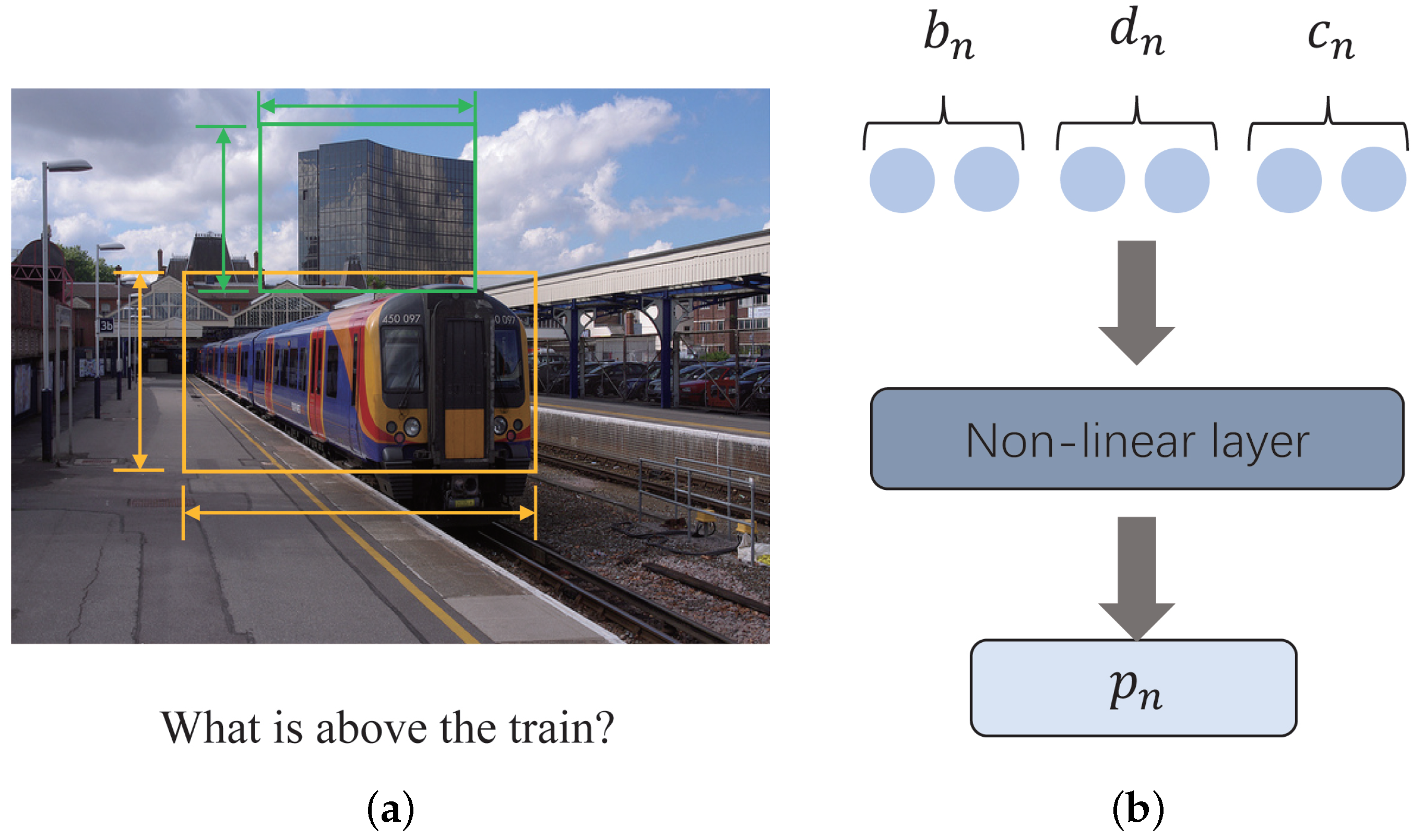
2.4. Position Embedding Mechanism
2.5. Multi-Modal Fusion and Classification
3. Results
3.1. The Dataset
3.2. Implementation Details
3.3. Ablation Study
3.4. Comparison with Other Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VQA | Visual Question Answering |
| BUTD | Bottom-Up and Top-Down |
| GRU | Gated Recurrent Unit |
| BAN | Bilinear Attention Networks |
| BGN | Bilinear Graph Networks |
| GloVe | Global Vectors for Word Representation |
| MAGNA | Multi-hop Attention Graph Neural Network |
References
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2048–2057. [Google Scholar]
- Antol, S.; Agrawal, A.; Lu, J.; Mitchell, M.; Batra, D.; Zitnick, C.L.; Parikh, D. Vqa: Visual question answering. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015; pp. 2425–2433. [Google Scholar]
- Das, A.; Kottur, S.; Gupta, K.; Singh, A.; Yadav, D.; Moura, J.M.F.; Parikh, D.; Batra, D. Visual dialog. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Guo, D.; Xu, C.; Tao, D. Image-question-answer synergistic network for visual dialog. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Lau, J.J.; Gayen, S.; Abacha, A.B.; Demner-Fushman, D. A dataset of clinically generated visual questions and answers about radiology images. Sci. Data 2018, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhang, Y.; Mou, L.; Xing, E.; Xie, P. PathVQA: 30,000+ Questions for Medical Visual Question Answering. arXiv 2020, arXiv:2003.10286. [Google Scholar]
- Vu, M.H.; Löfstedt, T.; Nyholm, T.; Sznitman, R. A Question-Centric Model for Visual Question Answering in Medical Imaging. IEEE Trans. Med. Imaging 2020, 39, 2856–2868. [Google Scholar] [CrossRef] [PubMed]
- Ren, F.; Zhou, Y. CGMVQA: A New Classification and Generative Model for Medical Visual Question Answering. IEEE Access 2020, 8, 50626–50636. [Google Scholar] [CrossRef]
- Gurari, D.; Li, Q.; Stangl, A.J.; Guo, A.; Lin, C.; Grauman, K.; Luo, J.; Bigham, J.P. VizWiz Grand Challenge: Answering Visual Questions From Blind People. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 3608–3617. [Google Scholar]
- Zhou, Y.; Mishra, S.; Verma, M.; Bhamidipati, N.; Wang, W. Recommending themes for ad creative design via visual-linguistic representations. In Proceedings of the Web Conference, Taipei, Taiwan, 20–24 April 2020; pp. 2521–2527. [Google Scholar]
- Barra, S.; Bisogni, C.; Marsico, M.D.; Ricciardi, S. Visual question answering: Which investigated applications? Pattern Recognit. Lett. 2021, 151, 325–331. [Google Scholar] [CrossRef]
- Fukui, A.; Park, D.H.; Yang, D.; Rohrbach, A.; Darrell, T.; Rohrbach, M. Multimodal Compact Bilinear Pooling for Visual Question Answering and Visual Grounding. arXiv 2016, arXiv:1606.01847. [Google Scholar]
- Vo, H.Q.; Phung, T.; Ly, N.Q. VQASTO: Visual question answering system for action surveillance based on task ontology. In Proceedings of the 2020 7th NAFOSTED Conference on Information and Computer Science, Ho Chi Minh City, Vietnam, 26–27 November 2020; pp. 273–279. [Google Scholar]
- Yu, J.; Zhu, Z.; Wang, Y.; Zhang, W.; Hu, Y.; Tan, J. Cross-modal knowledge reasoning for knowledge-based visual question answering. Pattern Recognit. 2020, 108, 107563. [Google Scholar] [CrossRef]
- Mao, J.; Gan, C.; Kohli, P.; Tenenbaum, J.B.; Wu, J. The neuro-symbolic concept learner: Interpreting scenes, words, and sentences from natural supervision. arXiv 2019, arXiv:1904.12584. [Google Scholar]
- Kovalev, A.K.; Shaban, M.; Osipov, E.; Panov, A.I. Vector Semiotic Model for Visual Question Answering. Cogn. Syst. Res. 2022, 71, 52–63. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeerer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Anderson, P.; He, X.; Buehler, C.; Teney, D.; Johnson, M.; Gould, S.; Zhang, L. Bottom-up and top-down attention for image captioning and visual question answering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6077–6086. [Google Scholar]
- Gao, P.; Jiang, Z.; You, H.; Lu, P.; Hoi, S.C.H.; Wang, X.; Li, H. Dynamic Fusion With Intra- and Inter-Modality Attention Flow for Visual Question Answering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Yu, Z.; Yu, J.; Cui, Y.; Tao, D.; Tian, Q. Deep Modular Co-Attention Networks for Visual Question Answering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Kim, J.; Jun, J.; Zhang, B. Bilinear Attention Networks. Adv. Neural Inf. Process. Syst. 2018, 31, 1–13. [Google Scholar]
- Kim, J.; On, K.; Lim, W.; Kim, J.; Ha, J.; Zhang, B. Hadamard Product for Low-rank Bilinear Pooling. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Pirsiavash, H.; Ramanan, D.; Fowlkes, C. Bilinear classifiers for visual recognition. Adv. Neural Inf. Process. Syst. 2009, 22, 1–9. [Google Scholar]
- Norcliffe-Brown, W.; Vafeias, E.; Parisot, S. Learning Conditioned Graph Structures for Interpretable Visual Question Answering. Adv. Neural Inf. Process. Syst. 2018, 31, 1–10. [Google Scholar]
- Hu, R.; Rohrbach, A.; Darrell, T.; Saenko, K. Language-Conditioned Graph Networks for Relational Reasoning. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Guo, D.; Xu, C.; Tao, D. Bilinear Graph Networks for Visual Question Answering. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Pennington, J.; Socher, R.; Manning, C.D. GloVe: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Socher, R.; Manning, C. Glove: Global Vectors for Word Representation. Available online: http://nlp.stanford.edu/projects/glove/ (accessed on 1 March 2022).
- Cho, K.; Merriënboer, B.V.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN EncoderDecoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Proceedings of the European Conference on Computer Vision, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Wang, G.; Ying, R.; Huang, J.; Leskovec, J. Multi-hop Attention Graph Neural Network. arXiv 2020, arXiv:2009.14332. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Goyal, Y.; Khot, T.; Summers-Stay, D.; Batra, D.; Parikh, D. Making the V in VQA Matter: Elevating the Role of Image Understanding in Visual Question Answering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Krishna, R.; Zhu, Y.; Groth, O.; Johnson, J.; Hata, K.; Kravitz, J.; Chen, S.; Kalantidis, Y.; Li, L.-J.; Shamma, D.A.; et al. Visual genome: Connecting language and vision using crowdsourced dense image annotations. Int. J. Comput. Vis. 2017, 123, 32–73. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Shen, X.; Tian, X.; Liu, T.; Xu, F.; Tao, D. Continuous Dropout. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3926–3937. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Han, J.; Moraga, C. The influence of the sigmoid function parameters on the speed of backpropagation learning. Nat. Artif. Neural Comput. 1995, 930, 195–201. [Google Scholar]
- Yin, X.; Goudriaan, J.; Lantinga, E.A.; Vos, J.; Spiertz, H.J. A Flexible Sigmoid Function of Determinate Growth. Ann. Bot. 2003, 91, 361–371. [Google Scholar] [CrossRef] [PubMed]
- VQA: Visual Question Answering. Available online: https://visualqa.org/ (accessed on 1 March 2022).
- Ilievski, I.; Feng, J. A Simple Loss Function for Improving the Convergence and Accuracy of Visual Question Answering Models. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Nguyen, D.; Okatani, T. Improved fusion of visual and language representations by dense symmetric co-attention for visual question answering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 6087–6096. [Google Scholar]
- Yu, Z.; Yu, J.; Fan, J.; Tao, D. Multi-Modal Factorized Bilinear Pooling with Co-Attention Learning for Visual Question Answering. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Piscataway, NJ, USA, 22–29 October 2017; pp. 1821–1830. [Google Scholar]


| Module | Setting | Accuracy |
|---|---|---|
| d = 1 | 65.23 | |
| Decay factor | d = 2 | 65.56 |
| d = 3 | 65.42 | |
| Multi-hop | n = 1 | 64.96 |
| n = 2 | 65.56 | |
| n = 3 | 65.33 | |
| n = 4 | 65.07 | |
| Position dimension = 512 | 64.86 | |
| Multi-hop + position | Position dimension = 1024 | 65.54 |
| Position dimension = 1280 | 65.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Q.; Yu, C.; Hou, Y.; Peng, P.; Zheng, Z.; Chen, W. Multi-Modal Alignment of Visual Question Answering Based on Multi-Hop Attention Mechanism. Electronics 2022, 11, 1778. https://doi.org/10.3390/electronics11111778
Xia Q, Yu C, Hou Y, Peng P, Zheng Z, Chen W. Multi-Modal Alignment of Visual Question Answering Based on Multi-Hop Attention Mechanism. Electronics. 2022; 11(11):1778. https://doi.org/10.3390/electronics11111778
Chicago/Turabian StyleXia, Qihao, Chao Yu, Yinong Hou, Pingping Peng, Zhengqi Zheng, and Wen Chen. 2022. "Multi-Modal Alignment of Visual Question Answering Based on Multi-Hop Attention Mechanism" Electronics 11, no. 11: 1778. https://doi.org/10.3390/electronics11111778
APA StyleXia, Q., Yu, C., Hou, Y., Peng, P., Zheng, Z., & Chen, W. (2022). Multi-Modal Alignment of Visual Question Answering Based on Multi-Hop Attention Mechanism. Electronics, 11(11), 1778. https://doi.org/10.3390/electronics11111778








