The Joint Phantom Track Deception and TDOA/FDOA Localization Using UAV Swarm without Prior Knowledge of Radars’ Precise Locations
Abstract
:1. Introduction
- (1)
- By utilizing TDOA/FDOA localization of UAV swarms in a 3D scenario to estimate the position of hostile radars without prior knowledge, which is beneficial for optimizing the localization deployment and provides guidance for phantom track design, the model of the joint phantom track deception and TDOA/FDOA localization to deceive air defense radar networks is developed.
- (2)
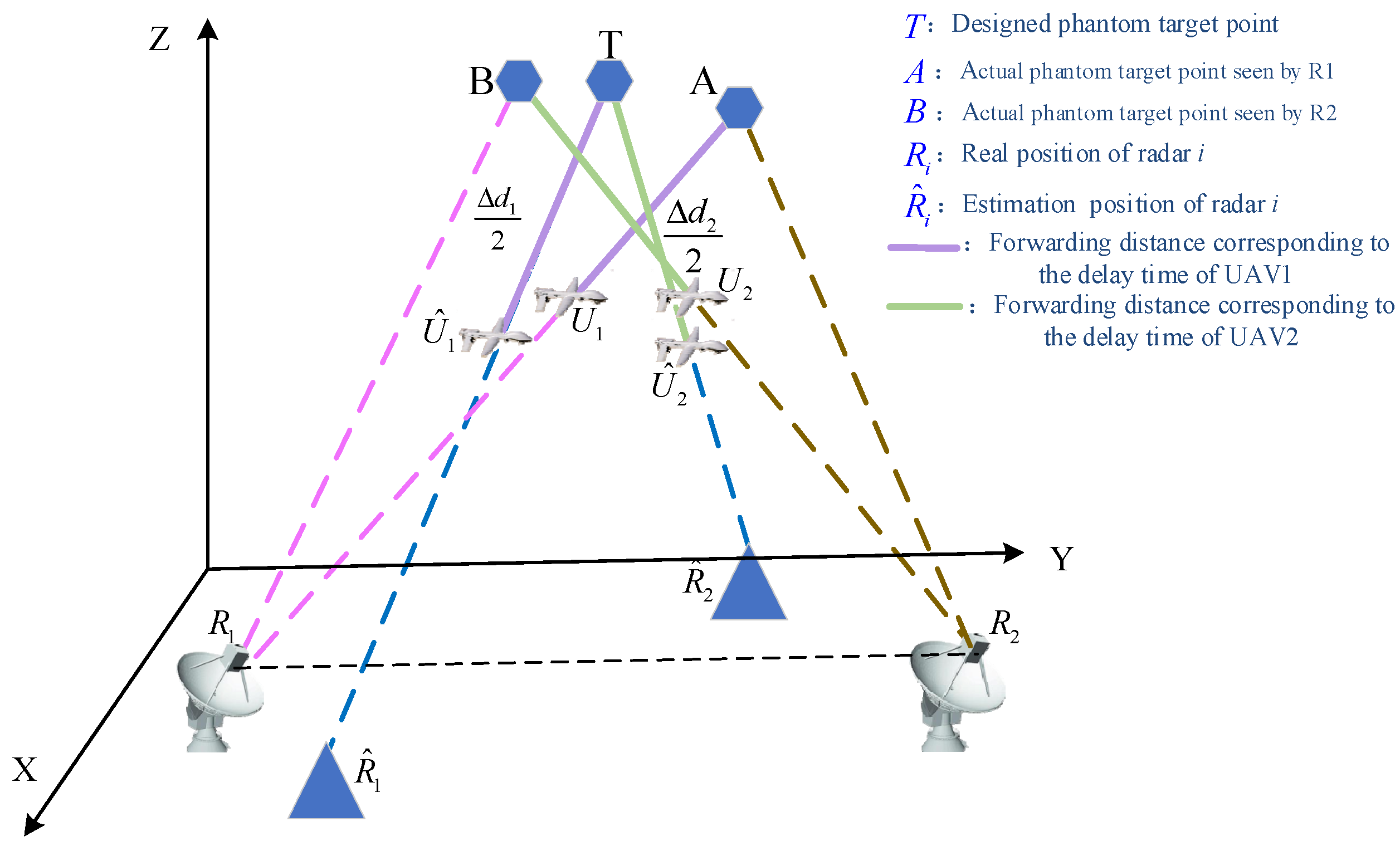
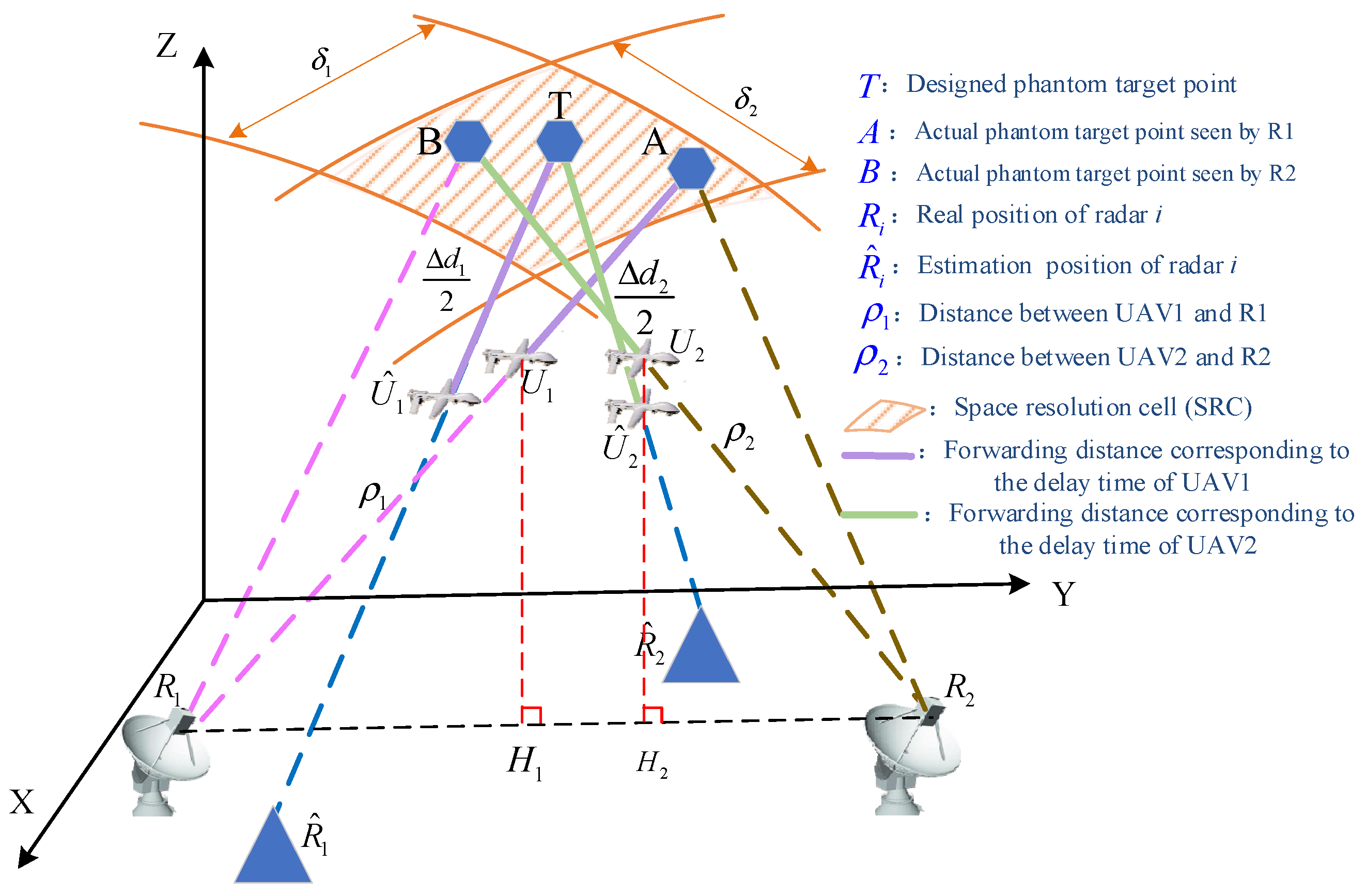
- In contrast to the existing studies, radar location error and UAV position error, which always exist in practical situations, are considered in uncertainty analysis for a 3D scenario. The same source testing by space resolution cell (SRC) from the perspective of a radar network is executed to evaluate the effectiveness of phantom track deception; the upper bound and lower bound of delay time to guarantee effective deception are derived in a 3D scenario.
- (3)
- The influence of the pass ration caused by localization error, UAV position error and SRC is analyzed and verified by simulation results. The pass ratio means the ratio of phantom targets number that can pass the same source testing to the total number of phantom targets. These analysis and simulation results provide guidance for phantom track deception in practice.
2. Model Establishing for Joint Phantom Track Deception and Radar Localization
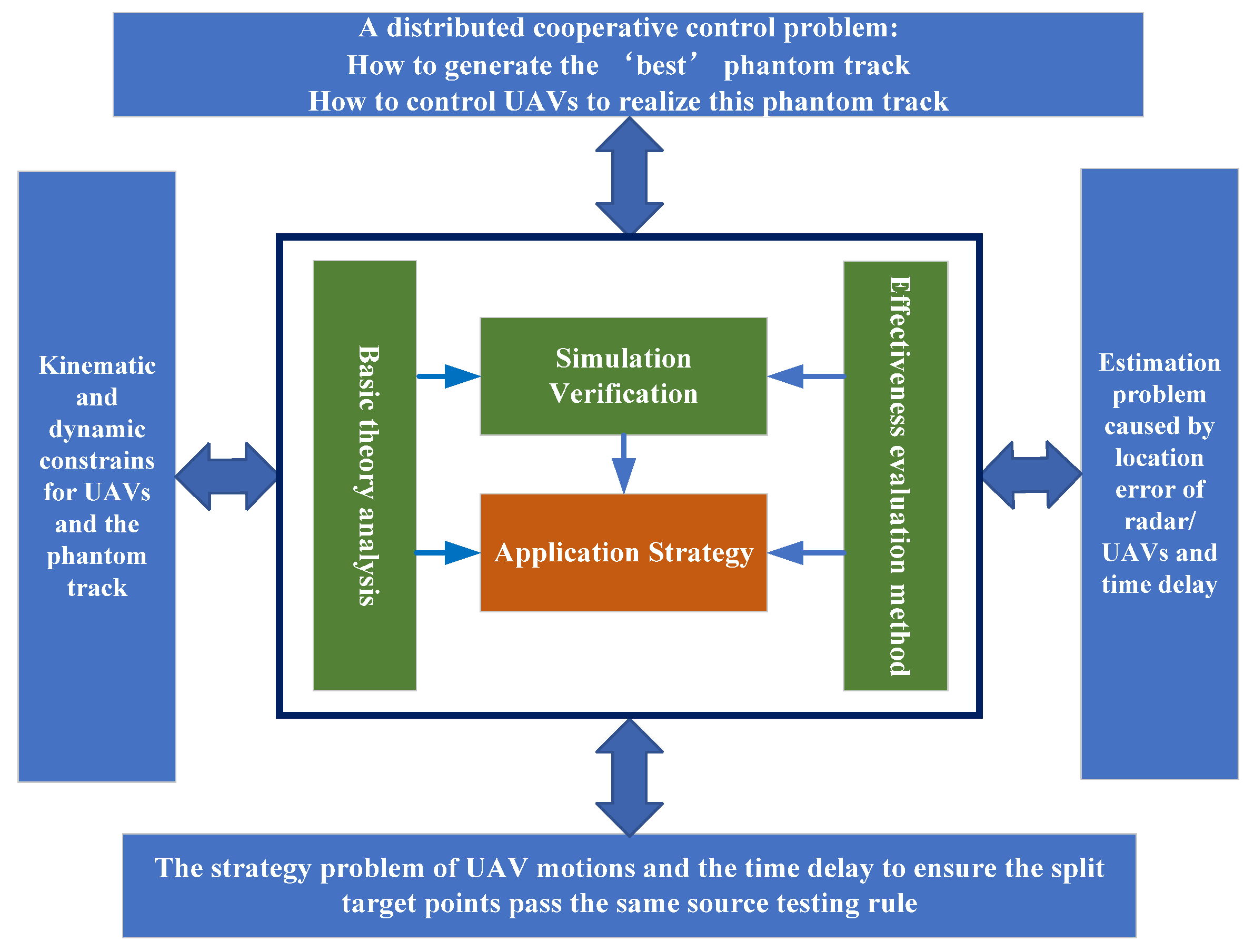
2.1. Problem Analysis and Related Work
- (1)
- A distributed cooperative control problem on how to generate the ‘best’ phantom track and how to control UAVs to realize this phantom track.
- (2)
- The estimation problem caused by location error of radar/UAVs and time delay.
- (3)
- The strategy problem of UAV motions and the time delay to ensure that the split target points pass the same source testing rule.
- (4)
- The kinematic and dynamic constrains for UAVs and the phantom track.
2.2. Model Establishment
3. TDOA/FDOA Localization Using UAV Swarm
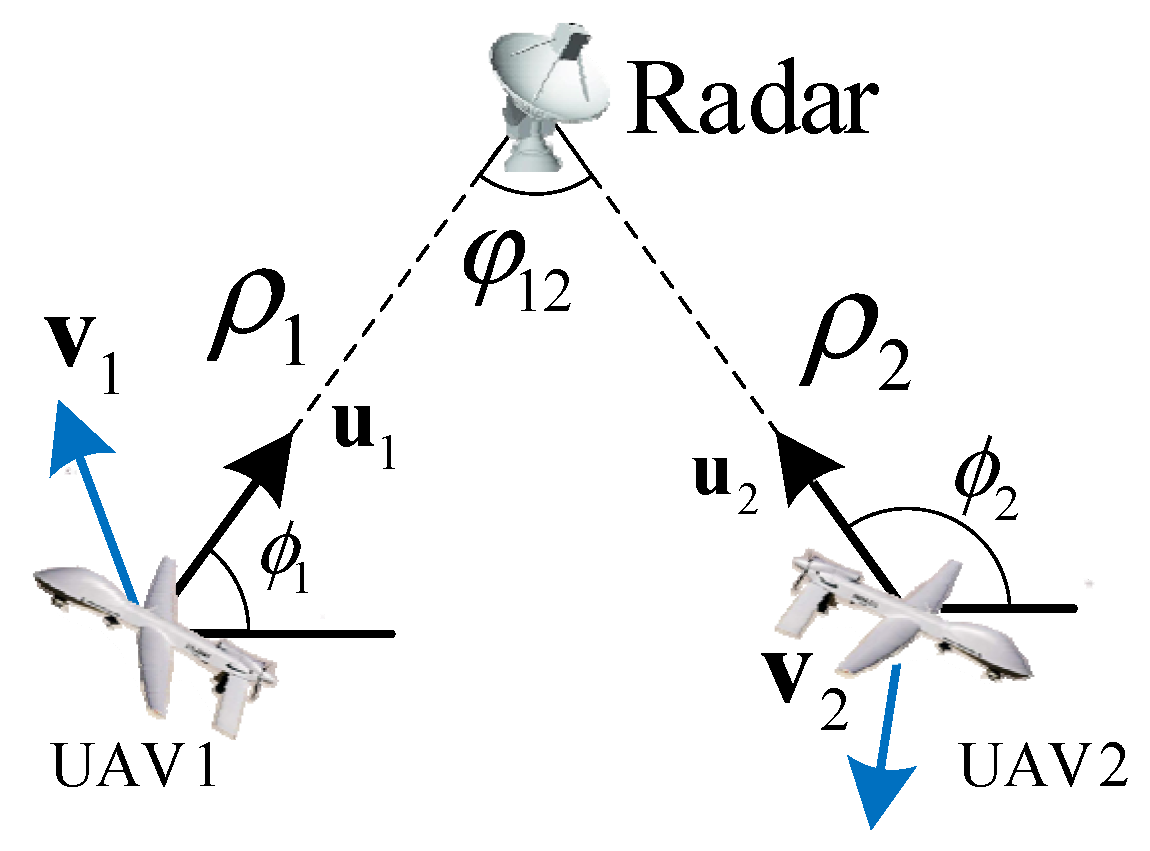
3.1. TDOA/FDOA Localization Model
3.2. Fisher Information Matrix (FIM) for TDOA/FDOA Localization
4. Phantom Track Deception with Uncertainty Analysis
4.1. Same Source Testing Using SRC Rule
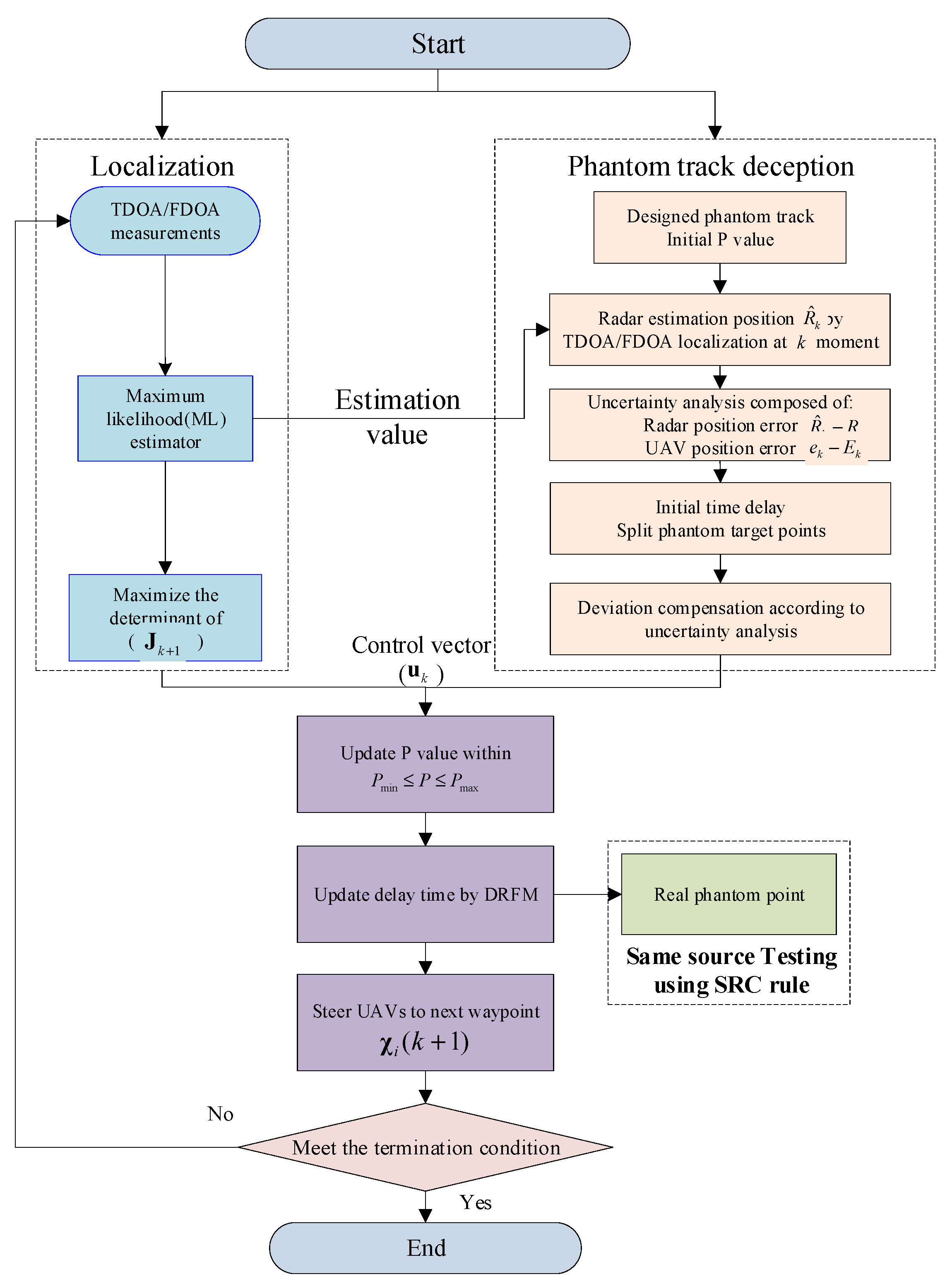
4.2. Process of Localization and Phantom Track Deception Method
- Step 1:
- According to the tactic intention or battlefield need, a designed phantom track is determined in advance as the first step of realizing the deception.
- Step 2:
- Radar position estimation is addressed by UAV swarm using TDOA/FDOA measurement. The FIM is used to optimize the localization deployment. Through TDOA/FDOA measurement, the estimated position at each time step keeps updated and the estimation value will be more and more accurate.
- Step 3:
- Using the obtained in Step 2, the uncertainty analysis composed of radar position error and UAV position error is made to calculate the delay time and the split degree of phantom target points.
- Step 4:
- Deviation compensation according to uncertainty analysis. The control vector is obtained by maximize the determinant of . The determinant of FIM matrix provides a lower bound for the localization and deception effectiveness.
- Step 5:
- Update the value within the maximum and minimum value. Using the same source testing to evaluate the deception effectiveness and providing feedback guidance for phantom track optimization. Although this step is executed by the radar network, it is necessary to evaluate the effectiveness as a close loop feedback which can help us to design the phantom track.
- Step 6:
- Update the time delay of DRFM and steer UAVs to the next waypoints. Finally, go back to step 2.
- Step 7:
- If the deception time meets the terminate condition, the deception process ends. Otherwise, go to step 2 and iterate until it meets the terminate condition.
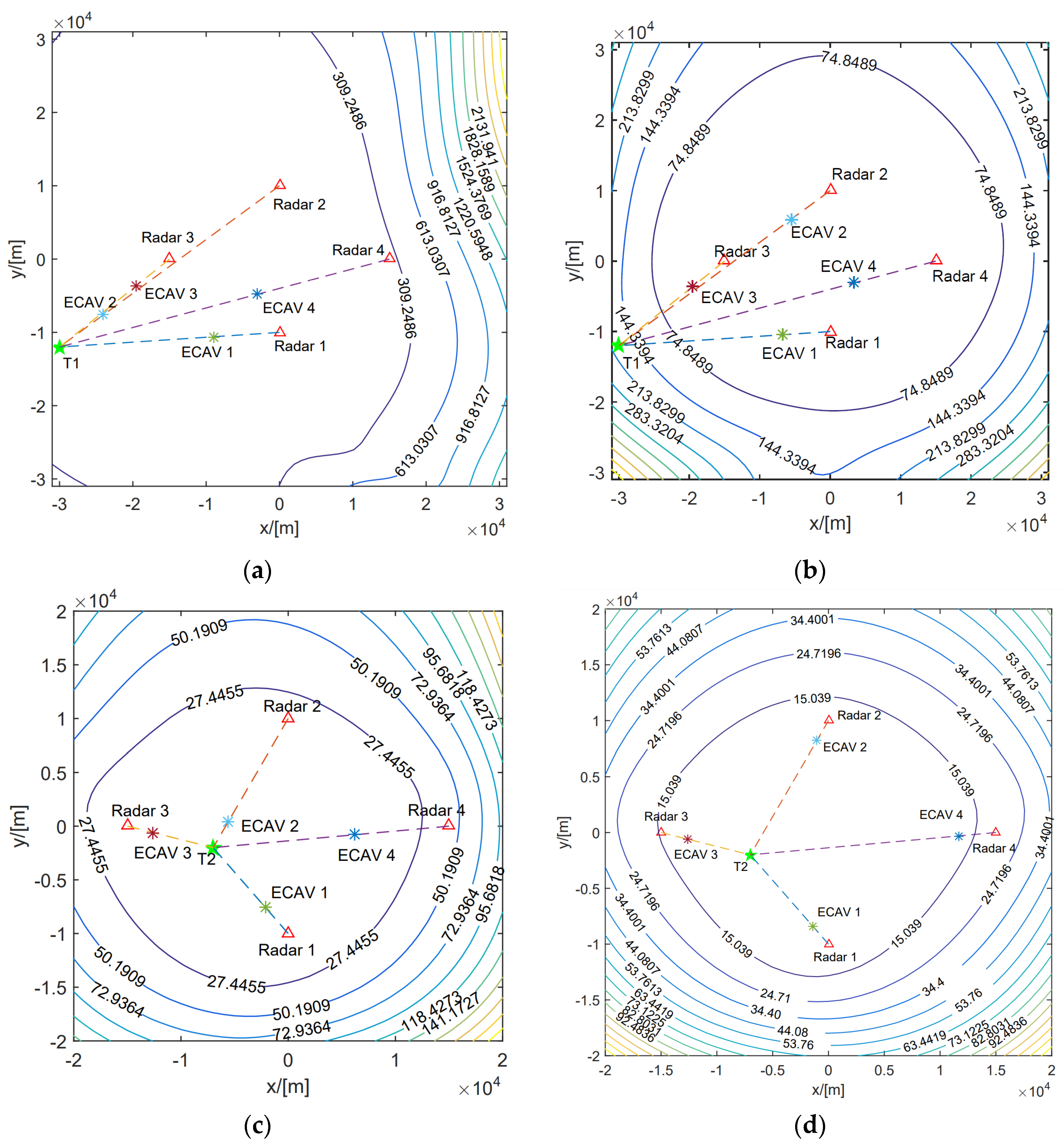
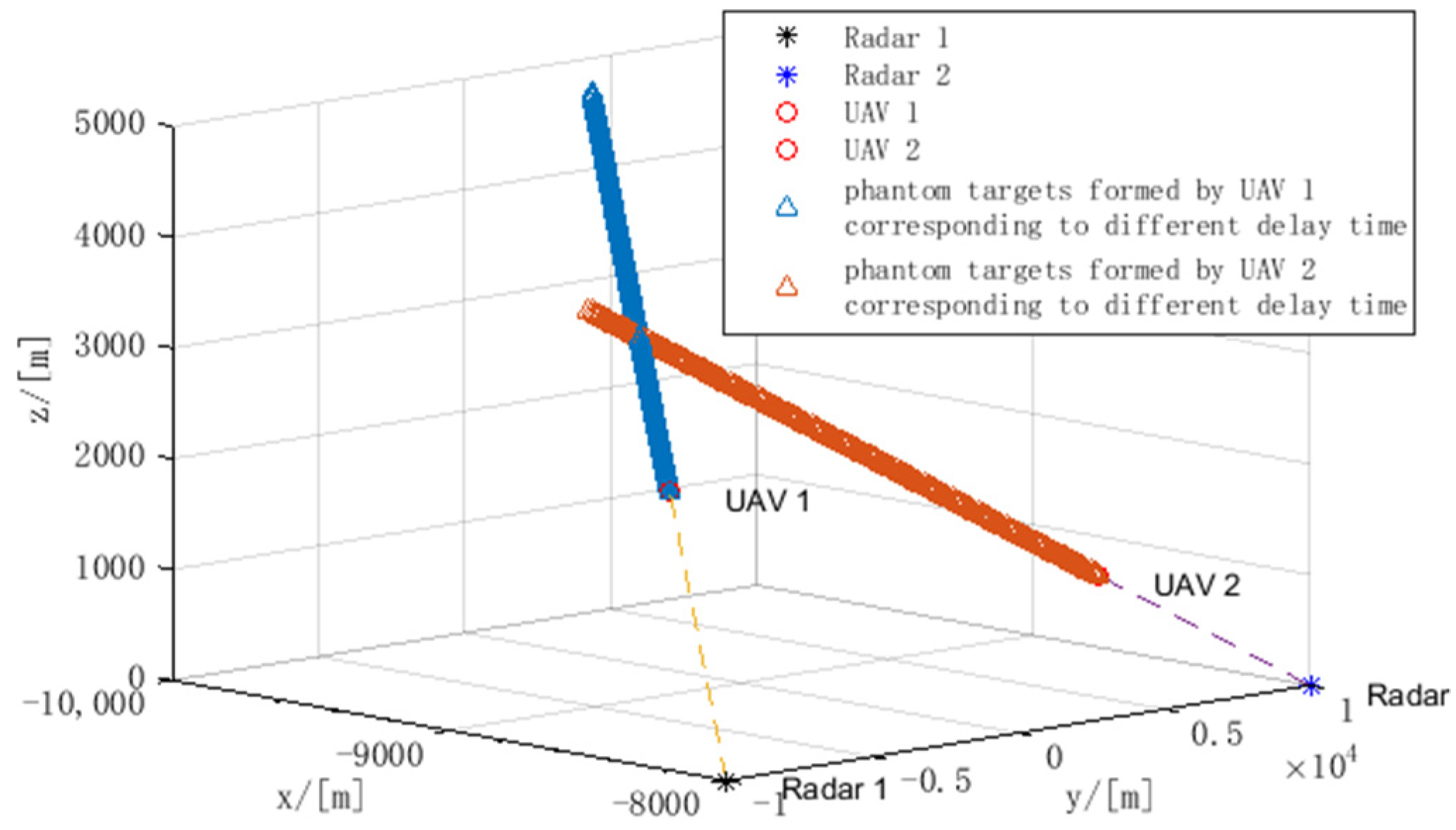
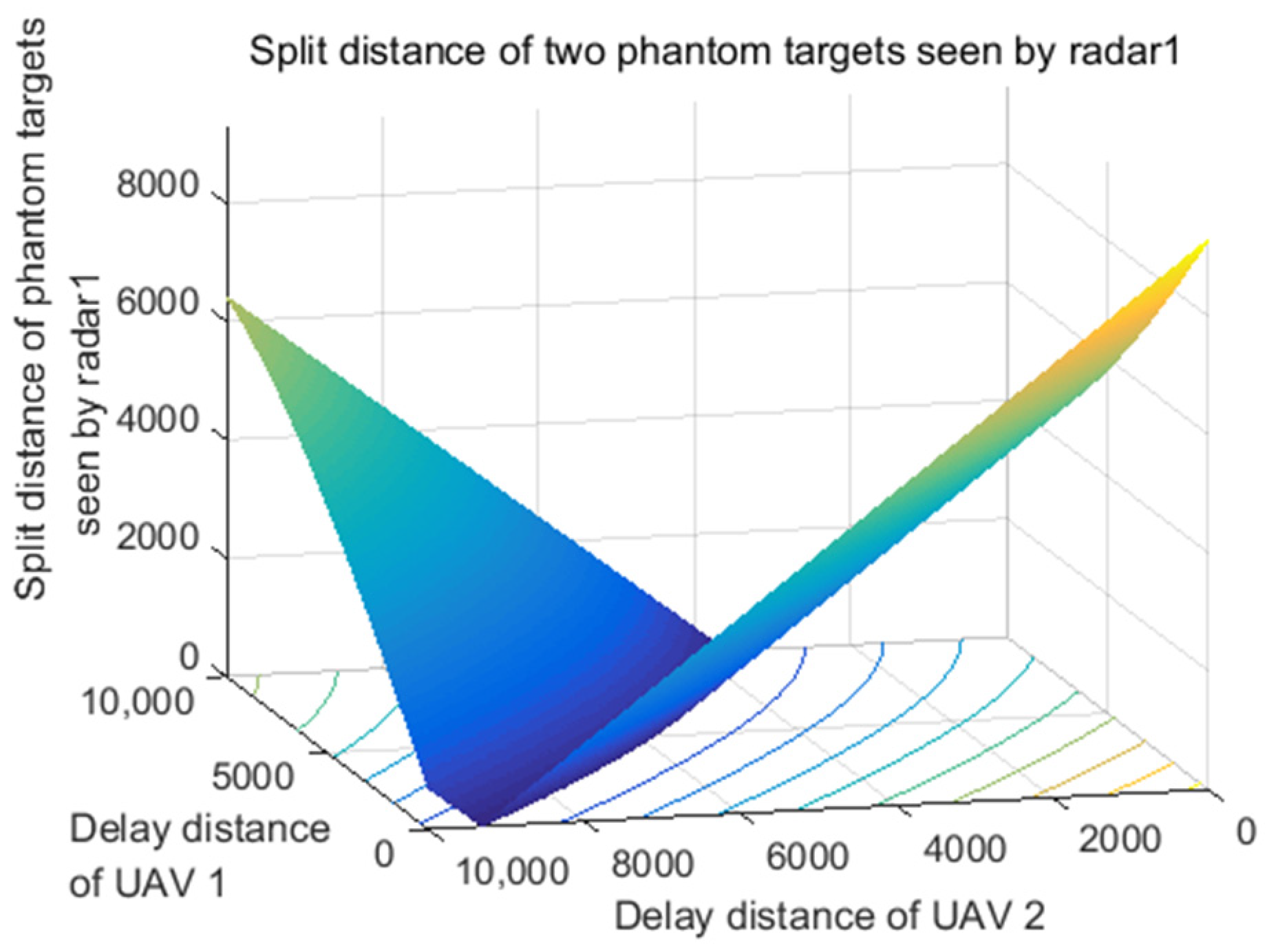
5. Simulation Results
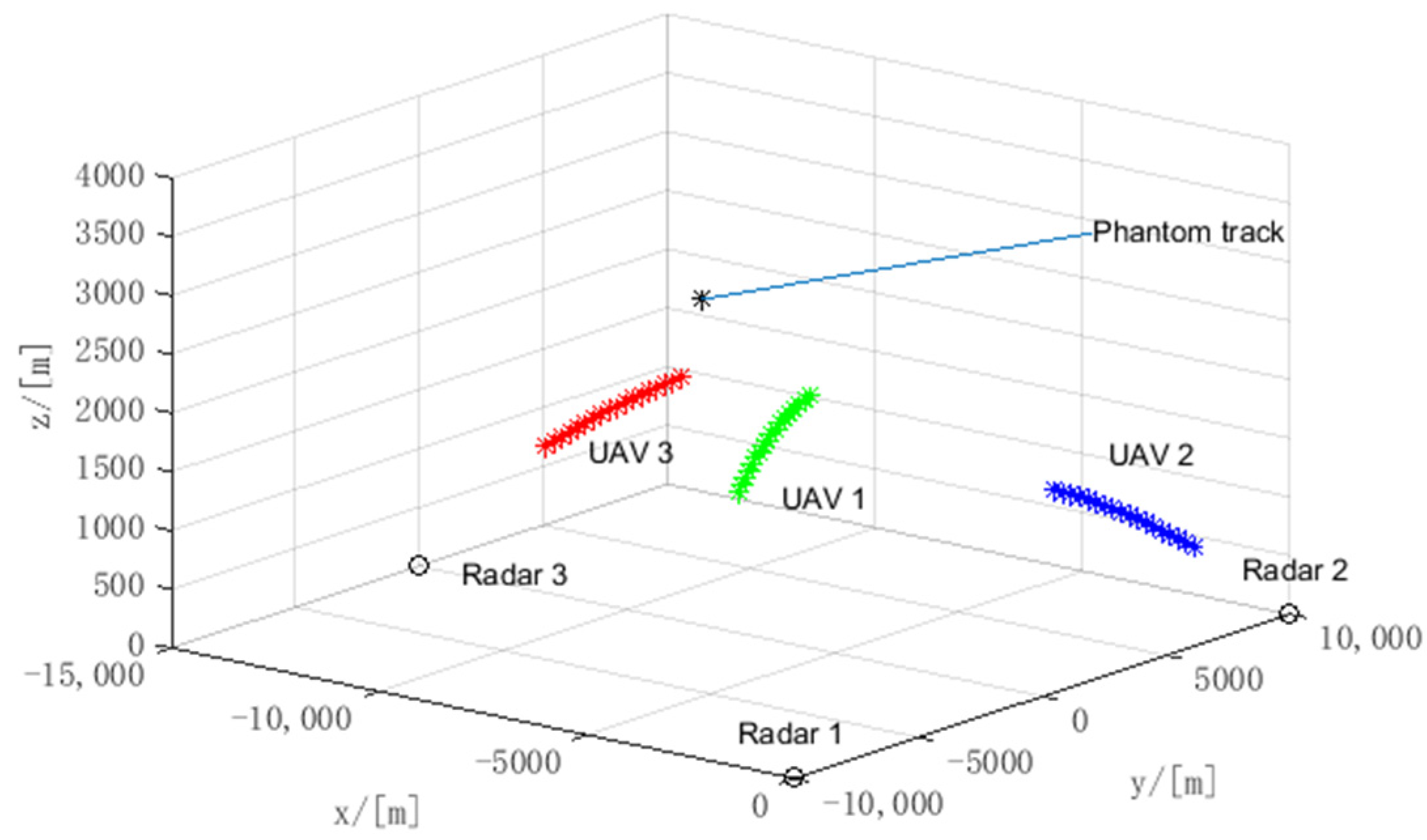
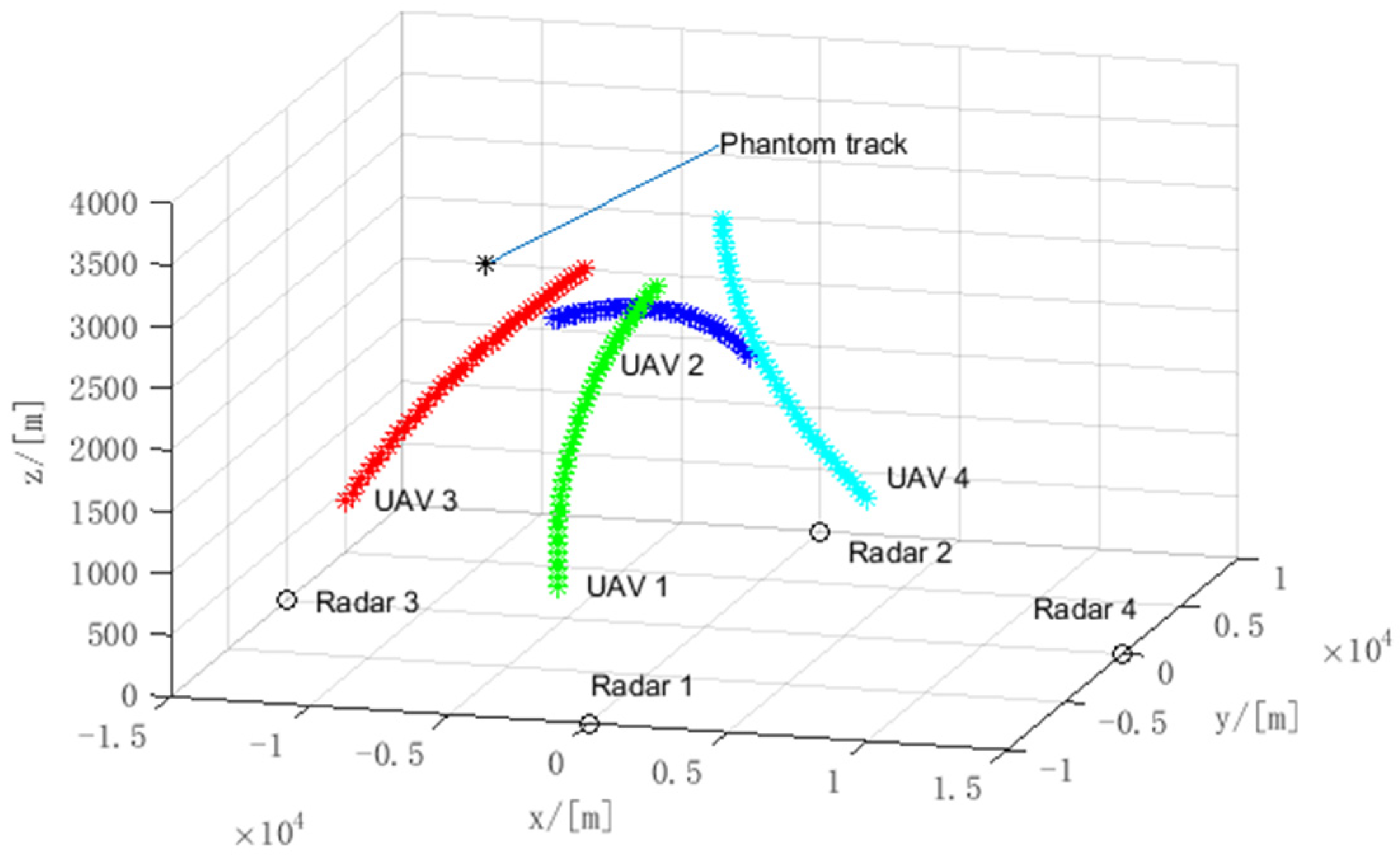
5.1. The Performance Analysis of the Designed Phantom
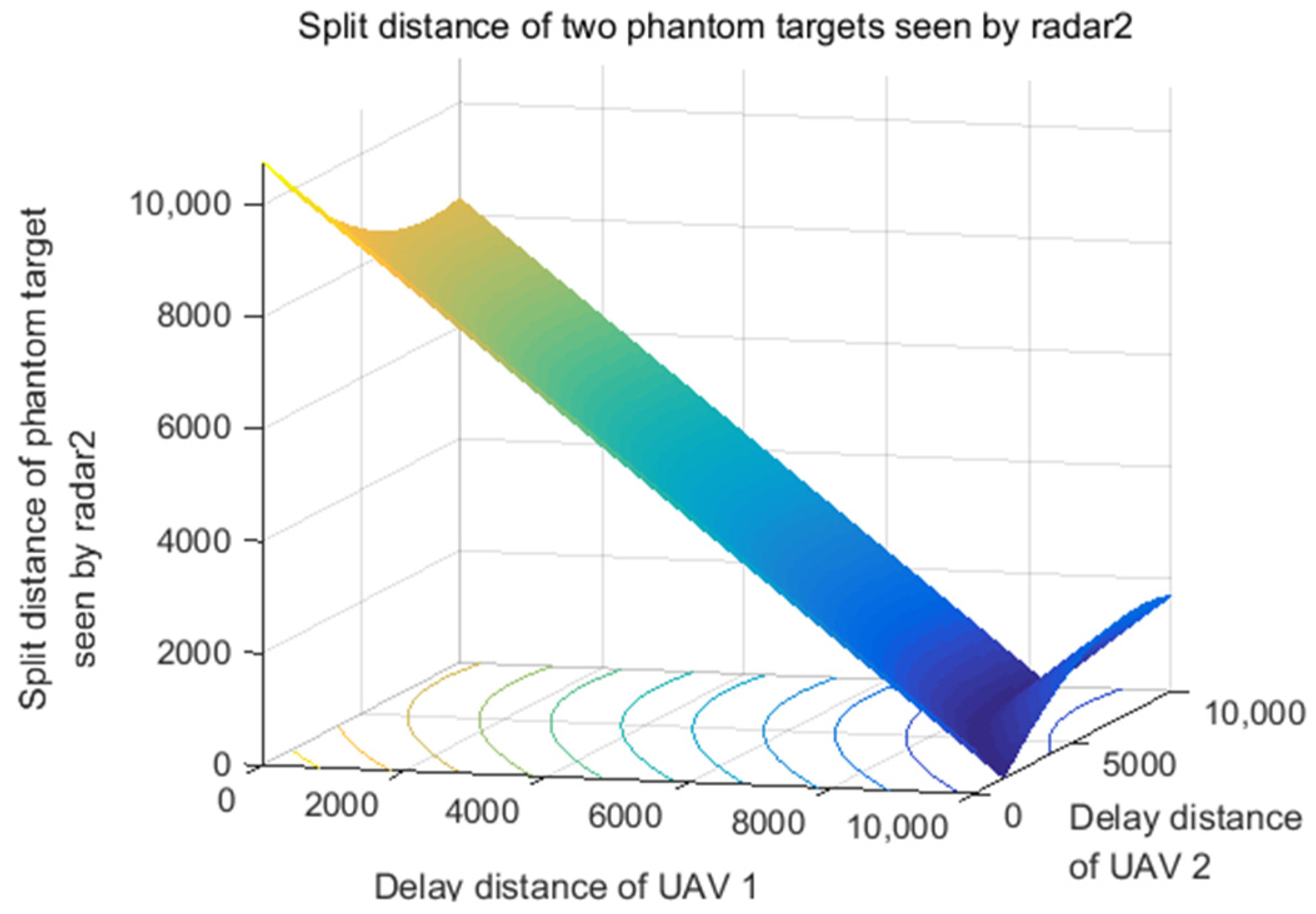
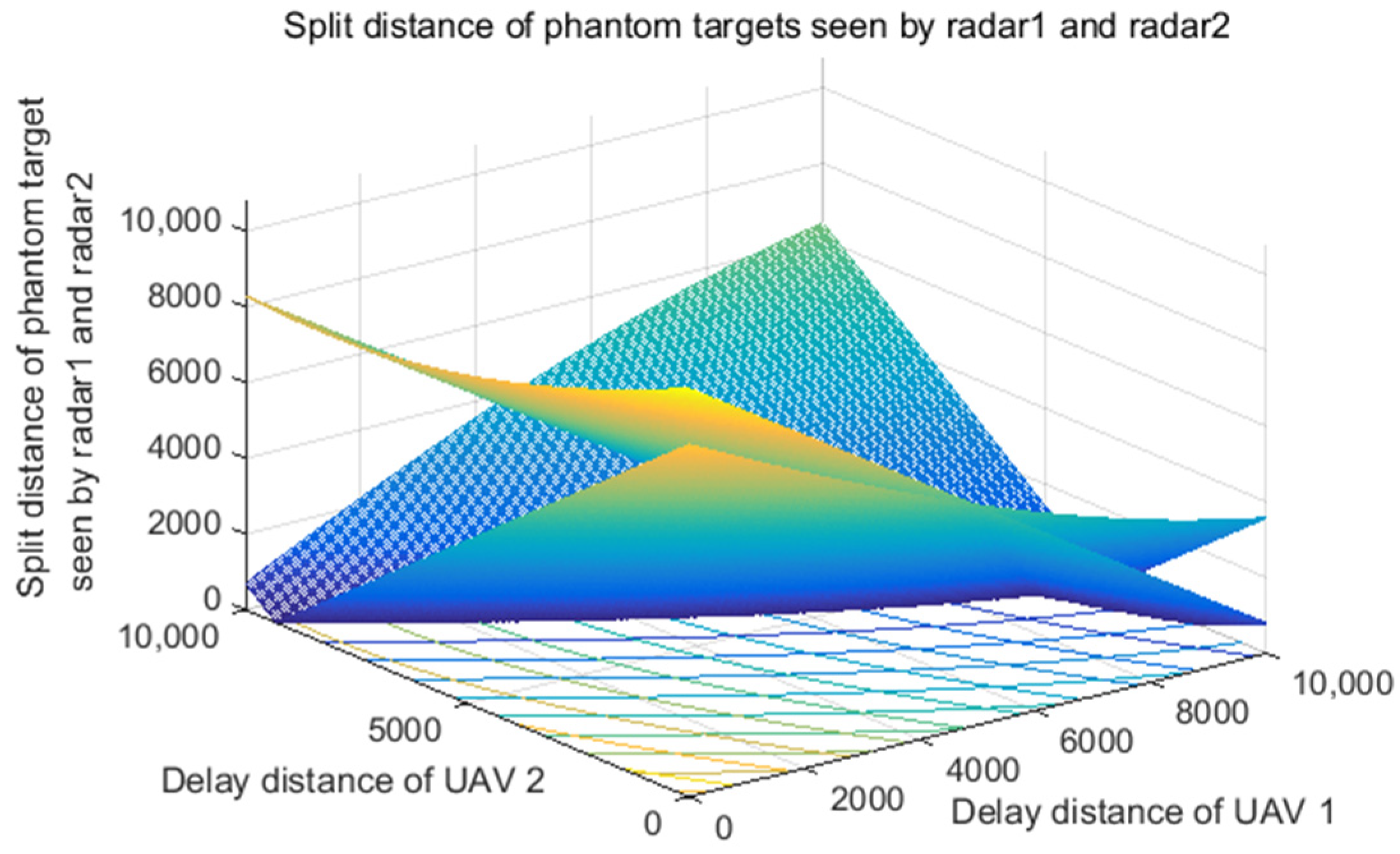
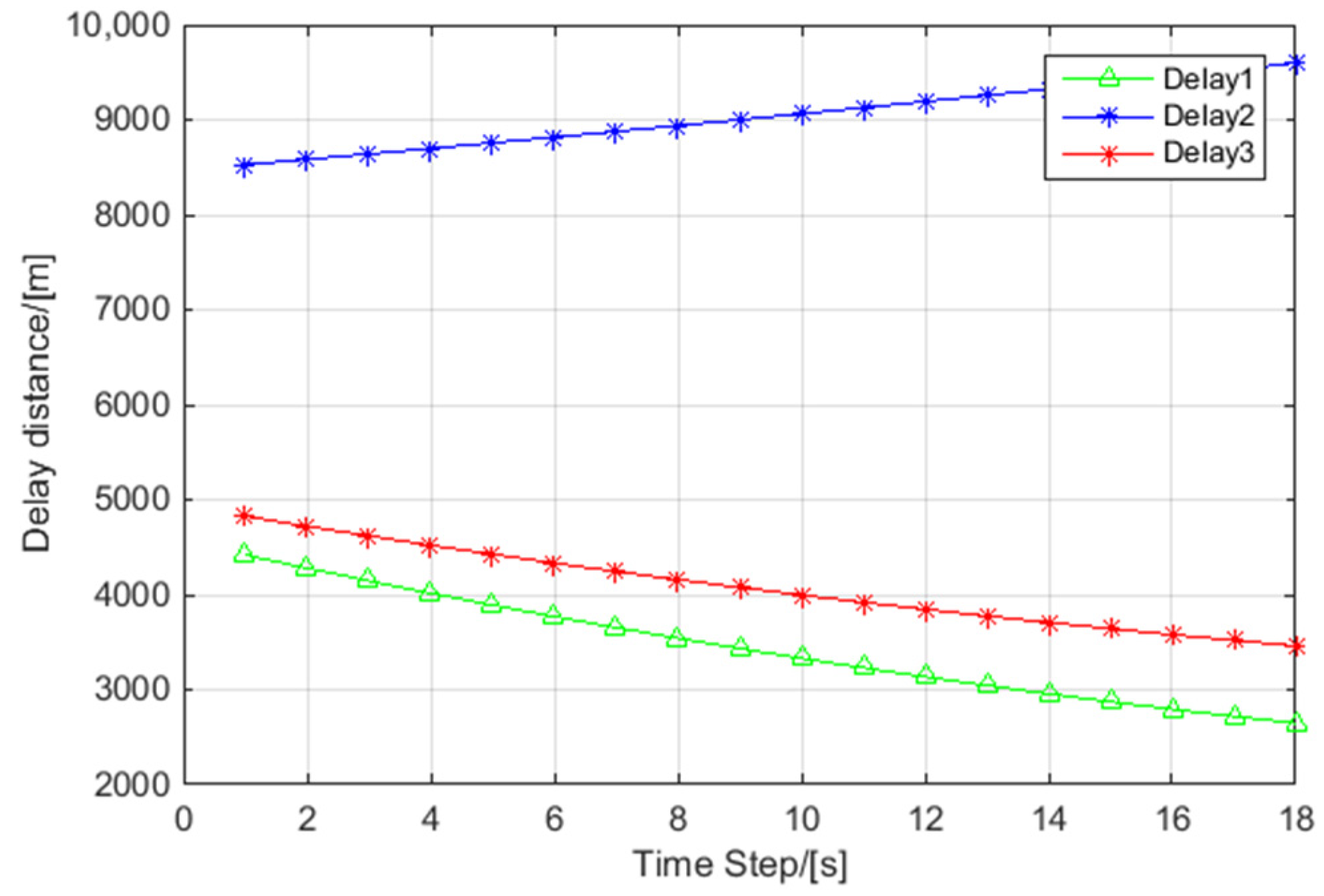
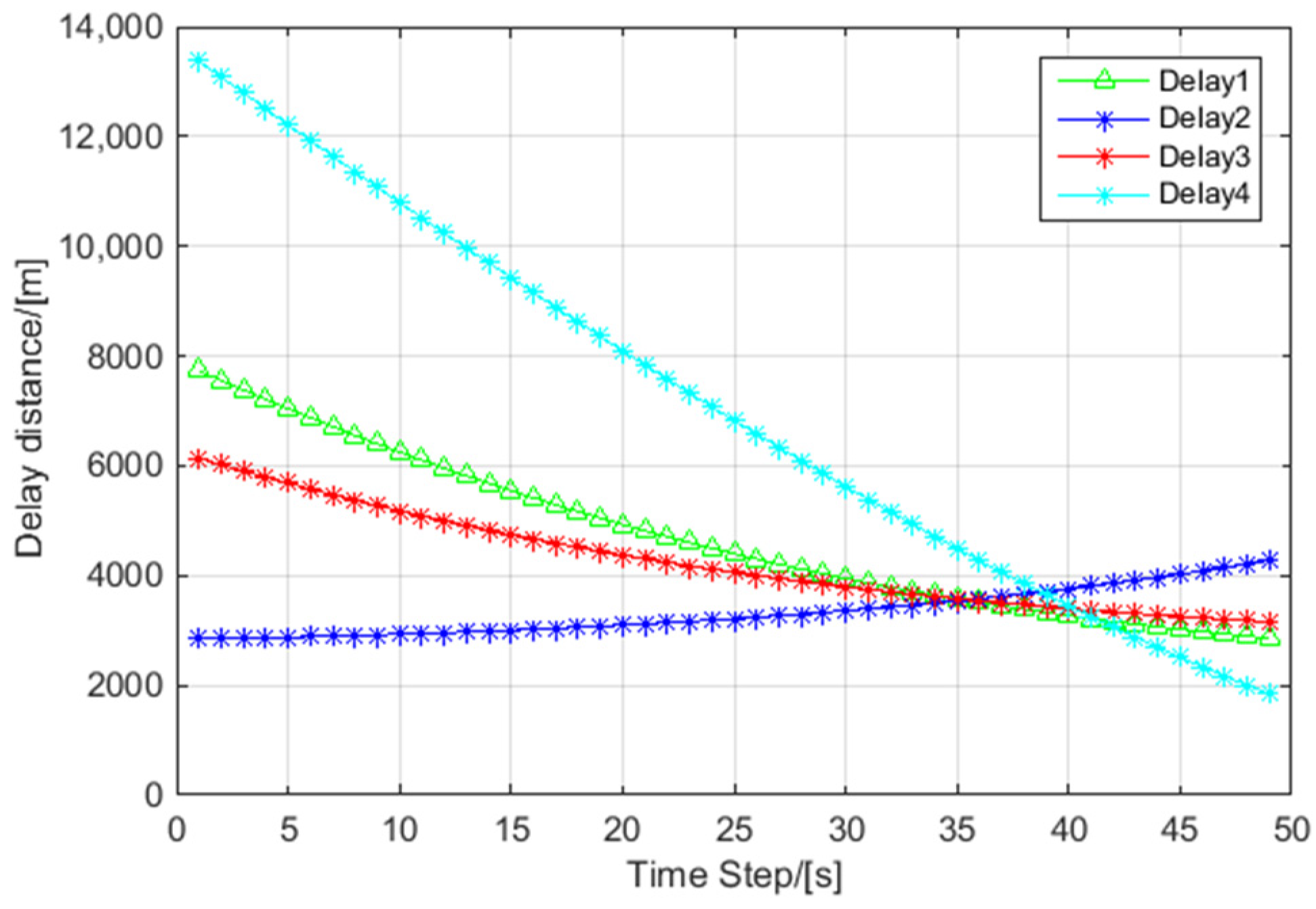
5.2. The Performance Analysis of Delay Distance
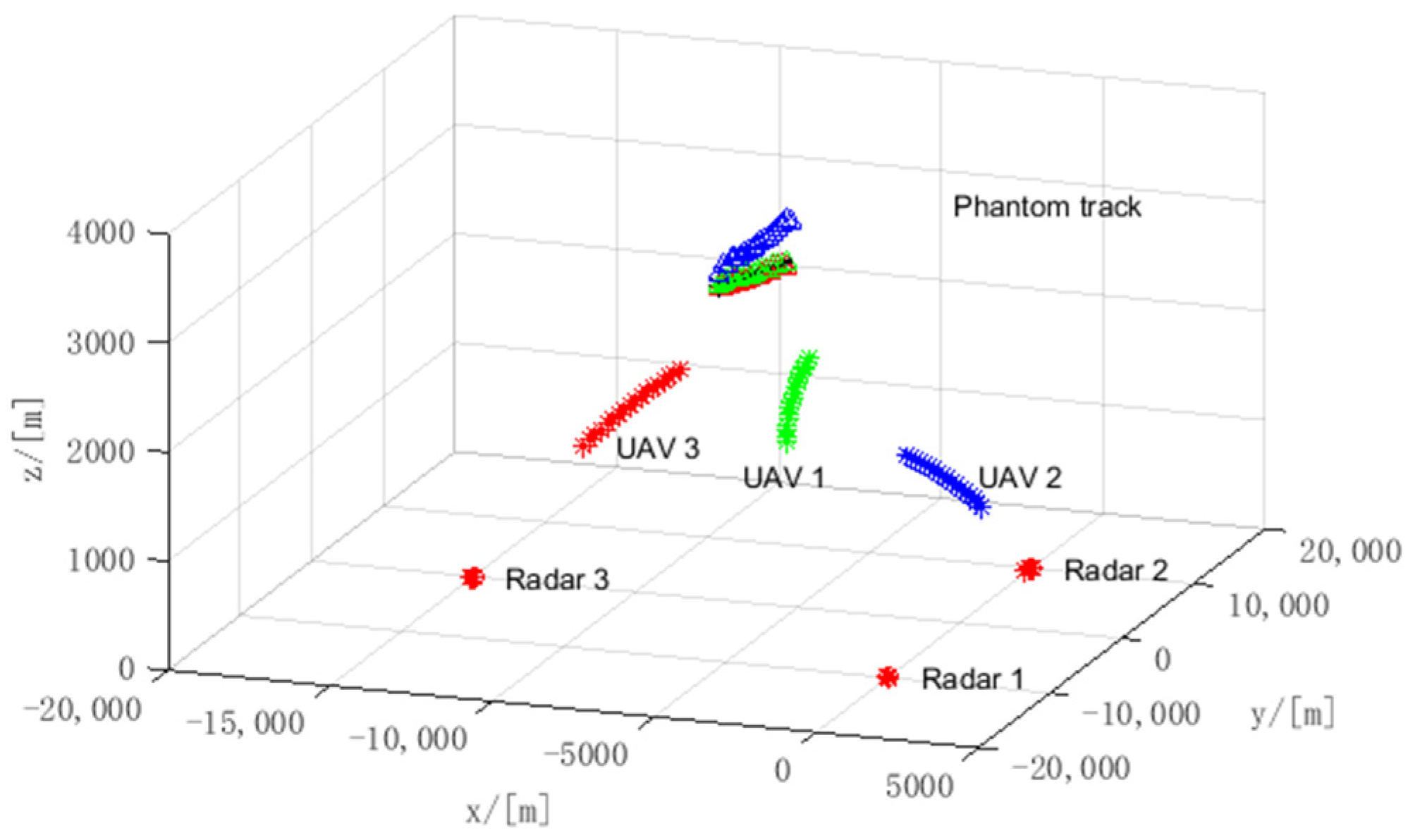
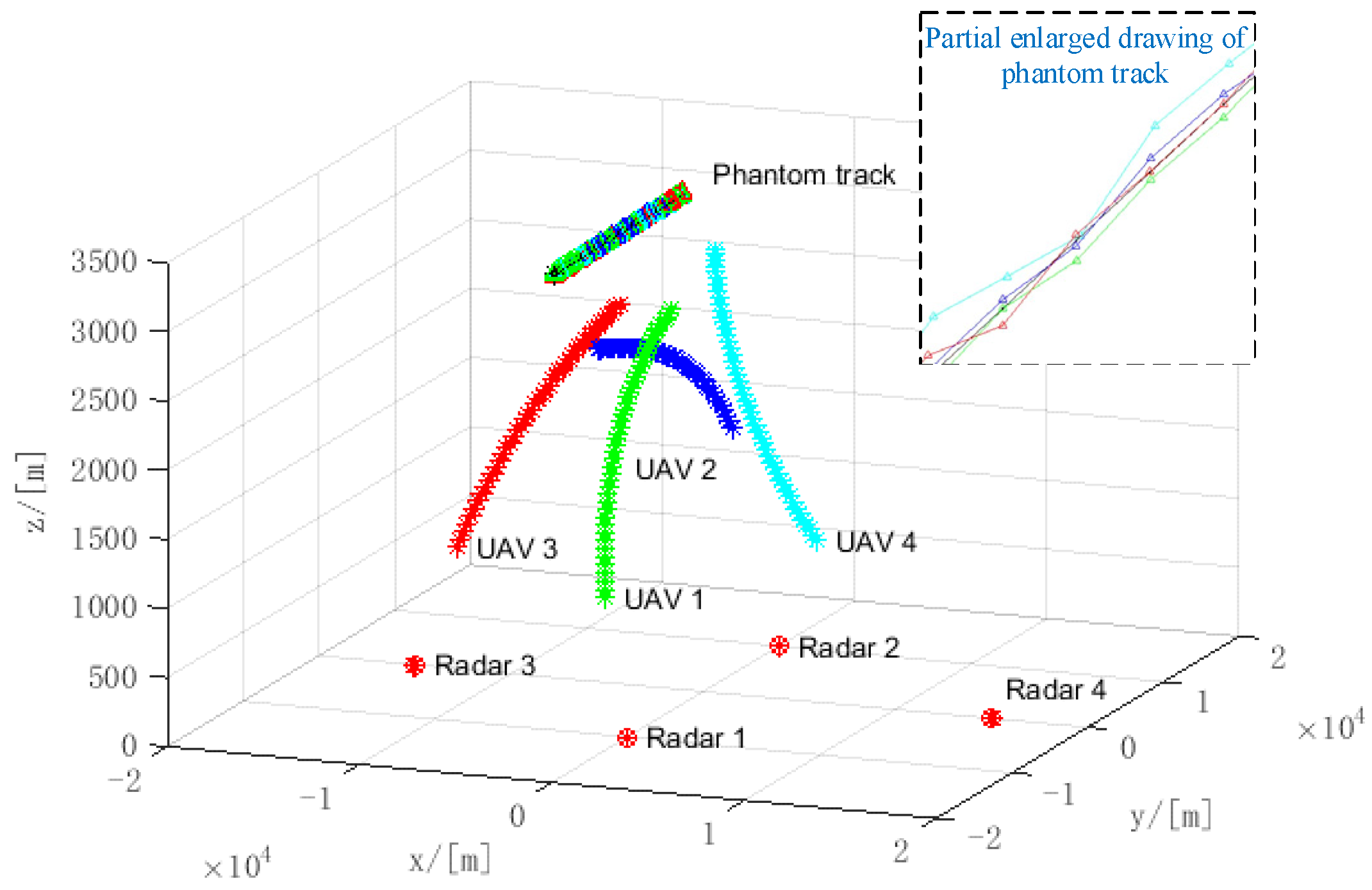
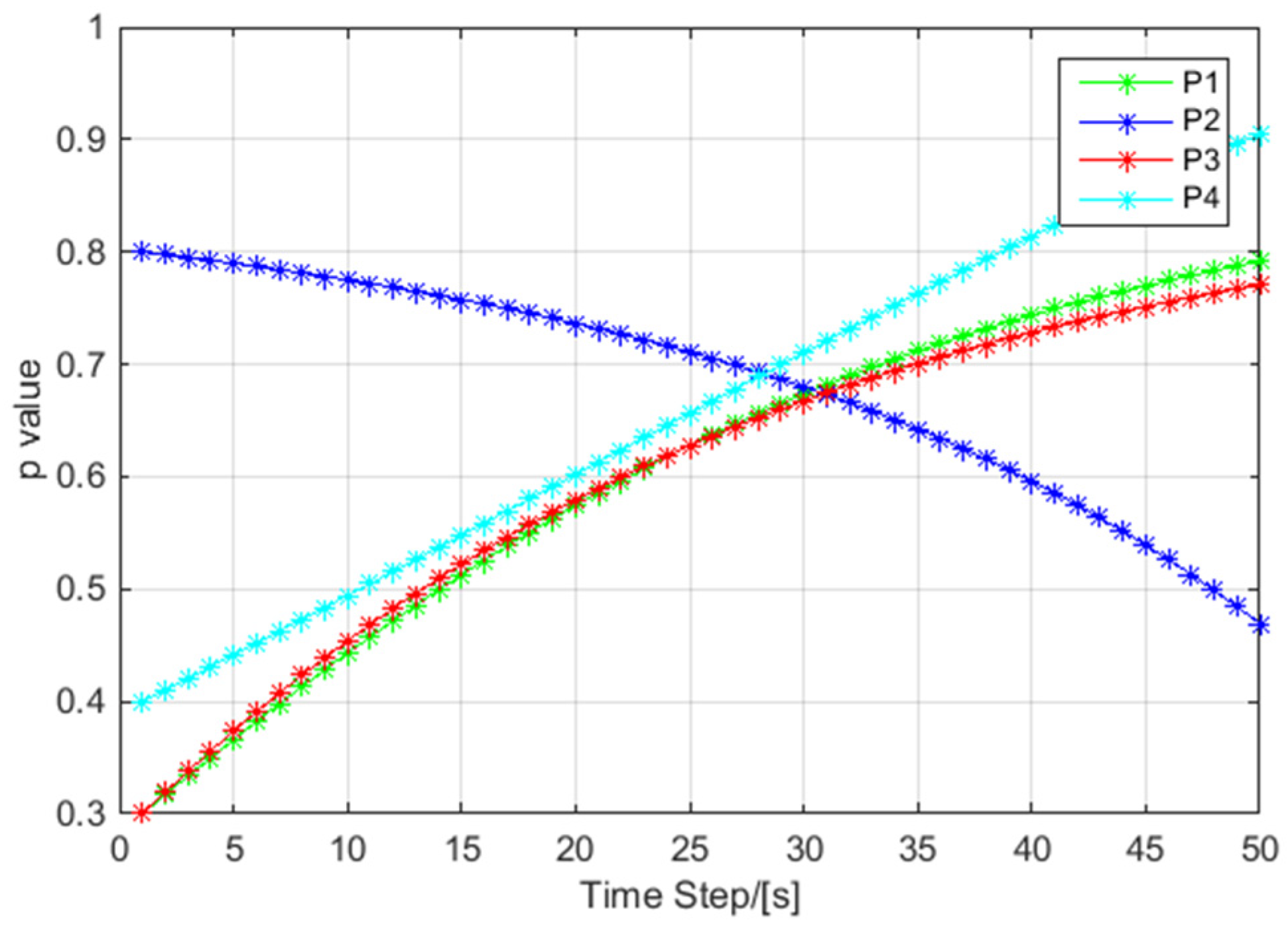
5.3. The Performance Analysis of Joint Phantom Track Deception and TDOA/FDOA Localization
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Clark, B.; Mcnamara, W.; Walton, T. Winning the Invisible War; The Center for Strategic and Budgetary Assessments: Washington, DC, USA, 2019; pp. 1–64. [Google Scholar]
- Bai, P.; Wang, Y.B.; Liang, X.L. Overview on phantom track deception against radar network using UAVs. Acta Aeronaut. Astronaut. Sin. 2020, 41, 6–21. [Google Scholar]
- Guo, S.F.; Yu, G.W.; Xiong, X. Research on method of track deception jamming based on cooperative control of UAVs. J. Air Force Early Warn. Acad. 2018, 32, 44–54. [Google Scholar]
- Purvis, K.B.; Astrom, K.J.; Khammash, M. Estimation and optimal configurations for localization using cooperative UAVs. IEEE Trans. Control Syst. Technol. 2008, 16, 947–958. [Google Scholar] [CrossRef] [Green Version]
- Purvis, K.B.; Chandler, P.R.; Pachter, M. Feasible flight paths for cooperative generation of a phantom radar track. J. Guid. Control Dyn. 2006, 29, 653–661. [Google Scholar] [CrossRef] [Green Version]
- Pachter, M.; Chandler, P.R.; Purvis, K.B. Multiple radar phantom tracks from cooperating vehicles using range-delay deception. Theory Algorithms Coop. Syst. 2004, 29, 368–390. [Google Scholar]
- Pachter, M.; Chandler, P.R.; Larson, R.A.; Purvis, K.B. Concepts for generating coherent radar phantom tracks using cooperating vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004. [Google Scholar]
- Purvis, K.B.; Astrom, K.J.; Khammash, M. Estimating radar positions using cooperative unmanned air vehicle teams. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005. [Google Scholar]
- Maithripala, D.; Jayasuriya, S. Feasibility considerations in formation control: Phantom track generation through multi-UAV collaboration. In Proceedings of the IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Maithripala, D.; Jayasuriya, S. Radar deception through phantom track generation. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005. [Google Scholar]
- Dhananjay, N.; Ghose, D.; Kuduvalli, A. Generation of a class of proportional navigation guided interceptor phantom tracks. J. Guid. Control Dyn. 2015, 38, 2206–2215. [Google Scholar] [CrossRef]
- Maithripala, D.; Jayasuriya, S. Phantom track generation in 3D through cooperative control of multiple ECAVs based on geometry. In Proceedings of the First International Conference on Industrial and Information Systems, Tirtayasa, Indonesia, 8–11 August 2006. [Google Scholar]
- Lee, I.; Bang, H. A cooperative line-of-sight guidance law for a three-dimensional phantom track generation using unmanned aerial vehicles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 6, 897–915. [Google Scholar] [CrossRef]
- Lee, I.; Bang, H. Optimal phantom track generation for multiple electronic combat air vehicles. In Proceedings of the International Conference on Control, Automation and Systems, Seoul, Korea, 14–17 October 2008. [Google Scholar]
- Lee, I.; Bang, H. Cooperative control of multiple electronic combat air vehicles for electronic attack. In Proceedings of the SICE Conference, Chofu, Japan, 20–22 August 2008. [Google Scholar]
- Lee, I.; Bang, H. Phantom track generation using predictive control concept. In Proceedings of the International Conference on Control, Automation and Systems, Gyeonggi, Korea, 26–29 October 2011. [Google Scholar]
- Kim, Y.H.; Kim, D.G.; Han, J.W.; Song, K.H.; Kim, H.N. Analysis of sensor-emitter geometry for emitter localisation using TDOA and FDOA measurements. IET Radar Sonar Navig. 2017, 11, 341–349. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, Z. Deception parameter estimation and discrimination in distributed multiple-radar architectures. IEEE Sens. J. 2017, 17, 6322–6330. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.S. A three-dimensional phantom track generation for radar network deception. IEEE Access 2019, 7, 27288–27301. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.S. Deviation compensation for phantom tracks jamming against distributed radar network. Syst. Eng. Electron. 2018, 40, 1255–1264. [Google Scholar]
- Wang, G.H.; Yang, Z.; Wu, J.P. Influence analysis of radar location error on multi-aircraft cooperative track deception. J. Nav. Aeronaut. Astronaut. Univ. 2015, 30, 501–510. [Google Scholar]
- Shima, T.; Chandler, P.; Pachter, M. Decentralized estimation for cooperative phantom track generation. In Cooperative Systems; Springer: New York, NY, USA, 2007; pp. 339–350. [Google Scholar]
- Purvis, K.B.; Chandler, P.R. A review of recent algorithms and a new and improved cooperative control design for generating a phantom track. In Proceedings of the American Control Conference, New York, NY, USA, 11–13 July 2007. [Google Scholar]
- Xu, Y.; Basset, G. Virtual motion camouflage based phantom track generation through cooperative electronic combat air vehicles. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010. [Google Scholar]
- Ratnoo, A.; Shima, T. Formation-flying guidance for cooperative radar deception. J. Guid. Control Dyn. 2012, 35, 1730–1739. [Google Scholar] [CrossRef]
- Dhananjay, N.; Kuduvalli, A.; Ghose, D. Realistic coherent phantom track generation by a group of electronic combat aerial vehicles. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Hadi, H.; Suhada, J. Guaranteed consensus in radar deception with a phantom track. In Proceedings of the ASME 2013 Dynamic Systems and Control Conference, Palo Alto, CA, USA, 21–23 October 2013. [Google Scholar]
- Hatem, H. Optimal sensor velocity configuration for TDOA-FDOA geolocation. IEEE Trans. Signal Process. 2017, 65, 628–637. [Google Scholar]
- Wang, W.; Bai, P.; Liang, X.; Zhang, J.; He, L. Performance analysis and path planning for UAVs swarms based on RSS measurements. Aerosp. Sci. Technol. 2018, 8, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Lui, W.K.; So, H.C. A study of two-dimensional sensor placement using time-difference-of-arrival measurements. Digit. Signal Process. 2009, 19, 650–659. [Google Scholar] [CrossRef]

| Reference | Type of Error | Scenario | Testing Rule | Method |
|---|---|---|---|---|
| [7] | --- | 2D | majority-rule scheme | Closed form solutions are obtained for the ECAV trajectory given a specified phantom track. |
| [22] | --- | 2D | --- | A decentralized estimation-decision strategy is derived for a team of electronic combat air vehicles (ECAVs) deceiving a network of radars. |
| [8] | TDOA localization error | 2D | minimum variance estimation theory | A nonlinear system model for estimation is formulated and used to perform simulations with “noisy” TDOAs; a linearized time-varying model for straight nominal ECAV trajectories is derived from the nonlinear model |
| [5] | UAV position error | 2D | --- | Generalized bounds for the initial conditions and time-dependent flyable ranges of a team of ECAVs are presented |
| [23] | UAV position error | 2D | --- | Generalized bounds for the initial conditions and time-dependent flyable ranges of a team of ECAVs are presented |
| [6] | UAV kinetic limit, wind influence | 2D | --- | Optimal control and then either (1) adding smooth penalty functions to the cost, or (2) using control parametrization. |
| [11] | TDOA localization error | 2D | --- | Analyzing the explicit solution leads to The Angle Rule, analyzing the Fisher Information Matrix leads to the Coordinate Rule |
| [24] | --- | 3D | --- | virtual motion camouflage based (VMC) subspace optimal trajectory design method |
| [25] | --- | 2D | --- | A generalized kinematic framework for the required formation. Flying is developed from the principles of line-of-sight guidance. |
| Reference | Type of Error | Scenario | Testing Rule | Method |
|---|---|---|---|---|
| [13] | --- | 3D | --- | A guidance law based on input–output feedback linearization is developed. A closed-form solution is constructed for the unmanned aerial vehicles trajectory corresponding to the pre-specified phantom track |
| [17] | TDOA/FDOA localization error | 2D | --- | FIM |
| [14] | --- | 3D | optimal control problem with dynamic equation and constrains | C code for Feasible Sequential Quadratic Programming (CFSQP) |
| [15] | --- | 3D | the trajectory generation problem is formulated as an optimal control problem | The parameter optimization problem with inequality constraints using the sequential quadratic programming method |
| [16] | --- | 3D | --- | line of sight (LOS) guidance based on predictive controller |
| Reference | Type of Error | Scenario | Testing Rule | Method |
|---|---|---|---|---|
| [9] | --- | 2D | --- | Distributed control architecture. |
| [10] | --- | 2D | --- | Translate kinematic constraints on the ECAV dynamic system into constraints on the phantom point |
| [11] | --- | 2D &3D | --- | sufficient conditions for the existence of feasible ECAV trajectories are first obtained in a planar engagement scenario and then extended to the more general three-dimensional framework |
| [12] | --- | 3D | --- | The trajectory of a ECAV can be represented by a parameterized differentiable space curve in R3 and capture ECAV actuator constraints through constraints on speed, curvature and torsion of this space curve |
| [26] | UAV position error | 2D | The Performance Measure |P1−P2| | The phantom track considered is the trajectory of a missile guided by proportional navigation. The line-of-sight guidance law is used to control the ECAVs for practical implementation |
| [27] | --- | 2D | --- | A motion planning algorithm provides some conditions on configuration parameters and the desired trajectory such that the proposed control guarantees consensus |
| Reference | Type of Error | Scenario | Testing Rule | Method |
|---|---|---|---|---|
| [18] | --- | 2D | Space resolution cell (SRC) | The effective range of time delay is derived under the condition of near field and far field |
| [19] | localization error/UAV position error | 3D | N/M rule | The beam rider guidance method is used to compensate the track deviation |
| [20] | --- | 3D | Nearest neighbor method and bearings-only associations method | Multiple discriminations for multi-range-false–target |
| [21] | localization error/UAV position error | 3D | N/M rule | The deviation compensation for phantom tracks and the tracks’ association detection are presented |
| [24] | UAV position error | 2D | K-NN track correlation | The correlative model is deduced |
| Space Resolution Cell | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |
|---|---|---|---|---|---|---|---|---|
| Localization Error | ||||||||
| 68.32 | 87.26 | 91.47 | 94.00 | 94.53 | 94.74 | 94.74 | ||
| 41.47 | 58.74 | 69.37 | 85.26 | 88.21 | 92.74 | 92.80 | ||
| 38.42 | 54.84 | 73.26 | 83.16 | 89.47 | 90.88 | 91.05 | ||
| 28.63 | 45.26 | 68.53 | 81.47 | 85.58 | 89.05 | 91.05 | ||
| 67.58 | 84.11 | 91.00 | 93.16 | 94.21 | 94.63 | 94.74 | ||
| 65.47 | 83.53 | 90.78 | 92.84 | 94.13 | 94.53 | 94.74 | ||
| 64.84 | 80.63 | 90.42 | 92.00 | 94.00 | 94.53 | 94.74 |
| Space Resolution Cell | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |
|---|---|---|---|---|---|---|---|---|
| Localization Error | ||||||||
| 42.16 | 63.05 | 73.47 | 82.21 | 90.11 | 92.84 | 93.47 | ||
| 41.47 | 58.74 | 69.37 | 80.26 | 88.21 | 92.74 | 92.80 | ||
| 35.58 | 50.63 | 66.84 | 77.89 | 87.68 | 90.95 | 91.05 | ||
| 35.47 | 60.63 | 69.58 | 78.74 | 88.53 | 90.74 | 92.00 | ||
| 38.42 | 54.84 | 73.26 | 83.16 | 89.47 | 90.88 | 91.05 | ||
| 34.84 | 56.42 | 69.47 | 79.89 | 83.37 | 89.47 | 91.32 |
| Space Resolution Cell | 1 | 3 | 5 | 7 | 10 | 15 | |
|---|---|---|---|---|---|---|---|
| Localization Error | |||||||
| 36.5 | 96.67 | 98.20 | 98.33 | 98.33 | 98.33 | ||
| 6.67 | 78.39 | 95.17 | 97.83 | 98.28 | 98.33 | ||
| 6.11 | 75.94 | 94.11 | 97.78 | 98.28 | 98.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, W.; Zhang, X.; Wu, L.; Yin, H. The Joint Phantom Track Deception and TDOA/FDOA Localization Using UAV Swarm without Prior Knowledge of Radars’ Precise Locations. Electronics 2022, 11, 1577. https://doi.org/10.3390/electronics11101577
Wang Y, Wang W, Zhang X, Wu L, Yin H. The Joint Phantom Track Deception and TDOA/FDOA Localization Using UAV Swarm without Prior Knowledge of Radars’ Precise Locations. Electronics. 2022; 11(10):1577. https://doi.org/10.3390/electronics11101577
Chicago/Turabian StyleWang, Yubing, Weijia Wang, Xudong Zhang, Lirong Wu, and Hang Yin. 2022. "The Joint Phantom Track Deception and TDOA/FDOA Localization Using UAV Swarm without Prior Knowledge of Radars’ Precise Locations" Electronics 11, no. 10: 1577. https://doi.org/10.3390/electronics11101577
APA StyleWang, Y., Wang, W., Zhang, X., Wu, L., & Yin, H. (2022). The Joint Phantom Track Deception and TDOA/FDOA Localization Using UAV Swarm without Prior Knowledge of Radars’ Precise Locations. Electronics, 11(10), 1577. https://doi.org/10.3390/electronics11101577






