Physical Layer Secrecy by Power Splitting and Jamming in Cooperative Multiple Relay Based on Energy Harvesting in Full-Duplex Network
Abstract
:1. Introduction
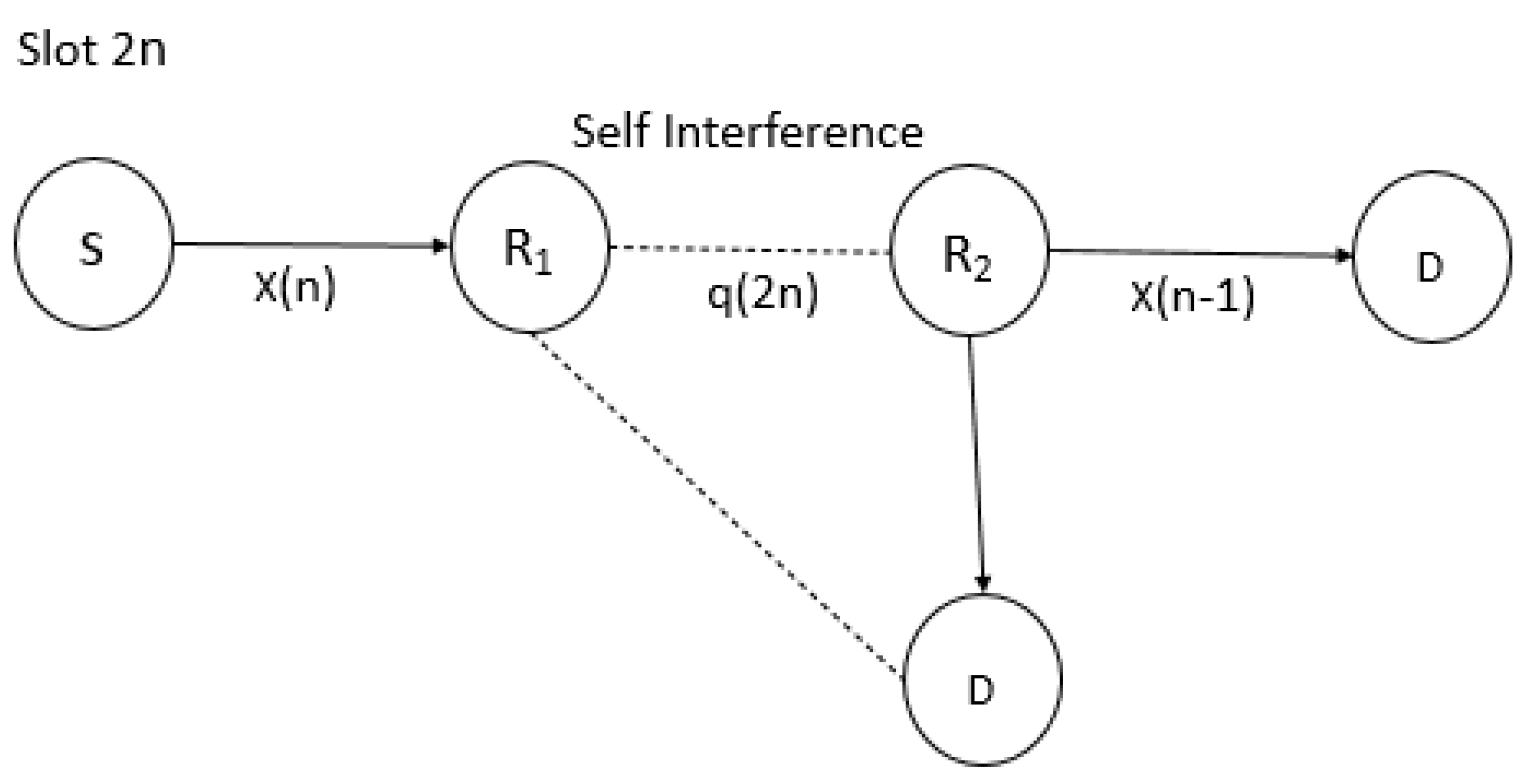
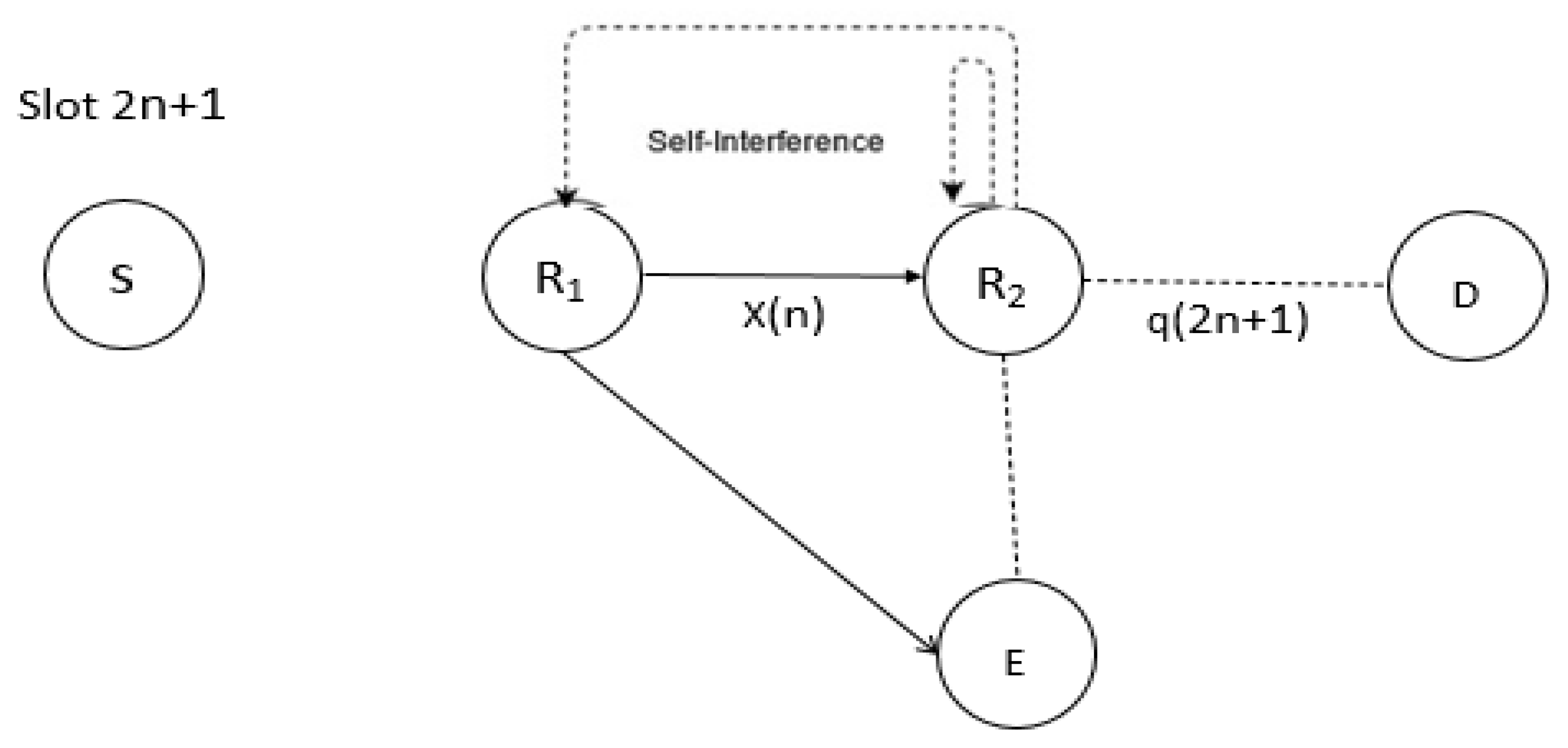
- This paper presents an investigation of a three-hop relaying system with a single relay active at each individual hop, where one source–destination pair tries to communicate securely in the presence of one eavesdropper.
- Each relay node operates in the AF and DF modes, and each node has a single antenna. Due to propagation loss, each relay and the destination only hear their previous nearby nodes in the standard multi-hop relaying paradigm.
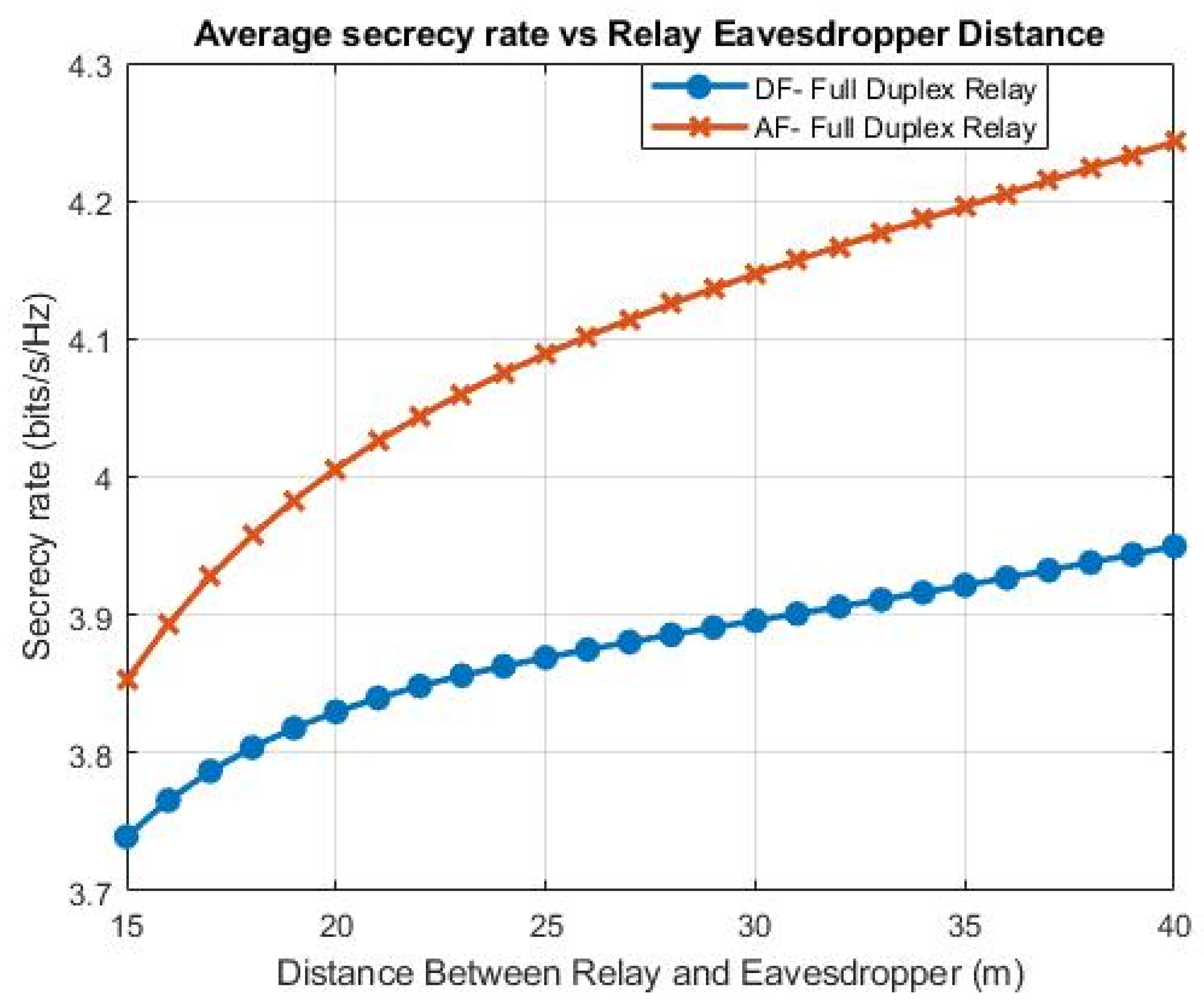
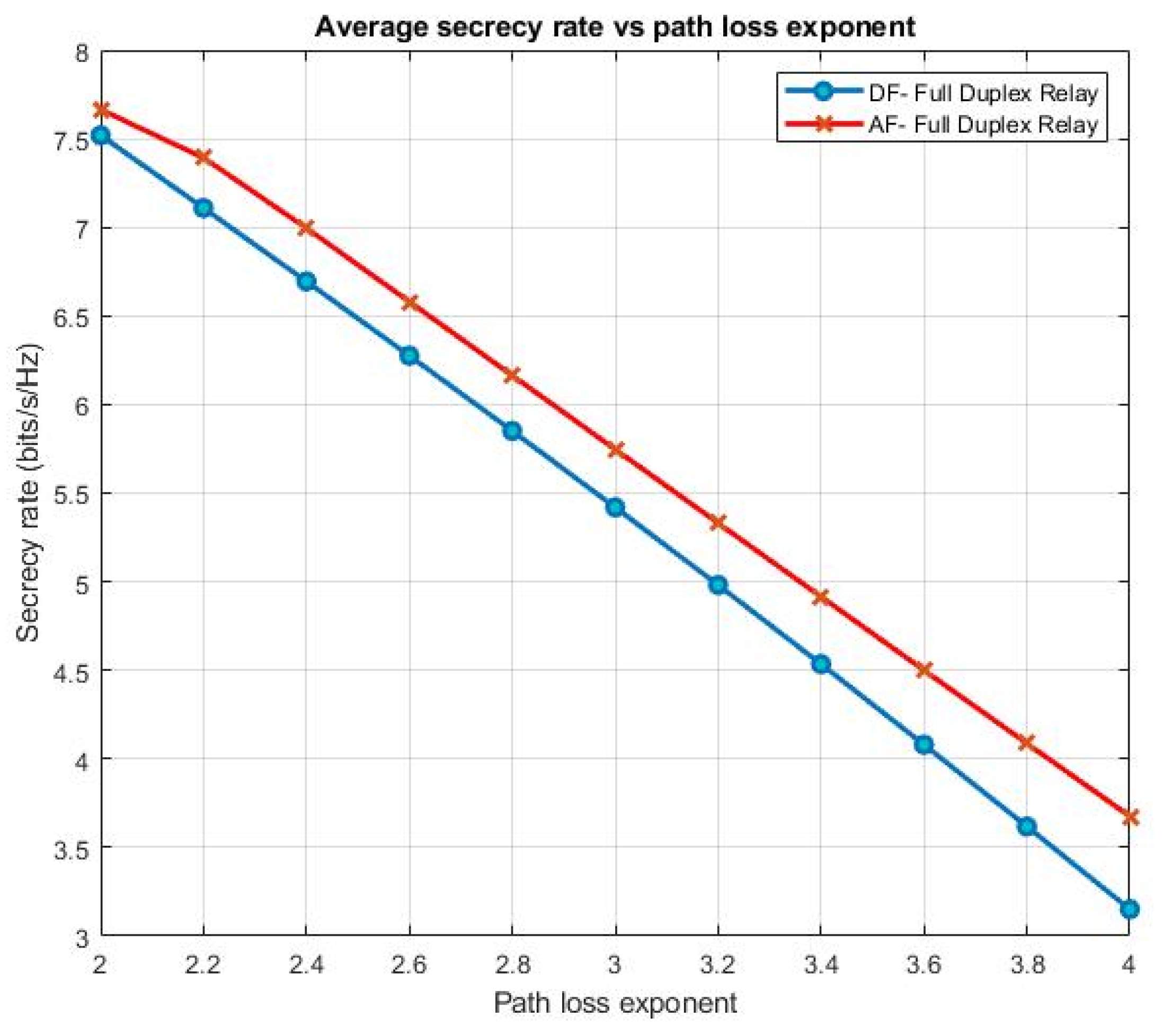
- The Secrecy Rates of two Cooperative Schemes, Amplify and Forward (AF) and Decode and Forward (DF), for both proposed systems are compared with those of the conventional Energy-Harvesting System, including an examination of the performance of the Outage Probability for proposed EH system.
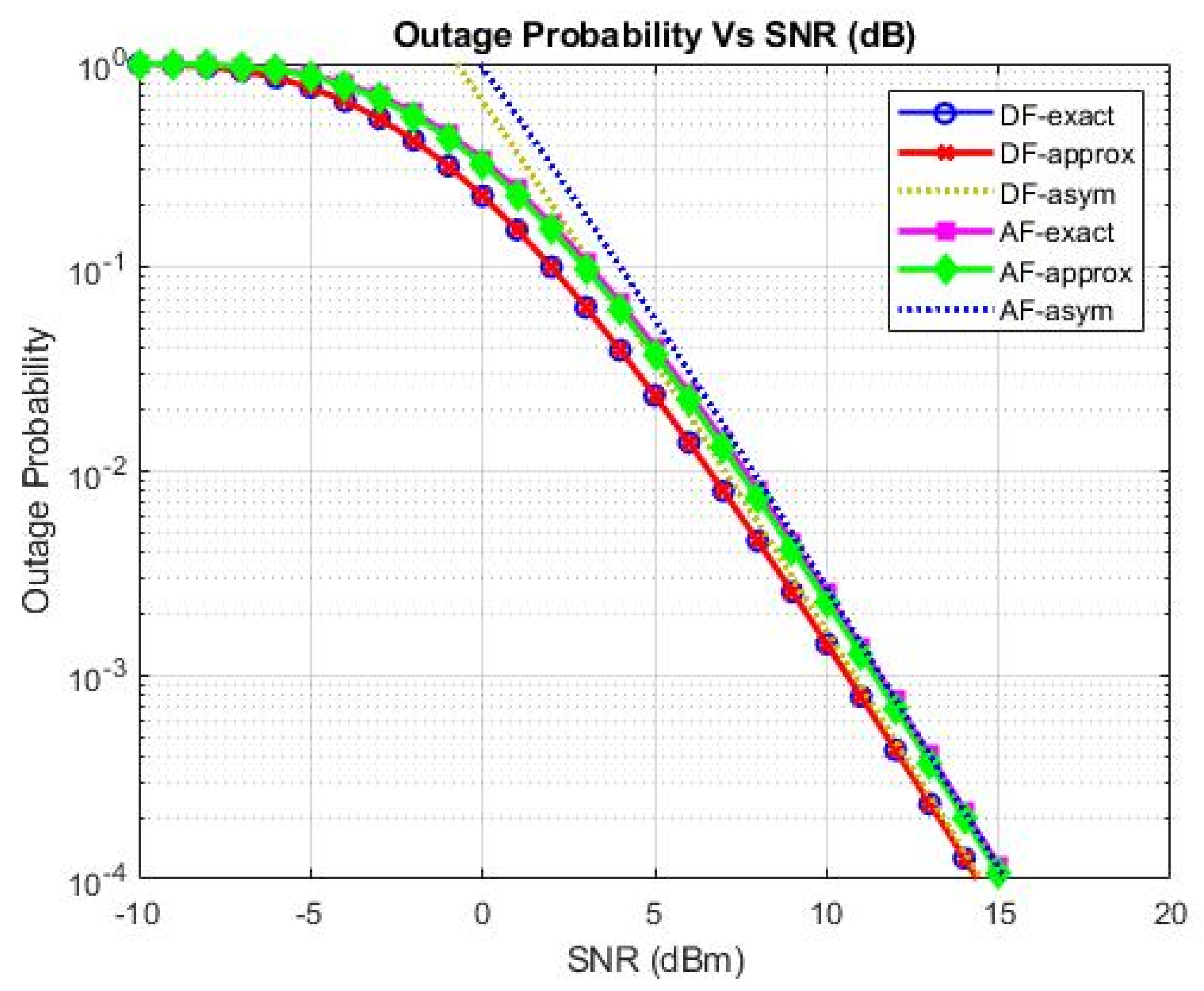
- In calculation, we extract accurate Secrecy Outage Probability (SOP) in a one-integral format and the closed-format asymptotic SOP for higher average Signal Noise Ratio (SNR).
1.1. Paper Organization
2. System Model
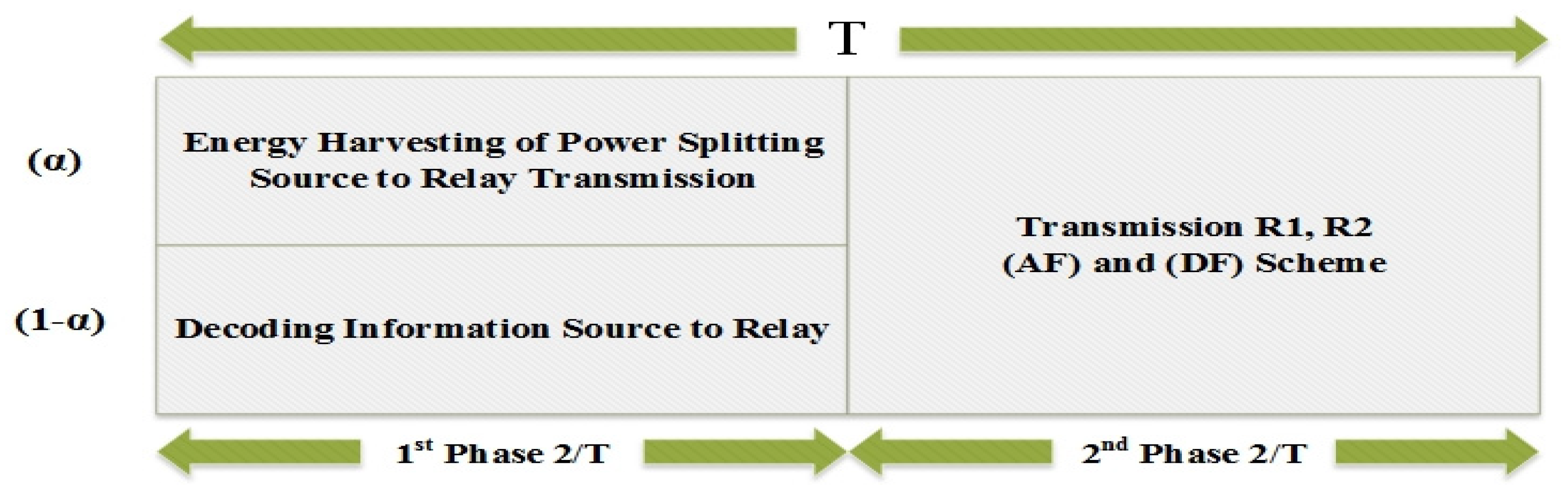
2.1. Power Splitting and Energy Harvesting Technique
2.2. Full Duplex Decode and Forward (DF) Relay Scheme
2.3. Amplify and Forward (AF) Relaying Scheme
3. Achievable Secrecy Rate
3.1. DF Scheme
3.2. AF Scheme
4. Analysis of Outage Probability
4.1. Decode and Forward Scheme
4.2. AF Strategy for Relaying
5. Numerical Evaluation and Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronym | Definition |
| AF | Amplify-and-Forward |
| DF | Decode-and-Forward |
| Time-Switching Factor | |
| FDR | Full Duplex Relay |
| DN | Destination Node |
| RN | Relay Network |
| SN | Source Node |
| T | Transmission Period |
| r | Power Harvest at Relay |
| Relay Eavesdropper | |
| Radio Frequency Energy Harvesting | |
| SWIPT | Simultaneous Wireless Information and Power Transmission |
| TSR | Time-Switching Relay-Oriented Protocol |
| PSR | Power-Splitting-Oriented Relay Protocol |
| AWGN | Additive White Gaussian Noise |
| PLS | Physical Layer Security |
| RF | Radiofrequency |
| RN | Relay Node |
| Power Beacon | |
| Relay Destination | |
| Distance Between Relay1 and Relay2 | |
| Power | |
| Energy Conversion efficiency | |
| Noise power or variance | |
| Jamming Signal of power | |
| Relay Eavesdropper AF |
Appendix A
Appendix B
References
- Li, X.; Zheng, Y.; Khan, W.U.; Zeng, M.; Li, D.; Ragesh, G.K.; Li, L. Physical layer security of cognitive ambient backscatter communications for green Internet-of-Things. IEEE Trans. Green Commun. Netw. 2021, 5, 1066–1076. [Google Scholar] [CrossRef]
- Waqar, O.; Tabassum, H.; Adve, R.S. Secure beamforming and ergodic secrecy rate analysis for amplify-and-forward relay networks with wireless powered jammer. IEEE Trans. Veh. Technol. 2021, 70, 3908–3913. [Google Scholar] [CrossRef]
- Nawaz, M.; Khan, W.U.; Ali, Z.; Ihsan, A.; Waqar, O.; Sidhu, G.A.S. Resource Optimization Framework for Physical Layer Security of Dual-Hop Multi-Carrier Decode and Forward Relay Networks. IEEE Open J. Antennas Propag. 2021, 2, 634–645. [Google Scholar] [CrossRef]
- Shim, Y.; Park, H.; Shin, W. Joint time allocation for wireless energy harvesting decode-and-forward relay-based IoT networks with rechargeable and nonrechargeable batteries. IEEE Internet Things J. 2020, 8, 2792–2801. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, P.T.; Voznak, M. Wireless energy harvesting meets receiver diversity: A successful approach for two-way half-duplex relay networks over block Rayleigh fading channel. Comput. Netw. 2020, 172, 107176. [Google Scholar] [CrossRef]
- Atapattu, S.; Ross, N.; Jing, Y.; He, Y.; Evans, J.S. Physical layer security in full-duplex multi-hop multi-user wireless network with relay selection. IEEE Trans. Wirel. Commun. 2019, 18, 1216–1232. [Google Scholar] [CrossRef]
- Phan, V.-D.; Nguyen, T.N.; Le, A.V.; Voznak, M. A Study of Physical Layer Security in SWIPT-Based Decode-and-Forward Relay Networks with Dynamic Power Splitting. Sensors 2021, 21, 5692. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.; Li, J.; Fu, X.; Zhang, L. Energy Harvesting for Physical Layer Security in Cooperative Networks Based on Compressed Sensing. Entropy 2017, 19, 462. [Google Scholar] [CrossRef] [Green Version]
- Truong, T.-V.; Vo, N.-V.; Ha, D.-B.; Tran, D.-D. Secrecy performance analysis of energy harvesting wireless networks with multiple power transfer stations and destinations in the presence of multiple eavesdroppers. In Proceedings of the 2016 3rd National Foundation for Science and Technology Development Conference on Information and Computer Science (NICS), Danang, Vietnam, 14–16 September 2016; pp. 107–112. [Google Scholar] [CrossRef]
- Shen, H.; Wang, J.; Levy, B.; Zhao, C. Robust optimization for amplify-and-forward MIMO relaying from a worst-case perspective. IEEE Trans. Signal Process. 2013, 61, 5458–5471. [Google Scholar] [CrossRef] [Green Version]
- Gong, S.; Wang, S.; Chen, S.; Xing, C.; Hanzo, L. Robust energy efficiency optimization for amplify-and-forward MIMO relaying systems. IEEE Trans. Wirel. Commun. 2019, 18, 4326–4343. [Google Scholar] [CrossRef] [Green Version]
- Jindal, P.; Sinha, R. Physical layer security with energy harvesting in single hop wireless relaying system. In Proceedings of the International Conference on Information Science and Applications, Changsha, China, 21–23 July 2017; Springer: Singapore, 2017; pp. 249–256. [Google Scholar]
- Sinha, R.; Jindal, P. A study of physical layer security with energy harvesting in single hop relaying environment. In Proceedings of the 2017 4th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 2–3 February 2017; pp. 530–533. [Google Scholar] [CrossRef]
- Pal, S.; Jindal, P. Secrecy Performance Analysis for Multi-hop and Single-Hop Relaying Model. Opt. Wirel. Technol. Proc. OWT 2019 2020, 648, 437. [Google Scholar]
- Gawtham, K.D.; Jindal, P. Analysis of amplify and forward technique to improve secrecy rate in multi-hop relaying system. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 20–21 May 2016; pp. 62–64. [Google Scholar]
- Zhou, N.; Wan, B.; Gong, L. Secrecy rate maximisation for non-linear energy harvesting relay networks with cooperative jamming and imperfect channel state information. ET Commun. 2020, 14, 923–929. [Google Scholar] [CrossRef]
- Ding, H.; Ge, J.; da Costa, D.B.; Jiang, Z. A new efficient lowcomplexity scheme for multi-source multi-relay cooperative networks. IEEE Trans. Veh. Technol. 2011, 60, 716–722. [Google Scholar] [CrossRef]








| Section 1 | Section 2 |
|---|---|
| Section 1. Introduction Section 1.1. Organization of Paper | Section 2. System Model Section 2.1. Power Splitting and Energy Harvesting Technique Section 2.2. Full Duplex Decoding and Forward (DF) Relay Scheme |
| Section 3 | Section 4 |
| Section 3. Achievable Secrecy Rate Section 3.1. DF Relaying Scheme Section 3.2. AF Relaying Scheme | Section 4. Analysis of Outage Probability |
| Section 5 | Section 6 |
| Section 5. Numerical Evaluation and Results | Section 6. Conclusions |
| Reference | Investigation | Technique | Cooperative Scheme | |
|---|---|---|---|---|
| AF Scheme | DF Scheme | |||
| [12] | Single-Hop Relay Network | Energy Harvesting | 8.89% | 9.83% |
| [13] | Single-Hop Relay Network | Energy Harvesting and Jamming Signal | 23.63% | 30.47% |
| [14] | Single-Hop Relay Network | Physical Layer Security | 11.9% | 42.86% |
| [15] | Half-Duplex Relay Network | Amplify and Forward (AF) and Decode and Forward (DF) | 40% | 41% |
| Proposed | Multiple-Relay Cooperative System. | Energy Harvesting, Power Splitting, Time Switching, Full Duplex Mode, Secrecy Outage Probability | 50.5% | 44.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sehito, N.; Yang, S.; Ali, E.M.; Khan, M.A.; Larik, R.S.A.; Bari, I.; Kamal, M.M.; Khan, S.; Alibakhshikenari, M.; Limiti, E. Physical Layer Secrecy by Power Splitting and Jamming in Cooperative Multiple Relay Based on Energy Harvesting in Full-Duplex Network. Electronics 2022, 11, 40. https://doi.org/10.3390/electronics11010040
Sehito N, Yang S, Ali EM, Khan MA, Larik RSA, Bari I, Kamal MM, Khan S, Alibakhshikenari M, Limiti E. Physical Layer Secrecy by Power Splitting and Jamming in Cooperative Multiple Relay Based on Energy Harvesting in Full-Duplex Network. Electronics. 2022; 11(1):40. https://doi.org/10.3390/electronics11010040
Chicago/Turabian StyleSehito, Nabila, Shouyi Yang, Esraa Mousa Ali, Muhammad Abbas Khan, Raja Sohail Ahmed Larik, Inam Bari, Mian Muhammad Kamal, Salahuddin Khan, Mohammad Alibakhshikenari, and Ernesto Limiti. 2022. "Physical Layer Secrecy by Power Splitting and Jamming in Cooperative Multiple Relay Based on Energy Harvesting in Full-Duplex Network" Electronics 11, no. 1: 40. https://doi.org/10.3390/electronics11010040
APA StyleSehito, N., Yang, S., Ali, E. M., Khan, M. A., Larik, R. S. A., Bari, I., Kamal, M. M., Khan, S., Alibakhshikenari, M., & Limiti, E. (2022). Physical Layer Secrecy by Power Splitting and Jamming in Cooperative Multiple Relay Based on Energy Harvesting in Full-Duplex Network. Electronics, 11(1), 40. https://doi.org/10.3390/electronics11010040










