Further Improvement of Customized Vibration Generator for Machine–Human Feedbacks with the Help of Resonant Networks
Abstract
1. Introduction
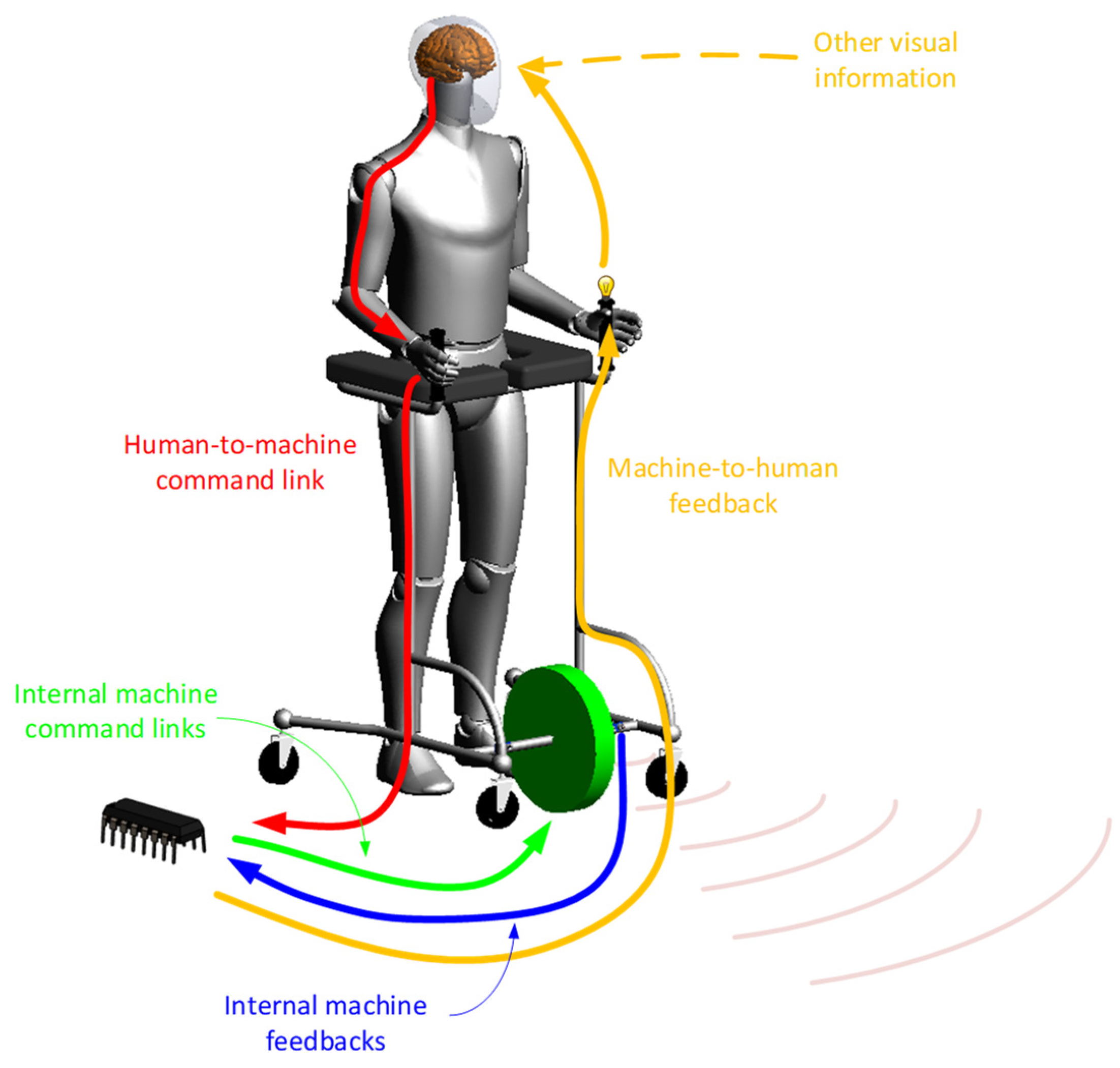
1.1. Human–Machine and Machine–Human Interaction
1.2. Kinds of Haptic Perceptions Sense
1.3. Kinds of Vibration Actuators
- Eccentric rotating mass vibration motor (ERM motor): Any motor (usually a DC motor) with a non-symmetric mass attached to the shaft [22]. The only parameter that affects both frequency and amplitude is input voltage, so the regulation of such a motor is limited.
- Piezoelectric motors (rotating and linear) directly convert voltage oscillations into mechanical vibrations and then, due to the mechanical contact of the piezoceramic material and moving parts, into the mechanical motion. However, these motors are regarded as low-speed/voltage, high-torque/force/current motors [23,24]. Additionally, these motors need high voltage to operate at higher frequencies.
- Voice coil motors: One challenge can be that these types of actuators usually have low active resistance (for example, 4 or 8 Ω). Therefore, lower supply voltage can be used to operate such a device. These vibration actuators are easier to regulate—the amplitude and frequency are dependent on amplitude and frequency of input voltage and can be controlled simultaneously.
- Linear resonant actuator: these actuators have movable mass, magnet, spring and coil. Connecting the coil to the sinusoidal voltage source, it produces a magnetic field, which forces the magnet with attached mass to move, and the spring makes it move in the opposite direction. These actuators are most efficient at resonant frequencies, when mechanical resonance appears, and the efficiency critically decreases when they are working in non-resonant frequencies. Therefore, it is impossible to regulate them in a wide frequency range.
2. Initial Proposal
3. Hypotheses, Methods and Technical Assumptions
3.1. Hypotheses
3.2. Mathemathical Considerations
3.3. Technical Considerations
- (I)
- The resonance allows increasing the apparent power and force developed by the VCM actuator.
- (II)
- Since the inductance of the actuator is constant the resonance is to be achieved at different values of capacitance that require an adjustable capacitor.
- (III)
- As a part of the machine–human feedback or diagnostic system, the actuator must react quickly to new operation conditions that require not only an adjustable, but also a real-time programmable capacitor.
- (IV)
- The real-time programmable capacitor can be implemented on the basis of capacitor bank and commutation unit, capable of operating at high frequency and integrating into switch-mode driver of the actuator. The generalized structure of such scheme is shown in Figure 5c.
- (V)
- It is reasonable to distribute the capacitance between the capacitors of the bank according to the binary weighted principle.
4. Test Bench Development
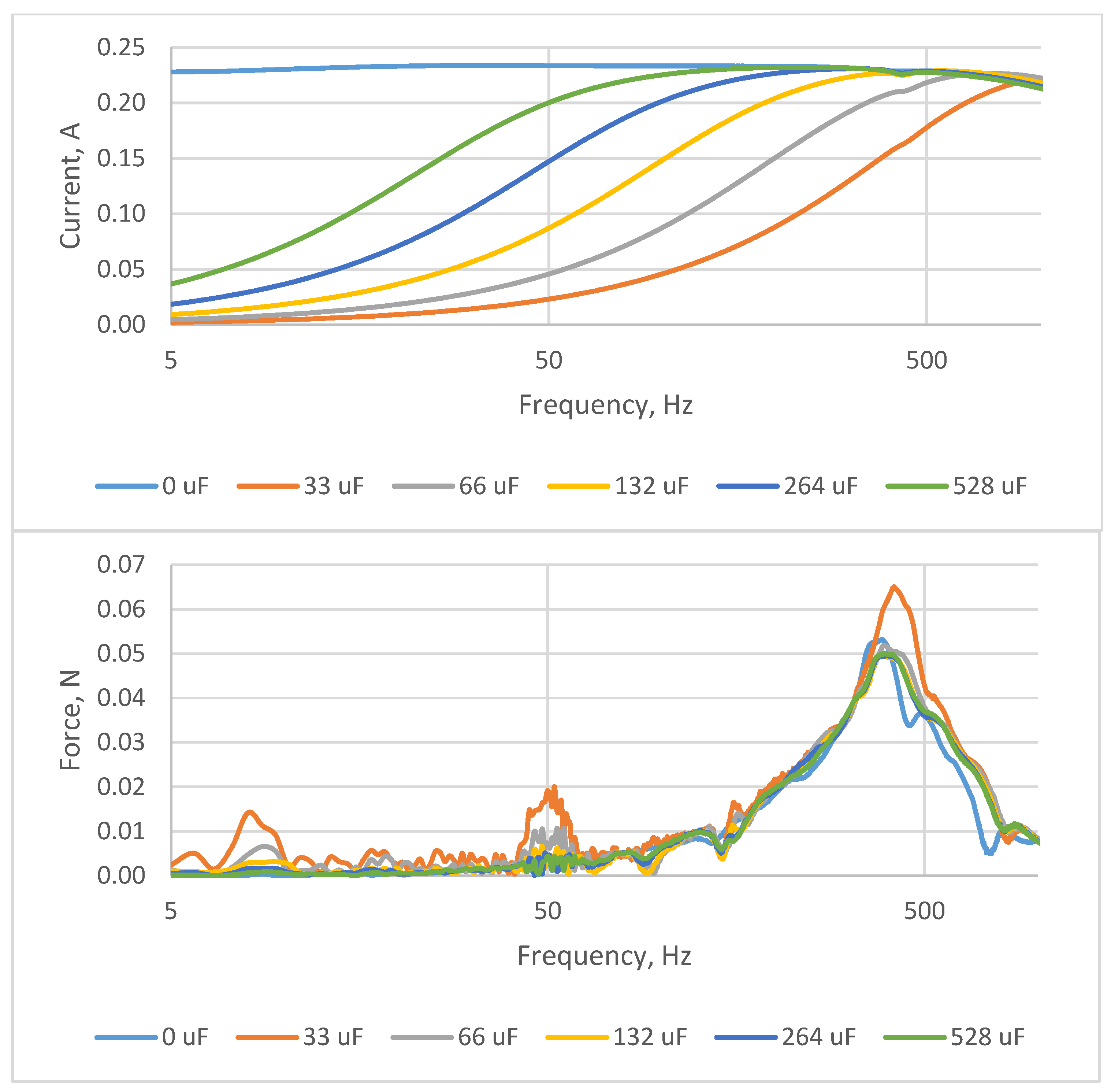
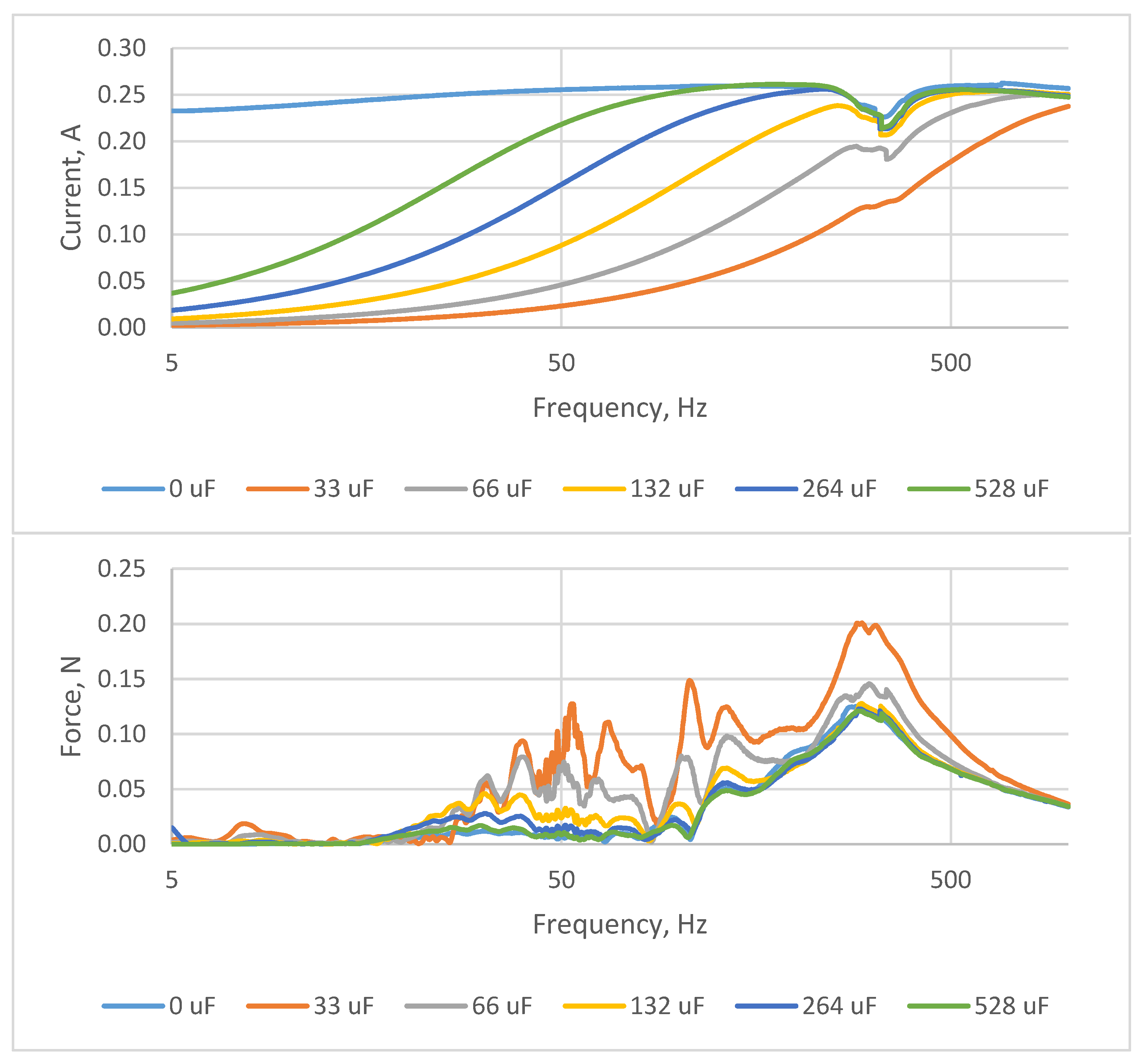
5. Results
6. Discussion and Conclusions
- (1)
- The point of maximal current output is defined by the resonant frequency that occurs at equality of inductive resistance of the actuator and capacitive resistance of the attached capacitor unit XL = XC.
- (2)
- Changing of the capacitance of the capacitor connected in series with the actuator allows shifting of the point of maximal current output.
- (3)
- The electrical damping factor (active resistance) and the mechanical damping factor of the actuator make the above-described effect less obvious, but do not reduce its importance.
- (4)
- The capacitances of the applied capacitors are significant, which makes the hypothesis less practically implementable.
- (5)
- A comprehensive comparison of four-quadrant and two-quadrant schemes is required. The use of a four-quadrant converter (full transistor bridge) requires bipolar capacitors, as well as a higher number of transistors and their drivers; in turn, two-quadrant converters may require more powerful transistors and they may be less compatible with adjustable capacitors packs.
- (1)
- Development of a two-quadrant converter with bipolar current and unipolar voltage that would allow the use of electrolytic capacitors that would facilitate the development of the driver.
- (2)
- Development of a real-time programmable capacitor pack that consists of several binary weighted capacitors and a commutating circuit and its integration into the previously developed two-quadrant converter.
Author Contributions
Funding
Conflicts of Interest
References
- Sowe, S.K.; Simmon, E.; Zettsu, K.; De Vaulx, F.; Bojanova, I. Cyber-Physical-Human Systems: Putting People in the Loop. IT Prof. 2016, 18, 10–13. [Google Scholar] [CrossRef] [PubMed]
- Serpanos, D. The Cyber-Physical Systems Revolution. Computer 2018, 51, 70–73. [Google Scholar] [CrossRef]
- Stoker, C.; Burch, D.; Hine, B.; Barry, J. Antarctic undersea exploration using a robotic submarine with a telepresence user interface. IEEE Expert 1995, 10, 14–23. [Google Scholar] [CrossRef]
- Iborra, A.; Pastor, J.; Alvarez, B.; Fernandez, C.; Merono, J.F. Robots in radioactive environments. IEEE Robot. Autom. Mag. 2003, 10, 12–22. [Google Scholar] [CrossRef]
- Utsumi, M.; Hirabayashi, T.; Yoshie, M. Development for teleoperation underwater grasping system in unclear environment. In Proceedings of the 2002 Interntional Symposium on Underwater Technology (Cat. No.02EX556), Tokyo, Japan, 19 April 2002; pp. 349–353. [Google Scholar]
- Radi, M.; Nitsch, V. Telepresence in Industrial Applications: Implementation Issues for Assembly Tasks. Presence Teleoperators Virtual Environ. 2010, 19, 415–429. [Google Scholar] [CrossRef]
- Hagn, U.; Ortmaier, T.; Konietschke, R.; Kubler, B.; Seibold, U.; Tobergte, A.; Nickl, M.; Jorg, S.; Hirzinger, G. Telemanipulator for remote minimally invasive surgery. IEEE Robot. Autom. Mag. 2008, 15, 28–38. [Google Scholar] [CrossRef]
- Vorobyov, M.; Galkin, I. Concept of cost-effective power-assisted wheelchair: Human-in-the-loop subsystem. In Proceedings of the 2017 5th IEEE Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE), Riga, Latvia, 24–25 November 2017. [Google Scholar]
- Vitols, K.; Podgornovs, A. Concept of cost-effective power-assist wheelchair’s electrical subsystem. In Proceedings of the 2017 5th IEEE Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE), Riga, Latvia, 24–25 November 2017. [Google Scholar]
- Galkin, I.; Podgornovs, A.; Blinov, A.; Vitols, K.; Vorobyov, M.; Kosenko, R. Consideretions on Cost effective power assisted wheelchair subsystems. Electr. Control Commun. Eng. 2018, 14, 71–80. [Google Scholar] [CrossRef]
- Bubovich, A.; Vorobyov, M.; Nikonorov, D.; Galkin, I. Evaluation of Accelerometer Control Interface with Powered Wheelchair. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. P.1–P.9. [Google Scholar]
- Jacinto-Villegas, J.M.; Satler, M.; Filippeschi, A.; Bergamasco, M.; Ragaglia, M.; Argiolas, A.; Niccolini, M.; Avizzano, C.A. A Novel Wearable Haptic Controller for Teleoperating Robotic Platforms. IEEE Robot. Autom. Lett. 2017, 2, 2072–2079. [Google Scholar] [CrossRef]
- Bolopion, A.; Régnier, S. A Review of Haptic Feedback Teleoperation Systems for Micromanipulation and Microassembly. IEEE Trans. Autom. Sci. Eng. 2013, 10, 496–502. [Google Scholar] [CrossRef]
- Mayer, H.; Nagy, I.; Knoll, A.; Braun, E.U.; Bauernschmitt, R.; Lange, R. Haptic Feedback in a Telepresence System for Endoscopic Heart Surgery. Presence: Teleoperators Virtual Environ. 2007, 16, 459–470. [Google Scholar] [CrossRef]
- Pacchierotti, C.; Prattichizzo, D.; Kuchenbecker, K.J. Cutaneous Feedback of Fingertip Deformation and Vibration for Palpation in Robotic Surgery. IEEE Trans. Biomed. Eng. 2015, 63, 278–287. [Google Scholar] [CrossRef] [PubMed]
- Edwards, J. Signal Processing Powers Next-Generation Prosthetics: Researchers Investigate Techniques That Enable Artificial Limbs to Behave More Like Their Natural Counterparts [Special Reports]. IEEE Signal Process. Mag. 2018, 35, 13–16. [Google Scholar] [CrossRef]
- Stephens-Fripp, B.; Mutlu, R.; Alici, G. Using Vibration Motors to Create Tactile Apparent Movement for Transradial Prosthetic Sensory Feedback. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; Volume 2018, pp. 213–218. [Google Scholar]
- Galkin, I.; Vorobyov, M.; Gainutdinovs, O.; Studers, P. Customized Vibration Generator for State of Health Monitoring of Prosthetic Implants and Pseudo-Bionic Machine–Human Feedbacks. Electronics 2019, 8, 810. [Google Scholar] [CrossRef]
- Cholewiak, R.W.; Collins, A.A. Sensory and physiological bases of touch. In Psychology of Touch; Heller, M.A., Schiff, W., Eds.; Lawrence Erlbaum: London, UK, 1991; pp. 23–60. ISBN 0805807500. [Google Scholar]
- Vinet, L.; Zhedanov, A. Engineering Haptic Devices; Springer: London, UK, 2014; Volume 44. [Google Scholar]
- Vorobyov, M.; Bubovich, A.; Galkin, I. Initial in-the-field evaluation of wheelchair’s machine-to-human haptic feedback with 3D printed vibration actuator. In Proceedings of the 2018 IEEE Industrial Cyber-Physical Systems (ICPS), St. Petersburg, Russia, 15–18 May 2018; pp. 579–584. [Google Scholar] [CrossRef]
- AB-004: Understanding ERM Vibration Motor Characteristics—Precision Microdrives. Available online: https://www.precisionmicrodrives.com/content/ab-004-understanding-erm-vibration-motor-characteristics/ (accessed on 18 March 2019).
- Belly, C.; Porchez, T.; Bagot, M.; Claeyssen, F. Improvement of Linear and Rotative Stepping Piezo Actuators using design and control. In Proceedings of the ACTUATOR2012, 13th International Conference on New Actuators, Bremen, Germany, 18–20 June 2012; pp. 246–249. [Google Scholar]
- Uchino, K. Piezoelectric ultrasonic motors: Overview. Smart Mater. Struct. 1998, 7, 273–285. [Google Scholar] [CrossRef]

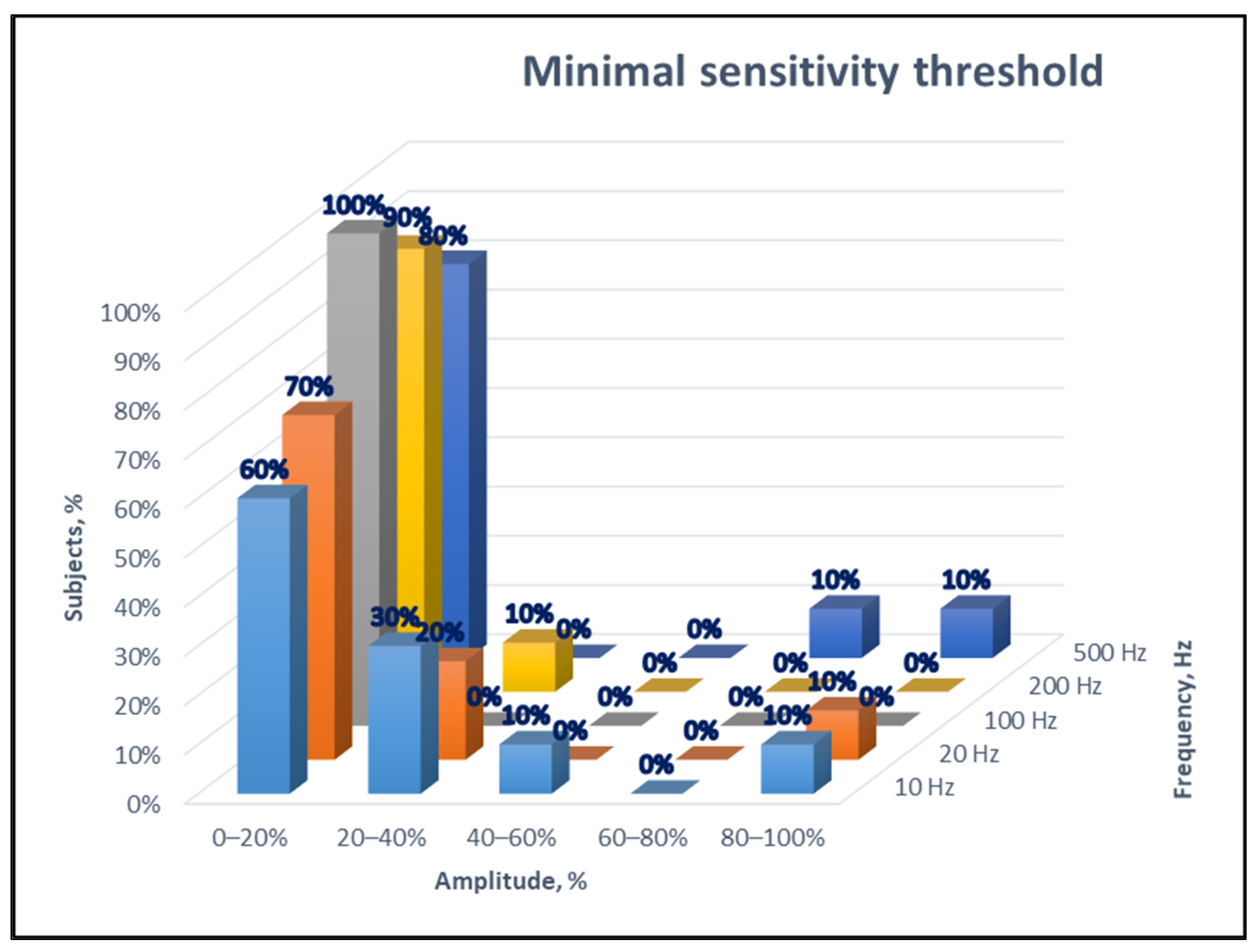


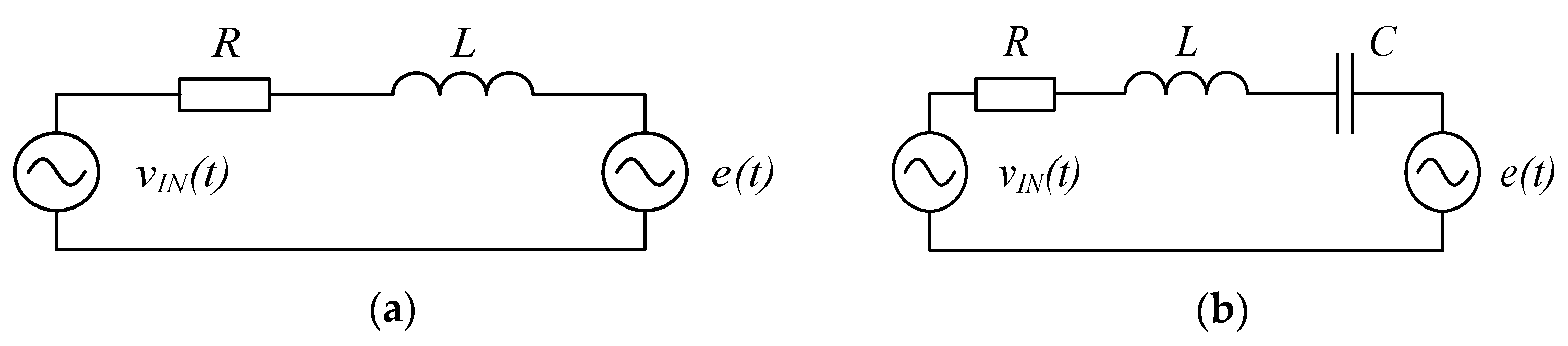

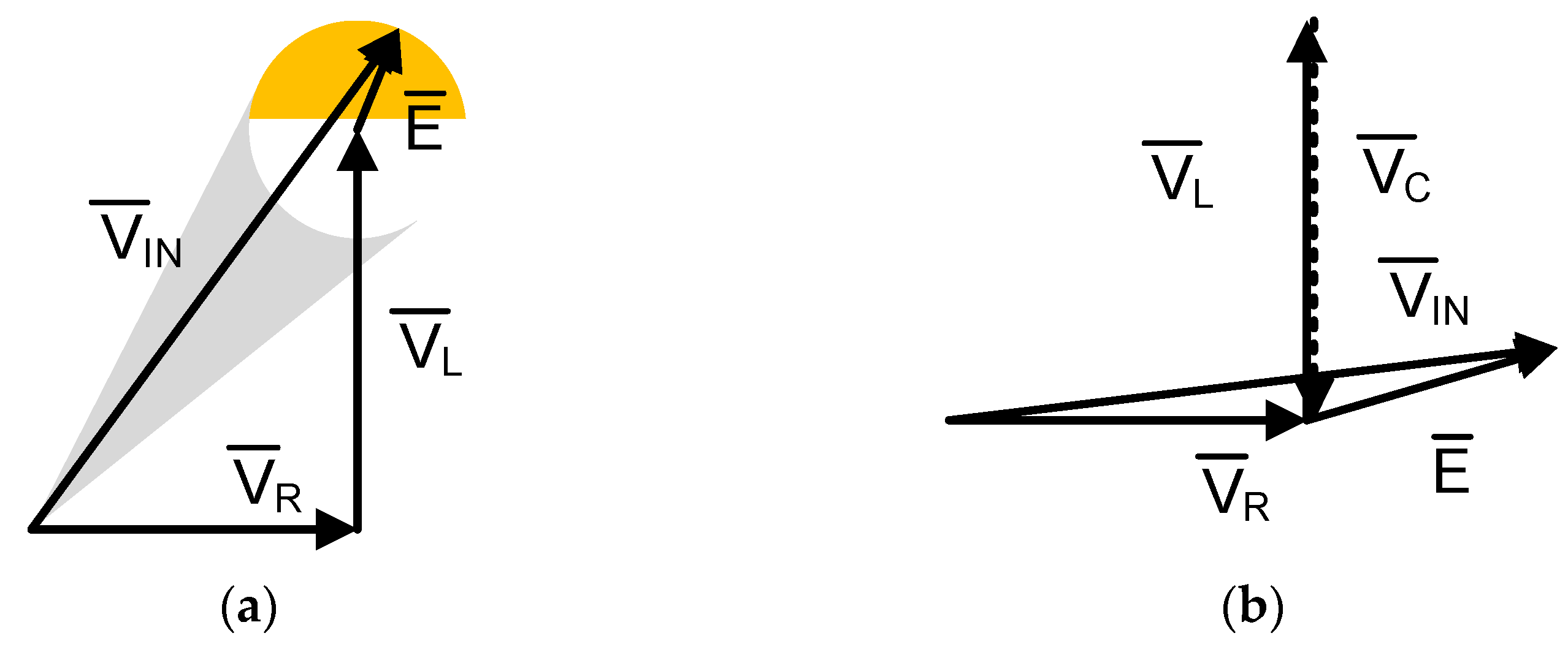

| Receptor Type | Sensory Cell | Size (mm2) | Boundary | Vibration FreQuency Filling Gap |
|---|---|---|---|---|
| SA-I | Merkel disk | 7–12 | Distinct | Steady state–20 Hz |
| SA-II | Ruffini endings | 50–75 | Diffuse | Steady state–50 Hz |
| RA-I | Meissner corpuscle | 7–19 | Distinct | 10–50 Hz |
| RA-II | Pacinian corpuscle | 100–300 | Diffuse | 40–1000 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bubovich, A.; Galkin, I.; Vorobyov, M. Further Improvement of Customized Vibration Generator for Machine–Human Feedbacks with the Help of Resonant Networks. Electronics 2021, 10, 962. https://doi.org/10.3390/electronics10080962
Bubovich A, Galkin I, Vorobyov M. Further Improvement of Customized Vibration Generator for Machine–Human Feedbacks with the Help of Resonant Networks. Electronics. 2021; 10(8):962. https://doi.org/10.3390/electronics10080962
Chicago/Turabian StyleBubovich, Alexander, Ilya Galkin, and Maxim Vorobyov. 2021. "Further Improvement of Customized Vibration Generator for Machine–Human Feedbacks with the Help of Resonant Networks" Electronics 10, no. 8: 962. https://doi.org/10.3390/electronics10080962
APA StyleBubovich, A., Galkin, I., & Vorobyov, M. (2021). Further Improvement of Customized Vibration Generator for Machine–Human Feedbacks with the Help of Resonant Networks. Electronics, 10(8), 962. https://doi.org/10.3390/electronics10080962






