Parameter Extraction of Photovoltaic Module Using Tunicate Swarm Algorithm
Abstract
1. Introduction
2. Problem Statement
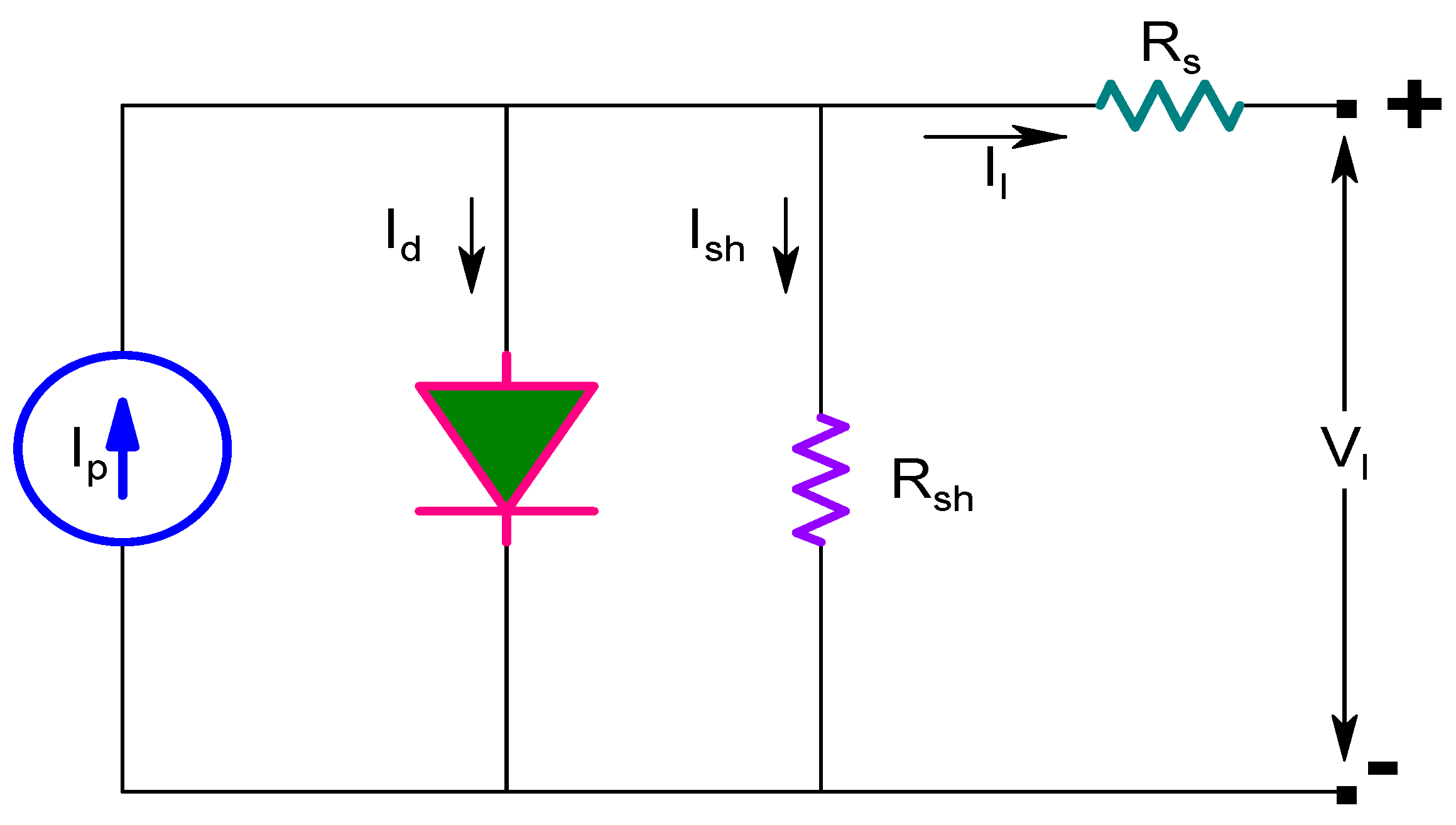
2.1. Photovoltaic Panel Module Model
2.2. Objective Function
3. Tunicate Swarm Algorithm
3.1. Prevent Collisions between Candidate Solutions
3.2. Step More toward the Location of the Best Solution
3.3. Stick Close to the Best Solution
3.4. Implementation of TSA for Parameter Extraction
4. Results and Discussion
4.1. TSA for Parameter Extraction of Photowatt-PWP201 PV Module
4.2. Convergence Analysis
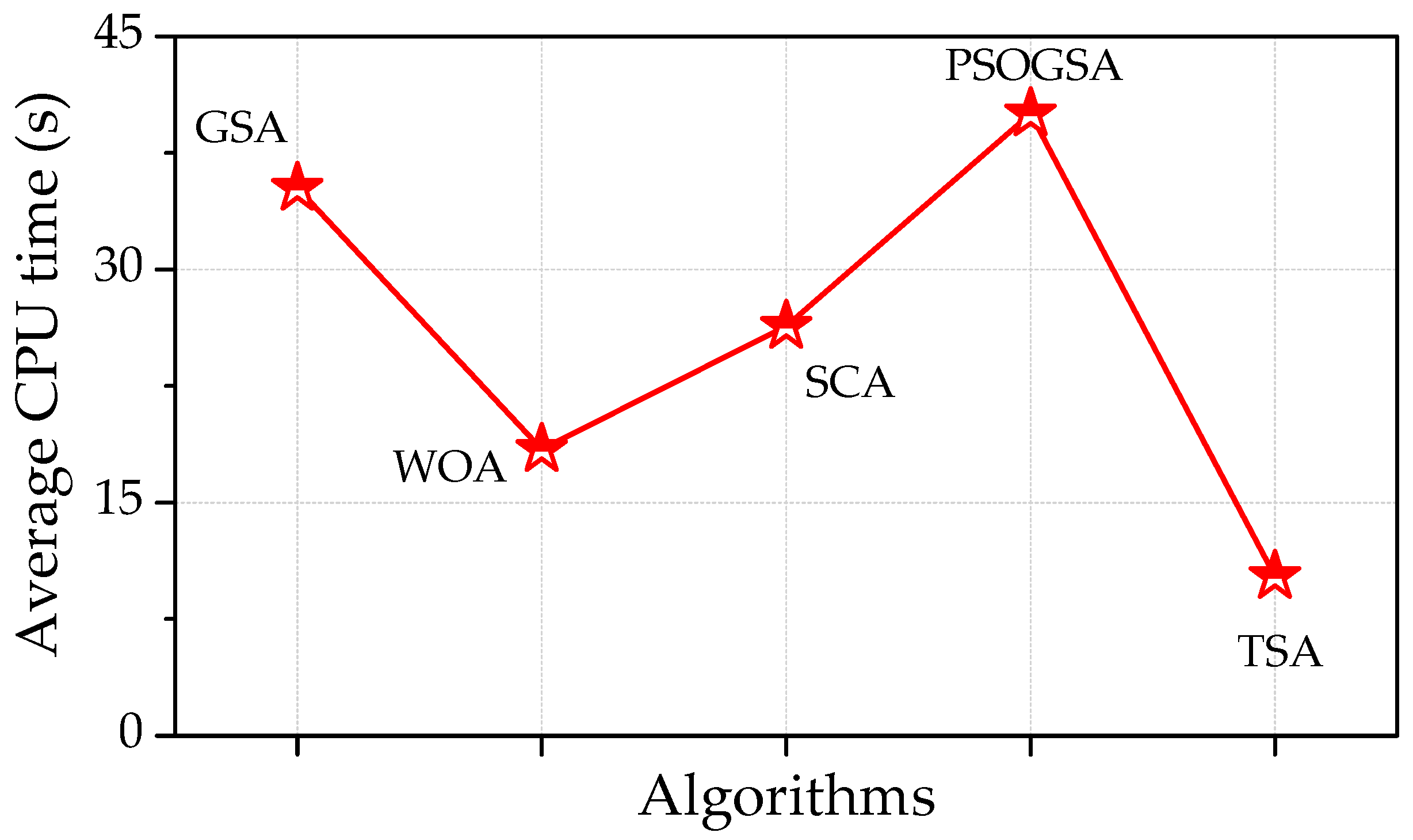
4.3. Robustness and Statistics Analysis
5. Discussion
6. Conclusions
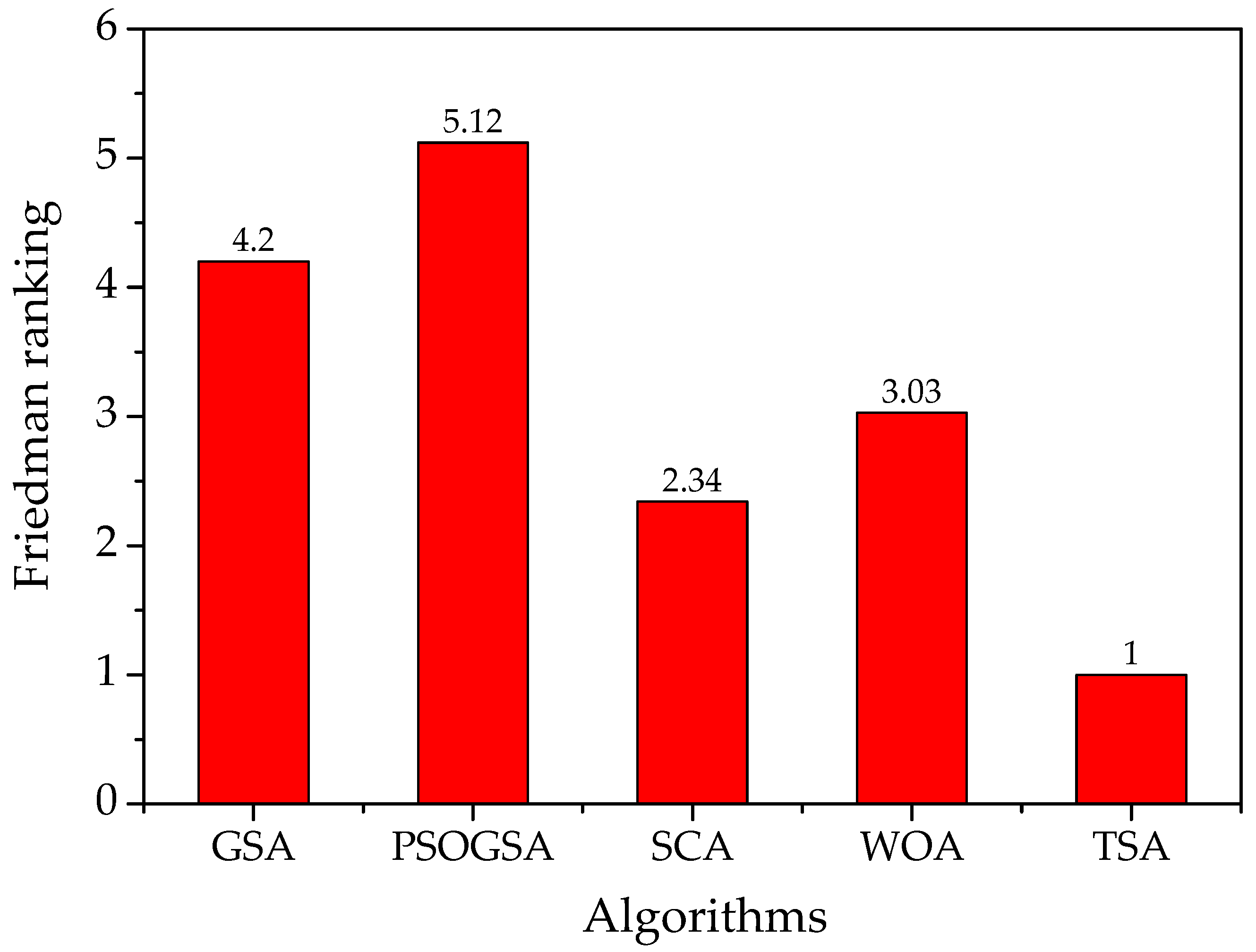
- TSA is relatively accurate and reliable at delivering the solution in terms of the RMSE compared with other algorithms such as GSA, PSOGSA, SCA, and WOA.
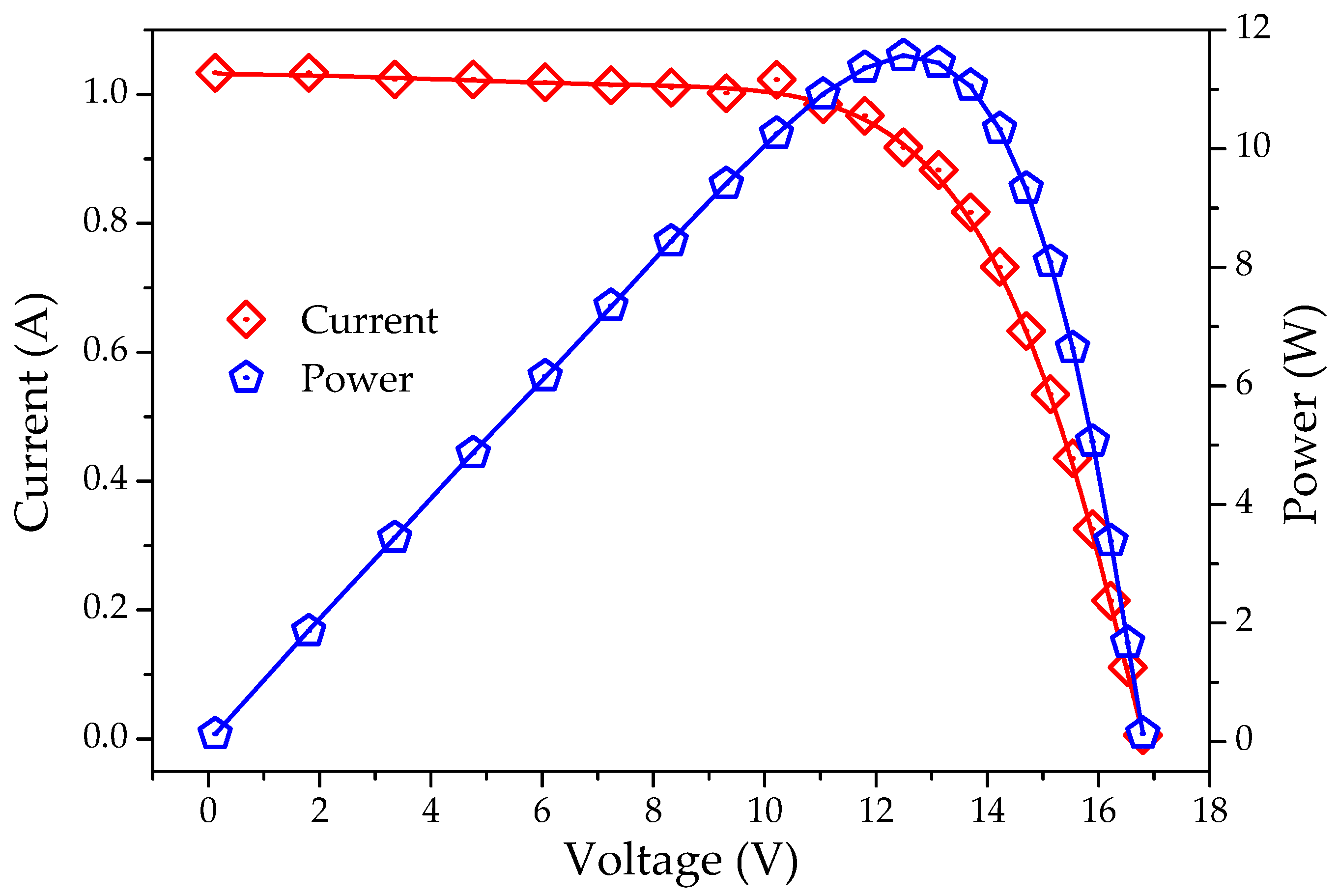
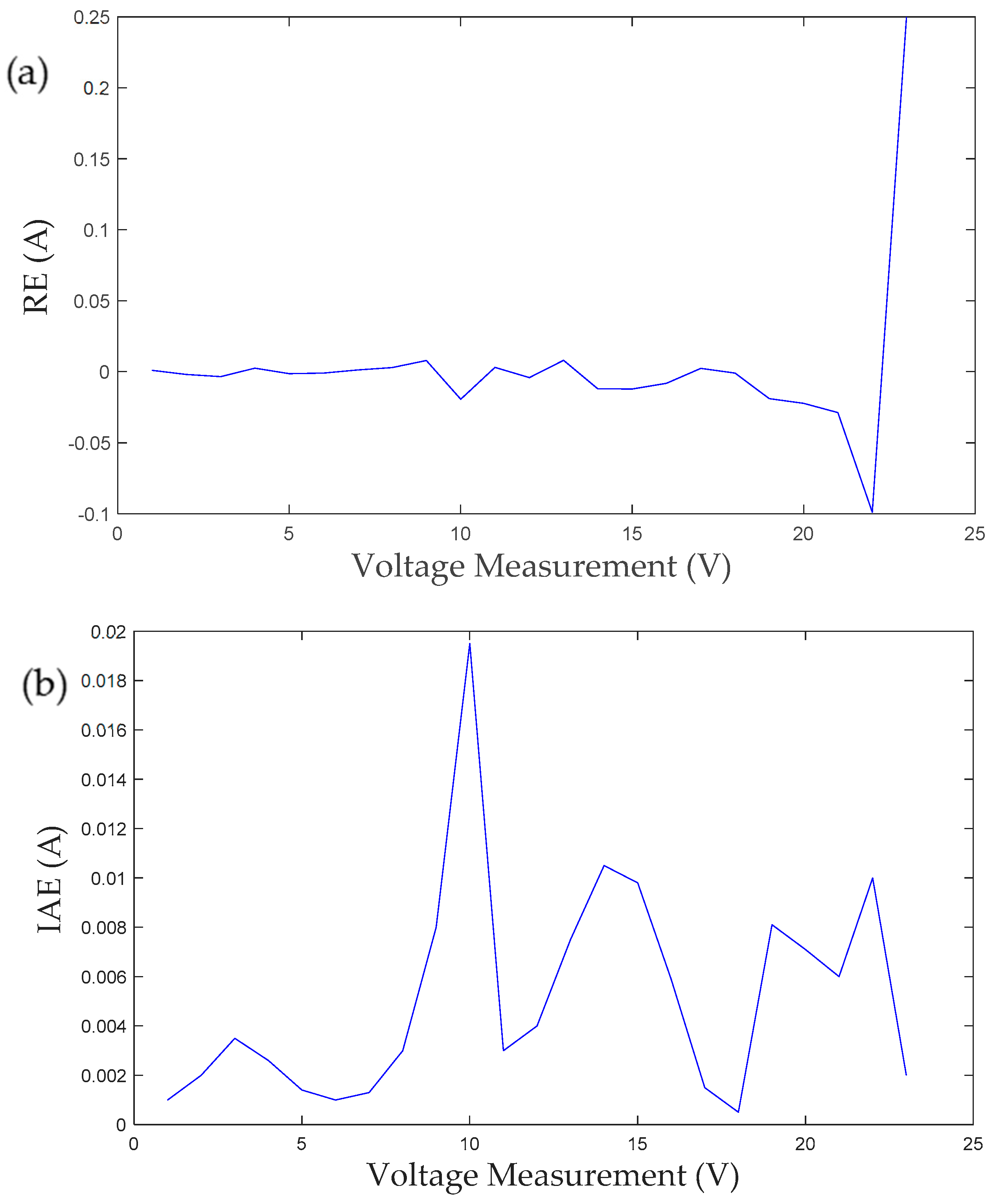
- The I-V and P-V characteristic curves and IAE results indicate that TSA can generate the optimized value of the estimated parameters for all the solar PV cell models compared with other algorithms.
- The statistical analysis depicts the robustness of the TSA technique in parameter estimation problems under standard operating conditions.
- The convergence curves demonstrate that the TSA obtains the best estimated parameters in terms of RMSE (5.06 10−4).
- From the above discussion, it can be concluded that the TSA is an effective and robust technique to estimate the unknown optimized parameters of the solar PV module model under standard operating conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Symbols
| Ip | Photo Diode Current |
| Isd | Reverse Saturation Current |
| Rs | Series Resistance |
| Rsh | Shunt Resistance |
| A | Diode Ideality Factor |
| RMSE | Root Mean Square Error |
| PV | Photovoltaic |
| I-V | Current-Voltage |
| P-V | Power-Voltage |
| MPPT | Maximum Power Point Tracking |
| Voc | Open Circuit Voltage |
| Impp | Maximum Power Point Current |
| Isc | Short Circuit Current |
| PSO | Particle Swarm Optimization |
| WOA | Whale Optimization Algorithm |
| SDM | Single diode Model |
| DDM | Double diode Model |
| IAE | Internal Absolute Error |
| RE | Relative Error |
| GSA | Gravitational Search Algorithm |
| SCA | Sine Cosine Algorithm |
| PSOGSA | Particle Swarm Optimization Gravitational Search Algorithm |
References
- Coello, C.; Lamont, G.; van Veldhuizen, D. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: New York, NY, USA, 2007. [Google Scholar]
- Khanna, V.; Das, B.K. A Method to Model the Maximum Power Output of Photovoltaic Modules Using Statistical Analysis and Matlab-Simulink Simulation; A Method to Model the Maximum Power Output of Photovoltaic Modules Using Statistical Analysis and Matlab-Simulink Simulation. 2018. Available online: http://www.academia.edu/download/59389096/a-method-to-model-the-maximum-power-output-of-simulation-IJERTV7IS05022020190525-102639-p9gz0d.pdf (accessed on 7 October 2020).
- Chen, X.; Yu, K.; Du, W.; Zhao, W.; Liu, G. Parameters identification of solar cell models using generalized oppositional teaching learning based optimization. Energy 2016, 99, 170–180. [Google Scholar] [CrossRef]
- KYu, K.; Liang, J.; Qu, B.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Merchaoui, M.; Sakly, A.; Mimouni, M.F. Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Convers. Manag. 2018, 175, 151–163. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Kennedy, C. Review of Mid-to High-Temperature Solar Selective Absorber Materials. 2002. Available online: https://www.osti.gov/biblio/15000706 (accessed on 6 September 2020).
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. Hybrid Particle Swarm Optimization and Gravitational Search Algorithm for Multilayer Perceptron Learning. Ph.D. Thesis, Universiti Teknologi Malaysia, Skudai, Malaysia, 2011. [Google Scholar]
- AlHajri, M.; El-Naggar, K.; AlRashidi, M.; Al-Othman, A. Optimal extraction of solar cell parameters using pattern search. Renew. Energy 2012, 44, 238–245. [Google Scholar] [CrossRef]
- Gong, X.; Kulkarni, M. Design optimization of a large scale rooftop photovoltaic system. Sol. Energy 2005, 78, 362–374. [Google Scholar] [CrossRef]
- Chellaswamy, C.; Ramesh, R. Parameter extraction of solar cell models based on adaptive differential evolution algorithm. Renew. Energy 2016, 97, 823–837. [Google Scholar] [CrossRef]
- Bayoumi, A.; El-Sehiemy, R.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Assessment of an Improved Three-Diode against Modified Two-Diode Patterns of MCS Solar Cells Associated with Soft Parameter Estimation Paradigms. Appl. Sci. 2021, 11, 1055. [Google Scholar] [CrossRef]
- Mughal, M.A.; Ma, Q.; Xiao, C. Photovoltaic Cell Parameter Estimation Using Hybrid Particle Swarm Optimization and Simulated Annealing. Energies 2017, 10, 1213. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, A.; Averbukh, M.; Jately, V.; Azzopardi, B. An Effective Method for Parameter Estimation of a Solar Cell. Electronics 2021, 10, 312. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S.M. Parameter Estimation of Three Diode Photovoltaic Model Using Grasshopper Optimization Algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef]
- Oliva, D.; Ewees, A.A.; Aziz, M.A.E.; Hassanien, A.E.; Peréz-Cisneros, M. A Chaotic Improved Artificial Bee Colony for Parameter Estimation of Photovoltaic Cells. Energies 2017, 10, 865. [Google Scholar] [CrossRef]
- Stornelli, V.; Muttillo, M.; de Rubeis, T.; Nardi, I. A New Simplified Five-Parameter Estimation Method for Single-Diode Model of Photovoltaic Panels. Energies 2019, 12, 4271. [Google Scholar] [CrossRef]
- Al-Taani, H.; Arabasi, S. Solar Irradiance Measurements Using Smart Devices: A Cost-Effective Technique for Estimation of Solar Irradiance for Sustainable Energy Systems. Sustainability 2018, 10, 508. [Google Scholar] [CrossRef]
- Park, C.-Y.; Hong, S.-H.; Lim, S.-C.; Song, B.-S.; Park, S.-W.; Huh, J.-H.; Kim, J.-C. Inverter Efficiency Analysis Model Based on Solar Power Estimation Using Solar Radiation. Processes 2020, 8, 1225. [Google Scholar] [CrossRef]
- Bocca, A.; Bergamasco, L.; Fasano, M.; Bottaccioli, L.; Chiavazzo, E.; Macii, A.; Asinari, P. Multiple-Regression Method for Fast Estimation of Solar Irradiation and Photovoltaic Energy Potentials over Europe and Africa. Energies 2018, 11, 3477. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Khan, I.; Elavarasan, R.M.; Das, N. Optimal PV Parameter Estimation via Double Exponential Function-Based Dynamic Inertia Weight Particle Swarm Optimization. Energies 2020, 13, 4037. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Korashy, A.; Yu, J. Photovoltaic cells parameter estimation using an enhanced teaching–learning-based optimization algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 767–779. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Sajjad, I.A.; Raza, A.; Khan, I.A. Chaotic inertia weight particle swarm optimization (CIWPSO): An efficient technique for solar cell parameter estimation. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sindh, Pakistan, 29–30 January 2020; pp. 1–6. [Google Scholar]
- Halko, S.; Halko, К. Research of electrical and physical characteristics of the solar panel on the basis of cogeneration photoelectric modules. Збірник наукових праць ΛΌГOΣ 2020, 2, 39–44. [Google Scholar] [CrossRef]
- El-Hameed, M.A.; Elkholy, M.M.; El-Fergany, A.A. Three-diode model for characterization of industrial solar generating units using Manta-rays foraging optimizer: Analysis and validations. Energy Convers. Manag. 2020, 219, 113048. [Google Scholar] [CrossRef]
- Abdulrazzaq, A.K.; Bognár, G.; Plesz, B. Evaluation of different methods for solar cells/modules parameters extraction. Sol. Energy 2020, 196, 183–195. [Google Scholar] [CrossRef]
- Babich, V.; Lobel, R.; Şafak, Y. Promoting Solar Panel Investments: Feed-in-Tariff vs. Tax-Rebate Policies. Manuf. Serv. Oper. Manag. 2020, 22, 1148–1164. [Google Scholar] [CrossRef]


| Parameters | Photowatt-PWP201 PV Module | |
|---|---|---|
| Lower Bound | Upper Bound | |
| Ip (A) | 0 | 10 |
| Isd (µA) | 0 | 50 |
| Rs (Ω) | 0.001 | 2 |
| Rsh (Ω) | 0 | 2000 |
| a | 0 | 100 |
| Algorithms | Iph (A) | Rs (Ω) | Rsh (Ω) | Isd (µA) | a | RMSE |
|---|---|---|---|---|---|---|
| WOAPSO [18] | 1.5032 | 0.0213 | 668.27 | 0.024 | 1.502 | 8.86 × 10−4 |
| GSA | 0.0278 | 2 | 1201.097 | 0.050 | 58.4588 | 8.80 × 10−3 |
| PSOGSA | 0.0218 | 0.6430 | 1100.437 | 0.01 | 79.7893 | 7.156 × 10−3 |
| SCA | 1.0063 | 0.0496 | 1107.399 | 0.039 | 1.0532 | 1.28 × 10−2 |
| WOA | 0.0264 | 0.0113 | 588.5011 | 0.0424 | 1.4496 | 9.54 × 10−4 |
| TSA | 0.0261 | 0.0017 | 2000 | 0.053 | 1.4727 | 5.06 × 10−4 |
| Observations | VL (V) | IL (A) | Isim (A) | IAE (A) | Pmeasured (W) | Psimulted (W) | IAE (W) |
|---|---|---|---|---|---|---|---|
| 1 | 0.1246 | 1.0345 | 1.0335 | 0.001 | 0.1288 | 0.1256 | 0.0032 |
| 2 | 0.1248 | 1.0315 | 1.0335 | 0.002 | 0.1287 | 0.1226 | 0.0061 |
| 3 | 1.8093 | 1.03 | 1.0335 | 0.0035 | 1.8635 | 1.8765 | 0.013 |
| 4 | 3.3511 | 1.026 | 1.0234 | 0.0026 | 3.4382 | 3.4354 | 0.0028 |
| 5 | 4.7622 | 1.022 | 1.0234 | 0.0014 | 4.8669 | 4.8766 | 0.0097 |
| 6 | 6.0538 | 1.018 | 1.019 | 0.001 | 6.1627 | 6.1456 | 0.0171 |
| 7 | 7.2364 | 1.0155 | 1.0142 | 0.0013 | 7.3485 | 7.3256 | 0.0229 |
| 8 | 8.3189 | 1.014 | 1.011 | 0.003 | 8.4353 | 8.4453 | 0.01 |
| 9 | 9.3097 | 1.01 | 1.002 | 0.008 | 9.4027 | 9.4124 | 0.0097 |
| 10 | 10.2163 | 1.0035 | 1.023 | 0.0195 | 10.252 | 10.245 | 0.007 |
| 11 | 11.0449 | 0.988 | 0.985 | 0.003 | 10.9123 | 10.9234 | 0.0111 |
| 12 | 11.8018 | 0.963 | 0.967 | 0.004 | 11.3651 | 11.3554 | 0.0097 |
| 13 | 12.4929 | 0.9255 | 0.918 | 0.0075 | 11.5621 | 11.5722 | 0.0101 |
| 14 | 13.1231 | 0.8725 | 0.883 | 0.0105 | 11.4499 | 11.445 | 0.0049 |
| 15 | 13.6983 | 0.8075 | 0.8173 | 0.0098 | 11.0613 | 11.0521 | 0.0092 |
| 16 | 14.2221 | 0.7265 | 0.7324 | 0.0059 | 10.3323 | 10.321 | 0.0113 |
| 17 | 14.6995 | 0.6345 | 0.633 | 0.0015 | 9.3268 | 9.313 | 0.0138 |
| 18 | 15.1346 | 0.5345 | 0.535 | 0.0005 | 8.0894 | 8.0754 | 0.014 |
| 19 | 15.5311 | 0.4275 | 0.4356 | 0.0081 | 6.6395 | 6.6367 | 0.0028 |
| 20 | 15.8929 | 0.3185 | 0.3256 | 0.0071 | 5.0618 | 5.0524 | 0.0094 |
| 21 | 16.2229 | 0.2085 | 0.2145 | 0.006 | 3.3824 | 3.3724 | 0.01 |
| 22 | 16.5241 | 0.101 | 0.111 | 0.01 | 1.6689 | 1.6564 | 0.0125 |
| 23 | 16.7987 | 0.008 | 0.006 | 0.002 | 0.1343 | 0.1347 | 0.0004 |
| Sum of IAE | 0.0594 | 0.0927 |
| Photowatt-PWP201 Module Model | Algorithm | RMSE | |||
| Min | Mean | Max | SD | ||
| GSA | 8.80 × 10−3 | 2.65 × 10−1 | 2.08 × 10−1 | 5.85 × 10−3 | |
| PSOGSA | 7.156 × 10−3 | 6.47 × 10-3 | 2.83 × 10−1 | 1.81 × 10−2 | |
| SCA | 1.28 × 10−2 | 2.26 × 10-1 | 6.35 × 10−1 | 1.78 × 10−2 | |
| WOA | 9.54 × 10−4 | 2.35 ×10-2 | 2.63 × 10−1 | 2.83 × 10−2 | |
| TSA | 5.06 × 10−4 | 1.45 × 10-3 | 2.34 × 10−2 | 1.25 × 10−3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, A.; Dasgotra, A.; Tiwari, S.K.; Sharma, A.; Jately, V.; Azzopardi, B. Parameter Extraction of Photovoltaic Module Using Tunicate Swarm Algorithm. Electronics 2021, 10, 878. https://doi.org/10.3390/electronics10080878
Sharma A, Dasgotra A, Tiwari SK, Sharma A, Jately V, Azzopardi B. Parameter Extraction of Photovoltaic Module Using Tunicate Swarm Algorithm. Electronics. 2021; 10(8):878. https://doi.org/10.3390/electronics10080878
Chicago/Turabian StyleSharma, Abhishek, Ankit Dasgotra, Sunil Kumar Tiwari, Abhinav Sharma, Vibhu Jately, and Brian Azzopardi. 2021. "Parameter Extraction of Photovoltaic Module Using Tunicate Swarm Algorithm" Electronics 10, no. 8: 878. https://doi.org/10.3390/electronics10080878
APA StyleSharma, A., Dasgotra, A., Tiwari, S. K., Sharma, A., Jately, V., & Azzopardi, B. (2021). Parameter Extraction of Photovoltaic Module Using Tunicate Swarm Algorithm. Electronics, 10(8), 878. https://doi.org/10.3390/electronics10080878








