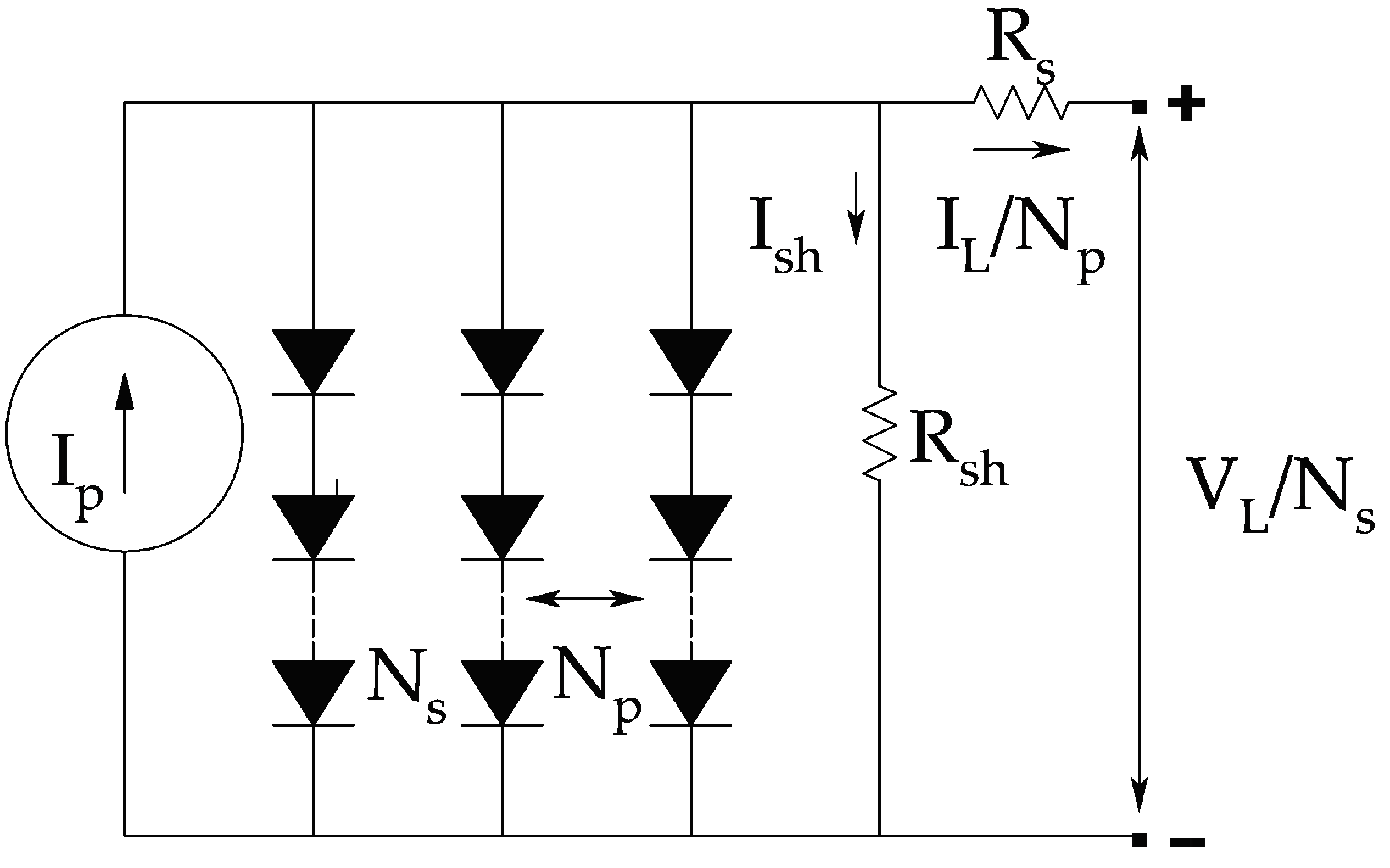
1. Introduction
The depletion of fossil fuel resources and resulting environmental impact due to their usages embarks the need for alternate energy resources [
1]. Solar energy is one of the most promising alternative sources for fossil fuel. The free access to the energy of sunlight can be extracted employing the photovoltaic (PV) panels. The rapid adoption of solar energy by the domestic and industrial sector makes it a vital source to be explored [
2]. Despite the very low operational and maintenance cost, there are various limitations for efficient energy generation. An enormous amount of research has been performed and carried out to better the power output from the PV panels [
3,
4]. The major limitation in the execution and implementation of the solar PV power plants is the very high capital cost for installation [
5]. PV cells are having nonlinear current-voltage (I-V) and power-voltage (P-V) characteristics curves with some operational limitations [
6]. This non-linearity makes it difficult for any probability and approximation to increase efficiency. Every PV panel can operate at maximum efficiency, as defined by the manufacturer, only if the practical parameters (voltage-current) are somewhat close to or coinciding with the maximum power point (MPP). The real behaviour of PV panels rather different from the optimal conditions, due to the non-linearity of I-V characteristics of solar cells makes it essential to determine the MPP in each moment. It could be done through simulation techniques for better operational efficiency [
7]. This technology is ensured by the model of the equivalent circuit having several inherent parameters. However, the parameters provided by the PV panel manufacturer don’t specify the model parameters. The given information states the open-circuit voltage (V
oc), short circuit current (I
sc), and current at maximum power point (I
mpp) under standard test conditions (i.e., 1000 W/m
2, 25 °C). The practical parameters vary at every instant with a change in weather conditions. The aging effects of PV also alter the parameters of the equivalent circuit [
3,
8,
9].
The core unit of the PV system is a solar cell, and it is of utmost priority to extract the parameters for a close analysis of the PV panel performance around its MPP. The simulation study of cells combined all together give the performance analysis of entire PV panels [
8,
10]. The equivalent circuit for the single- and double-diode model for parameter extraction is the recent and most widely used approach. The method of parameter extraction can be bifurcated into two major categories: analytical and optimization methods [
11,
12,
13,
14,
15]. Although the analytical methods are the simplest and yields result quickly, but it misses the accuracy under normal day conditions with variable lighting. The deterministic ways of parameter extraction such as Newton-Raphson, nonlinear least square, Lambert W-functions [
16], iterative curve fitting [
17], conductivity method [
18] and the Levenberg-Marquardt algorithm [
19] have many boundaries such as continuity, differentiability, and convexity related to objective functions. The boundary conditions further impose limitations on the usage of the above analytical methods, as they obtain local minima when dealing with multi-modal problems. Thus, analytical methods are not suitable to extract the parameters.
To get more accurate and precise parameters from nonlinear implicit equations with high accuracy, evolutionary algorithms [
20] were proposed. The bio-related algorithms are more accurate and powerful optimization algorithms to simplify nonlinear transcendental equations as it doesn’t include complex mathematics. Although, researchers have developed number of metaheuristic algorithm but there is no algorithm that provides optimal solution to all sets of problems which has also been proven by No free lunch theorem. This has motivated researchers to design new algorithms to efficiently solve complex science and engineering problems. A gradient-based optimizer (GBO) [
20] inspired from the gradient-based Newton’s method, Harris-Hawk optimizer (HHO) [
21] inspired from cooperative behavior and chasing style of the Harris Hawks Heap-based optimizer (HBO) [
22] inspired from corporate rank hierarchy and slime mould algorithm (SMA) [
23] inspired from diffusion and foraging conduct of slime mould are some of the recently developed metaheuristic algorithms. Some of the recent optimization algorithms used for parameter extraction are the genetic algorithm (GA) [
24], differential evolution (DE) [
25], simulated annealing (SA) [
26], pattern search (PS) [
27], harmony search (HS) [
28], cuckoo search (CS) [
29], flower pollination algorithm [
30], bacterial foraging optimization (BFO) [
31], bird mating [
32], and artificial bee swarm optimization (ABSO) [
33]. The proposed algorithms suffer from the problem of premature convergence. The primary disadvantage of GA is that it involves wide parameter optimization search space which makes the system quite complicated and slow. The problem of large search space was overcome by implementing PSO. However, it imposed the problem of the randomly chosen initial parameter value. The value exchange in SA between the cooling timetable and the original temperature makes it less popular. There is a likelihood that PSO will choose an incorrect pattern, leading to premature convergence or no convergence. PSO with reverse barrier restriction for series resistance (Rs), shunt resistance (Rsh), and diode ideality factor (a) is suggested for fast and coherent convergence of optimization issue to global optima, considering the temperature impact to reduce the modeling errors in differential evolution [
31,
32,
33,
34,
35]. Although the BFO technique offers excellent outcomes but involving too many parameters that have complicated the scheme and imposed a computational strain. Authors in [
36], implemented improved teaching-learning based optimization (ITLBO), where a good trade-off is established between the exploration and exploitation by eliminating the worst learner. This increases the global search ability of the population in a defined search space. A hybridization approach is carried out by the researchers in [
34] for parameter extraction of solar PV cell. In this approach, the hybridization of two algorithms are implemented, the firefly and pattern search. The exploration phase is completed by the firefly algorithm during the first half iteration and then the pattern search algorithm takes control of the population for the exploitation phase. A new opposition-based learning approach is incorporated with whale optimization and shuffled complex evolutionary algorithm for optimization of solar cell parameters [
35,
36]. This approach is tested on unimodal as well as on multimodal benchmark functions and simulation results clearly show the robustness of the algorithms.
The whale optimization algorithm (WOA) [
37] and particle swarm optimization (PSO) [
38] are the two most prominent used metaheuristics techniques as available in the literature. However, they differ from each other in the search mechanism for the best solution in a defined search space. WOA mimics the social behaviour of humpback whales while PSO mimics the searching behaviour of the birds in a group. It is shown by many previous research studies that WOA is good at exploring [
39] the search space but suffers from a slow convergence rate due to low exploitation ability while PSO don’t have good capability in exploring [
40] the search space but have good local search capability. the convergence speed of the algorithm. In [
41], the author proposed a chaotic WOA (CWOA) to improve maps utilized their dynamic behavior to prevent an optimization algorithm to trap in local optima and improves its global search capability. In [
42], the author proposed Levy flight trajectory based WOA (LWOA) to improve the accuracy and convergence speed of the algorithm. Levy flight allowed for the algorithm to get rid of local optima and prevents premature convergence.
There are certain complex and non-convex optimization problems that are not solved by continuous metaheuristic therefore, in [
43], the author proposed binary WOA (BWOA). In [
44], the author proposed a modified WOA that includes whale memory and new random search agent to enhance the exploitation capability of the algorithm. In [
45], the author improved the exploration capability of WOA and proposed three modified WOA which are based on opposition-based learning, exponentially decreasing parameters, and re-initialization of the worst particles. The hybridization of metaheuristic algorithms is another approach to improve the exploration and exploitation capability of population based stochastic algorithm. Furthermore, researchers have proposed hybrid approach grey wolf optimization (HAGWO) [
46], WOA-CBO (colliding bodies optimization) [
47], memetic-WOA (MWOA) [
48], WOA-SA (simulated annealing) [
39], WOA-MFO (moth flame optimization) [
49], Sine-Cosine (SC-WOA) [
50], WOA-PS (Pattern Search) [
51], and Brain Storm (BS-WOA) [
52,
53,
54] to improve the global and local search capability of WOA.
According to the literature survey, WOAPSO has not yet been implemented for the parameter extraction of the solar cell (and it cannot be used to establish a PV parameter estimation technique that can overcome all existing techniques). Therefore, this research paper aims to anticipate a new parameter estimation algorithm for solar cell/module. The novelty of the proposed study is that the exploitation capability of WOA is significantly improved by incorporating the exploitation capability of PSO with adaptive weight in sequential mode. As a result, equivalent circuit parameters converge equally good to the true values with minimum error. The proposed WOAPSO algorithm’s performance is measured based on convergence analysis, robustness, reliability, and statistical analysis for three PV models at diverse operating conditions.
The manuscript is organized as follows: the problem formulation and mathematical model for solar PV cell/module are presented in
Section 2.
Section 3 gives a brief introduction of the WOA, PSO, and proposed WOAPSO algorithm and discussed its implementation to estimate the optimized value of unknown parameters of a single-diode, double-diode, and PV module model. In
Section 4, the simulation results of the WOAPSO algorithm are discussed and compared with pre-existing metaheuristic algorithms. Finally,
Section 5 provides a conclusive remark to summarize the paper.
4. Discussion
To evaluate the reliability of the WOAPSO, the proposed hybrid algorithm is compared with six well established metaheuristics algorithms, i.e., GSA [
56], SCA [
57], GWO [
58], PSO [
59], WOA [
37], PSOGSA [
60] as well as other algorithms existing in the literature. It is observed that the estimated parameters based on the optimization process are highly consistent with the experimental data for SDM, DDM, and SS2018P PV module.
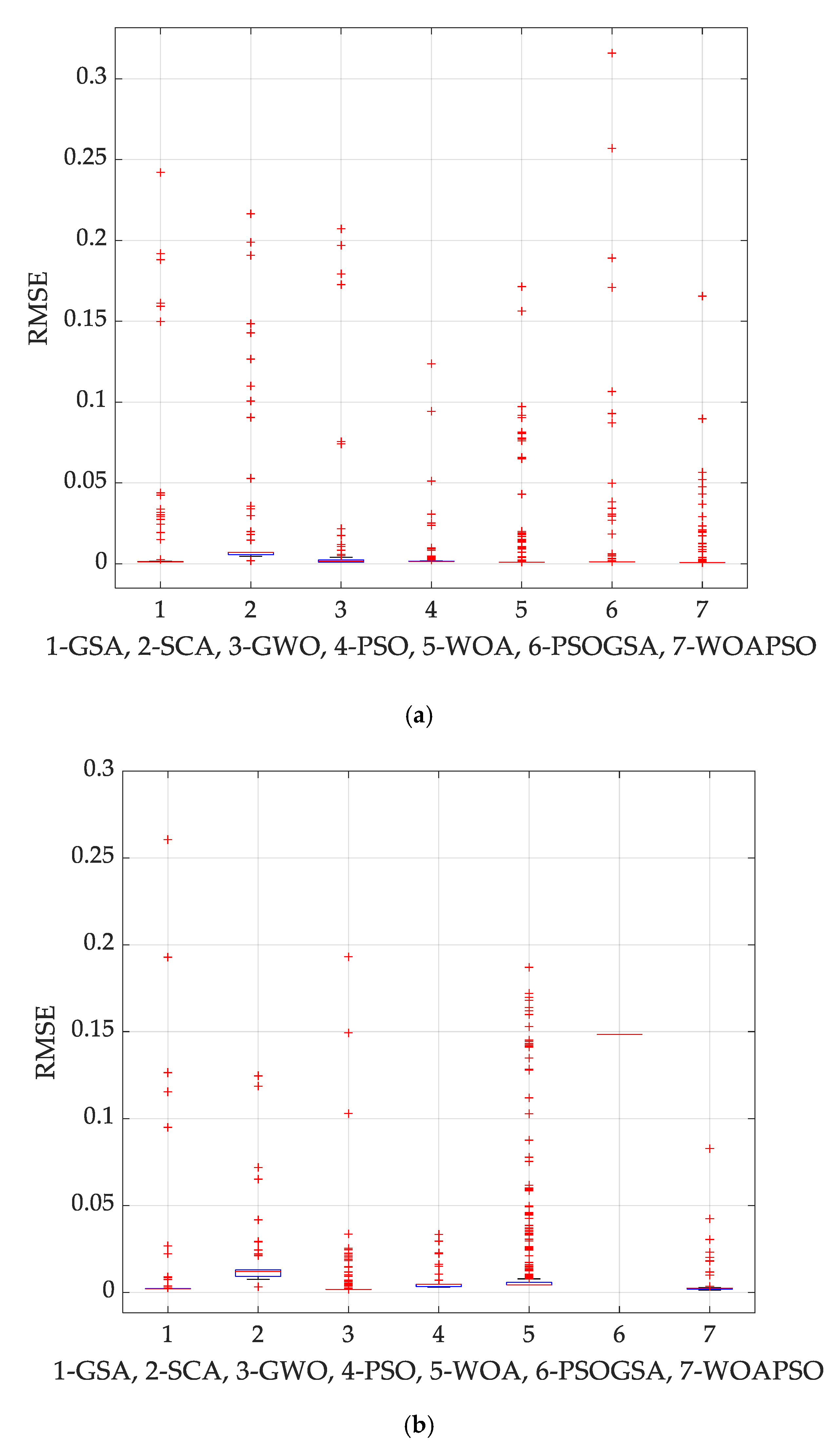
For SDM, the hybrid WOAPSO algorithm generates the lowest RMSE values (
) compared to the GSA, SCA, GWO, PSO, and WOA, PSOGSA algorithms (
Table 2). The RMSE of the proposed WOAPSO algorithm is also compared with previously studied algorithms (
Table S2). It is noted that the hybrid WOAPSO algorithm provides the lowest RMSE values than that of others.
Table S3 represents the absolute IAE for SDM analysis. The magnitude of IAE for different observations is less than 0.0018 (
Table S3), which indicates that the parameters optimized by the WOAPSO are very precise.
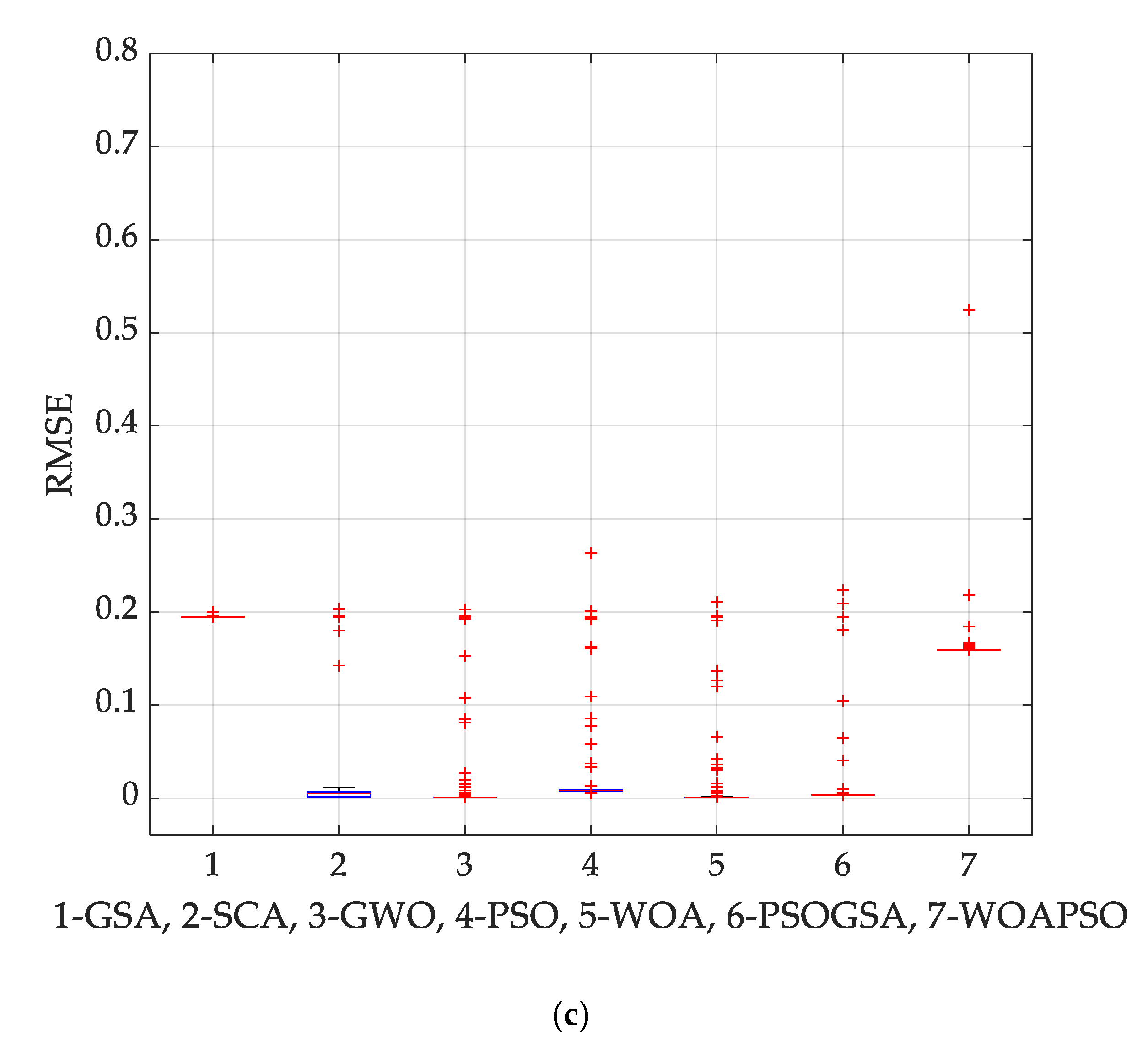
In the case of DDM analysis, the MLBSA, EHHO, IJAYA, and GOTLBO algorithms produce the best value of RMSE (
Table S4). However, WOAPSO generates the third-best value of RMSE (
), which is very close to MLBSA (
), EHHO (
), IJAYA (
), and GOTLBO (
). However, the computational cost in terms of function evaluation is 1/3 of MLBSA, EHHO, IJAYA, and GOTLBO. Moreover, WOAPSO shows superiority over other algorithms in terms of RMSE (
Table 3). For DDM, the magnitude of IAE for different observations is depicted in
Table S5. It is noticed that the IAE values are less than 0.0097, which demonstrates the accuracy of optimized parameters produced by WOAPSO.
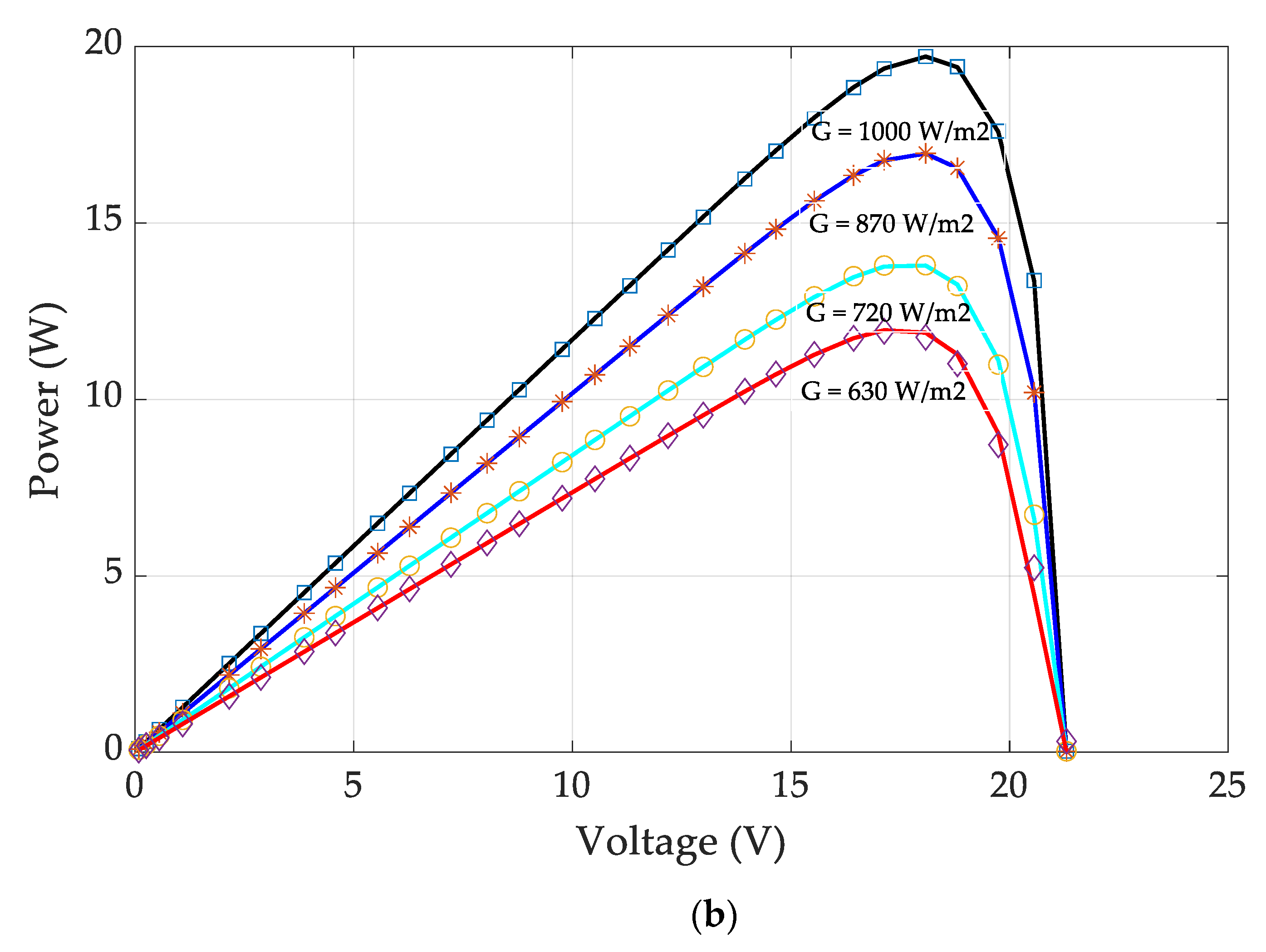
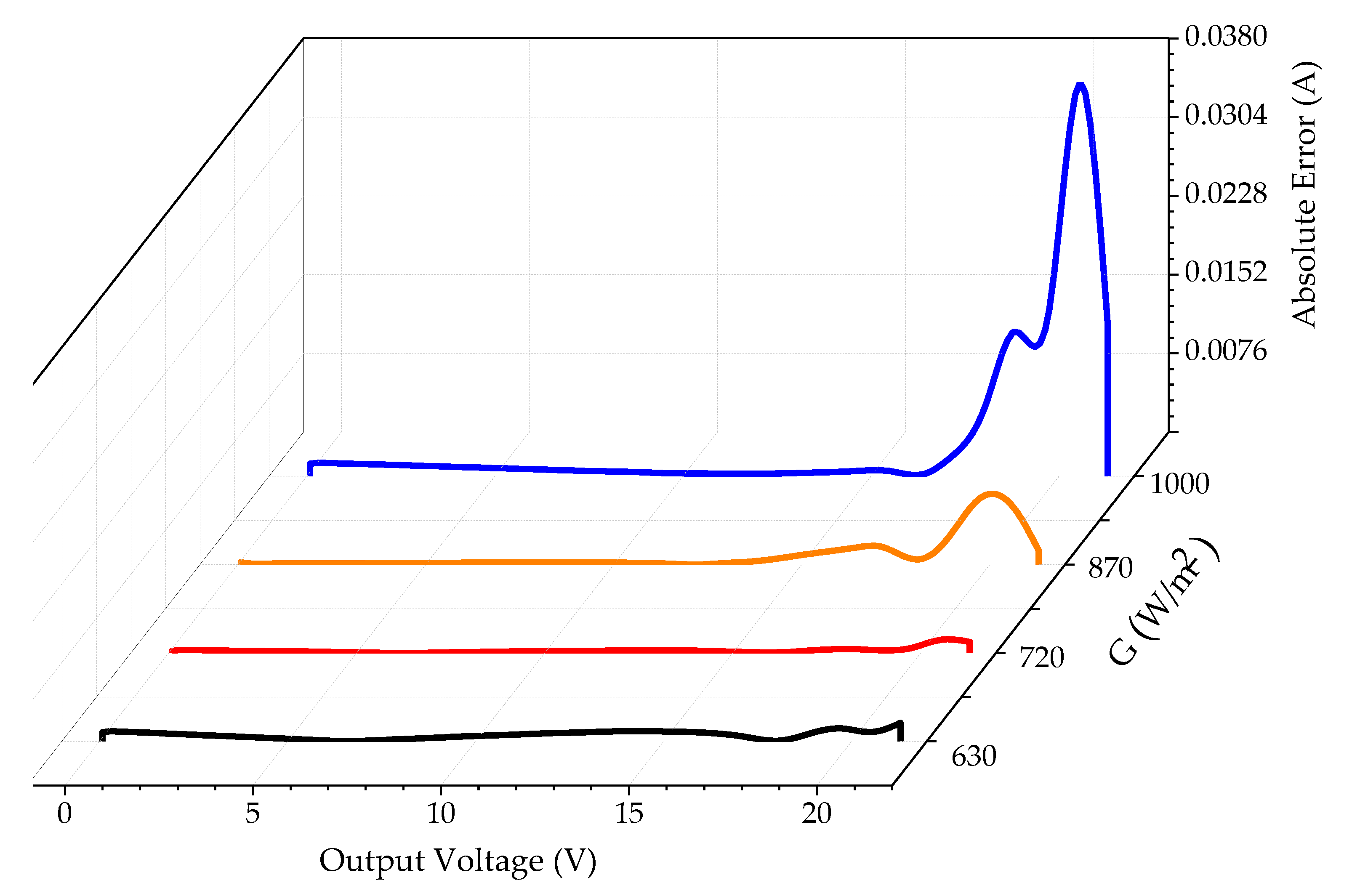
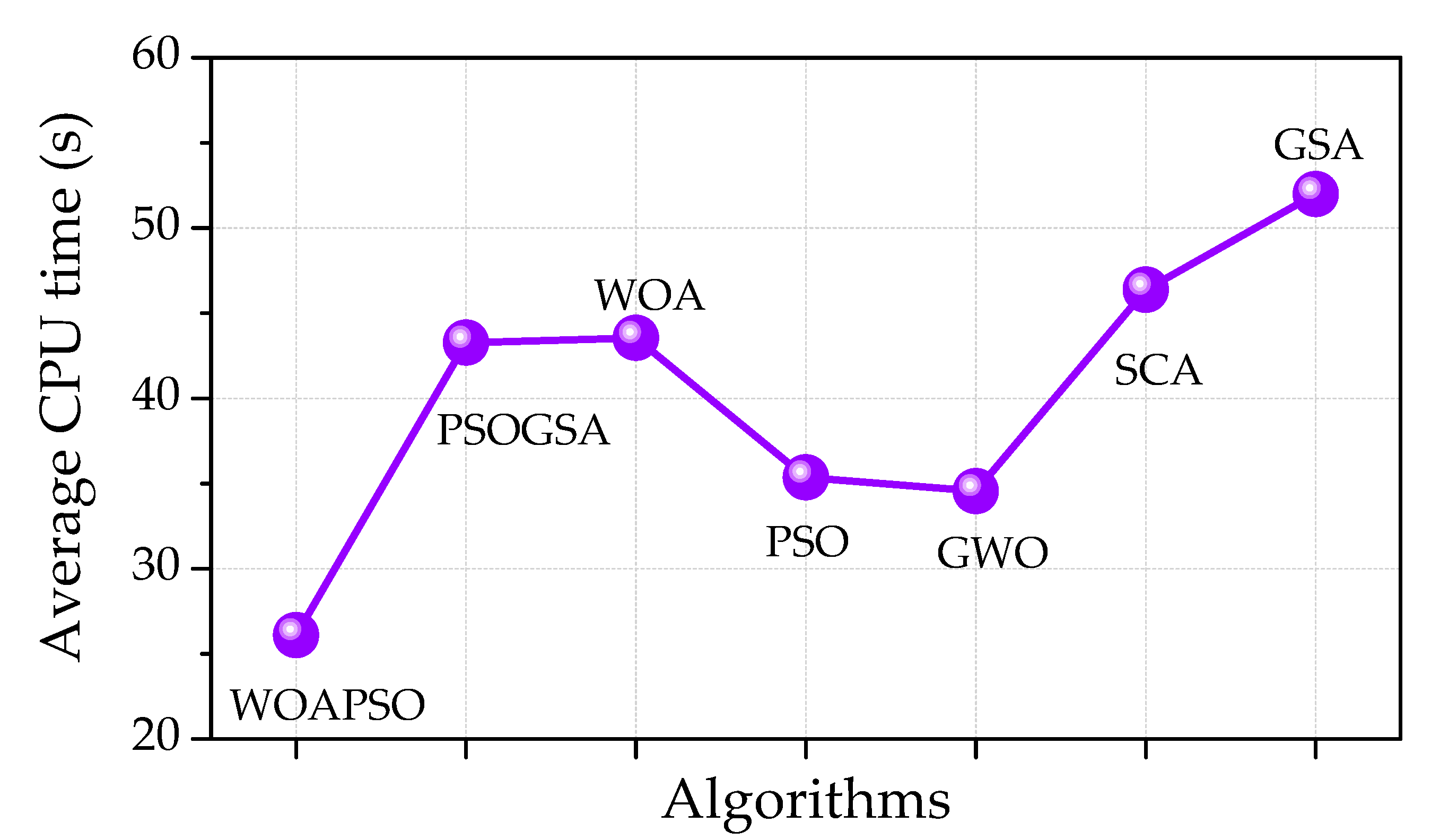
For the SS2018P PV module, the hybrid WOAPSO algorithm produces the lowest RMSE values compared to the GSA, SCA, GWO, PSO, WOA, and PSOGSA algorithms. The IAE magnitudes for different observations (at 1000 W/m
2) are less than 0.0018 (
Table S6). More importantly, the computational time for WOAPSO is less than other algorithms (
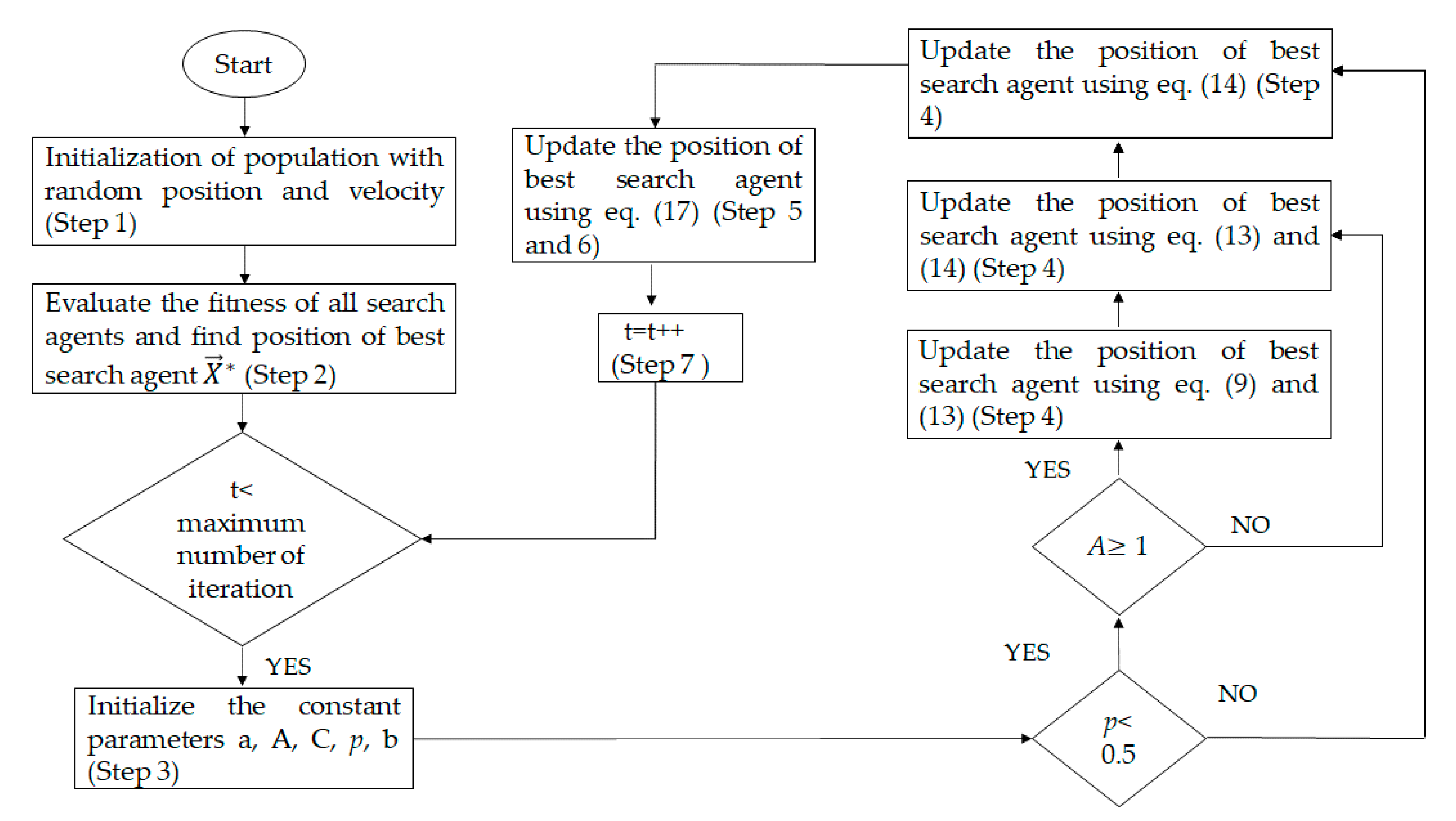
Table 4). The average execution time of each algorithm on the three PV models is calculated and illustrated in
Figure 9. The WOAPSO algorithm requires less time (about 26.1 s) than GWO, PSO, SCA, WOA, and PSOGSA, while GSA has the worst execution time of approximately 52 s.
Furthermore, the Friedman ranking test is also performed for all algorithms and depicted in
Table 6.
Table 6 shows that the proposed WOAPSO algorithm significantly outperforms the GSA, SCA, GWO, PSO, WOA, PSOGSA algorithms for all three models, i.e., single-diode, double-diode, and PV module models.
5. Conclusions
In this study, the hybridization of whale optimization and particle swarm optimization algorithm (WOAPSO) is anticipated. The exploitation ability of PSO is only implemented in pipeline mode when WOA stops to improve the best-found solution. The collaboration of both metaheuristic algorithms can establish an effective balance between exploitation and exploration ability. The proposed technique is further used to estimate the parameter of three PV cell models, i.e., single-diode, double-diode, and SS108P PV panel module model at different operating conditions. It should be noted that this suggested technique is, for the first time, intended to track the estimation of parameters for photovoltaic models reliably. The major conclusions are classified as follows:
The proposed WOAPSO is relatively accurate and reliable at delivering the solution in terms of RMSE as compared with other algorithms such as GSA, SCA, GWO, PSO, WOA, PSOGSA, and existing algorithms in the literature.
The I-V and P-V characteristic curves and IAE results indicate that WOAPSO can generate the optimized value of estimated parameters for all the models of solar PV cell as compared with other algorithms.
The statistical analysis clearly depicts the robustness of the proposed WOAPSO technique on parameter estimation problem at different operating conditions.
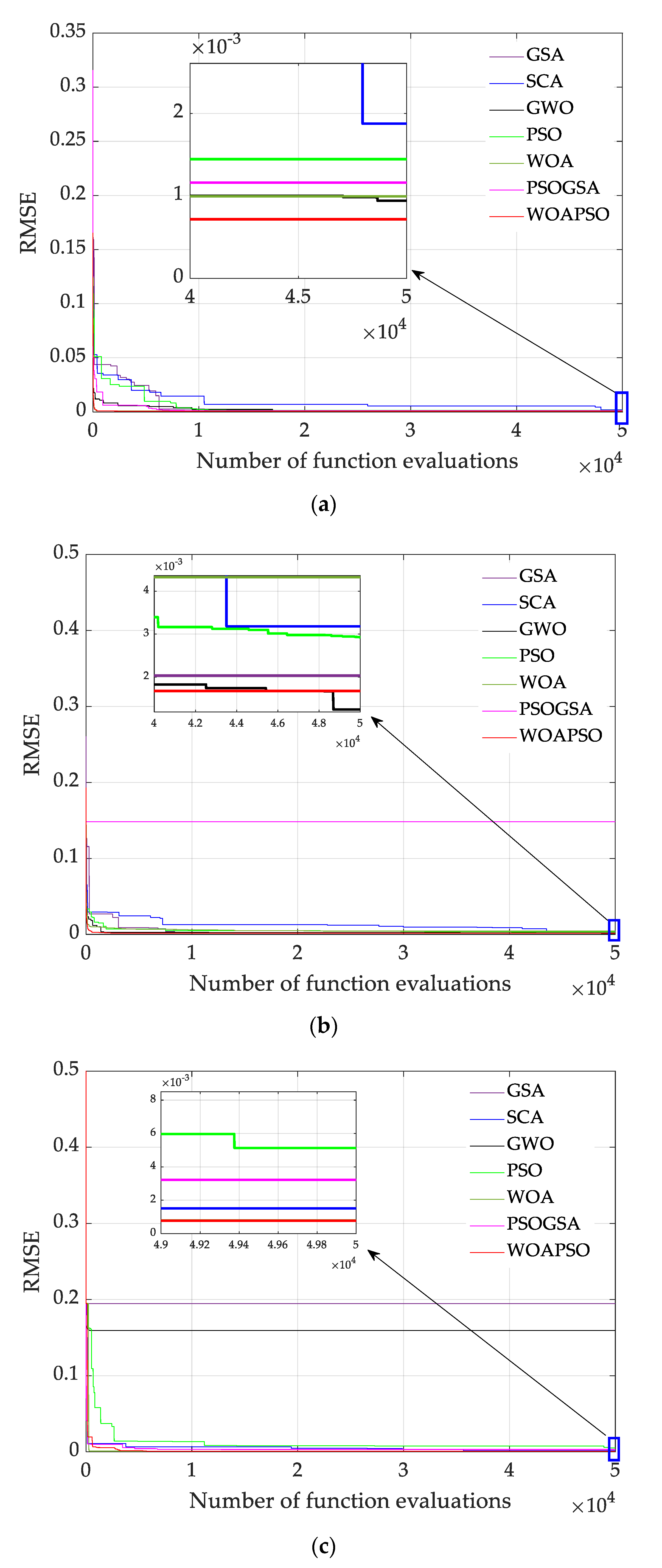
The convergence curves demonstrate that the best values of estimated parameters are obtained by WOAPSO, and RMSE is and in the case of single- and double-diode respectively.
At different irradiation levels (i.e., 1000 W/m2, 870 W/m2, 720 W/m2, and 630 W/m2), the proposed WOAPSO algorithm is best in producing optimized parameters (Ip, Isd, a, Rs, Rsh) and minimum value of RMSE for PV module even at a low level of irradiation (630 W/m2).
The proposed WOAPSO algorithm has limitation for DDM analysis. The RMSE value () of WOAPSO algorithm is lower than that of recently developed metaheuristics algorithms (MLBSA, EHHO, IJAYA, and GOTLBO algorithms).
The WOAPSO is an efficient and robust technique to estimate the unknown optimized parameters of the solar PV model at different operating conditions. For future study, the implementation of proposed WOAPSO to solve the other problems related to energy optimization such as economic load dispatch, energy scheduling and optimization of PV array configuration may also be interesting for scientists and research scholars.