Abstract
In this article, we present an analysis of the accuracy level of methods for modeling the multi-service overflow systems that service Erlang, Engset, and Pascal traffic. In systems with traffic overflow, new calls that cannot be serviced by the primary resources are overflown (directed) to other available resources that can service a given call, that is, to the secondary resources (alternative resources). In the article, we focus on studying the influence of methods for determining the parameters of traffic that overflows to the secondary resources on the accuracy of determining the traffic characteristics of overflow systems. Our analysis revealed that the main source of the inaccuracy of the existing methods is their approach to determining both the average value and the variance of multi-service Pascal traffic streams offered to the secondary resources. Therefore, we proposed a new method for determining the parameters of Pascal overflow traffic. The method is based on the decomposition of multi-service primary resources into single-service resources and the subsequent conversion of Engset and Pascal streams into equivalents of Erlang traffic. The results of the analytical calculations obtained on the basis of the new method are then compared with the results of simulation experiments for a number of selected structures of overflow systems that service Erlang, Engset, and Pascal traffic. The results of the study indicate that the proposed theoretical model has a significantly higher accuracy than the models proposed in the literature. The method can be used in the analysis, dimensioning, and optimization of multi-service telecommunication systems composed of separated resources, for example, mobile cellular systems.
1. Introduction
Traffic overflow is one of the oldest techniques for the optimization of traffic stream distributions in telecommunications and computer networks. The overflow mechanism is initiated in time intervals that correspond to the states of total occupancies of resources termed primary resources, historically primary group or direct group (Defining the resources of a network by the term “link group” originated from the construction of the first telecommunications networks, in which the basic resource was the link, with the link corresponding to a physical pair of cables linking, for example, telephone exchanges with one another. In this study, to describe the resources of present-day telecommunications networks, the term “network resources” is used, expressed in allocation units, for example, links, channels or basic bandwidth units [1]). In such states, new calls that cannot be serviced by the primary resources will be directed (will overflow) to other available resources that can service a given call at the time. The resources to which traffic overflows are called secondary resources or alternative resources, historically secondary groups or alternative groups.
Initially, traffic overflow was primarily used in single-service hierarchical telecommunications networks with traffic redirection through alternative routes [2,3,4,5]. An application of two or more levels of hierarchy in networks with traffic redirection through alternative routes largely led to the effective use of network resources satisfying at the same time the requirements of demanded service quality. The use of alternative resources also guaranteed easy adaptability of a network to changeable load conditions resulting from both changes in the intensity and structure of offered traffic and from damages to certain elements of the network (link groups, exchanges), without the costly necessity to develop and expand switching exchanges [6].
Today, the traffic overflow mechanism in telecommunications networks, defined as the so-called vertical call handover [7,8], is mainly used to optimize the use of resources that are offered by a number of different technologies that operate within the same area, as is the case with overlay networks [8,9]. As a result, a decision as to whether connections are to be redirected (overflow traffic) is frequently related not so much to the mobility of users but rather to the pursuit of operators to obtain required load (e.g., balanced/sustainable) for individual networks operating with different technologies or redirecting connections to resources that are optimal from a point of view of a service that is being executed (traffic class). It follows from the practice of many mobile network operators that for overlay networks, composed of picocells, microcells, and macrocells, one of the most frequently executed call admission policies is to treat cells with a larger range (macrocells) as cells that service traffic that could not be serviced in cells with a lower range (picocells, microcells) [7,9,10,11,12]. When this is the case, traffic redirected to a macrocell is then overflow traffic with different characteristics from traffic offered directly to the network by users [10,11]. In today’s circumstances, the traffic overflow mechanism is considered to be one of the most effective methods to balance (equalize) load in self-organizing (self-optimizing, self-configuring) networks [13,14]). The recent research studies show that the traffic overflow technique is often considered in 5G networks. The authors of [15] consider a system consisting of base stations encompassing both 5G millimeter-wave New Radio (NR) technology and Wireless Gigabit Alliance (WiGiG) technologies occupying a spectrum at 60 GHz. The authors assumed that NR users’ requests can be overflown to WiGiG technology. This overflow (off-loading) technique could also be used in 5G systems with network slicing [16,17].
The traffic overflow mechanism has also found its application in information technology (IT) systems as a strategy to increase the efficiency in data centers [18] and content delivery networks [19], among others. In the case of data centers, the two basic premises for the application of traffic overflow are equalization of load [19,20] and reduction of energy consumption [21,22,23]. Load equalization can be used both within the same center and between distributed data centers that are connected with one another using appropriate network technologies. The demands that arrive at a given data center can, when they coincide with intensified and increased load, overflow to another server (virtual machine) that is part of the data center’s infrastructure, or to another center within a distributed data center architecture (web-based solutions, cloud-based solutions). In the case of IT systems, the mutual overflow technique is more frequently used. This technique is appropriate for flat topologies, where network/systems are built with a certain number of primary resources without designating resources as secondary resources. In systems with mutual overflow, the request can be overflown (forwarded) bidirectionally between certain primary resources [24,25].
Many analyses of the effectiveness of the traffic overflow mechanism show that in traditional and modern telecommunications networks alike, both access and backbone networks, the traffic overflow technique has the advantage of increasing the reliability and use of network resources, as well as optimizing traffic distribution and improving the quality of service (QoS) and the quality of experience (QoE) in multi-service traffic streams, generated by end users [26,27,28,29].
To use the traffic overflow mechanism more effectively, it is necessary to develop analytical models of traffic overflow systems, in particular models of multi-service systems. The basic models of overflow systems with single-service traffic were developed in as early as the mid-20th century. The first studies on modeling multi-service systems with traffic overflow were initiated toward the end of the 20th century [30,31,32] and were soon further developed at the beginning of this century [28,33,34]. However, the above-mentioned studies were limited to modeling systems with PCT1 traffic streams (In traffic theory, offered traffic generated by an infinite number of sources (Poissonian call streams) is defined as PCT1 (Pure Chance Traffic of Type 1), while the model of a system that services such traffic streams—with the assumption that service time is exponential—is called the Erlang model. The term PCT2 (Pure Chance Traffic of Type 2), in turn, refers to traffic offered by a finite number of traffic sources (binomial distribution of call stream), that is, the type of traffic considered both in the Bernoulli model, in which the capacity of the system is higher than the number of traffic sources, and in the Engset model, in which the number of traffic sources of individual call classes is higher than the capacity of the system. In the literature, these terms are used interchangeably—PCT1 traffic or Erlang traffic streams, PCT2 traffic or Engset traffic streams.). The models of systems in which PCT2 traffic streams (Engset) and Pascal streams are also taken into consideration are proposed in [35]. The assumption in the latter study is that multi-service Engset and Pascal streams can be modeled by equivalent Erlang streams. The same assumption, however, leads to significant inaccuracies for Pascal streams.
The present study proposes a novel model of a multi-service overflow system to which a mixture of multi-service Erlang, Engset, and Pascal traffic streams are offered. To determine the parameters of overflow traffic, offered to the primary resources as Pascal traffic, a new method has been developed. This new method makes it possible to significantly increase the accuracy of determining the average value and variance of overflow traffic.
The rest of this article is divided into seven parts. Section 2 presents a review of research related to modeling systems with overflow traffic. Section 3 provides an outline of the subject of the study, that is, the multi-service overflow system with Erlang, Engset, and Pascal traffic. Section 4 examines a model of primary resources. In Section 5, the existing methods for determining the parameters of overflow traffic are analyzed, and a new method for estimating the average value and variance of Pascal traffic is proposed. A model of secondary resources is presented in Section 6. In Section 7, the results of the analytical calculations are compared with the results of simulation experiments for a number of selected structures of overflow systems with Erlang, Engset, and Pascal traffic. Section 8 sums up the article.
2. Related Work
Analytical modeling of overflow networks (overflow systems) is a complex problem. The division of resources into primary and secondary resources leads to a significant change in the characteristics of traffic streams that overflow from the primary resources and are offered to the secondary resources, thus preventing the PCT1 (Erlang) model or the PCT2 model from being applied. Unlike PCT1 traffic, which can be fully described by the average value of traffic intensity, overflow traffic requires many more parameters.
The analytical models of overflow systems published in the literature involve both single-service and multi-service systems. Single-service traffic overflow systems have been addressed in many analyses presented in the literature, for example in [3,4,5,36,37,38]. The basic mathematical models for overflow systems with single-service traffic were developed as early as the mid-20th century. These models were further expanded into three groups of methods for analyzing overflow systems, that is, methods based on the analysis of state equations resulting from the service process in the system [39,40,41], methods based on the analysis of the state space of the service process [3,5,37] and methods based on the analysis of the call admission process [36,42].
The methods modeling overflow systems that are commonly and widely used in engineering applications typically belong to the group of methods based on the analysis of the state space on account of their high accuracy and accompanying low complexity resulting from a description of the overflow traffic stream that is reduced to just its first two moments. In the three best known methods in this group, presented in [3,5,37], the following two parameters are used to describe the traffic stream offered to the secondary resources—the average value and the variance. Methods of this group are still used in modeling modern telecommunications systems. For example, in [15,43], the traffic overflow phenomenon is considered in the context of fifth-generation (5G) millimeter-wave networks. In [43], the authors analyzed the performance metrics of mobile traffic overflown from one base station to another. As the main metric, they used the blocking probability, which was defined as the proportion of user requests that cannot be served by any of the neighboring base stations due to either physical-layer blocking or capacity-limited blocking. To determine physical-layer blocking the authors applied line-of-sight model [44], while in order to determine capacity-limited blocking they applied the Erlang B formula [45]. The request blocked in the base station of the first choice form the overflow traffic offered to subsequent neighboring base stations. The parameters of the overflow traffic are determined according to the Erlang fixed-point approximation method. The model elaborated in [43] does not offer the possibility of calculating blocking probabilities individually for different traffic streams, with different requirements.
The authors of [15] consider a system consisting of base stations encompassing both 5G millimeter-wave New Radio (NR) technology and WiGiG technologies occupying spectrum at a 60 GHz, known as NR-U (New Radio Unlicensed). They assumed that user requests that cannot be serviced with a given bitrate at the NR part of the NR-U base station can be overflown to the WiGiG technology (depending on the technology implemented in user equipment). Using an M/G/K/K model to service processes of NR-U sessions at the NR part of NR-U base station, the authors were able to determine the fraction of load that NR-U cannot handle in the licensed spectrum using the NR part of the NR-U base station [15]. However, the model proposed in [15] does not take into account the difference in the volume of required resources by different traffic streams—only the minimum bitrate is considered.
The problem of multi-service traffic overflow in telecommunications networks has been addressed in many studies. Typically, the most convenient models for the analytical modeling of traffic characteristics of multi-service networks with traffic overflow are the so-called multi-rate models. The basic multi-rate models were initially developed for wired systems (networks) with integrated (multi-rate) services—ISDN (Integrated Services Digital Network) and B-ISDN (Broadband ISDN) [46,47,48,49]. Currently, they are also used to model wireless multi-service telecommunications systems [50,51,52]. The initial assumption in multi-rate models is that the resources demanded by calls of particular traffic classes are a multiple of the so-called allocation unit (AU), which can be defined as the greatest common divisor of the resources demanded by calls of all traffic classes offered to the system. Depending on the multi-service multi-rate system (multi-service systems, systems with integrated traffic) under investigation, the AU can refer to both bitrate and other physical quantities that limit the resources of a system.
In research on modeling multi-service overflow systems, models based on an analysis of the call admission processes are predominant (the methods based on the analysis of the call admission processes are characterized by exponential computational complexity, since they require—to determine moments—solutions to state equations related to the multi-dimensional Markov process that takes place in the system under consideration). The interrupted Poisson process [IPP], the Markov-modulated Poisson process [MMPP]) [31]), and methods based on an analysis of the state space of systems are under consideration. These methods are in fact extensions of existing solutions for single-service systems and take into consideration the influence of traffic streams with different parameters (call intensity, service time, the volume of demanded resources) and their mutual correlation.
The first effective methods to model and dimension multi-service overflow networks were proposed between 2007 and 2008, in [28] and concurrently in [34]. In [28,34], the primary resources are described by a model of a full-availability resource, that is, a state-independent model, in which a call will be admitted for service if the system has enough free resources to service this call. The solutions proposed in [28,34] make it possible to determine in a simple way the variance and intensity of traffic that overflows to alternative resources. To determine the traffic characteristics of the alternative resources that service overflow traffic, in [28,34] a modified full-availability group model, modified according to the approach proposed by Hayward [5] for single-service systems, is used. In this model, both the capacity of the full-availability group and the values of offered traffic intensities for individual classes are divided by appropriate peakedness coefficients. An alternative analytical model, one that also assumes full availability of the primary resources, is proposed in [53]. This model is based on an appropriately defined, bi-dimensional convolution operation and allows overflow systems with any type of traffic offered to the primary resources to be modeled. The models in [54,55,56] consider overflow systems in which overflow traffic changes the service parameters, such as service time and bitrate, in the secondary resources. The assumed changes in the parameters were not, however, linked to any network traffic shaping mechanisms. Over time, the model in [28] for multi-service overflow systems, based on the Fredericks–Hayward approach, was successively expanded. Subsequent studies considered, among others, (i) limited availability of the secondary resources [57], (ii) thresholdless compression (elastic traffic) [58], (iii) threshold compression (adaptive traffic) [35], and (iv) multi-service Erlang, Engset, and Pascal traffic streams [35,59].
The approach to modeling multi-service overflow systems used in the above studies includes three stages: Stage 1, which involves the development of a model of the primary resources; Stage 2, which includes the determination of the parameters of overflow traffic; and Stage 3, which involves the determination of the traffic characteristics of alternative resources. Although there is extensive literature on several solutions to the problems of the first and third stages, the main problem—concerning a determination of the parameters of traffic that overflows from primary resources that service multi-service mixtures of Erlang-Engset-Pascal traffic—still has only rough solutions.
This article aims to analyze the accuracy of determining the parameters of overflow traffic, in particular the accuracy of the calculations of traffic streams of multi-service Pascal traffic, and to develop a new and significantly more accurate method for determining the parameters of overflow traffic.
Further on in the article, a scheme of traffic overflow and a model of primary and secondary resources will be briefly described, and a new method for determining the traffic parameters of overflow traffic for multi-service Pascal streams will be proposed. This method will allow the accuracy of modeling traffic overflow systems to be significantly increased.
3. Scheme of Traffic Overflow under Consideration
This article considers an overflow system in which calls of different traffic classes are redirected to a system of secondary resources when the primary resources are fully occupied. When all secondary resources are also occupied, calls will be lost. Figure 1 shows a general scheme of the traffic overflow system.
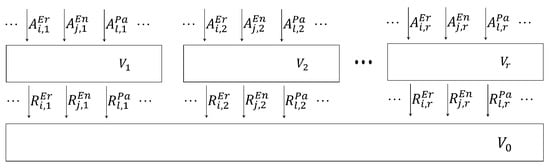
Figure 1.
Scheme of the multi-service overflow system.
The primary resources of the system shown in Figure 1 are composed of r components, where each resource s has a capacity , expressed in allocation units (AUs). The secondary resource has the capacity of the server, namely AUs.
This system is offered traffic streams generated by three types of traffic sources considered in traffic theory, that is, Erlang, Engset, and Pascal sources. Each of these traffic types is related to different call streams, described by the flow intensity (call arrival) and the number of demanded AUs. The assumption in the figure is that a primary resource s is offered traffic classes from the set , where classes that belong to the set are Erlang, classes that belong to the set are Engset, and classes that belong to the set are Pascal traffic classes, with , and . The parameters of the input traffic are described by the parameter , that is, the average traffic intensity of class c () type X () offered to the primary resource s that is in the occupancy state n AUs, and by the parameter , that is, the number of AUs demanded by a call of class c for service.
Traffic that cannot be serviced by a given resource s is offered to shared secondary resources with a capacity . This traffic is described by the parameter that determines the volume of demanded AUs in the secondary resources (the parameter ) and by the parameters that describe the probabilistic properties of these streams, that is, the parameter that determines the average intensity for traffic of class c () that overflows from the primary resource s, with the assumption that traffic of class c offered to the primary resource s is of type X (), and the parameter that determines the variance of traffic of class c of type X that overflows from the resource s of the system of primary resources.
4. Model of Primary Resources
In this article, to model the components of the primary resource, a recursive occupancy distribution is used [60]. In line with the notation adopted in this article, for Erlang, Engset, and Pascal traffic this distribution can be written in the following way:
where the distribution determines the occupancy probability n AU in the primary resource s with the capacity of the resource . In Figure 1, denotes the value of Erlang traffic, whereas the values of Engset (), and Pascal traffic (), offered to individual primary resources s, are determined on the basis of the following dependencies [61]:
where:
- indexes for call classes of Erlang, Engset, and Pascal traffic, respectively,
- average traffic intensity of class j for Engset traffic generated by one free source in the resource s,
- average traffic intensity of class l for Pascal traffic generated by one free source,
- the number of traffic sources of class j of the Engset type, related to the primary resource s,
- the number of traffic sources of class l of the Pascal type, related to the primary resource s,
- the number of traffic sources of class j of the Engset type, serviced in the occupancy state n AU of the primary resource s,
- the number of traffic sources of class l of the Pascal type, serviced in the occupancy state n AU of the primary resources s.
The blocking probability in such a system results from the finite capacity of the resource and can be determined for calls of class c by the following formula:
Formula (4) determines the sum of the blocking states for calls of class c, that is, those states in which the number of free AUs in the resource is lower than the number of AUs demanded to set up a connection of class c.
5. Model of Traffic That Overflows from Primary Resources
The effects of blocking of calls of individual traffic classes in primary resources lead to traffic overflow, with these surplus calls overflowing to a shared secondary resource with a capacity . With the computationally effective methods for modeling multi-service overflow traffic that have been developed so far [28,34], the assumption was that overflow traffic could be characterized by two parameters—the average value and the variance . The accompanying assumption was that to determine the value of these parameters, Riordan’s formulas could be used [3], developed for single-service systems, in which the primary resources were offered single-service Erlang traffic streams. These formulas, for single-service systems with Erlang streams, take on the following form:
where Z is a peakedness coefficient, A denotes the value of offered single-service traffic, denotes the variance of offered traffic, and is the value of blocking for a traffic stream with the intensity A.
Formula (5) is intuitively evident, since it is only traffic that is lost in the primary resource that can be offered traffic and, at the same time, can be serviced by a secondary resource. It should be noted that for (zero capacity of the primary resource), , which was to be expected, since the total traffic is directed to the secondary resource. Therefore, for each value of the parameters A and V of the full-availability resource, it is possible to unequivocally determine the parameters of overflow traffic R and .
The assumptions of the single-service nature of the systems and the presence of Erlang traffic adopted in Riordan’s formulas mean that they cannot be used directly in modeling multi-service systems with Erlang, Engset, and Pascal overflow traffic. A necessary adaptation of a model of a system with multi-service overflow traffic must therefore include a stage in which of the resource s that services traffic classes of multi-service traffic is decomposed into fictitious resources, each of them designed to service only one traffic class (a reduction to a single-service system), and a stage in which Engset and Pascal streams are changed into certain equivalents of Erlang traffic. Further on in the article, an analysis and review of existing methods for executing these stages will be provided, and new methods that significantly increase the accuracy of calculations, in particular for modeling Pascal traffic streams, will be proposed.
5.1. Methods for Determining the Parameters of Overflow Traffic
In [28,34], two different methods for the decomposition of primary resources are proposed. One method is based on the serviced traffic matching criterion [28], the other one on the blocking probability matching criterion [34]. In the method based on the matching criterion for serviced traffic, the capacity of the fictitious resource is defined as the part of the real resource that is not occupied by calls of the remaining classes (different from class c). Therefore, we obtain
where is the average number of calls of class c serviced in the resource s. According to the definition of the intensity of serviced traffic,
With methods based on the matching criterion of the blocking probability, to determine the capacity of the fictitious resources, the assumption was that the blocking probability for calls of class c in the fictitious resource with capacity is the same as the blocking probability for calls of this class in the primary resource s with capacity :
The above method, proposed in [34] initially for Erlang traffic streams, was then expanded in [35] to include systems with Erlang, Engset, and Pascal traffic streams.
In keeping with [35], to determine the capacity of the fictitious primary resource , the assumption is that the blocking probability for calls of class c of type X in the fictitious primary resource with capacity is the same as the blocking probability for calls of this class in the primary resource s with capacity :
The method for the decomposition of the primary resource s into fictitious primary resources and equivalent fictitious primary resources is presented in Figure 2.
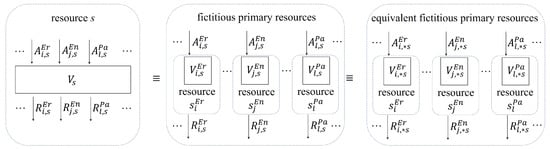
Figure 2.
Decomposition of the primary resource s into fictitious primary resources and equivalent fictitious primary resources.
We should note at this point that on the basis of Formula (4) that it is possible to determine the blocking probabilities for the individual traffic classes offered to the primary resource s. It follows from the assumption expressed by Formula (11) that the obtained blocking probabilities are the same as the probabilities for the matching fictitious primary resources. Since each resource services only one traffic class, the capacities of the decomposed fictitious primary resources can be determined on the basis of single-service full-availability models for Erlang, Engset, and Pascal traffic. In these models, it is possible to determine the blocking probability as the occupancy probability of all AUs:
In this way, the capacities of the fictitious resources to which single-service Erlang, Engset, and Pascal traffic is offered can be determined on the basis of appropriate formulas that determine the blocking probability in the Erlang, Engset and Pascal model:
Formulas (13)–(15) deal with single-service systems, in which admission of a new call denotes the occupancy of a single AU.
In keeping with [35], the next step in the decomposition of the primary resource s was to change the fictitious primary resource , servicing Engset or Pascal traffic, into an equivalent fictitious primary resource that services equivalent Erlang traffic. Equivalent Erlang traffic and is such traffic offered to certain fictitious additional resources with capacities , that overflows from these resources is equal, with regard to the average value and variance, to Engset traffic and Pascal traffic . Note that in the notation of the equivalent traffic, for example, in , the symbol En, which indicates the primary nature of this traffic, has been preserved in the superscript. The asterisk inserted into the subscript indicates that it is already equivalent Erlang traffic. For primary Erlang traffic, we then have , , and .
The parameters of the equivalent fictitious primary resource can be determined on the basis of the equivalent random technique (ERT) method [35]. Average values and variances of Erlang, Engset and Pascal traffic can be determined on the basis of the following dependencies:
- –
- Erlang traffic:
- –
- Engset traffic:
- –
- Pascal traffic:
In keeping with the ERT method, the average value R and the variance of traffic that overflows from the primary resource with capacity V to which traffic A of the Erlang type is offered can be determined on the basis of Riordan’s Formulas (5) and (6). In the traffic change scheme under consideration, the group with capacity is offered equivalent traffic of the Erlang type with intensity . From this group, traffic overflows with the average value and the variance . Therefore, in the notation adopted for this article, Riordan’s formulas can be written in the following way:
Formulas (19) and (20) allow us to determine the parameter pair (, ) on the basis of known values of the parameter pair (, ), which depending on the type of traffic under consideration, can be described by Formulas (16)–(18). Following the determination of the value of the parameters (, ), it is possible to estimate the capacity of the equivalent fictitious primary resource , that is, the parameter [3]:
Note that the parameter pair (, ) for each of the equivalent fictitious primary resources is determined by the Erlang model for a full-availability group [41].
Overflow traffic of class c that overflows from the primary resource s is equivalent to traffic that overflows from the equivalent fictitious primary resource and will be characterized by two parameters: the average value of traffic intensity and the variance . Since the equivalent fictitious primary resource is determined by a single-service Erlang model, the parameters and can be determined on the basis of Riordan’s formulas and, in the adopted notation, will take on the following form:
The peakedness coefficients (factors) of traffic of class c that overflows from the equivalent fictitious primary resource are defined as the ratio between the variance and the average value:
5.2. Accuracy Analysis of Glabowski-Kmiecik-Stasiak 2018 Method for Determining the Parameters of Overflow Traffic
The method for determining the parameters of overflow traffic in [35], based on the concept in [54], was subjected to in-house validation experiments. As a result of our simulation studies, we established that the main element of the method in [35] that influenced its inaccuracy was the procedure by which Pascal traffic classes were changed into equivalent classes of the Erlang type [62]. The problem is that both the average value and the variance of traffic offered to the primary resources, described by Formula (18), take into consideration the following dependency:
We note that in the above dependency, the value of traffic offered by one free source = 1 returns a value that is not allowed. An increase in , within the range , leads to an exponential increase in the above dependency, followed by negative values that tend toward zero, so that this range will be exceeded. Values exceeding the range in question, that is, for > 1, in successive stages of changing the fictitious resources into equivalent fictitious resources (Section 5.1), will cause the evaluation of the average value of overflow traffic to be near 0. To visualize the error in the determination of the average value of overflow traffic and its relation to and dependency on the average intensity of traffic offered by one free traffic source of the traffic class analyzed, Figure 3, Figure 4, Figure 5 and Figure 6 show the relative error between the analytical and the simulation results for two exemple systems (Table 1), with specific values of assigned to a given class.
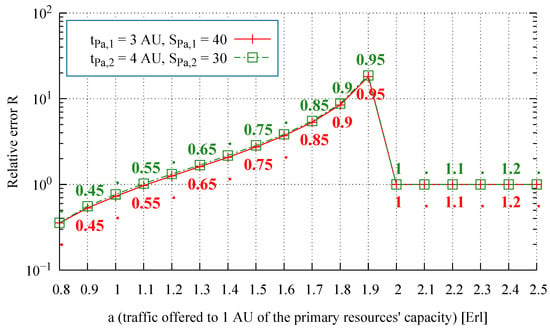
Figure 3.
Relative error of the average value of overflow traffic, System 1, Resource 1 ( values specified directly in the figure).
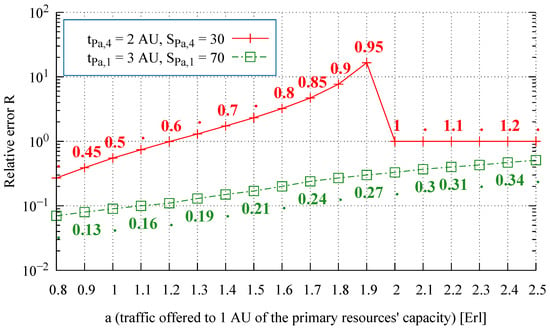
Figure 4.
Relative error of the average value of overflow traffic, System 1, Resource 2 ( values specified directly in the figure).
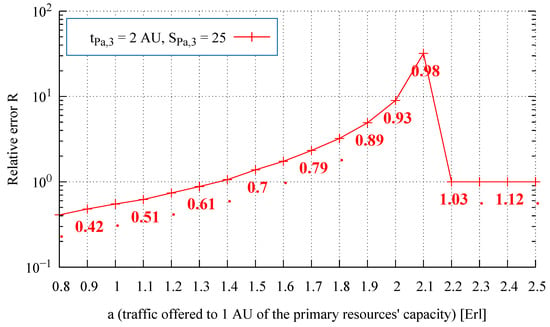
Figure 5.
Relative error of the average value of overflow traffic, System 2, Resource 1 ( values specified directly in the figure).
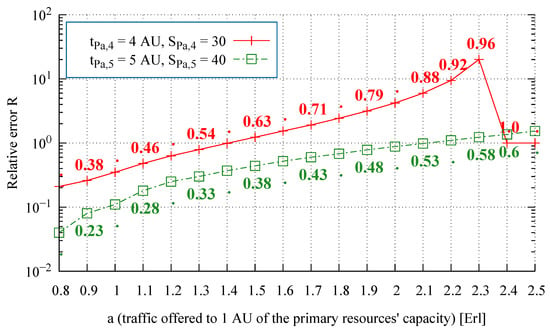
Figure 6.
Relative error of the average value of overflow traffic, System 2, Resource 2 ( values specified directly in the figure).

Table 1.
The parameters of the multi-service systems.
On the basis of numerous studies and their results presented in Figure 3, Figure 4, Figure 5 and Figure 6, one can observe that along with an increase in traffic offered to one AU of the primary resources, the relative error of the analytically obtained average value of overflow traffic R also increases, which is followed by a decrease in the accuracy of the analytically determined values. This increase is maintained for < 1.
5.3. New Method for Determining the Parameters of Multi-Service Overflow Systems
The analysis of the factors that decrease the accuracy in modeling systems with multi-service overflow traffic prompted us to develop a new method for the decomposition of primary resources that would help determine the first two traffic moments of traffic that overflows to the secondary resources. In order to present the most important results of this method, we note that for each class c that is serviced in the primary resource s, the difference between the average intensity of traffic and the value of carried traffic is the average value of the intensity of traffic that overflows from this resource:
At the same time, the value of can be estimated as the part of offered traffic that is moved to the resource s when calls of class c are blocked:
where is the blocking probability for calls of class c of type X in the primary resource s (Formula (4)). The value of this probability can be determined on the basis of the method in [60]. At the same time, this method allows the average value of carried traffic of class c of type X in the resource s to be precisely determined.
Having accurate values of and and using Formulas (26) and (27), we can determine, for any traffic type X, the value of the equivalent Erlang traffic that leads to the same value of carried traffic of type X:
The average value of offered traffic , determined by Formula (28), defines the first parameter of the parameter pair (, ) for the equivalent fictitious primary resource . The other parameter from the pair of parameters is determined by a juxtaposition of the blocking value , determined on the basis of Formula (4), and the values that result from the Erlang B formula (Formula (13)). After taking into consideration the description of the parameter pair of the equivalent fictitious primary resource, the dependency that results from Formula (13) can be written in the following form:
Thus, the values of the average value parameters of offered traffic and the capacity allow us to determine, using Riordan’s Formulas (22) and (23), the average value of traffic that overflows to the secondary resources as well as its variance .
The discussed model was incorporated into a method based on the matching criterion for the blocking probability, and its accuracy was validated by simulations for many configurations of overflow systems.
6. Model of Secondary Resources
As a result of the decomposition operation and the change of the primary resources into equivalent fictitious primary resources, the overflow traffic streams, initially generated according to Erlang, Engset, and Pascal distributions, are characterized by the following parameters: the average value of traffic intensity , the variance , and the number of AUs required for a given connection to be set up. These streams are offered to a system of secondary resources with a server capacity of AU.
To model the occupancy distribution in multi-service secondary resources to which a mixture of overflow traffic is offered, Hayward’s approach can be applied [28]. This approach is based on a division of the parameters of the secondary resource system (traffic intensity and capacity) by the peakedness coefficients of offered traffic. As a result, the occupancy distribution in the system of secondary resources, using the adopted notation, can be written as follows:
In Formula (30), the parameters of the traffic that overflows from the primary resources are determined by Formulas (22)–(24). The parameter Z is the aggregated peakedness coefficient [59]
The blocking probability for traffic of class c in the secondary resources (regardless of which primary resources this traffic overflows from) is equal to:
To sum up the above considerations, the method for calculating the blocking probability in multi-service overflow systems to which Erlang–Engset–Pascal traffic is offered can be presented as follows:
- Determination of the occupancy distribution in the primary resource s, where —Formula (1).
- Determination of the blocking probability for traffic streams of all classes in the primary resource s, where , —Formula (4).
- Determination of the capacity for each fictitious primary resource —Formula (13).
- Determination of the capacity for each fictitious primary resource —Formula (14).
- Determination of the variance of Erlang traffic offered to the primary resource—Formula (16).
- Determination of the variance of Engset traffic offered to the primary resource—Formula (17).
- Determination of the aggregated peakedness coefficient Z—Formula (31).
- Determination of the occupancy distribution in the system of secondary resources—Formula (30).
- Determination of the blocking probability for traffic streams of the classes offered to the system of secondary resources—Formula (32).
The main innovation of the method proposed in Section 5.3 and Section 6, in relation to the existing methods, including the method in [35], is the development of a new method for the decomposition of primary resources that can help determine the first two traffic moments of traffic that overflows to the secondary resources (the decomposition of primary resources is necessary to determine the variance of the multi-service traffic overflowing from the primary resources—Section 5.1). The developed method (Section 5.3) is dedicated to Pascal streams, for which the existing methods led to large calculation errors. These errors resulted from Formula (18) to determine the values and of Pascal traffic streams, used to determine the equivalent resource capacity. The applied formula made it impossible to determine the average traffic value and the variance of traffic offered by a single source, (denominator of Formula (18) equal to 0). At the same time, this formula failed to properly account for the increase in Pascal traffic intensity with the number of sources being served, and thus for the increase in overflow traffic associated with Pascal streams. As a consequence, the new method proposes that the value of equivalent traffic (related to Pascal classes) will be determined on the basis of the value of the overflow traffic, and not—as in the method in [35]—on the basis of information about the number of Pascal sources and their intensity (Formulaes (26)–(28)). This approach allowed us to obtain a much greater accuracy in determining the variance of the overflow traffic and, consequently, in determining the probability of blocking in secondary resources (a comparison of the accuracy of both methods is presented in Section 7). The new method of determining the parameters of traffic flowing to the secondary resources (Section 5.3) did not require changes in the general approach to determining the value of the blocking probability in secondary resources (Section 6), in relation to the method proposed in [35]. The only change introduced in the proposed method compared with to the method proposed in [35] is the procedure for determining the aggregated peakedness coefficient. The new method leads to less computational complexity.
7. Results of Modeling a Selected Number of Overflow System with Erlang–Engset–Pascal Traffic
The analytical method for modeling telecommunications systems with Erlang, Engset, and Pascal traffic overflow presented in this article is an approximate method. To evaluate its accuracy, the results of the analytical modeling were compared with the data obtained in the simulation experiments. The model accuracy was verified in a simulation tool designed by us. The Microsoft.NET programming platform was chosen to build the simulator. It allows the application to be executed on all devices with Microsoft operating systems. For the development of the simulator the C# language was chosen because of its efficiency and rich library resources. The program interface was designed in the WPF (Windows Presentation Foundation) structure in the XAML language, and its code was separated from the functional code according to the MVVM (model-view-view-model) architectural pattern. Building our own simulator allows us to examine the operation of the models as accurately as possible and allows for high flexibility of system construction.
The results of the simulation studies for three example overflow systems, whose parameters are given in Table 1 (Systems 1 and 2) and Table 2 (System 3), are shown in Figure 7, Figure 8 and Figure 9.

Table 2.
The parameters of the multi-service systems.
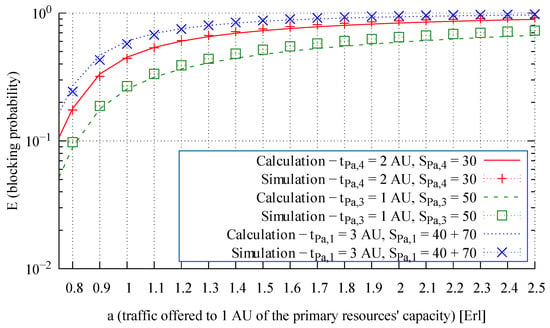
Figure 7.
Blocking probability of particular traffic classes in the alternative resources of System 1.
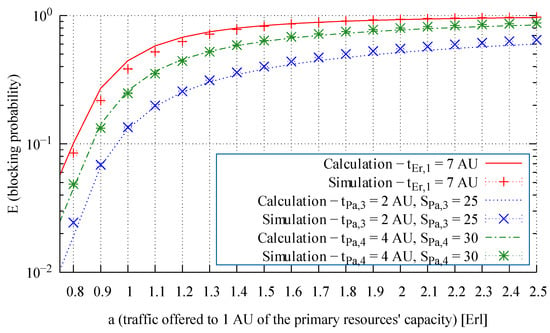
Figure 8.
Blocking probability of particular traffic classes in the alternative resources of System 2.
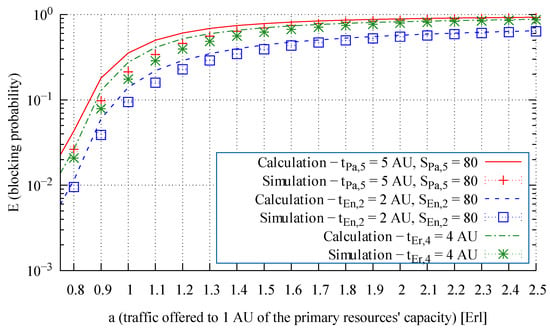
Figure 9.
Blocking probability of particular traffic classes in the alternative resources of System 3.
According to the general scheme of traffic overflow (Section 3), requests, the parameters of which are given in Table 1 and Table 2, are first directed to the primary resources, where an attempt is made to handle them. If there are not enough free resources to handle a given request, it is redirected to the secondary resources. If the current state of the secondary resources also does not support the request, it is lost.
In Table 1 and Table 2, the amount of resources requested by the calls of individual classes is marked as , where X stands for the type of traffic () and No. is the number of the traffic class. For Engset and Pascal traffic classes, the tables provide information on the number of sources generating traffic streams of a given class (parameters and , respectively). For Erlang traffic classes, the information about the number of traffic sources is not provided because these sources are assumed to be unlimited (infinite).
System 1 services exclusively Pascal traffic classes, while Systems 2 and 3 service Erlang–Engset–Pascal traffic classes. System 1 is composed of two primary resources with a capacity of AUs and AUs, and a secondary resource with a capacity of AUs. Only traffic from Pascal-type classes is offered to System 1. In System 2, the primary resource with a capacity of AUs supports all three types of traffic, that is, Erlang, Engset, and Pascal, while the other primary resource with a capacity of AUs supports only Pascal traffic flows. The secondary resource of System 2 has a capacity of AUs. In System 3, the first primary resource with a capacity of AUs handles Erlang, Engset, and Pascal streams, while the second primary resource with a capacity of AUs handles Erlang and Pascal classes. The requests that cannot be handled by the primary resources are overflown to the secondary resource with a capacity of AUs. The parameters of the tested systems were selected so as to be able to verify the accuracy of the method in the worst cases, that is, for a large share of the Pascal stream in the total traffic offered to the system. At the same time, using Erlang, Engset, and Pascal traffic streams allows taking into account the diverse nature of traffic sources at the level of reports. Erlang traffic can be used to characterize the traffic generated by a very large population of traffic sources associated with a given traffic class (constant traffic intensity). Engset traffic allows taking into account the impact of a limited number of traffic sources on the decrease in the traffic volume offered along with the number of traffic sources being served. Pascal traffic can be used to model traffic with a high peakedness coefficient (a high variance-to-mean ratio).
The blocking probabilities determined by the proposed method are compared with the results obtained by the simulation method. In the graphs, the blocking probability results are grouped for traffic classes of the same type and request. The results determined by each of the methods are compared with the values obtained by the simulation method for a traffic intensity range of 0.5–2.5 Erl offered to a single AU of the primary resources with a step of 0.1. For each step, a simulation was performed in 5 series, each with 1,000,000 calls. The simulated values are presented in the form of points with 95% confidence intervals calculated according to Student’s t-distribution for 5 series of calls. Each of the presented simulation results is at least one order of magnitude higher than its confidence interval. The results are presented in relation to an average traffic value of a offered to a single unit of the primary resources, which for one primary resource s can be written as follows:
where:
- m—the number of classes offered to primary resources,
- —the average intensity of traffic of class c of type X offered to primary resource s,
- —demands of calls of class c expressed in AUs,
- —capacity of primary resource s.
From an analysis of the modeling results presented in Figure 7, Figure 8 and Figure 9, we observe that the proposed method leads to highly accurate calculations of the blocking probability in the secondary resources, both for a mixture of Erlang, Engset, and Pascal traffic streams and for the independently occurring and the problematic Pascal streams. To evaluate the influence of the proposed method on the accuracy of the end results, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 compare for Systems 1, 2, and 3 the results obtained by the method proposed in [35] (“old method” in the legends) and with those obtained by the method developed in this article (“proposed method” in the legends).
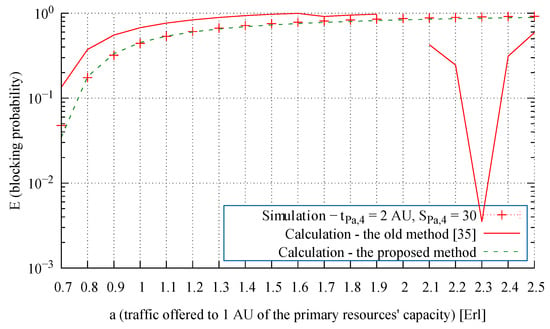
Figure 10.
Blocking probability of the Pascal traffic class in the secondary resources in System 1.
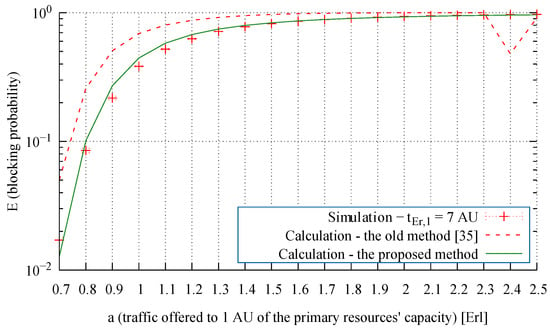
Figure 11.
Blocking probability of the Erlang traffic class in the secondary resources in System 2.
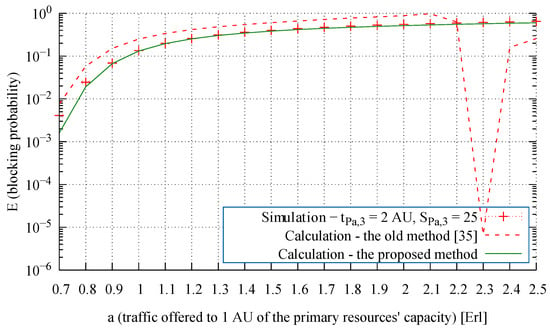
Figure 12.
Blocking probability of the Pascal traffic class in the secondary resources in System 2.
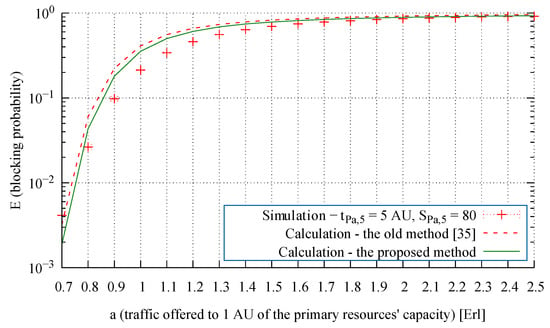
Figure 13.
Blocking probability of the Pascal traffic class in the secondary resources in System 3.
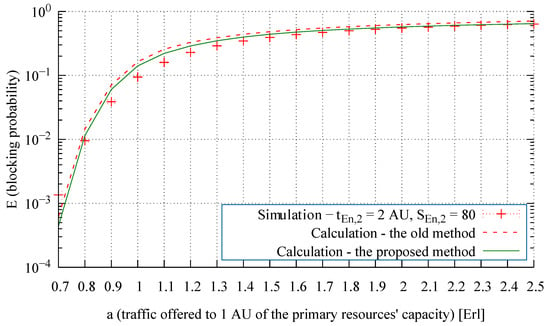
Figure 14.
Blocking probability of the Engset traffic class in the secondary resources in System 3.
On the basis of the blocking probability, in turn, other important characteristics, properties and performance indicators can be evaluated, for example, the call loss probability (the call congestion), the volume of traffic overflown from primary resources, and so forth. For example, one the basis of the blocking probability for class c calls in primary resource s (Formula (4)), we can calculate the loss probability in this resource (i.e., the ratio of the number of class c calls overflowing to the secondary resource to the number of class c calls offered to the primary resource). The call loss probability for class j Engset traffic stream and for class l Pascal traffic stream can be determined by the following formulas:
where and determine the intensity of calls generated by each idle source of class j (Engset) and class l (Pascal), respectively.
The simulation and analytical results of the call loss probability in the primary resources of three example systems, whose parameters are given in Table 1 and Table 2, are shown in Figure 15, Figure 16 and Figure 17.
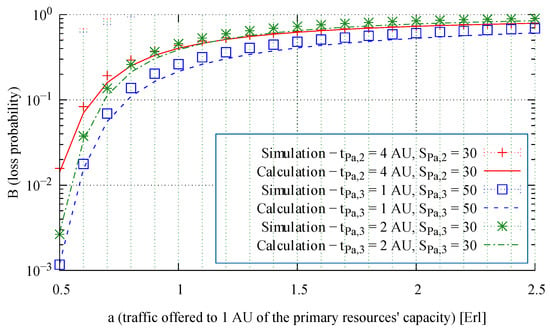
Figure 15.
Loss probability (call congestion) of three selected traffic classes in the primary resources of System 1.
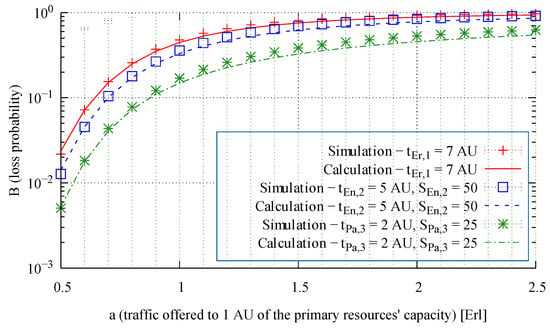
Figure 16.
Loss probability (call congestion) of three selected traffic classes in the primary resources of System 2.
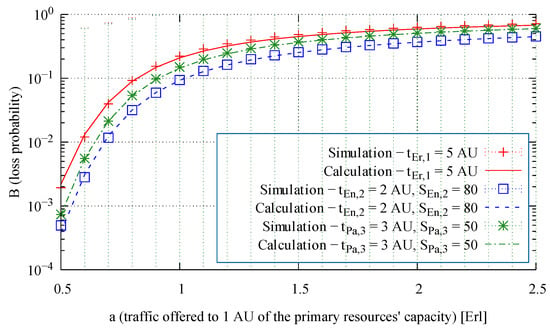
Figure 17.
Loss probability (call congestion) of three selected traffic classes in the primary resources of System 3.
An analysis of the presented results shows that the proposed method is distinguished by high accuracy and a stable level of errors, independently of the parameters of the system, the type of serviced traffic classes, and the volume of offered traffic.
8. Conclusions
This article proposes an analytical model of a multi-service hierarchical system with overflow traffic. The initial assumption is that the primary resources of the system are offered mixtures of Erlang, Engset, and Pascal multi-service traffic streams. Existing methods for modeling such systems are reviewed and analyzed, while the reasons for their insufficient accuracy are presented and discussed. The results of the analysis allowed us to develop a new method for calculating the parameters of overflow traffic that has the advantage of obtaining higher accuracy in modeling systems with multi-service overflow traffic.
To the best of our knowledge, the proposed method is also the first method that enables the analysis of systems with traffic overflow for any range of values of the offered traffic. The analysis of the previously developed solutions showed that for Pascal streams, they do not allow for the analysis of systems in which the traffic intensity offered by Pascal streams is equal or close to 1 Erl per system AU. Owing to its application versatility (Erlang, Engset and Pascal traffic streams) and high accuracy, the developed method can be employed in analyzing and dimensioning telecommunications networks at the flow (call) level. The use of Erlang, Engset, and Pascal streams allows taking into account the diverse nature of the traffic sources. Erlang traffic can be used to characterize the behavior of many flows whose average traffic volume is constant over time. Engset traffic allows us to take into account the impact of a limited (compared with the system capacity) number of traffic sources on the change (reduction) in the intensity of the offered traffic along with the number of serviced traffic sources. Engset traffic is often used to approximate flows with a long service time and a limited number of traffic sources. Pascal traffic can be used to model traffic with large values of the peakedness coefficient (variance-to-mean ratio).
The great interest in using traffic overflow to optimize 4G and 5G networks [15,16,17,43] indicates that the proposed method, by taking into account the different sizes of the requested resources and types of traffic offered as well as the high accuracy of calculations, can be widely used in the analysis and dimensioning of 4G and 5G access networks. The proposed method can also be used to develop call admission control mechanisms for multi-service telecommunications networks.
Author Contributions
Conceptualization, D.K. and M.G.; methodology, D.K.; software, D.K.; validation, D.K. and M.G.; formal analysis, D.K., M.G., and M.S.; investigation, D.K.; resources, D.K.; data curation, D.K.; writing—original draft preparation, D.K. and M.G.; writing—review and editing, D.K., M.G., and M.S.; visualization, D.K.; supervision, M.G.; project administration, D.K.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is in part funded by the Polish National Science Centre (supervised by the Ministry of Science and Higher Education), Grant 2016/23/B/ST7/03925, and by the Ministry of Education and Science, Grant 0313/SBAD/1301.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Stasiak, M.; Głąbowski, M.; Wiśniewski, A.; Zwierzykowski, P. Modeling and Dimensioning of Mobile Networks; Wiley: Chichester, UK, 2011. [Google Scholar]
- Bretschneider, G. Die Berechnung von Leitungsgruppen für berfließenden Verkehr in Fernsprechwählanlagen. Nachrichtentechnische Ztg. (NTZ) 1956, 11, 533–540. [Google Scholar]
- Wilkinson, R.I. Theories of Toll Traffic Engineering in the USA. Bell Syst. Tech. J. 1956, 40, 421–514. [Google Scholar] [CrossRef]
- Wallström, B. Congestion Studies in Telephone Systems with Overflow Facilities. Ericsson Tech. 1966, 22, 187–351. [Google Scholar]
- Fredericks, A. Congestion in Blocking Systems—A Simple Approximation Technique. Bell Syst. Tech. J. 1980, 59, 805–827. [Google Scholar] [CrossRef]
- Ash, G.R. Dynamic Routing in Telecommunications Networks, 1st ed.; McGraw-Hill Professional: New York, NY, USA, 1997. [Google Scholar]
- Fernandes, S.; Karmouch, A. Vertical Mobility Management Architectures in Wireless Networks: A Comprehensive Survey and Future Directions. IEEE Commun. Surv. Tutor. 2012, 14, 45–63. [Google Scholar] [CrossRef]
- Sgora, A.; Vergados, D. Handoff prioritization and decision schemes in wireless cellular networks: A survey. IEEE Commun. Surv. Tutor. 2009, 11, 57–77. [Google Scholar] [CrossRef]
- Wu, X.; Murherjee, B.; Ghosal, D. Hierarchical architectures in the third-generation cellular network. IEEE Wirel. Commun. 2004, 11, 62–71. [Google Scholar] [CrossRef]
- Tripathi, N.; Reed, J.; VanLandinoham, H. Handoff in cellular systems. IEEE Pers. Commun. 1998, 5, 26–37. [Google Scholar] [CrossRef]
- Lin, Y.B.; Chang, L.F.; Noerpel, A. Modeling hierarchical microcell/macrocell PCS architecture. In Proceedings of the International Conference on Communications, Seattle, WA, USA, 18–22 June 1995; Volume 1, pp. 405–409. [Google Scholar] [CrossRef]
- Li, S.; Grace, D.; Wei, J.; Ma, D. Guaranteed handover schemes for a multilayer cellular system. In Proceedings of the 7th International Symposium on Wireless Communication Systems, York, UK, 19–22 September 2010; pp. 300–304. [Google Scholar] [CrossRef]
- 3GPP. Self-Configuring and Self-Optimizing Network (SON) Use Cases and Solutions (Release 9). Available online: https://www.3gpp.org/specifications/releases/71-release-9 (accessed on 26 September 2014).
- Zia, N.; Mitschele-Thiel, A. Self-organized neighborhood mobility load balancing for LTE networks. In Proceedings of the 2013 IFIP Wireless Days (WD), Valencia, Spain, 13–15 November 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Daraseliya, A.; Korshykov, M.; Sopin, E.; Moltchanov, D.; Koucheryavy, Y.; Samouylov, K. Handling Overflow Traffic in Millimeter Wave 5G NR Deployments using NR-U Technology. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Song, C.; Zhang, M.; Zhan, Y.; Wang, D.; Guan, L.; Liu, W.; Zhang, L.; Xu, S. Hierarchical edge cloud enabling network slicing for 5G optical fronthaul. IEEE/OSA J. Opt. Commun. Netw. 2019, 11, B60–B70. [Google Scholar] [CrossRef]
- Ha, V.N.; Nguyen, T.T.; Le, L.B.; Frigon, J. Admission Control and Network Slicing for Multi-Numerology 5G Wireless Networks. IEEE Netw. Lett. 2020, 2, 5–9. [Google Scholar] [CrossRef]
- Kühn, P.; Mashaly, M.E. Multi-Server, Finite Capacity Queuing System with Mutual Overflow. In Proceedings of the 2nd European Teletraffic Seminar, Karlskrona, Sweden, 3 September–2 October 2013. [Google Scholar]
- Mashaly, M.; Kühn, P.J. Load Balancing in Cloud-based Content Delivery Networks Using Adaptive Server Activation/Deactivation. In Proceedings of the 24th International Teletraffic Congress. International Teletraffic Congress, Krakow, Poland, 4–7 September 2012; pp. 21:1–21:3. [Google Scholar]
- Soni, G.; Kalra, M. A novel approach for load balancing in cloud data center. In Proceedings of the International Advance Computing Conference, Gurgaon, India, 21–22 February 2014; pp. 807–812. [Google Scholar] [CrossRef]
- Głąbowski, M.; Sobieraj, M.; Stasiak, M.; Stasiak, M.D. Modeling of Clos Switching Structures with Dynamically Variable Number of Active Switches in the Spine Stage. Electronics 2020, 9, 1073. [Google Scholar] [CrossRef]
- Kühn, P.J. Systematic Classification of Self-adapting Algorithms for Power-saving Operation Modes of ICT Systems. In Proceedings of the 2nd International Conference on Energy-Efficient Computing and Networking, New York, NY, USA, 31 May–1 June 2011; pp. 51–54. [Google Scholar]
- Yoshino, M.; Nishibe, N.; Oba, M.; Komoda, N. Classification of energy-saving operations from the perspective of system management. In Proceedings of the 8th International Conference on Industrial Informatics, Osaka, Japan, 13–16 July 2010; pp. 651–656. [Google Scholar] [CrossRef]
- Głąbowski, M.; Walkowiak, P. Simulation Studies of Communication Systems with Mutual Overflows and Threshold Mechanisms. In Proceedings of the 2018 International Conference on Broadband Communications for Next Generation Networks and Multimedia Applications (CoBCom), Graz, Austria, 11–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Chan, Y.; Wong, E.W.M. Blocking Probability Evaluation for Non-Hierarchical Overflow Loss Systems. IEEE Trans. Commun. 2018, 66, 2022–2036. [Google Scholar] [CrossRef]
- Iversen, V.; Benetis, V.; Hansen, P. Performance of Hierarchical Cellular Networks with Overlapping Cells. In Wireless Systems and Mobility in Next Generation Internet; Kotsis, G., Spaniol, O., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3427, pp. 7–19. [Google Scholar] [CrossRef]
- Gauger, C.; Kühn, P.; Breusegem, E.; Pickavet, M.; Demeester, P. Hybrid optical network architectures: Bringing packets and circuits together. IEEE Commun. Mag. 2006, 44, 36–42. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kubasik, K.; Stasiak, M. Modeling of systems with overflow multi-rate traffic. Telecommun. Syst. 2008, 37, 85–96. [Google Scholar] [CrossRef]
- Głąbowski, M.; Hanczewski, S.; Stasiak, M. Modelling Load Balancing Mechanisms in Self-Optimising 4G Mobile Networks with Elastic and Adaptive Traffic. IEICE Trans. Commun. 2016, E99-B, 1718–1726. [Google Scholar]
- Lagrange, X.; Godlewski, P. Performance of a hierarchical cellular network with mobility-dependent hand-over strategies. In Proceedings of the Vehicular Technology Conference—VTC, Atlanta, GA, USA, 28 April–1 May 1996; pp. 1868–1872. [Google Scholar] [CrossRef]
- Chung, S.P.; Lee, J.C. Performance analysis and overflowed traffic characterization in multiservice hierarchical wireless networks. IEEE Trans. Wirel. Commun. 2005, 4, 904–918. [Google Scholar] [CrossRef]
- Kaufman, J.S.; Rege, K.M. Blocking in a shared resource environment with batched Poisson arrival processes. J. Perform. Eval. 1996, 24, 249–263. [Google Scholar] [CrossRef]
- Moscholios, I.D.; Vardakas, J.S.; Logothetis, M.D.; Boucouvalas, A.C. Congestion Probabilities in a Batched Poisson Multirate Loss Model Supporting Elastic and Adaptive Traffic. Ann. Telecommun. 2013, 68, 327–344. [Google Scholar] [CrossRef]
- Huang, Q.; Ko, K.T.; Iversen, V.B. Approximation of Loss Calculation for Hierarchical Networks with Multiservice Overflows. IEEE Trans. Commun. 2008, 56, 466–473. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kmiecik, D.; Stasiak, M. Modelling of Multiservice Networks with Separated Resources and Overflow of Adaptive Traffic. Wirel. Commun. Mob. Comput. 2018, 2018, 7870164. [Google Scholar] [CrossRef]
- Akimaru, H.; Takahashi, H. An Approximate Formula for Individual Call Losses in Overflow Systems. IEEE Trans. Commun. 1983, 31, 808–811. [Google Scholar] [CrossRef]
- Sanders, B.; Haemers, W.H.; Wilcke, R. Simple approximate techniques for congestion functions for smooth and peaked traffic. In Proceedings of the 10th International Teletraffic Congress, Montreal, QC, Canada, 8–15 June 1983. [Google Scholar]
- McArdle, C.; Tafani, D.; Barry, L. Overflow traffic moments in channel groups with Bernoulli-Poisson-Pascal (BPP) load. In Proceedings of the International Conference on Communications, Budapest, Hungary, 9–13 June 2013; pp. 2403–2408. [Google Scholar] [CrossRef]
- Kösten, L. Behaviour of Overflow Traffic and the Probabilities of Blocking in Simple Gradings. In Proceedings of the 8th International Teletraffic Congress, Melbourne, Australia, 10–17 November 1976; pp. 425/1–425/5. [Google Scholar]
- Schehrer, R. On the Exact Calculation of Overflow Systems. In Proceedings of the 6th International Teletraffic Congress, Munich, Germany, 9–15 September 1970; pp. 147/1–147/8. [Google Scholar]
- Brockmeyer, E.; Halstrom, H.; Jensen, A. The Life and Works of A.K. Erlang. Transcations Dan. Acad. Tech. Sci. 1948, 2, 1–278. [Google Scholar]
- Kuczura, A. The Interrupted Poisson Process As An Overflow Process. Bell Syst. Tech. J. 1973, 52, 437–448. [Google Scholar] [CrossRef]
- Wu, J.; Wang, M.; Chan, Y.C.; Wong, E.W.M.; Kim, T. Performance Evaluation of 5G mmWave Networks with Physical-Layer and Capacity-Limited Blocking. In Proceedings of the 2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR), Newark, NJ, USA, 11–14 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Bai, T.; Vaze, R.; Heath, R.W. Analysis of Blockage Effects on Urban Cellular Networks. IEEE Trans. Wirel. Commun. 2014, 13, 5070–5083. [Google Scholar] [CrossRef]
- Erlang, A. Solution of some problems in the theory of probabilities of significance in automatic telephone exchanges. Elektrotechnikeren 1917, 13, 5. [Google Scholar]
- Akimaru, H.; Kawashima, K. Teletraffic: Theory and Application; Springer: London, UK, 1999. [Google Scholar]
- Roberts, J.; Mocci, V.; Virtamo, I. (Eds.) Broadband Network Teletraffic, Final Report of Action COST 242; Commission of the European Communities, Springer: Berlin, Germany, 1996. [Google Scholar]
- Vassilakis, V.G.; Moscholios, I.D.; Logothetis, M.D. Call-Level Performance Modelling of Elastic and Adaptive Service-Classes with Finite Population. IEICE Trans. Commun. 2008, 91, 151–163. [Google Scholar] [CrossRef]
- Hanczewski, S.; Stasiak, M.; Weissenberg, J. Non-full-available queueing model of an EON node. Opt. Switch. Netw. 2019, 33, 131–142. [Google Scholar] [CrossRef]
- Panagoulias, P.I.; Moscholios, I.D.; Sarigiannidis, P.G.; Głąbowski, M.; Logothetis, M.D. An Analytical Framework in OFDM Wireless Networks Servicing Random or Quasi-Random Traffic. Appl. Sci. 2019, 9, 5376. [Google Scholar] [CrossRef]
- Efstratiou, P.; Moscholios, I.D. User Mobility in a 5G Cell with Quasi-Random Traffic under the Complete Sharing and Bandwidth Reservation Policies. Autom. Control Comput. Sci. 2019, 53, 376–386. [Google Scholar] [CrossRef]
- Moscholios, I.; Logothetis, M. Efficient Multirate Teletraffic Loss Models beyond Erlang; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Głąbowski, M.; Kaliszan, A.; Stasiak, M. Two-Dimensional Convolution Algorithm for Modelling Multiservice Networks with Overflow Traffic. Math. Probl. Eng. 2013, 2013, 852082. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, Y.C.; Ko, K.T.; Iversen, V. Loss Performance Modeling for Hierarchical Heterogeneous Wireless Networks With Speed-Sensitive Call Admission Control. IEEE Trans. Veh. Technol. 2011, 60, 2209–2223. [Google Scholar] [CrossRef][Green Version]
- Bakmaz, B.M.; Bakmaz, M.R. Solving some overflow traffic models with changed serving intensities. AEU Int. J. Electron. Commun. 2012, 66, 80–85. [Google Scholar] [CrossRef]
- Wang, M.; Li, S.; Wong, E.; Zukerman, M. Performance Analysis of Circuit Switched Multi-Service Multi-Rate Networks With Alternative Routing. J. Light. Technol. 2014, 32, 179–200. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kaliszan, A.; Stasiak, M. Modelling overflow systems with distributed secondary resources. Comput. Netw. 2016, 108, 171–183. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kmiecik, D.; Stasiak, M. Overflow of Elastic Traffic. In Proceedings of the International Conference on Broadband Communications for Next Generation Networks and Multimedia Applications, Graz, Austria, 14–16 September 2016. [Google Scholar]
- Głąbowski, M.; Kmiecik, D.; Stasiak, M. Overflows in Multiservice Systems. IEICE Trans. Commun. 2019, 102, 958–969. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kaliszan, A.; Stasiak, M. Modeling product-form state-dependent systems with BPP traffic. Perform. Eval. 2010, 67, 174–197. [Google Scholar] [CrossRef]
- Głąbowski, M.; Stasiak, M.; Weissenberg, J. Properties of Recurrent Equations for the Full-availability Group with BPP Traffic. Math. Probl. Eng. 2012, 2012, 547909. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kmiecik, D. Modelling Pascal traffic in overflow systems. Int. J. Electron. Telecommun. 2020, 66, 155–160. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).