Abstract
The stateless cloud-native design improves the elasticity and reliability of applications running in the cloud. The design decouples the life-cycle of application states from that of application instances; states are written to and read from cloud databases, and deployed close to the application code to ensure low latency bounds on state access. However, the scalability of applications brings the well-known limitations of distributed databases, in which the states are stored. In this paper, we propose a full-fledged state layer that supports the stateless cloud application design. In order to minimize the inter-host communication due to state externalization, we propose, on the one hand, a system design jointly with a data placement algorithm that places functions’ states across the hosts of a data center. On the other hand, we design a dynamic replication module that decides the proper number of copies for each state to ensure a sweet spot in short state-access time and low network traffic. We evaluate the proposed methods across realistic scenarios. We show that our solution yields state-access delays close to the optimal, and ensures fast replica placement decisions in large-scale settings.
1. Introduction
Traditionally, network functions (NFs) are implemented as monolithic applications—beyond their core packet processing functionality, auxiliary functions, such as load balancing, scaling, and redundancy logic are all baked into the application itself. This approach makes it possible to achieve great performance characteristics, especially given that the implementations are often tuned for the specific hardware they run on. However, there are key problems with this approach, namely: (1) It typically leads to the repeated implementation of the same (or a similar) set of functionalities across multiple NFs, significantly increasing both development and operation costs, and (2) the strong ties between application and hardware make it prohibitive to provide deployment flexibility. In order to tackle these issues, a modern NF virtualization (NFV) ecosystem needs to be fundamentally stateless [1,2,3,4]; if the virtual NFs (VNFs) do not maintain a persistent state on their own, then scale-in/scale-out and even fail-over events are less complex to handle, improving overall elasticity, scalability, resiliency, and upgradability [4].
With the advent of 5G, there is a strong drive in the industry to make applications more cloud-native [5,6]—that is, transform them so that they are stateless. The advantage of this approach is that the applications become independent of the underlying infrastructure (cloud vendor agnosticism), which paves the way for novel cloud, edge, and mobile management systems and use-cases, like vendor-agnostic resource consolidation [7], resource-aware cloud service admission control [8], and real-time (low-latency) 5G-enabled industrial IoT [9]. Furthermore, due to the cloud agnosticism, applications will be able to run in any telco’s or cloud administrator’s infrastructure, and various online application suppliers will ship the application systems, which, according to the authors of [10], by the union of the these actors, will result in a global virtualization platform in the future.
However, despite the cloud-native concept’s promises, eliminating the need for explicit state management within applications does not come for free; the downside is the complexity faced by all distributed systems, the performance, and data consistency [1,2,3,4]. These difficulties are especially compelling in telco deployments [11,12], where a carrier-grade telco NF ecosystem must provide extreme steady-state performance and strict service-level objectives (SLOs) simultaneously, at the order of hundreds of millions of packets per second throughput, and a 1–10 ms delay budget [13]. Although the perceived performance overhead of state externalization depends on various factors (such as the application’s state access pattern, the performance of the backing data store, and the deployment characteristics), we can anticipate that the cost of external state access may easily become the dominating, that is, limiting, factor in the overall NF performance. While fast user plane NFs spend, at most, a few hundred nanoseconds when processing a packet, the cost of accessing a remote state over a commodity 10 Gb network is around 21 microseconds [3].
The number of external state accesses can be decreased by (1) moving states close to the application instances accessing them, and (2) determining the frequently accessed ones to replicate them to the hosts of the most frequent reader NFs. By replicating everywhere, we facilitate local reads; however, this would cause significant replica update traffic when data are modified, and would also severely limit the amount of externalizable data. If we apply a uniform replication factor for all states, we ignore the fact that some states are more popular than others. All in all, to minimize the performance hit arising from state externalization, it is crucial to (1) determine an efficient replication factor for each state, and to (2) optimize the placement of the original data and their replicas, so that data access may be kept host-internal whenever possible. Joint optimization of the two results in a highly complex problem that cannot be solved in polynomial time. To decrease this complexity, we treat them as two sequential sub-problems, with the link of assuming a certain placement outcome while determining the replica factor.
1.1. Contributions
We propose a fast state placement algorithm and a system design for stateless cloud applications with the aim of minimizing externalized data access latency. The proposed techniques are suitable for any kind of key-value store with the ability of controlling data placement. Our contributions are the following:
- An architecture design for the state layer of cloud computing systems (e.g., stateless NFV systems) that store the externalized data of virtualized applications (e.g., NFs).
- A replica controller module that determines the optimal replication factor for each state, one by one, in order to keep the state access traffic and the read latency low.
- A state placement algorithm, which can handle a large number of states and their readable copies, and maximize reliability and read performance by adapting the location to their state access pattern.
- A comprehensive evaluation of the proposed state layer compares the performance results to naive solutions.
A preliminary version of this work was published in conference papers. In a prior paper [14], we presented an earlier version of the State Placement problem (detailed in Section 5) that does not consider the state access intensities for the locality optimization, and assumes serial, consecutive updates of readable copies. In ref. [15], we published a proof-of-concept prototype (https://netsoft.gsuite.tmit.bme.hu/demos/annabelladb (accessed on 16 December 2020)) implementation of a prior version of the proposed system design (elaborated in Section 2) without the feature of handling state copies. In this manuscript, the following aspects have been improved compared to our prior paper [14]: (1) We have modified the State Placement Problem model to make it more realistic, that is, to assume various state access intensities and parallel data copy updates; (2) we have extended the example use case in Section 3 for easier understanding of how the stateless design works; and (3) we have modified and extended the proposed heuristic algorithm in Section 5.3. As novel content, (1) we introduce the dynamic replication module in Section 4, (2) we propose an overall design for a cloud-based state store architecture in Section 2, (3) we add the pseudo-code of the extended heuristic algorithm, and make the source code publicly available in Section 5.3, (4) we provide the runtime complexity analysis of the proposed heuristic, (5) we present a comprehensive performance evaluation, and (6) we add a comparative analysis of state-of-the-art state stores and our proposed solution, with highlighted differences between the CDN and the State Placement Problem.
1.2. Terminology
In this paper, the terms state, data, copy, replica, master, and slave are used, so for the sake of clarity, we define their meaning and the differences between them in this subsection.
Definition 1
(State (data)). A specific instance of data that the cloud application creates and stores in a third-party storage application. For example, in the case of a firewall, a state could be the following key-value pair: (key: from_any_to_all, value: allow_tcp_port_22).
A state can be either a master or a slave. A master state can have multiple slaves.
Definition 2
(Master). Master is the original state that is created and externalized by the cloud application (e.g., NF). The master instance is both readable and writable by the cloud applications.
Definition 3
(Slave). A readable exact copy of the master instance. The master and slave instances are well-connected: the storage application server where the master is stored keeps the slaves updated if the master has been modified.
Definition 4
(Instance of a state). We use this term to refer to both master and slave instances for the given state. For example, the statement "state instance is readable" is true, since both the master and the slave instances of the state can be read by the applications.
Definition 5
(Copy/Replica). The exact copy of master data—that is, we use these two terms in the same way as the term, "slave".
1.3. Similarity to Content Delivery Networks
The state placement problem of the stateless NFV design is similar to the content placement problem in Content Delivery Networks (CDNs) [16]. While their optimization goals are the same, that is, reduced network traffic, minimized access latency, and increased reliability of data, there are key differences between the two research areas. We argue that the replica placement in CDN is a sub-problem of the state externalization problem in NFV stateless design.
In the case of CDN, all data (or contents) have a source, that is, an origin server from where the web users are able to download them. During the operation, the most popular contents are cached in order to improve the read access performance of the users. Writing content may happen from time to time only by the content owner, that is, from the origin server. Consequently, CDNs optimize for the reads and not for the content writes and updates. On the other hand, in the proposed stateless design, besides the slaves, the master instances have to be placed as well. During the state placement, we have to find the right balance of reads, writes, and updates too, since the state placement attempt to minimize the overall latency comes from all types of data access.
Another important difference between the two problems is in the type of the underlying topology, the accessed data, and the pattern of their accesses (how frequently and how long the accesses take). CDNs work over a geographically scattered network (even over continents) with typically large files (order of MBs or even GBs), such as graphics, documents, and videos, to reduce access times by up to several seconds. In contrast, our proposed state layer could operate in a single-cloud infrastructure handling a large number of small pieces of data (internal states/variables, such as integers and strings) which are accessed according to a constantly changing and dynamic NF reads/writes characteristic. In addition, the accesses should take no longer than a few milliseconds [13].
The summarized differences between the content placement problem of CDN and the state placement problem of stateless cloud-native NFV/applications is detailed in Table 1.

Table 1.
Comparative analysis of CDN and the state placement problem of cloud-native applications.
1.4. Organization of the Paper
The paper is organized as follows. In Section 2, we present our proposed cloud database architecture, called as state layer, supporting external states. In Section 3 we provide a simple use-case on how the stateless design could work in a cloud-based system. In Section 4 we discuss how the proper replication factor (i.e., number of data copies) is determined to minimize the data access latency. In Section 5 we formalize the State Placement Problem, prove that it is NP-hard, and introduce our heuristic solution to it. In Section 6 we provide a technical evaluation of our solution. In Section 7 we summarize related work, and finally in Section 8, we conclude our work.
2. Our Proposed Design for the State Layer
We propose a state handling layer and a corresponding state placement method, which spreads state instances across the hosts of a data center. In cloud-based telco deployments, application states are created in response to certain system events, like an incoming network packet of a network device or a subscriber performing a handover. The stateless cloud applications externalize these states to ensure reliability, fast self-healing, seamless scalability, and in-service upgradability. The externalized state instances stored in the state layer are called state data. We propose two types of externalized data: master and slave.The former is writable, and the latter is the read-only instance of the NF’s state; there is only one master, but multiple slaves may exist for a given state.
In order to sustain proper responsiveness of the application, such as an NF, a Service Function Chain (SFC) [17], or another software entity, access to the externalized states must be fast. Many public cloud databases, both from academia [4,15,18,19,20] and from the industry [3,21,22], offer in-memory state storage for cloud applications. Some of these technologies provide means to ensure data locality, that is, maximizing the chance that an application instance will find its respective state on the very same data center host where it is running. We argue that the placement of application states, which takes into account the locations of already deployed database instances and NF applications, is of paramount importance to improve application performance.
Consider general cluster containing hosts, that is, physical servers, virtual machines, containers, or any other virtualized entity, with an arbitrary intra-data-center network topology, where NF instances run. Each of these hosts contains a database (DB) instance that altogether forms a distributed cloud database, called a state layer over the cluster. In order to make NF instances elastic and resilient [1], some or all of their internal states are externalized into this state layer. To create an elastic and resilient service, it has to be built from stateless NFs. The relationship among those NFs does not affect the operation and the efficiency of our proposed solution, as it only deals with the placement of externalized states and not the NFs’. Due to state externalization, (1) states might be shared, that is, they are accessed by multiple NF instances, (2) states may have multiple instances to improve reliability, (3) NF instances may read the master or its slave instances, that is, read scaling, and (4) only the master is writable by NF instances; consequently, slaves are updated through their master instance.
Every host has a capacity limit that determines the maximum amount of memory allocated to the DB instance. Our objective is to determine the best host for each state data, taking into account their access pattern so that the sum of the access delay caused by inter-host communication is minimal. The access pattern of a state is determined by the following: (1) The number of NF instances accessing the state data throughout the cluster, (2) the type of these accesses, such as read, write, or both, and (3) the weights of these accesses, that is, the number of reads/writes initiated by a function in a given time interval.
We depict the design of our state layer system in Figure 1. The three main features of this approach are the following: (1) Ensures reliability of latency-sensitive cloud-native applications, (2) ensures access to shared states with minimal delay overhead, and (3) automatically determines the required number of slave instances to guarantee minimal states access time, and state survivability in the case of node failures. In the following, we show the role of each module in detail.
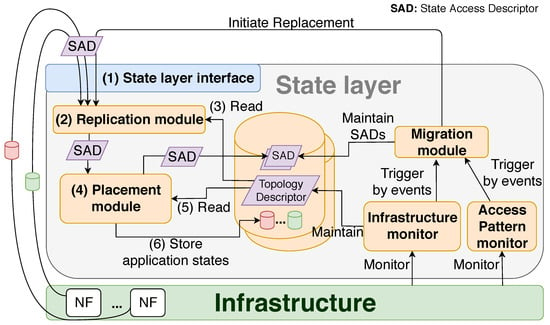
Figure 1.
Proposed state layer architecture.
2.1. State Layer Interface and State Access Descriptor
Our proposed system offers a State Layer Interface, through which the NF instances and/or the state layer itself (via Migration module) are able to make state placement requests, that is, to save the externalized data into the specified destination host(s) of the infrastructure. The input of the state layer is a State Access Descriptor (SAD), which includes the state value and its access pattern (only if known a priori, so items signed by * are not necessarily provided initially) as follows:
- One or multiple state data (with keys and values), which need to be saved in the state layer;
- The size of a state data in memory;
- Replication factor (a minimum number of slaves is optionally defined by policy);
- *
- NF instances accessing the state data (a state can belong to a single NF instance, or can be shared);
- *
- Type of access, that is, reads, writes, or both; and
- *
- Ease of access, number of accesses per second.
The formal SAD is given in Section 4 and Section 5. A directed graph is a tractable model of SADs—vertices divided into two disjoint and independent sets, state instances and NF instances, arcs depicting the type of access, that is, for writes, where the arc is directed from the NF instance towards the state instance, while for reads, we use arrows pointing in the opposite direction. The weight on an arc shows the access frequency. State instance vertices have size labels representing their required memory demand. See an example of SAD in Figure 2.
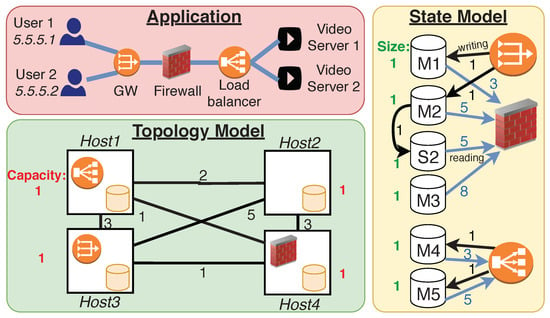
Figure 2.
An example of a server cluster (lower left side), a cloud-based application (upper left side), and the corresponding State Access Descriptor including all the required state instances (masters: M1–M5, slave: S2) to externalize (right side).
The state access pattern is not necessarily available when the system instantiates state data. Therefore, we designed our data layer with a feedback loop. First, default values are used, and as monitoring information is being collected, the Migration module continuously improves the SADs. In the case of an event-caused trigger (detailed in Section 2.5), it updates the affected SADs on the State Layer Interface to start the migration of state instances according to the modified access pattern.
2.2. Replication Module
The Replication module has two inputs—it gets the SAD originating from the State Layer Interface, and it also reads the delay distribution measured between the hosts in the underlying infrastructure. The delay characteristics are provided by the Infrastructure Monitor. The goal is to determine a replication factor individually for all SADs so that access time of the data and the inter-host communication are minimized, while state survivability is maximized in case of node failures. For example, if multiple NF instances read a master instance, the module may propose to create many slave instances to spread them and give a better chance to local reads. Policy can also determine a minimum replication factor for certain NFs.
The output of the Replication module is an extended version of the SAD, which contains the replication factor. In Section 4 we show different implementations of the Replication module, tuned for different objectives, and propose an all-in-all solution that takes all of them into account.
2.3. Infrastructure Monitor
The goal of the Infrastructure Monitor module is to maintain the Topology Descriptor that characterizes the underlying infrastructure where the stateless NF instances run. The accurate Topology Descriptor is critical for both the Replication module and the Placement module to calculate the optimal placement of master and slave instances. The Topology Descriptor contains the following:
- The list of hosts in the data center cluster;
- The memory capacities of these hosts;
- The measured network delays between the host pairs; and
- The hosts of already deployed NF instances.
If an infrastructure event, such as new host arriving, an NF migration among the hosts or modification in network delays, impacts the topology characteristics, then this module updates the Topology Descriptor. In the case of some specific events, the Infrastructure Monitor triggers the Migration module to initiate the full or partial reconfiguration of the replicas’ placement. In Section 2.5, we list possible infrastructure events to which the proposed system reacts.
2.4. Placement Module
The Placement module receives two inputs: the SADs and the Topology Descriptor. The Replication module forwards the former, while the latter is provided by the Infrastructure Monitor. This module calculates the placement that determines the best hosts for each state instance. The cost function of the placement algorithm determines the quality of the computed placement, that is, the sum of access and replica update times, which is defined by our proposed objective function (1) in Section 5. Minimizing this cost makes the proposed system suitable for latency-sensitive applications. Finally, the Placement module stores each master and its slaves into the DB instances of the computed respective hosts.
In Section 5 we prove that finding the optimal placement is an NP-hard problem, and we propose a heuristic algorithm to get a near-optimal solution in polynomial time.
2.5. Migration Module
The Migration module is responsible for the migration of already stored state instances in the case of specific system events: the Infrastructure and the Access Pattern Monitor trigger the Migration module to initiate the placement of some of the state replicas. The Migration module maintains all the SADs that the state layer handles, and these SADs together form a merged model of the externalized state instances: it is dynamically updated (i) for each placement request by the Placement module, and (ii) for each access pattern change recognized by the Migration module.
If a new host joins the cluster, then the Topology Descriptor is updated, but generally, there is no need for moving state instances. However, if a host goes down, then some replicas may become unreachable. Then, the state layer creates new replicas to maintain the required reliability level, and may move the existing ones to provide minimal inter-host accesses. To do that, the Migration module—using the State Layer Interface—sends the updated SAD to the Replication module to initiate the required migration process. The deployed NF instances may be migrated from one host to another. This event can easily cause additional inter-host state access time, as the local state instance becomes remote. In this case, the Migration module’s task is to initiate the migration of the state instances accessed by the migrated NFs. If the host-to-host delay distribution changes within the cluster, the controller has to start the placement process for all deployed state instances.
These events are triggered by the Infrastructure Monitor. However, the Access Pattern Monitor may also trigger the Migration module if the state’s access pattern has changed within a given time period. In these cases, the controller starts the migration process of the state instances that have been affected by the access pattern change.
2.6. Access Pattern Monitor
This module monitors the frequency of the already deployed state instance’s accesses and maintains lists of the reader, and the writer NF instances for each of them. In case of changes in access pattern, it notifies the Migration module to keep the SADs up-to-date. Then the Migration module initiates the migration of the respective replicas, resulting in more efficient state access for the stateless NF instances.
3. A Use-Case for Stateless Design
In this section, we explain the importance of an application’s state placement through an illustrative use case. In Figure 2, we present a simplified cloud-based application and a server cluster, including four hosts with different capacities. We model our cluster by a graph called the Topology Descriptor, in which nodes are the hosts, weights on edges are the delays, and each node has a capacity value and a list of locally run and stored NF and state instances. The example cluster of four hosts is a possible realization of the Infrastructure in Figure 1. In this example, we assume the state layer runs DB instances on each host of the cluster (depicted by yellow cylinders in the nodes of Topology Descriptor), and consequently, replicas can be stored in each host.
The upper, red part of Figure 2 presents an application running in the server cluster. It consists of three NF instances—namely, the Border Gateway (GW), the Firewall (FW), and the Load Balancer (LB)—and two video servers serving the same media. The gateway remaps the incoming users’ IP addresses into the private network space behind it. The firewall monitors and controls the network traffic based on predefined security rules and, finally, the load balancer distributes the workload across the video servers. The GW runs in , the FW is deployed in , while the LB is located in .
The right side of Figure 2 shows (1) master and slave instances to externalize into the state-layer, (2) relations between state and the accessing NF instances, and (3) access weights, that is, reading and/or writing frequencies. The size of the state data are also known. All these are described by the State Access Descriptor where arcs depict the type of access. Arcs from an NF instance to a state instance (either master or slave), and from a master to a slave mean write and update access. Arcs from a state to an NF instance depict read access. Weights of the arcs mean the access frequency. As a result of the slave updating policy, an NF instance may read a master or any of its slave replicas (blue arcs in the figure).
In our simple example, the input of the state layer is the yellow part in Figure 2. Three state types exist: (1) translation rules of GW, (2) security rules of FW, and (3) load-balancer rules of LB. The instances of these states are in Table 2. The task is to find the destination host for each state instance. Since there are only two users, GW writes two translation rules ( and ) into the state layer. is requested with a slave (). These rules might be key-value pairs as in Table 2, defining the mapping between users’ public IP addresses and their internal IPs. The security rules of FW may be based on GW states and on admin-defined security policies, such as how FW lets in the request only if its source IP is the same as the value in or . In our example, one admin-defined state replica exists (), indicating that requests between 4:00 and 5:00 AM are not allowed. Finally, LB creates and , two load-balancer rules defining that User 1’s request is directed to Video server 1, while Video server 2 serves User 2. In our example, and are shared states, that is, they are accessed by more than one NF instance. User 1 requests a video three times, while User 2, five times within a second. We need to spread state replicas across hosts in such a way that the sum of access delays arising from the inter-host communication is minimal. Thanks to state externalization, if an NF instance goes down, state replicas are still available, ensuring that newly launched NF instances can continue the operation. Furthermore, the cloud manager is independently able to scale NF instances in and out.

Table 2.
Written and read state instances by the NFs of Figure 2.
The optimal solution for placing replicas into the cluster in Figure 2 is the mapping of , , , , , and . In case of this placement, the gateway writes master instances (delay: ) and (delay: ) once within a second, while is updated from (delay: ). Firewall reads three times (delay: ), five times (delay: ), and eight times (delay: ). The load balancer reads and writes both and with zero delay. All in all, the total access delay of state replicas in the described placement is five.
In summary, in order to minimize the performance overhead due to state externalization, it is essential to use a state-layer whose placement algorithm is aware of the NFs’ locations within the cluster.
4. Optimal Number of Slave Instances
Thus far, we have assumed required replication factors are part of the state layer’s input, that is, they are individually defined for each state by a third party, which in fact requires awareness of state access patterns. Determining the optimal replication factor, according to how popular the state is, seems to be a complex problem. That is why well-known key-value stores apply the fixed replication factor strategy, which sets a unified replication number for all data independently of their popularity. Another simple design is the replication everywhere strategy, that is, copying each state to every DB instance within the cluster where at least one reader NF exists. This approach provides minimal read latency thanks to local accesses. On the other hand, this technique leads to significantly increased consistency time, as every slave must be updated when the master is written. The updates incur inter-host traffic, and the many slaves fill up host capacities. Therefore, we propose a state layer that dynamically determines the optimal replication factor for each state, one by one, with the aim of (1) increasing the read performance as much as possible by moving replicas close to the accessing NF instances, (2) minimizing replica update time, (3) restricting the maximum generated traffic related to the slave updates, and (4) providing the requested access frequency of the NF instances.
In this section, we introduce three outcomes of the stateless NF design that depend the most on replication factors: the generated network traffic between NFs and DB instances, the additional network delay suffered due to the state not necessarily being stored locally, and the maximum possible access frequency of the state that an application can achieve. Finally, we propose a model to determine the optimal replication factor for each externalized state. The summary of notations we use in this section is provided in Table 3.

Table 3.
Mathematical notations in Section 4.
4.1. Network Traffic Depending on Replication Factor
Thanks to state externalization, the more inter-host communication related to accessing states exists, the more significant the network load is. A large number of state instances, on the one hand, increases the network load due to slave updates, and on the other hand, decreases the number of remote state reads. A state is fully characterized by its SAD, including the following fields:
- The key and value of the state s;
- Its size, ;
- The set of its writer NFs , consisting of elements ;
- How frequently NFs write state s in a second, that is, a writing rate vector , where for example, means that the NF2 in writes the state times per second;
- The set of its reader NFs consisting of elements ;
- How frequently NFs read state s in a second, that is, a reading rate vector . Without the loss of generality, let be sorted in increasing order, that is, where .
In order to minimize the network load depending on the replication factor of states, we need to distinguish the three types of traffic related to data access: (1) Master writes, (2) slave updates, and (3) master or slave reads. Since only the master instance is writable by the NFs, only the latter two traffic types depend on the number of slaves. If the state and the accessing NF instance are deployed on the same host, there is no generated network traffic, since the communication stays within the host. For the sake of simplicity, we suppose the master instance of the state is located on a host remote from all its writer NFs.
The volume of the generated traffic caused by writing operations is , and the volume of the generated traffic caused by slave-updating operations is: , as state instances are spread with anti-affinity and slaves exist.
Assumption 1.
We consider a placement algorithm that places replicas on the hosts, from which the most frequent read accesses come.
Given Assumption 1, the volume of the generated traffic caused by reading operations is . Similarly, the placement algorithm should place replicas only to those hosts, on which at least one reader NF is situated, since more replicas would unnecessarily lead to higher update traffic without further improving reading access delays. Then, the upper bound for state instances is the count of reader NFs, that is, .
Definition 6.
Let L mean the sum of the generated traffic load per second, , where is the number of replicas of state s. Then, the optimal replication factor for state s according to the generated network load is .
4.2. Network Delay Depending on Replication Factor
The replication factor also influences the state access time; here, we consider the data access delays due to traversing of the data center network from the point of view of the accessing NFs. We examine the stateless NF instances, compared to their stateful counterparts, in terms of additional network delays experienced as the number of slaves as a given state increases. The stateful design gives an ideal reference, where stateful NF instances suffer zero network delay, as all state accesses happen locally. On the contrary, stateless NF instances must interrupt their operation to access their states that might be on a remote host.
Assumption 2.
We assume stochastic network delays between hosts of the data center cluster, modeled by random variable X, and we suppose the cumulative distribution of X to be known: .
The replication factor affects network delay during writing events only if those are synchronous operations. Then, the experienced network delay per second caused by writing operations is .
The DB instance, where the master instance is located, takes care of the slave maintenance, preferably by parallel updates to every slave instance. Due to the parallel execution, updating slaves lasts until the last one has finished. The network delay experienced by stateless NFs during updating multiple slave instances is: , where are independent and identically distributed random variables of Assumption 2. The maximum update time during the parallel update execution corresponds to the lifetime of the Parallel Switching Systems known from the Reliability Theory [23].
The total time that writer NFs wait for the network during slave update operations per second is therefore .
The total reading network delay per second that reader NF instances waiting for is .
Definition 7.
Let T represent the total waiting time due to assumable stochastic network delays, . Then, the optimal replication factor for state s according to the total waiting time is .
In Figure 3a, we show two simple state placement requests (Case 1 and Case 2) for state s that the Replication module may get as input. Both requests contain one writer NF () and six readers (). The difference lies within the writing and reading rate vectors—the first case gives a rather read-heavy state, while the second one describes a write-heavy one. We used the EC2-EUW-1 measured delay values between the hosts from [24], that is, we modelled them by an Erlang distributed random variable, of which the expected value is 367 . For the sake of simplicity, we set the size of the state to 1 MB.
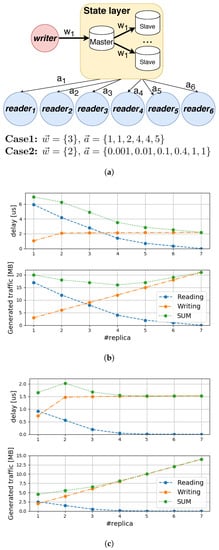
Figure 3.
An example input of Replica Controller and the corresponding delay and traffic values depending on the number of state instances. (a) A stored state whose master/slave instances are written by one and read by six NF instances with different writing and reading rates. (b) Total network delay and generated traffic depending on number of state instances in the read-heavy first case. (c) Total network delay and generated traffic depending on number of state instances in the write-heavy second case.
Figure 3b depicts total generated traffic and suffered delay depending on the replication factor of Case 1. In the upper part, the orange line depicts , while the blue one shows depending on replication factor . The green line is the total waiting time of the stateless NF instances. One might conclude that the more replicas exist, the less time NFs wait for network delay. The bottom part of the Figure shows the generated reading and writing traffic in one second, depending on the replication factor. Here, we can conclude that if the state has four replicas, then traffic is minimal. In Figure 3c, one might see how total delay and traffic can change in the case of a write-heavy access pattern. To conclude, the fewer replicas that exist, the less traffic is generated, and according to total delay, when beginning from five replicas, the total waiting time of NF instances is near minimal.
4.3. Maximum Access Rate Depending on the Slave Count
When an externalized state is too popular, its writing or reading rate might become higher than the theoretical maximum. For example, when slave updates take time with instances of state s, the theoretically maximal number of updates per second is . Hence, the total number of possible updates in the function of the replication factor is given by . If the required update frequency, that is, the total write frequency is higher than what is attainable with the host-to-host delays, then the network is a bottleneck.
Similarly, an NF instance’s theoretical maximum read count per second is . For simplicity, we assume that NF instances can read replicas locally with negligible delay. Consequently, if the NF’s read is local, then its reading rate is always satisfied. However, if NF’s read is remote, then we have to use the formula to get the upper limit on the number of reads that can be fulfilled per second by NF. While a remote state read operation is independent of the number of replicas as the NF reads only one of them, the number of replicas actually determines how many NFs can find and read the state locally. The total attainable read count per second in the case of the replication factor is given by .
4.4. Proposed Model for Determining the Replication Factor
Within our proposed data layer, we consider the optimization that determines the number of instances for each state, one by one, on the following normalized and weighted input:
First term of the argument gives the normalized total generated traffic of Definition 6, and the second term is the normalized total delay of Definition 7 if the number of state instances is i. The weight factor is freely adjustable within , depending on whether data center network traffic or access latency is more important to decrease. We present a numerical evaluation of the optimal replication factor in Section 6.
5. The Complexity of the State Placement Problem and Our Heuristic Solution
5.1. Problem Formulation
In this section, we show that the problem of optimally placing the state instances of cloud-native applications within a cluster is complex. The additional notations we use here are listed in Table 4. Input parameters, such as , , , and are not necessarily available for all states at first—however, as we mentioned in Section 2.1, the proposed state-layer architecture enables a feedback system, that is, when the Migration module triggers the replacement of the states, thanks to the Access Pattern monitor, the above-mentioned input variables will be available based on the past accesses.

Table 4.
Mathematical notations.
In the problem formulation, we treat network delays as deterministic parameters, as opposed to the study in Section 4. Furthermore, our proposed state-layer system enables a feedback loop, so multiple state placement optimizations might occur over time, and we treat the replication factor as an input parameter, not as a variable in the formalized model. Consequently, the number of replicas for each state is fixed in an optimization cycle.
The Quadratic Programming (QP) model of the State Placement Problem is formally defined as follows.
subject to
Our proposed objective function (1) contains three terms—namely, the total delay of (1) updating slaves parallel from the master instance, (2) writing master instances by NF instances, and (3) reading either the master or one of its slave instances by an NF instance, respectively. The solution for this problem is a state placement model, such that accessing and updating replicas yields the minimum latency in total.
The explanation for the constraints is the following. Each master must be mapped to a host (2), and each of its slaves is mapped to exactly one host (3). The Reference (4) is the anti-affinity rule—the master instance and any of its slaves cannot be on the same host. The total size of state instances stored on any given host must not be greater than the host’s capacity (5).
5.2. Proof of Complexity
The State Placement Problem is a generalization of the problem presented in our preliminary version of this paper. In order to make this work self-contained, we present the same proof as in [14]. We show that the Subset sum problem—a well-known NP-complete problem [25]—is polynomial time-reducible to our State Placement Problem. For the sake of clarity in the notation, we define the Subset sum problem below.
Definition 8.
The Subset sum problem consists of n items with weights , and a knapsack of capacity k. The elements of W and k are all non-negative integers. The problem is to select a subset of W whose sum is closest to k, without exceeding it.
In the Karp reduction, let us denote by K the instance of the Subset sum problem, and by L the instance of a relaxed version of the State Placement Problem in which there are no slaves . Let L contain as many states as there are items in K, that is, , and let their sizes be the same as the item weights . In addition, let L contain as many NFs as the sum of weights in K, that is, , where . Finally, let us assume that every state is accessed by as many NFs as its size, but each NF accesses only one state.
In the left side of Figure 4, we draw the constructed State Placement Problem for an example instance of the Subset sum problem, such as the size of state in —thus, it is accessed by two NFs, and , which access no other state than .
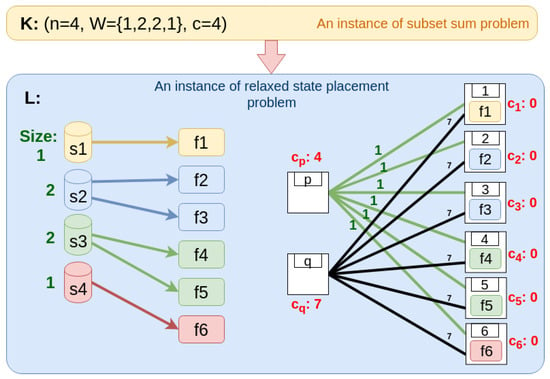
Figure 4.
An example for reduction of the Subset sum problem to the state placement problem.
We constructed L so that the number of hosts could be given by the number of NFs, and we added two more hosts: . The capacities of the additional hosts are the knapsack capacity , and the sum of item weights plus one, that is, of K. The other hosts have zero capacity, . Hosts p and q are connected to all the other hosts, except to each other. Every edge of p (depicted by green lines in Figure 4) has a delay of , while the edges of q (depicted by black lines) have a delay of . This topology can be modeled by a complete bipartite graph, where nodes p and q are one part, and the remaining hosts constitute the other part of the graph.
The right side of Figure 4 shows the host Topology Model of the constructed State Placement Problem.
When the State Placement Problem is solved, the result of L is a mapping matrix , where the rows represent hosts p and q, and the columns correspond to the states . The first row of the matrix is the vector . An optimal solution for the problem in Figure 4 is the following:
For tractability, we tagged the columns and rows with state and host labels, respectively.
Let denote the optimal solution of K, that is, the set of items to be selected into the knapsack. In addition, let mark the optimal solution of L. With the following lemmas, we establish the exact correspondence between and .
Lemma 1.
.
Proof.
Since a state is mapped to exactly one host, the sum of each column of M is 1: . □
Lemma 2.
.
Proof.
Let us assume . Then exists another item set , such that , , .
To complete the proof, consider the following cases: either , or . In the first case, due to the fact that the objective of is higher than that of , the optimal solution for K is . This contradicts the assumption that OPT(K) is the optimal solution for K. In the second case, , thus based on Lemma 1, is the optimal solution for L. In this case, the cost of is higher than , and consequently, is a better solution for L. This contradicts the assumption that is the optimal solution for L. □
Theorem 1.
The State Placement Problem is NP-Hard.
Proof.
As Lemma 2 shows, the Subset sum problem—a well-known NP-complete problem—is polynomial time-reducible to the State Placement Problem, constructed without slaves. Hence, the slave-free State Placement Problem is NP-hard. Since it is a sub-variant of the original problem, the general State Placement Problem is NP-hard. □
5.3. Proposed Heuristic Placement Algorithm
To find an approximately optimal mapping, we have created a heuristic solution that we named the flooding algorithm (https://github.com/hsnlab/flooding_state_placement (accessed on 16 December 2020)). In the flooding algorithm (Algorithm 1), we first performed multiple shortest-path searches, such as by using the Floyd–Warshall algorithm to find the minimal latency routes between the hosts and creating a delay matrix about the topology. Second, we sort the masters into descending order, according to the sum of their size and their slave instances’ total size (line 4). For example, if the size of a master is x and it has two slaves, then their total size considered in the sorting is . Third, we iterated through the sorted list. If a master has no slaves (line 9), its optimal host is found by the GetOptimalHost algorithm described in Algorithm 2 that has four inputs: the state s to be placed, a set of candidate hosts where the state could be placed, and a set of hosts from where the NFs access the state and the delay matrix D of the hosts. The algorithm iterates through the candidate hosts one by one, and examines how far they are from the hosts where reader and/or writer NFs are located. We weigh the costs of these paths by multiplying them with the corresponding reading/writing rates of the NFs. Finally, we choose the host, which owns the minimal cost.
The flooding algorithm initially does not take into account the capacities of the hosts, and assigns the destination location for each state instance based solely on delay, regardless of the host’s free capacity. If the master did have slave instance(s), and was read by only one NF instance (line 12), then we first determined the optimal host for the master as before (line 13, 14), then for each slave, one by one (line 15, 17). Finding a host for a slave instance was done by calculating the delays between each candidate host and the host where the master was placed, and the candidate with minimal cost was chosen.
| Algorithm 1: Flooding algorithm. |
 |
| Algorithm 2: GetOptimalHost procedure. |
 |
In case slave instances exist and the master is read by multiple NF instances (line 18), we first separated the NFs based on whether they read (line 19), and/or wrote (line 21) the master. For the reader NFs, we made the following data assignment with the goal of co-locating them with the reader NF instances. Let us assume that there are m slaves and n reader NFs. In case , the assignment is and , where and are the ith slave and reader NF, and s is the master of the elements of . If , we allocated the state instances to NFs as follows: . In the second step, we extended the state-to-NF assignment by including the writer NFs as well (line 32). For the state-to-NF assignment, we included the master instance as a shadow NF (line 34), as it is considered to be writing the slaves. The third and final step was to find the target hosts for all master/slave instances (line 36–39). We calculated the optimal host initially for the master, based on its weighted total distance from the hosts of the assigned NFs. Then for the slaves, the shortest path calculations were done from the host of the master replica and from the hosts of assigned NFs.
In line 40, for each host, we sorted the assigned master instances according to . Since data are placed on hosts without checking capacity, available memory may turn to negative values for certain hosts after the placement round. Therefore, the flooding algorithm repeats the following steps until negative values exist (line 41–49). (i) From the most loaded host, we pick the master, for which is minimal. (ii) We move the picked one to the closest host, in which the free capacity after the migration is larger than what it was in the original host and it does not contain any of its slaves. When there are no more hosts with negative capacity, the algorithm stops and returns the calculated placement of state instances.
The time complexity of the proposed heuristic solution is . In a realistic scenario, typically the following correlations exist: .
6. Evaluation
In order to get a comprehensive analysis of the performance of our flooding placement algorithm and replication strategy, we made simulations on a 6-core Intel Core Processor @2.4GHz server with 32 GB of RAM. We split our evaluations into two simulation groups. To the best of our knowledge, the State Placement Problem has not been addressed yet—thus, in our evaluation, we compare the heuristic algorithm to the optimal solution and to a simple heuristic’s solution in Section 6.1. In Section 6.2, the proposed replication strategy is compared to the two most widely used replicating everywhere, and fixed replication factor strategies.
6.1. Performance of the Flooding State Placement
To find the optimal placement, we used CPLEX, a solver developed by IBM [26], to solve the QP problem. To arrive at the quadratic formula of our problem, we used model transformation [27]. In simulations, we examined how close the flooding placement results are to the optimal one, and compared the run time of the flooding algorithm to the solver’s. We looked for the scale, at which the placement problem gets so complex that CPLEX would require more than one hour to find the optimal placement. We also investigated how the access pattern affects the quality of our heuristic algorithm.
During our simulations, we assumed a fat-tree [28] topology of data center hosts. Each physical link is abstracted to yield one unit of latency, and the received placement performance results are normalized by the number of state accesses. We assumed that synchronous operations, that is, writings, lasted until all slave replicas were updated. In the figures below, we used the average state access waiting time metric which is the value of the objective function (1) from Section 5 divided by the total number of state accesses.
Table 5 shows the average run time of the placement algorithms in seconds, depending on the number of states to be placed. The topology consists of six hosts, in which 12 NF instances are running. For each state, one to six instances are generated randomly according to uniform distribution. We divided the state placement requests into two different cluster load amounts: light and heavy. In the case of the former, the sum size of the master and slave instances that we like to store in the state layer, is between 40–50% of the hosts’ total memory capacity. In the case of heavy load, this value is between 50–60%. When CPLEX could not solve the problem within the one-hour time limit, we marked it with "N/A". With 100 state instances, the optimal algorithm’s run time was in the order of seconds, but the flooding finished the job in milliseconds. In the case of 1000 states, the former needs minutes, while the latter requires seconds to calculate the placement. Furthermore, from the 5000 states, the optimal algorithm could not solve the problem within one hour. These measurements prove that solving the state placement problem for realistic large-scale instances is possible only with heuristic solutions, like our flooding algorithm.

Table 5.
The average run time of placement algorithms in seconds, and the percentage of simulations exceeding the one hour time-limit. Opt. represents the Integer Linear Programming (ILP)/QP problem-solver CPLEX, while Flood. denotes our Flooding heuristics.
Table 5 also contains the percentage simulations, in which finding the optimal solution did not occur within the one-hour time limit. We can conclude, independently of the number of state replicas, that the placement problem becomes more complex for the solver over a cluster load. Initially, in the case of a light load, the complexity greatly depends on the state count, that is, how many states the NFs want to store. In the case of 100 states only 4%, and for 1000 states, 26% of the optimum calculations reached the one-hour limit, but for 5000 states, this increased to 100%. In contrast, the flooding algorithm never reached the one-hour time limit during the simulations with these inputs.
Figure 5 shows the empirical distribution of state access waiting time averages of the optimal, flooding, and random placements depending on the total number of states. The random placement algorithm selects the master replica’s destination host just like the flooding, but for the slave replicas, hosts are picked randomly from the set of nodes where at least one reader NF of the state is hosted. To get the optimal solution too, we used light cluster load requests. Topology and request settings are the same as in the simulations shown in Table 5. As the figure depicts, the flooding yields, on average, ~ worse delay than the optimal. Furthermore, we conclude the quality of placements is not significantly affected by the number of states. The bulk of the average access waiting time remains between and in all cases.
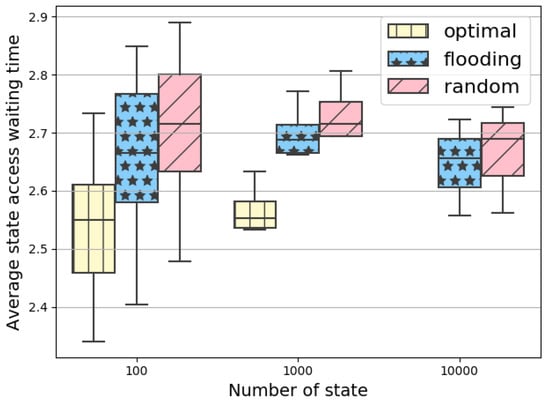
Figure 5.
Performance of the optimal, flooding, and random heuristics depending on the number of servers. Since the optimal from 10k states exceeds the one-hour time limit, its results are presented up to the input of 1k states.
Figure 6 shows the performance difference between the flooding and the random placement. We used a heavy cluster load and twice as many deployed NFs as the number of hosts. According to our configuration settings, one rack could contain five hosts. Apart from these, the topology and the request settings were the same as in the simulations shown in Table 5. In the case of five hosts, there was only a slight difference between the two placement solutions. However, as we increased the size of the cluster, the difference became larger. Interestingly, the more hosts were in the cluster, the higher was the average state access waiting time. The reason for that was that the more racks existed in the cluster, the higher was the chance of access NFs being located in different racks. This results in more inter-rack communications, which increases access delay.
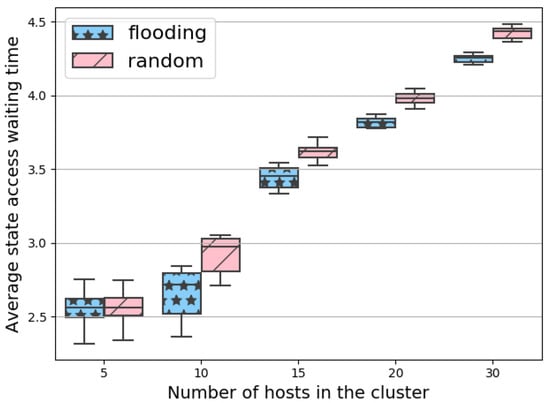
Figure 6.
Performance of the flooding and the simple algorithm depending on the number of hosts in the cluster.
We examined the effect of state access patterns on the average state access waiting time. Three access patterns were defined, namely, (1) write-heavy (18% read, 57% write, and 25% both), (2) read-heavy (57% read, 18% write, and 25% both) and balanced, where the state instances are read and written equally (33% read, 33% write, and 33% both). These access patterns indicate the relative frequency of each access type. For example, in the case of write-heavy, if a hundred NFs access a state, then 18 from them read, 57 write, and the remaining 25 both read and write it. Figure 7 summarizes our simulation results related to the placement quality of our proposed flooding algorithm depending on the access pattern type and on the number of states. We can conclude that the access pattern has a great effect on the average state access waiting time independently of the number of states that the algorithm places into the cluster. As we expect, the more NFs write the state instances, the higher the average access waiting time is. The reason for this is that NFs are not allowed to write the slave instances, therefore writes, and the slave updates that follow take, in total, a large amount of time, causing delays in state access in general.
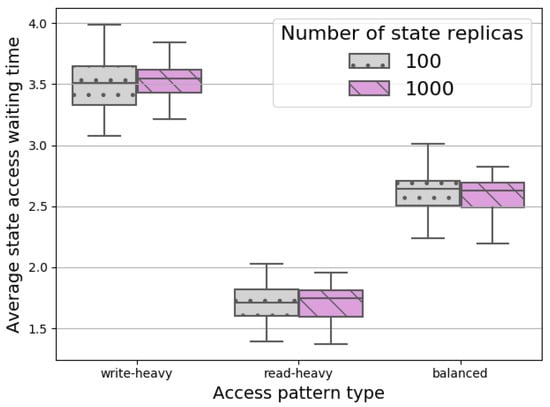
Figure 7.
Access delay results of the proposed placement in the case of different state access patterns and number of state instances.
6.2. Replication Module Evaluation
In this section, we show the performance comparison of our proposed replication strategy to the two most famous ones: the replication everywhere and the fixed replication factor. The proposed replication strategy is detailed in Section 4.4. We used parameter configuration. The simulation process is the following: We generate the state placement requests (i.e., SADs) an identical number of each previously introduced access pattern without any slave instance. The replication strategy extends the SADs with an appropriate number of slaves for each master instance. The extended SADs are served to our proposed flooding placement algorithm. Finally, we check the placement result of the state instances. We compare it to the stateful design—that is, we answer the question of how much additional delay and generated traffic emerges, thanks to the stateless architecture of the NFs. For the simulations, we use six fully connected hosts and 1000 states to be placed. The size of a state is randomly chosen between one and five MB, according to the uniform distribution.
In Figure 8, the y-axis shows the average generated traffic by the NFs to access their externalized data in the state layer. We used three different access pattern types. The fixed replication factor was set to two, that is, each master had one slave datum in the state layer. Our proposed strategy was more efficient in each access pattern case than the fixed replication factor strategy. Compared to the replicate everywhere, due to the update operations triggered by writings, the everywhere strategy resulted in times more traffic than ours, in the case of the write-heavy access pattern. Furthermore, this strategy was the worst in each scenario as well.
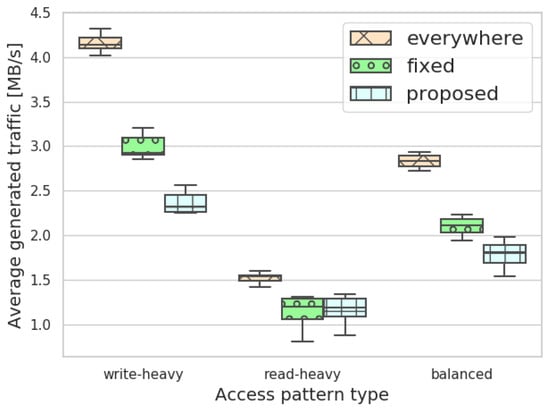
Figure 8.
Average generated traffic by state accesses in the case of different state access patterns and replication strategies.
If we examine the effects of the replication strategies on the access delay, we can notice our method is the most effective in the case of the write-heavy access pattern. On the other hand, with read-heavy and balanced states, the proposed solution is similar to the fixed replication factor strategy, while replication everywhere is the best.
To conclude our experiences, the replication everywhere strategy could result in better delay performance, but it is inapplicable in practice due to its generated traffic overhead. Comparing the fixed replication factor to our solution, the latter provides reduced delay and lowered traffic.
6.3. Discussion
The ultimate goal of the proposed state layer system is to minimize the inter-host data access communications between the cloud-native applications and hosts containing their externalized states. Thanks to the two main optimization components (dynamic replication module and data placement algorithm), the system design is able to decrease the state access time while keeping the network traffic load low. Here, we summarize our proposal’s pros and cons, and compare it to traditional—consistent hashing-based—key-value stores.
In the case of synchronous data access operations, the traditional key-value DB solutions, in terms of inter-host communications, store the externalized states randomly. The target hosts are calculated by hash functions, and not according to the data’s access pattern. In contrast, our data placement algorithm takes into account who reads and/or writes the data and how frequently one accesses it, and optimizes the states’ locations according to these.
In Section 6.1, we show that the CPLEX solver finds the optimal placement an order of magnitude longer than our placement algorithm. What is more, it cannot solve the problem within the one-hour time limit in the case of a heavy cluster load. Consequently, we can conclude that only heuristic solutions can be used in a realistic large-scale system, like our flooding algorithm, to get the placement decision as soon as possible.
In Figure 5, Figure 6 and Figure 7, (1) we show that the quality of flooding placement is not significantly affected by the number of states, (2) the more hosts are in the cluster, the higher the average state access time is, and (3) the access pattern types also have a significant effect on the final placement result.
However, not only the data placement algorithm, but also the number of slave instances affects the state access time. Thus, we propose a dynamic replication module to find the sweet spot in fast access time and low network traffic. Comparing it to the fixed replication factor strategy—applied mostly in traditional key-value stores—we show in Section 6.2 that, in terms of the generated network traffic, our strategy was more efficient, independent of the access pattern types. On the other hand, except for a write-heavy access pattern type, the two approaches perform similarly in terms of the access delay.
Naturally, the proposed system design has limitations as well. As opposed to the traditional key-value stores where the client’s side hash-function calculates which host owns the state, the server’s side Placement module is responsible for this in the proposed system. In other words, the placement logic is centralized in our design, while it is typically distributed in traditional key-value stores. In such a scenario where cloud applications use asynchronous operations to read and write states, the centralized placement strategy could cause unnecessary overhead in the state layer’s operation. In such a case, the applications do not care about the externalized states’ access time; they require the state store’s resiliency and reliability guarantee. For such purposes, the traditional key-value stores are suitable as well.
7. Related Work
7.1. Popular Key-Value Stores
Key-value stores from the industry, such as Redis [21], Memcached [29], Cassandra [30], and DynamoDB [22], typically use random state placement—in terms of data access time—based on either a consistent hashing, or a hash-slot/node association. These solutions allow fast state lookups; however, applying random placement, they do not tackle the minimization of remote state access. Therefore, these solutions may lead to orders of magnitude with higher latency than our proposed algorithm.
Similarly, the latest state-of-the-art, key-value stores from academia, such as [18,19,20,31,32,33], either concentrate on a single-node setup or—like the industry ones above—use hash functions to determine where to place data. This kind of placement does not take into account the delay distribution of the host cluster they are working on or the access pattern of the data to store, which is crucial to optimize the access latency.
Another kind of solution is to minimize the data movement over the network if you move the function close to the data (instead of the state to the function). Shredder [34], a low-latency, multi-tenant cloud store, applies this concept, since it “allows small units of computation to be performed directly within storage nodes”.
In [35], the authors presented a key-value store which monitored the data accesses and, according to the reader locations, determined the hosts where the data should be copied to. This way, their solution minimizes reading access delays, but contrary to our data layer, they optimize only the reading accesses. The master instance’s host is determined by a hash function, which can result in unnecessary writing latency that occurs due to the data center network between hosts.
Anna [19,20] is a distributed key-value store, positioned as an auto-scaling, multi-tier service for the cloud. According to the authors, it enables selective replication of hot keys to improve the access latency. Similarly to other popular key-value stores, this solution uses a hash function to calculate where to place data within the cluster.
Table 6 shows the comparative analysis of our solution and other state-of-the-art stores. Except for DAL and our proposed architecture, all stores maintain a pre-configured number of replicas of the stored data. On the other hand, different data replication factors might exist for each datum individually. Similarly, only DAL and our solution enables data access pattern-aware data placement; that is, they handle individual data items independently and attempt to find them the optimal target server to minimize the access latency. Finally, to accelerate the data accesses (of hot data), most of the presented key-value stores use client-side caches to avoid the network latency which occurred during a remote server request. In contrast, Anna detects hot data (by pre-configured thresholds on accesses) and increases their individual replication factor to multiply the number of replicas and to distribute the access workload. DAL maintains a list of servers where access requests arrive and moves the data to the most querying one. The proposed architecture automatically detects if the access pattern of a datum has changed, and triggers the re-optimization of the data localities—that is, they attempt to find the optimal target server for each state instance. During the re-optimization, the replication factors are calculated to each datum individually.

Table 6.
Comparative analysis of state-of-the-art stores and our proposed solution.
To our best knowledge, there is no prior research work that would propose placing both master and slave instances in a non-reactive way with the goal of minimizing state access latency. State-of-the-art solutions approach the problem from a different perspective, as they generally use a hash function to store data and cache it on the application’s site to speed up access. In this paper, we propose a solution, which (1) considers a large number of small states as data, (2) provides smart state placement to improve reliability and read performance, and (3) determines the destination host for each master and slave instance based on state access patterns.
7.2. Data/Replica Placement
In the era of Edge/Fog/Cloud computing, papers have appeared [35,36], in which the authors propose replica placement strategies to minimize access latency between data replicas and data sources and/or sinks. In contrast to our model, where both master and their slave instances’ locations are to be selected, these approaches determine the desired locations only for the slave instance.
In ref. [37], the authors present a reactive optimizer for data placement that leverages locality patterns in data accesses, to minimize inter-node communication. Because of the reactive nature of their optimization solution, the authors assume that data access frequencies do not change significantly during the entire optimization process. The autoplacer does not support replications, that is, slave copies from the master data instance.
In ref. [38], an automated mechanism is presented that places application data across data centers, taking into account the WAN bandwidth costs and data center capacity limits, while also minimizing user-perceived latency. Their solution analyses weekly/monthly cloud service logs to recommend migrations of user data based on data access patterns and client locations. They assume large amounts of long-living data files and rare user locality changes to perform more efficient data placement, compared to online heuristic placement solutions.
The scope of their solution is different from ours, since we deal with in-memory stored short-lived states, and with individual replica requirements that need to be calculated for optimal placement immediately.
7.3. Stateless Network Function Frameworks
According to the best of our knowledge, two NFV platforms enable the stateless working [2] of virtual functions: DAL [3], and S6 [4]. These solutions place the states close to the NF that created them and move them, in a reactive manner, across the cluster nodes—that is, they keep relocating states to one of the accessing NFs based on the access pattern and network traffic. DAL and S6 strive to optimize state placement during operation, not at deployment time.
7.4. Technologies Related to the Concept of State Externalization
Other emerging technologies, such as Software-Defined Networking and Network Function Virtualization (SDN/NFV) [39], containerization [40], Function as a Service, and serverless computing [41] seem to be conceptually close to the state externalization discussed in this paper. The essence of these technologies (among others) is to run our applications/services in a virtualized environment, where function placement algorithms like [42,43] ensure the locality of functions, to guarantee greater flexibility and reliability of them. However, to make these benefits happen, our software needs to run in stateless compute containers [44,45], or more precisely, any state of a virtualized function (e.g., FaaS) that has to be persistent, needs to be externalized into a persistent store [46].
8. Conclusions
The trend of network function virtualization has not stopped at breaking the link between software and custom hardware. In order to support fast recovery and seamless scalability, virtualized software components are also being dissected to separate processing and data-storing functionalities. In this paper, we focus on the placement of externalized states of network functions in cloud environments.
Our contributions are four-fold. First, we proposed an architecture design for the state layer of stateless NFV frameworks, which stores the externalized state data with the overall aim of remote access minimization. Second, to keep the amount of state access traffic and state read latency low, we designed a state access pattern-based replication scheme, which determines the optimal replication factor for each state. Third, by aiming at minimizing state access latency to ensure high performance of the applications, we formalized the combinatorial optimization problem of selecting hosts for the states, and we showed that the problem was NP-hard. To overcome this complexity, we designed a fast and efficient heuristic solution to find state placement solutions. Fourth, we evaluated both the proposed replication scheme and placement algorithm, comparing them to the widespread and optimal solutions. We showed, for large-scale systems, only the heuristic placement solution that could be the realistic choice—our proof-of-concept implementation reached running times a fraction of those of the optimization algorithm. Furthermore, we demonstrated that our replication scheme leads to lower generated traffic and access delay results than most of the schemes applied in the state-of-the-art.
Author Contributions
Conceptualization, M.S., P.M. and L.T.; methodology, M.S., P.M. and L.T.; software, M.S.; validation, M.S., P.M. and L.T.; formal analysis, M.S., P.M. and L.T.; investigation, M.S., P.M. and L.T.; writing—original draft preparation, M.S. and L.T.; writing—review and editing, M.S., P.M. and L.T.; visualization, M.S.; supervision, P.M. and L.T.; project administration, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
Project no. 135074 has been implemented with the support provided from the National Research, Development, and Innovation Fund of Hungary under the FK 20 funding scheme.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Kablan, M.; Caldwell, B.; Han, R.; Jamjoom, H.; Keller, E. Stateless Network Functions. In Proceedings of the 2015 ACM SIGCOMM Workshop on Hot Topics in Middleboxes and Network Function Virtualization—HotMiddlebox’15, London, UK, 21 August 2015; ACM Press: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Kablan, M.; Alsudais, A.; Keller, E.; Le, F. Stateless network functions: Breaking the tight coupling of state and processing. In Proceedings of the 14th USENIX Symposium on Networked Systems Design and Implementation (NSDI 17), Boston, MA, USA, 27–29 March 2017; pp. 97–112. [Google Scholar]
- Németh, G.; Géhberger, D.; Mátray, P. DAL: A Locality-Optimizing Distributed Shared Memory System. In Proceedings of the 9th USENIX Workshop on Hot Topics in Cloud Computing (HotCloud 17), Santa Clara, CA, USA, 10–11 July 2017. [Google Scholar]
- Woo, S.; Sherry, J.; Han, S.; Moon, S.; Ratnasamy, S.; Shenker, S. Elastic scaling of stateful network functions. In Proceedings of the 9th 15th USENIX Symposium on Networked Systems Design and Implementation (NSDI 18), Renton, WA, USA, 9–11 April 2018; pp. 299–312. [Google Scholar]
- Taleb, T.; Ksentini, A.; Sericola, B. On service resilience in cloud-native 5G mobile systems. IEEE J. Sel. Areas Commun. 2016, 34, 483–496. [Google Scholar] [CrossRef]
- Szalay, M.; Nagy, M.; Géhberger, D.; Kiss, Z.; Mátray, P.; Németh, F.; Pongrácz, G.; Rétvári, G.; Toka, L. Industrial-scale stateless network functions. In Proceedings of the 2019 IEEE 12th International Conference on Cloud Computing (CLOUD), Milan, Italy, 8–13 July 2019; pp. 383–390. [Google Scholar]
- Abbasi, A.A.; Al-qaness, M.A.; Elaziz, M.A.; Hawbani, A.; Ewees, A.A.; Javed, S.; Kim, S. Phantom: Towards Vendor-Agnostic Resource Consolidation in Cloud Environments. Electronics 2019, 8, 1183. [Google Scholar] [CrossRef]
- Abbasi, A.A.; Al-qaness, M.A.; Elaziz, M.A.; Khalil, H.A.; Kim, S. Bouncer: A Resource-Aware Admission Control Scheme for Cloud Services. Electronics 2019, 8, 928. [Google Scholar] [CrossRef]
- Varga, P.; Peto, J.; Franko, A.; Balla, D.; Haja, D.; Janky, F.; Soos, G.; Ficzere, D.; Maliosz, M.; Toka, L. 5g support for industrial iot applications–challenges, solutions, and research gaps. Sensors 2020, 20, 828. [Google Scholar] [CrossRef] [PubMed]
- Toka, L.; Recse, A.; Cserep, M.; Szabo, R. On the mediation price war of 5G providers. Electronics 2020, 9, 1901. [Google Scholar] [CrossRef]
- Intel. Network Function Virtualization: Quality of Service in Broadband Remote Access Servers with Linux and Intel Architecture; Intel: Santa Clara, CA, USA, 2014. [Google Scholar]
- Intel. Network Function Virtualization: Virtualized BRAS with Linux and Intel Architecture; Intel: Santa Clara, CA, USA, 2014. [Google Scholar]
- Mahmud, N.; Sandström, K.; Vulgarakis, A. Evaluating industrial applicability of virtualization on a distributed multicore platform. In Proceedings of the 2014 IEEE Emerging Technology and Factory Automation (ETFA), Barcelona, Spain, 16–19 September 2014; pp. 1–8. [Google Scholar]
- Szalay, M.; Mátray, P.; Toka, L. Minimizing state access delay for cloud-native network functions. In Proceedings of the 2019 IEEE 8th International Conference on Cloud Networking (CloudNet), Coimbra, Portugal, 4–6 November 2019; pp. 1–6. [Google Scholar]
- Szalay, M.; Matray, P.; Toka, L. AnnaBellaDB: Key-Value Store Made Cloud Native. In Proceedings of the 2020 16th International Conference on Network and Service Management (CNSM), Izmir, Turkey, 2–6 November 2020; pp. 1–5. [Google Scholar]
- Pallis, G.; Vakali, A. Insight and perspectives for content delivery networks. Commun. ACM 2006, 49, 101–106. [Google Scholar] [CrossRef]
- Bhamare, D.; Jain, R.; Samaka, M.; Erbad, A. A survey on service function chaining. J. Netw. Comput. Appl. 2016, 75, 138–155. [Google Scholar] [CrossRef]
- Ousterhout, J.; Gopalan, A.; Gupta, A.; Kejriwal, A.; Lee, C.; Montazeri, B.; Ongaro, D.; Park, S.J.; Qin, H.; Rosenblum, M.; et al. The RAMCloud storage system. ACM Trans. Comput. Syst. (TOCS) 2015, 33, 1–55. [Google Scholar] [CrossRef]
- Wu, C.; Sreekanti, V.; Hellerstein, J.M. Autoscaling tiered cloud storage in Anna. Proc. VLDB Endow. 2019, 12, 624–638. [Google Scholar] [CrossRef]
- Wu, C.; Faleiro, J.; Lin, Y.; Hellerstein, J. Anna: A kvs for any scale. IEEE Trans. Knowl. Data Eng. 2019, 33, 344–358. [Google Scholar] [CrossRef]
- Da Silva, M.D.; Tavares, H.L. Redis Essentials; Packt Publishing Ltd.: Birmingham, UK, 2015; ISBN 978-1-78439-245-1. [Google Scholar]
- Sivasubramanian, S. Amazon dynamoDB: A seamlessly scalable non-relational database service. In Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data, Scottsdale, AZ, USA, 20–24 May 2012; pp. 729–730. [Google Scholar]
- Rausand, M.; Høyland, A. System Reliability Theory: Models, Statistical Methods, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 396. [Google Scholar]
- Popescu, D.A.; Moore, A.W. A First Look at Data Center Network Condition Through The Eyes of PTPmesh. In Proceedings of the 2018 Network Traffic Measurement and Analysis Conference (TMA), Vienna, Austria, 26–29 June 2018; pp. 1–8. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Cplex, IBM ILOG. V12. 1: User’s Manual for CPLEX; International Business Machines Corporation: Armonk, NY, USA, 2009. [Google Scholar]
- Billionnet, A.; Elloumi, S.; Lambert, A. Linear reformulations of integer quadratic programs. In Proceedings of the International Conference on Modelling, Computation and Optimization in Information Systems and Management Sciences, Luxembourg, 8–10 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 43–51. [Google Scholar]
- Leiserson, C.E. Fat-trees: Universal networks for hardware-efficient supercomputing. IEEE Trans. Comput. 1985, 100, 892–901. [Google Scholar] [CrossRef]
- Memcached—A Distributed Memory Object Caching System. Available online: https://memcached.org/ (accessed on 16 December 2020).
- Lakshman, A.; Malik, P. Cassandra: A decentralized structured storage system. ACM SIGOPS Oper. Syst. Rev. 2010, 44, 35–40. [Google Scholar] [CrossRef]
- Perron, M.; Castro Fernandez, R.; DeWitt, D.; Madden, S. Starling: A Scalable Query Engine on Cloud Functions. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; pp. 131–141. [Google Scholar]
- Lersch, L.; Schreter, I.; Oukid, I.; Lehner, W. Enabling low tail latency on multicore key-value stores. Proc. VLDB Endow. 2020, 13, 1091–1104. [Google Scholar] [CrossRef]
- Chandramouli, B.; Prasaad, G.; Kossmann, D.; Levandoski, J.; Hunter, J.; Barnett, M. Faster: A concurrent key-value store with in-place updates. In Proceedings of the 2018 International Conference on Management of Data, Houston, TX, USA, 10–15 June 2018; pp. 275–290. [Google Scholar]
- Zhang, T.; Xie, D.; Li, F.; Stutsman, R. Narrowing the gap between serverless and its state with storage functions. In Proceedings of the ACM Symposium on Cloud Computing, Santa Cruz, CA, USA, 20–23 November 2019; pp. 1–12. [Google Scholar]
- Matri, P.; Costan, A.; Antoniu, G.; Montes, J.; Pérez, M.S. Towards efficient location and placement of dynamic replicas for geo-distributed data stores. In Proceedings of the ACM 7th Workshop on Scientific Cloud Computing, Kyoto, Japan, 1 June 2016; pp. 3–9. [Google Scholar]
- Mayer, R.; Gupta, H.; Saurez, E.; Ramachandran, U. Fogstore: Toward a distributed data store for fog computing. In Proceedings of the 2017 IEEE Fog World Congress (FWC), Santa Clara, CA, USA, 30 October–1 November 2017; pp. 1–6. [Google Scholar]
- Paiva, J.; Ruivo, P.; Romano, P.; Rodrigues, L. Autoplacer: Scalable self-tuning data placement in distributed key-value stores. ACM Trans. Auton. Adapt. Syst. (TAAS) 2014, 9, 1–30. [Google Scholar] [CrossRef]
- Agarwal, S.; Dunagan, J.; Jain, N.; Saroiu, S.; Wolman, A.; Bhogan, H. Volley: Automated data placement for geo-distributed cloud services. In Proceedings of the USENIX NSDI, San Jose, CA, USA, 28–30 April 2010. [Google Scholar]
- Mijumbi, R.; Serrat, J.; Gorricho, J.L.; Bouten, N.; De Turck, F.; Boutaba, R. Network function virtualization: State-of-the-art and research challenges. IEEE Commun. Surv. Tutor. 2015, 18, 236–262. [Google Scholar] [CrossRef]
- Turnbull, J. The Docker Book: Containerization Is the New Virtualization; James Turnbull: Melbourne, Australia, 2014. [Google Scholar]
- Baldini, I.; Castro, P.; Chang, K.; Cheng, P.; Fink, S.; Ishakian, V.; Mitchell, N.; Muthusamy, V.; Rabbah, R.; Slominski, A.; et al. Serverless computing: Current trends and open problems. In Research Advances in Cloud Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–20. [Google Scholar]
- Basta, A.; Kellerer, W.; Hoffmann, M.; Morper, H.J.; Hoffmann, K. Applying NFV and SDN to LTE mobile core gateways, the functions placement problem. In Proceedings of the 4th Workshop on All things Cellular: Operations, Applications, & Challenges, Chicago, IL, USA, 22 August 2014; pp. 33–38. [Google Scholar]
- Luizelli, M.C.; Bays, L.R.; Buriol, L.S.; Barcellos, M.P.; Gaspary, L.P. Piecing together the NFV provisioning puzzle: Efficient placement and chaining of virtual network functions. In Proceedings of the 2015 IFIP/IEEE International Symposium on Integrated Network Management (IM), Ottawa, ON, Canada, 11–15 May 2015; pp. 98–106. [Google Scholar]
- Roberts, M. Serverless Architectures. 2016, Volume 4. Available online: https://martinfowler.com/articles/serverless.html (accessed on 1 June 2020).
- Fox, G.C.; Ishakian, V.; Muthusamy, V.; Slominski, A. Status of serverless computing and function-as-a-service (faas) in industry and research. arXiv 2017, arXiv:1708.08028. [Google Scholar]
- Sreekanti, V.; Wu, C.; Lin, X.C.; Schleier-Smith, J.; Gonzalez, J.E.; Hellerstein, J.M.; Tumanov, A. Cloudburst: Stateful functions-as-a-service. Proc. VLDB Endow. 2020, 13, 2438–2452. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).