Deadlock-Free Planner for Occluded Intersections Using Estimated Visibility of Hidden Vehicles †
Abstract
1. Introduction
- A generic deadlock-free motion planner for blind intersections that utilizes both the ego vehicle’s and approaching vehicle’s visibility.
- A visibility-dependent behavior model for vehicles approaching occluded intersections based on an analysis of real driving data.
2. Related Work
2.1. POMDP-Based Approaches
2.2. Learning-Based Approaches
2.3. Model-Based Approaches
3. Proposed Deadlock-Free Blind Intersection Planner
3.1. Safe Intersection Crossing Strategy
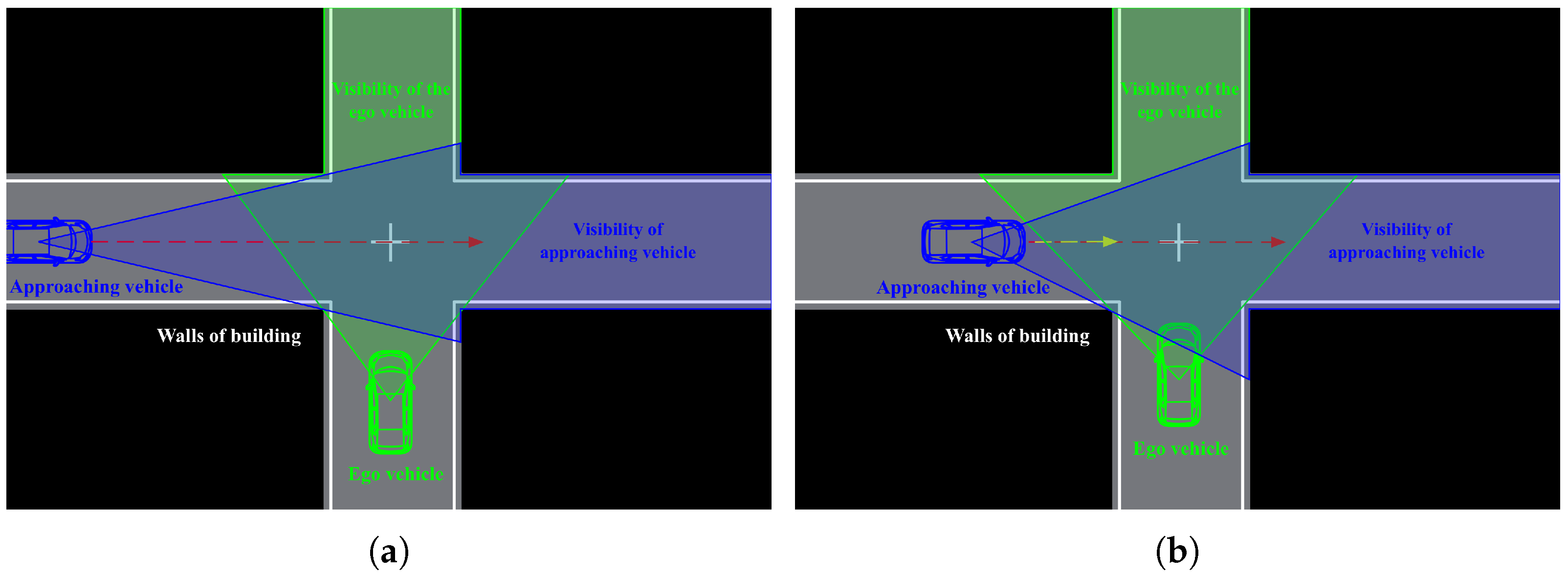
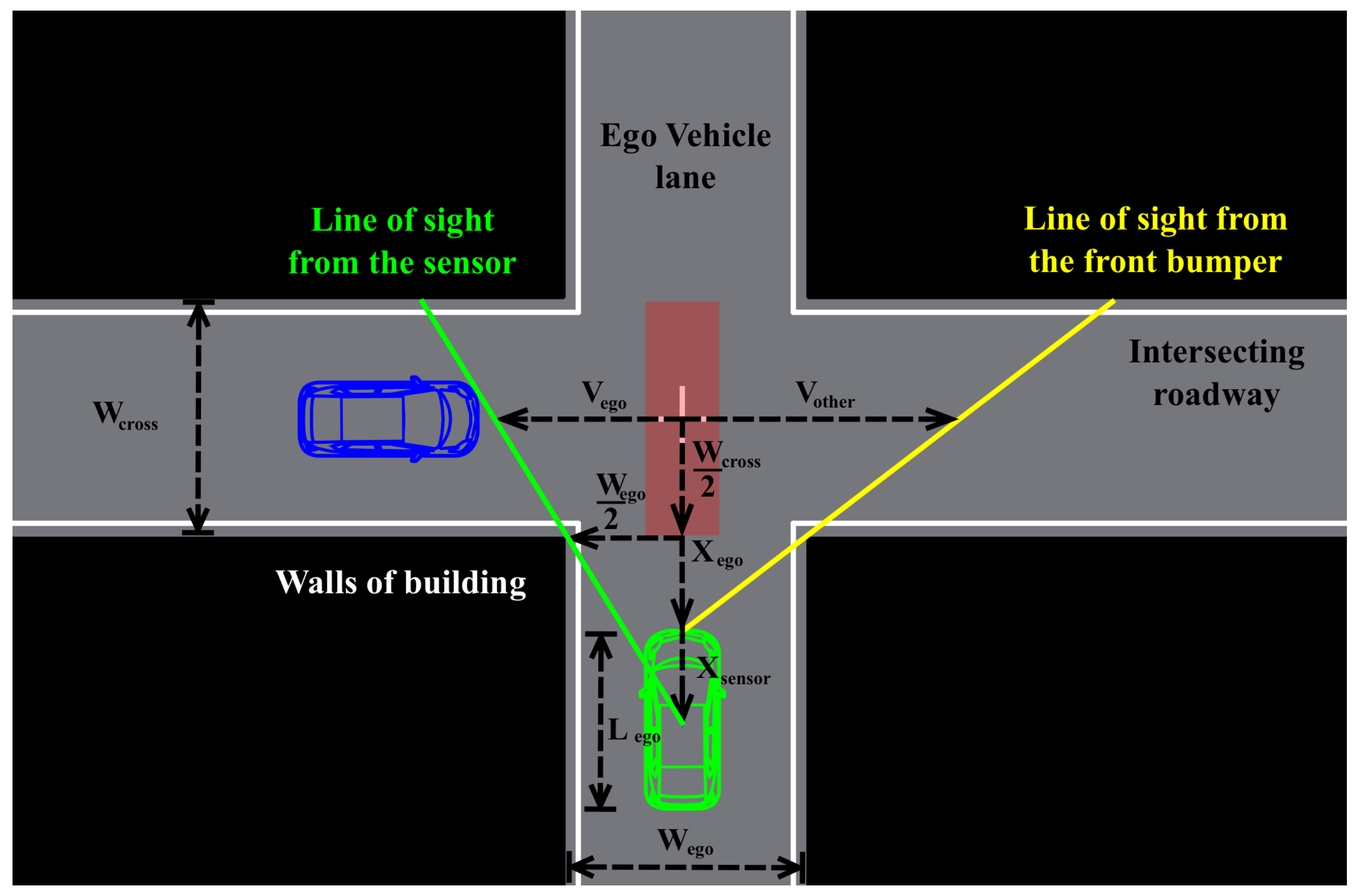
3.2. Visibility at Blind Intersections
| Algorithm 1. Proposed planner |
|
3.3. Particle-Filter-Based Occluded Vehicle Prediction
4. Proposed Visibility-Dependent Behavior Model for Approaching Vehicles
4.1. Collection of Driving Data
4.1.1. Driver Types
- Expert drivers: Driving school instructors;
- Elderly drivers: Drivers who are 65 years old or older;
- Typical drivers: Drivers who do not belong to the other two groups.
4.1.2. Experimental Vehicle
4.1.3. Experimental Environment
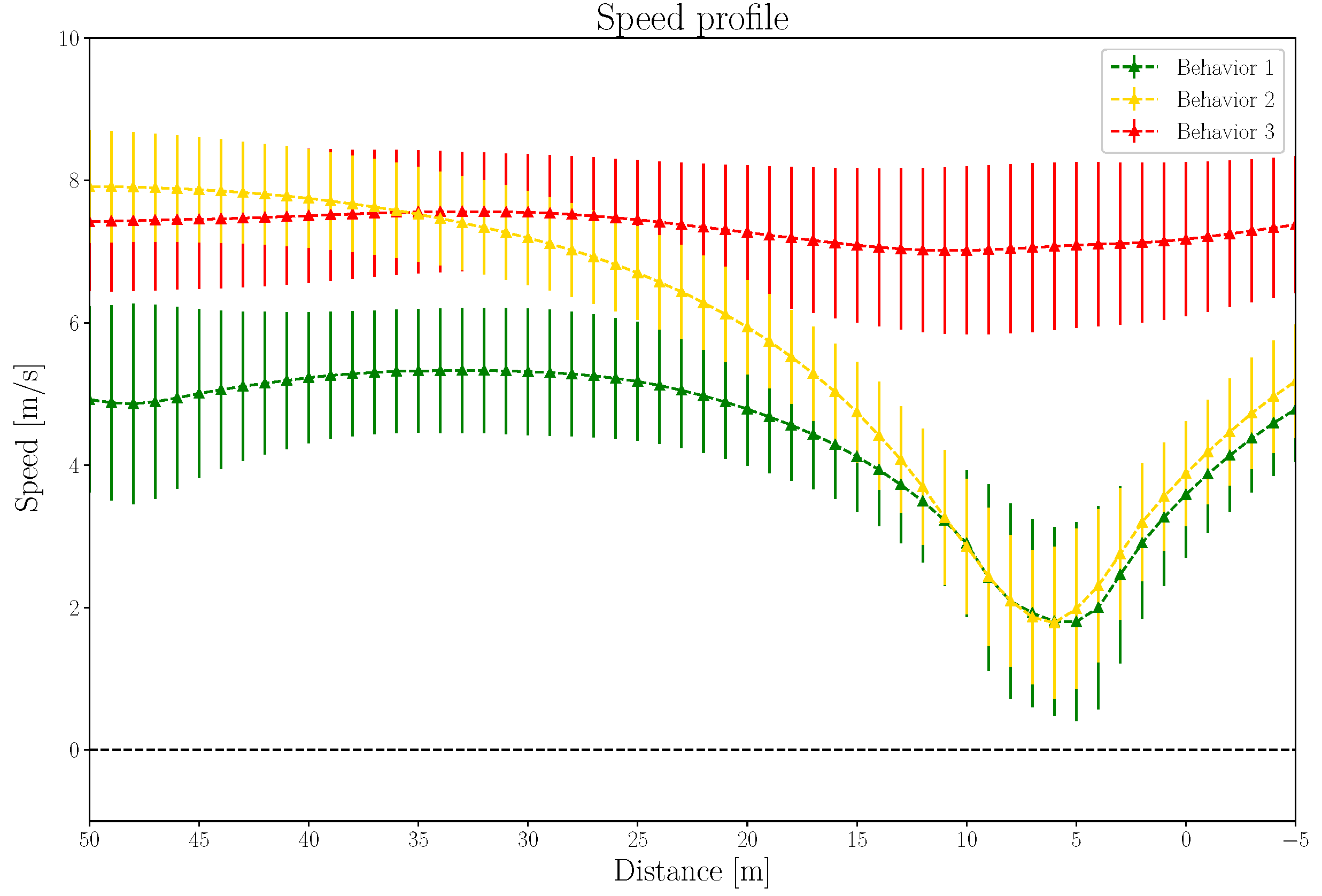
4.2. Driving Data Analysis
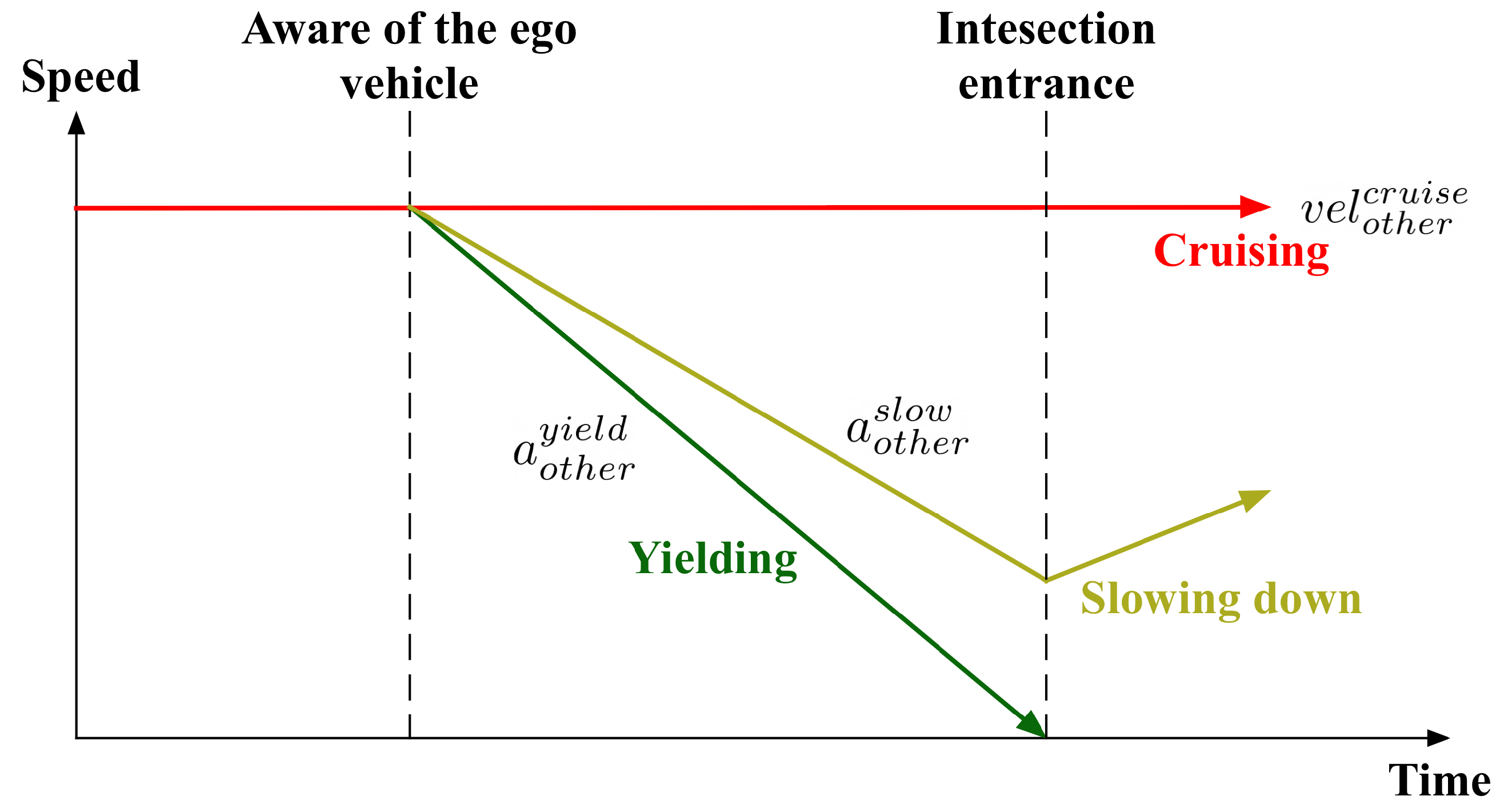
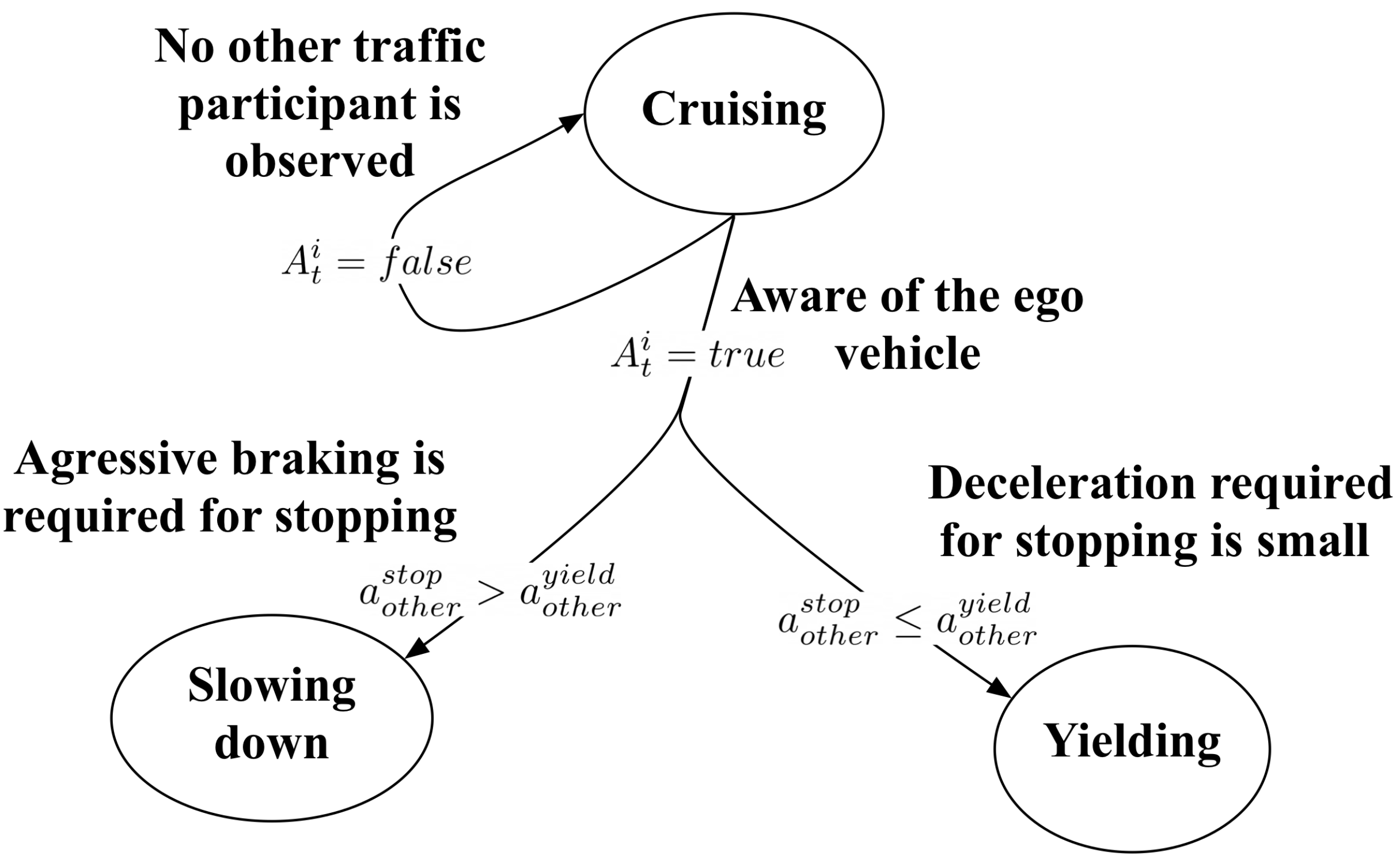
4.3. Proposed Visibility-Dependent Behavior Model
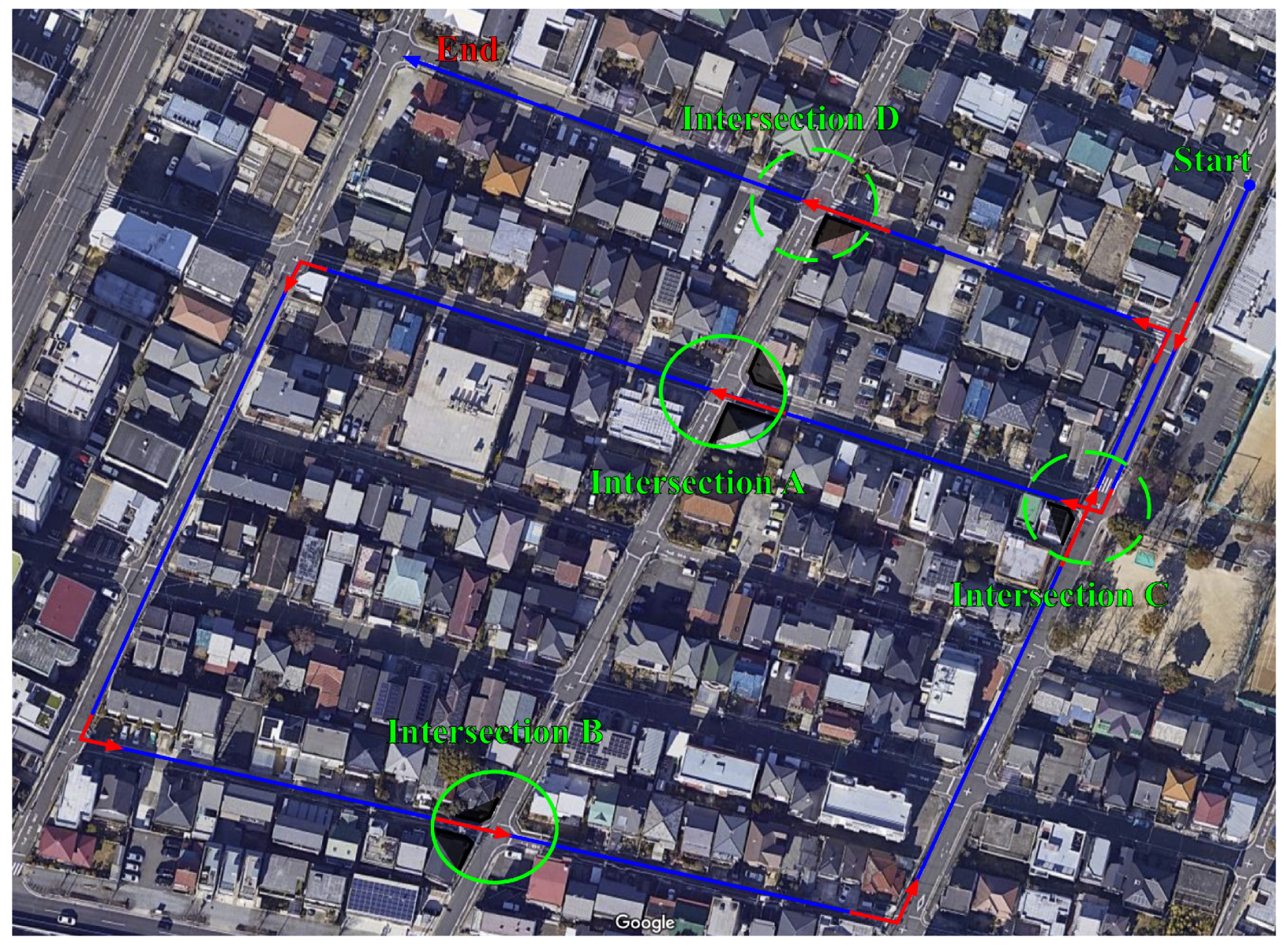
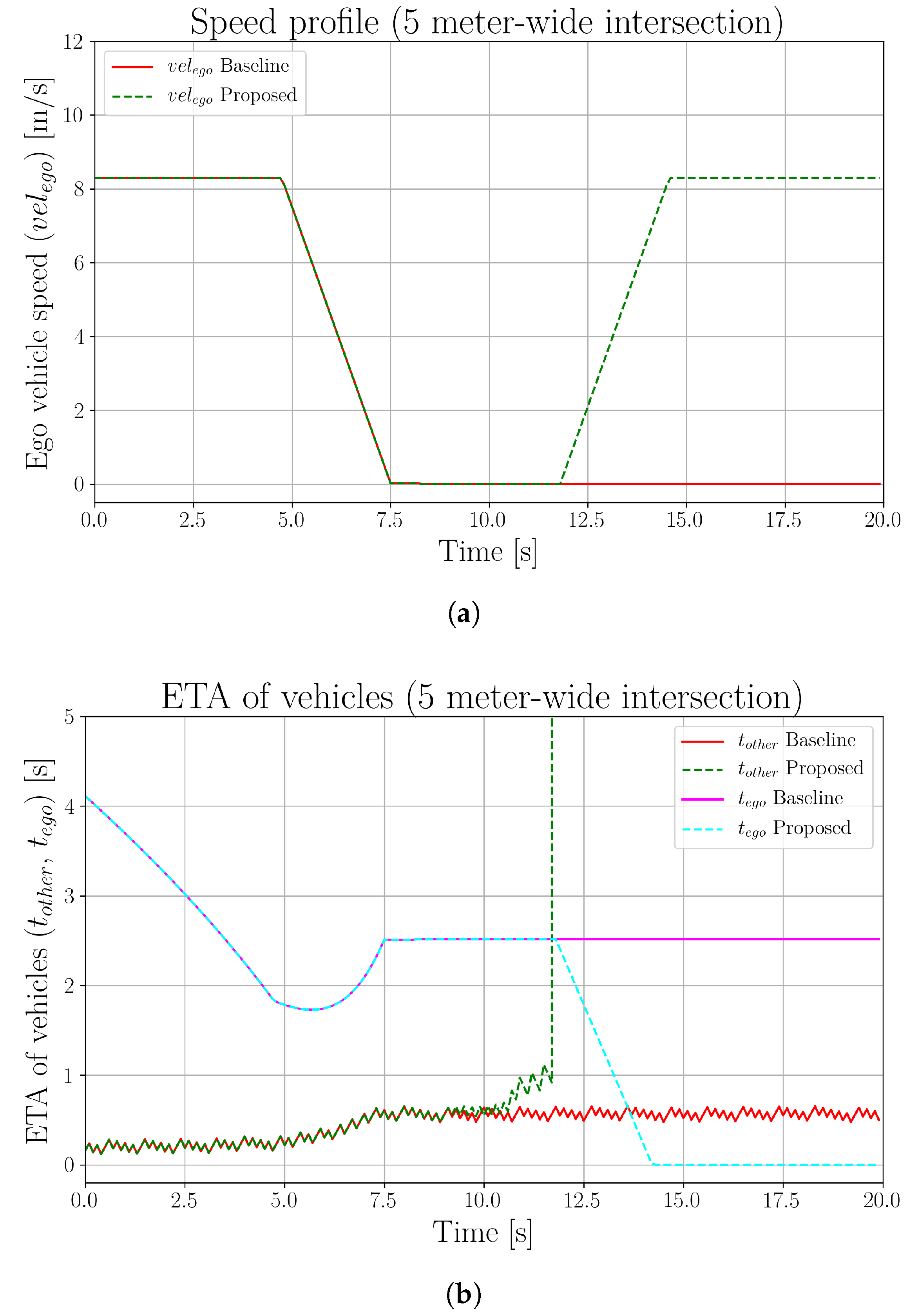
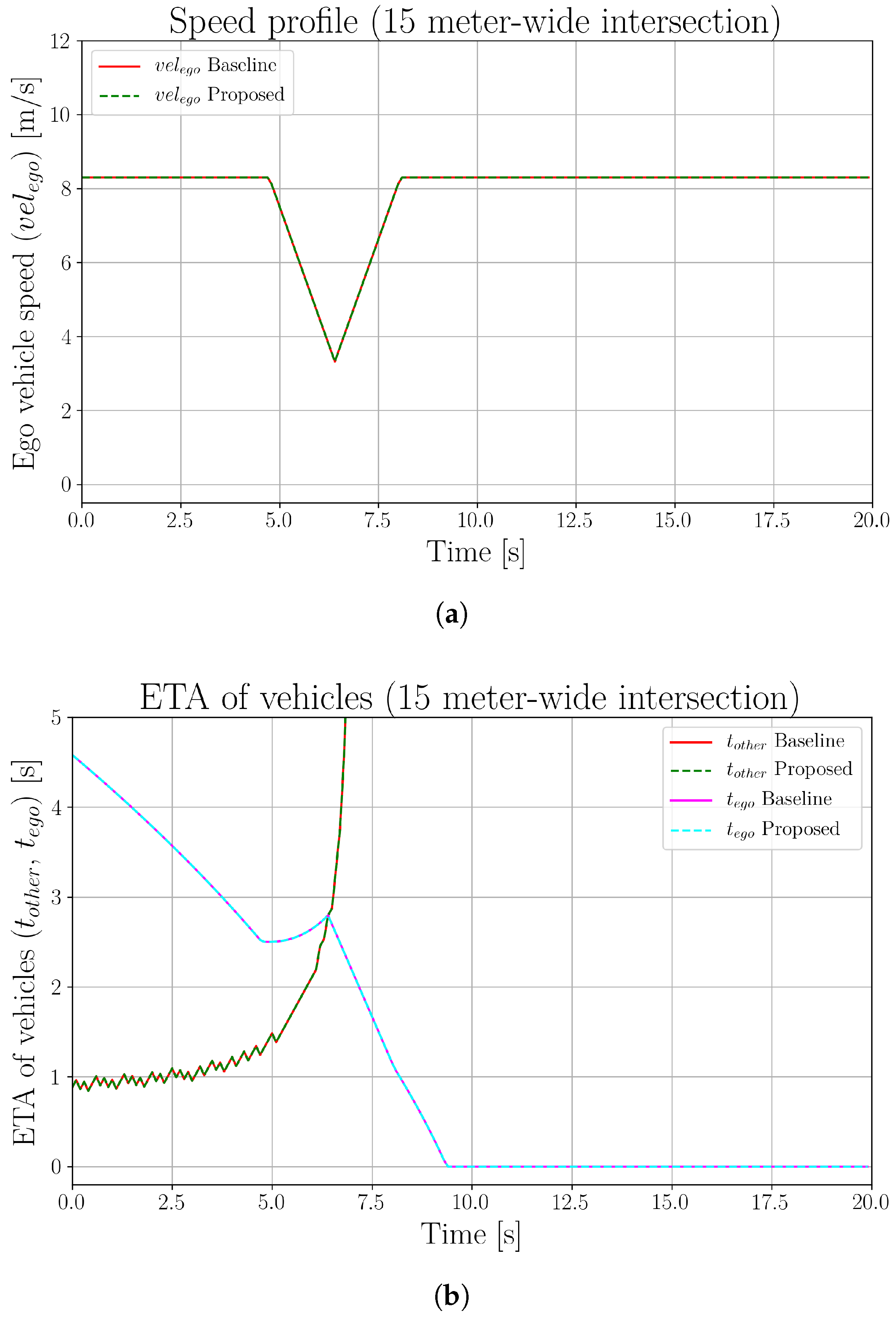
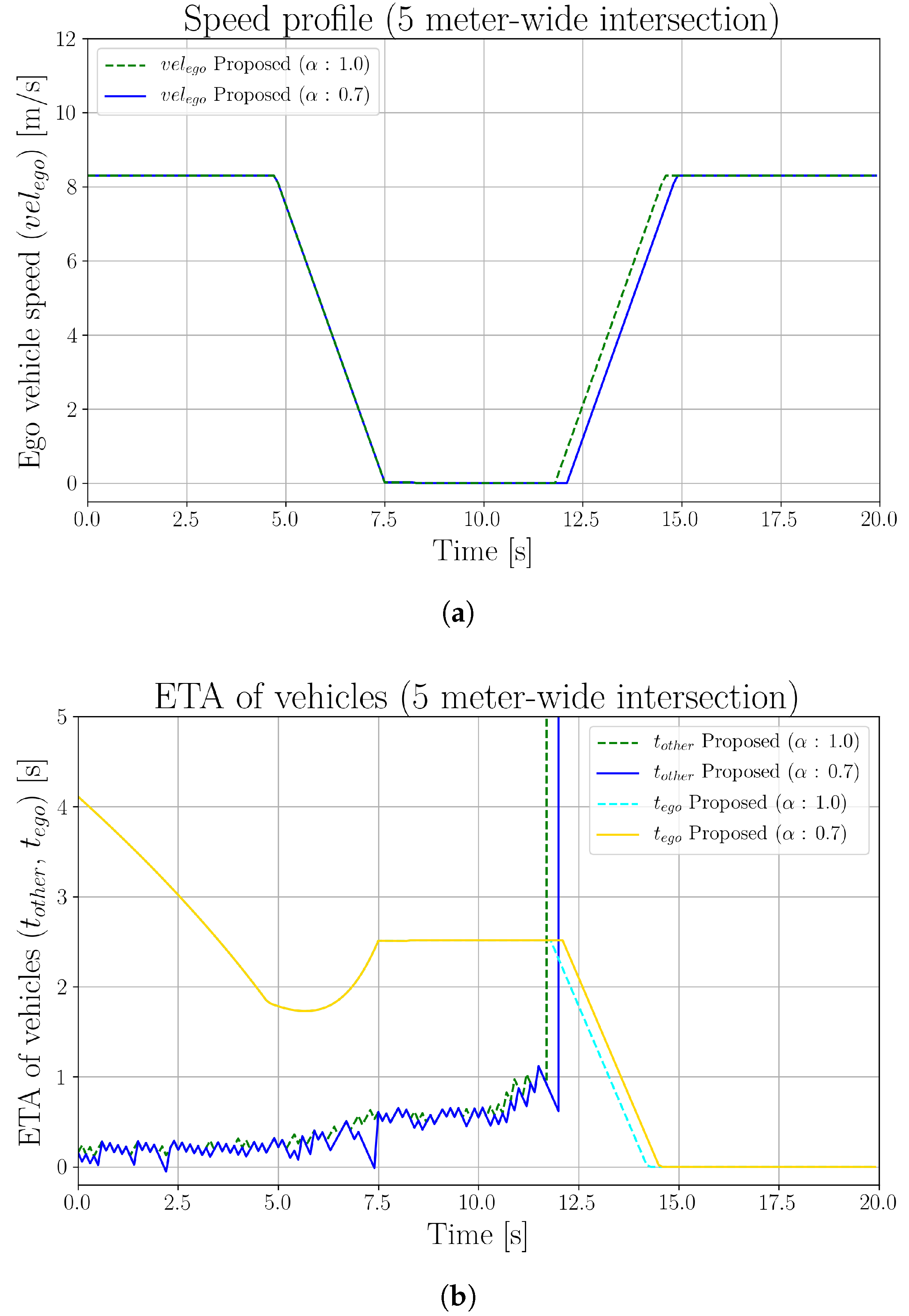
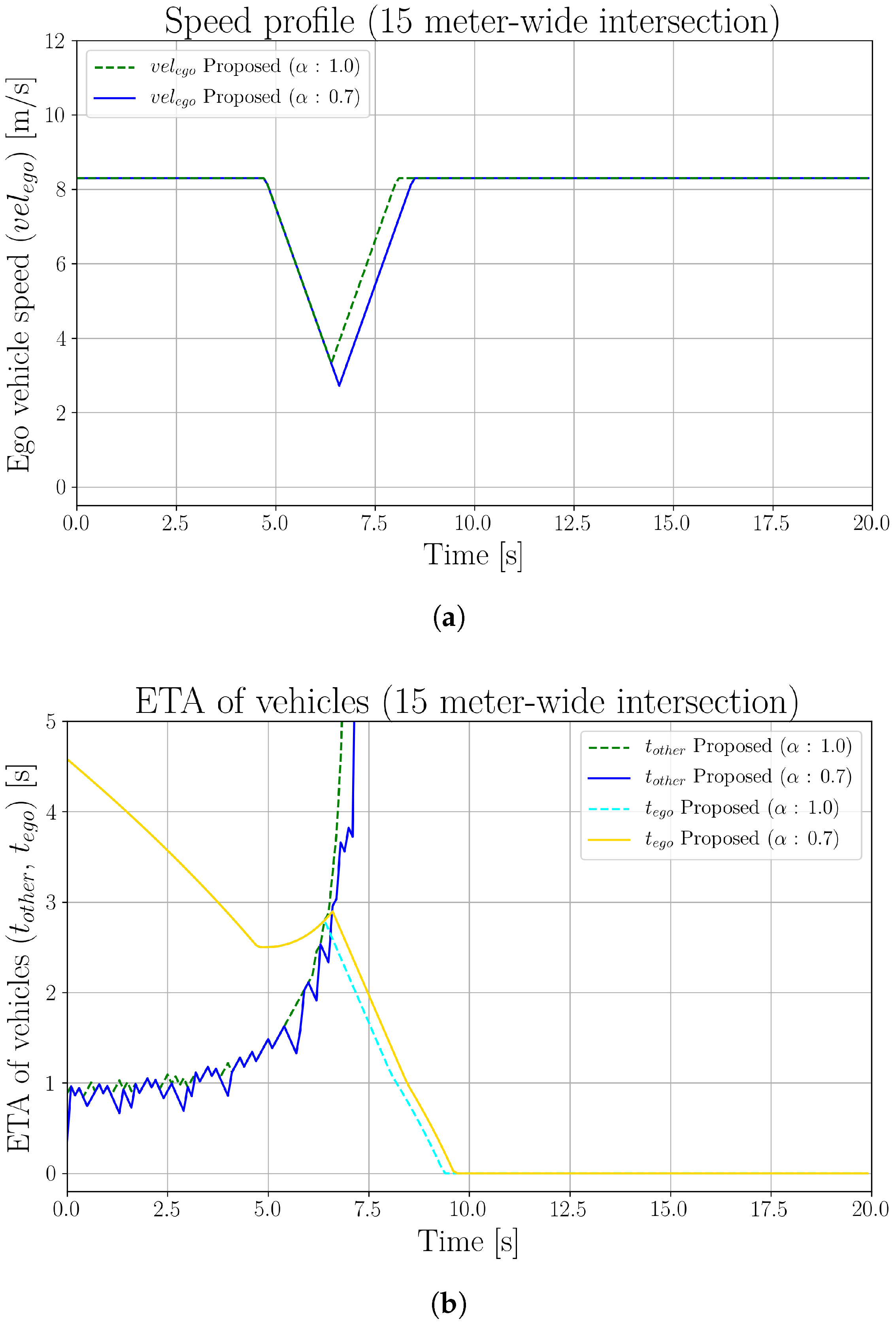
5. Experimental Results
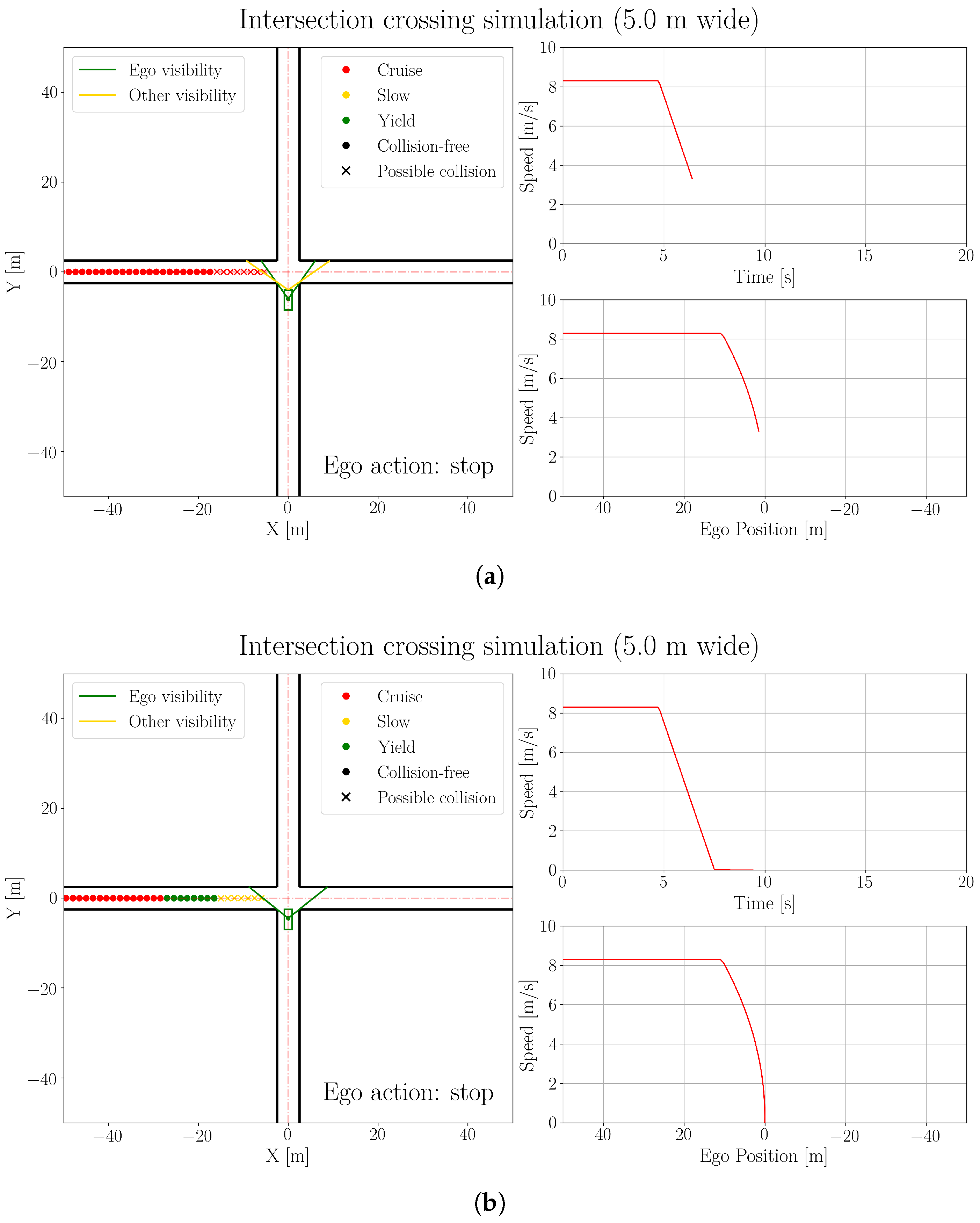
5.1. Baseline Comparison
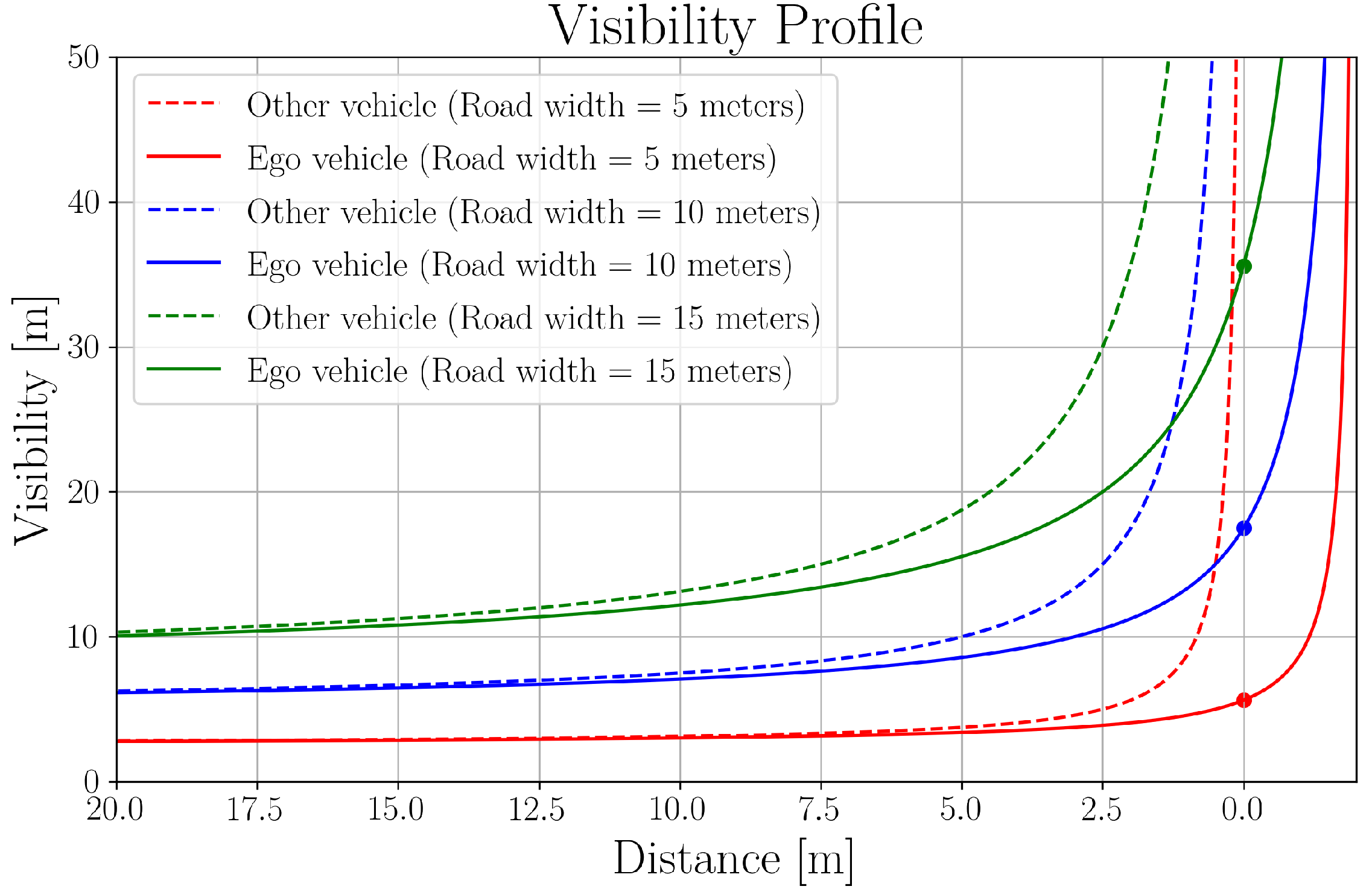
5.2. Effects of Perception Inaccuracy
5.3. Effects of Sensor Mounting Position
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, S. Critical Reasons for Crashes Investigated in the National Motor Vehicle Crash Causation Survey; Technical Report; NHTSA’s National Center for Statistics and Analysis: Washington, DC, USA, 2018.
- Fagnant, D.J.; Kockelman, K. Preparing a nation for autonomous vehicles: Opportunities, barriers and policy recommendations. Transp. Res. Part A Policy Pract. 2015, 77, 167–181. [Google Scholar] [CrossRef]
- Wadud, Z.; MacKenzie, D.; Leiby, P. Help or hindrance? The travel, energy and carbon impacts of highly automated vehicles. Transp. Res. Part A Policy Pract. 2016, 86, 1–18. [Google Scholar] [CrossRef]
- Chan, C.Y. Advancements, prospects, and impacts of automated driving systems. Int. J. Transp. Sci. Technol. 2017, 6, 208–216. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A Survey of Autonomous Driving: Common Practices and Emerging Technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Geissler, F.; Grafe, R. Optimized sensor placement for dependable roadside infrastructures. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC 2019), Auckland, New Zealand, 27–30 October 2019; pp. 2408–2413. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, J.; Yin, G.; Zhang, K. Cooperative Driving for Connected and Automated Vehicles at Non-signalized Intersection based on Model Predictive Control. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC 2019), Auckland, New Zealand, 27–30 October 2019; pp. 2121–2126. [Google Scholar] [CrossRef]
- Hafner, M.R.; Cunningham, D.; Caminiti, L.; Del Vecchio, D. Cooperative collision avoidance at intersections: Algorithms and experiments. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1162–1175. [Google Scholar] [CrossRef]
- Milanés, V.; Villagrá, J.; Godoy, J.; Simó, J.; Pérez, J.; Onieva, E. An intelligent V2I-based traffic management system. IEEE Trans. Intell. Transp. Syst. 2012, 13, 49–58. [Google Scholar] [CrossRef]
- Narksri, P.; Takeuchi, E.; Ninomiya, Y.; Takeda, K. Crossing Blind Intersections from a Full Stop Using Estimated Visibility of Approaching Vehicles. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC 2019), Auckland, New Zealand, 27–30 October 2019; pp. 2427–2434. [Google Scholar] [CrossRef]
- Brechtel, S.; Gindele, T.; Dillmann, R. Probabilistic decision-making under uncertainty for autonomous driving using continuous POMDPs. In Proceedings of the 2014 17th IEEE International Conference on Intelligent Transportation Systems (ITSC 2014), Qingdao, China, 8–11 October 2014; pp. 392–399. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J.; Shang, J.; Wang, Y.; Yu, H.; Zhang, X. Decision Making through Occluded Intersections for Autonomous Driving. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC 2019), Auckland, New Zealand, 27–30 October 2019; pp. 2449–2455. [Google Scholar] [CrossRef]
- Schorner, P.; Tottel, L.; Doll, J.; Zollner, J.M. Predictive trajectory planning in situations with hidden road users using partially observable markov decision processes. In Proceedings of the IEEE Intelligent Vehicles Symposium, Paris, France, 9–12 June 2019; pp. 2299–2306. [Google Scholar] [CrossRef]
- Klimenko, D.; Song, J.; Kurniawati, H. TAPIR: A software Toolkit for approximating and adapting POMDP solutions online. In Proceedings of the Australasian Conference on Robotics and Automation (ACRA), Melbourne, Australia, 2–4 December 2014. [Google Scholar]
- Hubmann, C.; Quetschlich, N.; Schulz, J.; Bernhard, J.; Althoff, D.; Stiller, C. A POMDP maneuver planner for occlusions in urban scenarios. In Proceedings of the IEEE Intelligent Vehicles Symposium, Paris, France, 9–12 June 2019; pp. 2172–2179. [Google Scholar] [CrossRef]
- Isele, D.; Rahimi, R.; Cosgun, A.; Subramanian, K.; Fujimura, K. Navigating Occluded Intersections with Autonomous Vehicles Using Deep Reinforcement Learning. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; pp. 2034–2039. [Google Scholar] [CrossRef]
- Qiao, Z.; Muelling, K.; Dolan, J.; Palanisamy, P.; Mudalige, P. POMDP and Hierarchical Options MDP with Continuous Actions for Autonomous Driving at Intersections. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2377–2382. [Google Scholar] [CrossRef]
- Yoshihara, Y.; Takeuchi, E.; Ninomiya, Y.; Board, T.R. Accurate Analysis of Expert and Elderly Driving at Blind Corners for Proactive Advanced Driving Assistance Systems. In Proceedings of the Transportation Research Board 95th Annual Meeting, Washington, DC, USA, 10–14 January 2016; p. 19. [Google Scholar]
- Morales, L.Y.; Naoki, A.; Yoshihara, Y.; Murase, H. Towards Predictive Driving through Blind Intersections. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 716–722. [Google Scholar] [CrossRef]
- Sama, K.; Morales, Y.; Liu, H.; Akai, N.; Carballo, A.; Takeuchi, E.; Takeda, K. Extracting Human-like Driving Behaviors From Expert Driver Data Using Deep Learning. IEEE Trans. Veh. Technol. 2020. [Google Scholar] [CrossRef]
- Orzechowski, P.F.; Meyer, A.; Lauer, M. Tackling Occlusions Limited Sensor Range with Set-based Safety Verification. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1729–1736. [Google Scholar] [CrossRef]
- Althoff, M.; Magdici, S. Set-based prediction of traffic participants on arbitrary road networks. IEEE Trans. Intell. Veh. 2016, 1, 187–202. [Google Scholar] [CrossRef]
- Naumann, M.; Konigshof, H.; Lauer, M.; Stiller, C. Safe but not overcautious motion planning under occlusions and limited sensor range. In Proceedings of the IEEE Intelligent Vehicles Symposium, Paris, France, 9–12 June 2019; pp. 140–145. [Google Scholar] [CrossRef]
- Tas, Ö.S.; Stiller, C. Limited Visibility and Uncertainty Aware Motion Planning for Automated Driving. In Proceedings of the IEEE Intelligent Vehicles Symposium, Changshu, China, 26–30 June 2018; pp. 1171–1178. [Google Scholar] [CrossRef]
- Akagi, Y.; Raksincharoensak, P. Stochastic driver speed control behavior modeling in urban intersections using risk potential-based motion planning framework. In Proceedings of the IEEE Intelligent Vehicles Symposium, Seoul, Korea, 28 June–1 July 2015; pp. 368–373. [Google Scholar] [CrossRef]
- Morales, Y.; Yoshihara, Y.; Akai, N.; Takeuchi, E.; Ninomiya, Y. Proactive driving modeling in blind intersections based on expert driver data. In Proceedings of the IEEE Intelligent Vehicles Symposium, Proceedings, Los Angeles, CA, USA, 11–14 June 2017; pp. 901–907. [Google Scholar] [CrossRef]
- Yoshihara, Y.; Morales, Y.; Akai, N.; Takeuchi, E.; Ninomiya, Y. Autonomous predictive driving for blind intersections. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; pp. 3452–3459. [Google Scholar] [CrossRef]
- Takeuchi, E.; Yoshihara, Y.; Yoshiki, N. Blind Area Traffic Prediction Using High Definition Maps and LiDAR for Safe Driving Assist. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Las Palmas, Spain, 15–18 September 2015; pp. 2311–2316. [Google Scholar] [CrossRef]
- Yu, M.Y.; Vasudevan, R.; Johnson-Roberson, M. Occlusion-aware risk assessment for autonomous driving in urban environments. IEEE Robot. Autom. Lett. 2019, 4, 2235–2241. [Google Scholar] [CrossRef]
- Hoermann, S.; Kunz, F.; Nuss, D.; Renter, S.; Dietmayer, K. Entering crossroads with blind corners. A safe strategy for autonomous vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium, Los Angeles, CA, USA, 11–14 June 2017; pp. 727–732. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics (Intelligent Robotics and Autonomous Agents); The MIT Press: Cambridge, MA, USA, 2005; pp. 1435–1452. [Google Scholar] [CrossRef]
- Akagi, Y.; Raksincharoensak, P. An analysis of an elderly driver behaviour in urban intersections based on a risk potential model. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 1627–1632. [Google Scholar] [CrossRef]
- Takeuchi, E.; Tsubouchi, T. A 3-D scan matching using improved 3-D normal distributions transform for mobile robotic mapping. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3068–3073. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]






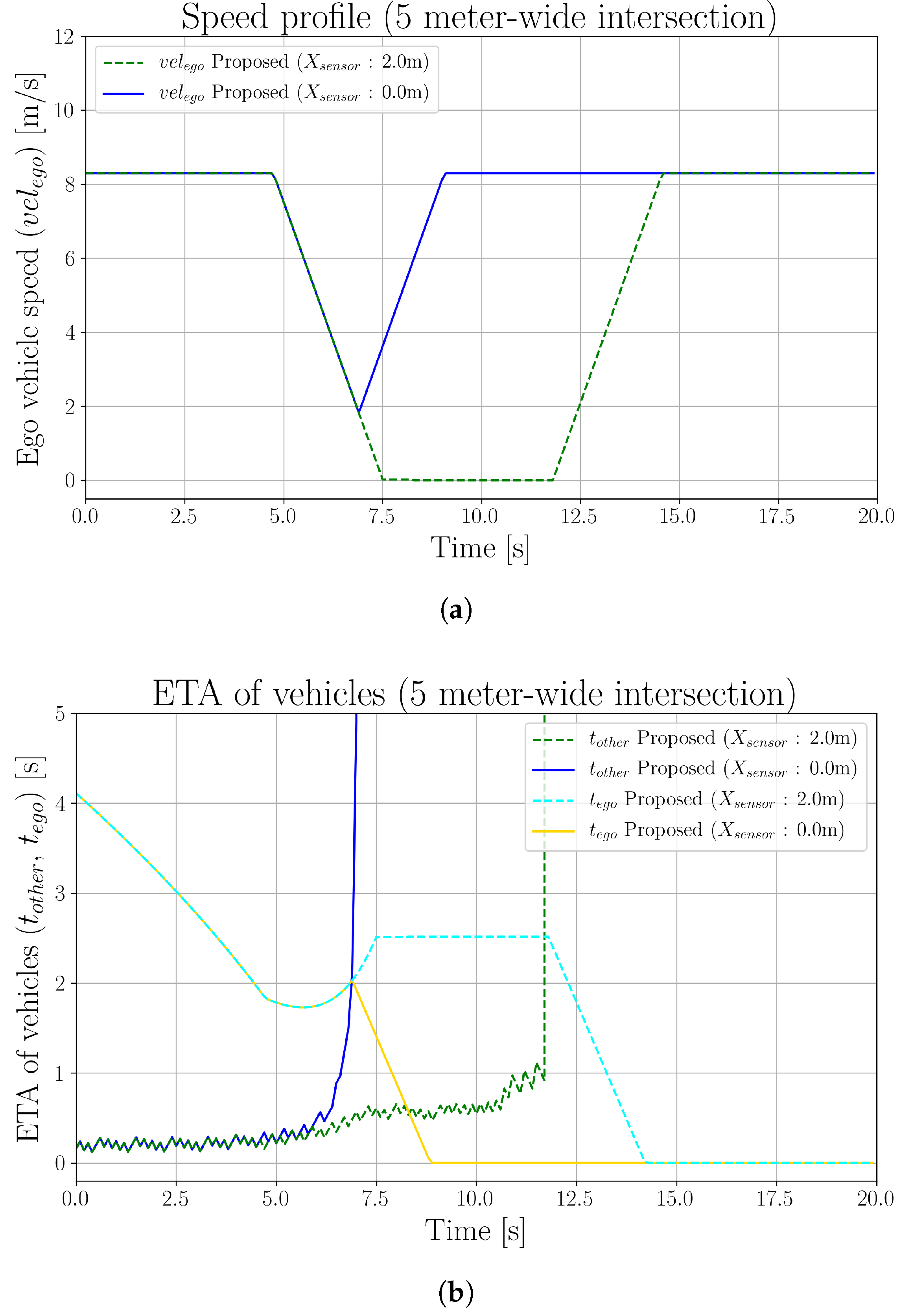
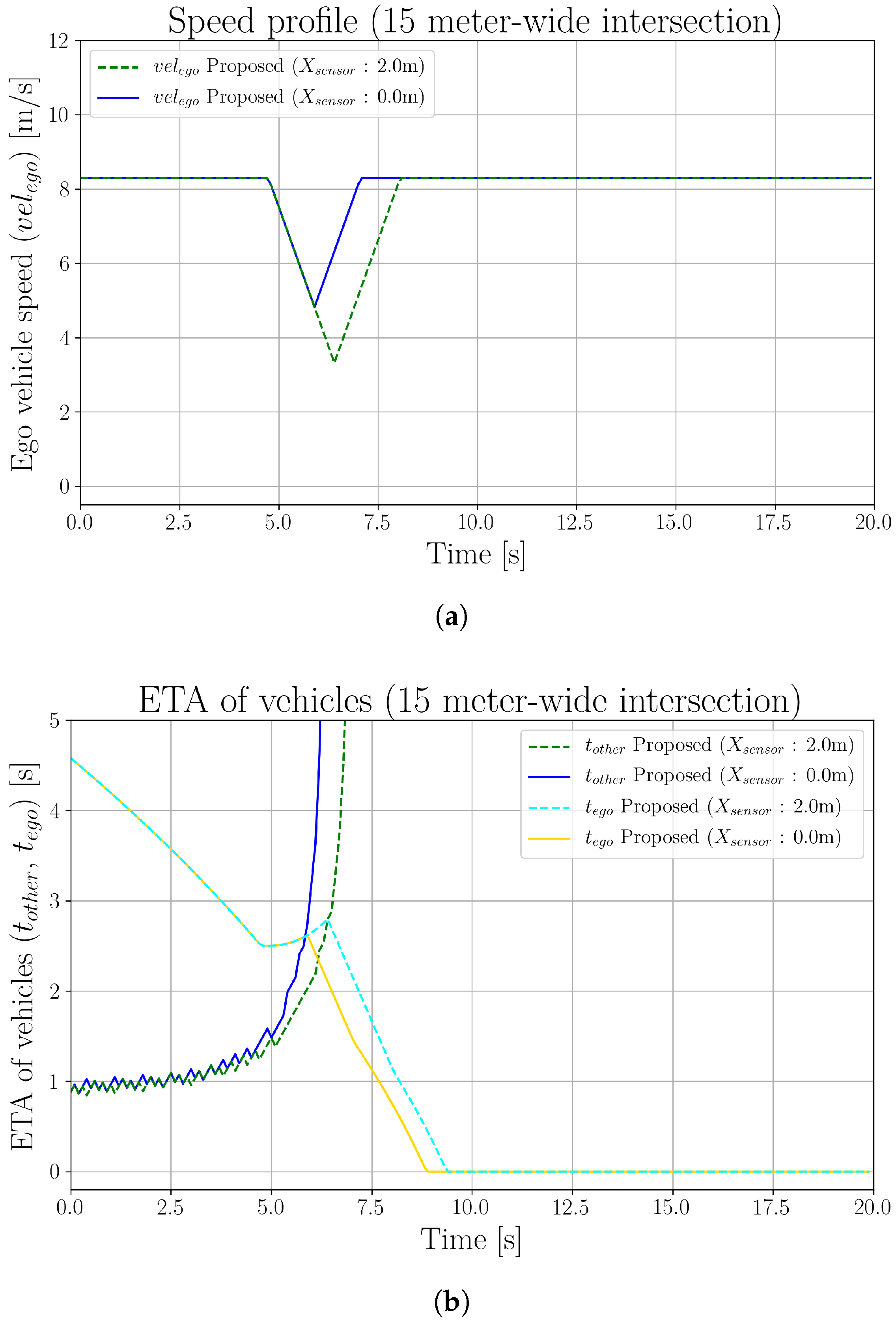
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 4.5 m | 1.7 m | ||
| 5.0, 15.0 m | 5.0, 15.0 m | ||
| 3.0 m/s | −3.0 m/s | ||
| −1.5 m/s | −0.8 m/s | ||
| 8.3 m/s | 2.3 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narksri, P.; Takeuchi, E.; Ninomiya, Y.; Takeda, K. Deadlock-Free Planner for Occluded Intersections Using Estimated Visibility of Hidden Vehicles. Electronics 2021, 10, 411. https://doi.org/10.3390/electronics10040411
Narksri P, Takeuchi E, Ninomiya Y, Takeda K. Deadlock-Free Planner for Occluded Intersections Using Estimated Visibility of Hidden Vehicles. Electronics. 2021; 10(4):411. https://doi.org/10.3390/electronics10040411
Chicago/Turabian StyleNarksri, Patiphon, Eijiro Takeuchi, Yoshiki Ninomiya, and Kazuya Takeda. 2021. "Deadlock-Free Planner for Occluded Intersections Using Estimated Visibility of Hidden Vehicles" Electronics 10, no. 4: 411. https://doi.org/10.3390/electronics10040411
APA StyleNarksri, P., Takeuchi, E., Ninomiya, Y., & Takeda, K. (2021). Deadlock-Free Planner for Occluded Intersections Using Estimated Visibility of Hidden Vehicles. Electronics, 10(4), 411. https://doi.org/10.3390/electronics10040411






