Abstract
This work presents a novel greedy randomized adaptive search procedure approach for dealing with the maximum diversity problem from a multi-objective perspective. In particular, five of the most extended diversity metrics were considered, with the aim of maximizing all of them simultaneously. The metrics considered have been proven to be in conflict, i.e., it is not possible to optimize one metric without deteriorating another one. Therefore, this results in a multi-objective optimization problem where a set of efficient solutions that are diverse with respect to all the metrics at the same time must be obtained. A novel adaptation of the well-known greedy randomized adaptive search procedure, which has been traditionally used for single-objective optimization, was proposed. Two new constructive procedures are presented to generate a set of efficient solutions. Then, the improvement phase of the proposed algorithm consists of a new efficient local search procedure based on an exchange neighborhood structure that follows a first improvement approach. An effective exploration of the exchange neighborhood structure is also presented, to firstly explore the most promising ones. This feature allowed the local search proposed to limit the size of the neighborhood explored, resulting in an efficient exploration of the solution space. The computational experiments showed the merit of the proposed algorithm, when comparing the obtained results with the best previous method in the literature. Additionally, new multi-objective evolutionary algorithms derived from the state-of-the-art were also included in the comparison, to prove the quality of the proposal. Furthermore, the differences found were supported by non-parametric statistical tests.
1. Introduction
The scientific community has been studying the family of the maximum diversity problems since 1988 [1], while the first integer programming models were originally introduced by Dhir et al. [2] and Kuo et al. [3]. The concept of diversity has evolved over the years, and several new proposals in the literature have improved its definition [4,5], constructing therefore a family of optimization problems. The wide interest in this family of problems is mainly due to their practical applications in a wide variety of areas: social network analysis, facility location problems, the generation of a set of heterogeneous students in class, etc. All of them have been proven -hard combinatorial optimization problems [3,6]. The main idea behind the diversity optimization problems relies on selecting a subset of elements from a given set, with the aim of maximizing a certain distance measure. The main difference among most of the proposed approaches is the way of computing the diversity of the selected elements.
Finding a diverse set of elements has been the focus of research in several fields in the last few years. In particular, diversity problems have been deeply studied in the context of Facility Location Problems (FLP). In an FLP, a company is interested in opening a certain number of facilities, selecting each location from a set of available ones. The set of selected facilities must maximize the diversity among them, where diversity can be measured as the physical distance among facilities or the type of service provided, among others [7]. Additionally, maximizing diversity can be useful for locating obnoxious facilities, such as prisons or airports, which were deeply studied in [8]. Diversity problems are also considered in the economics field, when it is necessary to decide the investments to maximize the expected benefit, which usually leads to selecting a set of diverse activities to minimize the potential risk [9]. In the last few years, there has been a special effort to analyze equity among individuals in organizations, which can also be processed by analyzing diversity [10]. In the field of logistics, locating special units such as warehouses with the aim of avoiding redundancy in their activities is also an interesting field of research [11,12]. Other applications include the selection of jury members [13] or the selection of heterogeneous results from a search [14].
As we can observe, diversity can be measured using different metrics. Before defining the metrics studied in this paper, let us introduce some preliminary definitions common to the problems belonging to the family of diversity optimization problems. Given a set of elements, the objective is to find a subset of p elements, with p , in such a way that the diversity of the elements included in is maximized. In order to evaluate the diversity, a distance metric , with , between every two elements must be defined. For the sake of generality, we did not consider any specific distance metric, but any well-known distance metric can be selected: the euclidean distance, the cosine distance, and the Jaccard similarity index, among others [15,16]. Then, a diversity problem looks for finding the solution that maximizes a certain diversity measure. More formally,
where represents the space search, i.e., the set of all possible combinations of p different elements selected from .
Diversity maximization problems have been traditionally tackled from a single-objective perspective, focusing on finding the subset of the most diverse elements with respect to a single diversity measure. However, it is interesting to analyze the results obtained when modeling diversity as a multi-objective optimization problem. Furthermore, in the context of real-life applications, it is difficult to select just one diversity metric that satisfies all the constraints required by the problem. Therefore, it would be desirable to be able to simultaneously optimize more than just one metric. In that case, we are dealing with a Multi-objective Optimization Problem (MOP), in which several objective functions need to be optimized at the same time. The main feature when dealing with a MOP is that the considered objective functions are in conflict, i.e., optimizing one of them usually results in deteriorating the other ones. Therefore, a single solution that optimizes all the objectives at the same time does not exist. As a result, the output of a MOP is not a single solution, but a set of efficient solutions.
The set of efficient solutions is constructed following the Pareto optimality principle, which presents a balance for a solution where an objective function cannot be improved while deteriorating another one. Therefore, the comparison of two solutions is given by the concept of dominance. Specifically, given two solutions and , we can state that dominates if and only if the evaluation of considering each objective function is better than or equal to the value of the corresponding objective function in . Otherwise, it is said that and are mutually non-dominated. Following this definition, a solution is considered as Pareto optimal (or an efficient solution) if there does not exists any other solution in the solution space such that dominates . The set conformed with all the solutions that are Pareto optimal is named the Pareto-optimal front.
In particular, this work was centered on proposing an algorithm that was able to deal with more than one diversity measure at the same time, with the aim of finding differences and similarities among the most extended diversity measures. This approach was originally presented in Vera et al. [17], where the authors studied five different diversity measures simultaneously. This problem was named the Multi-Objective Maximum Diversity Problem (MOMDP). In particular, the authors in Vera et al. [17] proposed a multi-objective evolutionary algorithm for dealing with the MOMDP.
In the literature, there are different approaches for dealing with multi-objective optimization problems [18]. The most direct adaptation of single-objective optimization strategies to multi-objective optimization is to consider a single objective function obtained as the weighted sum of the objectives. However, this approach usually leads to a low-quality set of efficient solutions that are poorly distributed along the search space. One of the most extended methods is the -constraint, which focuses on optimizing one of the objectives, including the remaining objectives, as constraints that depend on some specific thresholds. The main drawback of this approach is that finding suitable values for these thresholds is difficult.
Recently, a new approach for solving multi-objective optimization problems has been attracting the interest of the scientific community. This approach basically consists of considering the set of efficient solutions as the incumbent solution for a metaheuristic. This approach has been recently used in the context of evolutionary algorithms [19] and, specifically, genetic algorithms [20]. Additionally, other metaheuristics such as tabu search [21], scatter search [7], variable neighborhood search [8], the greedy randomized adaptive search procedure [22], and ant colony optimization [23] have been successfully applied for a wide variety of multi-objective optimization problems.
In addition to these new approaches for solving multi-objective optimization problems, several works have focused on improving the most extended evolutionary algorithms such as Non-dominated Sorting Genetic Algorithm III (NSGA-III) or the Multiobjective Evolutionary Algorithm with Decomposition (MOEA/D), including new operators of modifications of the traditional ones to adapt them to the most challenging problems. Yi et al. [24] proposed an adaptive mutation operator to be included in NSGA-III, evaluating its performance when comparing it with the traditional operators. The performance of this new proposal was evaluated with a set of problems derived from Big Data. Sun et al. [25] dealt with interval multi-objective optimization problems by including new promising local search strategies, proposing a new memetic algorithm to tackle them. In particular, they considered the hypervolume to be maximized in the context of the local search procedure. The proposal was evaluated with a benchmark of 10 interval multi-objective optimization problems, comparing it with the state-of-the-art method, which did not consider local search.
This work proposed an adaptation of the well-known greedy randomized adaptive search procedure for solving the MOMDP. The remainder of the manuscript is organized as follows: Section 2 describes the diversity metrics considered in this work. Section 3 details the algorithmic proposal. Section 4 presents the thorough computational experiments to analyze the performance of the proposed algorithm, and finally, Section 5 draws the most relevant conclusions derived from this research.
2. Diversity Metrics
In this section, we define the diversity measures studied in this work, which where previously considered together in [17].
The first diversity measure is the Max-Sum Diversity (MSD). In this case, the diversity of a given subset of elements is evaluated as the sum of distances between each pair of selected elements [26], as defined in Equation (2).
The objective then is to find a solution that maximizes the value of the MSD. This metric has been widely used in the context of the competitive location of facilities [11] and the selection of jury members [13]. Several metaheuristics, such as iterated tabu search or the GRASP with path relinking, have been proposed for this problem [27,28].
The second diversity measure considered, named the Max-Min Diversity (MMD), is evaluated as the minimum distance between the elements in (see Equation (3)).
The objective again is to find the solution that maximizes the MMD. This metric has been used in problems related to the location of obnoxious facilities [29], and it has been tackled using the GRASP and path relinking [30].
The Max-MinSum Diversity (MMSD) is the third diversity metric considered in this work. For each selected element , the sum of distances from i to the elements in is computed, returning the minimum value obtained among all possible sums (see Equation (4)).
The objective here is to maximize the value of the MMSD. This metric has been traditionally used in problems related to equity or in the selection of homogeneous groups [31]. Tabu search and variable neighborhood search have been widely used for this metric [32,33].
The fourth diversity measure considered in this work is named Minimum Differential Dispersion (MDD). In order to evaluate this measure, a method very similar to the one used to evaluate the MMSD is followed. For each selected element , the sum of distances to the remaining elements in is computed, evaluating the MDD as the difference between the maximum and minimum value obtained among all possible sums (see Equation (5)).
The objective of this measure is then to find the minimum value of the MDD. This problem has been tackled by means of the GRASP combined with path relinking and with Variable Neighborhood Search (VNS) in recent works [31,34].
The fifth and last diversity measure considered in this work is named the Minimum p-Center Diversity (MPCD). Evaluating this measure requires the set of selected elements and also a set of non-selected ones ∖. For each non-selected element ∖, the distance to its closest selected element is computed, returning the maximum distance found (see Equation (6)).
In this case, the objective is to minimize the value of the MPCD. This problem arises in the context of facility location problems, where the set of selected elements refers to the facilities that would be opened, while the set of non-selected ones represents demand points that are required from the services of the opened facilities. This problem has been addressed by using several metaheuristic approaches, iterated greedy [35] and VNS [36] being the most recent ones.
Let us illustrate the evaluation of these metrics with a graphical example. Figure 1 shows an example instance with and p . Figure 1a depicts the initial set of points, while Figure 1b,c illustrates two feasible solutions and for this example, respectively. Notice that the points are set in a bi-dimensional euclidean space to ease the evaluation of the distances between points. Then, the detailed evaluation of solutions and is performed as follows:
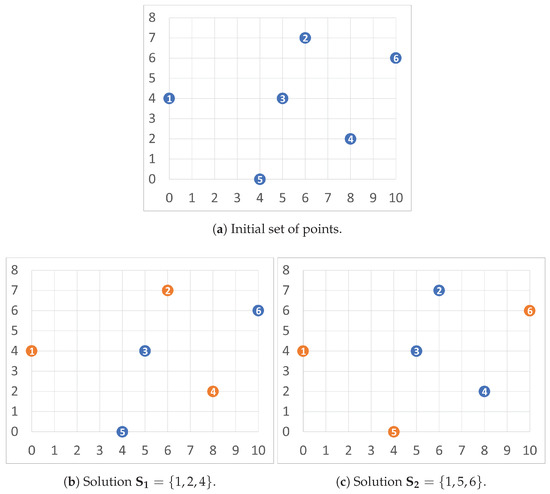
Figure 1.
Instance with 6 available points where 3 of them must be selected.
To sum up, Table 1 summarizes the results obtained in each one of the diversity metrics over and . Notice that the best result for each diversity metric is highlighted in bold font.

Table 1.
Evaluation of the five diversity metrics over the solutions and depicted in Figure 1.
The results presented in Table 1 confirm the behavior of a MOP. In particular, outperforms in the MDD metric, while is better than in the MSD, MMD, and MMSD. Finally, both solutions provide the same quality for the MPCD metric. Therefore, it is not possible to state that outperforms or vice versa, since they are non-dominated solutions.
3. Algorithmic Proposal
This work proposed a Greedy Randomized Adaptive Search Procedure (GRASP) for solving the MOMDP. The GRASP was originally presented in [37], but was not formally defined until [38]. It is a very extended metaheuristic that has been successfully applied to many hard optimization problems from a wide variety of areas [39,40,41]. The GRASP follows a multi-start strategy conformed with two different stages: construction and improvement. The former consists of a greedy randomized construction phase to generate an initial solution, while the latter is responsible for locally improving the constructed solution. Then, the two stages are repeated until reaching a certain stopping criterion, which is usually a fixed number of GRASP iterations. The success of this methodology relies on the balance between intensification and diversification in the generation of solutions, which is controlled by a search parameter named , which is described in detail in Section 3.1. We refer the reader to Festa and Resende [42] for a detailed survey, which described the most recent advances in GRASP methodology. Next, we present both the traditional scheme and the MOP adaptation, of each stage of the GRASP.
3.1. Constructive Procedure
The constructive procedure in the context of the GRASP is responsible for generating an initial high-quality solution to start the search. Instead of using a completely greedy procedure, the GRASP favors diversification by including randomness in this stage. Algorithm 1 introduces the pseudocode of the proposed constructive procedure.
The constructive procedure requires three input parameters, namely: , the set of candidate elements to be selected; p, the number of elements that must be selected; and , a real number in the range that controls the balance between diversification and intensification inside the GRASP methodology. In the context of the GRASP, the first element to be included in the solution is usually selected at random from the set of available ones to favor diversification (Step 1). This element is then included in the solution under construction (Step 2), and a candidate list CL is conformed with all the elements but i (Step 3). Then, the method iteratively adds a new element to the solution until it becomes feasible, i.e., the number of selected elements is equal to the input parameter p (Steps 4–12). In each iteration, the minimum () and maximum () values of a certain greedy function are computed (Steps 5–6). This greedy function g determines the contribution of each candidate element to the quality of the solution under construction. Without loss of generality, in a maximization problem, the larger the greedy function value, the better. Notice that, in the case of considering a minimization problem, it is only required to negate the value of the greedy function. We discuss later the selected greedy function for the MOMDP.
After evaluating the candidates, a threshold is computed (Step 7) with the aim of constructing the restricted candidate list (Step 8) with the most promising elements. The threshold depends on the value of the input search parameter , which controls the greediness/randomness of the method. On the one hand, if , then , therefore only contains those elements with the maximum value of the greedy function, which results in a totally greedy criterion. On the other hand, if , then , therefore resulting in a completely random criterion since all available elements are able to enter . The most adequate value for this input parameter is discussed in Section 4. Once the is constructed with the most promising elements, the next one to be included in the solution under construction is selected at random from it (Step 9). Finally, is updated by removing the selected element (Step 10), including it in the solution (Step 11). The methods ends when p elements have been selected, returning the constructed solution (Step 13).
| Algorithm 1GRASP-Constructive(). |
|
This traditional scheme of GRASP constructive must be adapted to a multi-objective optimization problem such as MOMDP. In particular, we proposed two different adaptations to construct feasible solutions. The first adaptation, named the Joint Alternate Evaluation of Objectives (JALEO), is focused in using the diversity metrics presented in Section 2 as greedy functions in each construction independently. It is performed by generating solutions that alternate each considered objective function as the greedy criterion. In particular, if c solutions are constructed and d diversity metrics are considered, then solutions are constructed considering each objective function as the greedy criterion. This idea allows the constructive procedure to generate a diverse set of initial efficient solutions. The second adaptation, named the Mixed Objective Function Algorithm (MOFA), uses all the diversity metrics as greedy functions simultaneously in every single construction. In order to do so, the greedy function varies from one diversity metric to another in each iteration of the constructive procedure. In other words, the first element is selected by following the first greedy criterion; the second one follows the second greedy criterion, and so on. Section 4 compares the performance of both strategies to construct initial solutions.
Finally, it is worth mentioning that each constructed solution is considered to be included in the set of efficient solutions. In particular, if a constructed solution is dominated by any of the solutions that are already in the set, then it is not included. On the contrary, if it is a non-dominated solution, it is included in the set of efficient solutions, removing those solutions already in the set that are dominated by the constructed one.
3.2. Local Improvement
The initial solutions constructed with the method described in Section 3.1 are not necessarily local optima, and therefore, they can be further improved to find a local optimum with respect to a certain neighborhood. The second stage of the GRASP algorithm is responsible for finding this local optimum for each constructed solution.
The first element required to define a local search is a move operator. In the context of the problem under consideration, we proposed the exchange move, which, given a solution and a set of elements , removes a selected element and includes a non-selected one . Notice that the exchange move always results in a feasible solution. More formally,
Then, the neighborhood of a given solution is defined as all the solutions that can be reached by applying a single exchange to . In mathematical terms,
The definition of a local search consists of determining how the neighborhood is traversed during the search. Traditionally, two different approaches have been investigated: first and best improvement. The former performs the first movement that leads to an improvement, while the latter firstly explores the complete neighborhood, moving to the best solution in the neighborhood. The best improvement approach usually results in a more computationally demanding algorithm, while an improvement in the quality of the results is not guaranteed, so we selected first improvement as the exploration strategy.
Traditional local search procedures need to define a criterion to determine if a solution improves another one, which usually is the value of the objective function that is being optimized. In the context of multi-objective optimization, there are several strategies that can be followed in order to adapt a local search procedure such as optimizing each objective independently or using a mixture function that aggregates all objectives, among others. This work proposed a new approach that consists of considering that an improvement has been found if the explored solution satisfies the criterion for entering in the set of efficient solutions.
Since the first improvement strategy moves to the first improving solution found in the neighborhood, it is relevant to determine the order in which the neighborhood is explored. In problems in which it is not possible to determine which are the most promising solutions in the neighborhood under exploration due to a lack of a priori information, it is customary to randomly explore the neighborhood to favor diversity. However, in the context of the MOMDP, we do have some insights about which are the solutions that should be firstly explored. Since a solution in is obtained by performing a single Exchange move, which involves a selected element , and a non-selected one , we can determine the order in which the elements in are explored (analogously, with the elements in ). In particular, for each i, we compute the minimum distance to the other selected elements, i.e., . Then, this distance is used to sort every in an ascending order, thus firstly exploring those elements with a smaller distance. On the other hand, those elements that are not in the solution are sorted in descending order with respect to the minimum distance to the elements in , i.e., . This ordering allows us to firstly explore the most promising moves.
4. Experimental Results
This section has two main objectives: (i) tuning of the input parameters in order to find the best configuration of the proposed algorithm and (ii) performing a competitive test with the best method found in the state-of-the-art to analyze the performance of the algorithm. All the algorithms were implemented in Java SE 11, performing the experiments proposed on an AMD EPYC 7282 (2.8 GHz) and 8 GB RAM.
The testbed of instances considered in this work was the same as the one presented in the best method found in the literature [17]. It was derived from the well-known MDPLIB. Specifically, the subset named GKD was used, resulting in 145 instances ranging from 10–500 elements in each instance where the number of elements to be selected ranged between two (for the smallest instances) and fifty (for the largest ones). This set of instances has been widely used in the context of diversity and facility location problems.
When dealing with single-objective optimization problems, it is easy to perform a comparison among two or more algorithms, since it is only necessary to compare the value of the objective function obtained for each algorithm involved in the comparison. However, in the context of multi-objective optimization, such as in the MOMDP, the output of the algorithm is a set of efficient solutions, and therefore, it is necessary to define specific metrics to compare sets of efficient solutions. In this work, we used some very well-known metrics used in the literature of the MOP: coverage, hypervolume, e-indicator, and inverted generational distance [43]. Next, we briefly describe each of them.
The coverage metric, , calculates the number of solutions of the approximation front under evaluation that are dominated by a reference front . This reference front is computed as the set of efficient solutions resulting from the union of all the fronts involved in the comparison. It is a good approximation of the Pareto front when the optimal one is not known. Following this definition, the smaller the coverage value is, the better. The hypervolume, HV, evaluates the volume in the objective space, which is covered by the set of efficient solutions under evaluation, and therefore, the larger it is, the better. The -indicator, EPS, computes which is the smallest distance required to transform every point of the set of efficient solutions under evaluation to the closest point in the reference front, resulting in a metric where small values are better. The last metric considered is the inverted generational distance, IGD+, which consists of inverting the generational distance metric with the aim of measuring the distance between the set of efficient solutions under evaluation and the reference front. Again, the smaller it is, the better. Finally, we also included the size of the set of efficient solutions and the computing time required by each algorithm measured in seconds. All the tables presented in this section include the average value of each metric along the set of considered instances, where the best value is highlighted in bold font.
4.1. Preliminary Experiments
First of all, it is necessary to adjust the input parameters of the algorithm, which are the value of and the number of solutions generated. In order to avoid over-fitting, we selected a set of 20 representative instances (13% of the complete set of instances) to perform all the preliminary experiments. The first experiment was devoted to selecting the best value for each constructive procedure presented in Section 3.1. In particular, we tested , where RND indicates that the value of was selected at random for each construction. For this comparison, we fixed the number of constructions to 100. Table 2 shows the results obtained by the JALEO constructive procedure.

Table 2.
Comparison among different values for the JALEO constructive procedure, without considering the local search procedure.
As can be derived from the table, the best values for the multi-objective metrics were always obtained when , followed by . If we analyzed the number of solutions in the efficient front, we can see that presented the smallest value. However, the quality of the solutions included in it was consistently better than the other approximation fronts, and the computing time was similar for all the variants. Therefore, we selected for the JALEO constructive procedure.
Having configured the JALEO procedure, the next experiment was designed to select the best value for the MOFA constructive procedure. Table 3 shows the results obtained by the different values for the parameter.

Table 3.
Comparison among different values for the MOFA constructive procedure.
This time, the best values for all the multi-objective optimization metrics were obtained by , with results considerably better than the rest of the values. The computing time was again similar among all the methods, as well as the size of the efficient set of solutions. Following these results, we selected for the MOFA constructive procedure. The third experiment, presented in Table 4, compared the results obtained by both constructive procedures to select which was the most promising one.

Table 4.
Comparison between the best configuration for the JALEO and MOFA constructive procedures.
The experimental results showed that the JALEO presented considerably better results than the MOFA in all the multi-objective optimization metrics. In particular, the coverage value of 0.0355 indicated that almost all the solutions included in the efficient set of the JALEO were non-dominated by the reference front. Although the number of solutions included in the approximation front of the JALEO was smaller than the number of solutions in the one of the MOFA, we selected the JALEO since the quality of the set of efficient solutions was better than the MOFA in all the metrics.
Vera et al. [17] analyzed the correlation among the different diversity metrics, concluding that the MPCD presented a high correlation with all the other metrics except the MDD. Furthermore, we used a profiler to analyze the performance in terms of the time consumption of the evaluated metrics and the effect of each metric over the final approximation of the Pareto front. In particular, we discovered that the MPCD required 99% of the total computing time, finally providing less than 5% of the solutions included in the approximation front. Therefore, we conducted an experiment to compare the impact of removing the constructions with the MPCD as the greedy function, distributing these constructions among the other diversity metrics homogeneously. Table 5 shows the effect of including and excluding the MPCD greedy function in the JALEO constructive procedure.

Table 5.
Comparison between the approximation fronts obtained by including and excluding the MPCD greedy function in the construction phase.
The results confirmed the hypothesis that the effect of the MPCD in the construction phase was negative for the final set of efficient solutions. In particular, the distribution of the constructions originally intended for the MPCD among the other objective functions allowed the JALEO procedure to obtain better results in all the multi-objective metrics. It is worth mentioning that the coverage obtained when the MPCD was not considered was really close to zero, indicating that the reference front was conformed by almost all the solutions derived from this variant. Finally, the computing time required by this new variant was almost negligible, being smaller than one second on average. Having analyzed these results, the MPCD was not be considered as a greedy function in the remaining experiments.
One of the decisions that must be made in the GRASP methodology is the number of solutions constructed. Since the proposed constructive procedure was considerably fast, we tested the quality of the approximation front generated when constructing from 100 to 1000 solutions in steps of 100 to analyze the convergence of the JALEO. In particular, Figure 2 shows the evolution of the coverage and hypervolume metrics when considering the aforementioned number of constructions.
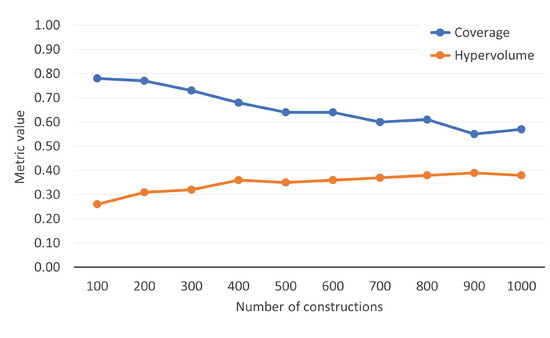
Figure 2.
Evolution of the coverage and hypervolume when constructing from 100 to 1000 GRASP solutions.
Analyzing the figure, we can see that when the number of constructions exceeded 700, neither the coverage, nor the hypervolume were able to significantly improve the previous results. Therefore, we constructed 700 solutions following the GRASP methodology to generate the set of efficient solutions. It is worth mentioning that, in this experiment, the local search procedure was not considered.
Once the initial set of efficient solutions was constructed with the JALEO constructive procedure, we then analyzed the impact of applying the local search procedure presented in Section 3.2. In particular, in a naive approach, the local search was applied to any of the solutions of the efficient set. However, since the local search was the most computationally demanding phase inside the GRASP algorithm, we proposed to limit the size of the neighborhood explored by reducing the number of solutions analyzed in each local search procedure. In order to do so, we included an input parameter in the local search method that determined the percentage of elements that would be considered in the move operator. In particular, we tested the exploration of different percentages of the efficient set (10% to 100% in steps of 10%). Notice that this percentage indicated the amount of solutions that were explored during each iteration of the local search, taking into account that the neighborhood was explored from the most to the least promising solutions, as stated in Section 3.2. Table 6 shows the results obtained in this experiment, where the local search method was applied to each solution that was able to enter the set of efficient solutions after the construction phase described in the previous experiment.

Table 6.
Evolution of the performance of the local search procedure when considering different percentages of elements to be explored.
As expected, the best results in terms of quality were obtained by exploring the complete neighborhood. However, the improvement obtained when increasing the percentage of solutions explored was not significant until reaching 80%. Even in that case, the impact of the computing time was considerably greater than the benefits obtained in terms of quality, being almost a hundred times slower. As a consequence, we decided to explore only 10% of the solutions in order to have a fast and high-quality method.
Having performed this preliminary experimentation, the best configuration of the GRASP algorithm was obtained when selecting the JALEO as the constructive procedure, with an value selected at random for each construction, excluding the MPCD from the set of greedy functions used, and performing 700 constructions. Finally, the local search was applied to each solution of the efficient set, considering the exploration of 10% of the most promising solutions in the neighborhood to have a fast algorithm.
4.2. Competitive Testing
The main aim of this section was to perform a competitive testing between the proposed algorithm and the best previous method found in the state-of-the-art to analyze the efficiency and efficacy of the proposed GRASP algorithm. The best method found in the literature was Vera et al. [17], where a Multi-Objective Evolutionary Algorithm (MOEA) was presented for solving the MOMDP. In particular, the authors designed a Non-Dominated Sorting Genetic Algorithm (NSGA-II) [44] leveraging the implementation provided in JMetal [45]. In order to have a fair comparison, all the experiments were run in the aforementioned computer, and we used the same implementation of NSGA-II; additionally, we included: the MOEA/D, a Multi-Objective Evolutionary Algorithm based on Decomposition [46], which has been proven to be better than NSGA-II in performance in recent works [47]; OMOPSO, a multi-objective particle swarm optimization algorithm which includes an -dominance archive to increase diversification [48]; SMPSO, a more recent multi-objective particle swarm optimization algorithm [49]; and AbYSS, a hybrid scatter search algorithm that uses genetic algorithm operators combined with local search strategies [50].
In this final experiment, we used the complete set of 145 instances described in Section 4. Table 7 shows the final results of the competitive testing.

Table 7.
Competitive testing of the GRASP, NSGA-II, MOEA/D, SMPSO, and AbYSS.
The first conclusion that can be derived from these results is that MOEA/D was the most competitive method among all the multi-objective evolutionary algorithms that were considered. If we first analyzed the coverage, the GRASP-JALEO obtained the best value (0.2698), closely followed by the MOEA/D. The results obtained by NSGA-II indicated that almost half of the solutions discovered by this algorithm were dominated by one or more solutions of the reference front. Regarding the hypervolume, we can see that both the MOEA/D and NSGA-II reached similar results (0.3582 vs. 0.3531), the GRASP-JALEO being considerably better than both of them in this case (0.4218). The same analysis was performed when considering the -indicator, the GRASP-JALEO emerging again as the best algorithm. However, the MOEA/D was able to reach the best value for the IGD+ metric, followed by the GRASP-JALEO algorithm. It is worth mentioning that the GRASP-JALEO was able to include in the set of efficient solutions an average of 762 solutions, while MOEA/D was able to include an average of just 20 solutions. Notice that the GRASP-JALEO was more than 10 times faster than the NSGA-II and MOEA/D approaches, requiring, on average, less than 2 s to solve an instance for the MOMDP. Although OMOPSO, SMPSO, and AbYSS were considerably faster than NSGA-II and the MOEA/D, they were not competitive enough in any metric, especially considering that the GRASP-JALEO was even faster and more competitive in all the metrics considered.
We conducted a non-parametric Friedman test in order to confirm that there were statistically significant differences among the compared algorithms. The obtained p-value smaller than 0.0001 confirmed this hypothesis, where the GRASP-JALEO was ranked first (2.12), followed by the MOEA/D (2.63), NSGA-II (3.25), AbySS (3.96), OMOPSO (4.34), and SMPSO (4.70). Analyzing these results, the GRASP-JALEO emerged as one of the most competitive algorithms for solving the MOMDP in short computing times. Finally, we conducted the non-parametric Wilcoxon test to confirm the superiority of the GRASP-JALEO over MOEA/D. A p-value smaller than 0.0001 supported this hypothesis.
5. Conclusions
In this paper, we presented a novel approach for solving a Multi-Objective variant of the Maximum Diversity Problem (MOMDP) using the well-known GRASP methodology. This kind of problem better adapts to real-life problems, where more than one objective is usually considered. Multi-objective optimization problems have been traditionally tackled with optimization methods claiming to be inspired by biological evolution such as: monarch butterfly optimization [51], elephant herding optimization [52], or Harris hawks optimization [53]. However, the adaptation of traditional metaheuristics, such as scatter search [7], variable neighborhood search [18], or GRASP [22] to handle this family of problems opens a new perspective for future research for multi-objective optimization problems.
Two different constructive procedures were proposed following two completely opposite ideas. On the one hand, the JALEO generated solutions optimizing each one of the greedy functions independently. On the other hand, the MOFA simultaneously optimized all the considered diversity metrics in each construction. The experimental analysis showed how the strategy followed in the JALEO was able to obtain the best results. Additionally, a deep analysis was performed to evaluate the impact of considering the most computationally demanding diversity metric in the proposed algorithm, concluding that its removal benefited the quality of the generated set of efficient solutions. An efficient local search procedure that was able to limit the neighborhood explored was presented to find a local optimum with respect to the solutions originally included in the approximation front, resulting in a novel adaptation of the well-known GRASP methodology for multi-objective optimization problems. The thorough computational experimentation was supported with non-parametric statistical tests that confirmed the superiority of our proposal, the GRASP-JALEO emerging as the best new method for solving the MOMDP.
Based on the analysis of the results, the future research work will be focused on changing the improvement stage of the GRASP using a full metaheuristic method, such as variable neighborhood search, instead of a general local search. This approach is worth researching since it could be better at escaping from local optima by changing the neighborhood explored. Furthermore, the generated solutions could be improved making use of a combination method such as path relinking to integrate intensification and diversification in the search.
Author Contributions
Conceptualization, J.S.-O. and E.G.P.; methodology, J.S.-O.; software, A.C.-C. and P.C.-M.; validation, A.C.-C. and P.C.-M.; formal analysis, E.G.P.; writing—original draft preparation, A.C.-C. and P.C.-M.; writing—review and editing, J.S.-O. and E.G.P.; visualization, E.G.P.; supervision, J.S.-O.; project administration, J.S.-O.; funding acquisition, E.G.P. All authors read and agreed to the published version of the manuscript.
Funding
This research was funded by “Ministerio de Ciencia, Innovación y Universidades” under Grant Ref. PGC2018-095322-B-C22, “Comunidad de Madrid” and “Fondos Estructurales” of European Union with Grant Refs. S2018/TCS-4566, Y2018/EMT-5062.
Data Availability Statement
All the data and source code will be available if the paper is finally published in https://grafo.etsii.urjc.es/momdp, accessed on 21 May 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kuby, M.J. Programming models for facility dispersion: The p-dispersion and maxisum dispersion problems. Math. Comput. Model. 1988, 10, 792. [Google Scholar] [CrossRef]
- Dhir, K.; Glover, F.; Kuo, C.C. Optimizing diversity for engineering management. In Proceedings of the Engineering Management Society Conference on Managing Projects in a Borderless World, New Delhi, India, 17–18 December 1993; pp. 23–26. [Google Scholar]
- Kuo, C.C.; Glover, F.; Dhir, K.S. Analyzing and modeling the maximum diversity problem by zero-one programming. Decis. Sci. 1993, 24, 1171–1185. [Google Scholar] [CrossRef]
- Martí, R.; Martínez-Gavara, A.; Sánchez-Oro, J. The capacitated dispersion problem: An optimization model and a memetic algorithm. Memetic Comput. 2021, 13, 131–146. [Google Scholar] [CrossRef]
- Parreño, F.; Álvarez Valdés, R.; Martí, R. Measuring diversity. A review and an empirical analysis. Eur. J. Oper. Res. 2021, 289, 515–532. [Google Scholar] [CrossRef]
- Martí, R.; Gallego, M.; Duarte, A.; Pardo, E.G. Heuristics and metaheuristics for the maximum diversity problem. J. Heuristics 2013, 19, 591–615. [Google Scholar] [CrossRef]
- López-Sánchez, A.; Sánchez-Oro, J.; Laguna, M. A New Scatter Search Design for Multiobjective Combinatorial Optimization with an Application to Facility Location. INFORMS J. Comput. 2020. [Google Scholar] [CrossRef]
- Sánchez-Oro, J.; López-Sánchez, A.D.; Colmenar, J.M. A multi-objective parallel variable neighborhood search for the bi-objective obnoxious p-median problem. Optim. Lett. 2021, 1–31. [Google Scholar] [CrossRef]
- Antia, M.J. Investment Management: Portfolio Diversification, Risk, and Timing—Fact and Fiction (a review). Financ. Anal. J. 2004, 85–86. [Google Scholar] [CrossRef]
- Sandoya, F.; Martínez-Gavara, A.; Aceves, R.; Duarte, A.; Martí, R. Diversity and Equity Models. In Handbook of Heuristics; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–20. [Google Scholar]
- Glover, F.; Kuo, C.C.; Dhir, K.S. Heuristic algorithms for the maximum diversity problem. J. Inf. Optim. Sci. 1998, 19, 109–132. [Google Scholar] [CrossRef]
- Menéndez, B.; Pardo, E.G.; Sánchez-Oro, J.; Duarte, A. Parallel variable neighborhood search for the min–max order batching problem. Int. Trans. Oper. Res. 2017, 24, 635–662. [Google Scholar] [CrossRef]
- Lozano, M.; Molina, D.; García, C. Iterated greedy for the maximum diversity problem. Eur. J. Oper. Res. 2011, 214, 31–38. [Google Scholar] [CrossRef]
- Huang, A. Similarity measures for text document clustering. In Proceedings of the Sixth New Zealand Computer Science Research Student Conference (NZCSRSC2008), Christchurch, New Zealand, 14–18 April 2008; Volume 4, pp. 9–56. [Google Scholar]
- Real, R.; Vargas, J.M. The Probabilistic Basis of Jaccard’s Index of Similarity. Syst. Biol. 1996, 45, 380–385. [Google Scholar] [CrossRef]
- Qian, G.; Sural, S.; Gu, Y.; Pramanik, S. Similarity between Euclidean and Cosine Angle Distance for Nearest Neighbor Queries. In Proceedings of the 2004 ACM Symposium on Applied Computing, Nicosia, Cyprus, 14–17 March 2004; Association for Computing Machinery: New York, NY, USA, 2004. [Google Scholar]
- Vera, K.; Lopez-Pires, F.; Baran, B.; Sandoya, F. Multi-objective maximum diversity problem. In Proceedings of the 2017 XLIII Latin American Computer Conference (CLEI), Cordoba, Argentina, 4–8 September 2017; pp. 1–9. [Google Scholar]
- Duarte, A.; Pantrigo, J.J.; Pardo, E.G.; Mladenović, N. Multi-objective variable neighborhood search: An application to combinatorial optimization problems. J. Glob. Optim. 2015, 63, 515–536. [Google Scholar] [CrossRef]
- Stewart, T.; Bandte, O.; Braun, H.; Chakraborti, N.; Ehrgott, M.; Göbelt, M.; Jin, Y.; Nakayama, H.; Poles, S.; Di Stefano, D.; et al. Multiobjective Optimization: Interactive and Evolutionary Approaches; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2008; pp. 285–327. [Google Scholar]
- Garcia-Najera, A.; Bullinaria, J.A. An improved multi-objective evolutionary algorithm for the vehicle routing problem with time windows. Comput. Oper. Res. 2011, 38, 287–300. [Google Scholar] [CrossRef]
- Pacheco, J.; Martí, R. Tabu search for a multi-objective routing problem. J. Oper. Res. Soc. 2006, 57, 29–37. [Google Scholar] [CrossRef]
- Martí, R.; Campos, V.; Resende, M.G.; Duarte, A. Multiobjective GRASP with path relinking. Eur. J. Oper. Res. 2015, 240, 54–71. [Google Scholar] [CrossRef]
- Bautista, J.; Fernández, E.; Pereira, J. Solving an urban waste collection problem using ants heuristics. Comput. Oper. Res. 2008, 35, 3020–3033. [Google Scholar] [CrossRef]
- Yi, J.H.; Deb, S.; Dong, J.; Alavi, A.H.; Wang, G.G. An improved NSGA-III algorithm with adaptive mutation operator for Big Data optimization problems. Future Gener. Comput. Syst. 2018, 88, 571–585. [Google Scholar] [CrossRef]
- Sun, J.; Miao, Z.; Gong, D.; Zeng, X.J.; Li, J.; Wang, G. Interval Multiobjective Optimization With Memetic Algorithms. IEEE Trans. Cybern. 2020, 50, 3444–3457. [Google Scholar] [CrossRef]
- Martí, R.; Sandoya, F. GRASP and path relinking for the equitable dispersion problem. Comput. Oper. Res. 2013, 40, 3091–3099. [Google Scholar] [CrossRef]
- Martí, R.; Gallego, M.; Duarte, A. A branch and bound algorithm for the maximum diversity problem. Eur. J. Oper. Res. 2010, 200, 36–44. [Google Scholar] [CrossRef]
- Palubeckis, G. Iterated tabu search for the maximum diversity problem. Appl. Math. Comput. 2007, 189, 371–383. [Google Scholar] [CrossRef]
- Erkut, E.; Neuman, S. Analytical models for locating undesirable facilities. Eur. J. Oper. Res. 1989, 40, 275–291. [Google Scholar] [CrossRef]
- Resende, M.; Martí, R.; Gallego, M.; Duarte, A. GRASP and path relinking for the max–min diversity problem. Comput. Oper. Res. 2010, 37, 498–508. [Google Scholar] [CrossRef]
- Duarte, A.; Sánchez-Oro, J.; Resende, M.G.; Glover, F.; Martí, R. Greedy randomized adaptive search procedure with exterior path relinking for differential dispersion minimization. Inf. Sci. 2015, 296, 46–60. [Google Scholar] [CrossRef]
- Lai, X.; Yue, D.; Hao, J.K.; Glover, F. Solution-based tabu search for the maximum min-sum dispersion problem. Inf. Sci. 2018, 441, 79–94. [Google Scholar] [CrossRef]
- Amirgaliyeva, Z.; Mladenović, N.; Todosijević, R.; Urošević, D. Solving the maximum min-sum dispersion by alternating formulations of two different problems. Eur. J. Oper. Res. 2017, 260, 444–459. [Google Scholar] [CrossRef]
- Mladenović, N.; Todosijević, R.; Urošević, D. Less is more: Basic variable neighborhood search for minimum differential dispersion problem. Inf. Sci. 2016, 326, 160–171. [Google Scholar] [CrossRef]
- Pérez-Peló, S.; Sánchez-Oro, J.; López-Sánchez, A.D.; Duarte, A. A Multi-Objective Parallel Iterated Greedy for Solving the p-Center and p-Dispersion Problem. Electronics 2019, 8, 1440. [Google Scholar] [CrossRef]
- Brimberg, J.; Mladenović, N.; Todosijević, R.; Urošević, D. A basic variable neighborhood search heuristic for the uncapacitated multiple allocation p-hub center problem. Optim. Lett. 2017, 11, 313–327. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G. A probabilistic heuristic for a computationally difficult set covering problem. Oper. Res. Lett. 1989, 8, 67–71. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G.C.; Smith, S.H. A Greedy Randomized Adaptive Search Procedure for Maximum Independent Set. Oper. Res. 1994, 42, 860–878. [Google Scholar] [CrossRef]
- López-Sánchez, A.; Sánchez-Oro, J.; Hernández-Díaz, A. GRASP and VNS for solving the p-next center problem. Comput. Oper. Res. 2019, 104, 295–303. [Google Scholar] [CrossRef]
- Pérez-Peló, S.; Sánchez-Oro, J.; Duarte, A. Finding weaknesses in networks using Greedy Randomized Adaptive Search Procedure and Path Relinking. Expert Syst. 2020, 37, e12540. [Google Scholar] [CrossRef]
- Sohrabi, S.; Ziarati, K.; Keshtkaran, M. A greedy randomized adaptive search procedure for the orienteering problem with hotel selection. Eur. J. Oper. Res. 2020, 283, 426–440. [Google Scholar] [CrossRef]
- Festa, P.; Resende, M.G.C. An annotated bibliography of GRASP–Part II: Applications. Int. Trans. Oper. Res. 2009, 16, 131–172. [Google Scholar] [CrossRef]
- Li, M.; Yao, X. Quality evaluation of solution sets in multiobjective optimisation: A survey. ACM Comput. Surv. (CSUR) 2019, 52, 26. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Durillo, J.J.; Nebro, A.J. jMetal: A Java framework for multi-objective optimization. Adv. Eng. Softw. 2011, 42, 760–771. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Li, H.; Deb, K.; Zhang, Q.; Suganthan, P.N.; Chen, L. Comparison between MOEA/D and NSGA-III on a set of novel many and multi-objective benchmark problems with challenging difficulties. Swarm Evol. Comput. 2019, 46, 104–117. [Google Scholar] [CrossRef]
- Sierra, M.R.; Coello, C.A.C. Improving PSO-based multi-objective optimization using crowding, mutation and ϵ-dominance. In Lecture Notes in Computer Science, Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, 9–11 March 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 505–519. [Google Scholar]
- Nebro, A.J.; Durillo, J.J.; Garcia-Nieto, J.; Coello, C.C.; Luna, F.; Alba, E. SMPSO: A new PSO-based metaheuristic for multi-objective optimization. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making (MCDM), Nashville, TN, USA, 30 March–2 April 2009; pp. 66–73. [Google Scholar]
- Nebro, A.J.; Luna, F.; Alba, E.; Dorronsoro, B.; Durillo, J.J.; Beham, A. AbYSS: Adapting scatter search to multiobjective optimization. IEEE Trans. Evol. Comput. 2008, 12, 439–457. [Google Scholar] [CrossRef]
- Feng, Y.; Deb, S.; Wang, G.G.; Alavi, A.H. Monarch butterfly optimization: A comprehensive review. Expert Syst. Appl. 2021, 168, 114418. [Google Scholar] [CrossRef]
- Meena, N.K.; Parashar, S.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Improved elephant herding optimization for multiobjective DER accommodation in distribution systems. IEEE Trans. Ind. Inform. 2017, 14, 1029–1039. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).