ASAD-RD: Accuracy Scalable Approximate Divider Based on Restoring Division for Energy Efficiency

Abstract

Approximate computing can considerably improve energy efficiency by mitigating the accuracy requirements of calculations in error resilient application programming, such as machine learning, audio–video signal processing, data mining, and search engines. In this study, we propose an approximate divider for dynamic energy-quality scaling, which involves a trade-off between accuracy and latency. Previous approximate dividers for dynamic energy-quality scaling are well-configured, but lack energy-quality scalability. The key is to create a more accurate dynamic approximate divider while extending the limits of accuracy to maximize energy efficiency and meet various accuracy requirements. The proposed divider, called the accuracy scalable approximate divider based on restoring division (ASAD-RD), uses restoring division to significantly improve the error of the approximate divider and to use less latency. For the 8-bit division, SAADI, the previous design, has an average accuracy of 90.78% to 98.77%; however, ASAD-RD can improve the accuracy between 95.2% and 99.23% and hardly requires additional power consumption. Furthermore, for the same target accuracy, ASAD-RD requires fewer cycle iterations than SAADI. Thus, ASAD-RD requires lower energy than SAADI and can operate as an energy-efficient approximate divider.

1. Introduction

Energy efficiency is a key component of a computer system. Approximate computing is a type of design that can improve the energy efficiency of a system [1]. Traditionally, arithmetic operations were considered to always produce accurate results and were designed to pursue accurate computational results in computer design. However, accuracy may not always be a priority when considering energy efficiency in arithmetic operations [2]. Some applications pursue perfectly accurate computations, while others may require only adequate accuracy and seek more computational speed or power consumption [3]. Applications such as machine learning, video signal processing, searching, and data mining do not require complete accuracy [4]. In such cases, pursuing perfectly accurate computation can waste energy. Approximate computing is a new approach to improve the energy efficiency of these applications [5]. Approximate computing using an adder [6], multiplier [7], or divider [8] can improve energy efficiency by saving power or latency while meeting the results of appropriate accuracy.

So far, many approximate computing designs have been presented, and these designs have been proven to benefit from performance improvement and power savings by causing minor errors. Furthermore, many approximate divider designs have been proposed [9,10,11,12]. However, previously proposed approximation dividers do not meet the applications’ various accuracy requirements and are limited in that they provide only a single level of accuracy. In addition, the accuracy requirement for arithmetic operations is not constant because the impact of approximation to the final quality at the application level is highly input-dependent [13], and the application-level quality requirements may also change over time. Therefore, in order to meet the quality requirements of the application, an approximate divider is required that enables dynamic quality scaling. SAADI has the advantage of being able to dynamically control the accuracy and latency, which helps to overcome the shortcomings of the previous approximate dividers [14].

Herein, we propose an approximate divider design that enhances the dynamic energy quality scalability with fewer errors. The accuracy scalable approximate divider based on restoring division (ASAD-RD) is based on the previous approximate divider, SAADI [14], which performs division by multiplying the dividend and the approximate reciprocal of the divisor and then repeats the process of the approximation of the reciprocal of the divisor. According to the iteration process, accuracy gradually increases, which enables SAADI to obtain a trade-off between latency and accuracy. Applications can use SAADI to perform high-accuracy division by increasing the time and power consumption or improving energy efficiency while reducing accuracy. Energy-efficient arithmetic operations have long been a challenge for researchers to derive better performance from limited resources in computer systems. Compared with SAADI [14], ASAD-RD is based on a novel idea. It is a hybrid method of SAADI and other division algorithms for improving the accuracy and reducing the repetition process of the approximate division. In the process of approximate division, a restoring division is performed at the beginning of SAADI to reduce the occurrence of truncation errors in the multiplicative division. As a result, the proposed design can meet more stringent accuracy requirements that cannot be reached by SAADI and can benefit from power or performance.

The remainder of the paper is organized as follows: Section 2 presents related works and explains the motivations of our study. The proposed approximate divider is introduced in Section 3. It elaborates on the algorithm and architecture with error compensation. Section 4 presents a complete analysis of accuracy and latency and a comparison with a conventional scalable accuracy approximate divider (e.g., SAADI), followed by conclusions in Section 5.

2. Related Works

Researchers have developed and proposed various approximate arithmetic units to improve the energy efficiency of arithmetic operations. Among them, approximate dividers have been studied relatively more recently than other arithmetic units, such as the adder [6] and multiplier [7]. An approximate divider called AAXD [9] normalizes the operands to remove leading zeros and uses only a few numbers of the most relevant bits. The truncated dividend is then divided by the truncated divisor using a narrow width divider. The dividend and divisor are then compared to prevent overflow. Accuracy is predetermined by the partition width of AAXD, which cannot be adjusted dynamically. An approximate divider design presented in [15] reduces power consumption and circuit complexity. It is designed with a simple structure consisting of three approximate subtractor cells that leads to performance improvement and power reduction. However, the accuracy is also determined at the design level. Therefore, the requirements of the application cannot be met dynamically. PLApp [10], TruncApp [11], and SEERAD [12] are examples of multiplicative dividers, where the reciprocal of the divisor is obtained first and then subsequently multiplied by the dividend. In PLApp, the reciprocal is approximated using a fragmented linear function and rounding. In TruncApp, the reciprocal is obtained by simple bit manipulations such as inversion, truncation, and concatenation. In SEERAD, the reciprocal is approximated using a table indexed by the upper bits of the divisor. For all three designs, the accuracy is determined at design time and cannot be configured at runtime. SAADI [14] is an example of an approximation divider, which can dynamically scale accuracy at runtime. It is also a multiplicative divider, but in the approximation process of the reciprocal of the divisor, repeated operations are performed using the Taylor series. Here, the accuracy is determined by the number of iterations, and the truncation errors are accumulated during the iteration process. As a result, there is a limitation of accuracy that cannot be solved no matter how many times a repeated operation is performed. For error compensation of SAADI, Reference [16] reference could not be subject. proposed the idea that the approximate quotient is multiplied by a constant in a Look-up Table indexed by the number of iterations. However, the error compensation after approximation may not be achieved properly due to the truncation caused by the limit of divider width. Therefore, we propose the idea of changing the input, not the error compensation of the output.

3. Proposed Approximate Divider

In this section, we introduce our divider design, ASAD-RD, and the algorithm of the divider and hardware implementation. We analyze the error compensation and improvement in accuracy.

3.1. Proposed Approximate Division

The proposed design, ASAD-RD, is a combination of a multiplicative division algorithm that obtains the reciprocal of the divisor first and then multiplies the dividend and uses the restoring division algorithm that provides accurate computational results. We explain the basics of the restoring division algorithm [17,18] and the multiplicative division algorithm [19].

First, we describe the basics of restoring division. In restoring division, register R contains the remainder and register Q the quotient. An n bit dividend is loaded in Q, and the divisor is loaded in register M. The value of the register is initially maintained at zero; this is register R whose value is restored during the iteration. For example, the dividend is 190, the divisor 11, and the bits 8. Subsequently, R is 0, M 11, and Q 190.

$$R=0,Q=10111110,M=1011,n=8,$$

(1)

Subsequently, the content of the registers R and Q is shifted to the left as if they are a single unit, such as $RQ$.

$$0000000010111110\to 0000000101111100\mathrm{shift}\mathrm{left}RQ$$

(2)

Subsequently, $R=R-M$, if $A<0$, $Q\left[0\right]=0$, and the value of R is restored. Else $Q\left[0\right]=1$.

$$R=R-M=1-11<0\to Q\left[0\right]=0,R=1\left(\mathrm{restore}R\right)$$

(3)

The process of the first step is over. Once this process is iterated n times, where n is the width of the divider, the restoring division is finished, and the register Q contains the quotient 17, while R contains the remainder of three. The remainder R and divisor M are the new inputs of multiplicative division as a dividend A and divisor B.

Next, we describe the basics of the multiplicative division. A and B can be represented in a normalized form as:

$$A=2^{e_a}\times aandB=2^{e_b}\times b,$$

(4)

where $0.5\le a<1$ and $0.5\le b<1$. During normalization, a and b are truncated to n bits. Subsequently, the quotient Q of division $A/B$ is:

$$Q=\frac{A}{B}=2^{e_a-e_b}\times \frac{a}{b}=2^{e_a-e_b}\times a\times R\left(b\right),$$

(5)

where $R\left(b\right)$ is the reciprocal of b, i.e., $R\left(b\right)=1/b$. Instead of computing $a/b$ directly, it can be expressed as a multiplication of a and $R\left(b\right)$. For energy-efficient division, the exact reciprocal is not required. Therefore, an approximation reciprocal with acceptable accuracy is required. We address this by the approximation of the reciprocal based on the Taylor series expansion. More specifically, the Taylor series expansion of $1/b$ is:

$$R\left(b\right)=\frac{1}{1+x}=\sum _{i=0}^{\infty }{(-x)}^i=1-x+x^2-x^3+x^4-···,$$

(6)

where $x=b-1$. It always converges because $-0.5\le x<0$ for normalized b such that $0.5\le b<1$. The approximate reciprocal can be obtained by adding up the first few low-order terms. If higher accuracy is required, more order terms can be added to gradually improve accuracy. However, this also improves latency. This trade-off can be used for applications depending on the required accuracy and latency restriction [14]. Let $\widetilde{R_t}\left(b\right)$ denote the t-th order approximation of $R\left(b\right)$, such that:

$$\widetilde{R_t}\left(b\right)=\sum _{i=0}^t{\left|x\right|}^i=1+\left|x\right|+{\left|x\right|}^2+{\left|x\right|}^3+{\left|x\right|}^4+···+{\left|x\right|}^t,$$

(7)

Finally, the t-th order approximate quotient $\widetilde{Q_t}$ is then obtained as:

$$\widetilde{Q_t}=2^{e_a-e_b}\times \frac{a}{b}=2^{e_a-e_b}\times a\times R_t\left(b\right).$$

(8)

Subsequently, we get two quotients, Q and $\widetilde{Q_t}$. The sum of Q and $\widetilde{Q_t}$ is the final quotient $\widetilde{Q_t^r}$ of the proposed approximate divider.

Table 1 shows the result of $190/11$ and the error of SAADI and ASAD-RD. In the multiplicative division of each divider, the divisor B is 11, and b is $0.68750$. Therefore, the initial normalization and two’s complement conversion produce $\left|x\right|=0.31250$. Since the first iteration, the approximate reciprocal $\widetilde{R_1}\left(b\right)$ is $1.31250$. In the case of SAADI, the dividend A is 190, and the quotient $\widetilde{Q_1}$ is 15.5000, which is the approximate quotient of SAADI. By contrast, in the case of ASAD-RD, because restoring division was executed first, dividend A becomes three. Therefore, the quotient $\widetilde{Q_1}$ of ASAD-RD is 0.1250.

Table 1. Comparison of the 190/11 division for each divider for 8 bits. ASAD-RD, accuracy scalable approximate divider based on restoring division.

Iteration Count	${\left|\mathit{x}\right|}^{\mathit{t}}$	${\mathit{R}}_{\mathit{t}}\left(\mathit{b}\right)$	SAADI [14]	ASAD-RD
t = 1	0.31250	1.31250	15.5000 (10.26%)	17.1250 (0.86%)
t = 2	0.09766	1.40265	16.6250 (3.75%)	17.2500 (0.13%)
t = 3	0.02930	1.43750	17.0000 (1.58%)	17.2500 (0.13%)
t = 4	0.00782	1.44531	17.1250 (0.86%)	17.2500 (0.13%)
t = 5	0.00195	1.44531	17.1250 (0.86%)	17.2500 (0.13%)

After multiplicative division, adding the restoring division quotient Q to the output of the multiplicative division quotient $\widetilde{Q_1}$ provides the result of 190/11 by ASAD-RD. Therefore, the final quotient of ASAD-RD $\widetilde{Q_1^r}$ is 17 + 0.1250 = 17.1250. The exact quotient is 17.2727$\cdots$; thus, the error rate of ASAD-RD is 0.86%. By contrast, the error rate of SAADI is 10.26%. In the second iteration, $\widetilde{R_2}\left(b\right)$ and the final quotient of each divider are increased, thus reducing the error rate of SAADI from 10.26% to 3.75% and the error rate of ASAD-RD from 0.86% to 0.13%. However, in more than three iterations, there is no change in the error rate of ASAD-RD because $\widetilde{Q_t^r}$ has already converged. As t increases, ${\left|x\right|}^t$ decreases. If ${\left|x\right|}^t$ is zero after being truncated from 2n to n bits, ${\left|x\right|}^t$ will have no effect on the value of $\widetilde{Q_t^r}$. Then, $\widetilde{Q_t^r}$ is converged. Thus, the maximum approximate quotient of 190/11 achieved by ASAD-RD is 17.25000 with an error rate of 0.13%. In SAADI, the quotient is converged to 17.1250 with an error rate of 0.86% in four iterations.

Comparing the final quotient of SAADI and ASAD-RD shows that there are differences in the 190/11 division operation. Because restoring division is performed before multiplicative division, the quotient gets a compensated initial value. Thus, the quotient of ASAD-RD has a lower error rate than SAADI for each cycle iteration. Restoring division before the multiplicative division increases the maximum accuracy and reduces the number of cycle iterations for maximum accuracy. More analysis regarding this is provided in Section 4.

3.2. Hardware Architecture

Figure 1 shows the hardware architecture for the restoring division of ASAD-RD, and Figure 2 shows the hardware architecture for the multiplicative division of ASAD-RD. Figure 3 shows the hardware architecture of SAADI. Except for Q and one adder, whose output is the final quotient $\widetilde{Q_t^r}$ in the multiplicative division part of ASAD-RD, the hardware architectures of ASAD-RD and SAADI are similar. The proposed design consists of a restoring division part and a multiplicative part. In the restoring division part, if the remainder R, whose initial value is zero, divisor M, and dividend Q are the inputs of ASAD-RD, R and Q are combined as $RQ$ and are shifted one bit left. Subsequently, most n bits of $RQ$ become R. The most significant bit (MSB) of the $R-M$ operation result is the selector of the two multiplexers. If the selector is one, the output of the multiplexers is $RQ$, and if the selector is zero, $(R-M)Q$ and one are the outputs. The architecture consists of a recursive structure in which the output of each multiplexer is returned to its input. This process is repeated for the number of bits of the input. When the restoring division is performed through this process, R, Q, and B are obtained as outputs, and the remainder R and quotient Q have different values from the initial values. However, B receives the value of M, and it remains the initial value. After the restoring division, R and B become the inputs of multiplicative division as a dividend A and divisor B, respectively; in this process, the dividend A gets the value of R. Furthermore, Q is stored and then combined with the results of the multiplicative division to provide the final quotient $\widetilde{Q_t^r}$. This multiplicative division process is the same as the previous design of SAADI. However, for the same operation, the input and output of the multiplicative division are different. Consequently, the existence of the restoring division provides different outputs from the previous design for the same division. Major hardware components for ASAD-RD include one 2n-bit barrel shifter, two n-bit adders, and two 2n bit two to one multiplexers more than those of SAADI. Therefore, ASAD-RD needs as much area as for these components as SAADI, and it is expected that ASAD-RD will consume more power and energy for the same division. The analysis of the power consumption and energy is provided in Section 4.3.

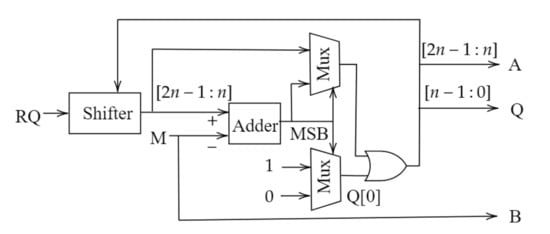
Figure 1. Hardware architecture of the restoring division of the proposed ASAD-RD.

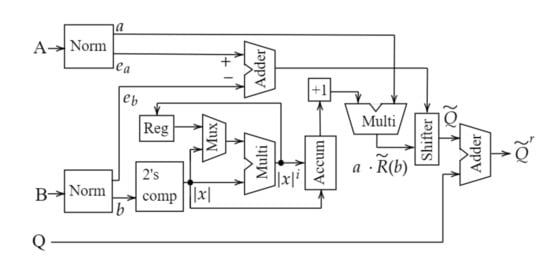
Figure 2. Hardware architecture of the multiplicative division of the proposed ASAD-RD.

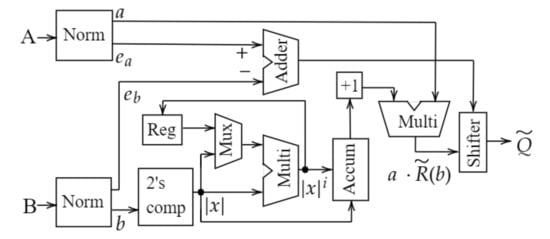
Figure 3. Hardware architecture of SAADI [14].

3.3. Error Compensation

In this section, we analyze the errors of SAADI and how the errors can be compensated for in our divider design. The loss of accuracy in SAADI is caused by the following factors:

• ${ϵ}_1$: The input operands A and B are truncated to n bits during normalization
• ${ϵ}_2$: The approximate reciprocal $\widetilde{R_t}\left(b\right)$ is the sum of a limited number of ${\left|x\right|}^i$ terms
• ${ϵ}_3$: Each ${\left|x\right|}^i$ term is computed using an approximate multiplier that truncates 2n bits to n bits
• ${ϵ}_4$: The approximate reciprocal $\widetilde{R_t}\left(b\right)$ is truncated from $n+2$ bits to n bits before being multiplied by a, and the result is truncated to n bits.

The sign of ${ϵ}_1$ is input-dependent. Truncating A contributes to negative factors of ${ϵ}_1$ because the truncation results in a smaller dividend, while truncating B has the reverse effect because a smaller divisor produces a larger quotient. The error due to a finite-order approximation (${ϵ}_2$) is the runtime-adjustable error factor that we exploit for the trade-off of accuracy and latency such that:

$${ϵ}_2=\widetilde{R_t}\left(b\right)-R\left(b\right)=-\sum _{i=t+1}^{\infty }{\left|x\right|}^i=-{\left|x\right|}^{t+1}-{\left|x\right|}^{t+2}-···.$$

(9)

Note that ${ϵ}_2$ is always negative, and the magnitude decreases as t increases. Because of the accuracy loss in the multiplier (${ϵ}_3$), ${\left|x\right|}^i$ eventually becomes zero within n cycles. Therefore, the effective range of t for the accuracy-latency trade-off is $1\le t\le n-1$, considering one additional cycle at the end for $a\times \widetilde{R_t}\left(b\right)$. The error induced by the truncation in the multiplier and the accumulator (${ϵ}_3$ and ${ϵ}_4$) is always negative because it results in an under-approximated reciprocal and thus an under-approximated quotient [14].

We attempted to compensate SAADI for its approximate error by adding restoring division to the front of SAADI. This approach can reduce the size of the input of SAADI. A smaller input reduces the truncation error that occurs during normalization, which improves the accuracy by reducing the effect of ${ϵ}_1$ on the approximate division results. Because restoring division is performed before the multiplicative division, the initial errors of division improve. Thus, the iterations of the approximation process for target accuracy will be reduced. This reduces the number of ${\left|x\right|}^i$ terms. Subsequently, ${ϵ}_3$ reduces. In the maximum iteration of the approximation process for the maximum accuracy, as the effect of error factors decreases, a more accurate division is possible beyond the accuracy limit of SAADI. The next section is followed by a performance comparison analysis of the approximate divider with the addition of the restoring division.

4. Comparison and Analysis

We used Intel Quartus Prime Lite tool ver. 18.1 [20] to implement SAADI and ASAD-RD with Verilog hardware description language (HDL) and to evaluate the dividers from the perspective of the trade-off of accuracy, latency, and power consumption. A comparison of our design with that of SAADI is as follows:

• Average cycle iteration counts for maximum accuracy.
• Mean absolute error (MAE) of SAADI and ASAD-RD.
• Power consumption and energy efficiency.
• Required cycle iteration counts for target accuracy.

4.1. Previous Approximate Dividers

Table 2 shows the MAE and power consumption of the previous single cycle designs. AAXD has an MAE of 0.18% at a maximum accuracy level of 16. PLApp also has an MAE of 0.18% at the maximum accuracy level (8,8). On the other hand, TruncApp and SEERAD provide accuracies of 4.3% and 2.42%, respectively, when the accuracy level is four. Compared to TruncApp and SEERAD, AAXD and PLApp appear to have higher accuracy limits. TruncApp and AAXD result in higher accuracy scalability than the others. However, the energy consumption of AAXD at maximum accuracy is significantly higher than that of other dividers. These dividers can provide dynamic accuracy scalability by parameter changes. However, they do not have dynamic accuracy scalability at runtime because the accuracy is determined at design-time. Therefore, the following sections mainly deal with comparisons with SAADI, which has dynamic quality scalability at runtime.

Table 2. Comparison of previously proposed approximate dividers.

Parameters	Dividers	Cycle	MAE (%)	Power (mW)	Energy (nJ)
6	AAXD	1	6.61	0.5	1.15
10	AAXD	1	1.52	1.02	4.29
16	AAXD	1	0.18	2.31	21.02
2, 4	PLApp	1	2.87	0.89	1.13
4, 5	PLApp	1	1.42	1.15	1.89
8, 8	PLApp	1	0.18	2.86	7.21
3	TruncApp	1	10.1	0.56	0.47
4	TruncApp	1	4.3	0.8	0.84
3	SEERAD	1	4.66	2.12	1.69
4	SEERAD	1	2.42	7.53	8.06

4.2. Accuracy and Latency

In this section, we analyze the errors of the previous design and detail how the errors can be compensated to use the proposed design. Within the range, we first evaluate both dividers for varying runtime parameters with 500,000 random combinations of dividends and divisors. For a fair comparison, the same combinations are supplied to both dividers. As described in Section 3.1, the design parameters of the dividers are n i.e., the number of bits of operands, and t i.e., the cycle iteration count for reciprocal approximation.

Figure 4 shows the average iteration counts of SAADI and ASAD-RD required to reach the maximum accuracy for n = [4, 8, 12, 16]. In both dividers, the maximum number of the effective iteration counts for improved accuracy is $n-1$. The average number of iteration counts to reach the maximum accuracy is less than $n/2$ for SAADI. For ASAD-RD, it is approximately 0.5 lower than the value for SAADI. In other words, ASAD-RD has the benefit of reducing the iteration count in the same n. Therefore, ASAD-RD can offset the additional latency for maximum accuracy due to the extended hardware for restoring division.

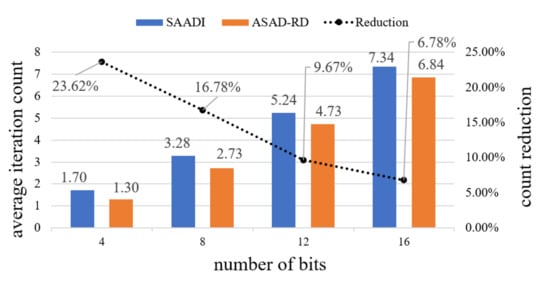
Figure 4. Average iteration count for maximum accuracy for a varying number of bits.

Figure 5 shows the variation of MAE of both dividers after varying n and the iteration count using the log scale. As n is increased, not only the maximum accuracy, but also the speed of improvement increases. For all terms with the same parameter, the proposed design obtains a lower MAE than the previous design. Therefore, ASAD-RD can obtain more accurate results for the same operation. The relation between reduced MAE and energy efficiency is discussed in the following section.

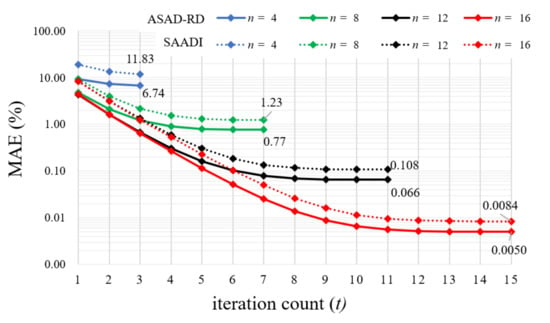
Figure 5. MAE for varying numbers of bits and iteration counts in SAADI and ASAD-RD.

4.3. Power Consumption

Using the Quartus power analyzer tool [20], we measured the power consumption of the designed models. We adopted the power consumption per cycle as the basic unit for comparison with the previous design.

Table 3 shows the minimum and maximum MAE and power consumption of the first cycle of each divider using n = [4, 8, 12, 16]. For every n, ASAD-RD exhibits an approximately 40% to 50% lower MAE than SAADI. Although ASAD-RD consumes 4.3% to 4.9% more power than SAADI under the same conditions, the additional power consumption is due to the added division process compared with the previous design, in which division occurs only once. Thus, the more the total power consumption due to the increase of cycle iterations, the lower the percentage of additional power consumption in the total. As an example, for the 8 bit division, when only one iteration cycle is performed, the additional power consumption from the added process accounts for 4% of the total power consumption. However, for four iteration cycles, the rate is only 1%.

Table 3. Comparison of MAE and power consumption for a varying number of bits.

Bits	Divider	Cycles		MAE (%)	Power (mW)
4	SAADI	Min	1	19.24	0.90
		Max	3	11.83
	ASAD-RD	Min	1	9.33	0.94
		Max	3	6.74
8	SAADI	Min	1	9.22	1.41
		Max	7	1.23
	ASAD-RD	Min	1	4.78	1.47
		Max	7	0.77
12	SAADI	Min	1	8.36	2.06
		Max	11	0.108
	ASAD-RD	Min	1	4.37	2.15
		Max	11	0.066
16	SAADI	Min	1	8.33	2.67
		Max	15	0.008
	ASAD-RD	Min	1	4.39	2.80
		Max	15	0.005

According to Section 4.2, the average number of iterations for maximum accuracy is less than $n/2$. Then, the average number of iterations of ASAD-RD is approximately 0.5 lower than the previous design. As a result, with the same parameters, the maximum accuracy of ASAD-RD is not only higher than that of the previous design, but also the number of iterations for maximum accuracy is lower. Lower iterations save power, and the amount saved is greater than the additional power consumption due to additional hardware. Therefore, ASAD-RD has advantages over SAADI in power or performance.

Table 4 shows how many iteration counts are required for each divider to reach the target accuracy in n = [4, 8, 12, 16] and the required energy. To compare ASAD-RD with the previous design from the viewpoint of energy, we expressed energy as the number of cycles to reach the target accuracy and the power consumption per cycle. Target accuracy that cannot be achieved due to the divider design limitation is left blank. For the same target accuracy, ASAD-RD, in most cases, performs one to two fewer iterations than SAADI. The proposed design and the previous design have the same cycle structure, and the proposed design has fewer iteration counts. Consequently, ASAD-RD consumes less energy than SAADI for the same target accuracy.

Table 4. Comparison of required cycles and energy for target accuracy in SAADI and ASAD-RD for a varying number of bits.

		SAADI [14]				ASAD-RD
Number of Bits (n)		4	8	12	16	4	8	12	16
Target accuracy: 88%	Cycles	3	1	1	1	1	1	1	1
	Energy (mW)	2.70	1.41	2.06	2.67	0.94	1.47	2.15	2.80
Target accuracy: 91%	Cycles		2	2	2	3	1	1	1
	Energy (mW)		2.42	4.12	5.34	2.74	1.47	2.15	2.80
Target accuracy: 95%	Cycles		2	2	2		1	1	1
	Energy (mW)		2.42	4.12	5.34		1.47	2.15	2.80
Target accuracy: 98%	Cycles		4	3	3		3	2	2
	Energy (mW)		5.64	6.18	8.01		4.29	4.21	5.47
Target accuracy: 99%	Cycles			4	4		4	3	3
	Energy (mW)			8.24	10.58		5.70	6.27	8.14
Target accuracy: 99.80%	Cycles			6	6			5	5
	Energy (mW)			12.36	16.02			10.39	13.48
Target accuracy: 99.99%	Cycles				11				9
	Energy (mW)				29.37				24.16

Compared to the previous designs in Table 2, dynamically scalable dividers are multi-cycle, which consume relatively more power and energy than the single-cycle designs. However, the previous designs have low accuracy limits and a short range of accuracy scalability. This may result in a lack of performance if the accuracy requirements become strict at runtime. In this case, a multi-cycle divider, as proposed in this study, with large accuracy scalability and a high accuracy limit, which can be expanded at run-time, can be useful.

SAADI has a larger range of dynamic scalable accuracy because of the higher gap between the maximum MAE and minimum MAE. By contrast, ASAD-RD has a smaller range of dynamic scalable accuracy, but can reach a higher target accuracy at the same divider width. For instance, for the 8 bit divider, SAADI cannot reach a target accuracy of 99%, but ASAD-RD can. Thus, the proposed design uses less energy at the same divider width for target accuracy and achieves higher target accuracy with a smaller divider width.

5. Conclusions

Today, energy efficiency is a very important factor in computing and signal processing. This study presents an energy quality scalable approximate divider called ASAD-RD to improve the energy efficiency of systems. The proposed design is based on SAADI and the restoring division algorithm. It is an approximate divider that can control the accuracy and latency by repeating the process of approximating the reciprocal of dividends and has better performance than the previous design. It has been demonstrated that the number of iterations can be set to create a trade-off between latency and accuracy; thus, the required accuracy for the application can be met. For the 8 bit division, SAADI has an average accuracy of 90.78% to 98.77%; however, ASAD-RD can improve the accuracy to 95.22% to 99.23% and hardly requires additional power consumption. However, for 99% target accuracy, SAADI requires an over 12 bit division. However, ASAD-RD can achieve 99% target accuracy using just an 8 bit division. Additionally, for the same target accuracy, ASAD-RD requires fewer cycle iterations than SAADI. Thus, ASAD-RD uses lower energy than SAADI and can operate as an energy-efficient approximate divider.