Stiffness of Human Hair Correlates with the Fractions of Cortical Cell Types
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hair Samples
2.2. Hair Diameter
2.3. Bending Elasticity
2.4. Fluorescence Light Microscopy (FLM) of Cortical Cell Types
2.5. Atomic Force Microscopy (AFM)
3. Results
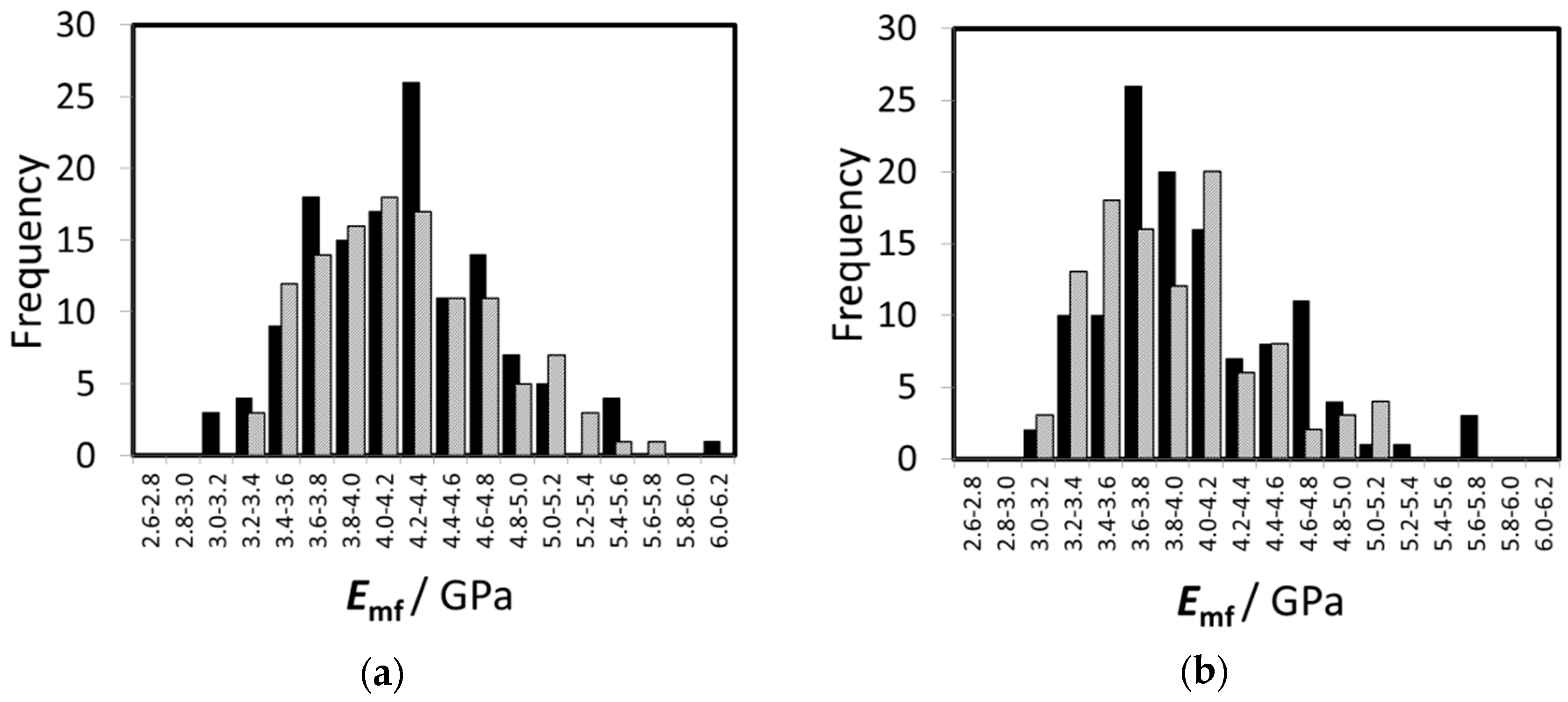
3.1. Bending Elasticity
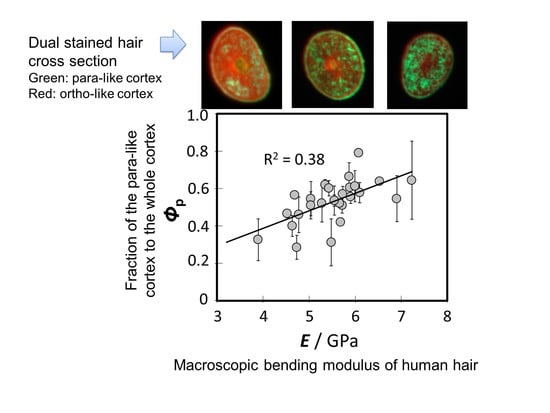
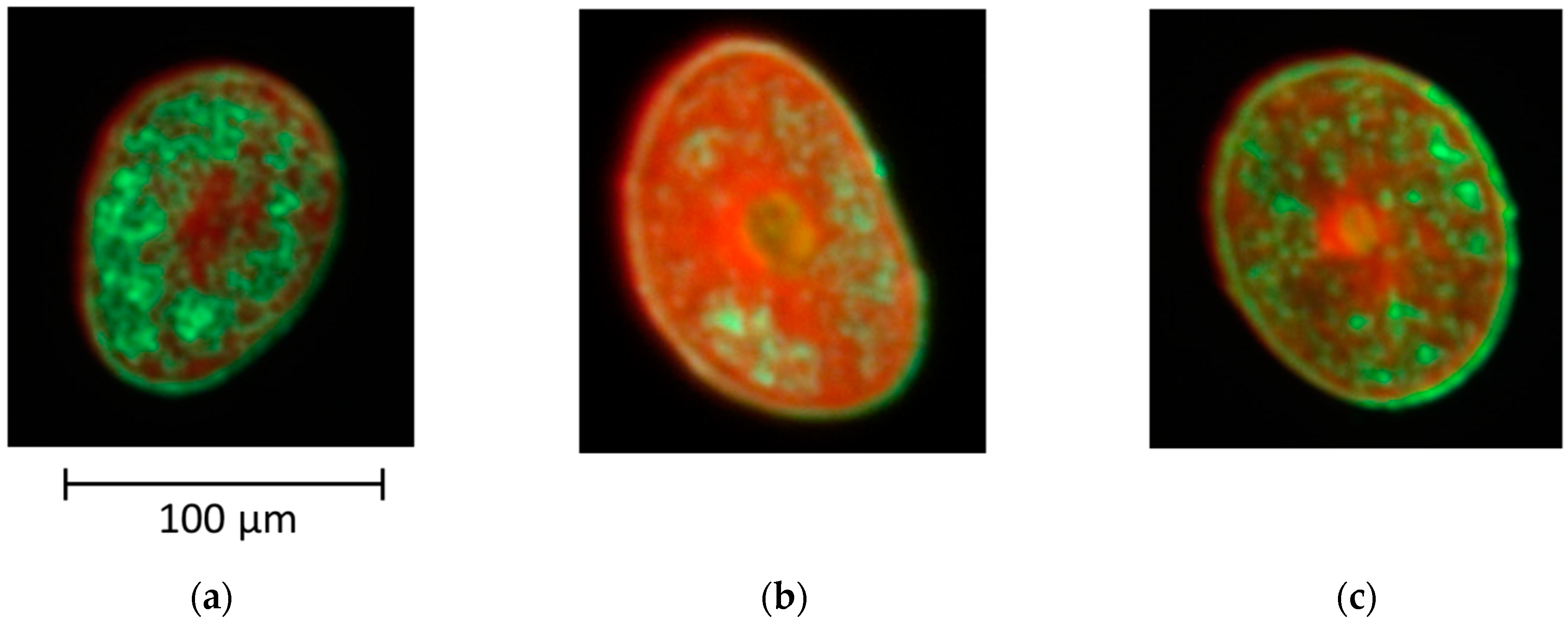
3.2. Observation of Cortical Cell Types in Hairs of Various Elastic Moduli
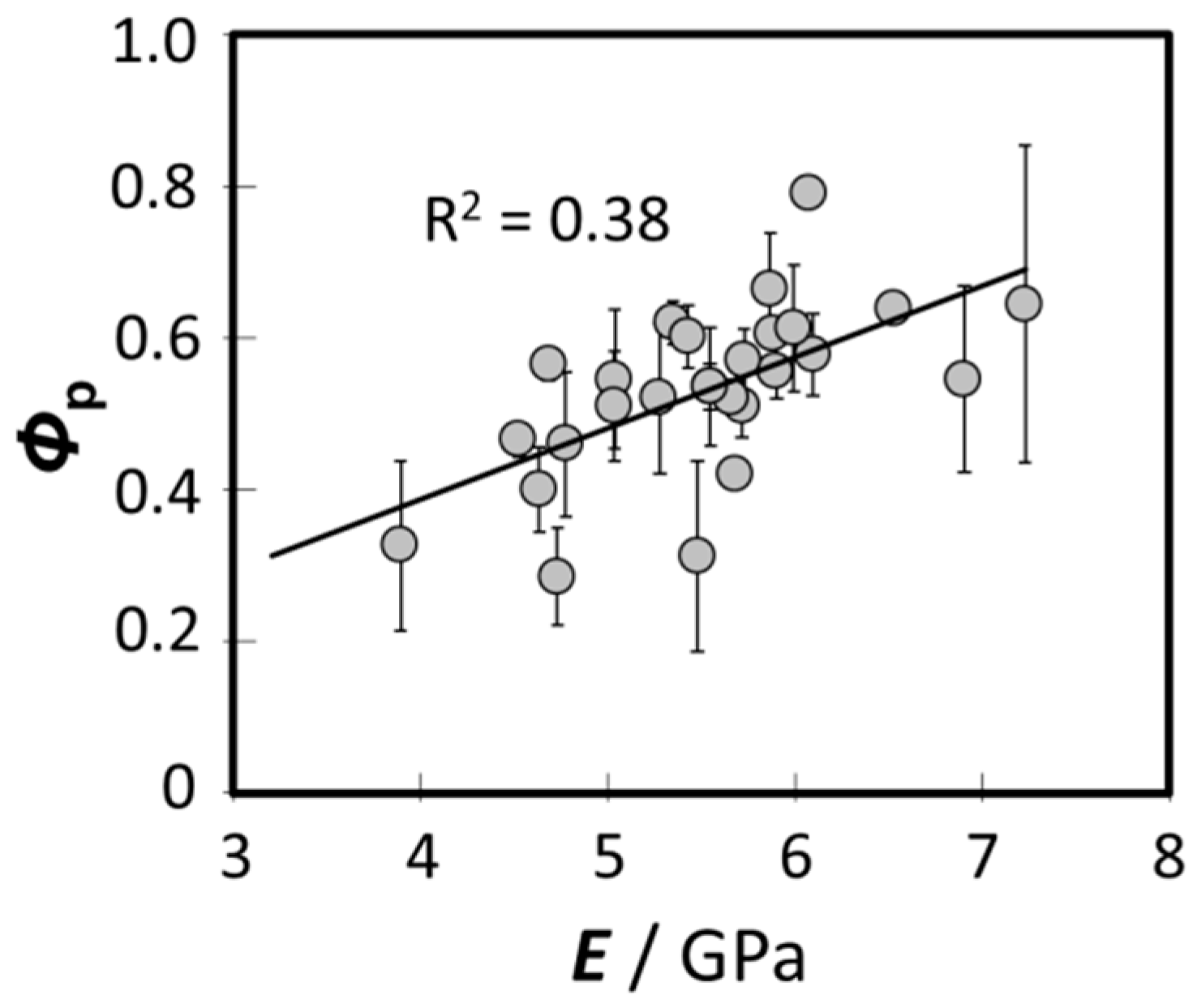
3.3. Relationship between the Bending Modulus and the Fraction of Para-Like and Ortho-Like Cortices
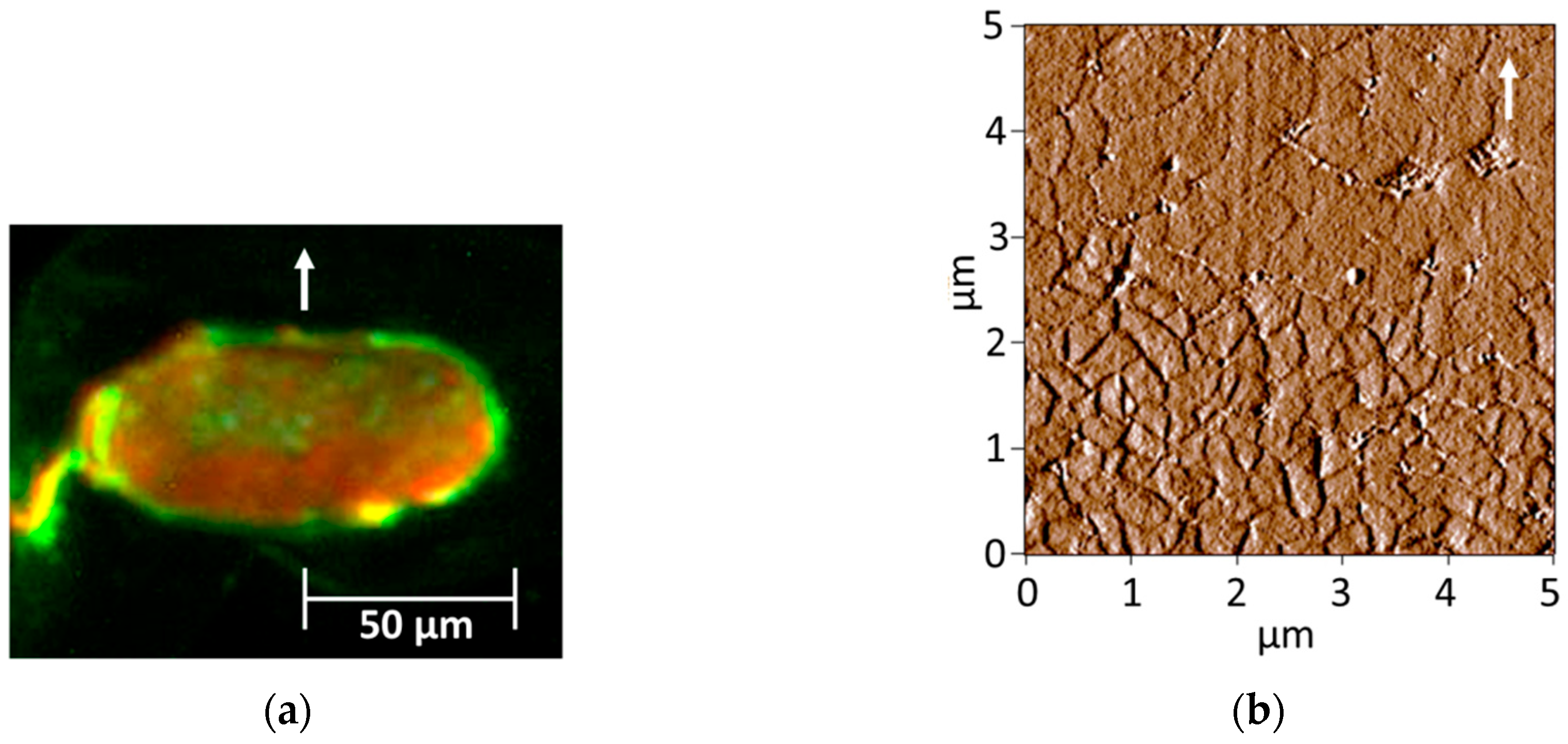
3.4. Modulus Inside Macrofibrils
4. Discussion
4.1. The Effect of Cuticle
4.2. The Effect of Cortical Cell Type Distribution
4.3. The Reason Why the Para-Like Cortex Is Stiffer Than the Ortho-Like Cortex
4.4. The Decrease in Hair Volume with Aging and a Potential Approach to Solve It
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parry, D.A.D.; Steinert, P.M. Intermediate filaments: Molecular architecture, assembly, dynamics and polymorphism. Q. Rev. Biophys. 1999, 32, 99–187. [Google Scholar] [CrossRef] [PubMed]
- Robbins, C.R. Chemical and Physical Behavior of Human Hair, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 53–63. ISBN 978-3-642-25611-0. [Google Scholar]
- Powell, B.C.; Rogers, G.E. The role of keratin proteins and their genes in the growth, structure and properties of hair. In Formation and Structure of Human Hair; Jollès, P., Zahn, H., Höcker, H., Eds.; Birkhäuser Verlag: Basel, Switzerland, 1997; pp. 59–148. ISBN 3-7643-5119-5. [Google Scholar]
- Rogers, M.A.; Langbein, L.; Praetzel-Wunder, S.; Hermelita, W.; Schweizer, J. Human Hair Keratin-Associated Proteins (KAPs). Int. Rev. Cytol. 2006, 251, 209–263. [Google Scholar] [CrossRef] [PubMed]
- Mercer, E.H. The heterogeneity of the keratin fibers. Text. Res. J. 1953, 23, 388–397. [Google Scholar] [CrossRef]
- Horio, M.; Kondo, T. Crimping of wool fibers. Text. Res. J. 1953, 23, 373–386. [Google Scholar] [CrossRef]
- Rogers, G.E. Electron Microscopy of Wool. J. Ultrastruct. Res. 1959, 2, 309–330. [Google Scholar] [CrossRef]
- Bryson, W.G.; Mastronarde, D.N.; Caldwell, J.P.; Nelson, W.G.; Woods, J.L. High voltage microscopical imaging of macrofibril ultrastructure reveals the three-dimensional spatial arrangement of intermediate filaments in Romney wool cortical cells–A causative factor in fibre curvature. In Proceedings of the 10th International Wool Textile Research Conference, Aachen, Germany, 26 November–1 December 2000. [Google Scholar]
- Swift, J.A. Morphology and histochemistry of human hair. In Formation and Structure of Human Hair; Jollès, P., Zahn, H., Höcker, H., Eds.; Birkhäuser Verlag: Basel, Switzerland, 1997; pp. 149–175. ISBN 3-7643-5119-5. [Google Scholar]
- Thibaut, S.; Barbarat, P.; Leroy, F.; Bernard, B.A. Human hair keratin network and curvature. Int. J. Dermatol. 2007, 46 (Suppl. 1), 7–10. [Google Scholar] [CrossRef]
- Nagase, S.; Tsuchiya, M.; Matsui, T.; Shibuichi, S.; Tsujimura, H.; Masukawa, Y.; Satoh, N.; Itou, T.; Koike, K.; Tsujii, K. Characterization of curved hair of Japanese women with reference to internal structures and amino acid composition. J. Cosmet. Sci. 2008, 59, 317–332. [Google Scholar]
- Bryson, W.G.; Harland, D.P.; Caldwell, J.P.; Vernon, J.A.; Walls, R.J.; Woods, J.L.; Nagase, S.; Itou, T.; Koike, K. Cortical cell types and intermediate filament arrangements correlate with fiber curvature in Japanese human hair. J. Struct. Biol. 2009, 166, 46–58. [Google Scholar] [CrossRef]
- Kajiura, Y.; Watanabe, S.; Itou, T.; Iida, A.; Shinohara, Y.; Amemiya, Y. Structural analysis of single wool fibre by scanning microbeam SAXS. J. Appl. Cryst. 2005, 38, 420–425. [Google Scholar] [CrossRef]
- Kajiura, Y.; Watanabe, S.; Itou, T.; Nakamura, K.; Iida, A.; Inoue, K.; Yagi, N.; Shinohara, Y.; Amemiya, Y. Structural analysis of human hair single fibres by scanning microbeam SAXS. J. Struct. Biol. 2006, 155, 438–444. [Google Scholar] [CrossRef]
- Mamada, A.; Nakamura, K. A study of the volume and bounce decrease in hair with aging using bending elasticity measurements. J. Cosmet. Sci. 2007, 58, 485–494. [Google Scholar]
- Nagase, S.; Kajiura, Y.; Mamada, A.; Abe, H.; Shibuichi, S.; Satoh, N.; Itou, T.; Shinohara, Y.; Amemiya, Y. Changes in structure and geometric properties of human hair by aging. J. Cosmet. Sci. 2009, 60, 637–648. [Google Scholar] [CrossRef] [PubMed]
- ImageJ. Available online: https://imagej.nih.gov/ij/ (accessed on 4 August 2006).
- Caldwell, J.P.; Bryson, W.G. Elastic modulus mapping of the wool fibre cellular structure by atomic force microscopy. In Proceedings of the 11th International Wool Textile Research Conference, Leeds, UK, 4–9 September 2005. [Google Scholar]
- Sogabe, A.; Yasuda, M.; Noda, A. Physical properties of human hair. 1. Evaluation of bending stress by measuring the major and the minor axis of human hair. J. Soc. Cosmet. Chem. Jpn. 2002, 36, 207–216. [Google Scholar] [CrossRef]
- Breakspear, S.; Mamada, A.; Itou, T.; Noecker, B. Contribution of the cuticle to the stiffness of human hair: Significant or minor? IFSCC Mag. 2015, 18, 25–34. [Google Scholar]
- Swift, J.A. Some simple theoretical considerations on the bending stiffness of human hair. Int. J. Cosmet. Sci. 1995, 17, 245–253. [Google Scholar] [CrossRef]
- Rogers, G.E. Electron microscope studies of hair and wool. Ann. N. Y. Acad. Sci. 1959, 83, 378–399. [Google Scholar] [CrossRef] [PubMed]
- Dobb, M.G. Electron-diffraction studies of keratin cells. J. Text. Inst. 1970, 61, 232–234. [Google Scholar] [CrossRef]
- Fraser, R.D.B.; MacRae, T.P.; Sparrow, L.G.; Parry, D.A.D. Disulphide bonding in α-keratin. Int. J. Biol. Macromol. 1988, 10, 106–112. [Google Scholar] [CrossRef]
- Kitano, H.; Yamamoto, A.; Niwa, M.; Fujinami, S.; Nakajima, K.; Nishi, T.; Naito, S. Young’s modulus mapping on hair cross-section by atomic force microscopy. Compos. Interfaces 2009, 16, 1–12. [Google Scholar] [CrossRef]
- Hamilton, J.B. Patterned loss of hair in man: Types and incidence. Ann. N. Y. Acad. Sci. 1951, 53, 708–728. [Google Scholar] [CrossRef]
- Ludwig, E. Classification of the types of androgenetic alopecia (common baldness) occurring in the female sex. Br. J. Dermatol. 1977, 97, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Birch, M.P.; Messenger, J.F.; Messenger, A.G. Hair density, hair diameter and the prevalence of female pattern hair loss. Br. J. Dermatol. 2001, 144, 297–304. [Google Scholar] [CrossRef] [PubMed]
- Ootsuka, H.; Nemoto, T. Study on Japanese hair. Koshokaishi 1988, 12, 192–197. [Google Scholar]
- Li, S.W.; Ouyang, H.S.; Rogers, G.E.; Bawden, C.S. Characterization of the structural and molecular defects in fibres and follicles of the merino felting lustre mutant. Exp. Dermatol. 2008, 18, 134–142. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezawa, Y.; Nagase, S.; Mamada, A.; Inoue, S.; Koike, K.; Itou, T. Stiffness of Human Hair Correlates with the Fractions of Cortical Cell Types. Cosmetics 2019, 6, 24. https://doi.org/10.3390/cosmetics6020024
Ezawa Y, Nagase S, Mamada A, Inoue S, Koike K, Itou T. Stiffness of Human Hair Correlates with the Fractions of Cortical Cell Types. Cosmetics. 2019; 6(2):24. https://doi.org/10.3390/cosmetics6020024
Chicago/Turabian StyleEzawa, Yusuke, Shinobu Nagase, Akira Mamada, Shigeto Inoue, Kenzo Koike, and Takashi Itou. 2019. "Stiffness of Human Hair Correlates with the Fractions of Cortical Cell Types" Cosmetics 6, no. 2: 24. https://doi.org/10.3390/cosmetics6020024
APA StyleEzawa, Y., Nagase, S., Mamada, A., Inoue, S., Koike, K., & Itou, T. (2019). Stiffness of Human Hair Correlates with the Fractions of Cortical Cell Types. Cosmetics, 6(2), 24. https://doi.org/10.3390/cosmetics6020024