Forecasting Monthly River Flows in Ukraine under Different Climatic Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset Characteristics
2.3. Descriptive Statistics
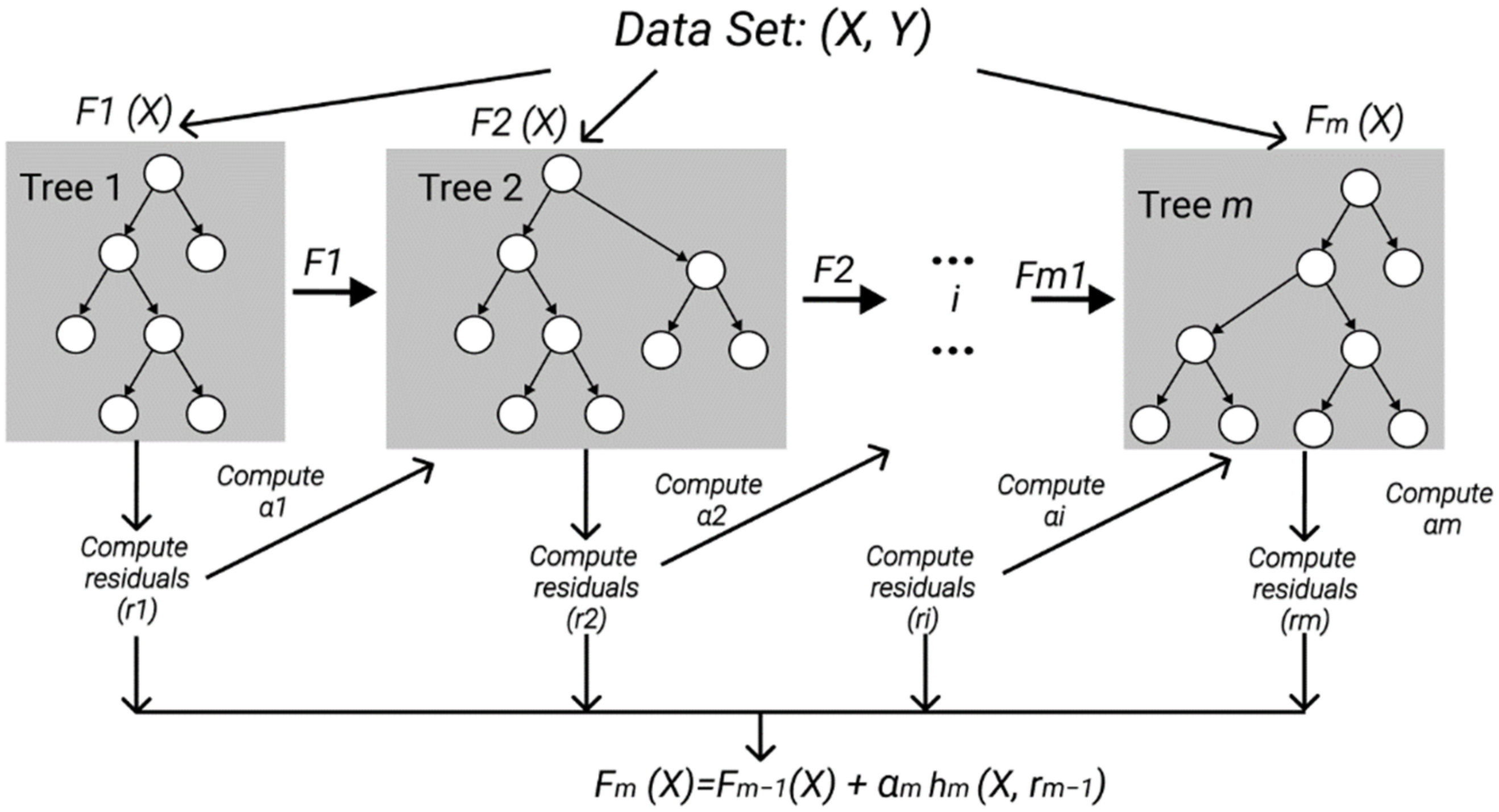
2.4. Forecast Algorithm
XGBoost Algorithm
3. Results
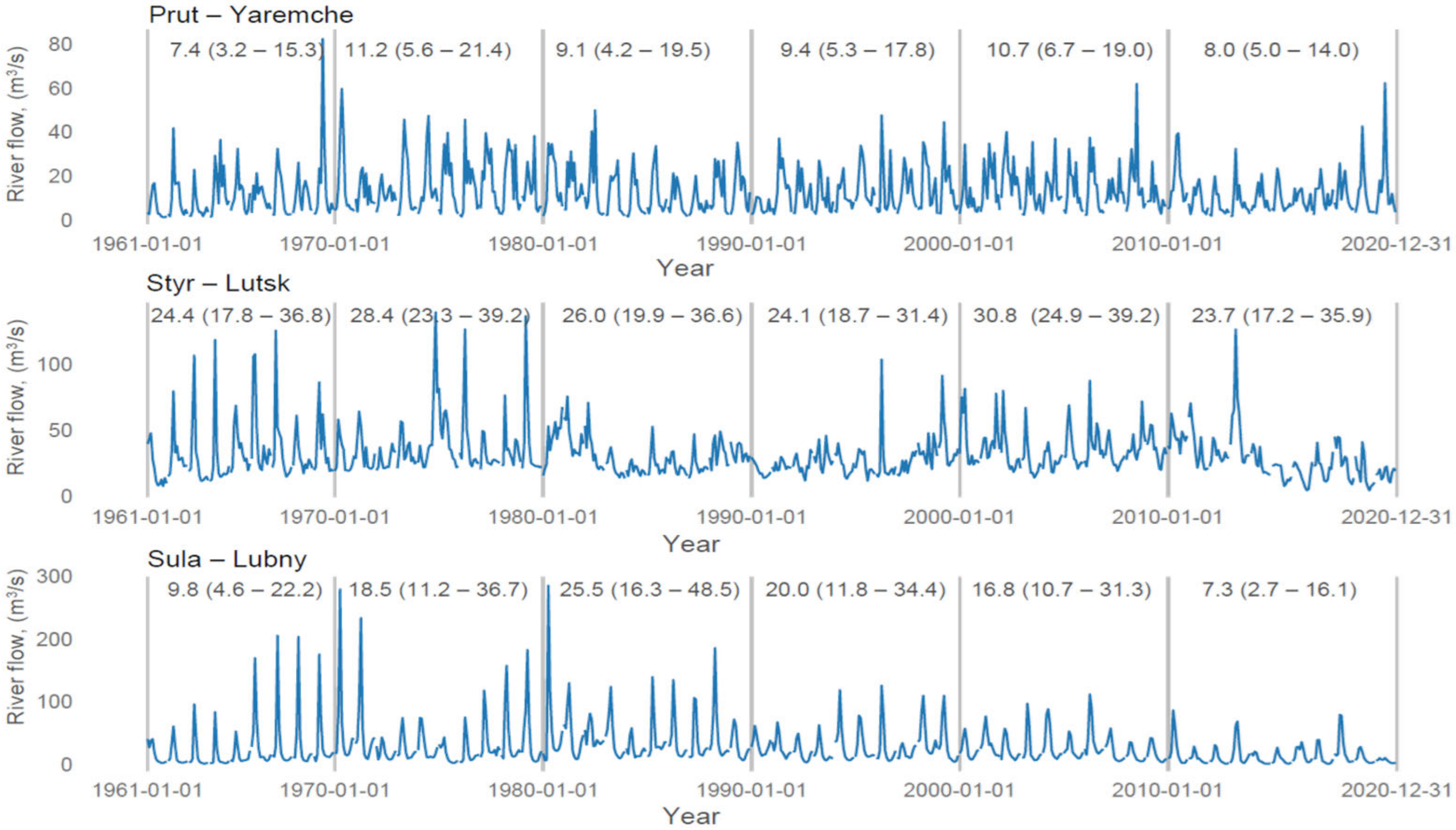
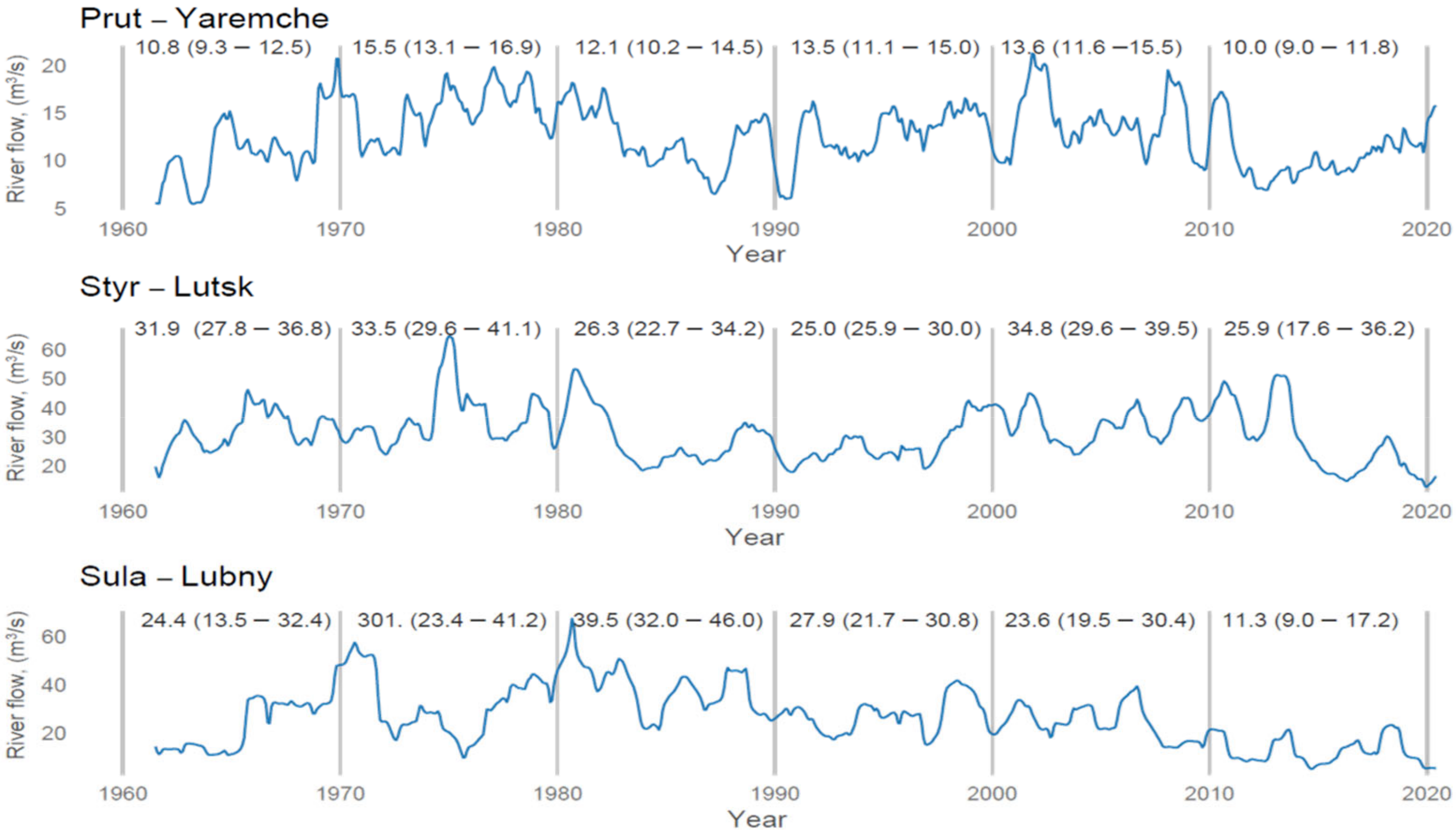
3.1. River-Flow Dynamics in Relation to Changes in Precipitation and Air Temperature over the Decades 1961–2020
3.2. Forecasting Monthly River Flows and Meteorological Variables
3.2.1. River-Flow Forecasting
3.2.2. Precipitation Forecasting
3.2.3. Air Temperature Forecasting
4. Discussion
4.1. Long-Term Changes of Monthly River Flow under Different Precipitation and Air Temperature Conditions
4.2. Forecasting of Monthly River Flow with Precipitation and Air Temperature Forecasts
4.3. Assessment of the Forecasts of Monthly River Flow
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shmueli, G. To explain or to predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three Unsolved Problems in Hydrology (UPH)–a community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar]
- Papacharalampous, G.A.; Tyralis, H.; Koutsoyiannis, D.; Montanari, A. Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: A large-sample experiment at monthly timescale. Adv. Water Resour. 2020, 136, 103470. [Google Scholar] [CrossRef]
- Montanari, A. Hydrology of the Po River: Looking for changing patterns in river discharge. Hydrol. Earth Syst. Sci. 2012, 16, 3739–3747. [Google Scholar] [CrossRef]
- Steirou, E.; Gerlitz, L.; Apel, H.; Sun, X.; Merz, B. Climate influences on flood probabilities across Europe. Hydrol. Earth Syst. Sci. 2019, 23, 1305–1322. [Google Scholar] [CrossRef]
- Hussain, F.; Wu, R.-S.; Wang, J.-X. Comparative Study of Very Short-Term Flood Forecasting Using Physics-Based Numerical Model and Data-Driven Prediction Model. Nat. Hazards 2021, 107, 249–284. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ebtehaj, I.; Bonakdari, H.; Deo, R.C.; Mehr, A.D.; Melini, W.H.; Mohtar, W.; Diop, L.; El-shafie, A.; Singh, V.P. Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. J. Hydrol. 2017, 554, 263–276. [Google Scholar] [CrossRef]
- Tu, H.; Wang, X.; Zhang, W.; Peng, H.; Ke, Q.; Chen, X. Flash Flood Early Warning Coupled with Hydrological Simulation and the Rising Rate of the Flood Stage in a Mountainous Small Watershed in Sichuan Province, China. Water 2020, 12, 255. [Google Scholar] [CrossRef]
- Sivakumar, B.; Jayawardena, A.W.; Fernando, T.M.K.G. River flow forecasting: Use of phase-space reconstruction and artificial neural networks approaches. J. Hydrol. 2002, 265, 225–245. [Google Scholar] [CrossRef]
- Chau, K.W. A split-step particle swarm optimization algorithm in river stage forecasting. J. Hydrol. 2007, 346, 131–135. [Google Scholar] [CrossRef]
- Abbas, S.A.; Xuan, Y. Development of a new quantile-based method for the assessment of regional water resources in a highly-regulated river basin. Water Resour. Manag. 2019, 33, 3187–3210. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.-J.; Ganguly, S.; Hsu, K.-L.; Kifer, D.; Fang, Z.; et al. HESS Opinions: Incubating Deep-Learning-Powered Hydrologic Science Advances as a Community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Siuta, T.J. Modelowanie serii czasowych przepływów w krótkoterminowej prognozie hydrologicznej. Acta Sci. Polonorum. Form. Circumiectus 2020, 19, 3–14. [Google Scholar] [CrossRef]
- Khrystiuk, B.; Gorbachova, L. Long-term Forecasting of Extraordinary Spring Floods by Commensurability Method on the Dnipro River Near Kyiv City, Ukraine. J. Environ. Res. Eng. Manag. EREM 2019, 75, 74–81. [Google Scholar]
- Abrahart, R.S.; See, L. Multi-model data fusion for River flow forecasting; an evaluation of six alternative methods based on two contrasting catchment. Hydrol. Earth Syst. Sci. 2002, 6, 655–670. [Google Scholar] [CrossRef]
- Zeynoddin, M.; Bonakdari, H.; Azari, A.; Ebtehaj, I.; Gharabaghi, B.; Riahi Madavar, H. Novel hybrid linear stochastic with non-linear extreme learning machine methods for forecasting monthly rainfall a tropical climate. J. Environ. Manag. 2018, 222, 190–206. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, L.; Yin, J.; Wang, H. Commensurability-Based Flood Forecasting in Northeastern China. Pol. J. Environ. Stud. 2017, 26, 2689–2702. [Google Scholar] [CrossRef][Green Version]
- Apel, H.; Thieken, A.H.; Merz, B.; Blöschl, G. Flood risk assessment and associated uncertainty. Nat. Hazards Earth Syst. Sci. 2004, 4, 295–308. [Google Scholar] [CrossRef]
- Khrystiuk, B.F. The forecasting of the average, maximum and minimum for a ten-day period of water discharges on Upper Danube. Proc. Ukr. Hydrometeorol. Inst. 2012, 262, 206–220. (In Ukrainian) [Google Scholar]
- Khrystiuk, B.; Gorbachova, L.; Koshkina, O. The impact of climatic conditions of the spring flood formation on hydrograph shape of the Desna River. Meteorol. Hydrol. Water Manag. 2017, 5, 63–70. [Google Scholar] [CrossRef]
- Shevnina, E. Methods of long-range forecasting of dates of the spring flood beginning and peak flow in the estuary sections of the Ob and Yenisei rivers. Russ. Meteorol. Hydrol. 2009, 34, 51–57. [Google Scholar] [CrossRef]
- Scitovski, R.; Maričić, S.; Scitovski, S. Short-term and long-term water level prediction at one river measurement location. Croat. Oper. Res. Rev. (CRORR) 2012, 3, 80–90. [Google Scholar]
- Sharma, P.; Machiwal, D. Streamflow forecasting. In Advances in Streamflow Forecasting; Sharma, P., Machiwal, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–50. [Google Scholar]
- Toth, E.; Brath, A.; Montanari, A. Comparison of short-term rainfall prediction models for real-time flood forecasting. J. Hydrol. 2000, 239, 132–147. [Google Scholar] [CrossRef]
- Imrie, C.E.; Durucan, S.; Korre, A. River flow prediction Rusing artificial neural networks: Generalisation beyond the calibration range. J. Hydrol. 2000, 233, 138–153. [Google Scholar] [CrossRef]
- Ozgur, K. River Flow Modeling Using Artificial Neural Networks. J. Hydrol. Eng. 2004, 9, 60–63. [Google Scholar]
- Teschl, R.; Randeu, W.L. An Artificial Neural Networkbased Rainfall-Runoff Model Using Gridded Radar Data. In Proceedings of the Third European Conference on Radar in Meteorology and Hydrology (ERAD), Visby, Sweden, 6–10 September 2004. [Google Scholar]
- Krzanowski, S.; Wałęga, A. Zastosowanie sztucznych sieci neuronowych do predykcji szeregów czasowych stanów wody i przepływów w rzece. Acta Sci. Pol. Form. Circumiectus 2007, 6, 59–73. [Google Scholar]
- Kim, G.; Barros, A.P. Quantitative flood forecasting using multisensor data and neural networks. J. Hydrol. 2001, 246, 45–62. [Google Scholar] [CrossRef]
- Firat, M.; Güngör, M. River flow estimation using adaptive neuro fuzzy inference system. Math. Comput. Simul. 2007, 75, 87–96. [Google Scholar] [CrossRef]
- Lohani, A.K.; Kumar, R.; Singh, R.D. Hydrological time series modeling: A comparison between adaptive neuro-fuzzy, neural network and autoregressive techniques. J. Hydrol. 2012, 442, 23–35. [Google Scholar] [CrossRef]
- Dehghani, M.; Seifi, A.; Riahi-Madvar, H. Novel forecasting models for immediate-short-term to long-term influent flow prediction by combining ANFIS and grey wolf optimizations. J. Hydrol. 2019, 576, 698–725. [Google Scholar] [CrossRef]
- Riahi-Madvar, H.; Dehghani, M.; Memarzadeh, R.; Gharabaghi, B. Short to Long-Term Forecasting of River Flows by Heuristic Optimization Algorithms Hybridized with ANFIS. Water Resour. Manag. 2021, 35, 1149–1166. [Google Scholar] [CrossRef]
- Achouri, I.; Hani, I.; Bougherira, N.; Djabri, L.; Chaffai, H.; Lallahem, S. River flow model using artificial neural networks. Energy Proc. 2015, 74, 1007–1014. [Google Scholar] [CrossRef]
- Abudu, S.; Cui, C.; King, J.P.; Abudukadeer, K. Comparison of performance of statistical models in forecasting monthly streamflow of Kizil River. China. Water Sci. Eng. 2010, 3, 269–281. [Google Scholar]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Aghelpour, P.; Varshavian, V. Evaluation of stochastic and artificial intelligence models in modeling and predicting of river daily flow time series. Stoch. Hydrol. Hydraul. 2020, 34, 33–50. [Google Scholar] [CrossRef]
- Hsu, K.; Gupta, H.V.; Soroochian, S. Aplication of a recurrent neural network to rainfall-runoff modeling. Proc. Aesthet. Constr. Environ. 1997, 31, 2517–2530. [Google Scholar]
- Kratzert, R.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff model ling Rusing Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Sanders, W.; Li, D.; Li, W.; Fang, Z.N. Data-Driven Flood Alert System (FAS) Using Extreme Gradient Boosting (XGBoost) to Forecast Flood Stages. Water 2022, 14, 747. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar]
- Graf, R.; Kolerski, T.; Zhu, S. Predicting Ice Phenomena in a River Using the Artificial Neural Network and Extreme Gradient Boosting. Resources 2022, 11, 12. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Singh, V.P.; Shi, P. River flow modelling: Comparison of performance and evaluation of uncertainty using data-driven models and conceptual hydrological model. Stoch Environ. Res. Risk Assess. 2018, 32, 2667–2682. [Google Scholar]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J. Streamflow forecasting using extreme gradient boosting model coupled with Gaussian mixture model. J. Hydrol. 2020, 586, 124901. [Google Scholar]
- Fares, A. Climate Change and Extreme Events; Elsevier: San Diego, CA, USA, 2021. [Google Scholar]
- Shakirzanova, J. Forecasting of the maximum water flow of the spring flood in basin Dnieper with use of the automated program complexes. Hydrol. Hydrochem. Hydroecol. 2011, 4, 48–55. (In Ukrainian) [Google Scholar]
- Fischer, S.; Pluntke, T.; Pavlik, D.; Bernhofer, C. Hydrologic effects of climate change in a sub-basin of the Western Bug River, Western Ukraine. Environ. Earth Sci. 2014, 72, 4727–4744. [Google Scholar] [CrossRef]
- Snizhko, S.; Kuprikov, I.; Shevchenko, O.; Evgen, P.; Didovets, I. Assessment of local water resources runoff in Ukraine by using the water-balance Turk model and the regional model REMO in the XXI century. Bryansk State Univ. Her. 2014, 4, 191–201. [Google Scholar]
- Loboda, N.; Bozhok, Y. Water resources of Ukraine in the XXI century based on climate change scenarios. Ukr. Hydrometeorol. J. 2016, 17, 114–121. [Google Scholar]
- Didovets, I.; Lobanova, A.; Bronstert, A.; Snizhko, S.; Maule, C.F.C.F.; Krysanova, V. Assessment of climate change impacts on water resources in three representative Ukrainian catchments using eco-hydrological modelling. Water 2017, 9, 204. [Google Scholar] [CrossRef]
- Didovets, I.; Krysanova, V.; Bürger, G.; Snizhko, S.; Balabukh, V.; Bronstert, A. Climate change impact on regional floods in the Carpathian region. J. Hydrol. Reg. Stud. 2019, 22, 100590. [Google Scholar]
- Vyshnevskyi, V.I.; Donich, O.A. change in the Ukrainian Carpathians and its possible impact on river runoff. Acta Hydrol. Slovaca. 2021, 22, 3–14. [Google Scholar] [CrossRef]
- Loboda, N.; Kozlov, M. Assessment of water resources of the Ukrainian rivers according to the average statistical models of climate change trajectories RCP4.5 and RCP8.5 over the period of 2021 to 2050. Ukr. Hydrometeorol. J. 2020, 25, 93–104. [Google Scholar] [CrossRef]
- Vyshnevskyi, V.I.; Kutsiy, A.V. Long-Term Changes in the Water Regime of Rivers in Ukraine; Naukova Dumka: Kyiv, Ukraine, 2022; 252p, Available online: https://er.nau.edu.ua/handle/NAU/56293 (accessed on 22 October 2022).
- Redell, N. forecastML: Time Series Forecasting with Machine Learning Methods; R Package Version 0.9.0,<URL; 2020. Available online: https://CRAN.R-project.org/package=forecastML (accessed on 3 September 2022).
- Bergmeir, C.; Hyndman, R.J.; Koo, B. A note on the validity of cross-validation for evaluating autoregressive time series prediction. Comput. Stat. Data Anal. 2018, 120, 70–83. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd SIGKDD Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Bahrami-Pichaghchi, H.; Aghelpour, P. An estimation and multi-step ahead prediction study of monthly snow cover area, based on efficient atmospheric-oceanic dynamics. Clim. Dyn. 2022. [Google Scholar] [CrossRef]
- Aghelpour, P.; Norooz-Valashedi, R. Predicting daily reference evapotranspiration rates in a humid region, comparison of seven various data-based predictor models. Stoch. Environ. Res. Risk Assess. 2022, 36, 4133–4155. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 5 August 2022).
- Abolghasemi, M.; Hyndman, R.; Garth, T.; Bergmeir, C.H. Machine learning applications in time series hierarchical forecasting. arXiv 2019, arXiv:1912.00370v1. [Google Scholar]
- XGBoost Documentation. Available online: https://xgboost.readthedocs.io/en/latest/index.html (accessed on 1 August 2022).
- Vyshnevskyi, V.I. The impact of climate change on evaporation from the water surface in Ukraine. J. Geol. Geogr. Geoecol. 2022, 31, 163–170. [Google Scholar] [CrossRef]
- Kovats, R.S.; Valentini, R.; Bouwer, L.M.; Georgopoulou, E.; Jacob, D.; Martin, E.; Rounsevell, M.J.-F.S. Europe. In Climate Change 2014: Impacts, Adaptation, and Vulnerability; Part B: Regional Aspects; Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1267–1326. [Google Scholar]
- IPCC. Climate Change and Land, IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems. Summary for Policymakers. 2018. Available online: https://www.ipcc.ch/site/assets/uploads/2019/08/4.-SPM_Approved_Microsite_FINAL.pdf (accessed on 10 August 2022).
- Jacob, D.; Kotova, L.; Teichmann, C.; Sobolowski, S.P.; Vautard, R.; Donnelly, C.; Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Damm, A.; et al. Climate impacts in Europe under +1.5 °C global warming. Earth’s Futur. 2018, 6, 264–285. [Google Scholar] [CrossRef]
- Graf, R.; Wrzesiński, D. Relationship between Water Temperature of Polish Rivers and Large-Scale Atmospheric Circulation. Water 2019, 11, 1690. [Google Scholar] [CrossRef]
- Didovets, I.; Krysanova, V.; Hattermann, F.F.; López, M.R.R.; Snizhko, S.; Schmied, H.M. Climate change impact on water availability of main river basins in Ukraine. J. Hydrol. Reg. Stud. 2020, 32, 100761. [Google Scholar]
- Wrzesiński, D.; Graf, R. Temporal and spatial patterns of the river flow and water temperature relations in Poland. J. Hydrol. Hydromech. 2022, 70, 12–29. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Wagener, T.; Tallaksen, L.M.; Engeland, K. Evaluation of nine large-scale hydrological models with respect to the seasonal runoff climatology in Europe. Water Resour. Res. 2012, 48, W11504. [Google Scholar]
- Van Vliet, M.T.H.; Donnelly, C.; Strömbäck, L.; Capell, R.; Ludwig, F. European scale climate information services for water use sectors. J. Hydrol. 2015, 528, 503–513. [Google Scholar] [CrossRef]
- Donnelly, C.; Greuell, W.; Andersson, J.; Gerten, D.; Pisacane, G.; Roudier, P.; Ludwig, F. Impacts of climate change on European hydrology at 1.5, 2 and 3 degrees mean global warming above preindustrial level. Clim. Change 2017, 143, 13–26. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.; Besio, G.; Feyen, L. alphaBetaLab: Automatic estimation of subscale transparencies for the Unresolved Obstacles Source Term in ocean wave modelling. SoftwareX 2019, 9, 1–6. [Google Scholar] [CrossRef]
- Bayazit, M. Nonstationarity of Hydrological Records and Recent Trends in Trend Analysis: A State-of-the-art Review. Environ. Process. 2015, 2, 527–542. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Elbeltagi, A.; Yaseen, Z.M.; Shamsuddin, S.; Kisi, O. Development of new machine learning model for streamflow prediction: Case studies in Pakistan. Stoch. Environ. Res. Risk Assess. 2022, 36, 999–1033. [Google Scholar] [CrossRef]
- Meira-Neto, A.A.; Niu, G.; Roy, T.; Tyler, S.; Troch, P.A. Interactions between snow cover and evaporation lead to higher sensitivity of streamflow to temperature. Commun. Earth Environ. 2020, 1, 1–7. [Google Scholar]
- Gorbachova, L. Place and role of hydro-genetic analysis among modern research methods runoff. Proc. Ukr. Hydrometeorol. Institute 2015, 268, 73–81. (In Ukrainian) [Google Scholar]
- Frieler, K.; Lange, S.; Piontek, F.; Reyer, C.P.O.; Schewe, J.; Warszawski, L.; Zhao, F.; Chini, L.; Denvil, S.; Emanuel, K.; et al. Assessing the impacts of 1.5 °C global warming-Simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). Geosci. Model Dev. 2017, 10, 4321–4345. [Google Scholar] [CrossRef]
- Haddeland, I.; Heinke, J.; Biemans, H.; Eisner, S.; Flörke, M.; Hanasaki, N.; Konzmann, M.; Ludwig, F.; Masaki, Y.; Schewe, J.; et al. Global water resources affected by human interventions and climate change. Proc. Natl. Acad. Sci. USA 2014, 111, 3251–3256. [Google Scholar] [CrossRef]
- Hattermann, F.F.; Krysanova, V.; Gosling, S.N.; Dankers, R.; Daggupati, P.; Donnelly, C.; Flörke, M.; Huang, S.; Motovilov, Y.; Buda, S.; et al. Cross-scale intercomparison of climate change impacts simulated by regional and global hydrological models in eleven large river basins. Clim. Chang. 2017, 141, 561–576. [Google Scholar] [CrossRef]
- Hattermann, F.F.; Vetter, T.; Breuer, L.; Su, B.; Daggupati, P.; Donnelly, C.; Fekete, B.; Florke, F.; Gosling, S.N.; Hoffmann, P.; et al. Sources of uncertainty in hydrological climate impact assessment: A cross-scale study. Environ. Res. Lett. 2018, 13, 015006. [Google Scholar] [CrossRef]
- Osman, A.I.A.; Najah Ahmed, A.; Chow, M.F.; Feng Huang, Y.; El-Shafie, A. Extreme Gradient Boosting (Xgboost) Model to Predict the Groundwater Levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Vieux, B.E.; Cui, Z.; Gaur, A. Evaluation of a Physics-Based Distributed Hydrologic Model for Flood Forecasting. J. Hydrol. 2004, 298, 155–177. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. Short-Term Flood Forecasting with a Neurofuzzy Model: Flood Forecasting with a Neurofuzzy Model. Water Resour. Res. 2005, 41, W04004. [Google Scholar] [CrossRef]
- Hosseiny, H.; Nazari, F.; Smith, V.; Nataraj, C. A Framework for Modeling Flood Depth Using a Hybrid of Hydraulics and Machine Learning. Sci. Rep. 2020, 10, 8222. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Asanjan, A.A.; Welles, E.; Gao, X.; Sorooshian, S.; Liu, X. Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information. Water Resour. Res. 2017, 53, 2786–2812. [Google Scholar] [CrossRef]
- Aghelpour, P.; Bahrami-Pichaghchi, H.; Varshavian, V.; Graf, R.; Gholami Sefidkouhi, M.A.; Khoshravesh, M. Evaluating the impact of large-scale climatic indices as inputs for forecasting monthly river flow in Mazandaran Province, Iran. Pure Appl. Geophys. 2022, 179, 1309–1331. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Tang, Z.-Y.; Xu, Y.; Zhang, H.-R. Evolutionary Artificial Intelligence Model via Cooperation Search Algorithm and Extreme Learning Machine for Multiple Scales Nonstationary Hydrological Time Series Prediction. J. Hydrol. 2021, 595, 126062. [Google Scholar]
- Kilinc, H.C.; Haznedar, B. A Hybrid Model for Streamflow Forecasting in the Basin of Euphrates. Water 2022, 14, 80. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Yuan, P.; Wang, L.; Cheng, D. An Adaptive Daily Runoff Forecast Model Using VMD-LSTM-PSO Hybrid Approach. Hydrol. Sci. J. 2021, 66, 1488–1502. [Google Scholar] [CrossRef]

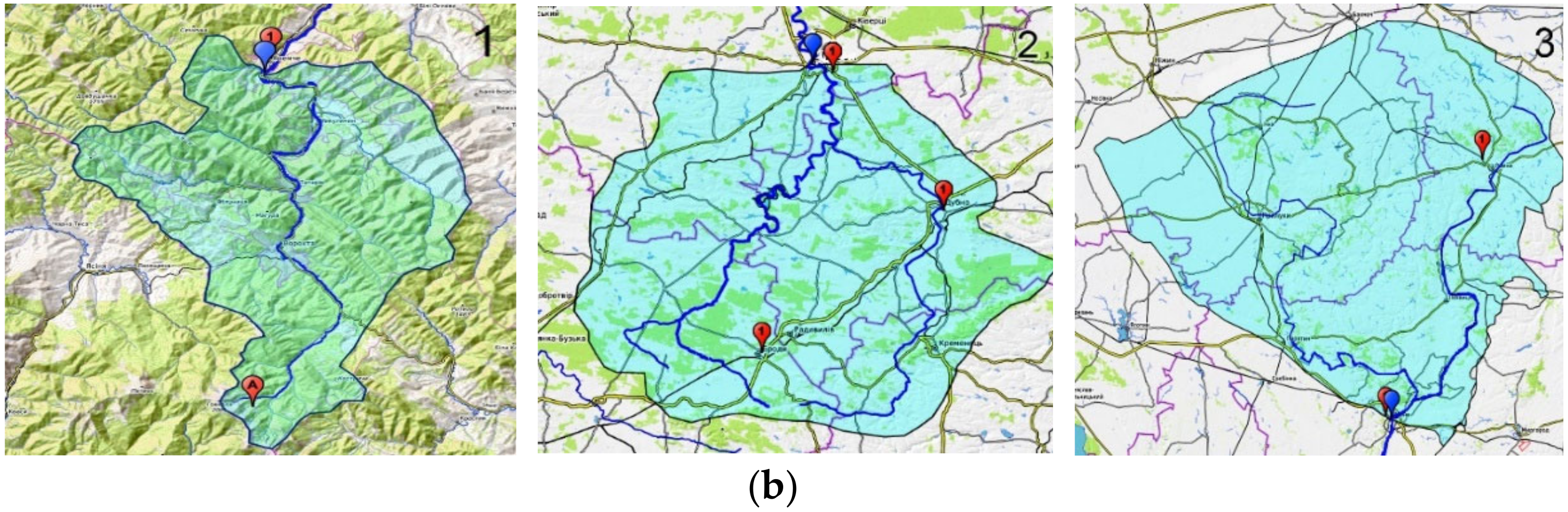

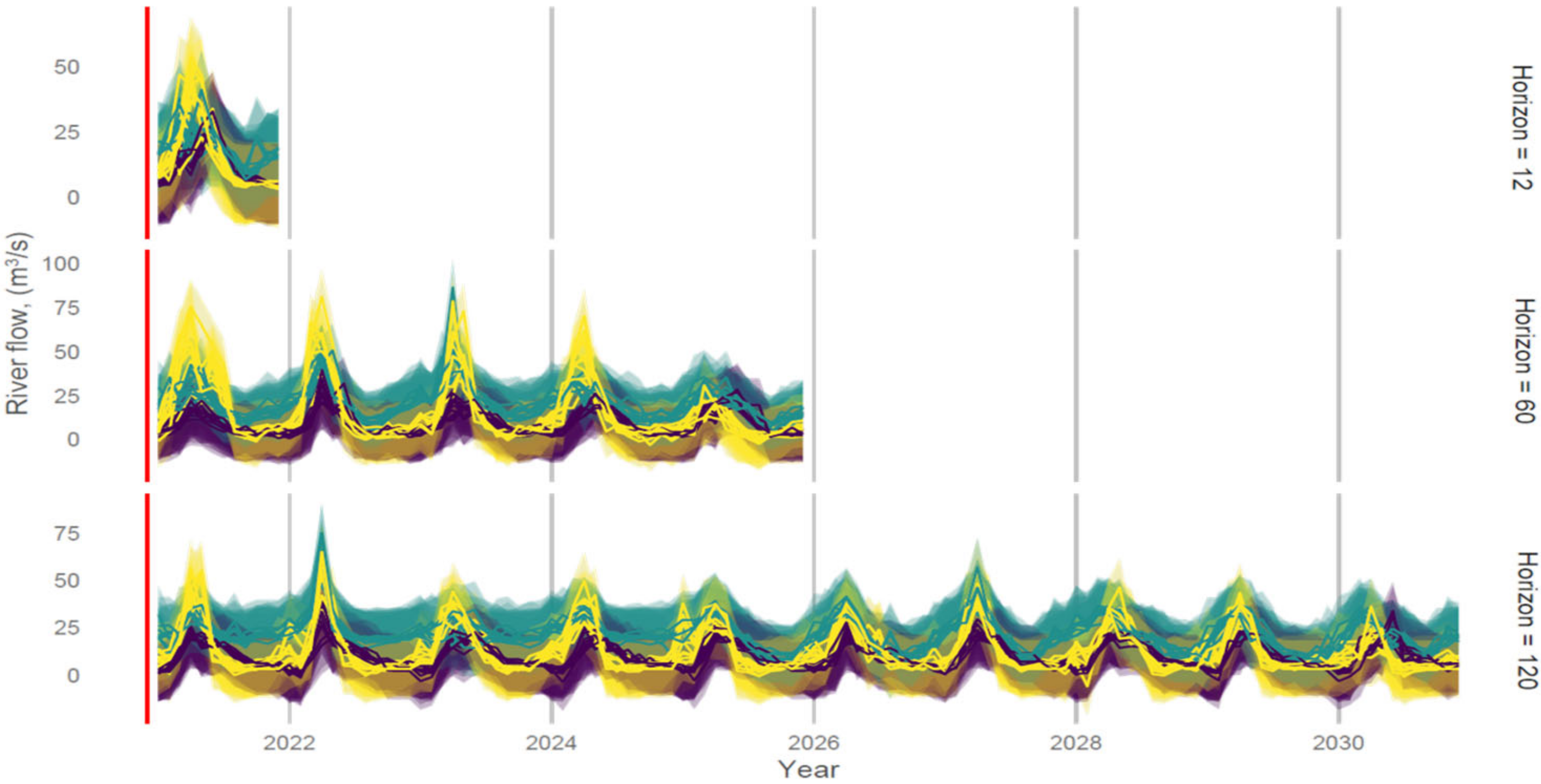
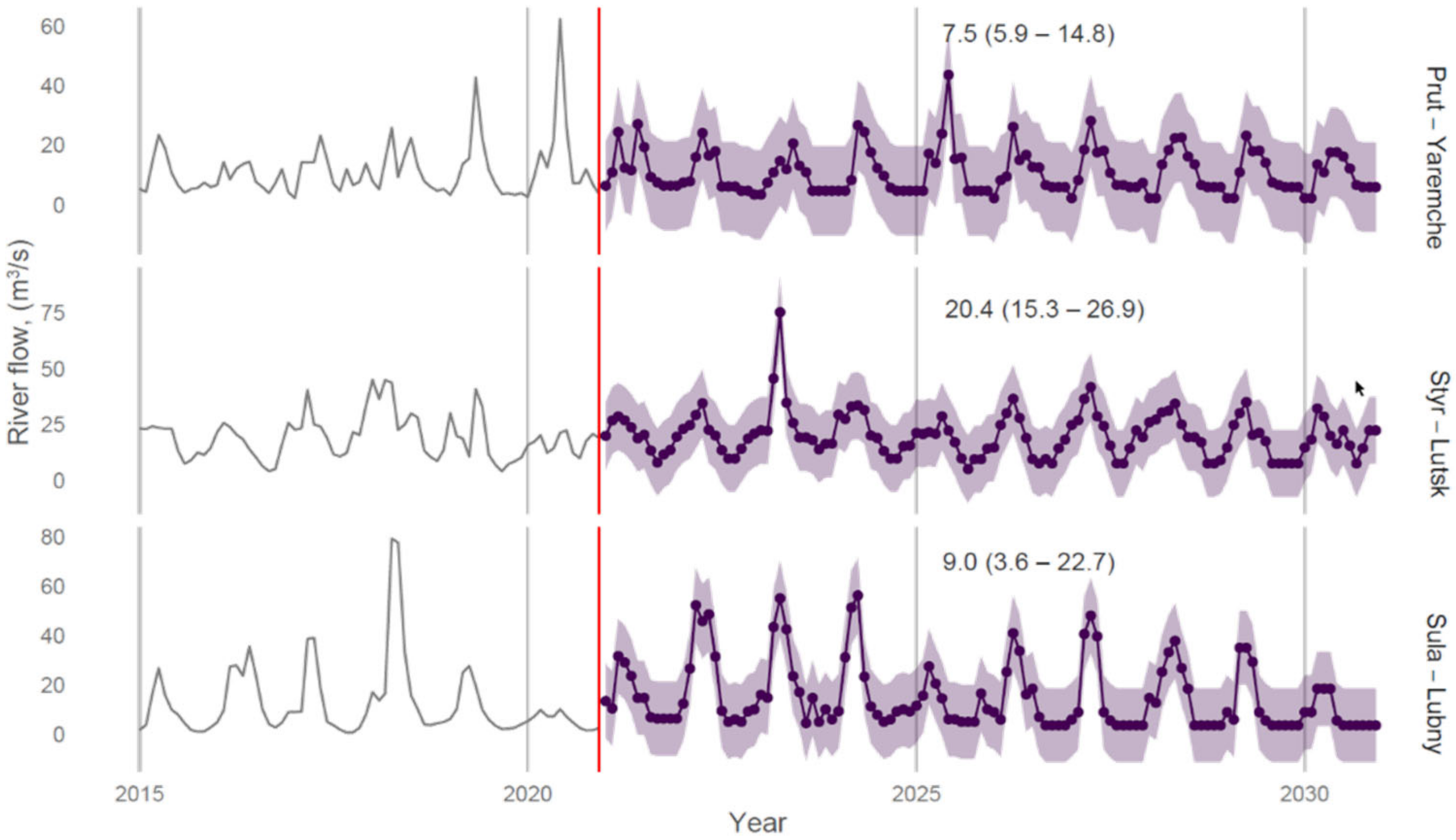
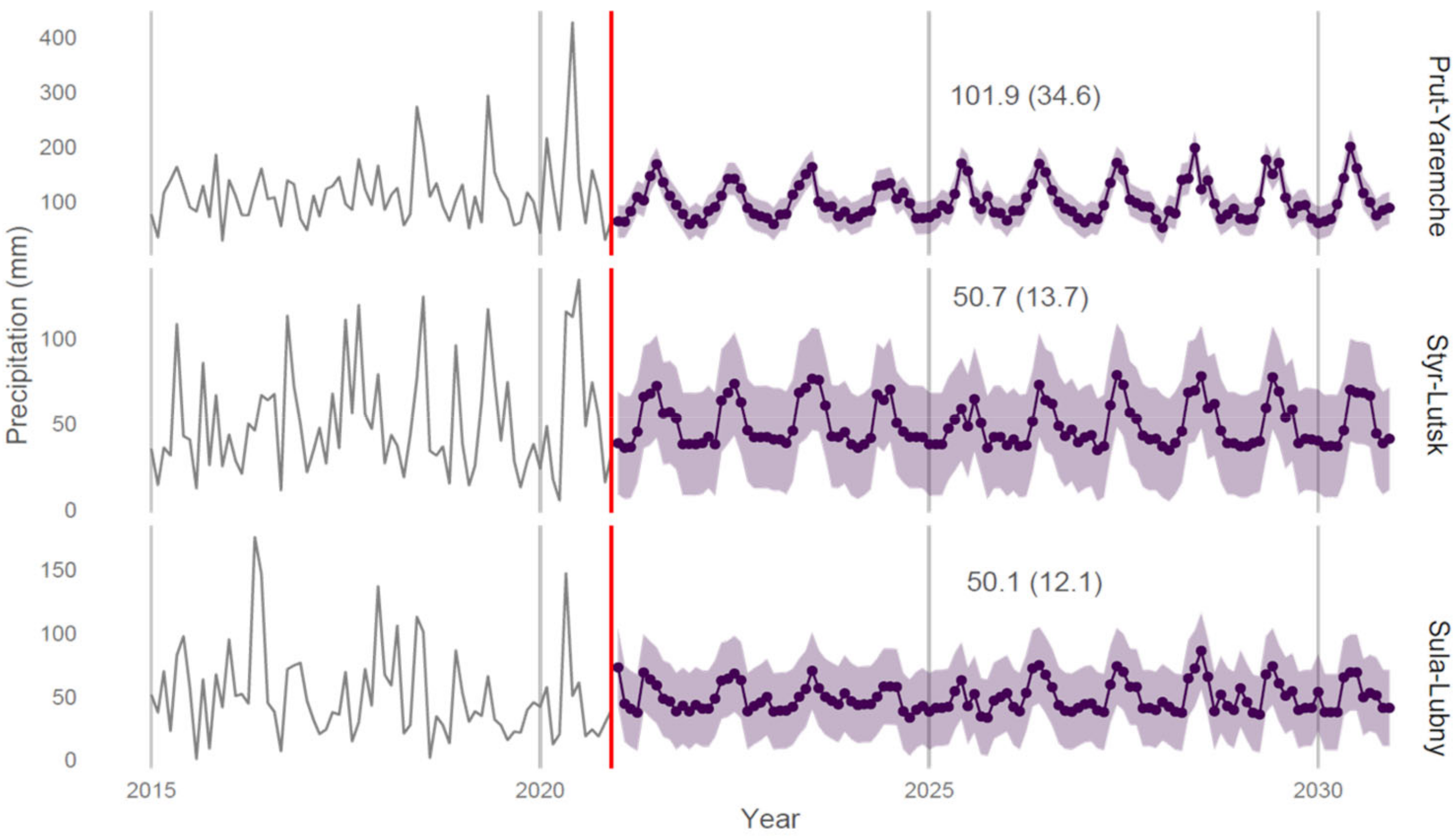

| River and Water Gauge Stations | Catchment Area [km2] | Discharge [m3/sec] | |||
|---|---|---|---|---|---|
| Long-Term Period Observation | 1961–2020 | ||||
| Mean Annual (Period) | Observed Maximum (Date) | Observed Minimum (Date) | Mean Annual | ||
| Prut–Yaremche | 597 | 12.4 (1951–2020) | 1530 (08.06.1969) | 0.68 (24.01.1976) | 12.7 |
| Styr–Lutsk | 7200 | 30.5 (1923–2020) | 876 (08.04.1932) | 2.26 (18–19.09.2019) | 31.2 |
| Sula–Lubny | 14,200 | 27.4 (1936–2020) | 1140 (21.04.1942) | 0.38 (21.09.2019) | 26.4 |
| River | M | SD | Mdn | IQR | Min | Max | Skew. | Kurt. |
|---|---|---|---|---|---|---|---|---|
| Prut–Yaremche | 12.66 | 10.54 | 9.37 | 12.12 | 1.2 | 82.5 | 1.75 | 4.51 |
| Styr–Lutsk | 31.15 | 17.82 | 26.95 | 15.73 | 4.03 | 140 | 2.43 | 8.78 |
| Sula–Lubny | 26.40 | 32.49 | 16,00 | 22.36 | 0.71 | 286 | 3.52 | 17.66 |
| River Catchment | M | SD | Mdn | Min | Max | Skew. | Kurt. |
|---|---|---|---|---|---|---|---|
| Precipitation [mm] | |||||||
| Prut | 102.4 | 60.3 | 92.5 | 3.5 | 458.5 | 1.38 | 3.82 |
| Styr | 52.6 | 33.1 | 45.5 | 1.67 | 197.67 | 1.25 | 1.70 |
| Sula | 51.1 | 30.7 | 45.15 | 0.75 | 174.65 | 0.96 | 0.89 |
| Air temperature | |||||||
| Prut | 7.4 | 7.5 | 7.8 | −11.9 | 19.9 | −0.21 | −1.16 |
| Styr | 8.5 | 8.5 | 8.4 | −14.0 | 22.0 | −0.19 | −1.16 |
| Sula | 8.6 | 8.4 | 8.4 | −16.0 | 24.7 | −0.15 | −1.25 |
| Horizon (Months) | River | N | Mdn | IQR |
|---|---|---|---|---|
| 12 | Prut–Yaremche | 120 | 8.3 | 5.6–18.6 |
| 60 | 600 | 6.8 | 4.6–14.6 | |
| 120 | 1200 | 8.0 | 5.5–15.7 | |
| 12 | Styr–Lutsk | 120 | 17.9 | 15.0–22.1 |
| 60 | 600 | 19.8 | 14.3–25.5 | |
| 120 | 1200 | 20.8 | 16.7–26.6 | |
| 12 | Sula–Lubny | 120 | 9.6 | 5.9–21.8 |
| 60 | 600 | 8.5 | 4.7–20.4 | |
| 120 | 1200 | 8.5 | 5.1–17.9 |
| Horizon (Months) | River Catchment | N | M | SD |
|---|---|---|---|---|
| 12 | Prut | 120 | 100.3 | 32.0 |
| 60 | 600 | 103.3 | 33.6 | |
| 120 | 1200 | 103.0 | 37.0 | |
| 12 | Styr | 120 | 51.2 | 13.3 |
| 60 | 600 | 52.3 | 14/7 | |
| 120 | 1200 | 53.3 | 15.2 | |
| 12 | Sula | 120 | 50.3 | 10.1 |
| 60 | 600 | 53.6 | 12.8 | |
| 120 | 1200 | 52.3 | 11.8 |
| Horizon (Months) | River Catchment | N | M | SD |
|---|---|---|---|---|
| 12 | Prut | 120 | 9.12 | 6.98 |
| 60 | 600 | 9.16 | 7.33 | |
| 120 | 1200 | 9.02 | 7.50 | |
| 12 | Styr | 120 | 9.73 | 7.61 |
| 60 | 600 | 9.28 | 8.15 | |
| 120 | 1200 | 9.21 | 8.19 | |
| 12 | Sula | 120 | 9.70 | 8.22 |
| 60 | 600 | 9.28 | 8.77 | |
| 120 | 1200 | 9.12 | 8.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graf, R.; Vyshnevskyi, V. Forecasting Monthly River Flows in Ukraine under Different Climatic Conditions. Resources 2022, 11, 111. https://doi.org/10.3390/resources11120111
Graf R, Vyshnevskyi V. Forecasting Monthly River Flows in Ukraine under Different Climatic Conditions. Resources. 2022; 11(12):111. https://doi.org/10.3390/resources11120111
Chicago/Turabian StyleGraf, Renata, and Viktor Vyshnevskyi. 2022. "Forecasting Monthly River Flows in Ukraine under Different Climatic Conditions" Resources 11, no. 12: 111. https://doi.org/10.3390/resources11120111
APA StyleGraf, R., & Vyshnevskyi, V. (2022). Forecasting Monthly River Flows in Ukraine under Different Climatic Conditions. Resources, 11(12), 111. https://doi.org/10.3390/resources11120111








