Abstract
In this paper, a method of mathematical modeling for solving the problem of reusing man-made waste from mining and the processing of ores is proposed. The use of intermediate products (man-made waste: tailings of processing plants, rocks from sinking operations and the technical water of mine drainage) in cyclic production presupposes their use as fill material components and placement in the mined-out voids of underground mines. The influence of mining factors on the fill material composition and the parameters of the created fill mass is justified. The results of a practical implementation of the proposed mathematical model are presented, and an algorithm is compiled. Deformation changes and stress concentration are key criteria in the proposed mathematical model. The proposed algorithm allows for the determination of the preferred system of deposit development, and the selection of its parameters and the fill material composition.
1. Introduction
The growing number of mining enterprises has led to an increase in air and water pollution, the formation of sinkholes on the Earth’s surface [1], a change in the stress–strain condition of rock mass [2], a violation of the waterproof strata [3], the accumulation of explosive gases (methane) and subsequent ignition in the stopes [4]; liquid and solid waste is stored on the Earth’s surface [5], and the resulting vapors and gases are released into the atmosphere [6]. All this leads to an increase in the man-made impact on the environment [7]. Methane explosions in stopes, roof collapses and rock bumps are often accompanied by man-made earthquakes [3]. Mining operations and man-made disasters cause vibrations in the Earth’s crust [3,8,9]. Vibrations spread over long distances and have an impact on underground mine stopes and the buildings and structures located on the surface [10]. Methods of controlling and reducing vibrations are considered in [11,12].
It is necessary to search for various technical methods [13] and financial and economic tools in order to mitigate or completely eliminate the consequences of the impact of geotechnology on the environment [14]. The main task facing geotechnology is the creation of efficient engineering [15], and economically [16] and environmentally [17] feasible technological solutions for deposit development [18] with safe mining operations [19].
When developing deposits, it is necessary to use a comprehensive method that considers the total value of the natural and man-made resources [20,21,22] of the developed area. The technologies used must protect people, both in production [23] and in their habitat [24].
It is often proposed to preserve the pristine nature and mineral diversity of the Earth by transferring mining production to space bodies [25]. However, the lack of technical possibilities and unresolved legal problems [26,27] postpone the implementation of this idea to the distant future.
The choice of rational geotechnology involves the following:
- -
- The application of the principles of safe production organization [28];
- -
- The elimination of waste generation or its disposal [29];
- -
- The use of intermediate products (industrial waste) in a closed production cycle [30].
The introduction of rational geotechnology will allow the following:
- -
- The increasing economic and environmental requirements [31] for mining enterprises to be met;
- -
- Safe mining production with an integrated preventive environmental strategy to be organized [32].
The application of technology with backfill based on mining waste leads to the following:
- -
- An increase in the efficiency of deposit development;
- -
- A decrease in the negative impact of geotechnology on the environment;
- -
- A decrease in the harmful impact on humans [33];
- -
- An increase in the extraction ratio of minerals [34].
The strength of the fill mass depends on the quality of the binder and aggregate, the quantitative ratio between them and the liquid. If processing tailings are used in the backfill material, they need to be pre-dewatered and dried. The issues of drying mineral waste were previously considered in [35]. The quality of the binder and aggregate grinding has a positive effect on the created artificial mass. Therefore, it is necessary to improve the methods for evaluating grinding mechanisms [36]. A high abrasibility of the aggregate leads to an increase in the wear of parts and mechanisms. It is necessary to ensure the preservation of the operational resource of grinding mechanisms and the transport system through the use of new manufacturing technologies and wear diagnostics [37].
An analysis of the current state of mineral extraction shows continuous growth, both in terms of the number of new enterprises and the scale of existing industrial facilities. First of all, this is due to the development of new and advanced mining technologies, as well as tools that make it possible to work in previously inaccessible regions with harsh climatic conditions in order to extract minerals from greater depths and with a lower percentage of the useful component. The development of such deposits leads to the emergence of technogenic manifestations, which are very different in form and dynamics from those previously encountered [38,39]. This requires a more rigorous approach to ensure safe mining [40]. The development and implementation of various solutions in the field of automated control systems, including robotic and fully autonomous mining transport complexes, make it possible to ensure the continuous execution of production processes in changing conditions [41]. The consequence of such technical solutions is a significant increase in the load on the undermined rock mass [42], which predetermines the need for innovative technologies that allow for the changes in the stress–strain state of the rock mass to be predicted [43].
Today, many scientific works are devoted to the problem of selecting a rational technology for the mining of a deposit [44,45,46]. Innovative technologies are being developed, and new methods for a rapid assessment of the rock mass state [47,48] using remote sensing [49,50,51,52] are being introduced. Most solutions in this area involve the study of spot measurements of stress in the mass, performed by specialists in the field or with stationary monitoring sensors in automatic mode [53]. It is obvious that such an approach is not perfect in view of the limited amount of data, which poorly allow for an assessment of the general stress state of the rock mass and for a visual interpretation of the dynamics of changes in this state, including in the operational mode. If these data in the mining industry were previously sufficient to assess the reliability of a short-term forecast, then, in the context of constantly changing conditions and factors, it is necessary to develop a methodology taking into account a large amount of data and the transience of their changes.
As a consequence, rock mass still remains subject to various abrupt changes, with control being largely left to the mining companies themselves. Thus, the management of enterprises, aimed most of all at increasing profits through the intensification of works, has to find a balance between the growth of production rates and the prospect of dynamic manifestations in the undermined mass. Dynamic manifestations can be divided into local and large-scale. If local dynamic manifestations lead to a temporary stoppage of mineral extraction, then large-scale ones often cause technogenic disasters and the cessation of mine exploitation. At present, the developed analytical models that are used in the mining industry [2,7,41,42,47,48] cannot fully control or predict the stress–strain state of the mass. The lack of a simple, visual and easily interpretable tool for assessing the stress dynamics in the mass under the conditions of intensified works significantly complicates the decision-making processes of company management and certainly leads to risks of technogenic catastrophes.
In view of the above, the purpose of this work is to improve the reliability and efficiency of the monitoring of the stress–strain state of undermined mass and to create an algorithm for determining the optimal structure and composition of stowing mixture in the development of deposits with systems of artificial support.
2. Formalization of the Task for Monitoring the Stress–Strain State of Rock Mass
Producing a description of the cause-and-effect relations of the dynamics of changes in the stress–strain state of rock mass is a very time-consuming and complex task. The emphasis in this work is one of the most important aspects—stress–strain state control in rock mass with the application of backfill technology. The proposed model for assessing the stress–strain state of rock mass is based on the interrelation of three key elements:
- -
- The degree of impact on the mass;
- -
- The exposure time and parameters of the mined stopes;
- -
- The applied development system for an integrated assessment of the rock mass state.
The severity of the impact on the mass is determined as a quantitative assessment of the mineral extraction work performed in the modal time tact. Thus, the undermined rock mass is presented as a geoinformation multi-agent system, which reproduces the dynamics of the stress–strain state in accordance with the intensity of the mining operations. Mineral extraction leads to the formation of large voids, and this causes an intense redistribution of the stress–strain behavior of the mass. Such changes predetermine rock disturbances characterized by a variety of intensities, shapes and sizes [2,3]. Their influence decreases depending on the distance from the mining area [10,12,54]. Therefore, it may be concluded that rock mass is characterized by zonal disintegration around the area of the underground mining [3,54]. The zonal division of the mass, depending on the intensity of the underground mining impact, is a set of alternating disturbed and relatively undisturbed zones.
The whole geoinformation multi-agent system has such parameters as the total volume of the investigated mass, and the massif of coordinates that describe single areas (points) of this volume and the location of influence zones (stopes, workings, etc.). For each coordinate point, a parameter for estimating the stress–strain state at a point in time is introduced in the form of a relative stress concentration in the mass.
Furthermore, the geoinformation system is presented in the form of Moore space as a multi-agent interaction environment. The agents of the system are single sections of the mass volume (with a scale of 1 km3 in experimental modeling), and they interact with each other through the transfer of stresses and strains in the mass.
Based on the initial massif of coordinates, the structure (location) of the initial population of agents in space is determined, which is a conditionally static part of the system.
Zone division of the mass is proposed to determine the initial structure of the multi-agent system (Figure 1): zone 1—mining area (mined-out stope); zone 2—rock mass, located in the vicinity of the mined-out stope; and zone 3—rock mass, located at a distance from the mining area.
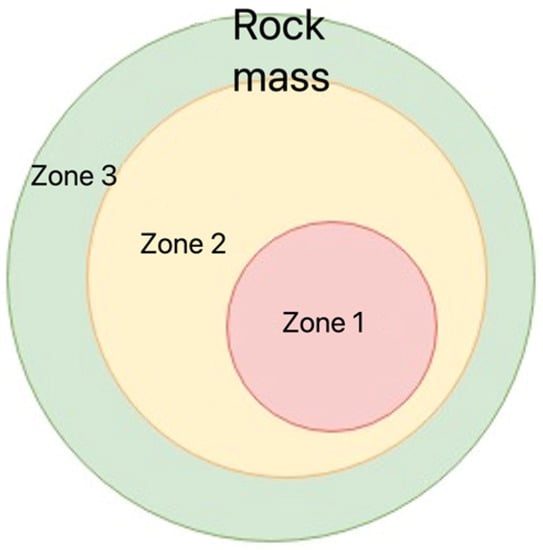
Figure 1.
Dividing the rock mass into impact zones.
The entire geoinformation multi-agent system has such parameters as the total occupied area, an array of coordinates corresponding to each point of this area and the number of stopes. For each individual coordinate point, it is possible to set a parameter for estimating the stress–strain state at the time, which is defined as a relative change in the initial density or a relative displacement of strata. For rock mass, which is already defined as “disturbed”, it is possible to identify the disturbed area and its coordinates. In this case, the geoinformation system can be easily fitted into the Murov space, which is a multi-agent interaction environment. The zones of influence of extraction operations on the rock mass state will indicate its separate single areas, which interact with each other by transferring the stress–strain state indicators.
According to the initial coordinates and initial values, it is possible to determine the point of fracture initiation, i.e., the point of mass transition from the equilibrium state to the stress-strained state. The dynamics of the transition of the system from the equilibrium state are characterized by the evaluation of the stresses in the mass: “stable”, “subject to fracture” and “fractured”. In the entire volume of the rock mass, of great importance is the value of the stress, which is reproduced in each tact of the modal time and extends to the neighboring areas.
3. Construction of a Simulation Model
In the proposed conditions for the intensification of mining works, it is reasonable to choose t-year as the unit of model time, which determines both the properties of the technological processes themselves and the possibility of operational long-term forecasting. The number of agents (of a separate volume/section of the mass) in the initial population is determined in accordance with the studied volume of the massif , where is the population of agents in Equation (1):
Based on the number and the occupied volumes of the mined-out space, the number of agents affecting the massif can be determined using Equation (2):
It is worth noting that and can be set as both static parameters and dynamic parameters in order to study the impact on the region due to an increase or decrease in the scale of production.
In the proposed simplified model, agents are in a two-dimensional discrete space, which is a massif of cells (grouped x, y coordinates). Neighboring agents are determined according to the Moore model.
In the formula below, is the number of blocks that are in the actual mining per modal time unit, and is the average value of the fractures formed in the weakened mass during the mining of one block. Since the mining processes are not stationary within the experiment, is randomly set to an interval from 0 to 6, with an average value of 2. The parameter is defined as the total volume of fractures from one block and varies randomly per modal time unit. The volume of the fractures formed because of the mass weakening during the actual mining per modal time unit can be determined using Equation (3):
Since dynamic stresses are generated in the mass due to blasting, it is necessary to consider the volume of the fractures formed during these works in the model.
The volume of the fractures produced by blasting during mining per modal time unit is set in a similar way in Equation (4):
where:
- j—the number of explosions;
- y2—the average volume of fractures produced by a single explosion.
It should be noted that the number of simultaneous explosions is the target tunable parameter under intensification conditions. However, in experimental modeling, this parameter is randomly set between 0 and 5000, which may be due to production volumes that are related to market prices, market demands, operations under difficult conditions and other technological conditions.
Thus, the values of and are set as random variables using a triangular probability distribution function. An estimation of the increase in the harmful substance volume per modal time unit produced by one mining enterprise can be made using Equation (5):
However, for each individual agent influencer, the increase in the volume of cracks can be determined using Equation (6):
For a more accurate calculation, the subvertical fracture development factor, which has an influence on the total fracture volume, has to be additionally included in the general model. However, in the experimental modeling, the calculation is carried out for the most favorable conditions (the ideal model was applied); i.e., the influence of subvertical fracturing is excluded. At the same time, a correction factor equal to 0.2 is considered to explain the weakening of the already weakened (fractured) mass. The coefficient can be set depending on the strength of the rock mass, its disturbance or other geological factors. To describe the state transfer process between the agents, the actual distance of each agent from the agent influencers is used, which is defined by a weighted sum of coordinate differences using Equation (7):
An estimation of the stability of each agent (individually taken volume of the massif) can be made using Equation (8):
At the same time, the following categorical assessments are introduced:
An integral assessment of the mass stability is determined through the weighted sum of the states of each section of the mass (agent) using Equation (9):
Software implementation of the proposed model and experimental functional runs to assess its performance are carried out in the AnyLogic environment. Figure 2 demonstrates separate user tools for the dynamic adjustment of the model parameters (runners) and for a visualization of the model run results.
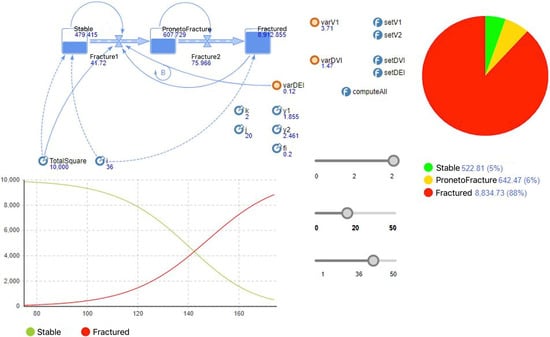
Figure 2.
Model settings panel and visualization of run results.
The numerical variation of such parameters as the degree of impact on the mass, the number of worked stopes and exposure time is available in the model run. The flow and storage diagram displays the dynamics of the change in the stress–strain state of the mass from “equilibrium” to “collapsed” during the model time units.
Figure 3 demonstrates a test run of the model with visualization of the geoinformation multi-agent environment representation in the Moore space.
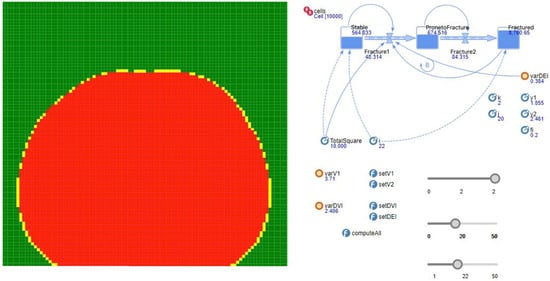
Figure 3.
Visualization of the model run in the Moore space.
In the course of the experimental modeling, it was determined that the proposed conceptual model is workable. At the same time, the results obtained during the modeling process obviously do not reflect the full complexity of the dynamics of the stress–strain state of the rock mass due to the lack of real data from mining enterprises, such as the hardness and strength of the mined rocks, the quality characteristics of the mined minerals, the composition of the used explosives, the method and blasting scheme, and the characteristics of the mining equipment. In addition, for a more accurate description of the distribution of the deformation changes in the rock mass, it is necessary to consider the order of mining stopes, the number of stopes in operation, the total exposure area, the strength characteristics of the stowing mass and other factors.
However, the obtained geoinformation multi-agent model for assessing the stress–strain state of rock mass clearly demonstrates the dynamics of the propagation of deformation changes, which greatly facilitates the perception of the data obtained as a result of the modeling and, with significant improvements, can be integrated into production management processes for predicting the consequences of intensification works.
The obtained results allow for the progression to the next stage of the study: the development of an algorithm for determining the optimal structure and composition of the stowing mix and its components in the development of a deposit using systems with artificial support. The issue is vital for planning, development and the current supervision of mining production.
4. Statement of the Problem and Initial Data
The aim of this work is to create an algorithm for determining the optimal structure and composition of the backfill material and its components during deposit development by systems with artificial support. The solution to the problem of determining the optimal values or probabilistic manifestations is currently possible using modeling. Various methods of modeling are used in science: physical modeling, modeling based on random numbers and modeling based on developed programs [2,18].
The modeling results are aimed at solving a number of applied problems: determining the required strength of the fill mass, calculating the size of inter-stope pillars when mining flat and inclined ore bodies, and establishing the order of deposit development.
The idea of modeling is to create an algorithm for determining the optimal structure and composition of the backfill and its components. The model takes into account the size of the inter-stope pillars and the required strength of the fill mass when underground mining.
In the initial period, the load from the overlying rocks is perceived by inter-stope ore pillars. They interact with the surrounding mass through the zones of support pressure. All this must be taken into account to minimize the risk of the unplanned loss of the stability of the inter-stope pillars. Horizontal displacements of the contour and the near-contour mass can be caused by deformations in the mass without cracks in the walls of the mined-out stopes.
This approach makes it possible to correct the parameters of the inter-stope pillars, the fill mass and the backfill material composition based on an efficiency and safety analysis at any stage of deposit development. The considered inter-stope pillars and artificially created mass, as an object of modeling, are different in their physical compositions and perceived loads. Therefore, universal criteria for assessing the stress–strain behavior of the mass are needed to simplify and ensure high reliability of the mathematical modeling.
It is proposed to evaluate the different-strength sections of the stress–strain system by a complex of interrelated universal criteria: the ore body dip angle; the dip and strike length; the thickness; the width of the inter-stope pillars; and the width of the extraction blocks of the first stage. The width of the left inter-stope pillars and the width of the extraction blocks are affected by the depth of development, the hardness of the adjacent strata and the characteristic strength of the cemented fill mass. The characteristic strength of the fill mass depends on the backfill material components.
Backfill technology involves the creation of fill material capable of hardening in underground conditions. The backfill composite includes the following components: binder (cement, lime, gypsum, blast-furnace slags, slags from power generation plants, etc.), aggregate (specially mined raw materials: gravel; sand; or mining waste, such as tailings of concentrator or crushed rock from stripping operations), water and chemical additives.
The length and intensity of the material flow determine its resource intensity. The resource intensity of a flow in monetary terms estimates its movement and processing costs. The sum of these costs on several segments of the logistics chain, or throughout the entire length from the moment of generation to the moment of the repayment of the flow, is called the accumulated resource intensity. The accumulated resource intensity of the backfill is a key criterion determining the choice of the deposit development system and the backfill composition.
The initial data for modeling are represented by the physical and mechanical properties of the ores and host rocks. The sources of the initial data are the results of studies of the physical and mechanical properties of the ores and host rocks. The studies were carried out during the period of exploration and exploitation in various areas of the Zhdanovskoye deposit Eastern ore cluster and the Tundrovoe deposit. An analysis of these data shows that they are almost completely identical. The main parameters of the ore bodies composing the deposit are presented in Table 1.

Table 1.
Parameters of the ore bodies composing the mineral deposit.
The density of the ore and rock varies from 3.5 to 2.7 ton/m3, Young’s modulus varies from 12 to 7 × 10−4 MPa, and the all-around compression modulus varies from 10 to 6 × 10−4 MPa. The strength characteristics of the ores and host rocks determine stability in terms of the ultimate stress parameter. However, the structural factor plays a decisive role in assessing the mass stability and depends on the structural attenuation coefficient. The calculated data of the strength of the rocks in the mass, taking into account the structural attenuation coefficient, are given in Table 2.

Table 2.
Strength of rocks in the mass.
5. The Mathematical Model Structure and Algorithm
Depending on the application conditions, fill mass is affected by the static (gravitational and tectonic) forces and dynamic loads (from blasting) superimposed on the existing static stress field. Artificial mass can experience the strain of compression, tension, shear, bending and “work” under conditions of uniaxial, biaxial and volumetric compression. The universal backfill characteristic is its strength; the characteristic strength is determined under uniaxial compression according to the permissible limit. The required backfill strength is calculated by one factor or, more often, by several factors: the stability of the vertical exposed surface, horizontal under-mining, permissible backfill deformations and the possibility of equipment movement. The highest of the calculated ones is taken as the characteristic strength.
The load on the artificial mass and its elements is calculated depending on the rock pressure hypothesis:
- -
- Set as the rock weight in the volume of the pressure arch, a weak bind and a rock column to the surface;
- -
- Found through the host rocks’ displacement under conditions of rock and artificial mass deformation.
When calculating the elements of artificial mass, the following factors are taken into account:
- -
- The staging of excavation and its spatial position;
- -
- The size of the undermined rock mass;
- -
- The lag in the formation of the fill mass in time and space from the work front;
- -
- The smooth subsidence of the underworked rocks.
When determining the loads on the supporting pillars from the backfill, the dimensions of the mined-out rock mass are limited to the borehole zone of reduced stresses. In the initial period, inter-stope and panel ore pillars perceive the load from the overlying rocks when using stoping in gentle and inclined deposits. Such pillars interact with the surrounding mass through the support pressure zones. In this case, artificial supports are loaded with their own weight and the rock weight in the roof arch volume or a layer of weak rocks above the ore body. Backfilling at this development stage increases the load-bearing capability of the inter-stope pillars. Thus, the main bearing elements are the ore panel (block) pillars, which are surrounded by artificial pillars during the mining of the remaining ore inter-stope pillars. As the mining span increases, there is an increase in deformations in the ore and artificial supports and the subsidence of the overlying strata of rocks under conditions of combined pillar deformation. The longitudinal strain of the combined pillar (∆hp) from compressive loads can be determined using Equation (10):
where:
- h—the pillar height, m;
- γ = ρg—the unit weight of the overlying rocks, N/m3;
- ρ—the rock density, kg/m3;
- g—the acceleration of gravity, m/sec2;
- H—the depth of the excavation, m;
- Sr—the roof square supported by the pillar, m2;
- Sp—the cross-section square of the ore pillar, m2;
- Ep—the proportional modulus for the ore, MPa;
- Μp—the coefficient affecting the longitudinal deformation, considering the artificial mass characteristics.
The hardening effect of the backfill on the ore pillars surrounded by artificial ones is estimated by the hardening coefficient, which shows the increase in the bearing capability of the ore supports. The excavation of the pillars that perceive the maximum load leads to an increase in the load on the artificial mass. In this case, the artificial mass is deformed together with the overlying rock strata.
The process of roof subsidence and backfill compression has a damping characteristic. In the mined-out rocks, a zone of tensile stresses is formed, in which the rocks are softened. The zone size and the stratification intensity are a function of the mining span, the deposit slope angle and the lateral repulse coefficient. The influence of the underground stope usually extends to a height of 1.5 spans of the exposed surface. The load from delaminated rocks is summed up with the load from deformations and their own weight. With small sizes of gentle and inclined deposits, the calculation of the load is reduced to determining the arch height and the rock weight in the volume of the caving zone. The height of the cave arch is determined by comparing the tensile stresses in the stope roof with the ultimate tensile strength of the rocks using Equation (11):
where:
- ɳ—the horizontal stress coefficient;
- σt—the ultimate tensile strength of the roof rocks, Pa.
The formula is valid with a horizontal stress equal to 0.2 ÷ 0.3, and the ratio of the depth of the stope roof to its span is greater than two. There are methods for calculating the cave arch height through the shear angle and rock hardness, such as Equation (12):
where:
- l—the minimum size of the stope, m;
- φ—the angle of the internal friction of the roof rocks, deg.;
- f = σc/100—the rock hardness on a scale of Professor M. M. Protodiakonov;
- σc—the compressive strength.
The scheme for determining the pressure arch depending on the width of the mined-out mass is shown in Figure 4.
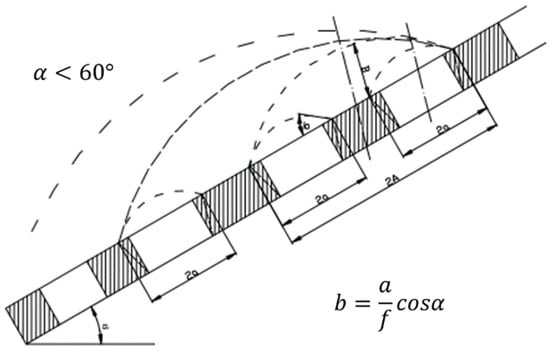
Figure 4.
Scheme for determining the height of pressure arch.
The reactive effect of the backfill, which reduces the rock stratification zone, is insignificant due to its high compliance, and it can be determined by the dependence using Equation (13):
where:
- —the size of the zone of the tensile stresses (caving) in the absence of pressure on the contour, m;
- —the backfill pressure on the roof contour, MPa;
- —stress in the tight mass at the roof level, MPa.
The loads on artificial mass are mainly created by horizontal components in steeply dipping deposits, developed by stopes and slicing systems with cemented backfill. The action of horizontal components is manifested in the wall convergence of the mined-out void in the area of influence of gravitational and tectonic fields. Due to the high compression properties, the backfill does not significantly affect the stress behavior of the rocks, and it does not change the stress distribution in the surrounding mass. The ore pillars and the rock mass remain the main bearing elements. The purpose of the backfill in this case is to prevent the movement of the softened mass of the stope side and to increase its stability. The quantitative values of the stresses and strains in the fill mass are determined by using the approach of the values of the sides of the mined-out void under conditions of elastic or elastoplastic rock deformation. This takes into account the deformation changes in the unloading zone in the field of gravitational and tectonic forces and the reaction of the artificial mass. The reverse action of the fill mass reduces the displacement of rocks toward the mined-out void. The impact of development extends into the host rocks to a depth equal to 1/4 span, as shown in Equation (14):
where:
- and —the height and width, respectively, of the mined-out void, m.
With continuous mining, a reduced pressure zone (unloading) is formed in the roof, and an increased pressure zone (support) is formed in the ore mass. The roof rocks interact with the backfill mass as the span of the exposed surface increases and the mined-out void is filled with backfill. Created artificial mass behaves similar to pliable timber.
The pliability of the fill mass is maintained at the full set of strength until it fully realizes the ability to deform under load and accept the full weight of the rock column. The overlying strata act similar to a plate, fixed at one end over the ore mass and supported by the other end on the fill mass. The unloading zone size is proportional to the shrinkage of the backfill material. The stress concentration coefficient of the ore mass is proportional to shrinkage up to ε = 3%. At ε ≤ 3%, the overlying strata are displaced smoothly without breaks, and at ε > 3%, the rocks are stratified in the roof. The stress concentration coefficient in the ore mass is determined by the under-mining span using Equations (15) and (16):
where:
- —the base of the natural logarithm;
- —the under-mining span, m;
- —the depth of the work, m;
- —the width of the mined band, m;
- —the number of simultaneously mined belts.
As the practice of underground mining shows, the fill mass is only exposed to the weight of the overlying rock strata 40–60 m from the bottom. In the area of actual mining, the mass is loaded with its own weight and the weight of the technological equipment.
Simplified methods are used in engineering calculations. For pillars from the backfill, the research method is limited to the determination of normal stresses over dangerous sections under the assumptions that the pillars work under uniaxial compression and that the stresses are distributed evenly. The actual uneven distribution of stresses in the pillars is considered by introducing a safety factor. Then, the normal stresses in the backfill can be determined (17):
where:
- is the load on the artificial pillar, Pa;
- is the section area of the pillar, m2.
The algorithm for determining the optimal structure and composition of the backfill, its components during deposit development with artificial support and the choice of the preferred development system with backfill consists of several stages (Figure 5).
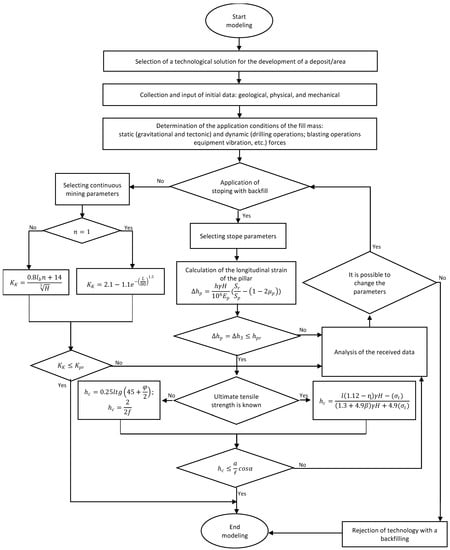
Figure 5.
Algorithm for choosing a development system and selecting the optimal fill material.
6. Conclusions
1. A method of mathematical modeling aimed at solving the following problems is proposed:
- -
- The selection of the optimal development system with backfill when extracting minerals;
- -
- The determination of the rational composition of the fill material.
2. The method of mathematical modeling presented by the algorithm involves the sequential execution of various stages.
3. Feasibility evaluation of using a certain system in an underground mine is based on a comparison of static forces and dynamic loads acting on the artificial mass and stresses imposed on the existing static field.
4. The method of mathematical modeling is based on the use of a complex of interrelated universal criteria of the stress–strain behavior of the rock mass, as well as the values of the stress concentration in it, taking into account the reaction of the artificial mass. The values of these criteria depend on the mining parameters: the development depth; the ore body dip angle; the dip and strike length; the thickness and width of the inter-stope pillars; the width of the extraction blocks of the first stage; artificial mass heights; and the composition of the backfill material.
5. Deformation changes and stress concentration are key criteria in the proposed mathematical model, since exceeding the permissible values of the accumulated concentration and strain changes can lead to a man-made disaster.
6. It is possible to select a system with backfill for deposit development and to select the optimal composition of the backfill material using the proposed method for certain conditions.
7. A further direction for research is a case study of the proposed method for its feasibility and a mathematical description of the choice of a mining system with backfill and optimal backfill composition considering the weight (significance coefficient) of each factor.
Author Contributions
Conceptualization, M.M.K. and V.I.G.; methodology, M.M.K. and A.V.A.; software, E.V.T. and Y.V.A.; validation, M.M.K. and A.V.A.; formal analysis, V.I.G.; investigation, V.I.G. and A.V.A.; resources, N.V.L.; data curation, E.V.T. and Y.V.A.; writing—original draft preparation, E.V.T.; writing—review and editing, V.I.G. and N.V.L.; visualization, E.V.T.; supervision, M.M.K. and V.I.G.; project administration, M.M.K.; funding acquisition, M.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mikolas, M.; Mikusinec, J.; Abrahamovsky, J.; Dibdiakova, J.; Tyulyaeva, Y.; Srek, J. Activities of a Mine Surveyor and a Geologist at Design Bases in a Limestone Quarry. IOP Conf. Ser. Earth Environ. Sci. 2021, 906, 012073. [Google Scholar] [CrossRef]
- Khayrutdinov, A.M.; Kongar-Syuryun, C.B.; Kowalik, T.; Tyulyaeva, Y.S. Stress-strain behavior control in rock mass using different-strength backfill. Min. Inf. Anal. Bull. 2020, 10, 42–55. [Google Scholar] [CrossRef]
- Marcak, H.; Mutke, G. Seismic activation of tectonic stresses by mining. J. Seismol. 2013, 17, 1139–1148. [Google Scholar] [CrossRef]
- Gao, Y.; Hao, M.; Wang, Y.; Dang, L.; Guo, Y. Multi-Scale Coal Fire Detection Based on an Improved Active Contour Model from Landsat-8 Satellite and UAV Images. ISPRS Int. J. Geo-Inf. 2021, 10, 449. [Google Scholar] [CrossRef]
- Ignjatovi’c, L.D.; Krsti’c, V.; Radonjanin, V.; Jovanovi´c, V.; Malešev, M.; Ignjatovi´c, D.; Ðurdevac, V. Application of Cement Paste in Mining Works, Environmental Protection, and the Sustainable Development Goals in the Mining Industry. Sustainability 2022, 14, 7902. [Google Scholar] [CrossRef]
- Tcvetkov, P.; Cherepovitsyn, A.; Fedoseev, S. The changing role of CO2 in the transition to a circular economy: Review of carbon sequestration projects. Sustainability 2019, 11, 5834. [Google Scholar] [CrossRef]
- Grayson, R.L. Addressing the Dual Challenges of Meeting Demand for Minerals and Sustainable Development. Minerals 2011, 1, 1–2. [Google Scholar] [CrossRef]
- Han, L.; Liu, H.; Zhang, W.; Ding, X.; Chen, Z.; Feng, L.; Wang, Z. Seismic behaviors of utility tunnel-soil system: With and without joint connections. Undergr. Space 2022, 7, 798–811. [Google Scholar] [CrossRef]
- Zhang, W.; Han, L.; Feng, L.; Ding, X.; Wang, L.; Chen, Z.; Liu, H.; Aljarmouzi, A.; Sun, W. Study on seismic behaviors of a double box utility tunnel with joint connections using shaking table model tests. Soil Dyn. Earthq. Eng. 2020, 136, 106118. [Google Scholar] [CrossRef]
- Dobrzycki, P.; Ivannikov, A.L.; Rybak, J.; Shkodkina, V.O.; Tyulyaeva, Y.S. The impact of Rapid Impulse Compaction (RIC) of large non-cohesive material deposits on the surrounding area. IOP Conf. Ser. Earth Environ. Sci. 2019, 362, 012132. [Google Scholar] [CrossRef]
- Li, X.; Huo, D.; Goldberg, D.W.; Chu, T.; Yin, Z.; Hammond, T. Embracing Crowdsensing: An Enhanced Mobile Sensing Solution for Road Anomaly Detection. ISPRS Int. J. Geo-Inf. 2019, 8, 412. [Google Scholar] [CrossRef]
- Herbut, A.; Khairutdinov, M.M.; Kongar-Syuryun, C.; Rybak, J. The surface wave attenuation as the effect of vibratory compaction of building embankments. IOP Conf. Ser. Earth Environ. Sci. 2019, 362, 012131. [Google Scholar] [CrossRef]
- Łupieżowiec, M.; Rybak, J.; Różański, Z.; Dobrzycki, P.; Jędrzejczyk, W. Design and Construction of Foundations for Industrial Facilities in the Areas of Former Post-Mining Waste Dumps. Energies 2022, 15, 5766. [Google Scholar] [CrossRef]
- Golik, V.I.; Razorenov, Y.I.; Lukyanov, V.G. Environmental and economic aspects of resource saving in mining. Bull. Tomsk. Polytech. Univ. Geo Assets Eng. 2017, 328, 18–27. (In Russian) [Google Scholar]
- Huang, J.; Tian, C.; Xing, L.; Bian, Z.; Miao, X. Green and Sustainable Mining: Underground Coal Mine Fully Mechanized Solid Dense Stowing-Mining Method. Sustainability 2017, 9, 1418. [Google Scholar] [CrossRef]
- Bučinskas, A.; Kriipsalu, M.; Denafas, G. Proposal for Feasibility Assessment Model for Landfill Mining and Its Implementation for Energy Generation Scenarios. Sustainability 2018, 10, 2882. [Google Scholar] [CrossRef]
- Sekhohola-Dlamini, L.M.; Keshinro, O.M.; Masudi, W.L.; Cowan, A.K. Elaboration of a Phytoremediation Strategy for Successful and Sustainable Rehabilitation of Disturbed and Degraded Land. Minerals 2022, 12, 111. [Google Scholar] [CrossRef]
- Adigamov, A.E.; Yudenkov, A.V. Stress-strain behavior model of disturbed rock mass with regard to anisotropy and discontinuities. Min. Inf. Anal. Bull. 2021, 8, 93–103. (In Russian) [Google Scholar] [CrossRef]
- Golik, V.I.; Burdzieva, O.G. Increase of Work Safety by Enlargement of Field of Application of Hardening Mixtures from Processing Waste. Bezop. Tr. Promyshlennosti 2016, 8, 45–50. (In Russian) [Google Scholar]
- Han, G.; Zhang, J.; Sun, H.; Shen, D.; Wu, Z.; An, X.; Meye, S.M.; Huang, Y. Application of Iron Ore Tailings and Phosphogypsum to Create Artificial Rockfills Used in Rock-Filled Concrete. Buildings 2022, 12, 555. [Google Scholar] [CrossRef]
- Zglinicki, K.; Małek, R.; Szamałek, K.; Wołkowicz, S. Mining Waste as a Potential Additional Source of HREE and U for the European Green Deal: A Case Study of Bangka Island (Indonesia). Minerals 2022, 12, 44. [Google Scholar] [CrossRef]
- Tcvetkov, P. Engagement of resource-based economies in the fight against rising carbon emissions. Energy Rep. 2022, 8, 874–883. [Google Scholar] [CrossRef]
- Khayrutdinov, M.M.; Kongar-Syuryun, C.B.; Khayrutdinov, A.M.; Tyulyaeva, Y.S. Improving safety when extracting water-soluble ores by optimizing the parameters of the backfill mass. Bezop. Tr. Promyshlennosti 2021, 2021, 53–59. [Google Scholar] [CrossRef]
- deCarvalho, F.A.; Nobre, J.N.P.; Cambraia, R.P.; Silva, A.C.; Fabris, J.D.; dosReis, A.B.; Prat, B.V. Quartz Mining Waste for Concrete Production: Environment and Public Health. Sustainability 2022, 14, 389. [Google Scholar] [CrossRef]
- Anan’ev, P.P.; Vasilev, S.V.; Meshcheryakov, R.V.; Plotnikova, A.V.; Belyakov, K.O.; Kuznetsov, E.B. Prospects of development of space mining and processing industry. Innovations 2016, 4, 4–8. (In Russian) [Google Scholar]
- Gugunskiy, D.; Chernykh, I.; Khairutdinov, A. Legal Models for Activities on the Exploration and Utilization of Space Resources: Towards the “Space-2030” Agenda. Adv. Intell. Syst. Comput. 2020, 1100, 657–664. [Google Scholar] [CrossRef]
- Khayrutdinov, A.M. Current Issues of Mining Activities on Celestial Bodies: International Law Aspects. In Advances in the Astronautical Sciences, Proceedings of the First IAA/AAS SciTech Forum on Space Flight Mechanics and Space Structures and Materials, Moscow, Russia, 13–15 November 2018; American Astronautical Society: Springfield, VA, USA, 2020; Volume 170, pp. 895–902. [Google Scholar]
- Šajn, R.; Ristović, I.; Čeplak, B. Mining and Metallurgical Waste as Potential Secondary Sources of Metals—A Case Study for the West Balkan Region. Minerals 2022, 12, 547. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, H.; Su, H.; Zeng, Q. Green Mining Takes Place at the Power Plant. Minerals 2022, 12, 839. [Google Scholar] [CrossRef]
- Blinova, E.; Ponomarenko, T.; Knysh, V. Analyzing the Concept of Corporate Sustainability in the Context of Sustainable Business Development in the Mining Sector with Elements of Circular Economy. Sustainability 2022, 14, 8163. [Google Scholar] [CrossRef]
- Khairutdinov, A.; Ubysz, A.; Adigamov, A. The concept of geotechnology with a backfill is the path of integrated development of the subsoil. IOP Conf. Ser. Earth Environ. Sci. 2021, 684, 012007. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Y.; Zhang, J.; Chen, Y.; Duan, C.; Qi, J.; Cheng, Z.; Pan, Z. Comprehensive Evaluation of the Eco-Geological Environment in the Concentrated Mining Area of Mineral Resources. Sustainability 2022, 14, 6808. [Google Scholar] [CrossRef]
- Tcvetkov, P.; Cherepovitsyn, A.; Fedoseev, S. Public perception of carbon capture and storage: A state-of-the-art overview. Heliyon 2019, 5, e02845. [Google Scholar] [CrossRef] [PubMed]
- Khayrutdinov, A.; Paleev, I.; Artemov, S. Replacement of traditional components of the backfill mixture with man-made waste. IOP Conf. Ser. Earth Environ. Sci. 2021, 942, 012005. [Google Scholar] [CrossRef]
- Prokopowicz, P.; Pires, P.; Michałek, A.; Rybak, A.; Khairutdinov, A.M. Time necessary for microwave drying of mineral soils. IOP Conf. Ser. J. Phys. 2020, 1614, 012021. [Google Scholar] [CrossRef]
- Rakhutin, M.G.; Boyko, P.F. Ways to improve assessment methods of the main characteristics of grinding balls. Russ. Coal J. 2017, 12, 49–52. [Google Scholar] [CrossRef]
- Boyko, P.F.; Titievsky, E.M.; Timiryazev, V.A.; Mnatsakanyan, V.U.; Khostikoev, M.Z. Provision of operational life-time period of crushers liners by applying new technologies of their manufacturing and wear-out diagnosing. Equip. Technol. Oil Gas Complex 2019, 5, 42–47. [Google Scholar] [CrossRef]
- Adach-Pawelus, K. Back-Calculation Method for Estimation of Geomechanical Parameters in Numerical Modeling Based on In-Situ Measurements and Statistical Methods. Energies 2022, 15, 4729. [Google Scholar] [CrossRef]
- Carmo, F.F.; Lanchotti, A.O.; Kamino, L.H.Y. Mining Waste Challenges: Environmental Risks of Gigatons of Mud, Dust and Sediment in Megadiverse Regions in Brazil. Sustainability 2020, 12, 8466. [Google Scholar] [CrossRef]
- Litvinenko, V. Advancement of geomechanics and geodynamics at the mineral ore mining and underground space development. Geomech. Geodyn. Rock Masses 2018, 1, 3–16. [Google Scholar]
- Du, X.; Zhou, K.; Cui, Y.; Wang, J.; Zhou, S. Mapping Mineral Prospectivity Using a Hybrid Genetic Algorithm–Support Vector Machine (GA–SVM) Model. ISPRS Int. J. Geo-Inf. 2021, 10, 766. [Google Scholar] [CrossRef]
- Rybak, J.; Khayrutdinov, M.M.; Kuziev, D.A.; Kongar-Syuryun, C.B.; Babyr, N.V. Prediction of the geomechanical state of the rock mass when mining salt deposits with stowing. J. Min. Inst. 2022, 253, 61–70. [Google Scholar] [CrossRef]
- Komolov, V.; Belikov, A.; Demenkov, P. Research on Load-Bearing Constructions Behavior During Pit Excavation Under «Slurry Wall» Protection. Technol. Adv. Constr. 2022, 180, 313–323. [Google Scholar] [CrossRef]
- Wu, P.; Chen, L.; Li, M.; Wang, L.; Wang, X.; Zhang, W. Surrounding Rock Stability Control Technology of Roadway in Large Inclination Seam with Weak Structural Plane in Roof. Minerals 2021, 11, 881. [Google Scholar] [CrossRef]
- Czajka, K.; Kawalec, W.; Król, R.; Sówka, I. Modelling and Calculation of Raw Material Industry. Energies 2022, 15, 5035. [Google Scholar] [CrossRef]
- Liu, S.; Bai, J.; Wang, G.; Wang, X.; Wu, B. A Method of Backfill Mining Crossing the Interchange Bridge and Application of a Ground Subsidence Prediction Model. Minerals 2021, 11, 945. [Google Scholar] [CrossRef]
- Pal, A.; Rošer, J.; Vulić, M. Surface Subsidence Prognosis above an Underground Longwall Excavation and Based on 3D Point Cloud Analysis. Minerals 2020, 10, 82. [Google Scholar] [CrossRef]
- Dumakor-Dupey, N.K.; Arya, S.; Jha, A. Advances in Blast-Induced Impact Prediction—A Review of Machine Learning Applications. Minerals 2021, 11, 601. [Google Scholar] [CrossRef]
- Pang, D.; Zhou, Y.; Niu, X.; He, K.; Li, C.; Chen, Z. Research on the Mechanical Properties of Flexible Material Backfilling Wall in Gob-Side Entry Retaining. Minerals 2022, 12, 1020. [Google Scholar] [CrossRef]
- Chakrawarthi, V.; Jesuarulraj, L.R.; Avudaiappan, S.; Rajendren, D.; Amran, M.; Guindos, P.; Roy, K.; Fediuk, R.; Vatin, N.I. Effect of Design Parameters on the Flexural Strength of Reinforced Concrete Sandwich Beams. Crystals 2022, 12, 1021. [Google Scholar] [CrossRef]
- Chen, F.; Liu, J.; Zhang, X.; Wang, J.; Jiao, H.; Yu, J. Review on the Art of Roof Contacting in Cemented Waste Backfill Technology in a Metal Mine. Minerals 2022, 12, 721. [Google Scholar] [CrossRef]
- Jelínek, P.; Marschalko, M.; Lamich, D.; Yilmaz, I.; Zastěrová, P.; Bednárik, M.; Heviánková, S.; Kyncl, M.; Drusa, M.; Růčková, H. Monitoring and analysis of burning in coal tailing dumps: A case study from the Czech Republic. Environ. Earth Sci. 2015, 73, 6601–6612. [Google Scholar] [CrossRef]
- Mustafin, M.; Bykasov, D. Adjustment of Planned Surveying and Geodetic Networks Using Second-Order Nonlinear Programming Methods. Computation 2021, 9, 131. [Google Scholar] [CrossRef]
- Ding, X.; Luo, Z.; Ou, Q. Mechanical property and deformation behavior of geogrid reinforced calcareous sand. Geotext. Geomembr. 2022, 50, 618–631. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).