Abstract
Geophysical methods for local rock burst prediction are currently being developed along two lines: improving recording equipment and improving data processing methods. Progress in developing processing methods is constrained by the lack of informative prognostic models that describe the condition of rock mass, the process of rock mass fracturing, and the phenomena that can substantiate the choice of both criteria and test parameters of the condition of rock mass and give an estimate of the time remaining until rock pressure manifestation. In particular, despite achievements in hardware design, researchers using the seismo-acoustic method to predict rock bursts measure the acoustical activity or energy capacity of elastic wave scattering after a man-made explosion and are faced with the dependence of forecast results on destabilizing factors. To solve this problem, we applied an information and kinetic approach to forecasting. In this article, we discuss the principles of selecting test parameters that are resistant to destabilizing factors. We propose a micromechanical model of fracture accumulation in a rock mass block that reflects the dependence of acoustic emission (AE) parameters on time, which makes it possible to detect the influence of various factors on forecast data and filter the signals. We also propose criteria and a methodology for rock burst risk assessment. The results were tested in analyzing the seismo-acoustic phenomena caused by man-made explosions at the Taimyrsky and Oktyabrsky mines in Norilsk. The article gives examples of using the proposed criteria. The effectiveness of their application is compared with traditional methods for assessing rock burst risks and evaluating the stress–strain parameters of rock mass in terms of their being informative, stable, and representative by means of statistical processing of experimental data.
1. Introduction
There is a sharp intensification of the extraction of minerals with an increase in consumption. The use of resources in excess of the replacement rate causes their depletion. Since minerals are non-renewable resources, one of the possible forms of depletion is mining. To meet the growing demand in order to ensure sustainable development of resources, mining enterprises are moving to the development of reserves that were previously considered unsuitable for extraction, such as off-balance reserves, ores of complex material composition, areas of the deposit in difficult mining and geological conditions, and more [1,2,3,4]. One of the ways to increase the mineral resource base and resource support for the sustainable development of a mining enterprise is the transition to the development of reserves which are located at great depths. However, the extraction of minerals at great depths is associated with the complexity of monitoring and managing the stress–strain state of the undermined rock massif [5,6,7].
As underground mining goes deeper and man-made stresses around mine workings are growing, the issue of combating rock pressure manifestations in ore deposits becomes increasingly important in mining theory and practice [8,9]. The consequence of the change in the stress–strain state of the massif as a result of mining operations is the development of subvertical disturbances, leading to the destruction of the waterproof layer and failures on the surface [10]. The problem of predicting the intensity of rock pressure manifestations has become of particular significance due to the need to consider the implementation of preventive measures when preparing plans for developing deep levels at both new and already operating mines [2,11,12]. No less important are the development and selection of practical methods and technical means for predicting stress–strain parameters of rock mass and assessing rock burst risks [13,14,15,16].
Extracting ore from deep levels that are prone to rock bursts necessitates improving the safety of workers, which requires improving methods and techniques for monitoring rock mass parameters [17,18,19]. Among them is the acoustic emission (AE) method, which is approved by Rostekhnadzor [20] as one of the geophysical methods for rock burst risk assessment. The AE method is being upgraded in terms of both hardware and methodology [21,22,23,24], but the developments are not effective enough due to the lack of a reliable methodological basis for searching for correlations between the AE parameters being measured and the parameters of rock mass [25,26,27]. In particular, despite progress in hardware design, tests are still based on measuring acoustical activity, the total number of pulses, or the energy capacity of elastic wave scattering after a man-made explosion, and researchers have to deal with the dependence of tests results on the influence of destabilizing factors [28,29,30]. It seems possible to solve the problem by using an information and kinetic approach to predicting rock fracturing and designing kinetic models of processes and phenomena preceding a rock burst, which can serve as guiding principles in the search for informative criteria and test parameters [31]. The purpose of the study is to justify effective AE analysis criteria and rock burst prediction methods that have low sensitivity to noise and are most closely related to the time remaining until rock pressure manifestation.
2. Materials and Methods
The proposed approach assesses rock burst risks by means of simulating the process of rock fracturing and monitoring the resulting phenomenon of elastic wave scattering, which manifests itself most intensely in the initial period of stress redistribution caused by new voids in a rock mass block after a man-made explosion. The basis of modeling is the relationship between the primary informative parameters of AE (ξ) and the parameter of damage to the material or rock, which is fracture density C(t) caused by the fracturing of structural elements [31,32], described by the following equation:
where t is the current time and kAE is the acoustic emission factor (AEF), which reflects the similarity between the fracturing and elastic wave scattering processes or the acoustically active volume of the material and is described by the equation below:
where V is the volume of the material being tested and Φ(Δt,f,u) is the density function of AE signal distribution by pauses ∆t, frequency f, and amplitude u. Model (1) is informative as it stabilizes AEF and connects the fracture density accumulation rate C(t) with time to failure.
ξ(t) = kAEC(t),
The time dependence of fracture density is described as follows:
where C0 is the initial density of structural elements, ω is the strength parameter of the structural element of the test object material that depends on the time-varying tensile stresses σ(t) in the structural element, and ω(t) is the time dependence of the strength parameter:
where γ is the structurally sensitive coefficient; K is the Boltzmann constant; T is the absolute temperature; Ψ(ω) is the distribution density function of the values of ω by structural elements; θavg(U0,ω(t)) = τ0 exp[U0/(KT) − ω(t)] is the average time before one structural element fails, which is found by the Zhurkov formula [33]; τ0 is the atomic oscillation period; U0 is the energy that activates the process of fracturing; ω0 is the lower limit of the range of ω; Δω is a representative dispersion range of ω values by structural elements.
ω(t) = γσ(t)/KT
Equation (1), used for testing structural materials at the microscale level, also extends to the scale of an elastic wave scattered around the void formed by an explosion. Thus, Equation (1) is a universal multilevel model of time dependence of acoustic emission parameters recorded at the stage of scattered fracturing of any scale for a material characterized by strength heterogeneity. With a known critical fracture density C* ≈ 0.01C0, it is possible to find time to failure. Various primary AE parameters (ξ) act as analogs of C(t), namely the number of discrete AE pulses recorded (N∑), the total AE count (N), the relative total amplitude, or any dimensionless combination of these parameters. A significant dependence of the activity and amplitude of AE signals on the conditions of signal registration and elastic wave propagation reduces the reliability of the AE forecast and the effectiveness of safety measures based on it. Signal registration conditions are affected by the individuality of each recording channel (Figure 1), which affects AEF (2), thus destabilizing the relationship between the primary parameters or AE energy and the parameters of rock mass.
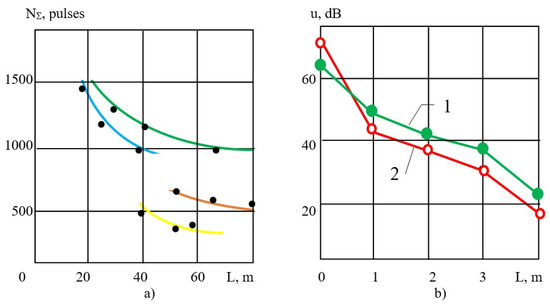
Figure 1.
AE parameters as a function of the distance L from the AE transducer to its source: (a) the total number of AE pulses (N∑) registered by different recorders over the stress relaxation period as a function of the distance L from the AE transducer to its source at a blast area in the Taimyrsky mine operated by Norilsk Nickel; (b) the amplitude u of AE signals as a function of the distance L to the AE transducers with resonant frequencies of 320 kHz (1) and 180 kHz (2).
This approach to forecasting makes it possible to identify the predicted stage of homogeneous fracturing, formulate the conditions for AE testing correctness, and propose a number of informative indicators to be used in the AE testing of the strength parameters of structural materials. They are connected with the fracture rate at the stage of homogeneous fracturing, the moment of critical fracture density, and the degree of risk, and are also resistant to the influence of destabilizing factors [34]. As the testing optimization principles underlying the process are universal, the proposed indicators can be extrapolated onto rocks as well. We use relative stress (FAE), as well structure parameters and decline in activity, or the structure factor (XAE), as AE indicators of the stress–strain parameters of a rock mass block. The WAE durability factor is used as an indicator of rock burst risk that reflects time to failure in the borehole zone (Table 1).

Table 1.
Multi-model multilevel concentration and kinetic AE strength indicators resistant to interference and destabilizing factors in AE testing.
3. Results and Discussion
AE signals were recorded and their parameters were measured after man-made explosions at the Taimyrsky and Oktyabrsky mines, located in Norilsk and operated by Norilsk Nickel. The aim of the explosions was to break down the ore being mined. The equipment used for AE signal recording is described in [31].
In most cases, the number of AE signals recorded per unit time t of decline in activity varied according to the exponential law described by the micromechanical model (1) for the case of homogeneous fracturing (Figure 2):
where σ0 is stress after the explosion, is the average rate of their decline, is the seismo-acoustic activity at the initial time of its decline, and α = γ/KT = XAE = dln/dt is the AE decline rate indicator. The correlation coefficient between the real value and that calculated by Equation (5) for in various recording cases averaged 0.9, which confirms the adequacy of the model (5). This is notable for the difference in the number of pulses recorded by different sensors at the same distance (Figure 1) or from a single signal source (Figure 2), which indicates that this parameter is unstable in relation to the state of the array.
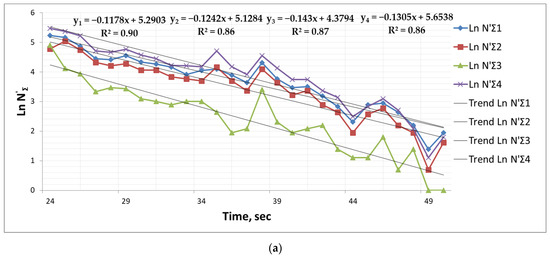
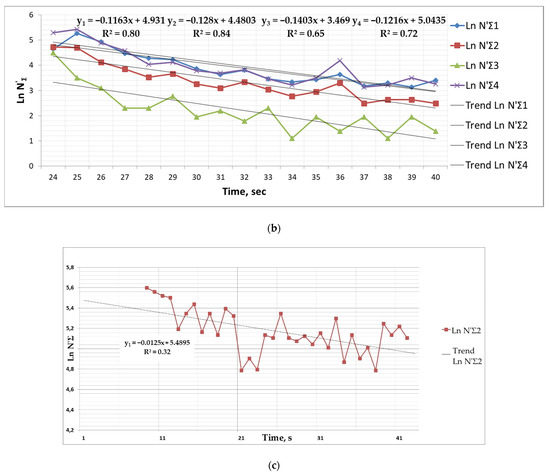
Figure 2.
The results of testing the time dependence of the AE caused by man-made explosions at mines in Norilsk: (a) for various channels when passing through the partially safe zone; (b) for various channels when passing through the zone with high bearing pressure; (c) for the zone associated with rock burst risks.
It was found that the AE caused by an explosion reached the maximum value of at the first moment (1 to 2 min) and then decreased to . The results were described by the equations of the micromechanical model:
The number of AE pulses accumulated in time t according to the law is found as follows:
where is the acoustic emission activity factor.
Figure 3 shows experimentally recorded data illustrating changes in the parameters , α, and NΣ(τp) depending on the stress levels in the mine working being developed, which depend on the stress ratio σ/[σ]avg and were analyzed using core disking [20].
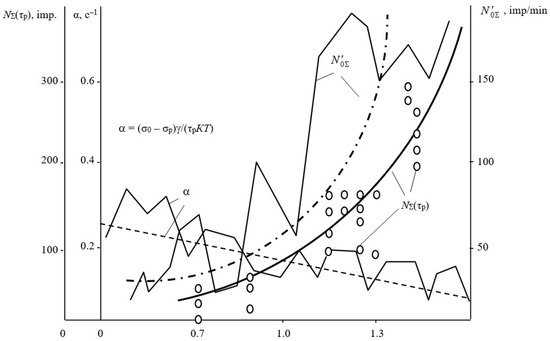
Figure 3.
Relationship between the stress–strain parameters of rock mass, the maximum activity , the decline rate α, and the total emission N(τp).
As Figure 3 shows, the relationship between the AE parameters and the stresses in rock mass corresponds to the relationship described by Equations (5)–(8). For rock mass in a quasi-static homogeneous stressed state, with average stresses σp in it being constant, the time τ* reflecting rock burst risk is found based on the condition that fracture density C(t) has reached the critical value C* using the following equation [19,31]:
The values of τ0, U0, K, T, A = on the right side of Equation (9) are relatively stable and, as a rule, are known or can be found a priori before testing. Therefore, rock burst risk assessment is reduced to a posteriori determination of only the value ωp of Equation (9), for example, using the AE index WAE = γσ/(KT) (Table 1).
The value of the durability factor WAE is found as follows.
- -
- For the rock mass block at the time of the explosion:where ΔK0= σ0/[σ] − σp/[σ] ≈ [1 − FAE] is the change in the stress factor during the stress relaxation period after the explosion, FAE= ln (/) ≈ σp/σ0;
- -
- In equilibrium:where ΔKp = σ0/σp − σp/σp ≈ 1/FAE − 1 is the change in the stress factor for a rock mass block in equilibrium.
To formulate an indicator that is informative regarding rock burst risks, the WAE values should be compared with the allowable threshold values [WAE], which are found for a rock block being fractured in θexp time and do not depend on factors affecting the results of AE testing:
[W0AE] = ln (τ0/θexp) + U0/(KT).
For τ0 =10 −13 ÷ 10 −15 s, θexp ≈ 1 ÷ 1000 s, U0/KT = 50 ÷ 60 [9,34], we have [W0AE] ≈ 10 ÷ 30, [WpAE] ≈ 1 ÷ 2, which is taken as the universal constant for a rock mass block.
Let us consider the results of recording seismo-acoustic signals in rock mass after explosions in zones with different levels of rock pressure (the Taimyrsky mine of Norilsk Nickel). In the safe zone, AE signals registered by Channel 1 have the following values (Figure 2a):
- -
- At the initial moment of the decline in activity = 62 min–1, = 4.1.
- -
- At the final moment of the decline in activity = (16) = 2 min−1, = 0.69.
The value of the AE indicator of the stress parameters in the rock mass block is:
The value of the durability factor for the borehole zone is:
As FAE < 0.5, WpAE < [WpAE], W0AE < [W0AE], there are no rock burst risks. The zone belongs to Category III, meaning that there is no immediate danger of rock bursts.
Similarly, in the zone with high bearing pressure (Figure 2b),
The value of the durability factor for the borehole zone is:
.
Taking into account the change in the AE testing procedure caused by a decrease in the average amplitude of the AE signals over time in the process of stress relaxation [35], the adjusted values are:
FcorAE = 1.1 FAE = 0.654
The values of the durability factor for the borehole zone are as follows:
As FAE > 0.5, WpAE > [WpAE], W0AE < [W0AE], the zone is classified as belonging to Category II, meaning that there are rock burst risks, the mine working must be stress-relieved, and mining operations are carried out according to standard methods.
Similarly, in terms of rock bursts (Figure 2c), FAE = 0.94, WpAE = 12.86, W0AE = 13.67, FAE > 0.5, WpAE > [WpAE], W0AE > [W0AE]; the zone belongs to Category I, which means there are increased rock burst risks.
Table 2 and Table 3 compare AE testing parameters in terms of their being informative (correlations with σ/[σ]avg values in different rock mass zones), stable (variability across recording channels), and representative of the rock mass parameters.

Table 2.
Correlation between relative stresses in the mine working being developed and AE parameters calculated factoring in the metrological heterogeneity associated with a decrease in the amplitude of AE signals in the process of stress relaxation.

Table 3.
Values of the coefficient of variation V for the recording channels and the representativity ratio |ρ|/V of the AE parameters.
As can be seen from the tables, the concentration and kinetic indicators are the most valuable (Table 1), which is due to the optimization principles underlying the information and kinetic approach. Table 4 shows an example of how rock bursts can be predicted.

Table 4.
Rock burst risk assessment (local forecast).
4. Conclusions
We have demonstrated the efficiency of using an information and kinetic approach and a micromechanical model of time dependence of the AE parameters recorded after a man-made explosion for interpreting the results of recording AE signals in rock mass. Testing parameters have been substantiated that are connected with time until the moment of rock pressure manifestation, as well as the indicators reflecting the stress–strain parameters of a rock mass block. What makes the presented material original is that the previously formulated parameters XAE and WAE (concentration and kinetic indicators) that were used in testing objects of other types (welded structures, composite materials, pipelines, pressure vessels, etc.) have been successfully applied to rock burst risk assessment. The results produced confirm the universality of these parameters and the underlying principles of information optimization in testing. The difference between the presented research methodology and the previously published ones lies in changing the type of loading of the object under test by switching from uniform or sustained loading to unloading in the process of stress relaxation after a man-made explosion, changing the frequency range of signals and the type of equipment, and using a new mathematical model of the WAE parameter presented in the article. The article also contains new information on the statistical processing of experimental data, confirming that the concentration and kinetic indicators of strength are more informative compared to the energy indicators that are traditionally used.
Author Contributions
Conceptualization, V.V.N. and A.I.B.; methodology, V.V.N.; software, A.P.A.; validation, A.P.A.; formal analysis, V.V.N. and A.P.A.; resources, V.V.N.; data curation, V.V.N.; writing—original draft preparation, V.V.N.; writing—review and editing, A.I.B.; visualization, A.I.B. and A.P.A.; supervision, V.V.N.; funding acquisition, A.I.B. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partially funded by the Ministry of Science and Higher Education of the Russian Federation as part of the World-Class Research Center Program: Advanced Digital Technologies (contract no. 075-15-2022-311 dated 20 April 2022).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, J.; Zhang, W.; Ma, J. Experimental study on butterfly shape of failure zone and fractal characteristics of rock burst. Eng. Fail. Anal. 2022, 140, 106636. [Google Scholar] [CrossRef]
- Khayrutdinov, A.M.; Kongar-Syuryun, C.B.; Kowalik, T.; Tyulyaeva, Y.S. Stress-strain behavior control in rock mass using different-stregth backfill. Mining Inf. Anal. Bull. 2020, 10, 42–55. [Google Scholar] [CrossRef]
- Sidorov, D.V. Methodology of reducing rock bump hazard during room and rillar mining of north ural deep bauxite deposits. J. Min. Inst. 2017, 223, 58–69. [Google Scholar] [CrossRef]
- Ivanov, S.L.; Fadeev, D.V.; Kudryavtseva, R.-E.A. Peat mining, a look through the centuries. Quest Hist. 2022, 7, 45–63. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, J.; Pan, Y.; Yu, H. Experimental study on intensity and energy evolution of deep coal and gas outburst. Fuel 2022, 324, 124484. [Google Scholar] [CrossRef]
- Gendler, S.G.; Gabov, V.V.; Babyr, N.V.; Prokhorova, E.A. Justification of engineering solutions on reduction of occupational traumatism in coal longwalls. Mining Inf. Anal. Bull. 2022, 1, 5–19. [Google Scholar] [CrossRef]
- Song, D.; He, X.; Qiu, L.; Zhao, Y.; Cheng, X.; Wang, A. Study on real time dynamic monitoring and early warning technology of regional and local outburst danger. Meitan Kexue Jishu 2021, 49, 110–119. [Google Scholar] [CrossRef]
- Gendler, S.G.; Fazylov, I.R. Application efficiency of closed gathering system toward microclimate normalization in operating galleries in oil mines. Mining Inf. Anal. Bull. 2021, 9, 65–78. [Google Scholar] [CrossRef]
- Protosenya, A.G.; Stavrogin, A.N. Mechanics of Deformation and Destruction of Rocks; Nedra: Moscow, Russia, 1992; p. 224. [Google Scholar]
- Rybak, J.; Khayrutdinov, M.M.; Kuziev, D.A.; Kongar-Syuryun, C.B.; Babyr, N.V. Prediction of the geomechanical state of the rock mass when mining salt deposits with stowing. J. Min. Inst. 2022, 253, 61–70. [Google Scholar] [CrossRef]
- Mengel, D.A. The results of rock burst prediction on the sokolovskaya underground mining by the acoustic emission method. Mining Inf. Anal. Bull. 2020, 3–1, 149–160. [Google Scholar] [CrossRef]
- Shkuratnik, V.L.; Nikolenko, P.V. Using acoustic emission memory of composites in critical stress control in rock masses. J. Min. Sci. 2013, 49, 544–549. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Yu, M.; Li, X.; Hu, J.; Yang, H. Acoustic emission monitoring technology for coal and gas outburst. Energy Sci. Eng. 2019, 7, 443–456. [Google Scholar] [CrossRef]
- Li, M.; Su, C.; Li, G. Prediction of the stability of the loaded rock based on the acoustic emission characteristics of the loaded rock based on data mining. Shock. Vib. 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Du, S.; Feng, G.; Li, Z.; Sarkodie-Gyan, T.; Wang, J.; Ma, Z.; Li, W. Measurement and prediction of granite damage evolution in deep mine seams using acoustic emission. Meas. Sci. Technol. 2019, 30, 114002. [Google Scholar] [CrossRef]
- Clavijo, J.; Wang, H.; Sánchez, S. Observation of significant differences between electromagnetic and acoustic emissions during fracture processes: A study on rocks under compression loading. J. Phys. Conf. Ser. 2019, 1386, 012107. [Google Scholar] [CrossRef]
- Efimov, V.P. Effect of loading rate on fracture toughness within the kinetic concept of thermal fluctuation mechanism of rock failure. J. Min. Sci. 2016, 52, 274–278. [Google Scholar] [CrossRef]
- Wang, H.; Tang, L.; Ren, X.; Yang, A.; Niu, Y. Mechanism of rock deformation memory effect in low stress region and its memory fading. Rock Soil Mech. 2014, 35, 1007–1014. [Google Scholar]
- Nosov, V.V. Control of inhomogeneous materials strength by method of acoustic emission. J. Min. Inst. 2017, 226, 469–479. [Google Scholar] [CrossRef]
- FNiP, No. 505. Federal Norms and Regulations in the Field of Industrial Safety « Safety Rules for Mining Operations and Processing of Solid Minerals»; Federal Service for Environmental, Technological and Nuclear Supervision (Rostekhnadzor): Moscow, Russia, 2020. (In Russian)
- Kuksenko, V.S.; Makhmudov, K.F.; Mansurov, V.A.; Sultonov, U.; Rustamova, M.Z. Changes in structure of natural heterogenous materials under deformation. J. Min. Sci. 2009, 45, 355–358. [Google Scholar] [CrossRef]
- Shcherbakov, I.P.; Kuksenko, V.S.; Chmel’, A.E. Temperature dependence of microdamage accumulation in granite under impact fracture. J. Min. Sci. 2013, 49, 919–925. [Google Scholar] [CrossRef]
- Kocharyan, G.G.; Ostapchuk, A.A. Acoustic emission during different-type inter-block movements. J. Min. Sci. 2015, 51, 1–9. [Google Scholar] [CrossRef]
- Krivosheev, I.A.; Ivanov, G.A. Statistical method for processing acoustic emission signals in a rock massif. Defektoskopiya 2002, 2, 62–65. [Google Scholar]
- Nagovitsyn, Y.N.; Kakoshina, L.V. Regional rockburst hazard forecast at the mines of the Polar Division of PJSC MMC Norilsk Nickel. Development prospects. In Proceedings of the International Scientific and Practical Conference Dedicated to the 110th Anniversary of the Mining Faculty, Mining in the 21st Century: Technology, Science, Education, Saint Petersburg Mining University, Saint Petersburg, Russia, 28–29 October 2015. [Google Scholar]
- Gilyarov, V.L.; Damaskinskaya, E.E.; Kadomtsev, A.G.; Rasskazov, I.Y. Analysis of statistic parameters of geoacoustic monitoring data for the antey uranium deposit. J. Min. Sci. 2014, 50, 443–447. [Google Scholar] [CrossRef]
- Oparin, V.N.; Yemanov, A.F.; Vostrikov, V.I.; Tsibizov, L.V. Kinetics of seismic emission in coal mines in kuzbass. J. Min. Sci. 2013, 4, 40–45. [Google Scholar] [CrossRef]
- Rasskazov, I.Y.; Kursakin, G.A. Features of seismoacoustic control of the geomechanical state of a rock mass in geodynamically active areas. News High Inst. Min. Mag. 2006, 6, 22–28. [Google Scholar]
- Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Chen, Y. Acoustic emission characteristics of red sandstone specimens under uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2018, 51, 969–988. [Google Scholar] [CrossRef]
- Archer, J.W.; Dobbs, M.R.; Aydin, A.; Reeves, H.J.; Prance, R.J. Measurement and correlation of acoustic emissions and pressure stimulated voltages in rock using an electric potential sensor. Int. J. Rock Mech. Min. Sci. 2016, 89, 26–33. [Google Scholar] [CrossRef]
- Nosov, V.V. Bump hazard evaluation of a rock mass area as a result of its seismic acoustic activity registration. J. Min. Inst. 2015, 216, 62–75. (In Russian) [Google Scholar]
- Nosov, V.V.; Chaplin, I.E.; Gilyazetdinov, E.R.; Grigoriev, E.V.; Pavlenko, I.A. Micromechanics, nanophysics and non-destructive testing of the strength of structural materials. Mater. Phys. Mech. 2019, 42, 808–824. [Google Scholar] [CrossRef]
- Regel’, V.R.; Slutsker, A.I.; Tomashevskii, E.E. The kinetic nature of the strength of solids. Sov. Phys. Uspekhi 1972, 15, 45–65. [Google Scholar] [CrossRef]
- Grigorev, E.; Nosov, V. Improving quality control methods to test strengthening technologies: A multilevel model of acoustic pulse flow. Appl. Sci. 2022, 12, 4549. [Google Scholar] [CrossRef]
- Trapeznikov, Y.A.; Manzhikov, B.T.; Bogomolov, L.M. Amplitude spectra of acoustic emission under stepwise loading of rocks. Volc. Seism. 2000, 2, 75–78. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).