Changes in Terrestrial Evaporation across Poland over the Past Four Decades Dominated by Increases in Summer Months
Abstract
1. Introduction
- (1)
- Is the ET across Poland increasing or decreasing at annual and monthly time scales, and, if this is the case, what is the magnitude of such temporal trends?
- (2)
- Which components of ET are contributing to the country-scale inter-annual trend?
- (3)
- What are the monthly spatial patterns of the ET trends and regions of significantly increasing/decreasing ET?
2. Materials and Methods
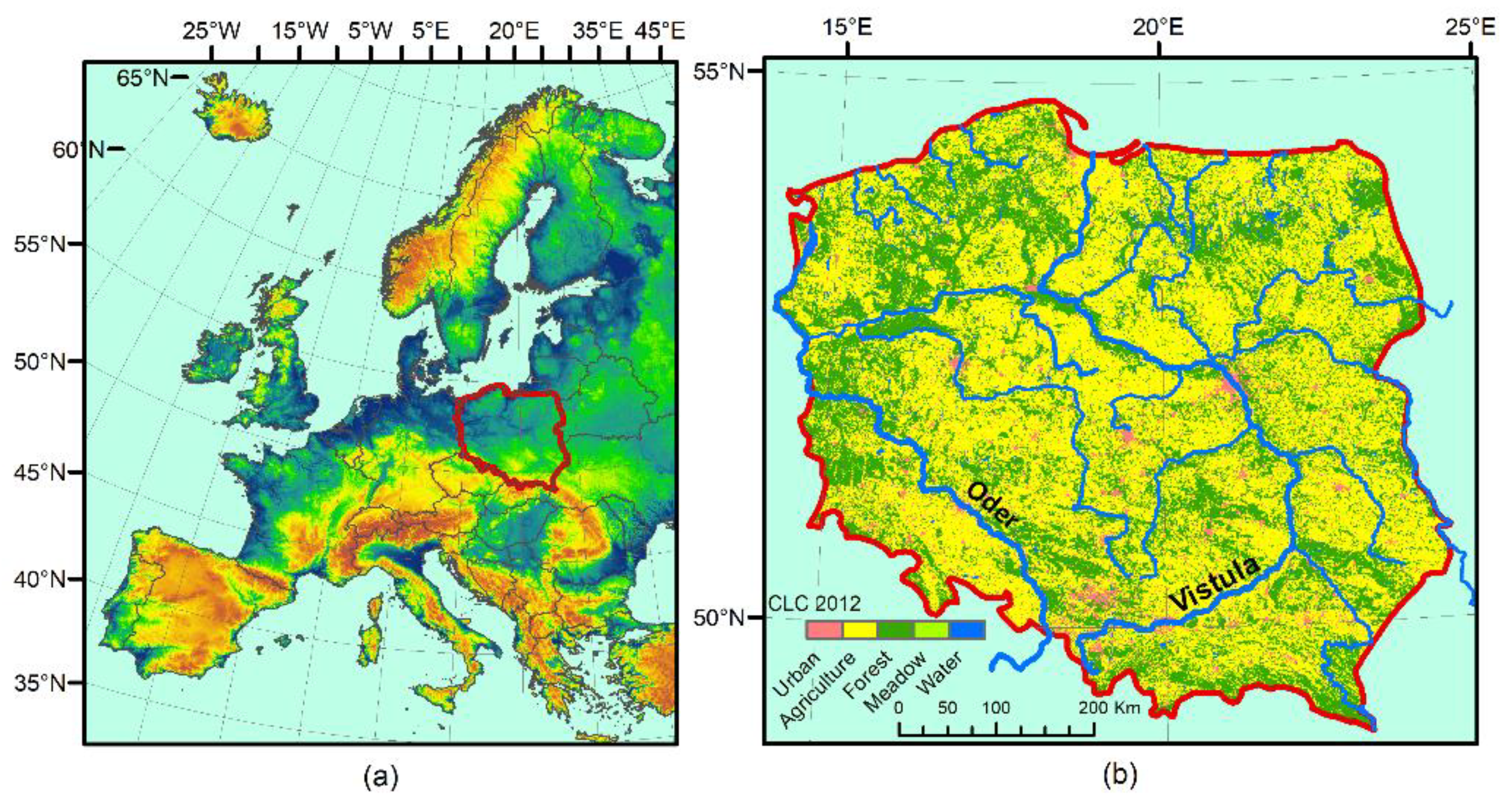
2.1. Basic Geographical Characteristics of Poland
2.2. Data
2.3. Methods
3. Results
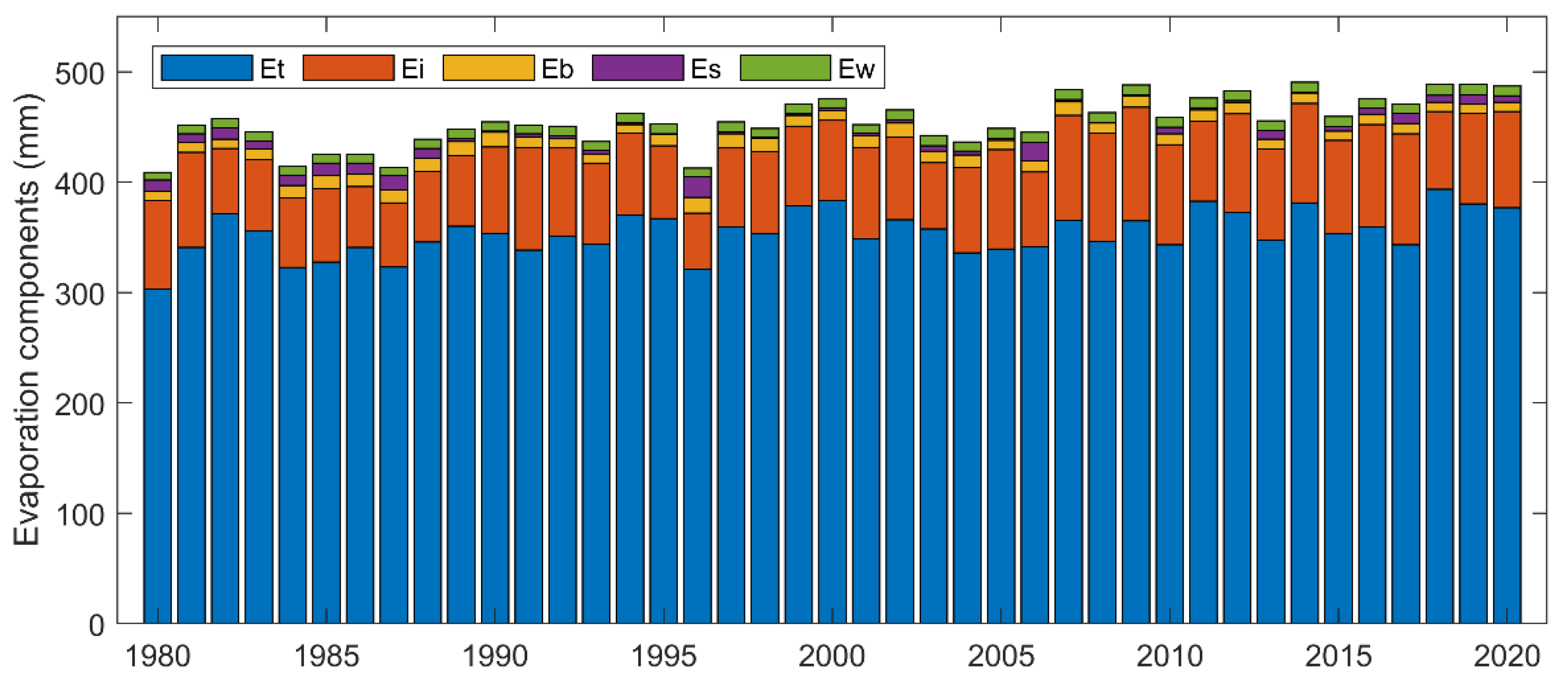
3.1. Country Scale, Inter-Annual Terrestrial Evaporation over the Period 1980–2020
3.2. Country-Scale, Monthly Terrestrial Evaporation over the Multi-Year Period 1980–2020
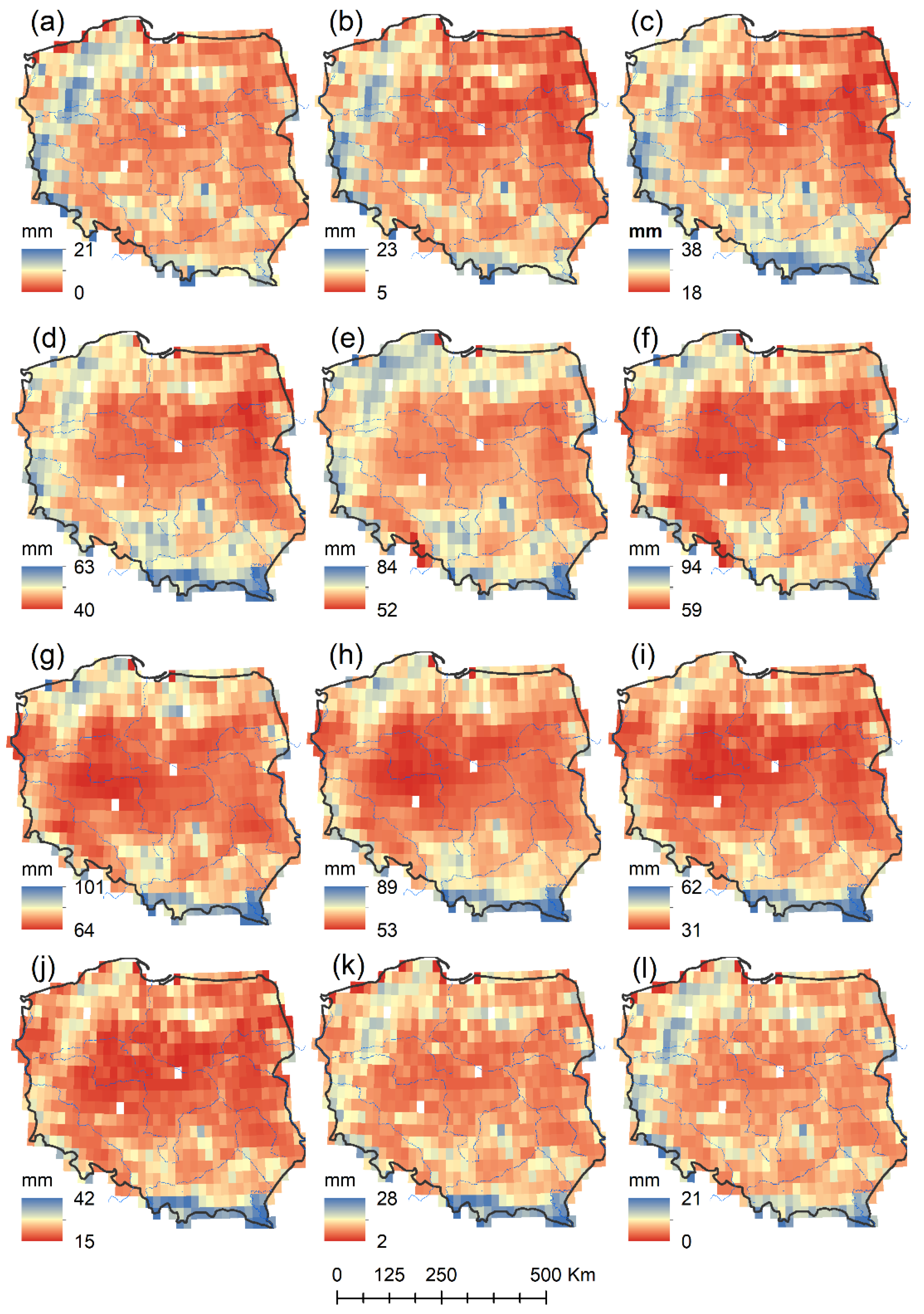
3.3. Monthly and Annual Spatial Patterns of Terrestrial Evaporation
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miralles, D.G.; Brutsaert, W.; Dolman, A.J.; Gash, J.H. On the Use of the Term “Evapotranspiration”. Water Resour. Res. 2020, 56, e2020WR028055. [Google Scholar] [CrossRef]
- Paschalis, A.; Fatichi, S.; Pappas, C.; Or, D. Covariation of vegetation and climate constrains present and future T/ET variability. Environ. Res. Lett. 2018, 13, 104012. [Google Scholar] [CrossRef]
- Wang-Erlandsson, L.; Van Der Ent, R.J.; Gordon, L.J.; Savenije, H.H.G. Contrasting roles of interception and transpiration in the hydrological cycle—Part 1: Temporal characteristics over land. Earth Syst. Dyn. 2014, 5, 441–469. [Google Scholar] [CrossRef]
- Laguë, M.M.; Pietschnig, M.; Ragen, S.; Smith, T.A.; Battisti, D.S. Terrestrial Evaporation and Global Climate: Lessons from Northland, a Planet with a Hemispheric Continent. J. Clim. 2021, 34, 2253–2276. [Google Scholar] [CrossRef]
- Zhan, S.; Song, C.; Wang, J.; Sheng, Y.; Quan, J. A Global Assessment of Terrestrial Evapotranspiration Increase Due to Surface Water Area Change. Earth’s Futur. 2019, 7, 266–282. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W.; Hong, Y.; Gourley, J.J.; Yu, Z. Vegetation Greening and Climate Change Promote Multidecadal Rises of Global Land Evapotranspiration. Sci. Rep. 2015, 5, 15956. [Google Scholar] [CrossRef]
- Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef]
- Pan, S.; Pan, N.; Tian, H.; Friedlingstein, P.; Sitch, S.; Shi, H.; Arora, V.K.; Haverd, V.; Jain, A.K.; Kato, E.; et al. Evaluation of global terrestrial evapotranspiration using state-of-the-art approaches in remote sensing, machine learning and land surface modeling. Hydrol. Earth Syst. Sci. 2020, 24, 1485–1509. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Wang, R.; Gentine, P.; Yin, J.; Chen, L.; Chen, J.; Li, L. Long-term relative decline in evapotranspiration with increasing runoff on fractional land surfaces. Hydrol. Earth Syst. Sci. 2021, 25, 3805–3818. [Google Scholar] [CrossRef]
- Teuling, A.J.; Hirschi, M.; Ohmura, A.; Wild, M.; Reichstein, M.; Ciais, P.; Buchmann, N.; Ammann, C.; Montagnani, L.; Richardson, A.D.; et al. A regional perspective on trends in continental evaporation. Geophys. Res. Lett. 2009, 36, L02404. [Google Scholar] [CrossRef]
- Vadeboncoeur, M.A.; Green, M.B.; Asbjornsen, H.; Campbell, J.L.; Adams, M.B.; Boyer, E.W.; Burns, D.A.; Fernandez, I.J.; Mitchell, M.J.; Shanley, J.B. Systematic variation in evapotranspiration trends and drivers across the Northeastern United States. Hydrol. Process. 2018, 32, 3547–3560. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Sun, S.; Fiifi Tawia Hagan, D.; Chen, T.; Dolman, H.; Liu, Y. Long-term changes in evapotranspiration over China and attribution to climatic drivers during 1980–2010. J. Hydrol. 2021, 595, 126037. [Google Scholar] [CrossRef]
- Zhang, F.; Geng, M.; Wu, Q.; Liang, Y. Study on the spatial-temporal variation in evapotranspiration in China from 1948 to 2018. Sci. Rep. 2020, 10, 17139. [Google Scholar] [CrossRef]
- Teuling, A.J.; De Badts, E.A.G.; Jansen, F.A.; Fuchs, R.; Buitink, J.; Van Dijke, A.J.H.; Sterling, S.M. Climate change, reforestation/afforestation, and urbanization impacts on evapotranspiration and streamflow in Europe. Hydrol. Earth Syst. Sci. 2019, 23, 3631–3652. [Google Scholar] [CrossRef]
- Blyth, E.M.; Martínez-de la Torre, A.; Robinson, E.L. Trends in evapotranspiration and its drivers in Great Britain: 1961 to 2015. Prog. Phys. Geogr. 2019, 43, 666–693. [Google Scholar] [CrossRef]
- Ziche, D.; Riek, W.; Russ, A.; Hentschel, R.; Martin, J. Water budgets of managed forests in northeast germany under climate change—Results from a model study on forest monitoring sites. Appl. Sci. 2021, 11, 2403. [Google Scholar] [CrossRef]
- Malinin, V.N.; Gordeeva, S.M.; Mitina, Y.V.; Kuleshova, A.V. Interannual variability of moistening in the European Russia. Russ. J. Earth Sci. 2021, 21, 1. [Google Scholar] [CrossRef]
- Dezsi, Ş.; Mîndrescu, M.; Petrea, D.; Rai, P.K.; Hamann, A.; Nistor, M.M. High-resolution projections of evapotranspiration and water availability for Europe under climate change. Int. J. Climatol. 2018, 38, 3832–3841. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Hursh, A.; Ballantyne, A.; Cooper, L.; Maneta, M.; Kimball, J.; Watts, J. The sensitivity of soil respiration to soil temperature, moisture, and carbon supply at the global scale. Glob. Chang. Biol. 2017, 23, 2090–2103. [Google Scholar] [CrossRef]
- Liu, X.; Biondi, F. Transpiration drivers of high-elevation five-needle pines (Pinus longaeva and Pinus flexilis) in sky-island ecosystems of the North American Great Basin. Sci. Total Environ. 2020, 739, 139861. [Google Scholar] [CrossRef] [PubMed]
- Łabędzki, L.; Bąk, B.; Smarzyńska, K. Spatio-temporal variability and trends of Penman-Monteith reference evapotranspiration (FAO-56) in 1971-2010 under climatic conditions of Poland. Polish J. Environ. Stud. 2014, 23, 2083–2091. [Google Scholar] [CrossRef]
- Bogawski, P.; Bednorz, E. Atmospheric conditions controlling extreme summertime evapotranspiration in Poland (central Europe). Nat. Hazards 2016, 81, 55–69. [Google Scholar] [CrossRef]
- Szwed, M. Projections of changes of areal evapotranspiration for different land-use units in the Wielkopolska Region (Poland). Theor. Appl. Climatol. 2017, 130, 291–304. [Google Scholar] [CrossRef][Green Version]
- Okoniewska, M.; Szuminska, D. Changes in potential evaporation in the years 1952–2018 in North-Western Poland in terms of the impact of climatic changes on hydrological and hydrochemical conditions. Water 2020, 12, 877. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Song, X.P.; Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Tyukavina, A.; Vermote, E.F.; Townshend, J.R. Global land change from 1982 to 2016. Nature 2018, 560, 639–643. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Xia, Y.; Ferreira, V.G.; Liu, S.; Wang, K.; Yao, Y.; Zhang, X.; Zhao, C. Evaluation of twelve evapotranspiration products from machine learning, remote sensing and land surface models over conterminous United States. J. Hydrol. 2019, 578, 124105. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Wang, J.; Feng, J.; Zhang, M. A comprehensive evaluation of five evapotranspiration datasets based on ground and grace satellite observations: Implications for improvement of evapotranspiration retrieval algorithm. Remote Sens. 2021, 13, 2414. [Google Scholar] [CrossRef]
- Kim, S.; Anabalón, A.; Sharma, A. An assessment of concurrency in evapotranspiration trends across multiple global datasets. J. Hydrometeorol. 2021, 22, 231–244. [Google Scholar] [CrossRef]
- Dembélé, M.; Ceperley, N.; Zwart, S.J.; Salvadore, E.; Mariethoz, G.; Schaefli, B. Potential of satellite and reanalysis evaporation datasets for hydrological modelling under various model calibration strategies. Adv. Water Resour. 2020, 143, 103667. [Google Scholar] [CrossRef]
- Roy, T.; Gupta, H.V.; Serrat-Capdevila, A.; Valdes, J.B. Using satellite-based evapotranspiration estimates to improve the structure of a simple conceptual rainfall-runoff model. Hydrol. Earth Syst. Sci. 2017, 21, 879–896. [Google Scholar] [CrossRef]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Lockhoff, M.; Zolina, O.; Simmer, C.; Schulz, J. Representation of precipitation characteristics and extremes in regional reanalyses and satellite-and gauge-based estimates over western and central Europe. J. Hydrometeorol. 2019, 20, 1123–1145. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.D. Testing E-OBS European high-resolution gridded data set of daily precipitation and surface temperature. J. Geophys. Res. Atmos. 2009, 114, D21101. [Google Scholar] [CrossRef]
- Gampe, D.; Ludwig, R. Evaluation of gridded precipitation data products for hydrological applications in complex topography. Hydrology 2017, 4, 53. [Google Scholar] [CrossRef]
- Berezowski, T.; Szczeniak, M.; Kardel, I.; Michalowski, R.; Okruszko, T.; Mezghani, A.; Piniewski, M. CPLFD-GDPT5: High-resolution gridded daily precipitation and temperature data set for two largest Polish river basins. Earth Syst. Sci. Data 2016, 8, 127–139. [Google Scholar] [CrossRef]
- Piniewski, M.; Szcześniak, M.; Kardel, I.; Chattopadhyay, S.; Berezowski, T. G2DC-PL+: A gridded 2 km daily climate dataset for the union of the Polish territory and the Vistula and Odra basins. Earth Syst. Sci. Data 2021, 13, 1273–1288. [Google Scholar] [CrossRef]
- McDonald, J.E. On the Ratio of Evaporation to Precipitation1. Bull. Am. Meteorol. Soc. 1961, 42, 185–189. [Google Scholar] [CrossRef][Green Version]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. R. Neth. Acad. Sci. 1950, 53, 386–392, 521–525, 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Radziejewski, M.; Kundzewicz, Z.W. Detectability of changes in hydrological records. Hydrol. Sci. J. 2004, 49, 39–52. [Google Scholar] [CrossRef]
- Greene, C.A.; Thirumalai, K.; Kearney, K.A.; Delgado, J.M.; Schwanghart, W.; Wolfenbarger, N.S.; Thyng, K.M.; Gwyther, D.E.; Gardner, A.S.; Blankenship, D.D. The Climate Data Toolbox for MATLAB. Geochem. Geophys. Geosyst. 2019, 20, 3774–3781. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Robson, A.J. Change detection in hydrological records—A review of the methodology/Revue méthodologique de la détection de changements dans les chroniques hydrologiques. Hydrol. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- Radziejewski, M.; Kundzewicz, Z.W. Development, Use and Application of the Hydrospect Data Analysis System for the Detection of Changes in Hydrological Time-Series for Use in WCP-Water and National Hydrological Services; WCASP-65; WMO: Geneva, Switzerland, 2004; pp. 1–44. [Google Scholar]
- Kolecka, N. Greening trends and their relationship with agricultural land abandonment across Poland. Remote Sens. Environ. 2021, 257, 112340. [Google Scholar] [CrossRef]
- Dębski, K. Hydrologia Kontynentalna. Cz. II. Fizyka Wody, Opady Atmosferyczne i Parowanie; Wydawnictwa Komunikacyjne: Warszawa, Poland, 1959; pp. 1–547. [Google Scholar]





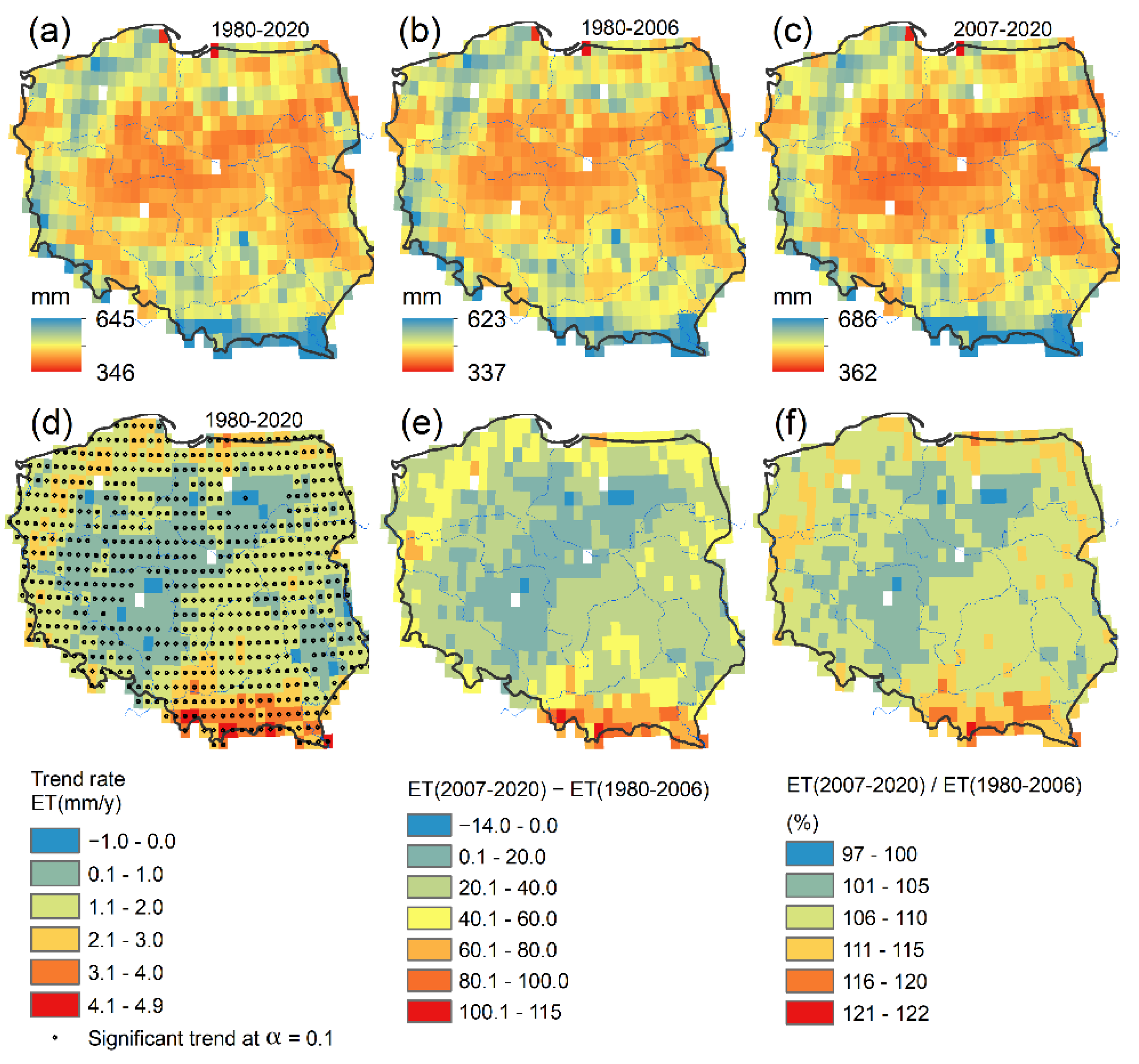
| Month | Percent of Area with Increasing ET Trend % | Percent of Area with Decreasing ET Trend % | Percent of Area with No Changes in ET % |
|---|---|---|---|
| January | 58 | 0 | 42 |
| February | 30 | 0 | 70 |
| March | 5 | 9 | 86 |
| April | 22 | 7 | 71 |
| May | 16 | 2 | 82 |
| June | 96 | 0 | 4 |
| July | 89 | 0 | 11 |
| August | 84 | 0 | 16 |
| September | 75 | 0 | 25 |
| October | 35 | 0 | 65 |
| November | 31 | 0 | 69 |
| December | 24 | 4 | 72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somorowska, U. Changes in Terrestrial Evaporation across Poland over the Past Four Decades Dominated by Increases in Summer Months. Resources 2022, 11, 6. https://doi.org/10.3390/resources11010006
Somorowska U. Changes in Terrestrial Evaporation across Poland over the Past Four Decades Dominated by Increases in Summer Months. Resources. 2022; 11(1):6. https://doi.org/10.3390/resources11010006
Chicago/Turabian StyleSomorowska, Urszula. 2022. "Changes in Terrestrial Evaporation across Poland over the Past Four Decades Dominated by Increases in Summer Months" Resources 11, no. 1: 6. https://doi.org/10.3390/resources11010006
APA StyleSomorowska, U. (2022). Changes in Terrestrial Evaporation across Poland over the Past Four Decades Dominated by Increases in Summer Months. Resources, 11(1), 6. https://doi.org/10.3390/resources11010006






