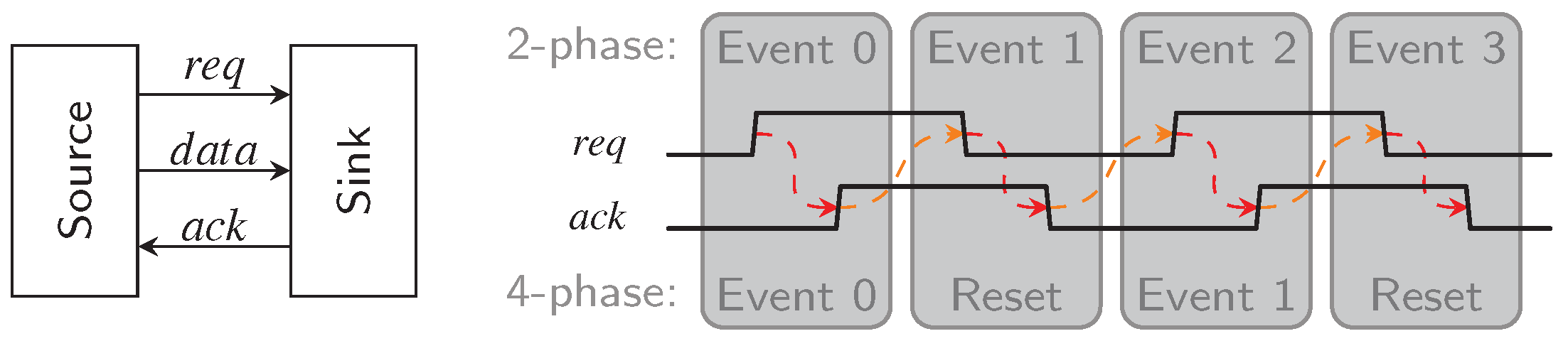
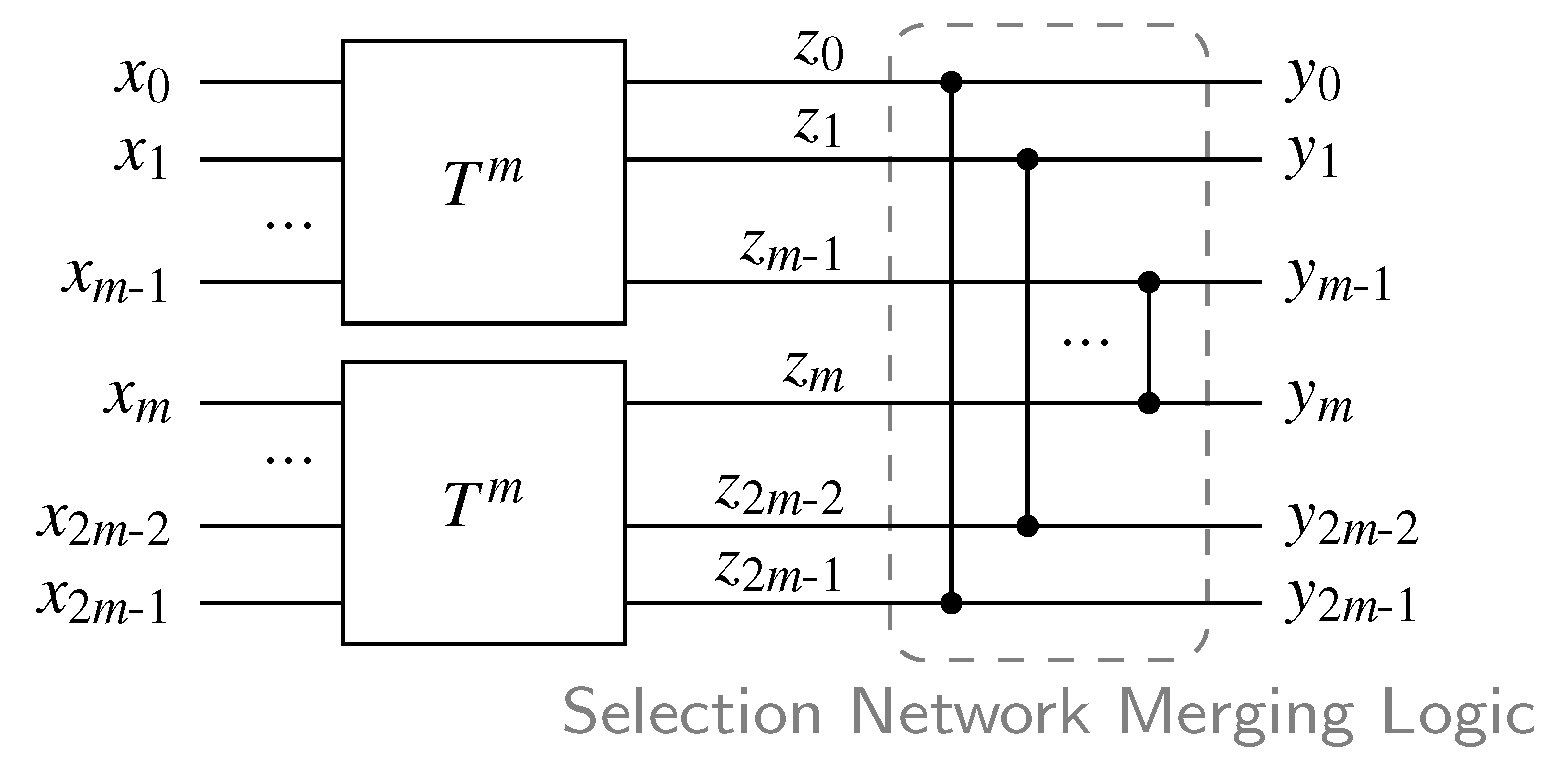
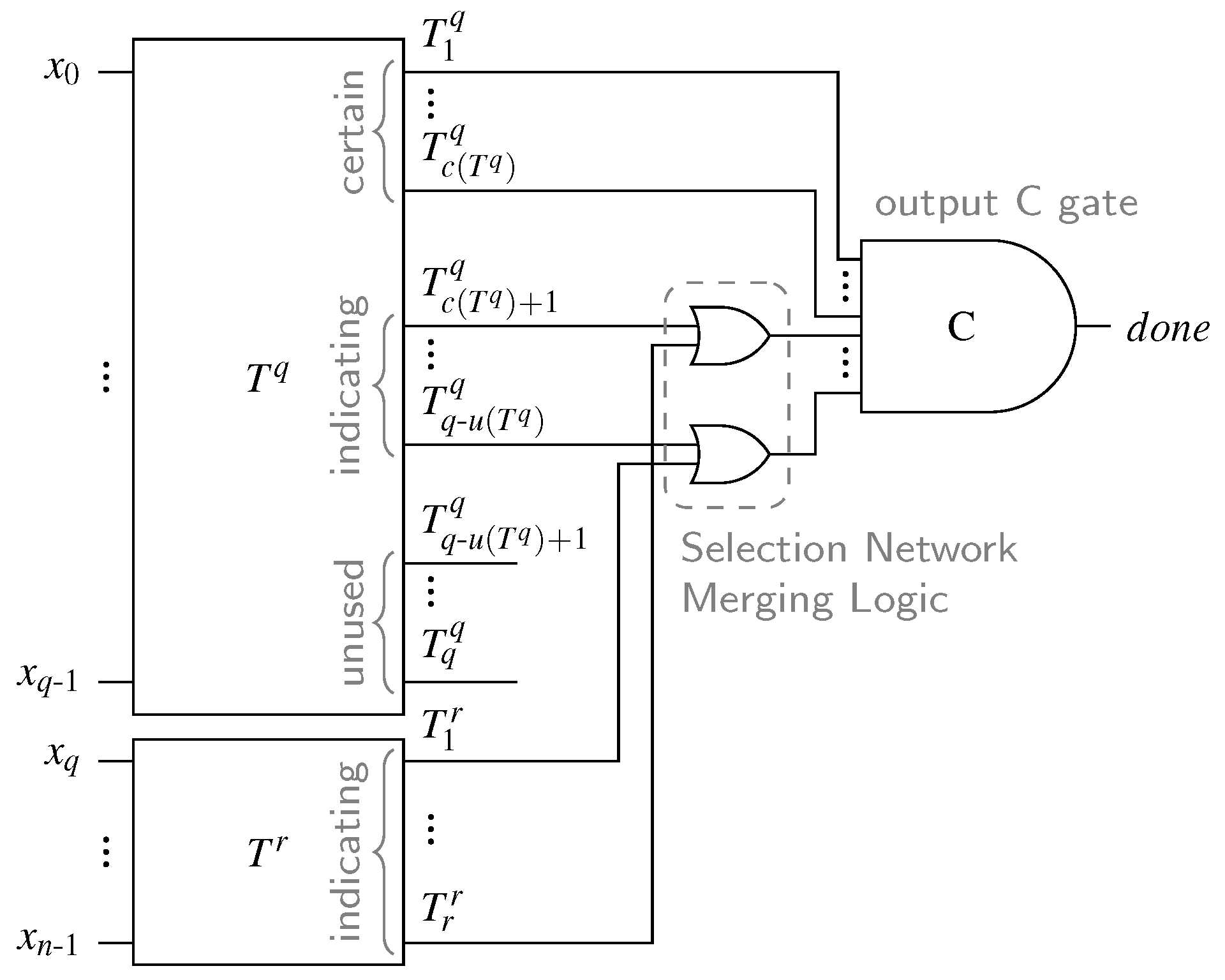
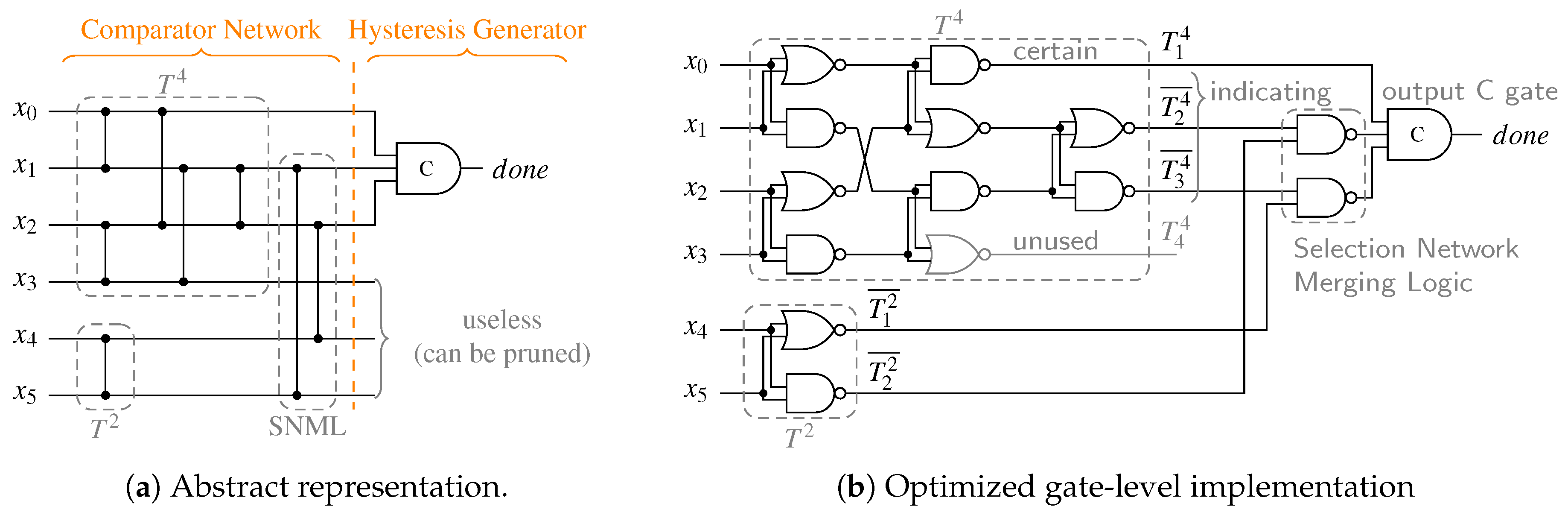
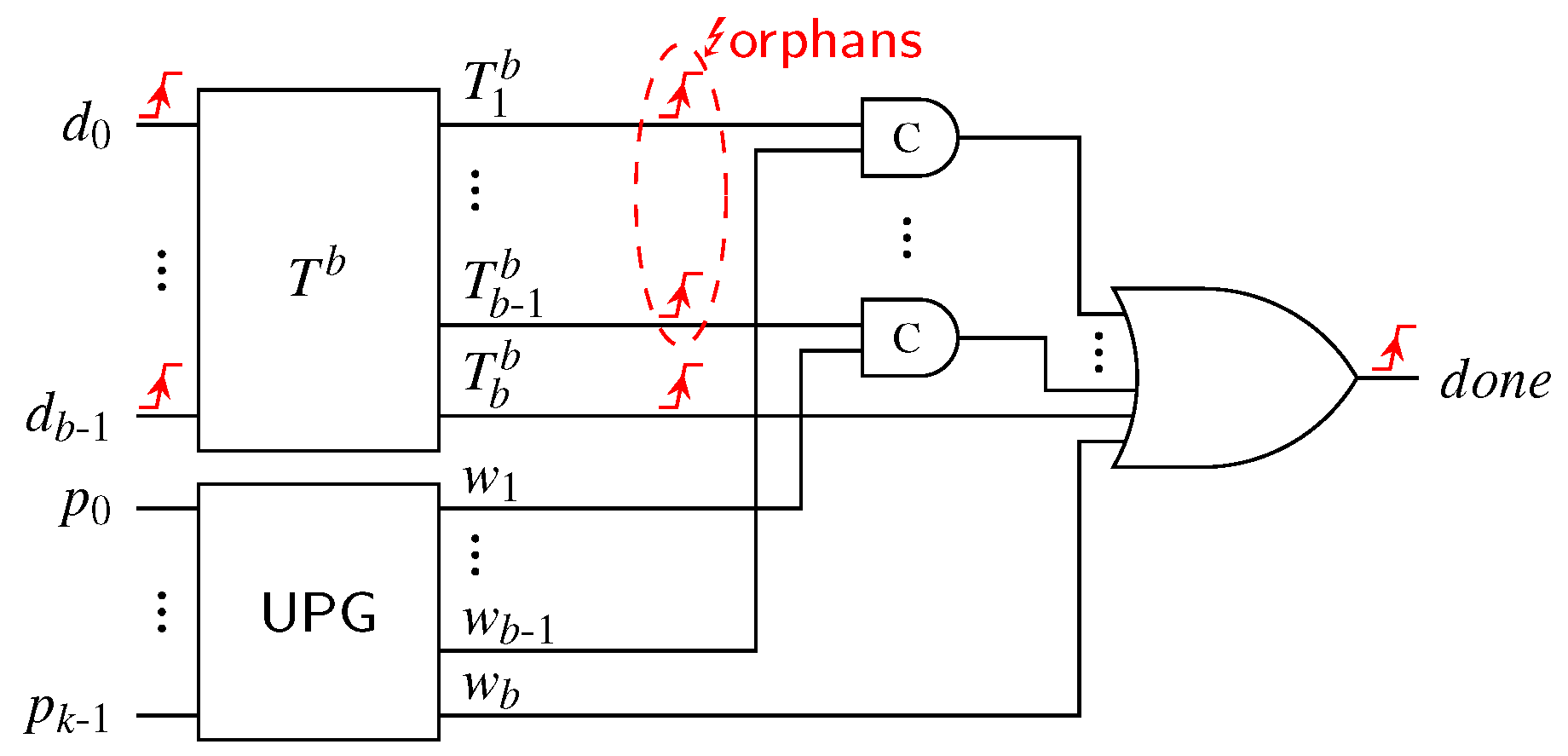
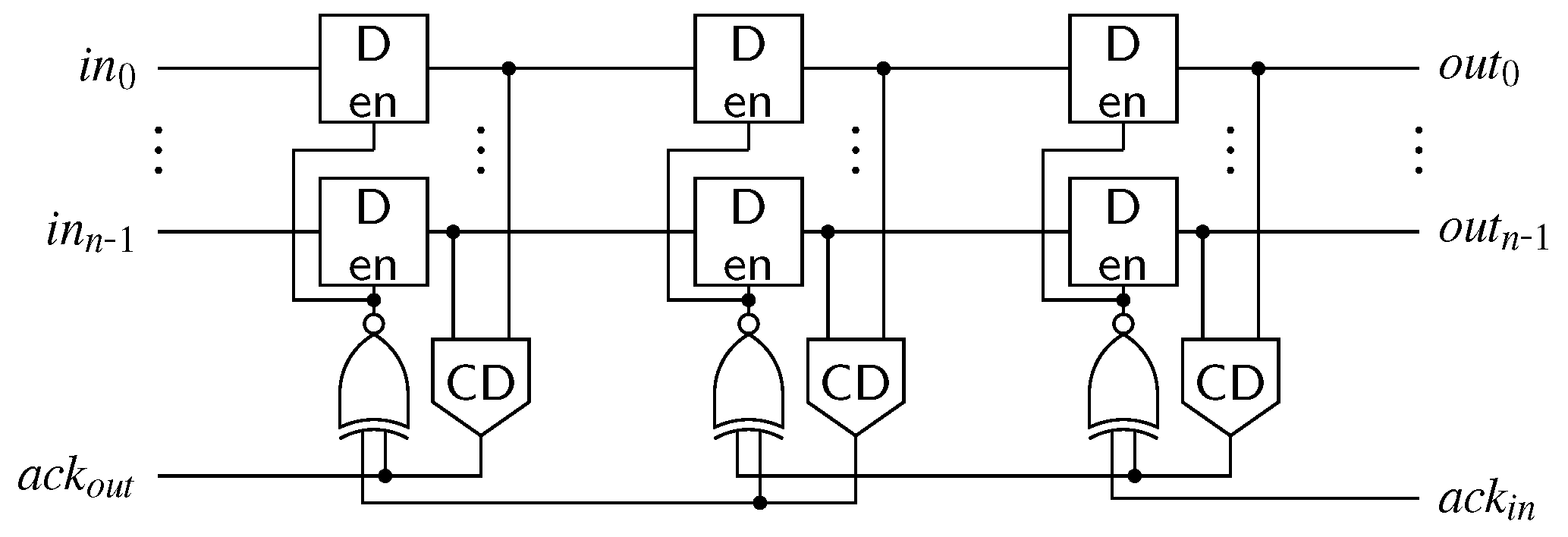
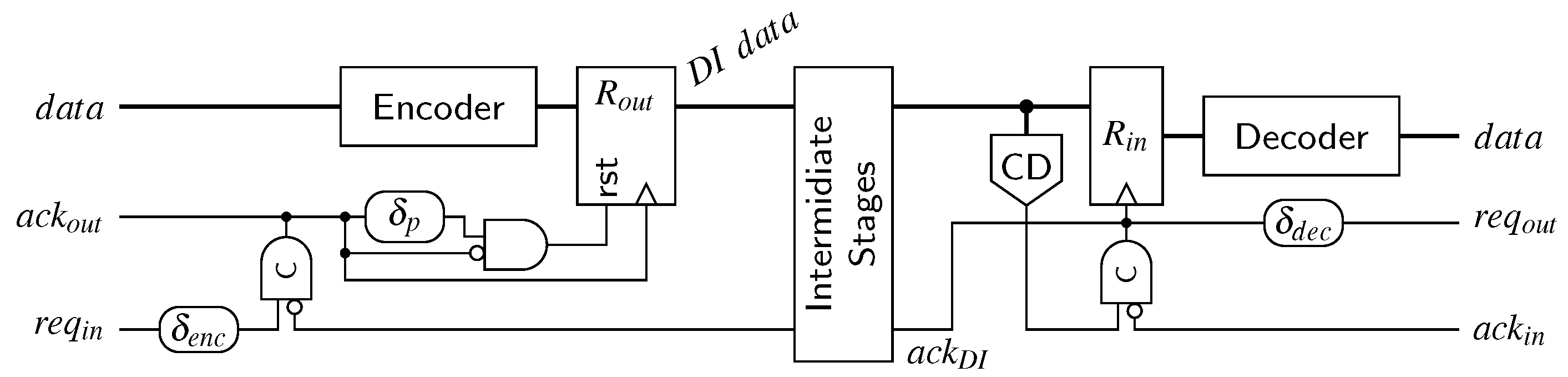
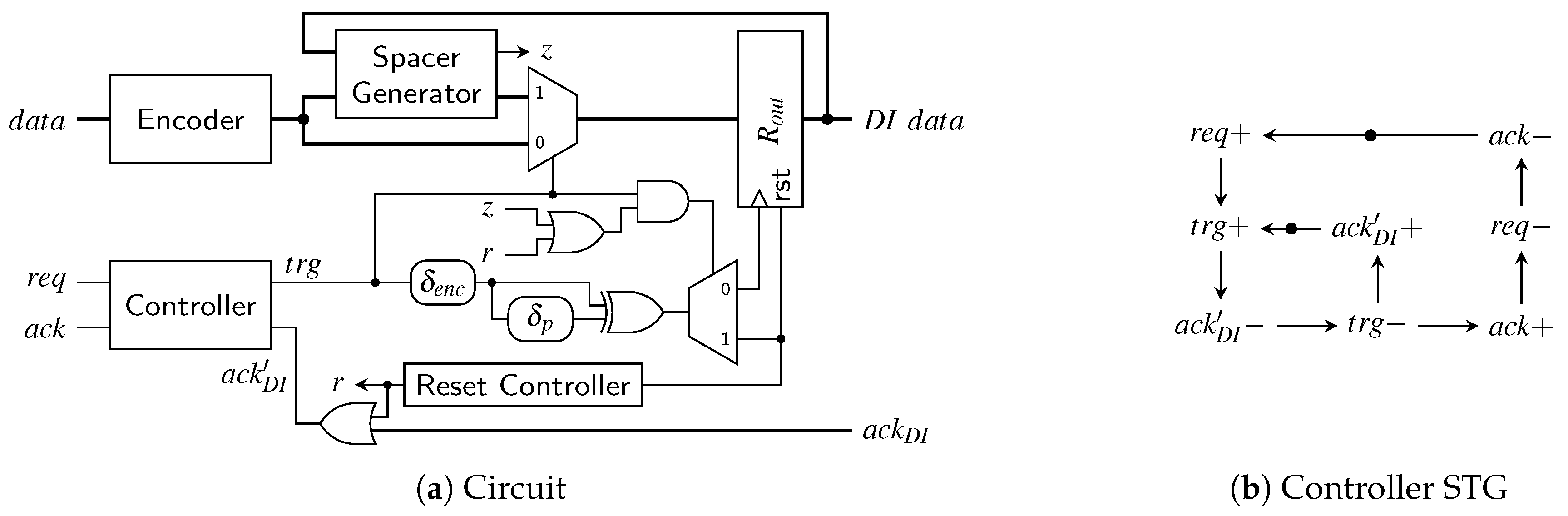
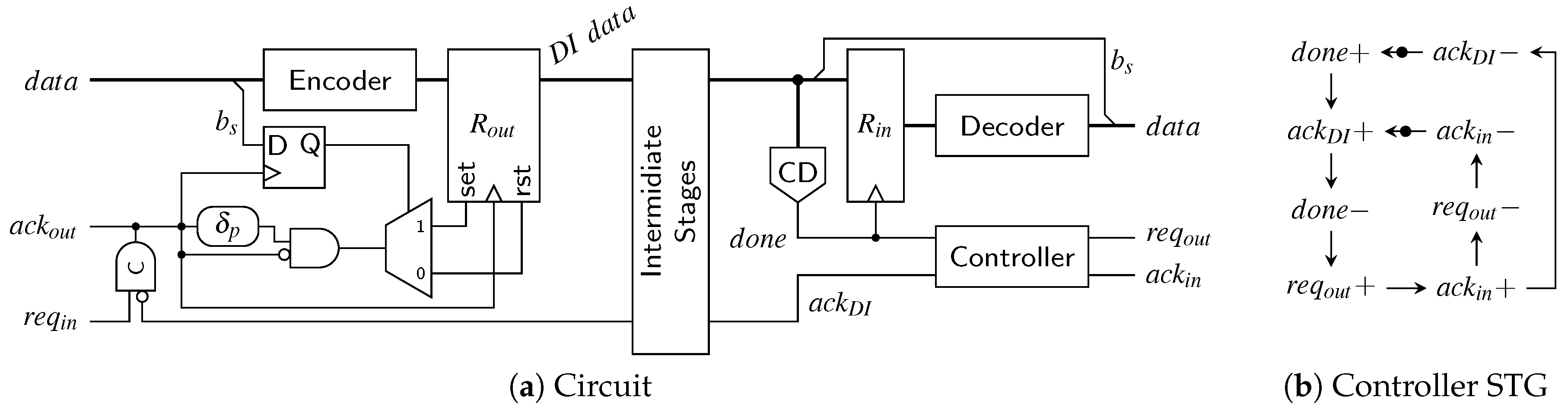
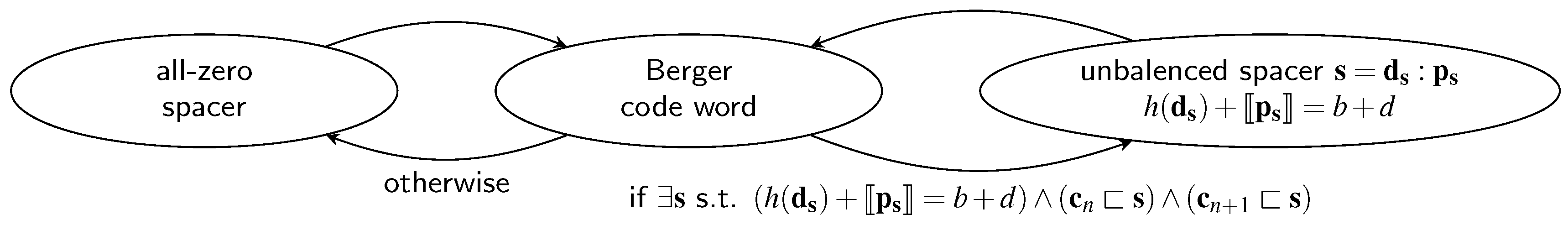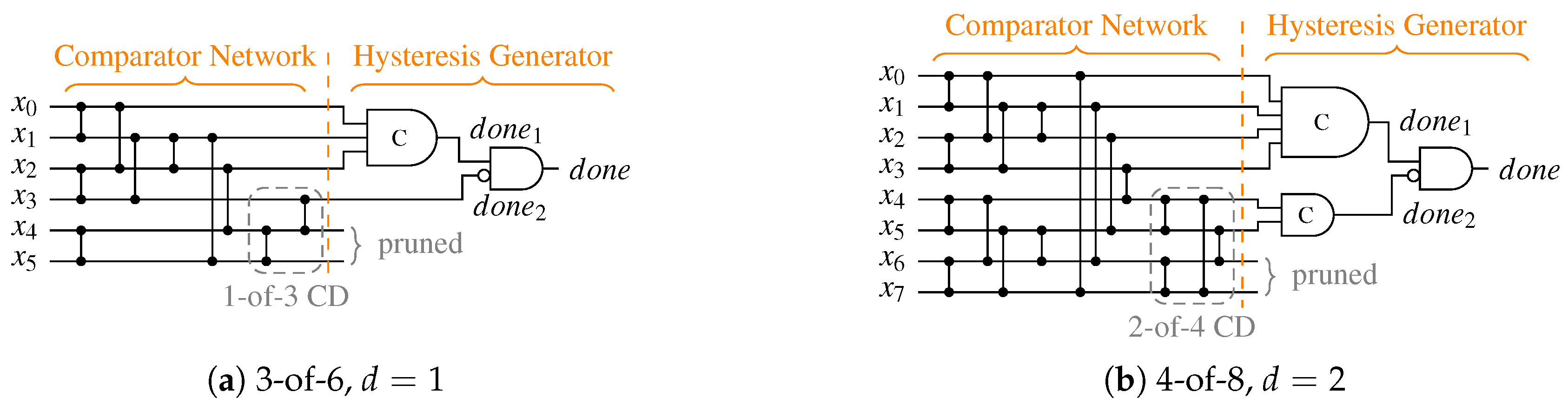There is no single, globally optimum solution for a DI protocol and encoding. Each choice has its specific place within the parameter space spanned by coding efficiency, power metric, area overhead, and data throughput. Ultimately, the application needs determine the most desirable region within this space. In the previous sections we have already investigated coding efficiency and power metric. While that was possible on a purely abstract level, area overhead and data throughput will be studied in this section, based on implementation examples.
7.1. Area Analysis
The synthesis results and area estimations in this section are generated using the NanGate 45 nm Open Cell Library. However, to abstract away from the library details, we use the gate equivalents (GE) metric, which relates the actual area to the one of a single 2-input NAND gate. Encoders and decoders have been synthesized from VHDL descriptions with the Synopsys Design Compiler, with high effort on area optimization (we only consider the pre-layout results for our analysis). The CDs are already generated on the gate level by our CD construction approach, hence no logic synthesis is required to estimate their area overhead. Since the library does not contain C gates, we assumed an area overhead of 3 GE (12 transistors) for a 2-input version of this gate [
23]. For multi-input C gates, we further assume an implementation using a single 2-input C gate (as state-holding element) which is set and reset with two carefully routed AND/OR networks.
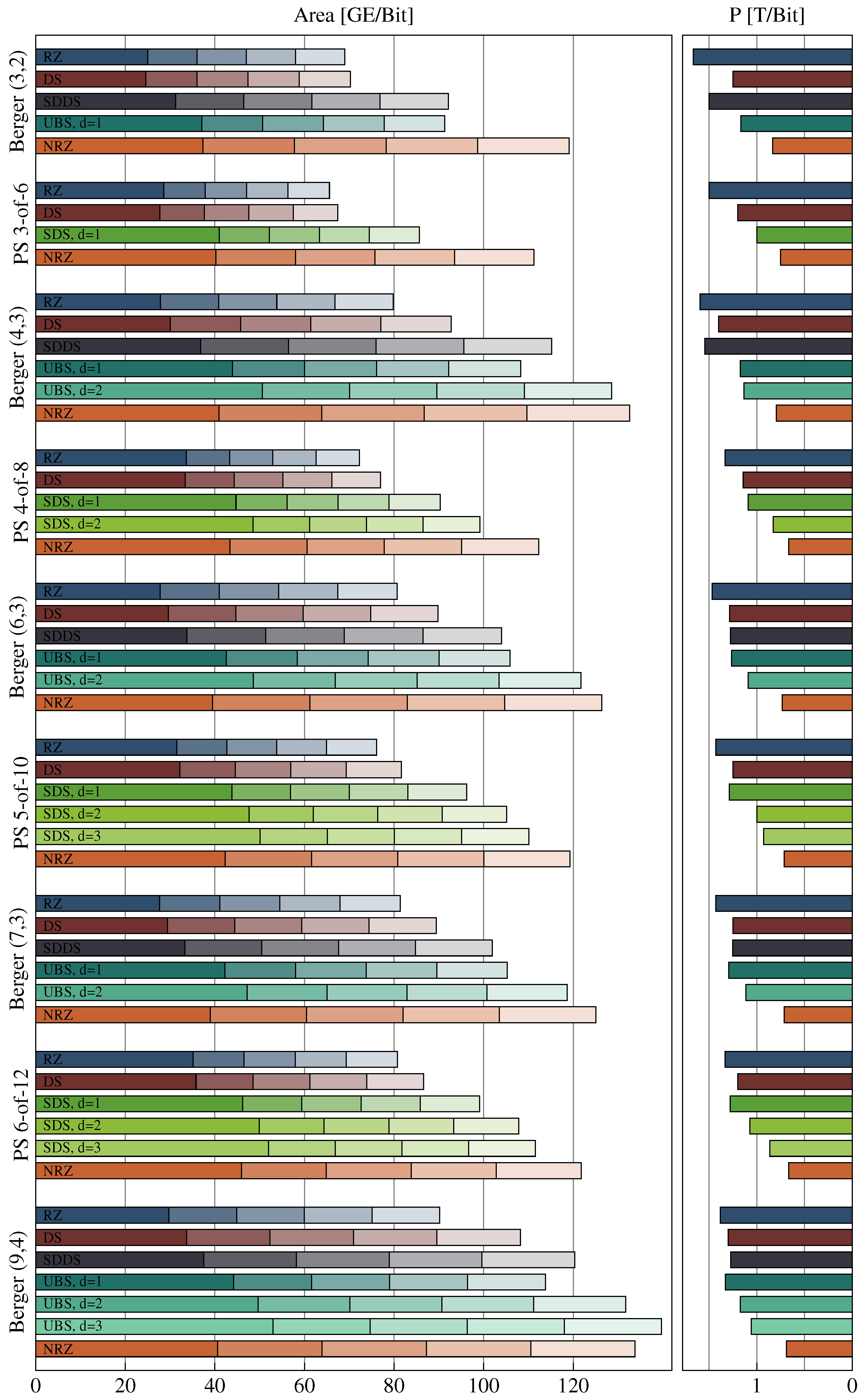
Table 8 lists the hardware costs for the encoders and decoders for all codes (and protocols) analyzed in this paper. Recall that the decoders are always the same regardless of the protocol, hence the table only contains one column for their overhead.
Table 9 provides the accompanying information for the respective CDs. The numbers in parentheses in the Berger code rows denote the number of data bits
b and parity bits
k, respectively. All values given use the GE/bit metric, because this makes it easier to compare code with different bit widths.
Let us first concentrate on the encoders and decoders. For the RZ and the NRZ protocols, it can be seen that the encoders for the PSCWCs are always more expensive than for a Berger code with the same bit width. Furthermore, since Berger codes are systematic no decoders are required. However, the table also shows that the PSCWCs codes generally have a better coding efficiency
R (except for the 5-of-10 and 7-bit Berger code) and as can be seen in
Table 9 also have smaller CDs. The decoders for the PSCWCs are also considerably simpler than their respective encoders.
The values for the SDS, UBS, and SDDS protocols also include the logic for the spacer generation. The encoder costs for the SDS and UBS protocol require very similar hardware efforts for codes with a certain bit width. This also holds true for different values of the parameter d. It is obvious that these protocols require a very large amount of additional logic when compared to (simple) RZ or even NRZ encoders. However, their CD costs are still below that of NRZ protocol. Another interesting fact is that the encoders for the SDDS protocol are only marginally more expensive than the ones for the RZ protocol.
Please note that we did not include the encoding costs for the DS protocol. Recall that this protocol basically uses the exact same encoder as the RZ protocol but can encode one additional bit via the use of a special output register. Since this table does not include the costs for the output register, we did not include the values for the DS protocol because they would give a skewed picture of the actual costs. Note that to some extent this argument also applies to the SDDS protocol, since it also requires a special output register.
The CD implementation costs in
Table 9 always list two values per entry. The first one corresponds to the combinational costs, i.e., mainly the CNs and the XORs for the NRZ CDs, while the second includes the costs for the C gates and the latches in case of the NRZ CDs. It is immediately apparent that the NRZ CDs require the most logic, since the 2-phase/4-phase wrapper circuit basically adds an additional D latch and XOR gate for every input rail. Also notice the entries for the DS and SDDS protocols. These protocols use the exact same CD. However, the values for the DS protocol are smaller because one additional bit of data can be transported.
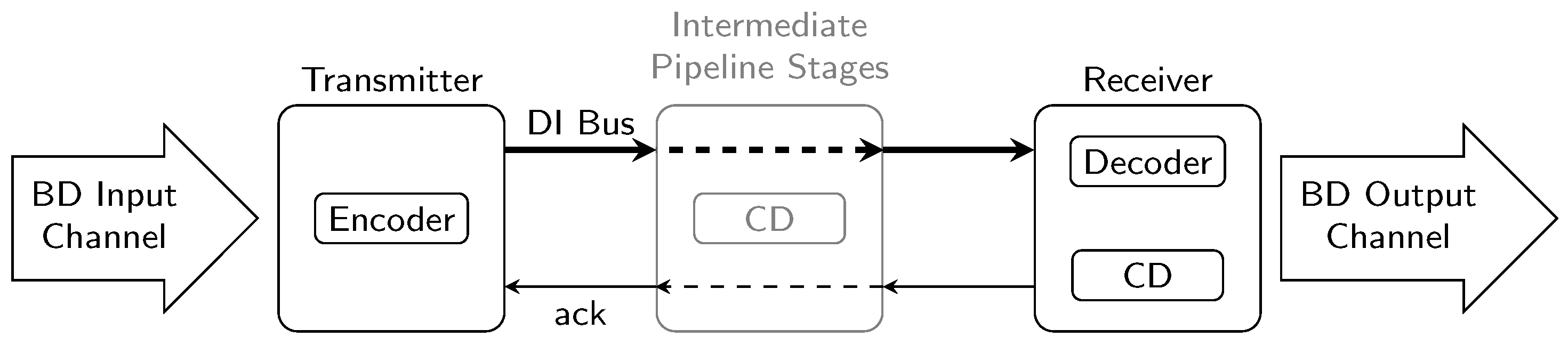
With the link architecture established in
Section 6 we now want to calculate the total combined link costs for each protocol and code. This not only includes the encoder, decoder, and CD costs but also the overhead for input and output registers and pipeline stages. However, in this analysis we do not include the static costs for the control logic of the links (i.e., controllers, delay-lines, etc.), since these costs are very similar for all the presented links. We are only interested in the dynamic cost that are directly impacted by the choice of a certain protocol and code.
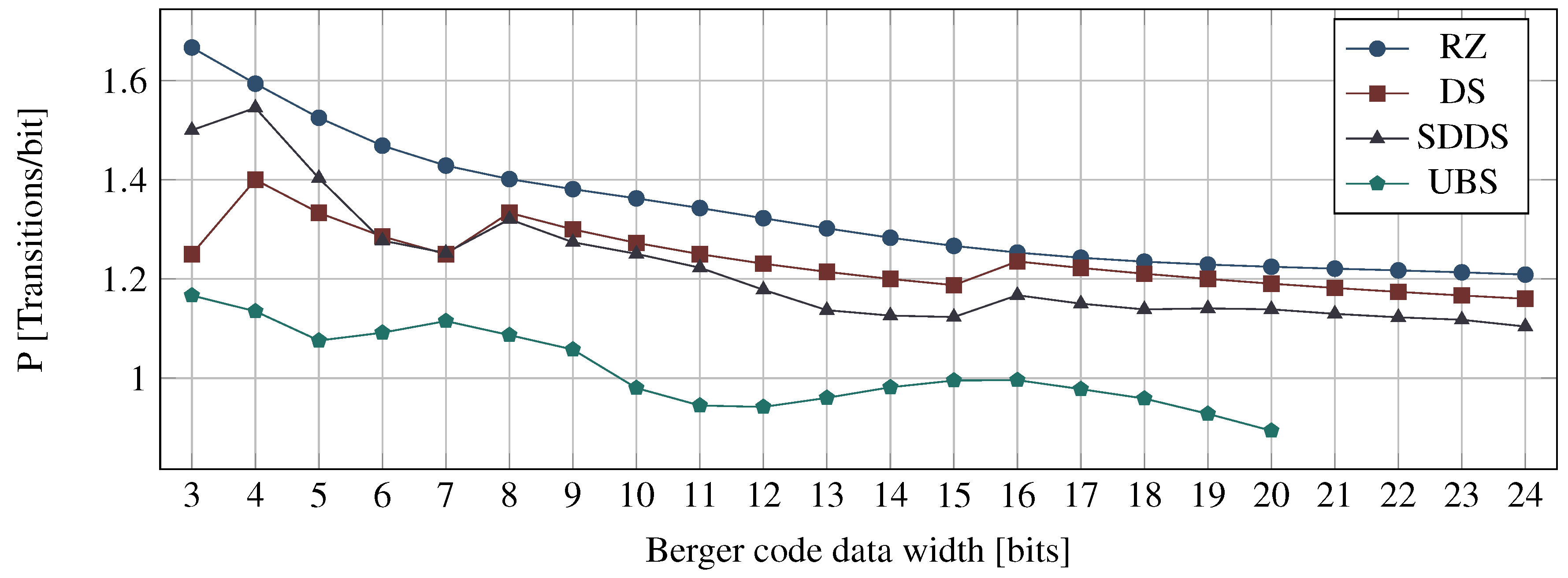
Figure 30 shows the results of this analysis.
The base bar of each bar stack corresponds to the combined costs of a transmitter receiver pair. Hence this bar includes the encoder, decoder, input, and output register as well as one CD. Each additional section represents the costs for one intermediate pipeline stage, which includes the pipeline D latches (or C gates in the case of the RZ protocol because of the simple WCHB design) and one CD.
It can be seen that for all codes the hop costs for the NRZ protocol are the most expensive. However, with greater initial costs the cheaper CDs of the SDS and UBS protocols often only pay off after a certain amount of pipeline stages. The DS protocol performs quite well, as it only requires a little more hardware investment than the RZ protocol and still improves the power metric quite significantly (see bars on the right-hand side), especially for codes with a small bit width. When the PSCWCs are compared to the Berger codes it can be seen that the higher initial costs for encoding and decoding pay off after just a few hops, regardless of the protocol.
7.2. Performance/Delay Analysis
This section discusses how the hybrid protocols impact the data transmission performance, i.e., the throughput, of a DI link. We start out by comparing the “classical” RZ and NRZ protocol. For this purpose, we analyze the WCHB as well as the MTDI pipeline style (see
Section 6.1) by creating a model for their dynamic behavior. After that we show how the hybrid protocols change the attainable performance when compared to the RZ protocol.
To quantify the pipeline performance, we use the
local cycle time metric [
20]. The
local cycle time corresponds to the minimal time required for a single pipeline stage to complete one handshake cycle with its neighbors. This hence gives a lower bound for the
system cycle time, which is basically the inverse of a pipeline’s throughput.
For this analysis we consider DI links as homogeneous linear pipelines, i.e., every pipeline stage is implemented identically and hence has similar delays. Because handshaking protocols involve the communication of a pipeline stage with the next and the previous stage the
local cycle time is usually a function of the delays of three neighboring blocks. This is reflected by the model circuits we use in this analysis shown in
Figure 31 and
Figure 32. The environments shown in these figures are assumed to be ideal, i.e., they generate immediate responses to the inputs they are presented with. Hence they are no limiting factor for the cycle time.
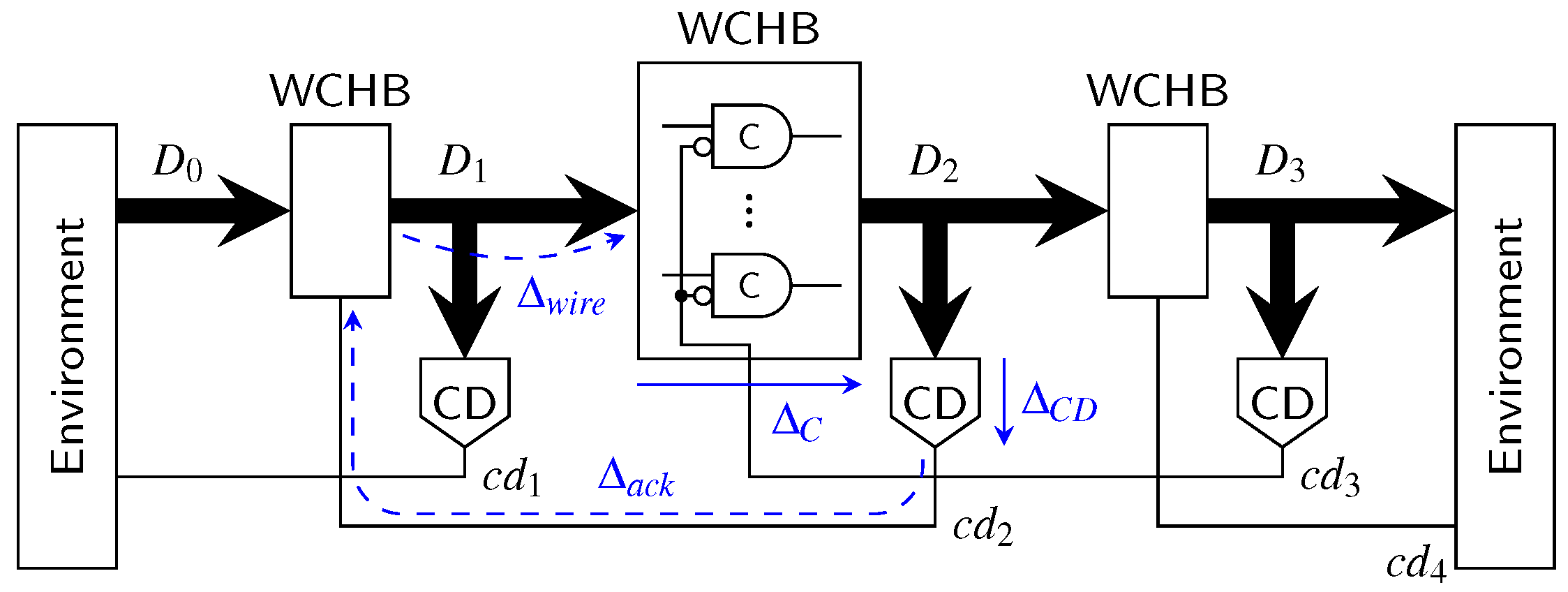
Let us first consider a classical 4-phase WCHB pipeline as shown in
Figure 31. The delay
models the wire delay on the data bus
connecting two pipeline stages. In this paper, we focus on data
transport, so we do not account for computations performed on the data and the associated delay. Adding
and
(i.e., the delay through the C gates comprising the buffer) thus yields the forward latency of a pipeline stage. The delay
corresponds to the delay of the acknowledgment signal measured from the output of the CD to the C gates of the previous pipeline stage. To simplify the analysis, we assume equal delays for rising and falling transitions.
To extract an analytical expression for the cycle time of this circuit, its dynamic behavior can be modeled by a marked graph (perti-net) as discussed in more detail in [
20]. For the WCHB pipeline this yields the graph shown in
Figure 33. This type of graph can be interpreted in a similar way as an STG. However, here the nodes do not (always) correspond to transitions of single signal wires but model more abstract events, such as the transition of the data bus from the spacer (i.e., null) phase to the data phase (
) or vice versa (
). This allows to capture the behavior of the pipeline in a compact way, independent of the actual data traversing it. The dashed lines in the graph indicate transitions performed by the environment.
Every node (event) of the graph is associated with a certain delay/latency: The nodes
and
add the delay
, and each node
adds
. Note, however that some of the arcs also cause a delay (e.g.,
, which adds
or
, which adds
). These particular delays are marked with dashed lines in
Figure 31.
The
local cycle time is now obtained by analyzing the longest cycle in this graph, which is marked by the orange arrows in the figure. Equation (26) shows the resulting expression for the
local cycle time of the WCHB pipeline, which corresponds to the time it takes for one code word and one spacer to pass though one pipeline stage.
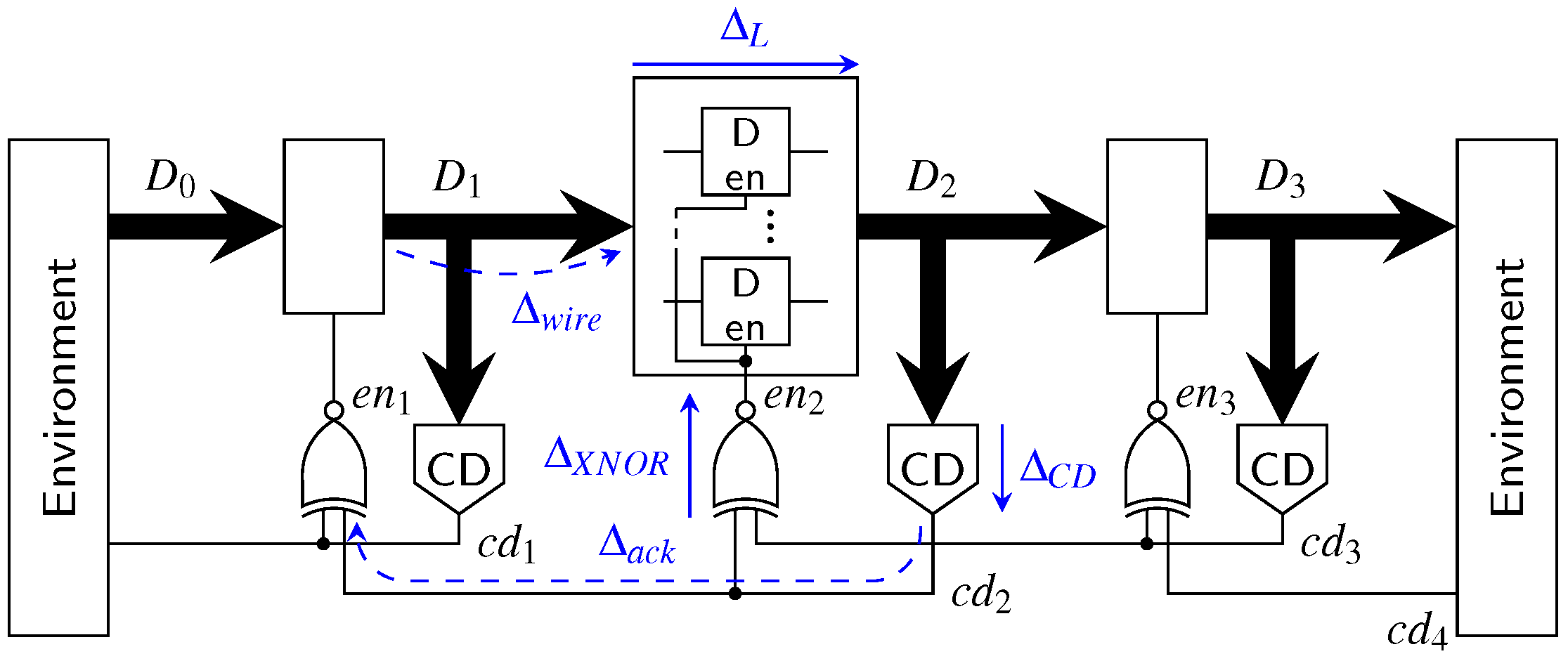
The graph model, associated with the MTDI pipeline of
Figure 32, is shown in
Figure 34. Since this pipeline works with both RZ and NRZ protocols we refer to the data events as
and
.
Again, the longest cycle is marked orange and the resulting cycle time expression is shown in Equation (27).
This expression yields the time it takes one pipeline stage to go through the two phases
and
. In NRZ protocols both of these phases transmit actual data, while in RZ protocols
corresponds to the spacer phase. Hence to make the protocols comparable this fact must be taken into account. We do this by introducing a factor of
for the actual cycle time of the NRZ protocol. Equations (
28) and (29) show the resulting expressions.
When Equation (
28) is compared to the cycle time of the WCHB pipeline (Equation (26)), it can be seen that the expressions are very similar. The only difference is the delay for the additional XNOR gate (assuming
). This reveals a fist small downside of the hybrid protocols because they must use the MTDI pipeline.
Notice that in Equations (
28) and (29)
has been replaced by variables denoting the actual delays of CDs for the specific protocol.
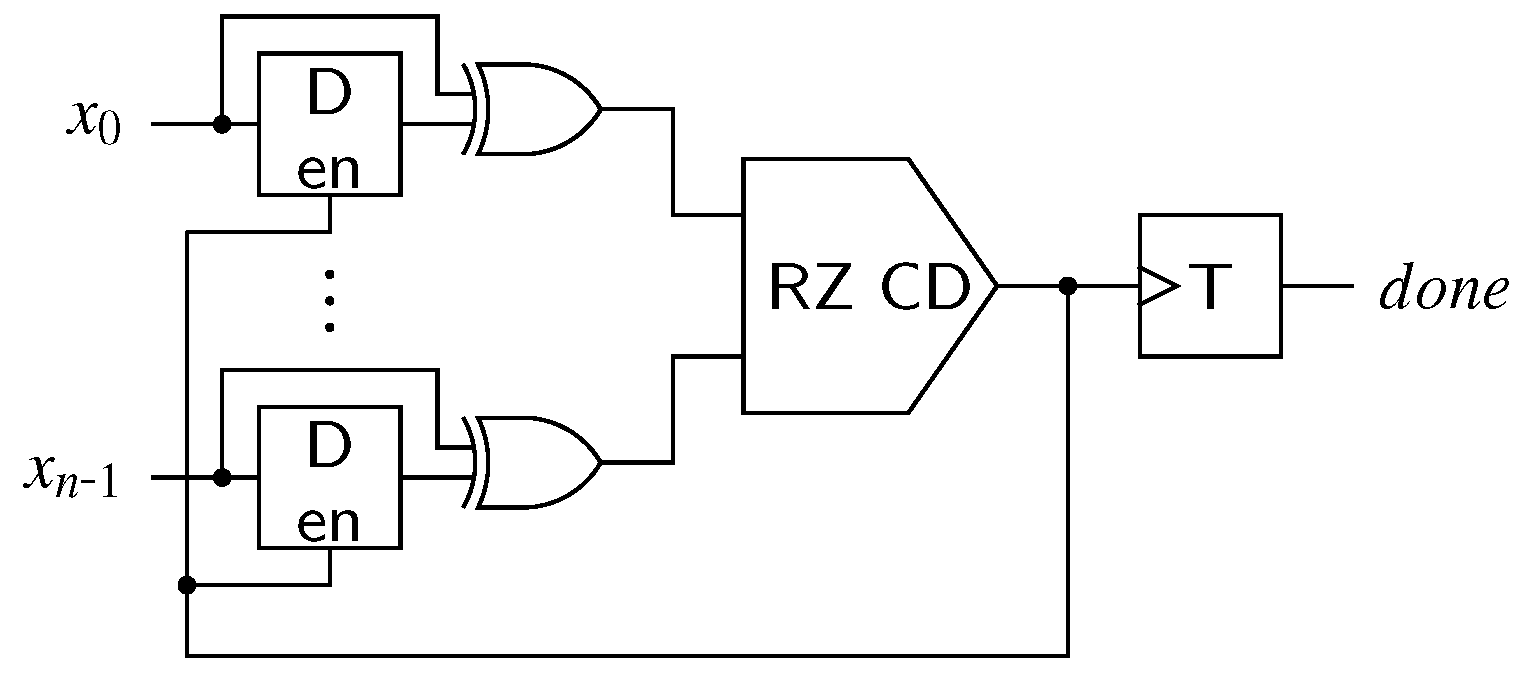
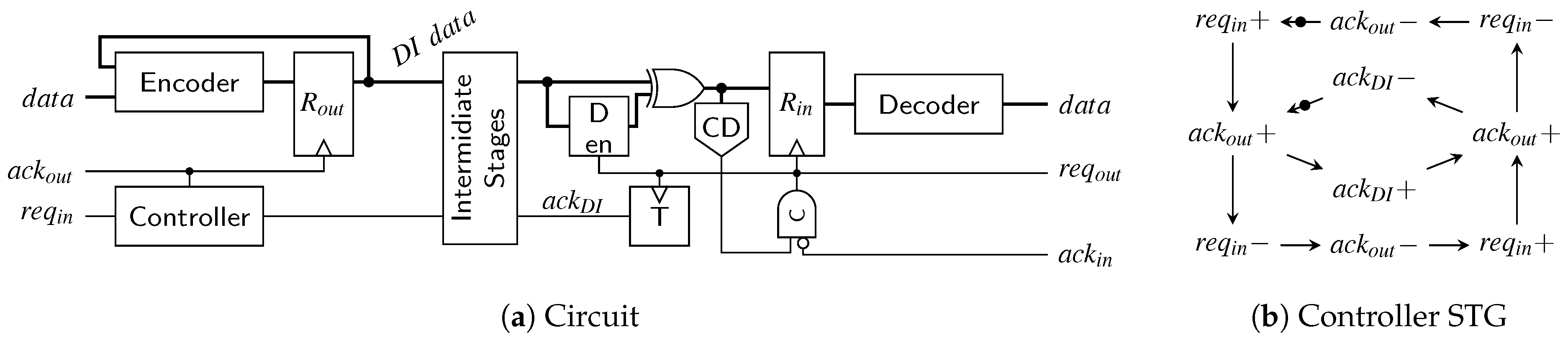
Section 5 discussed how an NRZ CD can be implemented using an RZ CD and an appropriate wrapper circuit consisting of shadow latches and XOR gates to detect input transitions. From the circuit in
Figure 13 we can thus derive the following equation for the delay of NRZ CDs:
Plugging this into Equation (29) yields:
When this expression is now compared to Equation (
28) (or Equation (26)), it can be seen that the main difference is that the terms
and
appear without the factor 2. Depending on how large these values are (compared to the sum of the other delays of the expression) this can of course have a large impact on the overall performance gains that can be achieved using the NRZ protocol.
For a very detailed picture of the NRZ protocol one might also investigate the impact of the protocol on the delay
. Even if the signal wires between two pipeline stages have the same geometrical dimensions and the same driver strength is used, it makes a difference whether an RZ or NRZ protocol is used. If neighboring wires of a bus switch in opposite directions capacitive crosstalk effects [
24] can have a negative impact on the delay. For the RZ and hybrid protocols such a situation can never occur since in one protocol phase
all transitioning wires must switch to the same value.
To calculate the cycle time of the hybrid protocols, we can basically take Equation (27) and plug in the correct value for . Hence in the following we will examine which factors contribute to the CD delay and how to estimate it. We start off with the analysis of the CDs for constant-weight codes and then briefly discuss Berger CDs as well.
From the general structure of the RZ CDs (see
Figure 18) we can deduce that the delay
can be divided into the delay
of the HG (i.e., the
m-input C gate at the output) and the delay of the purely combinational CN
. The latter delay is bounded by the depth of the of the CN, denoted by
(i.e., the maximum number of comparator cells an input signal has to pass through in order to reach the HG), multiplied by the delay of a single comparator cell
, which amounts to roughly one gate delay.
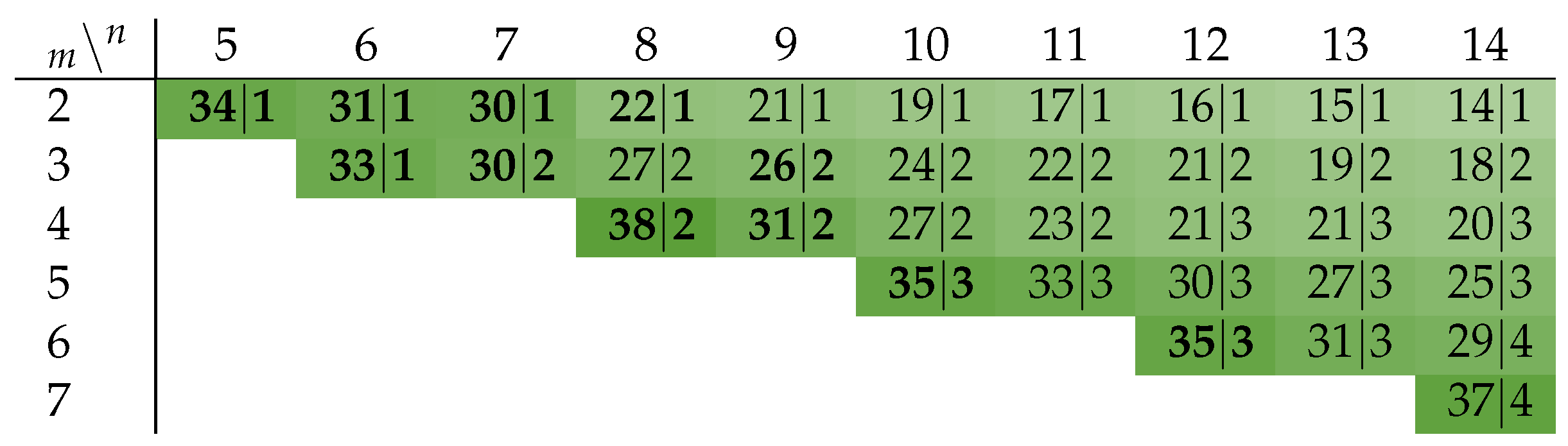
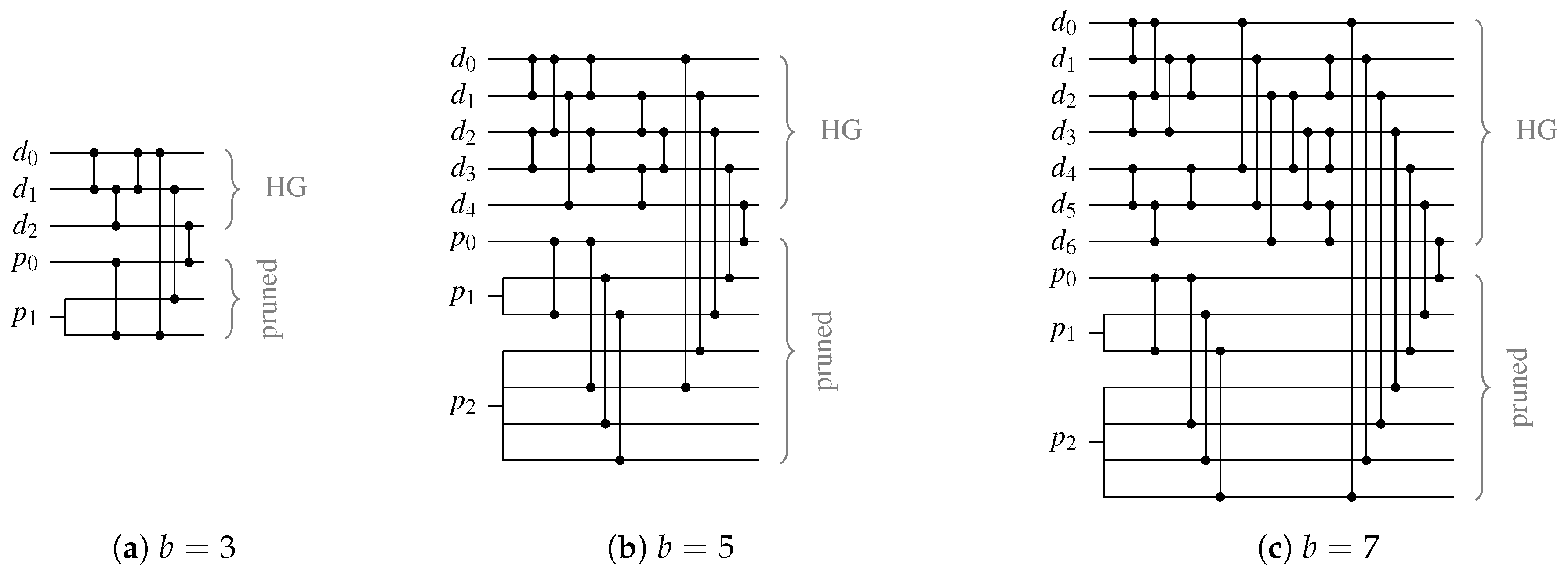
Table 10 lists the CN depths for the PSCWCs investigated in this paper. Note, however that for asymmetrical CDs (like the one for the 3-of-6 code) the actual value of
is data dependent. Hence, the actual selection of the code word set also plays a role. This is because for certain input vectors there are paths through the CN that are shorter than its (worst-case) depth. For the PS 3-of-6 code an exhaustive analysis of every critical path for every code word reveals that the average number of comparator cells an input vector must pass through is actually only
comparators instead of 4. However, for simplicity’s sake we only consider the worst-case path in our analysis.
For CDs for the SDS protocol the data dependency is an even bigger issue, because depending on whether the all-zero or the special spacer is used two different paths through the CD are relevant. Equation (33) shows how the average CD delay can be calculated. Recall that the variable
p denotes the percentage of cases in which the special spacer is used, which can either be estimated using Equation (18) or be calculated exactly by considering the actual code word set. For the cases where the input of the CD transitions from the all-zero spacer to a code word (or vice versa) the normal depth
must be used. When the input of the CD switches from a code word to the SD spacer or vice versa, the second-level CD must be considered, which increases the depth of the CN to
. However, in this case only the delay of the
d-input C gate in the HG is relevant. Finally, the delay
of the output AND gate of the HG must be added, to arrive at the following equation:
Table 10 shows the parameters for
p and
extracted from our CD circuits. Please note that for the case where
, there is no second C gate in the HG (hence
). Furthermore, the second-level CD only consists of an
m-input OR gate for which we estimated 1 (for
) and 2 (for
) comparator delays, respectively.
Generally it can be concluded that will only be marginally larger than , since the delay of an m-input OR gate (for the second-level 1-of-m CD) will certainly not exceed the delay of an m-input C gate. If the delay of the OR gate is significantly lower it can even compensate for . For higher values of d it strongly depends on whether the smaller C gate in the SD spacer path is sufficiently faster than the m-input C gate in the regular path to make up for the increased CN delay .
Because of a similar reason
is only marginally larger than
. Both possible paths to the output AND gate contain the same circuit elements, i.e., a CN with the same depth and an
m-input C gate. Hence the only difference in terms of delay is the output AND gate itself.
The CDs for Berger code-based protocols are by their nature very asymmetric, which again hints on some data dependent delay behavior. However, in most cases the overall depth of their CN is dominated by the depth of the SN
used to determine the Hamming weight of the data part of the code words. Equation (35) shows the CD delay for the RZ protocol.
Table 11 lists the CN depths for the Berger codes with
data bits.
Similar to
,
can be defined as:
The variable
p again denotes the percentage of cases where the unbalanced spacer can be used, and the second-level CD is activated. The parameters
and
p are listed in
Table 11. Again, an argument can be made that for
the delay of the CD is only marginally increased compared to
.
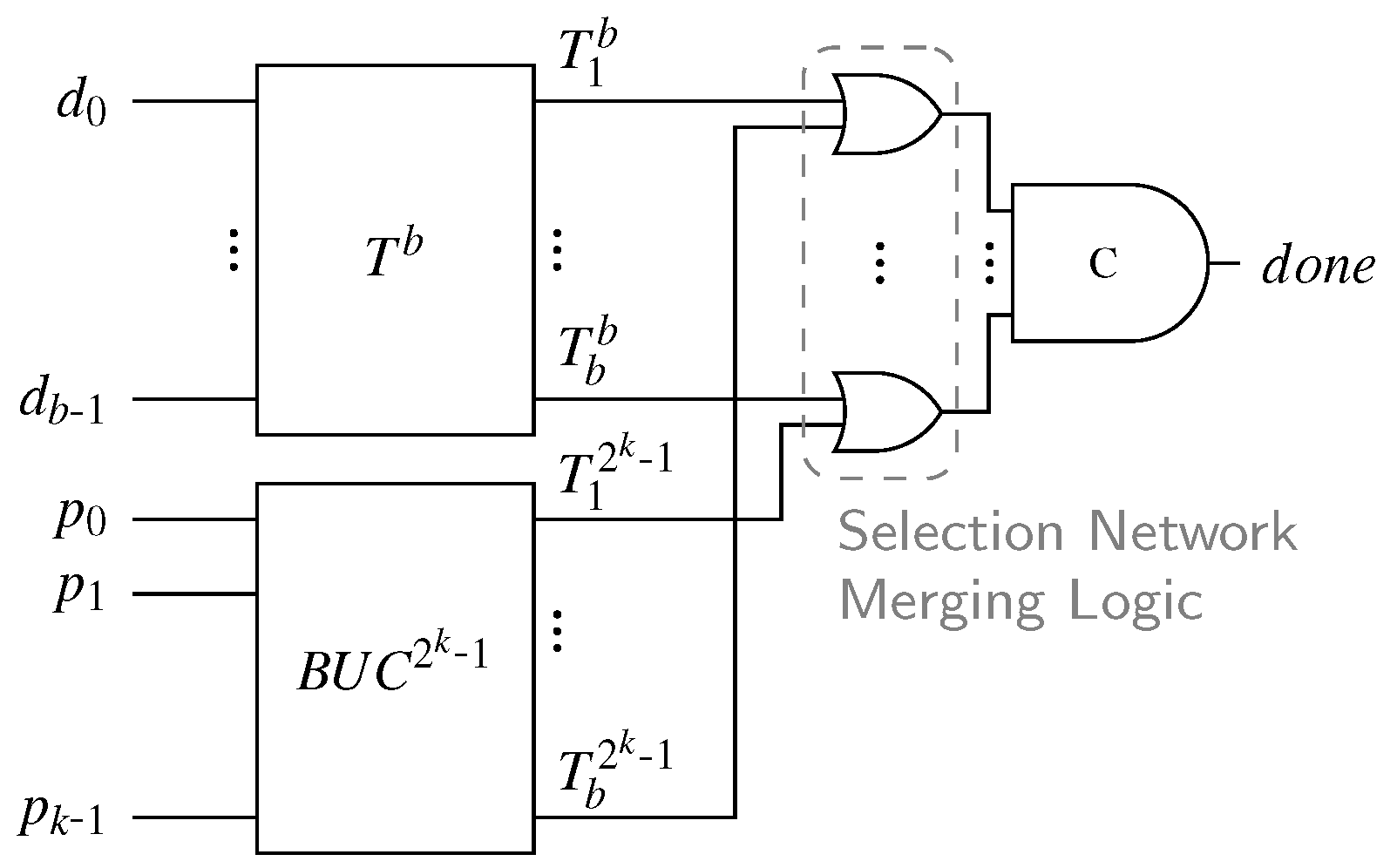
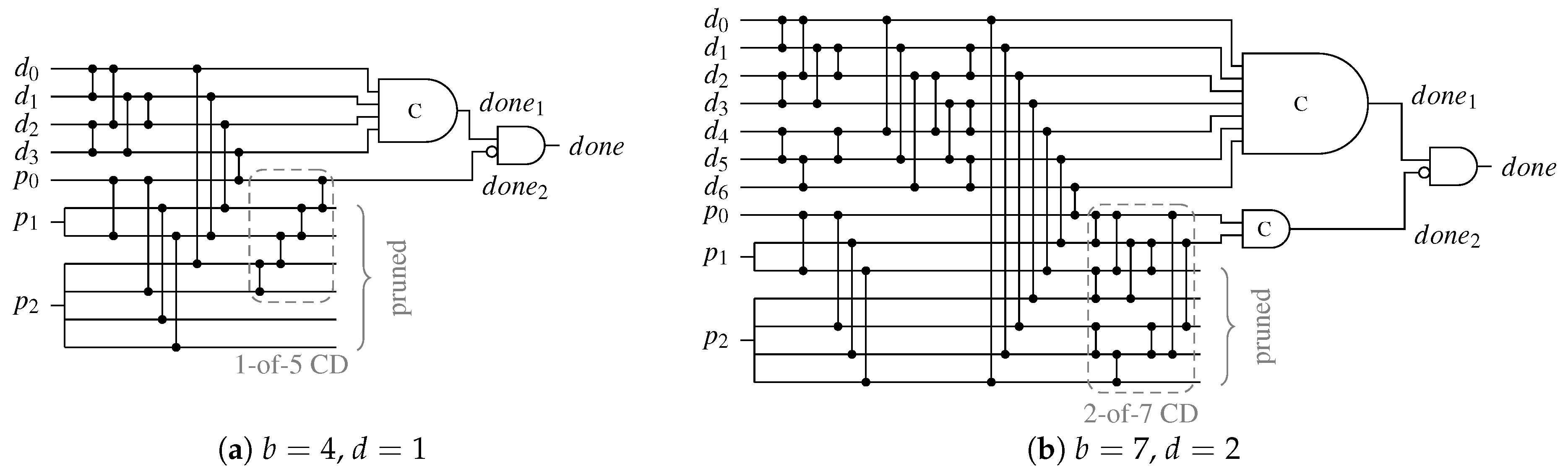
Recall that for the CD for the DS (and SDDS) protocol, the same CN as for the RZ CD is used. The only difference is that the
outputs that would be pruned from the network in case of an RZ CD, are merged using a C gate with
inputs. Depending on the spacer either this C gate or the usual
b-input C gate of the base circuit contributes to the critical path. Assuming equally distributed spacer-types (all-zero and all-one) we arrive at the following equation.
Notice that in the case where (i.e., in the case where Berger codes offer the best coding efficiency), both C gates have the same number of inputs. In this case, the only difference to is the delay of the output AND gate. In all other cases we have that , which (depending on b) can significantly worsen the delay of the CD.
Overall we can conclude from our analysis that the more (power) efficient encodings and protocols do incur a performance penalty. We have, however, also seen that with a careful selection of the protocol parameters this penalty can be made negligible