Abstract
In this paper, parameters related to the sensitivity of the interface circuits for capacitive sensors are determined. Both the input referred noise and capacitance of the input transistors are important for capacitive sensitivity. Chopping is an effective technique for signal conditioning circuits because of its capability of reducing circuit noise at low frequencies. The capacitive sensitivity and power consumption of various chopping techniques including the dual chopper amplifier (DCA), single chopper amplifier (SCA) and two-stage single chopper amplifier (TCA) are extracted for different values of total gain and sensor capacitance. The minimum sensitivity for each technique will be extracted based on the gain and sensor capacitance. It will be shown that designation of the amplifier and distribution of gain in the TCA and DCA are important for sensitivity. A design procedure for chopper amplifiers that illustrates the steps required to achieve either the best or the desired sensitivity while minimizing power consumption will be presented. It will be shown that for a small sensor capacitance and large total gain, the DCA has the best sensitivity, while for a large sensor capacitance and a lower gain, the SCA is preferable. The TCA is the desired architecture for an average total gain and a large sensor capacitance. Moreover, when the power consumption is the key requirement and the maximum sensitivity is not the goal; the TCA works best due to its potential to decrease the power consumption.
1. Introduction
Consumer electronics are increasingly making use of multiple integrated sensors to enhance their functionalities. Microelectromechanical systems (MEMS) have enabled the design of sensors with very high sensitivities, enabling a range of sensing applications [1]. Sensors that convert a physical stimulus into a capacitance are widely used for different purposes including detecting motion, pressure and acceleration [2,3,4,5]. Capacitive sensing has the benefits of a low temperature coefficient, low power dissipation and low noise. Additionally, the devices can be easily integrated with CMOS circuits and they are compatible with VLSI technology scaling [6,7,8].
Typical capacitive sensor output signals are in the microvolt range and have bandwidths ranging from DC up to a few kilohertz [9]. Amplifying such signals requires low noise and low offset amplifiers. Due to this frequency range, flicker noise is the dominant noise source in CMOS technology. There are two methods to remove the flicker noise: auto-zeroing and chopping [10]. Auto-zeroing is a sampling technique that removes flicker noise; but causes noise folding. Chopping is a continuous-time modulation technique in which the signal and offset are modulated to high frequencies. As a result, the chopping technique achieves low noise at low frequencies. Chopping techniques have been widely applied in recent publications to remove flicker noise and DC offsets [6,11,12,13,14,15,16,17,18]. One or more chopping frequencies can be applied when using chopping. An amplifier with a single chopping frequency is a single chopper amplifier (SCA) that can also be implemented as a two-stage chopper amplifier (TCA). In this system, the signal is modulated to a higher frequency, amplified and then demodulated to the baseband. When two different chopping frequencies are used, the system is a dual chopper amplifier (DCA). This technique can simultaneously remove flicker noise and reduce power consumption [14,18]. Additionally, two different clocks can be applied in series as proposed by the nested chopping technique [19] in order to remove the residual offset of the high frequency clock. The inner modulation, which has the higher frequency, is applied to remove the flicker noise and the outer modulation with the lower frequency is applied to remove the residual offset of the higher frequency. In this paper, the analysis of the nested chopper technique is not carried-out. However, it is expected that the technique would yield sensitivity characteristics that are similar to the SCA when the inner frequency of the nested chopper technique is equal to the chopping frequency of the SCA. In addition, other more intricate chopping techniques such as those presented in [9,13,20,21] have also been proposed and their sensitivity and power consumption could be ascertained by applying the analysis detailed in this paper.
Figure 1 shows a signal conditioning circuit that is connected to a differential sensor capacitance, C0 that can vary by ΔC in the presence of a stimulus. An important factor that must be considered in systems with capacitive sensors is parasitic capacitances at the sensing nodes that include the input capacitance of the signal conditioning circuit, Cgg, and the interconnect parasitic capacitance, CP. The sensed signal is sensitive to loading caused by parasitic capacitances at these nodes, which can degrade the circuit performance. In this paper, the effect of input capacitance of such an interface circuit on the sensitivity performance is investigated. When chopping is applied in other types of sensors such as inductive sensors [22], bioimpedance sensors [23] and resistive bridge sensors [16,24], the parasitic capacitance and input capacitance of the amplifier can also affect performance. Notably, in such sensors, the effect of the input amplifier capacitance and of the parasitic capacitance on the sensitivity is dependent on the chopping frequency and the bridge resistance values or inductors values.
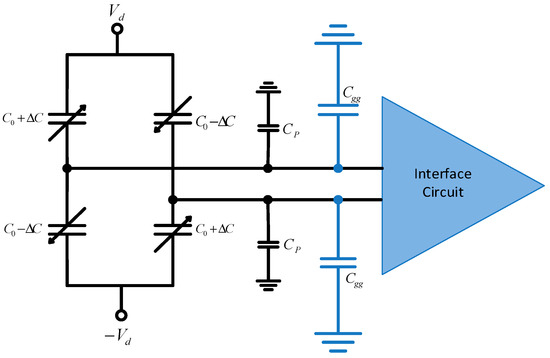
Figure 1.
Connection of differential sensor capacitance to an interface circuit with parasitic capacitances.
Power consumption is another important factor when sensors are used in portable devices [25]. Adding this requirement means the power must be minimized while maintaining satisfactory sensitivity in the interface system. There is a trade-off between the noise level and the power consumption, which poses a design challenge when trying to simultaneously obtain low noise and low power consumption.
This paper presents an analysis of sensitivity and power consumption when using the three chopping techniques of the SCA, TCA and DCA. These architectures are described in Section 2. Parameters related to the sensitivity of these systems are presented in Section 3, where a sensitivity factor used to extract the minimum detectable capacitance variation in the sensor capacitance is introduced. The sensitivity of the different chopping techniques is analyzed in Section 4. In each chopping technique, the achievable sensitivity and power consumption are extracted based on the total desired gain, the sensor capacitance and the minimum sensitivity. Section 5 compares the sensitivity of the three techniques and the preferred chopping technique is identified based on design constraints. Section 6 provides a method to select the appropriate circuit architecture based on a sensor’s capacitance and desired total gain. Finally, a conclusion is presented in Section 7.
2. Architecture of the Three Different Chopping Techniques
The system diagrams of the SCA, DCA and TCA are shown in Figure 2. In the SCA, the detected signal from the capacitive sensor is chopped at frequency fL, which is chosen to be higher than the 1/f noise corner frequency. After amplification, the signal is downconverted to the baseband and then filtered. In the TCA, the detected capacitive sensor signal is chopped at frequency fL, which is chosen to be higher than the 1/f noise corner frequency of the first and second stages and is then amplified by the first and second stages. After amplification, the signal is downconverted to the baseband and at last, the harmonics will be filtered. In the DCA, the sensed signal is modulated by frequency fM, which is a frequency that is generated by the mixing of two chopper frequencies, fH and fL. After chopping with frequency fM and amplification by the first stage A1, the signal is then chopped with frequency fH. In this step, the 1/f noise of the first stage can be filtered, as it is shifted to the odd harmonics of frequency fH. Finally, the signal is amplified by the second stage A2 and is then chopped by frequency fL, which is higher than the 1/f noise corner frequency of the second stage. With this last chopping operation, the signal has been downconverted to the baseband and the 1/f noise of the second stage is moved to the odd harmonics of fL and can be filtered for further processing. This dual chopping technique has advantages that will be highlighted in Section 3. In all of these three techniques, the signal is chopped by a complementary clock that is inputted to the capacitive bridge (i.e., Vd in Figure 1) and no switch is used for the modulation at the input. This is beneficial as it prevents charge injection and clock feedthrough of the switches at the input. If switches were applied to create the modulation at the input, the charges produced by the non-idealities of the switches could be comparable with the charge in the capacitive sensor and thus deteriorate performance.
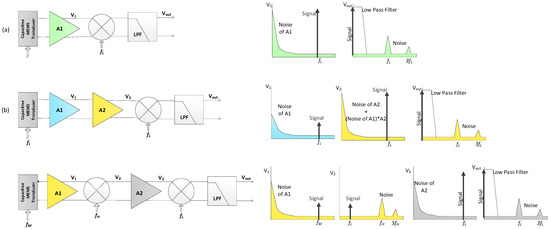
Figure 2.
Diagram of the (a) single chopper amplifier, (b) two stage single chopper amplifier and (c) dual chopper amplifier with a capacitive transducer connected to the input. The frequency domain signal and noise representation for each system is also presented.
3. Parameters Related to the Sensitivity of the Chopping Technique
In the following sections, the effective parameters for the sensitivity of the chopping amplifiers are shown and a sensitivity factor is defined to be able to compare the capacitive sensitivity of the signal conditioning circuits.
3.1. Noise and Corner Frequency
One of the important effective factors on sensitivity is the noise. The dominant noise sources in MOS transistors are thermal and flicker noise, which are given as [26]:
where Vn is the thermal noise voltage, Vf is the flicker noise voltage, gm is the transconductance of the MOS transistor, K is Boltzmann’s constant and ϒ is the MOSFET thermal noise coefficient which is 2/3 for long channel transistors. In (2), Kf is the flicker noise constant and W and L are the transistor width and length, respectively.
The goal of the chopping technique is to remove the flicker noise such that small signals at low frequencies can be detected. To remove the flicker noise, a suitable chopping frequency must be chosen. In addition, the chopping frequency should be in the bandwidth of the amplifier to prevent suppression of the signal. A chopping frequency which is smaller than the noise corner frequency cannot remove the flicker noise properly. On the other hand, using a large chopping frequency requires a large amplifier bandwidth, which results in a higher power consumption. As a result, choosing the proper chopping frequency is important to optimize both the power consumption and noise performance. Once the noise corner frequency is extracted, the appropriate chopping frequency can be selected.
The noise corner frequency is the frequency at which the thermal noise and flicker noise become equal [27]. Based on the relation of the thermal noise and flicker noise, the noise corner frequency can be extracted as:
As shown in (3), both dimensions of the transistor and its transconductance affect the noise corner frequency. Larger dimensions and a smaller transconductance result in a lower noise corner frequency. If the chopping frequency is 10 times larger than the corner frequency, then the flicker noise is 10% of the thermal noise and can be neglected [27]. In this analysis, a chopping frequency that is 10 times larger than the noise corner frequency is considered and the amplifier bandwidth is chosen to be a slightly larger than the chopping frequency as shown below to optimize the power consumption:
where fchop is the chopping frequency and BW is the 3-dB bandwidth of the amplifier.
3.2. Input Capacitance
The other determining factor on the capacitance sensitivity is the parasitic capacitance of the input transistor. Based on the value of the sensor capacitance and capacitance of the input transistor, the sensitivity can be decreased. The gate capacitance of a MOS transistor is equal to [27]:
where W and L are width and length of the transistor, Cox is the thin-oxide field-capacitance per unit area and Lov is the gate overlap length.
Considering Equations (5), (2) and (3), it is observed that the noise corner frequency and the flicker noise have an inverse relationship with the gate capacitance. If the dimensions of the input transistor are increased to decrease the flicker noise and the corner frequency, the input capacitance will increase. This effect can have a negative effect on the sensitivity, as will be shown in Section 3.3.
In an amplifier, the equations for the bandwidth and gain can be written as follows:
where CL is the load capacitance, Ro is the output impedance and gm is the transconductance of the input transistor. The coefficient α is included in (7) because the exact gain depends on the amplifier topology. In fully differential amplifiers, α is equal to 1 and in other types such as two stage amplifiers and folded cascade amplifiers, it is larger than 1. Substituting the equations for bandwidth (6) and the noise corner frequency (3) into Equation (4), the following is obtained:
Equation (8) can be rewritten as:
In (9), is the gain or part of the gain and the left-hand side can be considered as the capacitance of the input transistor (Cgg) if the value of is negligible. If not, the input capacitance is larger than this value. As a result, the input capacitance and gain are related such that:
This equation highlights the fact that the input capacitance and the gain are dependent on each other. For a given gain, the input capacitance is larger than the value in (10). As the gain is increased, the input capacitance will also increase and this can degrade the sensitivity.
3.3. Sensitivity Factor
The detected voltage signal from the capacitive sensor must be larger than the input noise floor of the circuit in order to be sensed, as shown by:
where Vn is the noise floor voltage, C0 is the sensor nominal capacitance, Cp is the parasitic capacitance of the interconnects, Cgg is the capacitance of the interface circuit, ΔCmin is the minimum detectable variation at the sensor capacitance, Vdd is the excitation voltage and BWsystem is the desired bandwidth of the system and is defined by the application. Equation (11) can be rewritten as:
Here, it is assumed that the parasitic capacitance of the interconnect can be neglected. This is a viable assumption in monolithically integrated sensors where very high levels of sensitivity are required and interconnect parasitics are minimal.
In this analysis, a loading factor Kc is defined as:
Based on (12) and (13), the following relationship can be derived:
In this equation, C0, Vdd and BWsystem are constants. As a result, , which is the ratio of the smallest detectable capacitance variation to the nominal capacitance, depends on the noise and the loading factor. Note that the sensitivity of a system is defined by the minimum detectable variation of capacitance. The ability to detect a smaller capacitance variation translates to greater sensitivity. In order to be able to compare the sensitivity of different systems, a sensitivity factor is introduced to extract the minimum detectable sensor capacitance variation. Based on (14), for a given minimum detectable variation in sensor capacitance, the maximum possible values of noise and loading factor are limited. Accordingly, a sensitivity factor can be defined as
As such, both the noise floor and the loading factor are influential in detecting the minimum variation in the sensor capacitance. A smaller sensitivity factor implies that the circuit has the capability to detect a smaller capacitance variation, translating into a higher sensitivity. Thermal noise has a direct effect on the sensitivity factor as it is multiplied by (1 + Kc). Therefore, the value of the loading factor is important. If it is much smaller than 1, the thermal noise is the sole factor for determining the sensitivity factor; however, if it is close to 1, it will affect the sensitivity factor.
In this paper, the sensitivity factor is applied to extract the minimum detectable variation of capacitance in the SCA, TCA and DCA configurations for different gains and sensor capacitances.
3.4. Power-Sensitivity Factor
To achieve a design suited to low-power operation, the effect of both sensitivity factor and power consumption should be considered. It is possible to achieve a very small sensitivity factor in a system but this may demand high power consumption. As a result, a power-sensitivity factor is defined as:
where P is the power consumption of the system. Based on the application, the system is designed to attain the minimum power-sensitivity factor, or the smallest possible value of sensitivity factor considering a constraint on the power-sensitivity factor.
4. Sensitivity of the SCA, TCA and DCA
In this section, the sensitivity factor of the SCA, TCA and DCA are extracted based on the total gain and sensor capacitance. To design a chopper amplifier, it is important that the relation between the bandwidth and the noise corner frequency given in (4) is respected. As a result, a reference amplifier with a particular gain and a valid relationship between the bandwidth and the noise corner frequency is considered to compare the performance of different chopping techniques for different gains.
4.1. Reference Amplifier
It is assumed that the reference amplifier has a gain of G0 and the current and dimensions of the input transistors maintain a valid relationship between the bandwidth and the noise corner frequency.
The characteristics of the chopping amplifiers for different gains are extracted based on characteristics of the reference amplifier. It is assumed that all amplifiers used in the chopping systems in this paper have a bandwidth of at least ten times larger than their noise corner frequency. There are different methods of changing the current and dimensions of the transistors to achieve an amplifier gain such that:
where G is the amplifier gain which is K times the gain of the reference amplifier. The possible approaches of changing the gain while maintaining the condition set in (4) are listed as cases in Table 1 along with the effect they have on different circuit metrics. In all of these cases, the load capacitance CL is kept constant. It is noted that any second order non-idealities are neglected in Table 1. Moreover, the minimum allowed value of length and width of the transistors depend on the technology considered for the design.

Table 1.
Methods of changing the gain of the SCA w.r.t. the reference amplifier.
Figure 3 and Figure 4 show the effect of changing the gain on the sensitivity factor for two values of the loading factor in the reference amplifier (Kc = 0.01 and 1). The sensitivity factor and gain of these figures are normalized based on the sensitivity factor and gain of the reference amplifier. In each figure, the sensitivities for the four possible cases in Table 1 are considered to achieve the desired gain.
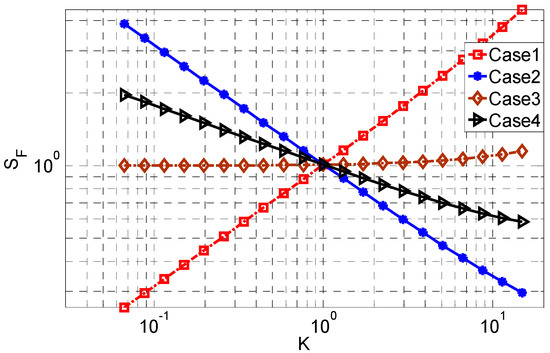
Figure 3.
Sensitivity factor of the chopper amplifier normalized by the reference amplifier for a loading factor of 0.01.
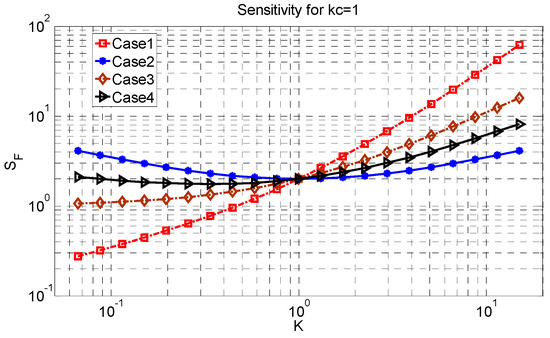
Figure 4.
Sensitivity factor of the chopping amplifier normalized by the reference amplifier for a loading factor of 1.
As shown in Figure 3, with increasing gain, the thermal noise and input capacitance vary as shown in Table 1. Cgg is changed by a factor of K in all of the cases which implies that the loading factor is increased by a factor of K. As a result of the gain variation, the loading factor is changed from 0.001 to 0.1, having a negligible impact on the sensitivity factor in this case as it remains much smaller than 1. Variation of the thermal noise depends on the considered case. As shown in Figure 3, with increasing K, the sensitivity factor is increased in case 1, decreased in cases 2 and 4 and almost constant in case 3. The trend in the sensitivity factor is thus the same as the trend of the thermal noise. This means that the effect of the loading factor on the sensitivity factor is negligible and the sensitivity factor is affected solely by the thermal noise.
The sensitivity factor based on varying K for a loading factor of 1 in the reference amplifier is shown in Figure 4. In this case, the loading factor varies from 0.1 to 10. As a result, it affects the sensitivity factor. As shown in Figure 4, with increasing K, the sensitivity factor is increased in case 1 but in cases 2, 3 and 4, there is an optimum value. This stems from both the thermal noise and loading factor variation with K. In case 1, both the thermal noise and loading factor are increased by increasing K, causing an ascending trend in the sensitivity factor. However, in cases 2, 3 and 4, the loading factor is increased but thermal noise is decreased. Since the effect of loading factor in this case is not negligible, an optimum value of K to achieve the lowest sensitivity factor can be observed. Accordingly, when the loading factor is 1, the effect of the loading factor on the sensitivity factor cannot be neglected.
To be able to compare the sensitivity factors of the different chopping techniques in the following analysis, the total gain of the circuit is considered to be set to Gt and the gain of the reference amplifier is considered to be of G0. Equation (18) shows the relation between G0 and Gt implying that the total gain is G0 times larger than the gain of the reference amplifier.
In the following sections, the sensitivity factor and power consumption of the three chopping techniques considered in relation to the reference amplifier will be analyzed.
4.2. Single Chopper Amplifier
In the SCA, the signal is chopped at the frequency fchop. After modulation, the signal is amplified by the amplifier. Next, the signal is demodulated to the baseband where it will be filtered by a low pass filter. For an SCA gain of Gt, K is made to be equal to G0. Out of the four cases in Table 1, cases 1, 2, 4 can be applied in the SCA to vary the gain. Case 3 cannot be applied because achieving a large gain by changing the dimensions and keeping the power constant is not possible.
The sensitivity factor of the SCA is given by:
where Vn,SCA is the thermal noise of the amplifier and KC,SCA is the loading factor of the amplifier. The sensitivity factor for cases 1, 2 and case 4 based on the reference amplifier are given below in (20)–(22), respectively.
where Vn,0 is the reference amplifier noise floor voltage and KC0 is the reference loading factor.
The sensitivity factor of the SCA versus the total gain is shown in Figure 5 for three sensor capacitances of 100 fF, 250 fF and 800 fF and for cases 1, 2 and 4. As shown, increasing the gain increases the sensitivity factor and the increase is larger for a smaller sensor capacitance because it has a larger loading factor. Comparing these three cases, SF,SCA2 represents the lowest sensitivity factor, since the thermal noise is smaller in case 2.
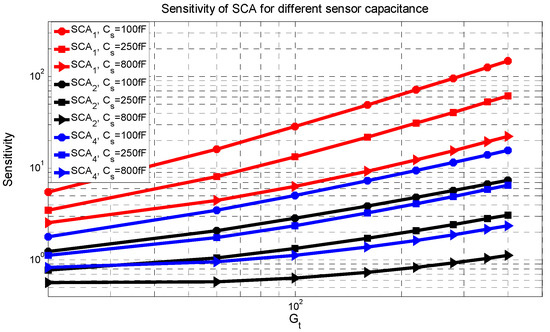
Figure 5.
Sensitivity factor of SCA for different cases vs. total gain for sensor capacitances of 100 fF, 250 fF and 800 fF.
The power consumption is independent of the sensor capacitance and in cases 1, 2 and 4, it is equal to:
From these equations, it can be concluded that although SCA,2 has better sensitivity, it consumes more power.
The power-sensitivity factor for the SCA in cases 1, 2 and 4 is given by:
From these equations, it can be concluded that increasing the gain will increase the power-sensitivity factor in cases 2 and 4 but in case 1 it depends on both the value of the gain and the loading factor. The power-sensitivity in case 2 is larger than in case 4. Moreover, a smaller sensor capacitance results in a larger power-sensitivity factor outlining the limitations of the SCA topology to accommodate small sensor capacitances.
4.3. Two-Stage Single Chopper Amplifier
In the TCA, the signal is also chopped by the frequency fchop. After modulation, the signal is amplified by the first and second amplifiers. Next, the signal is demodulated to the baseband where it will be filtered by a low pass filter. Since both amplifiers in the TCA are operating at the same frequency, it is important to select a chopping frequency that is at least 10 times larger than both noise corner frequencies of the amplifiers. To analyze the performance of the TCA with the same total gain as the SCA, it is assumed that the first amplifier and the second amplifier have gains of G1 and G2 that are varied from 1 to Gt (i.e., ) as outlined by:
G1 and G2 are the gain of the first and second amplifiers, respectively and K (distribution of gain between two stages) should be in the range shown in (31) to have the total gain of each amplifier range from 1 to .
The second amplifier in the TCA has a constant load capacitance of CL but the load capacitance of the first amplifier is the input capacitance of the second amplifier. As a result, changing the dimensions of the second amplifier to change the gain will affect the characteristics of the first amplifier. A larger gain in the second amplifier will result in a larger input capacitance and a larger load capacitance for the first amplifier. This will decrease the bandwidth of the first amplifier. As a result, the effect of changing the load capacitance of the first amplifier should be considered when distributing the gain between the two stages. The TCA is designed in such a way that the bandwidths of both amplifiers are at least 10 times larger than the noise corner frequency. The characteristics of the possible methods to change the gain of the first amplifier by a factor of K when compared to the reference amplifier and the gain of the second amplifier by a factor of 1/K are listed by case in Table 2 and Table 3; respectively.

Table 2.
Methods of changing the gain of the TCA first amplifier w.r.t. the reference amplifier.

Table 3.
Methods of changing the gain of the TCA second amplifier w.r.t. the reference amplifier.
As shown in Table 2 and Table 3, different combinations of cases for the first and second amplifiers are possible to attain the required gain from each amplifier. However, only case combinations where the chopping frequency fulfills (4) for both amplifiers can be considered. With these conditions, only the combinations of cases in Table 4 are suitable. The first case index in this table represents the applied case in the first amplifier and the second index shows the applied case in the second amplifier. Because of the limitation in the noise corner frequencies and the chopping frequency, all of these cases are valid for K larger than 1. This means that in the TCA, the gain of the first amplifier should be larger than the gain of the second stage. As a result, it is impossible to implement a small gain in the first stage to realize a small loading factor. Between these cases, the maximum sensitivity is achieved by applying case combination 21. However, the power consumption for this case combination is the largest.

Table 4.
Different case combinations (first amplifier and second amplifier) for changing TCA total gain.
The sensitivity factor of the TCA for total gains of 60 dB and 40 dB and two different sensor capacitances of 100 fF and 500 fF versus K are shown in Figure 6. Since the second amplifier does not have a sizable effect on the sensitivity factor of the TCA, only the sensitivity factors based on the possible cases for the first amplifier are shown. As shown at this figure, at the same gain and sensor capacitance, case 2 has a smaller sensitivity factor than case 4. With increasing K, the trend in sensitivity factor is dependent on both the gain and the sensor capacitance. At a gain of 40 dB and a sensor capacitance of 500 fF, the sensitivity factor decreases for an increasing K. This is because the effect of the loading factor is negligible and when the gain of first amplifier is increased; the thermal noise is decreased resulting in a decreasing trend in the sensitivity factor. However, for larger total gain or smaller sensor capacitance, the loading factor is not negligible when the gain of the first amplifier is increased. This results in an optimum value based on the value of K. At a gain of 60 dB and a sensor capacitance of 100 fF, where the effect of the loading factor is dominant over the thermal noise on the sensitivity factor. As a result, increasing the gain of the first amplifier causes the sensitivity factor to have an increasing trend.
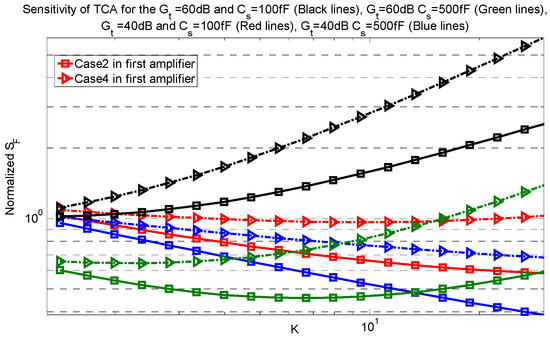
Figure 6.
Normalized sensitivity factor of the TCA for different total gains and sensor capacitances.
Note that minimum power consumption is achieved when K equals 1, which occurs when both amplifiers have the same gain. Comparing the power consumption in different cases shows that case 4 in the first amplifier results in a lower power consumption, although its sensitivity factor is larger.
The minimum sensitivity factor of the TCA for different total gains and different sensor capacitances is shown in Figure 7a and the ratio of gain of the first amplifier to the total gain related to the minimum sensitivity of TCA is shown in Figure 7b. For each gain and sensor capacitance, the sensitivity factor is based on the possible gain adjustment cases, the range of K is considered and the minimum sensitivity factor is extracted. As a result, for each gain and sensor capacitance, the value of K and the applied cases can be different.
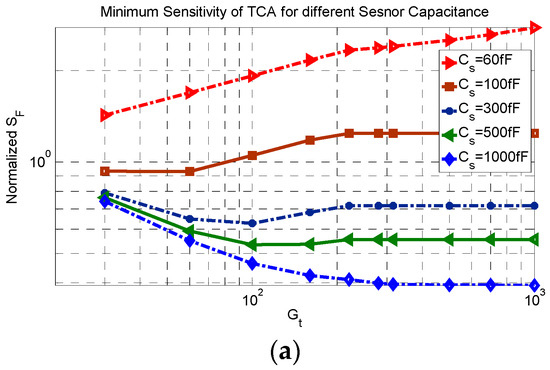
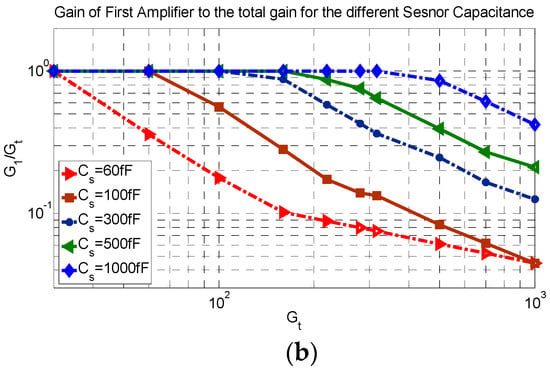
Figure 7.
Minimum Sensitivity factor in the TCA for (a) different total gains and sensor capacitances and (b) ratio of first amplifier gain to total gain related to minimum sensitivity factor.
As shown in Figure 7b, at a smaller Gt, the ratio of the first amplifier gain to the total gain is 1 which means that the minimum sensitivity factor is reached when all the amplification is done at the first stage and the second stage has the gain of 1. Note that this case corresponds to the SCA, since all the gain is achieved using only one stage and the second gain stage is not necessary. As the total gain is increased, the ratio of gains starts to decrease based on the value of the sensor capacitance. For a smaller sensor capacitance, the ratio starts to decrease for a smaller gain but for the larger sensor capacitance, the ratio remains at a value of 1 and then starts to decrease for a larger gain. This difference is justified by the loading factor.
Increasing the gain increases the power consumption and the power consumption for a large sensor capacitance is higher. This is because in this condition, all amplification is done by the first amplifier which results in a larger power consumption. Systems with a smaller sensor capacitance can have lower power consumption because the amplification is distributed between the two stages.
4.4. Dual Chopper Amplifier
In the dual chopper amplifier, two different and independent chopping frequencies are applied. Each chopping frequency is defined by the corner frequency of the related amplifier. This characteristic gives an extra degree of freedom when distributing the gain between the two stages which makes it possible to have a smaller sensitivity factor. As with the TCA, the capacitance of the input pair of the second amplifier is the load capacitance of the first amplifier. As a result, changing the gain distribution between the two stages changes the load of the first amplifier, which affects its bandwidth and power consumption. If the first and second amplifiers have a gain of G1 and G2, respectively, as described in (29) and (30), there are different ways to change their gains and all of the combinations in Table 2 and Table 3 can be applied to reach the desired gain.
The sensitivity factor of the DCA for sensor capacitances of 100 fF and 500 fF for gains of 40 dB and 60 dB are shown in Figure 8a,b. In these two figures, the sensitivity factor based on K and three possible cases for the gain modification of the first amplifier are shown. Since the effect of the second amplifier on the sensitivity factor is small, it is not considered here. This is the case because the total gain can be distributed to ensure that the gain of the first amplifier is high enough to suppress the thermal noise of the second stage, or that the gain of the second amplifier is high enough to result in a small thermal noise from the second stage.
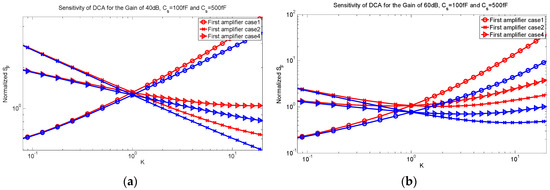
Figure 8.
Normalized sensitivity factor of the DCA for the gains of (a) 40 dB and (b) 60 dB for sensor capacitances of 100 fF (red lines) and 500 fF (blue lines).
As shown in Figure 8a, increasing K decreases the sensitivity factor for cases 2 and 4 and increases it for case 1. With increasing K, the thermal noise is decreased in cases 2 and 4 and increased in case 1 but the loading factor is increased in all cases. At this total gain, the effect of the thermal noise is dominant rather than the loading factor. As a result, the sensitivity factor has the same trend as the thermal noise. At a gain of 40 dB and a sensor capacitance of 500 fF, the minimum sensitivity factor is reached when K is maximized. In other words, all amplification is done in the first stage and the second stage has a gain of 1. This condition simplifies to the SCA. For a gain of 40 dB and a sensor capacitance of 100 fF, the minimum sensitivity factor is reached with the minimum possible K and applying case 1 for the first amplifier. The sensitivity factor in this case is given by:
A minimum K means the gain of the first amplifier is equal to 1 and all amplification is done in the second stage. For a small sensor capacitance (i.e., 100 fF), the effect of the loading factor is more important and the first amplifier acts as a buffer to keep the parasitic capacitance at the sensor node low, while being able to drive the larger capacitance of the second amplifier that implements the required gain.
The sensitivity factor for a gain of 60 dB is shown in Figure 8b. For cases 2 and 4, increasing the K decreases the thermal noise and increases the loading factor, which creates the presence of an optimum value. When K is smaller than the optimum value, the effect of the thermal noise is dominant and when K is larger than the optimum value, the effect of the loading factor becomes dominant. A minimum sensitivity factor is reached when the first amplifier has the gain of 1 and case 1 is applied. This mitigates the loading factor and results in the smallest sensitivity factor. It should be emphasized that case 1 is reached by decreasing the transistor lengths and it should be checked whether it is possible or limited by technology geometry.
The power consumption of the DCA for the different cases can be extracted from Table 2 and Table 3. The DCA has the maximum power consumption when the first amplifier is in case 1 and K is the smallest possible value, or when first amplifier is in case 2 and K is the maximum value. The optimum power consumption is reached for the DCA for the same gain in the first and second stages.
The minimum sensitivity factor of the DCA versus the total gain and for different sensor capacitances is shown in Figure 9a. These values are obtained by analyzing the sensitivity factors for the different gain modification cases and different values of K. As shown in Figure 9a, increasing the total gain decreases the minimum sensitivity factor. This can be explained by Figure 9b, which shows the ratio of the gain of the first amplifier to the total gain for the related minimum sensitivity factor. As shown, the ratio changes based on the total gain and the sensor capacitance, which is justified by the loading factor. Many distributions result in a negligible loading factor but the minimum sensitivity factor is reached when the first amplifier has a gain of 1 which is attained by case 1 and all amplification is done at the second amplifier via case 2. In this condition, the minimum thermal noise is achieved.
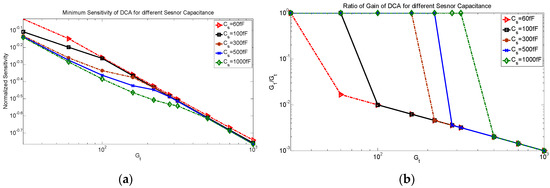
Figure 9.
(a) Normalized minimum sensitivity factor of the DCA for different total gains and (b) ratio of gain of the first amplifier to the total gain to reach the minimum sensitivity.
As shown in Figure 9a, increasing the total gain decreases the sensitivity factor because the thermal noise is decreased and the DCA can maintain the loading factor small.
To reach the smallest sensitivity factor in the DCA when case 1 is applied, the length of the input transistors should be decreased to have a smaller loading factor. However, the technology can limit the level of scaling that can be achieved. As a result, another option is considered. The sensitivity factor of the DCA is extracted while the length of the input transistors is kept constant and this DCA is named DCA2. Figure 10a shows the minimum sensitivity factor of DCA2 and Figure 10b shows the ratio of the gain of the first amplifier to the total gain to achieve the minimum sensitivity factor. As shown in Figure 10a, for a small sensor capacitance, the sensitivity factor is increased by increasing the gain. For this condition, the effect of the loading factor is dominant over the thermal noise and because of the assumed technology limitation, the loading factor cannot be reduced. For a larger sensor capacitance, an increasing gain leads to an initial decrease in the sensitivity factor and then an increase is observed. This is because the effect of the thermal noise is dominant for small gain increases but for a large increase, the effect of loading factor becomes important. As shown in Figure 10b, for a small gain, the gain of the first amplifier is equal to the total gain. As the gain is increased, the ratio drops. The value of the total gain for which the ratio starts dropping depends on the sensor capacitance. However, the gain of the first amplifier cannot be as small as 1 because of the limitation in decreasing the transistor length and this results in a larger sensitivity factor compared to the original DCA for the same condition.
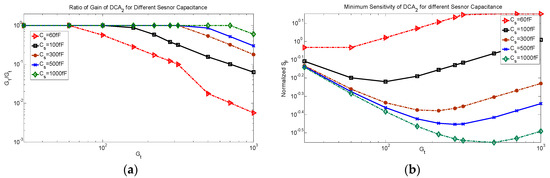
Figure 10.
(a) Normalized minimum sensitivity factor of DCA2 for different total gain and (b) ratio of the gain of first amplifier to the total gain to reach the minimum sensitivity.
To illustrate the difference in the minimum sensitivity factor between the DCA and DCA2, the ratio of the sensitivity factor of DCA to DCA2 is shown in Figure 11. Based on the sensor capacitance and the total gain, this ratio can be very different. For a small gain, this ratio is 1 because all amplification is done in the first stage. When the gain is increased, this ratio is increased and becomes larger for a smaller sensor capacitance. This is because the DCA can be designed to have an insignificant loading factor, which is important in systems that require a high gain and have a small sensor capacitance.
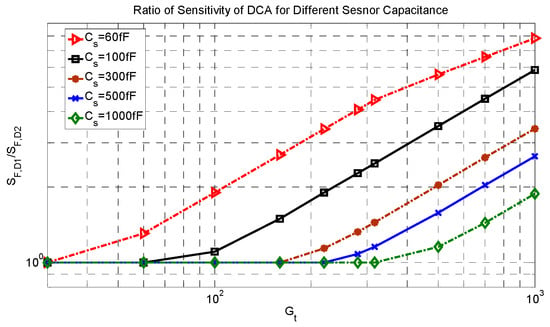
Figure 11.
Ratio of the minimum sensitivity factor between the DCA and DCA2.
5. Comparison of the Three Chopping Techniques
Based on the total gain required and the sensor capacitance, the sensitivity factor of each chopping technique is different. For a given gain and sensor capacitance, one of the chopping techniques has the smallest sensitivity factor. In this section, the suitable chopping technique is identified for different required gains and sensor capacitances in order to reach the best possible sensitivity. The minimum sensitivity factor is extracted for a particular value of K in each technique. Based on the total gain and sensor capacitance, each of these techniques can have the smallest sensitivity factor for a given range of K. To determine the best chopping technique, their sensitivities are compared to each other for different gains and sensor capacitances. For this purpose, the sensitivity factors are compared and the chopping technique with the smaller sensitivity factor within a given range of K is determined. For example, to achieve a better sensitivity factor in DCA2 compared to the SCA, the following should be valid:
Rewriting (33) based on the minimum sensitivity of DCA2 and the SCA, the following is obtained:
Solving for K gives the values of K for which DCA2 has a better sensitivity factor than the SCA. The left side of (34) is a quadratic equation with variable and (34) is valid if the discriminant Δ shown in (35) is larger than 0.
If is smaller than 0, Equation (34) cannot be valid which implies that the SCA has better performance than DCA2. If is larger than 0, DCA2 has better performance for that particular range of K.
In a similar fashion, by comparing the sensitivity factors of the chopping techniques, the equation related to their sensitivities can be derived and the preferred chopping technique can be determined for a given range of K.
Figure 12 shows the chopping technique with the smaller sensitivity factor based on the sensor capacitance and total gain. Sensitivity factors of the SCA, TCA and DCA2 are compared to each other and the chopping technique with the smaller sensitivity factor is shown in Figure 12a. As shown in this figure, at the smaller gain, the SCA can have the better sensitivity, as shown in the blue region. The yellow region represents the area where both TCA and DCA2 have the best possible sensitivity factor and are better suited than the SCA. At a larger gain and smaller sensor capacitance, DCA2 has a better possible sensitivity factor, shown in the red region. The sensitivity factors of the SCA, TCA and DCA are compared in Figure 12b. The red region is where the DCA has a better sensitivity factor. The TCA and DCA have the same sensitivity factor over the yellow region and the SCA has the smaller sensitivity factor over the blue region. Accordingly, when the desired gain increases or the sensor capacitance decreases, the DCA achieves better performance. At a small required gain, the SCA is preferred. For an increased gain, both the TCA and DCA can be used to reach a smaller sensitivity factor. However, for a large gain and small sensor capacitance, the DCA is preferred because it can be designed to attain a better sensitivity because of its reduced loading factor. To show the scale at which the sensitivity factor can be improved with the DCA or TCA in comparison to the SCA, different ratios of sensitivity factors are shown in Figure 13.
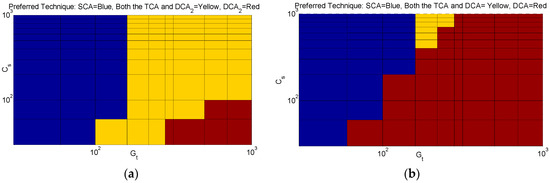
Figure 12.
(a) Preferred chopping technique between SCA, TCA and DCA2 and (b) preferred chopping technique between SCA, TCA and DCA (for different total gain and sensor capacitance).
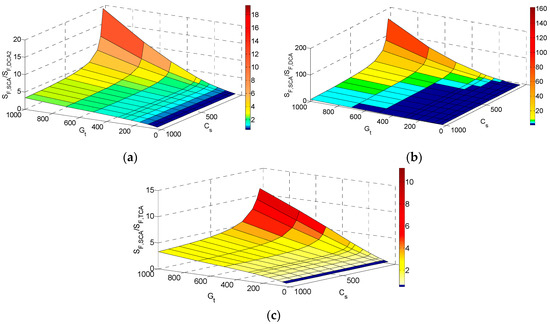
Figure 13.
Ratio of minimum sensitivity factor between (a) SCA & DCA2, (b) SCA & DCA and (c) SCA & TCA.
6. Design Methodology
In this section, a methodology for designing a signal conditioning chopping circuit with the best performance is described. If the sensor capacitance and the desired gain are known specifications, the signal conditioning circuit can be designed with the proper chopping technique to have the minimum sensitivity factor or to have the desired sensitivity with the lowest power consumption.
The design flow graph for this design is shown in Figure 14. As shown in this graph, a reference amplifier is considered based on the total required gain and the given sensor capacitance. This reference amplifier should have a valid relationship between the bandwidth and the noise corner frequency as defined in (4) and it is used to extract the characteristics of the amplifiers for different gains while also ensuring valid relationships between the bandwidth and noise corner frequency. Moreover, characteristics of the amplifier with the minimum possible length for the input transistors are extracted. In addition, the sensitivity factor of the circuit with the minimum power consumption is determined based on the reference amplifier.
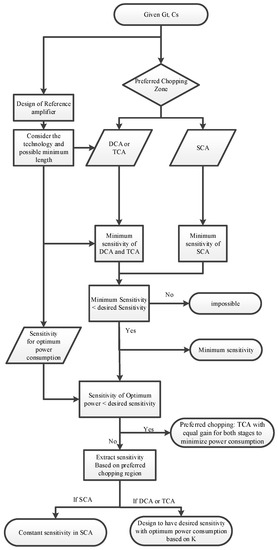
Figure 14.
Flow graph of the preferred chopping technique based on total gain and sensor capacitance.
As shown in the flow graph, the preferred chopping technique in order to have the smallest sensitivity factor for a given total gain and sensor capacitance can be extracted based on Figure 12. If the preferred chopping technique is the SCA, then the minimum sensitivity factor is calculated from (33) and if the preferred chopping technique is the DCA or TCA, the minimum sensitivity factor can be calculated based on (35) for the DCA or (34) for the TCA. It is noted that in designing the minimum sensitivity factor of the DCA, the input transistor length of the first amplifier must be compatible with the minimum length allowed in the chosen technology.
In the next step, the calculated minimum sensitivity factor is compared with the desired sensitivity factor. It is impossible to have a sensitivity factor smaller than the calculated minimum sensitivity factor; but if the desired sensitivity factor is larger, then the circuit can be designed to optimize power consumption for the desired sensitivity factor. In the case of the TCA, minimum power consumption is reached by setting the same gain for the two stages. If the desired sensitivity factor is larger than the sensitivity factor of the amplifier with optimized power consumption, then the preferred chopping technique with the smallest power consumption is the TCA with the same amplification in each stage. However, if the desired sensitivity factor is smaller than the sensitivity factor of the optimized power consumption amplifier; then the sensitivity factor will be defined based on the preferred chopping region. If the preferred chopping region warrants the use of the SCA, then the value of the sensitivity factor is constant and defined by the relevant equation (e.g., (21)). If the preferred chopping region requires the use of the TCA or the DCA, then based on the distribution of gain between the two stages, there is a range for which the sensitivity factor can be equal or smaller than the desired sensitivity factor. In this case, K must be chosen properly to achieve the desired power consumption and sensitivity factor.
7. Conclusions
In this work, it was shown that both the noise and input parasitic capacitance are important factors in determining the sensitivity factor of an interface circuit for a capacitive sensor. Moreover, different methods of varying the gain of the circuit can also affect power consumption and should be considered carefully.
A sensitivity factor was defined based on the noise and input parasitic capacitance to be able to compare the sensitivity factor obtained in different conditions. The three chopping techniques of the DCA, SCA and TCA were considered and their sensitivities for different gains and sensor capacitances were analyzed. Different possible designs were analyzed and the resulting sensitivity factor was extracted. It was shown that the distribution of gain between the two stages in the DCA and TCA has a significant effect on the sensitivity factor and based on this distribution, the sensitivity factor and power consumption vary significantly. For a large gain and small sensor capacitance, the effect of the loading factor is dominant and the DCA has an extra degree of freedom to decrease the input capacitance of the first amplifier and decrease the loading factor, contributing to a smaller sensitivity factor. For a small gain and large sensor capacitance, the capacitance loading factor is small so the SCA can be suitable. The DCA has the smallest sensitivity factor and is the most suitable for a small sensor capacitance and large required gains. In this condition, the gain of the first amplifier of the DCA can be set 1 to act as a parasitic capacitance buffer and reduce the capacitive loading effect of the amplifier to minimize the sensitivity factor. For a moderate gain and large sensor capacitance, the TCA is preferred. Moreover, the lowest power consumption is obtained by using the TCA with the same gain for the first and second amplifiers, if that architecture is well suited to the required sensitivity.
Accordingly, this work has presented an analysis of three chopping architectures that can be selected when designing a capacitive interface circuit and it has outlined the design constraints and guidelines to achieve a well-designed sensing system that ensures that the required gain can be achieved without degrading sensitivity because of capacitive loading. It has also outlined considerations to reduce the power consumption of the designed circuit by preventing the over-design of the amplifier characteristics.
Acknowledgments
This work was supported by funding from the Regroupement Stratégique en Microsystèmes du Québec (ReSMiQ) and the Natural Sciences and Engineering Research Council of Canada (NSERC).
Author Contributions
P.V. performed the analysis; K.A. and F.N. gave direction and analyzed the data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, L.; Rieutort-Louis, W.; Gualdino, A.; Teagno, L.; Hu, Y.; Mouro, J.; Sanz-Robinson, J.; Sturm, J.C.; Wagner, S.; Chu, V.; et al. A System Based on Capacitive Interfacing of CMOS with Post-Processed Thin-Film MEMS Resonators Employing Synchronous Readout for Parasitic Nulling. IEEE J. Solid-State Circuit 2015, 50, 1002–1015. [Google Scholar] [CrossRef]
- Meng, Y.; Dean, R.N. A Technique for Improving the Linear Operating Range for a Relative Phase Delay Capacitive Sensor Interface Circuit. IEEE Trans. Instrum. Meas. 2016, 65, 624–630. [Google Scholar] [CrossRef]
- Liu, J.C.; Hsiung, Y.S.; Lu, M.S.C. A CMOS Micromachined Capacitive Sensor Array for Fingerprint Detection. IEEE Sens. J. 2012, 12, 1004–1010. [Google Scholar] [CrossRef]
- Hao, X.; Tanaka, S.; Masuda, A.; Nakamura, J.; Sudoh, K.; Maenaka, K.; Takao, H.; Higuchi, K. Application of Silicon on Nothing Structure for Developing a Novel Capacitive Absolute Pressure Sensor. IEEE Sens. J. 2014, 14, 808–815. [Google Scholar] [CrossRef]
- Han, J.; Shannon, M.A. Smooth Contact Capacitive Pressure Sensors in Touch- and Peeling-Mode Operation. IEEE Sens. J. 2009, 9, 199–206. [Google Scholar] [CrossRef]
- Jiangfeng, W.; Fedder, G.K.; Carley, L.R. A low-noise low-offset capacitive sensing amplifier for a 50 monolithic CMOS MEMS accelerometer. IEEE J. Solid-State Circuits 2004, 39, 722–730. [Google Scholar] [CrossRef]
- Hafizi-Moori, S.; Cretu, E. Weakly-Coupled Resonators in Capacitive Readout Circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 337–346. [Google Scholar] [CrossRef]
- Tavakoli, M.; Sarpeshkar, R. An offset-canceling low-noise lock-in architecture for capacitive sensing. IEEE J. Solid-State Circuits 2003, 38, 244–253. [Google Scholar] [CrossRef]
- Witte, J.F.; Makinwa, K.A.A.; Huijsing, J.H. A CMOS Chopper Offset-Stabilized Opamp. IEEE J. Solid-State Circuits 2007, 42, 1529–1535. [Google Scholar] [CrossRef]
- Enz, C.C.; Temes, G.C. Circuit techniques for reducing the effects of op-amp imperfections: autozeroing, correlated double sampling, and chopper stabilization. Proc. IEEE 1996, 84, 1584–1614. [Google Scholar] [CrossRef]
- Belloni, M.; Bonizzoni, E.; Fornasari, A.; Maloberti, F. A Micropower Chopper—CDS Operational Amplifier. IEEE J. Solid-State Circuits 2010, 45, 2521–2529. [Google Scholar] [CrossRef]
- Pertijs, M.A.P.; Kindt, W.J. A 140 dB-CMRR Current-Feedback Instrumentation Amplifier Employing Ping-Pong Auto-Zeroing and Chopping. IEEE J. Solid-State Circuits 2010, 45, 2044–2056. [Google Scholar] [CrossRef]
- Fan, Q.; Huijsing, J.H.; Makinwa, K.A.A. A 21 nV/ Chopper-Stabilized Multi-Path Current-Feedback Instrumentation Amplifier With 2 μV Offset. IEEE J. Solid-State Circuits 2012, 47, 464–475. [Google Scholar]
- Sun, H.; Fang, D.; Jia, K.; Maarouf, F.; Qu, H.; Xie, H. A Low-Power Low-Noise Dual-Chopper Amplifier for Capacitive CMOS-MEMS Accelerometers. IEEE Sens. J. 2011, 11, 925–933. [Google Scholar] [CrossRef]
- Yaul, F.M.; Chandrakasan, A.P. A sub-µW 36nV/ chopper amplifier for sensors using a noise-efficient inverter-based 0.2V-supply input stage. In Proceedings of the 2016 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 94–95. [Google Scholar]
- Ong, G.T.; Chan, P.K. A Power-Aware Chopper-Stabilized Instrumentation Amplifier for Resistive Wheatstone Bridge Sensors. IEEE Trans. Instrum. Meas. 2014, 63, 2253–2263. [Google Scholar] [CrossRef]
- Qu, H.; Fang, D.; Xie, H. A Monolithic CMOS-MEMS 3-Axis Accelerometer with a Low-Noise, Low-Power Dual-Chopper Amplifier. IEEE Sens. J. 2008, 8, 1511–1518. [Google Scholar]
- Hongzhi, S.; Fares, M.; Deyou, F.; Kemiao, J.; Huikai, M. An improved low-power low-noise dual-chopper amplifier for capacitive CMOS-MEMS accelerometers. In Proceedings of the 2008 3rd IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Sanya, China, 6–9 January 2008; pp. 1075–1080. [Google Scholar]
- Bakker, A.; Thiele, K.; Huijsing, J.H. A CMOS nested-chopper instrumentation amplifier with 100-nV offset. IEEE J. Solid-State Circuits 2000, 35, 1877–1883. [Google Scholar] [CrossRef]
- Wu, R.; Makinwa, K.A.A.; Huijsing, J.H. A Chopper Current-Feedback Instrumentation Amplifier with a 1 mHz 1/f Noise Corner and an AC-Coupled Ripple Reduction Loop. IEEE J. Solid-State Circuits 2009, 44, 3232–3243. [Google Scholar] [CrossRef]
- Fan, Q.; Huijsing, J.; Makinwa, K. A capacitively coupled chopper instrumentation amplifier with a ±30 V common-mode range, 160 dB CMRR and 5 µV offset. In Proceedings of the 2012 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 19–23 February 2012; pp. 374–376. [Google Scholar]
- Rahal, M.; Demosthenous, A. A Synchronous Chopping Demodulator and Implementation for High-Frequency Inductive Position Sensors. IEEE Trans. Instrum. Meas. 2009, 58, 3693–3701. [Google Scholar] [CrossRef]
- Kassanos, P.; Constantinou, L.; Triantis, I.F.; Demosthenous, A. An Integrated Analog Readout for Multi-Frequency Bioimpedance Measurements. IEEE Sens. J. 2014, 14, 2792–2800. [Google Scholar] [CrossRef]
- Wu, R.; Huijsing, J.H.; Makinwa, K.A.A. A 21b ±40 mV range read-out IC for bridge transducers. In Proceedings of the 2011 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2011; pp. 110–112. [Google Scholar]
- Shiah, J.; Mirabbasi, S. A 5-V 290-µW Low-Noise Chopper-Stabilized Capacitive-Sensor Readout Circuit in 0.8-µm CMOS Using a Correlated-Level-Shifting Technique. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 254–258. [Google Scholar]
- Gray, P.R.; Hurst, P.J.; Lewis, S.H.; Meyer, R.G. Analysis and Design of Analog Integrated Circuits, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990; ISBN 0470245999. [Google Scholar]
- Fang, D. Low-Noise and Low-Power Interface Circuits Design for Integrated CMOS-MEMS Interial Sensors. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2006. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).