Abstract
Power optimization is a very important and challenging step in the physical design flow, and it is a critical success factor of an application-specific integrated circuit (ASIC) chip. Many techniques are used by the place and route (P&R) electronic design automation (EDA) tools to meet the power requirement. In this paper, we will evaluate, independently from the library file, the impact of redefining the max transition constraint (MTC) before the power optimization phase, and we will study the impact of over-constraining or under-constraining a design on power in order to find the best trade-off between design constraining and power optimization. Experimental results showed that power optimization depends on the applied MTC and that the MTC value corresponding to the best power reduction results is different from the default MTC. By using a new MTC definition method on several designs, we found that the power gain between the default methodology and the new one reaches 2.34%.
1. Introduction
The energy consumption in integrated circuits has been a challenge for designers for many years due to the continuous increase of devices density, speed, and complexity. This challenge is more accentuated in battery-powered devices since low-power devices provide more reliability for the battery life cycle.
Power dissipation in CMOS logic arises from the following sources:
- dynamic power dissipation due to the charging and discharging of different parasitic capacitances [1];
- dynamic power dissipation due to a short-circuit current, when both n-channel and p-channel transistors are momentarily on at the same time [1];
- static power dissipation due to a leakage current and a subthreshold current [1].
In order to minimize power dissipation, low-power considerations should be applied at all levels of design abstraction and design activities. Low-power design techniques and methodologies have been widely reported, each taking place at a very specific stage of the design flow (register transfer level (RTL), logical synthesis or physical synthesis). Examples of such methodologies include dynamic voltage and frequency scaling (DVFS) [2], parallel architecture [3], clock gating [4], and power gating [5].
During physical design, power reduction techniques are quite limited if compared with other techniques at higher abstraction levels. However, such techniques can have a major impact because some circuits are repeated thousands of times on a chip. Therefore, circuit techniques with small percentage improvements should not be overlooked.
The voltage and frequency in the place and route (P&R) phase are defined as a hard constraint in the specification. The only remaining factors to play with during power optimization are the transition time of signals (slew), the threshold voltage of standard cells, the switching activity of different inputs, the cell placement, and the net routing.
The best known power optimization techniques used in physical design are gate sizing/spacing, buffer/inverter insertion, equivalent pin reordering, logic remapping, critical net re-routing, the use of non-default routing rules, and high-voltage threshold (HVT) cells.
During power optimization, the P&R tools try different methods on each target/cell in order to reduce power (dynamic or leakage). An optimization is accepted if it improves the power without violating the costing criteria, which is a function of the timing (setup and hold), and the electrical design rule constraints (EDRCs) (max transition and max capacitance constraints).
The max transition constraint (MTC) is defined by the designer from the library (.lib) file, which characterizes the standard cells used in the design. This MTC is used by different P&R engines through the physical design flow to provide a clean design layout to the foundry.
In this paper, we will assess the quality of the default MTC definition methodology used by P&R tools, and we will study its impact on power reduction capabilities. We will also evaluate the impact and benefits of redefining the MTC before power optimization phase independently from the library file. By redefining the MTC, we aim to examine the impact of over-constraining and under-constraining a design on power and to find the best trade-off between design constraining and power optimization.
The remainder of this work is organized as follows. Section 2 presents some basic concepts of power calculation and optimization. Section 3 provides two case studies. Section 4 applies the new approach on a wide variety of designs with different technological nodes. Finally, Section 5 draws the conclusion.
2. The Basic Concept of Power Calculation and Optimization
The energy consumed in an integrated circuit (IC) can be split into two main branches:
A static power dissipation related to the logical states of the circuit. In CMOS logic, the leakage current and subthreshold current are the only sources of static power dissipation.
A dynamic power dissipation, which is caused by the switching activity of the circuit. A higher operating frequency leads to more frequent switching activities in the circuit and results in increased power dissipation. The most significant source of dynamic power dissipation in CMOS circuits is the charging and discharging of capacitances. Sometimes, capacitors are intentionally fabricated to achieve certain non-digital operations. However, most digital CMOS circuits do not require capacitors for their intended operations. The capacitance forms due to the parasitic effects of interconnection wires and transistors, such parasitic capacitance cannot be avoided and it has a significant impact on power dissipation [6].
As demonstrated in [6], from the simplified inverter RC network, the dynamic power due to switching current of a CMOS gate (Psw) can be estimated by Equation (1).
where
- Sw is the switching activity of the input,
- f is the frequency of operation,
- CL is the load parasitic capacitance, and
- VDD is the voltage swing across the capacitor.
In [6], the dynamic power due to short circuit current (Psc) is estimated by Equation (2):
where
- β is the size of the transistors,
- τ is the duration of the input signal (transition time), and
- Vth is the threshold voltage of the PMOS and NMOS transistors.
Thus, we can reduce power dissipation of a gate by
- reducing switching activity;
- reducing parasitic capacitance;
- reducing transition time;
- increasing the threshold voltages of PMOS and NMOS.
The most known circuit level techniques to reduce the dynamic power are gate sizing, equivalent pin reordering, logic remapping, and HVT cell usage.
Gate sizing is very useful in reducing power [7,8]. It consists of substituting the big cells that are in the non-timing critical path by smaller gates that satisfy the delay requirement with identical logical function. Such a technique is widely used in the industry for timing, area [9,10], and power optimization [7,10].
Equivalent pin reordering consists of connecting the input with high capacitance to the net with low switching activity since most combinational digital gates found in a cell library have input pins that are equivalent (e.g., ANDs, ORs, and XORs). Logically equivalent pins may not have identical circuit characteristics, which means that the pins have a different delay or power consumption. Such a property can be exploited for a low-power design [11].
Net Re-routing: This technique tries to re-route nets with high parasitic capacitances in a lower congested area to reduce the parasitic capacitance caused by neighboring wires [12,13].
The use of HVT cells in non-timing critical paths: A leakage current is inversely exponential to Vth; therefore, by using high-threshold voltage cells, the amount of leakage current and hence the leakage power is reduced [14,15].
During the physical design phase, the above techniques are used to optimize power consumption depending on the stage of the design. For example, power optimization at placement stage aims to optimize the placement from a power point of view, which implies the downsizing or remapping of big cells on sub-critical paths [16,17]. Similarly, in CTS (clock tree synthesis) stage, the clock tree quality plays a very important role in power reduction because it is the longest net and drives the biggest load in the circuit (all the synchronized elements). Many considerations are taken to reduce power dissipation in the clock network [18].
At the routing stage, most power optimization techniques deal with wires and via capacitance and resistance reduction. Some non-default routing rules and long net re-routing techniques are used for this purpose [19].
After routing is complete, new timing, electrical, and routing design rule violations (DRVs) appear. The timer at this stage deduce the coupling noise between metal lines and provide more accurate timing and power pictures, so another round of optimization is needed to clean the design [20].
3. Max Transition Variation Impact on Power Optimization (Case Study)
The transition time is the time needed for a signal to pass from 10% to 90% or from 20% to 80% of its final state. The delay of a cell can be deduced from the standard cell library, it is a function of input transition time and output capacitance load. During the cell characterization phase, the library’s developers calculate using the cell’s SPICE models, the cell’s delay, and the output transition for each input transition and output load combination.
Additionally, they define the max transition and max capacitance, which represent the limits of where the cell is characterized. Those values are used as constraints by P&R tools to extract the delay and power of the design. Users can also impose new max transition or max capacitance constraints; in this case, the P&R tools use the most pessimistic value between the user-defined values and the library values.
When applying a max transition constraint on a design, the tool considers all transitions greater than this max transition as violations and tries to fix them by upsizing the drivers, downsizing the loads, or inserting buffers to split the loads. If the tool is over-constrained, it will see many violations and will try to fix them, which will lead to upsizing and buffer insertion of many cells. Under-constraining the tool will also hide certain targets where downsizing is possible. Both scenarios impact power reduction capabilities.
Most of the published research on power reduction techniques at the circuit level adopt a bottom-up methodology and treat the power issue on a gate level [7,8,9], which means that they prove the effectiveness of a technique on a design with few gates and then try to generalize on multi-million gates designs. In some cases, if we apply such a technique on a gate, the power and timing of neighboring gates may be impacted, as presented in [8].
By examining the global picture of the physical design flow, we noticed that global constraints that affect power optimization, such as the MTC, are left to their default values. Usually, the MTC is defined based on the timing library file (.lib) by taking the average max transition of all lib cells’, or may be defined by the user in the standard delay constraints file (.sdc), and the tool takes the most pessimistic value between the user-defined and lib-defined MTC values. This value might not be optimal for power optimization and could over-constrain or under-constrain the design.
This section will explore the impact of changing MTC on power reduction capabilities on two different designs, with different sizes and technological nodes. It will first provide a P&R flow used to run the experiments and will then examine the results.
With the aim of evaluating the MTC variation impact on power optimization, we developed the following flow (Flow 1):
| Flow 1: Check MTC Impact on Power Reduction. |
| 1: For Tran ∊ {0… MTCD} do |
| 2: Read Design Database |
| 3: Enable power in all corners |
| 5: Set MTC MTCD |
| 4: Estimate power (Initial value) |
| 5: Set MTC Tran |
| 6: Optimize Power |
| 5: Set MTC MTCD |
| 7: Estimate power (Final value) |
| 8: Evaluate timing impact (setup and hold) |
| 9: END for |
We developed a flow (Flow 1) that varies the max transition constraint (MTC) and evaluates the power improvement after its optimization. First, we set the range of MTC values to explore between 0 and MTC default (MTCD). Then, we loaded the design database, which consists of the netlist, the timing and technology library files, and the timing constraints in Nitro SoC. After that, we enabled the power in all of the design’s corners and estimated the initial power and timing values given by the default MTC. We then applied the max transition constraint (MTC) on the design. We made a pass of power optimization using Nitro SoC optimization engine, and we reset the MTC to MTCD again for comparable results. Finally, we calculated the power reduction and the timing impact for the specific MTC applied using Nitro SoC’s static timing analysis (STA) and power estimation (PE) engines.
3.1. Test Case 1 Results
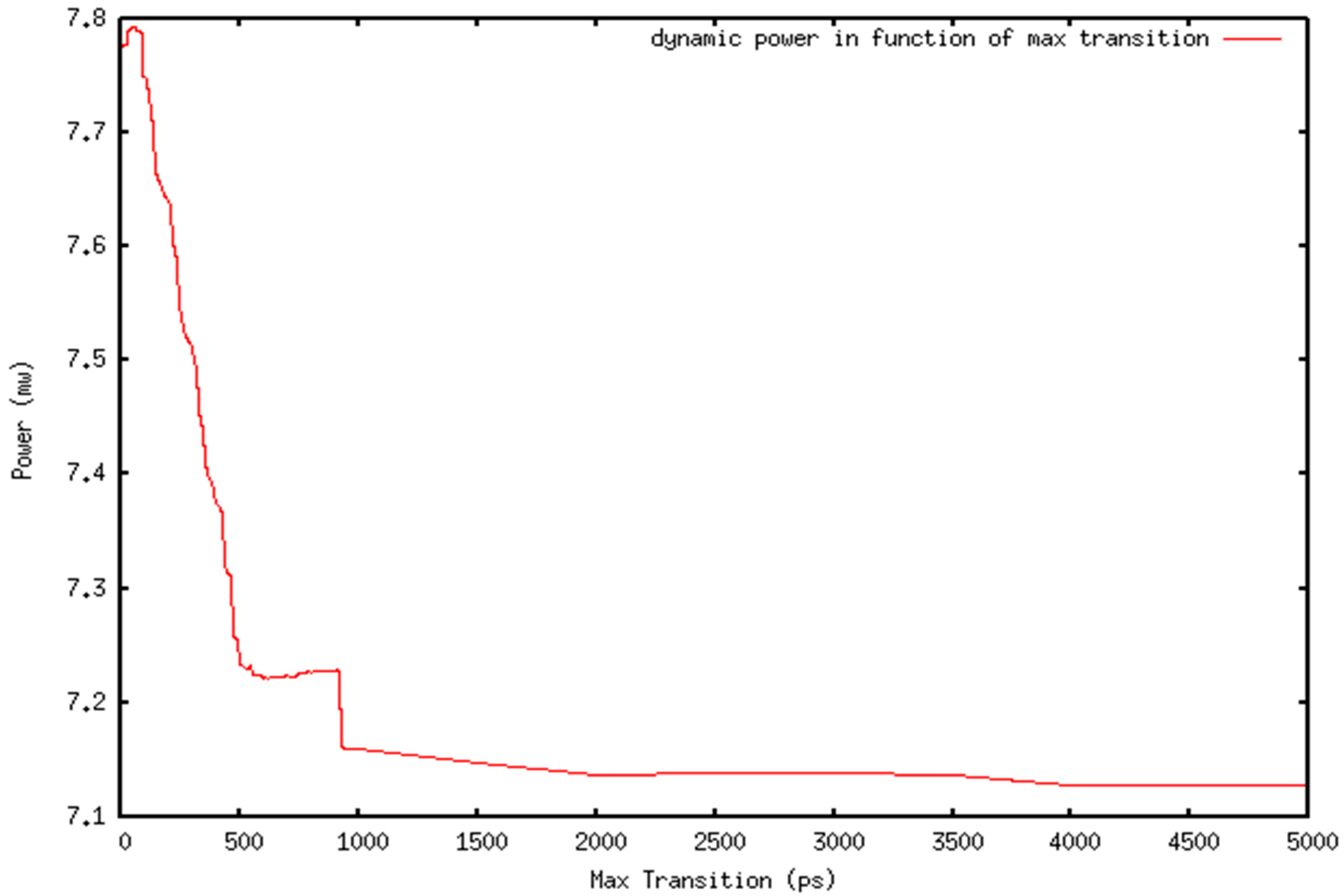
We applied Flow 1 on Test Case 1 (Figure 1), the characteristics of which are summarized in Table 1. We evaluated for an MTC interval of [0 ps–5000 ps], the corresponding power reduction achieved after optimization. The graph in Figure 2 summarizes the results. We noticed that the power dissipation is reduced rapidly as MTC increases until 1000 ps. Then, it still decreases slowly until it reaches 4000 ps. Then, the power reduction is constant. This means that, in order to achieve the optimum power reduction, the MTC should at least be equal to this threshold value. Constraining the design with an MTC less than this threshold value will result in a sub-optimal power dissipation reduction.
Figure 1.
Test Case 1: Schematic and layout views.

Table 1.
Test Case 1 characteristics.
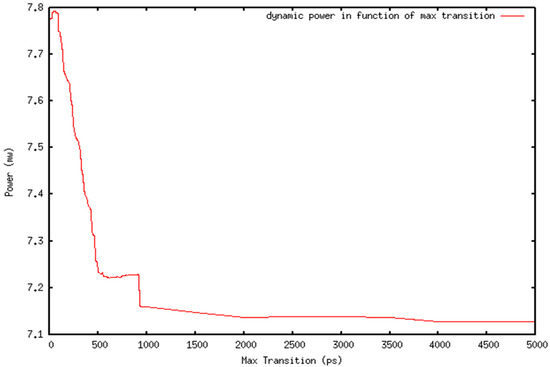
Figure 2.
Power reduction in function of max transition constraint (MTC) applied on Test Case 1.
3.2. Test Case 2 Results
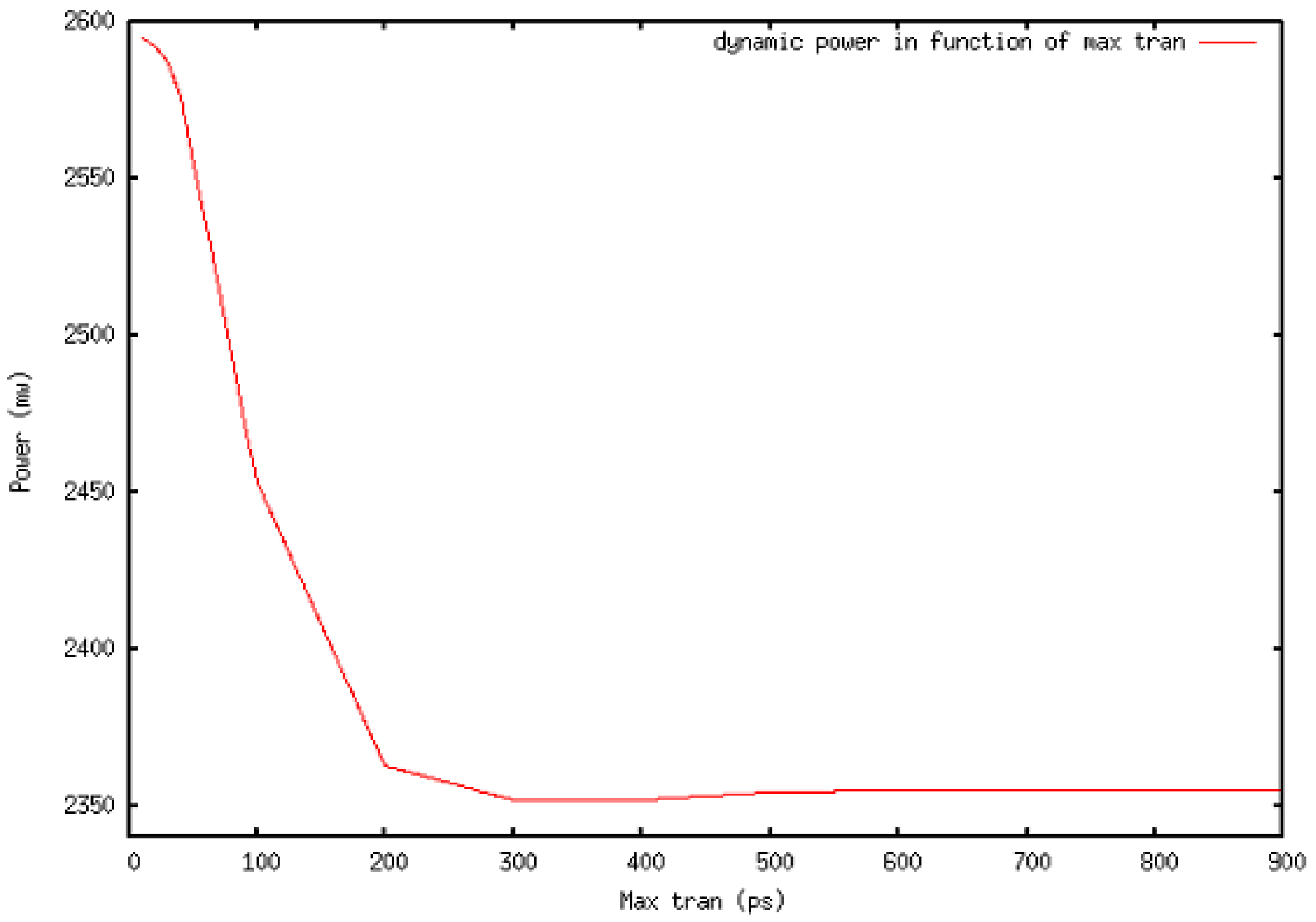
We repeated the same experiment on Test Case 2 (Figure 3), which has the characteristics summarized in Table 2. We estimated for the same MTC interval as Test Case 1, the corresponding power achieved after optimization. The graph in Figure 4 summarizes the results. We noticed that the power dissipation is reduced as MTC increases up to a given threshold (between 200 and 400 ps) and then starts increasing again as MTC continues to rise, which means that for certain MTC intervals the power reduction is optimal and that, by increasing the MTC beyond this interval, we under-constrain the design and hide certain areas of power reduction. Moreover, by decreasing the MTC below this interval, we over-constrain the design, and this results in sub-optimal power reduction.
Figure 3.
Test Case 2: Schematic and layout views.

Table 2.
Test Case 2 characteristics.
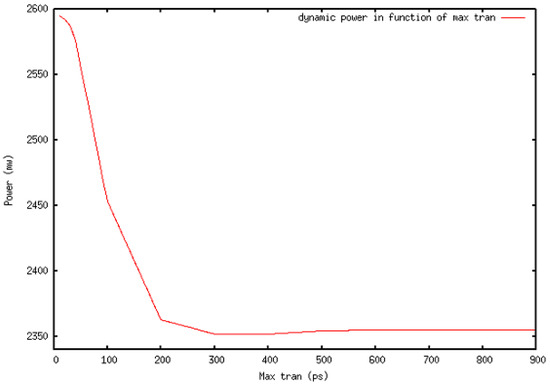
Figure 4.
Power reduction in function of MTC applied on Test Case 2.
4. Experimental Results
The two motivational examples presented in Section 3 provide evidence that the default MTC value is not optimal for power optimization and prove the existence of another MTC range where power optimization achieves the best power reduction gain. However, to detect this MTC interval, many runs are needed, which is runtime- and resource-consuming. Therefore, in order to reduce the runtime and the used resources, we proposed a new algorithm in which we adopted a dichotomous approach, described in Algorithm 1. The algorithm automatically detects the best MTC value needed to attain better power reduction results.
The algorithm first loads the database (file.db), which includes the synthesized netlist, the liberty files, and the technological files. In a second step, it detects the default MTC value in the design (MTCd), then it runs the power optimization and assesses the reference power improvement value (Powerd) and the timing impact. Using a dichotomous approach, it starts to split the interval between MTCd and 0 and calculates the power optimization gain (Power(i)); based on the results, it repeats the same operation in the sub-interval that provides the best power reduction until the interval size is less than a given threshold value. At the end, it returns the MTC sub-interval that provides the best power reduction results.
| Algorithm 1: Optimal MTC Detector |
| 1: Procedure MTCDechotomy () |
| 2: Load the Data Base (file.db) |
| 3: MTCd ← Default MTC value in the design |
| 4: Powerd ← Run_power_optimization (MTCd) |
| 5: Estimate reference power reduction and timing impact |
| 6: Initialize the first 3 MTC values |
| 7: MTC(0) ← 0 |
| 8: MTC(1) ← (MTC(0) + MTC(2))/2 |
| 9: MTC(2) ← 1000 × MTCd |
| 10: While (MTC(i) − MTC(i − 1) > Threshold) do |
| 11: Power(i) ← Run_power_optimization(MTC(i)) |
| 12: Reset the MTC to default value (MTCd) |
| 13: Estimate power reduction and timing impact |
| 14: If Power(i) < Power(i − 1) then |
| 15: MTC(i) ← (MTC(i − 1) + MTC(i − 2))/2 |
| 16: Else |
| 17: MTC(i) ← (MTC(i − 2) + MTC(i − 3))/2 |
| 18: End if |
| 19: End while |
| 20: Return Trans value that gives the min power |
| 21: End procedure |
Applying Algorithm 1 on Test Case 2 produces the results in Table 3. The results indicate that the power varies between 2403 mw when MTC is less than 268, which means that, by choosing an MTC <268, we are over-constraining the design. Additionally, Table 3 indicates that an optimum MTC value is between [251.7–268.5] ps, which corresponds to a power between [2353.2–2352.1] mw. Relaxing the MTC with a value greater than 268.5 means that we are under-constraining the design and that a sub-optimal value, such as MTC = 1074.0, will result. By adopting this dichotomous approach, we were able to detect a good transition value in a few iterations (8 in Test Case 2).

Table 3.
Results of Algorithm 1 on Test Case 2.
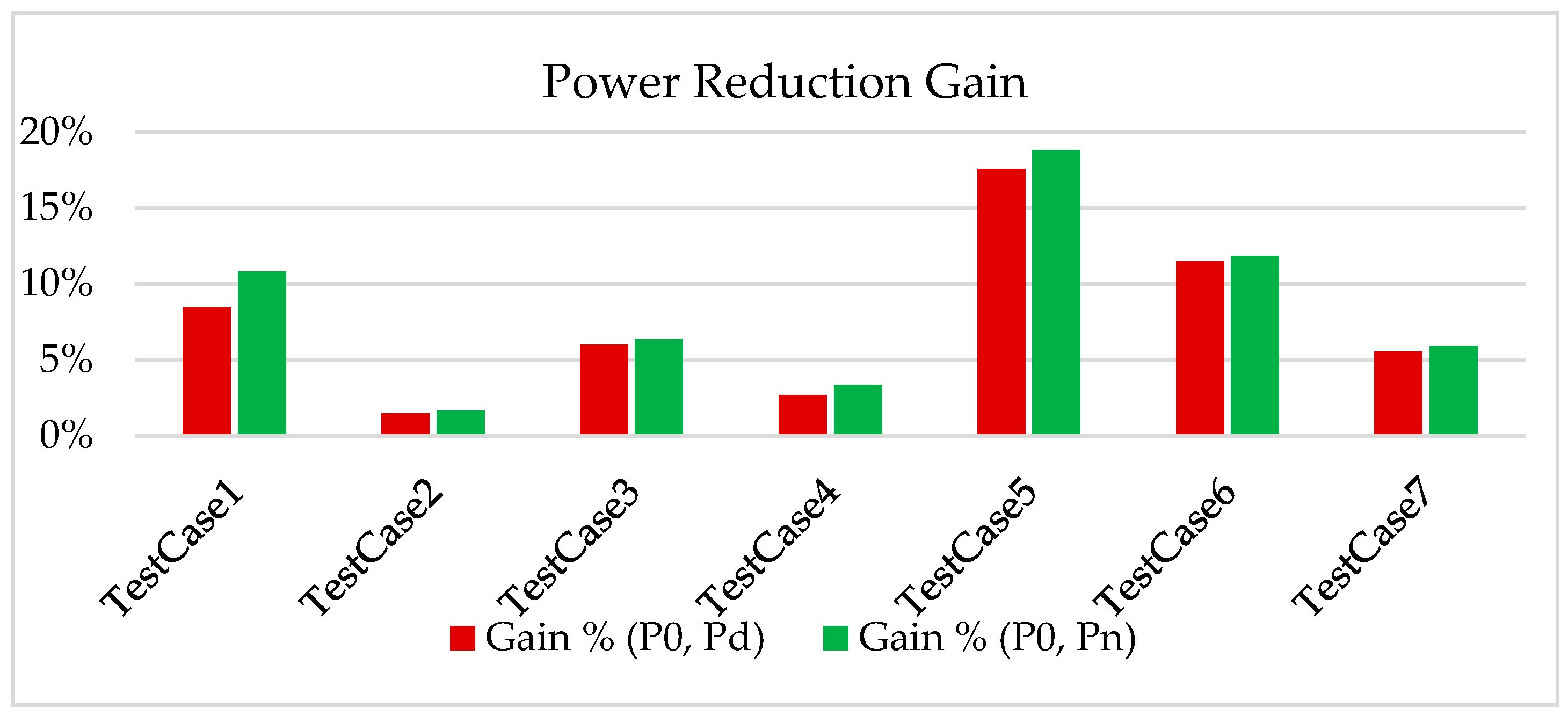
We applied Algorithm 1 on a wide variety of designs, with different sizes and technological nodes using Nitro SoC’s P&R tool. For each design, we reported the initial power (P0) and the default MTC (MTCd) values, ran the power optimization for this default MTCd, reported the final power reduction (Pd (MTCd)), and calculated the default power gain (Gain % (P0, Pd)). After that, we used Algorithm 1 to detect the optimal MTC value (MTCn) and applied it, ran power optimization, and reported the new power reduction (Pn (MTCn)) and the new power gain (Gain % (P0, Pn)). We also reported the timing (setup and hold) for both the default and the newly generated MTC.
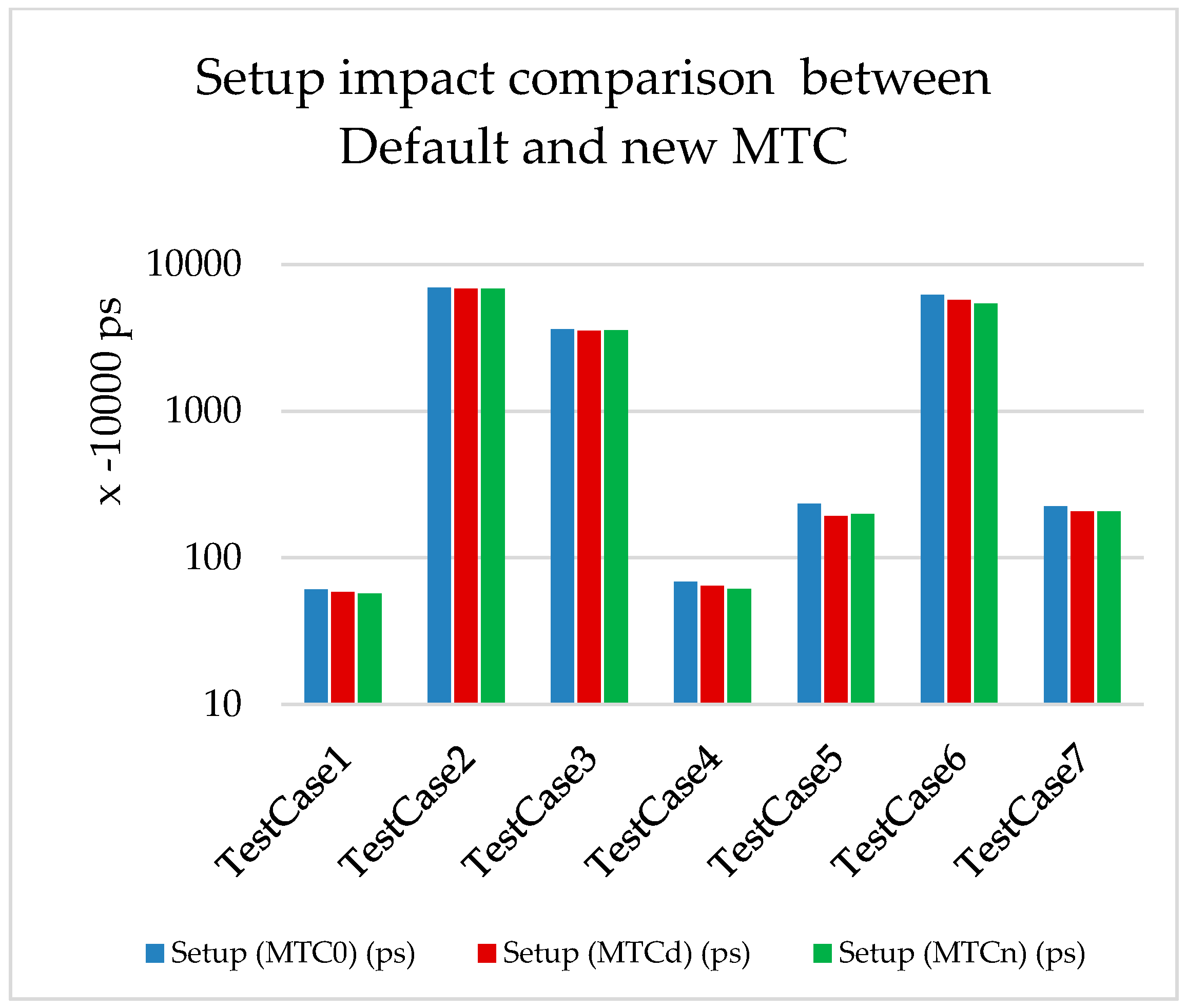
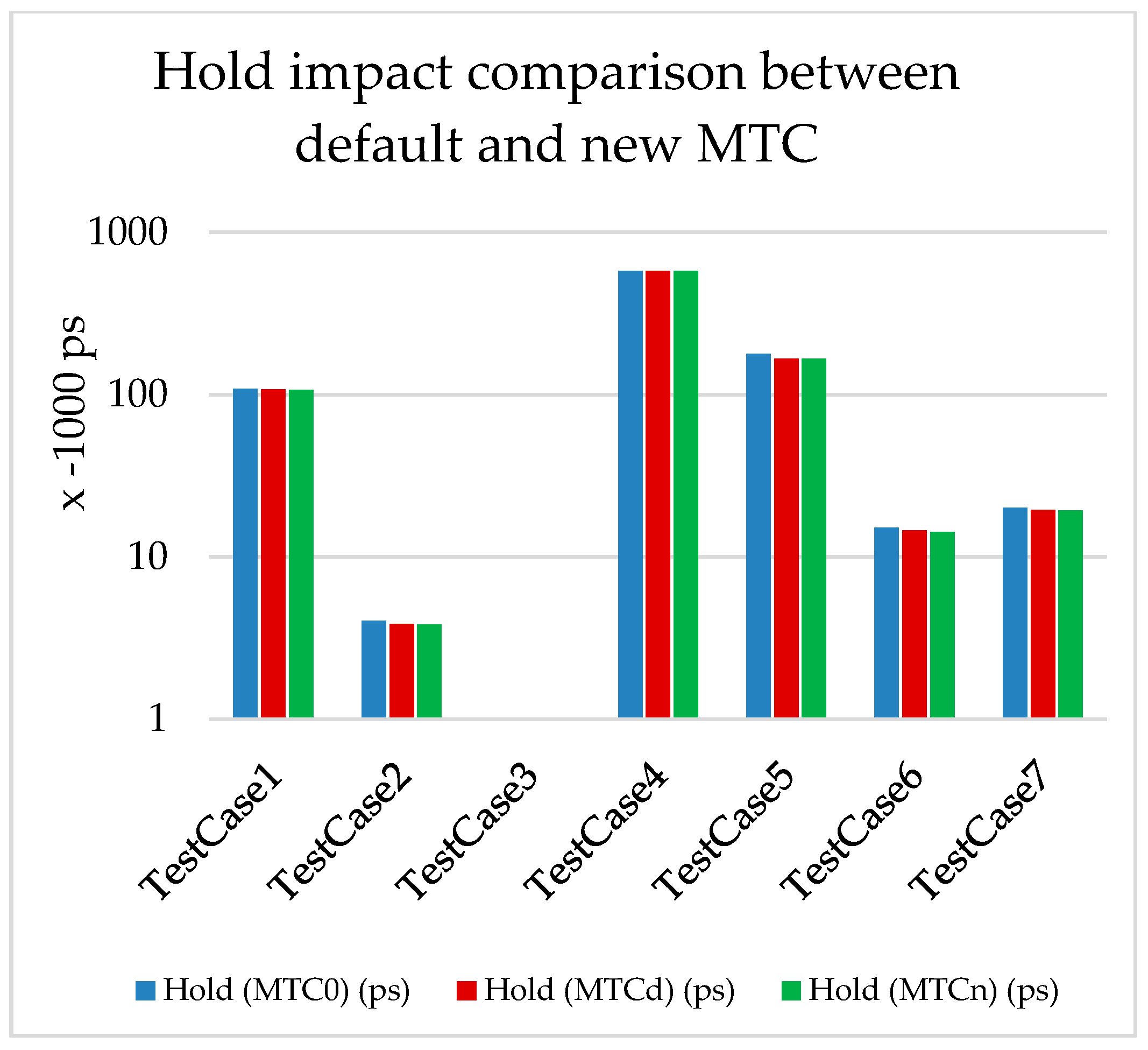
We deduced from the results shown in Table 4 and Figure 5 that, with the default MTC, the average power gain is 38.3%, while it reaches 43.3% with the newly generated MTC. Additionally, we noticed that the timing is better in most cases for both setup and hold (Figure 6 and Figure 7).

Table 4.
Comparison between power reduction with default and newly generated MTCs.
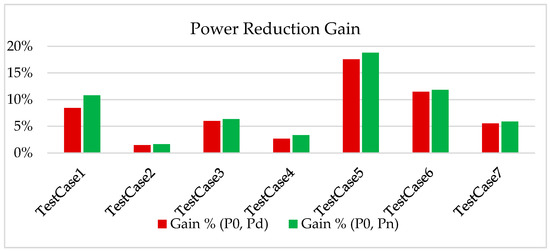
Figure 5.
Power reduction gain of default and new MTCs.
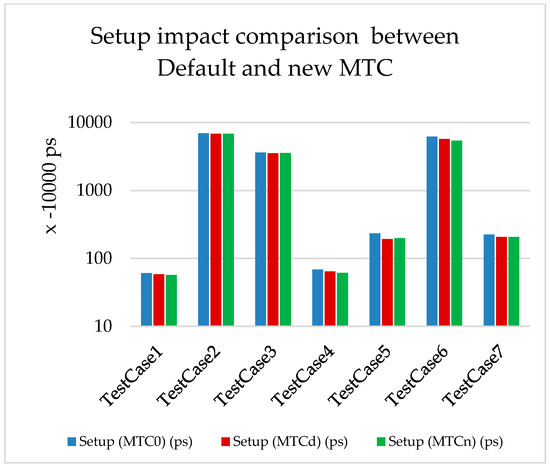
Figure 6.
Timing (Setup) impact for MTCd and MTCn.
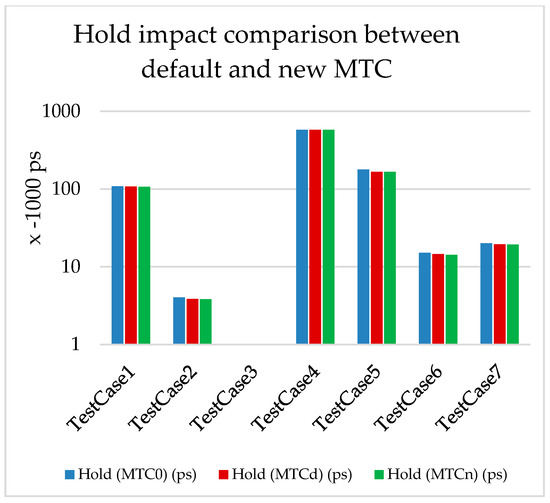
Figure 7.
Timing (Hold) impact for MTCd and MTCn.
The power gain is mainly due to the decrease in short-circuit time, which leads to the decrease in internal power, as per Equation (2). The gain in the setup timing is because of the signal speedup, since the MTCn is smaller than the MTCd in all test cases. The gain in the hold timing is a side effect of the power optimization, as one of the techniques of power optimization is to downsize the cells in the sub-critical paths, which automatically leads to improvements in the paths with hold violations.
In the experiments, we noticed that, by applying MTCs that are too small, we are over-constraining the design. Over-constraining the design forces the optimization engine to reject power improvement solutions due to a max transition-costing violation, which means that, if a solution improves power but violates the MTC, it will be rejected. A large MTC, on the other hand, causes a power increase due to increased short-circuit power, which is a linear function of the transition time. By under-constraining the MTC, we are allowing the design to have large transitions—hence the short circuit power, which is an important component of the dynamic power. Therefore, there is an optimum value in between, which we can find using our algorithm (Algorithm 1).
5. Conclusions
By evaluating the effect of max transition constraint on power optimization over various designs and technological nodes, we demonstrated experimentally that, in order to reduce the power consumption of a System on Chip (SoC) optimally, one should evaluate different values of max transition to well constrain the design before starting power optimization. We also showed that, by adopting this method of max trans evaluation, the gain in power reduction reaches 2.35% in some designs.
The algorithm presented in Section 4 was applied on more than 100 designs, and the obtained results confirmed that careful attention should be taken when constraining a design to drive physical design tools, such as Nitro SoC from Mentor Graphics, and to attain the optimum power reduction.
6. Perspectives
This paper proved the existence of a good MTC value (MTCn) that gives better power reduction results, which is different from the default MTC (MTCd). More work can be done to reduce the runtime of finding the MTCn value by using more efficient analytical techniques other than the dichotomy approach adopted in this paper. Additionally, another dimension may be explored by studying the relationship between the design node, size, structure, and MTC, which may lead to a direct method or equation to find the best MTC without running any experiments.
Acknowledgments
This research was supported by Mentor Graphics Corporation. We thank our colleagues from the ICDS division who provided insight and expertise that greatly assisted the research, although they may not agree with all of the interpretations/conclusions of this paper. We thank Hazem El Tahawy (Mentor Graphics, Managing Director MENA Region) for initiating and supporting this work, Bhardwaj Sarvesh (Group Architect, ICDS P&R Solutions Optimization) for assistance, help and guidelines through the research, and Yanamandala Jay (Architect, Product Validation, ICDS P&R Solutions) for the opportunity to work on such advanced topic.
Author Contributions
Mohamed Chentouf and Alaoui Ismaili Zine El Abidine conceived and designed the experiments; Mohamed Chentouf performed the experiments; Mohamed Chentouf and Alaoui Ismaili Zine El Abidine analyzed the data; contributed reagents/materials/analysis tools; Mohamed Chentouf wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, M.J.S. Application-Specific Integrated Circuits, 9th ed printing; Addison-Wesley: Berkeley, CA, USA, 2001; p. 816. [Google Scholar]
- Ma, D.; Bondade, R. Enabling Power-Efficient DVFS Operations on Silicon. IEEE Circuits Syst. Mag. 2010, 10, 14–30. [Google Scholar] [CrossRef]
- Choi, H.S.; Choi, J.H.; Kim, J.T. Low-Power AES Design Using Parallel Architecture. In Proceedings of the International Conference on Convergence and Hybrid Information Technology (ICHIT ‘08), Daejeon, Korea, 28–30 August 2008. [Google Scholar]
- Melikyan, V.; Babayan, E.; Melikyan, A.; Babayan, D.; Petrosyan, P.; Mkrtchyan, E. Clock gating and multi-VTH low power design methods based on 32/28 nm ORCA processor. In Proceedings of the 2015 IEEE East-West Design & Test Symposium (EWDTS), Batumi, Georgia, 26–29 September 2015. [Google Scholar]
- Jeon, B.; Hong, S.; Kwon, O. A low-power 10-bit single-slope ADC using power gating and multi-clocks for CMOS image sensors. In Proceedings of the 2016 International SoC Design Conference (ISOCC), Jeju, Korea, 23–26 October 2016. [Google Scholar]
- Yeap, G.K. Practical Low Power Digital VLSI Design; Springer: New York, NY, USA, 1998; pp. 175–178. [Google Scholar]
- Beg, A. Automating the CMOS Gate Sizing for Reduced Power/Energy. In Proceedings of the 2014 12th International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 17–19 December 2014. [Google Scholar]
- Livramento, V.D.S.; Guth, C.; Guntzel, J.L.; Johann, M.O. Evaluating the impact of slew on delay and power of neighboring gates in discrete gate sizing. In Proceedings of the 2012 IEEE 3rd Latin American Symposium on Circuits and Systems (LASCAS), Playa del Carmen, Mexico, 29 February–2 March 2012. [Google Scholar]
- Posser, G.; Flach, G.; Wilke, G.; Reis, R. Gate Sizing Minimizing Delay and Area. In Proceedings of the 2011 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Chennai, India, 4–6 July 2011. [Google Scholar]
- Coudert, O. Gate sizing for constrained delay/power/area optimization. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 1997, 5, 465–472. [Google Scholar] [CrossRef]
- Chang, C.; Hsiao, M.; Hu, B.; Wang, K.; Marek-Sadowska, M.; Cheng, C.; Chen, S. Fast postplacement optimization using functional symmetries. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2004, 23, 102–118. [Google Scholar] [CrossRef]
- Kuh, E.S.; Wang, D.; Xue, T. Post Global Routing Crosstalk Risk Estimation and Reduction. In Proceedings of the 1996 IEEE/ACM International Conference on Computer-Aided Design, 1996 (ICCAD-96), Digest of Technical Papers, San Jose, CA, USA, 10–14 November 1996; p. 302. [Google Scholar] [CrossRef]
- Cheng, C.K.; Lillis, L.; Lin, S.; Chang, N. Interconnect Analysis and Synthesis; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Wei, L.; Chen, Z.; Johnson, M.; Roy, K.; De, V. Design and optimization of low voltage high performance dual threshold CMOS circuits. In Proceedings of the Design Automation Conference, San Francisco, CA, USA, 15–19 June 1998. [Google Scholar] [CrossRef]
- Brodersen, R.W.; Horowitz, M.A.; Markovic, D.; Nikolic, B.; Stojanovic, V. Methods for true power minimization. In Proceedings of the IEEE/ACM International Conference on Computer Aided Design, 2002 (ICCAD 2002), San Jose, CA, USA, 10–14 November 2002; pp. 35–42. [Google Scholar]
- Minhas, M.R. Iterative Algorithms for Timing and Low Power Driven VLSI Standard Cell Placement. Master’s Thesis, Department of Computer Engineering, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia, 2001; p. 31261. [Google Scholar]
- Sait, S.M.; Minhas, M.R.; Khan, J.A. Performance and low power driven VLSI standard cell placement using tabu search. In Proceedings of the 2002 Congress on Evolutionary Computation, 2002 (CEC ’02), Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Mahmoodi, H.; Tirumalashetty, V.; Cooke, M.; Roy, K. Ultra Low-Power Clocking Scheme Using Energy Recovery and Clock Gating. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 33–44. [Google Scholar] [CrossRef]
- Zuber, P.; Bahlous, O.; Ilnseher, T.; Ritter, M.; Stechele, W. Wire Topology Optimization for Low Power CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 1–11. [Google Scholar] [CrossRef]
- Nitro-SoC™ and Olympus-SoC™ User’s Manual; Mentor Graphics Corporation: Wilsonville, OR, USA, 2016.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).