Flexible, Scalable and Energy Efficient Bio-Signals Processing on the PULP Platform: A Case Study on Seizure Detection †
Abstract
:1. Introduction
2. Related Work
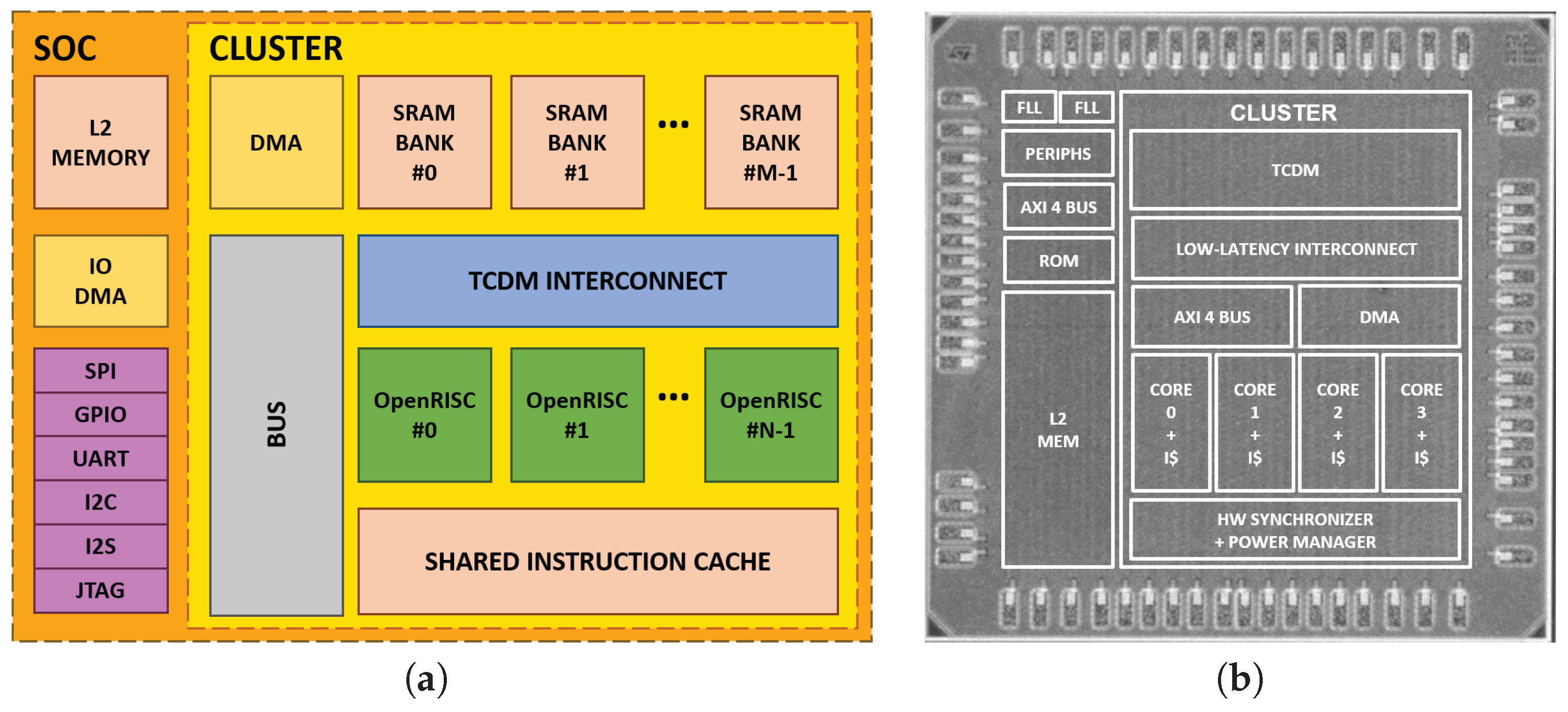
3. PULP Platform
3.1. Cluster Architecture
3.2. SoC Architecture
3.3. Programming Model and Toolchain
4. Seizure Detection on the PULP Architecture
4.1. Seizure Detection Algorithm
4.2. Parallel Implementation on PULP
4.2.1. Dimensionality Reduction
4.2.2. Feature Extraction
4.2.3. Pattern Recognition
4.3. Fixed-Point Implementation
5. Experimental Results
5.1. Experimental Setup
5.2. Seizure Detection Accuracy
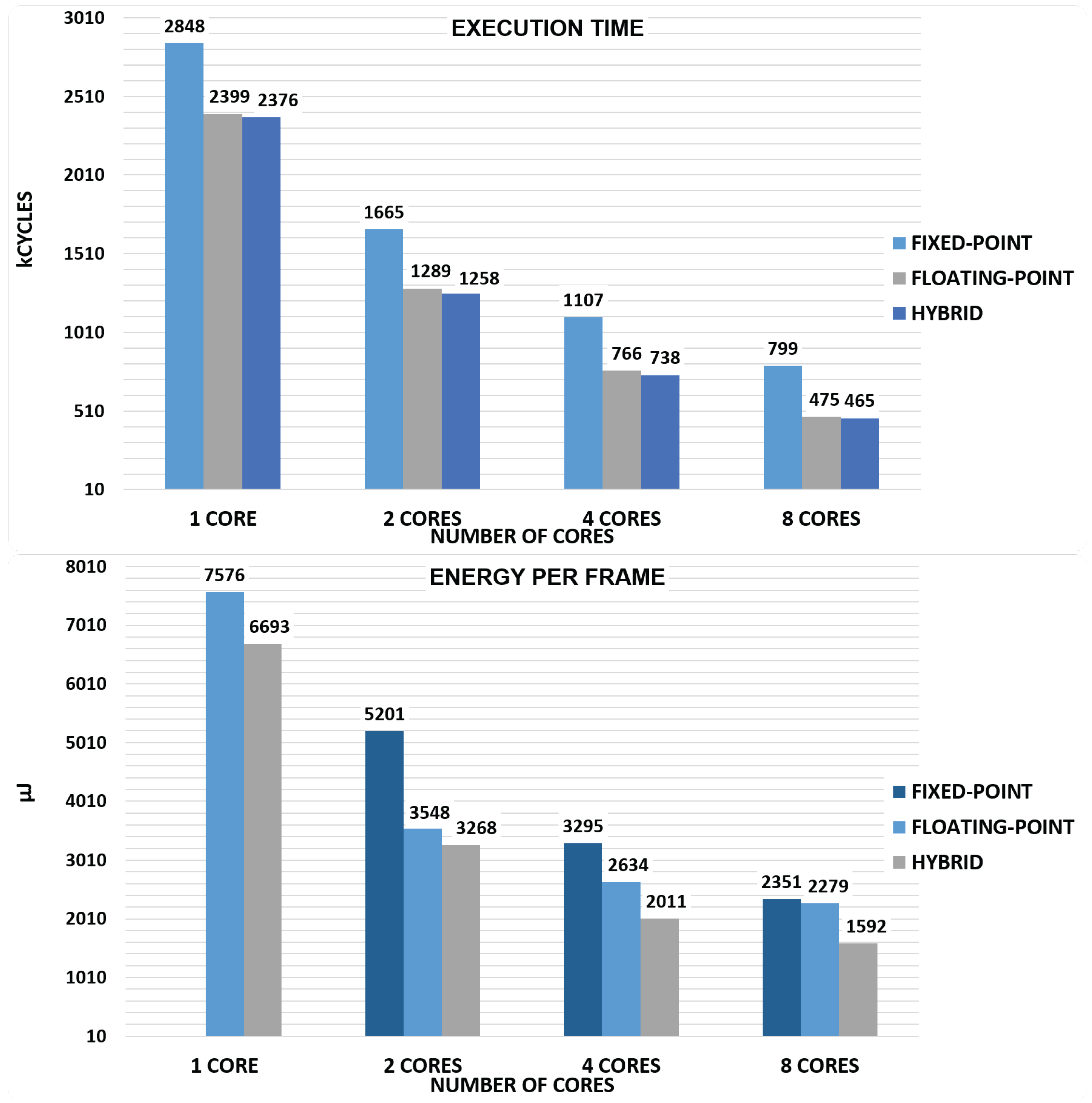
5.3. Evaluation of Execution Performance
5.4. Hybrid Implementation Performance
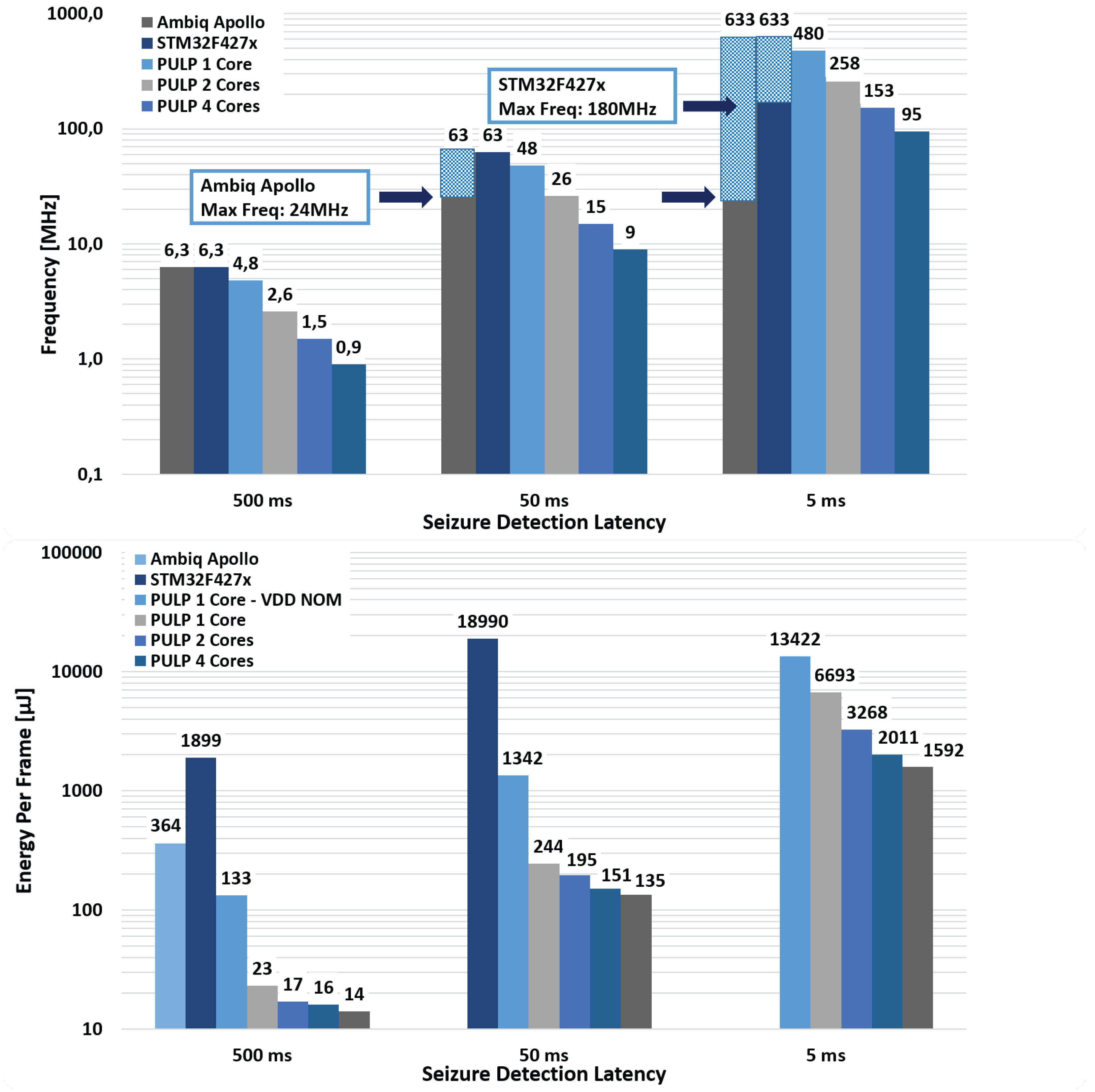
5.5. Energy Considerations and Comparison with Commercial MCUs
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rossi, D. Sub-pJ per operation scalable computing: The PULP experience. In Proceedings of the 2016 IEEE SOI-3D-Subthreshold Microelectronics Technology Unified Conference (S3S), Burlingame, CA, USA, 10–13 October 2016; pp. 1–3. [Google Scholar]
- United Nations. Available online: http://www.un.org/ (accessed on 1 December 2016).
- Al-Otaibi, F.A.; Hamani, C.; Lozano, A.M. Neuromodulation in epilepsy. Neurosurgery 2011, 69, 957–979. [Google Scholar] [CrossRef] [PubMed]
- Nune, G.; DeGiorgio, C.; Heck, C. Neuromodulation in the treatment of epilepsy. Curr. Treat. Options Neurol. 2015, 17, 43. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.T.; Morrell, M.J. Closed-loop neurostimulation: The clinical experience. Neurotherapeutics 2014, 11, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Sree, S.V.; Alvin, A.P.C.; Suri, J.S. Use of principal component analysis for automatic classification of epileptic EEG activities in wavelet framework. Expert Syst. Appl. 2012, 39, 9072–9078. [Google Scholar] [CrossRef]
- Subasi, A.; Gursoy, M.I. EEG signal classification using PCA, ICA, LDA and support vector machines. Expert Syst. Appl. 2010, 37, 8659–8666. [Google Scholar] [CrossRef]
- Wang, C.; Zou, J.; Zhang, J.; Wang, M.; Wang, R. Feature extraction and recognition of epileptiform activity in EEG by combining PCA with ApEn. Cogn. Neurodyn. 2010, 4, 233–240. [Google Scholar] [CrossRef]
- Neurospace. Available online: http://www.neuropace.com/ (accessed on 1 November 2015).
- Medtronic. Available online: http://www.medtronic.com/ (accessed on 1 November 2015).
- Yoo, J.; Yan, L.; El-Damak, D.; Altaf, M.B.; Shoeb, A.; Yoo, H.J.; Chandrakasan, A. An 8-channel scalable EEG acquisition SoC with fully integrated patient-specific seizure classification and recording processor. In Proceedings of the 2012 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 19–23 February 2012; pp. 292–294. [Google Scholar]
- Lee, K.H.; Verma, N. A low-power processor with configurable embedded machine-learning accelerators for high-order and adaptive analysis of medical-sensor signals. IEEE J. Solid State Circuits 2013, 48, 1625–1637. [Google Scholar] [CrossRef]
- Benatti, S.; Milosevic, B.; Farella, E.; Benini, L. A Prosthetic Hand Body Area Controller Based on Efficient Pattern Recognition Control Strategies. Sensors 2017, 17, 869. [Google Scholar] [CrossRef] [PubMed]
- Dreslinski, R.G.; Wieckowski, M.; Blaauw, D.; Sylvester, D.; Mudge, T. Near-threshold computing: Reclaiming moore’s law through energy efficient integrated circuits. Proc. IEEE 2010, 98, 253–266. [Google Scholar] [CrossRef]
- Rossi, D.; Pullini, A.; Loi, I.; Gautschi, M.; Gurkaynak, F.K.; Teman, A.; Constantin, J.; Burg, A.; Miro-Panades, I.; Beigné, E.; et al. 193 MOPS/mW @ 162 MOPS, 0.32 V to 1.15 V voltage range multi-core accelerator for energy efficient parallel and sequential digital processing. In Proceedings of the 2016 IEEE Symposium in Low-Power and High-Speed Chips (COOL CHIPS XIX), Yokohama, Japan, 20–22 April 2016; pp. 1–3. [Google Scholar]
- Golub, G.H.; Van der Vorst, H.A. Eigenvalue computation in the 20th century. J. Comput. Appl. Math. 2000, 123, 35–65. [Google Scholar] [CrossRef]
- Ilyas, M.Z.; Saad, P.; Ahmad, M.I. A survey of analysis and classification of EEG signals for brain-computer interfaces. In Proceedings of the 2015 2nd IEEE International Conference onBiomedical Engineering (ICoBE), Penang, Malaysia, 30–31 March 2015; pp. 1–6. [Google Scholar]
- Escabí, M.A.; Read, H.L.; Viventi, J.; Kim, D.H.; Higgins, N.C.; Storace, D.A.; Liu, A.S.; Gifford, A.M.; Burke, J.F.; Campisi, M.; et al. A high-density, high-channel count, multiplexed μECoG array for auditory-cortex recordings. J. Neurophysiol. 2014, 112, 1566–1583. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.M.; Chiueh, H.; Chen, T.J.; Ho, C.L.; Jeng, C.; Ker, M.D.; Lin, C.Y.; Huang, Y.C.; Chou, C.W.; Fan, T.Y.; et al. A fully integrated 8-channel closed-loop neural-prosthetic CMOS SoC for real-time epileptic seizure control. IEEE J. Solid State Circuits 2014, 49, 232–247. [Google Scholar] [CrossRef]
- Patel, K.; Chua, C.P.; Fau, S.; Bleakley, C.J. Low power real-time seizure detection for ambulatory EEG. In Proceedings of the 2009 3rd IEEE International Conference on Pervasive Computing Technologies for Healthcare, PervasiveHealth 2009, London, UK, 1–3 April 2009; pp. 1–7. [Google Scholar]
- Verma, N.; Shoeb, A.; Bohorquez, J.; Dawson, J.; Guttag, J.; Chandrakasan, A.P. A micro-power EEG acquisition SoC with integrated feature extraction processor for a chronic seizure detection system. IEEE J. Solid State Circuits 2010, 45, 804–816. [Google Scholar] [CrossRef]
- Kwong, J.; Chandrakasan, A.P. An Energy-Efficient Biomedical Signal Processing Platform. IEEE J. Solid State Circuits 2011, 46, 1742–1753. [Google Scholar] [CrossRef]
- Kwong, J.; Ramadass, Y.; Verma, N.; Koesler, M.; Huber, K.; Moormann, H.; Chandrakasan, A. A 65 nm Sub-Vt Microcontroller with Integrated SRAM and Switched-Capacitor DC-DC Converter. IEEE J. Solid State Circuits 2009, 44, 115–126. [Google Scholar] [CrossRef]
- Volder, J.E. The CORDIC trigonometric computing technique. IRE Trans. Electron. Comput. EC-8, 330–334. [CrossRef]
- Walther, J.S. A unified algorithm for elementary functions. In Proceedings of the Spring Joint Computer Conference, Atlantic City, NJ, USA, 18–20 May 1971; ACM: New York, NY, USA, 1971; pp. 379–385. [Google Scholar]
- Causo, M.; Benatti, S.; Frappé, A.; Cathelin, A.; Farella, E.; Kaiser, A.; Benini, L.; Rabaey, J. Sampling Modulation: An Energy Efficient Novel Feature Extraction for Biosignal processing. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016. [Google Scholar]
- Liu, Y.; Zhou, W.; Yuan, Q.; Chen, S. Automatic seizure detection using wavelet transform and SVM in long-term intracranial EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 749–755. [Google Scholar] [PubMed]
- Benatti, S.; Montagna, F.; Rossi, D.; Benini, L. Scalable EEG seizure detection on an ultra low power multi-core architecture. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 86–89. [Google Scholar]
- Gautschi, M.; Rossi, D.; Benini, L. Customizing an Open Source Processor to Fit in an Ultra-low Power Cluster with a Shared L1 Memory. In Proceedings of the GLSVLSI ’14, 24th Edition of the Great Lakes Symposium on VLSI, Houston, TX, USA, 21–23 May 2014; ACM: New York, NY, USA, 2014; pp. 87–88. [Google Scholar]
- Gautschi, M.; Schaffner, M.; Gürkaynak, F.K.; Benini, L. 4.6 A 65 nm CMOS 6.4-to-29.2pJ/FLOP@0.8V shared logarithmic floating point unit for acceleration of nonlinear function kernels in a tightly coupled processor cluster. In Proceedings of the 2016 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 82–83. [Google Scholar]
- Loi, I.; Rossi, D.; Haugou, G.; Gautschi, M.; Benini, L. Exploring Multi-banked shared-L1 Program Cache on Ultra-low Power, Tightly Coupled Processor Clusters. In Proceedings of the CF ’15, 12th ACM International Conference on Computing Frontiers, Ischia, Italy, 18–21 May 2015; ACM: New York, NY, USA, 2015; pp. 64:1–64:8. [Google Scholar]
- Teman, A.; Rossi, D.; Meinerzhagen, P.; Benini, L.; Burg, A. Power, Area, and Performance Optimization of Standard Cell Memory Arrays Through Controlled Placement. ACM Trans. Des. Autom. Electron. Syst. 2016, 21, 59:1–59:25. [Google Scholar] [CrossRef]
- Rossi, D.; Loi, I.; Haugou, G.; Benini, L. Ultra-low-latency Lightweight DMA for Tightly Coupled Multi-core Clusters. In Proceedings of the CF ’14, 11th ACM Conference on Computing Frontiers, Cagliari, Italy, 20–22 May 2014; ACM: New York, NY, USA, 2014; pp. 15:1–15:10. [Google Scholar]
- Conti, F.; Palossi, D.; Marongiu, A.; Rossi, D.; Benini, L. Enabling the heterogeneous accelerator model on ultra-low power microcontroller platforms. In Proceedings of the 2016 Design, Automation Test in Europe Conference Exhibition (DATE), Dresden, Germany, 14–18 March 2016; pp. 1201–1206. [Google Scholar]
- Marongiu, A.; Benini, L. An OpenMP Compiler for Efficient Use of Distributed Scratchpad Memory in MPSoCs. IEEE Trans. Comput. 2012, 61, 222–236. [Google Scholar] [CrossRef]
- Alotaiby, T.N.; Alshebeili, S.A.; Alshawi, T.; Ahmad, I.; El-Samie, F.E.A. EEG seizure detection and prediction algorithms: A survey. EURASIP J. Adv. Signal Proc. 2014, 2014, 183. [Google Scholar] [CrossRef]
- Benatti, S.; Farella, E.; Benini, L. Towards EMG control interface for smart garments. In Proceedings of the 2014 ACM International Symposium on Wearable Computers: Adjunct Program, Seattle, WA, USA, 13–17 September 2014; ACM: New York, NY, USA, 2014; pp. 163–170. [Google Scholar]
- Scholkopf, B.; Sung, K.K.; Burges, C.J.; Girosi, F.; Niyogi, P.; Poggio, T.; Vapnik, V. Comparing support vector machines with Gaussian kernels to radial basis function classifiers. IEEE Trans. Signal Proc. 1997, 45, 2758–2765. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Wilkinson, J.H.; Bauer, F.L.; Reinsch, C. Linear Algebra; Springer: Heidelberger, Germany, 2013; Volume 2. [Google Scholar]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Brunelli, C.; Campi, F.; Mucci, C.; Rossi, D.; Ahonen, T.; Kylliäinen, J.; Garzia, F.; Nurmi, J. Design space exploration of an open-source, IP-reusable, scalable floating-point engine for embedded applications. J. Syst. Archit. 2008, 54, 1143–1154. [Google Scholar] [CrossRef]
- Oberstar, E.L. Fixed-point representation & fractional math. Oberstar Consulting Rev. 2007, 1. [Google Scholar]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A practical guide to support vector classification. Tech. Rep. Taipei 2003. [Google Scholar]
- Shoeb, A.H. Application of Machine Learning to Epileptic Seizure Onset Detection and Treatment. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Chandaka, S.; Chatterjee, A.; Munshi, S. Cross-correlation aided support vector machine classifier for classification of EEG signals. Expert Syst. Appl. 2009, 36, 1329–1336. [Google Scholar] [CrossRef]
- Acharya, U.R.; Molinari, F.; Sree, S.V.; Chattopadhyay, S.; Ng, K.H.; Suri, J.S. Automated diagnosis of epileptic EEG using entropies. Biomed. Signal Proc. Control 2012, 7, 401–408. [Google Scholar] [CrossRef]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Rapoport, B.I.; Kedzierski, J.T.; Sarpeshkar, R. A glucose fuel cell for implantable brain–machine interfaces. PLoS ONE 2012, 7, e38436. [Google Scholar] [CrossRef] [PubMed]


| Yoo J. [11] | Chen W.M. [19] | Patel K. [20] | Verma N. [21] | Lee K.H. [12] | Proposed Work | |
|---|---|---|---|---|---|---|
| Applications: | EEG | EEG | EEG | EEG | EEG, ECG | EEG |
| Processing Chain: | spectral | FFT | FIR, RMS, | spectral | spectral | PCA, |
| energy, | ApEn | maxima&minima, | energy, | energy, | DWT + energy, | |
| SVM | LLS | line length, | SVM | variance, | SVM | |
| nonlinear energy, | SVM | |||||
| LDA | ||||||
| Number of Electrodes: | 8 | 8 | 6 | 18 | 18 | 23 |
| Fully Programmable: | X | X | X | X | X | ✓ |
| Fully Embedded: | ✓ | ✓ | X | X | ✓ | ✓ |
| MATLAB | FLOATING-POINT | FIXED-POINT | |||
|---|---|---|---|---|---|
| Subjects | Accuracy% | Precision% | Accuracy% | Precision% | Accuracy% |
| S01 | 93 | 100 | 93 | 91 | 80 |
| S02 | 100 | 100 | 100 | 90 | 100 |
| S03 | 74 | 100 | 74 | 97 | 74 |
| S04 | 100 | 100 | 100 | 96 | 100 |
| Mean | 91.75 | 100 | 91.75 | 93.50 | 88.50 |
| PULP 1 Core | PULP 2 Cores | PULP 4 Cores | PULP 8 Cores | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kernel | kCycles | load% | kCycles | Speed-up | E.Save% | kCycles | Speed-up | E.Save% | kCycles | Speed-up | E.Save% |
| PCA | 1902 | 79.25 | 1057 | 1.80 | 611 | 3.11 | 374 | 5.08 | |||
| Mean + Covariance | 1018 | 53.50 | 514 | 1.98 | 0 | 284 | 3.59 | 0 | 146 | 6.95 | 0.60 |
| Householder Reduction | 151 | 8.00 | 85 | 1.78 | 4.00 | 52 | 2.92 | 11.45 | 35 | 4.32 | 20.30 |
| Accumulate | 90 | 4.70 | 50 | 1.81 | 2.50 | 29 | 3.05 | 7.45 | 19 | 4.60 | 14.80 |
| Diagonalize | 228 | 12.00 | 162 | 1.38 | 11.00 | 132 | 1.73 | 22.85 | 116 | 1.97 | 32.00 |
| Compute PC | 413 | 21.80 | 207 | 1.99 | 0 | 105 | 3.93 | 0 | 58 | 7.12 | 0 |
| DWT + ENERGY | 169 | 7.05 | 94 | 1.80 | 5.00 | 57 | 2.98 | 14.30 | 39 | 4.38 | 26.50 |
| SVM | 328 | 13.70 | 175 | 1.87 | 0 | 98 | 3.33 | 0 | 60 | 5.43 | 0.65 |
| TOTAL | 2400 | 100 | 1326 | 1.86 | 4.50 | 766 | 3.13 | 12.00 | 475 | 5.05 | 21.00 |
| PULP 1 Core | PULP 2 Cores | PULP 4 Cores | PULP 8 Cores | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kernel | kCycles | load% | kCycles | Speed-up | E.Save% | kCycles | Speed-up | E.Save% | kCycles | Speed-up | E.Save% |
| PCA | 2159 | 83.25 | 1392 | 1.55 | 923 | 2.34 | 681 | 3.17 | |||
| Mean + Covariance | 995 | 42.2 | 536 | 1.86 | 0 | 284 | 3.50 | 0.40 | 143 | 6.97 | 0.60 |
| Householder Reduction | 246 | 13.00 | 170 | 1.45 | 4.25 | 125 | 1.97 | 14.40 | 106 | 2.33 | 28.60 |
| Accumulate | 109 | 6.60 | 85 | 1.28 | 1.50 | 50 | 2.18 | 6.80 | 33 | 3.30 | 17.70 |
| Diagonalize | 405 | 20.60 | 395 | 1.03 | 9.75 | 355 | 1.14 | 25.20 | 337 | 1.20 | 44.60 |
| Compute PC | 397 | 17.60 | 204 | 1.95 | 0 | 104 | 3.82 | 0 | 58 | 6.84 | 0 |
| DWT + ENERGY | 136 | 4.78 | 76 | 1.79 | 2.50 | 46 | 2.97 | 10.00 | 31 | 4.38 | 25.15 |
| SVM | 304 | 11.97 | 164 | 1.86 | 0 | 85 | 3.58 | 0 | 45 | 6.75 | 1.15 |
| TOTAL | 2599 | 100 | 1631 | 1.60 | 3.00 | 1053 | 2.47 | 11.20 | 756 | 3.44 | 26.30 |
| PULP 1 Core | PULP 2 Cores | PULP 4 Cores | PULP 8 Cores | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kernel | kC.Fl | kC.Fx | R | kC.Fl | kC.Fx | R | kC.Fl | kC.Fx | R | kC.Fl | kC.Fx | R |
| PCA | ||||||||||||
| Mean + Covariance | 1018 | 995 | 0.98 | 514 | 536 | 0.98 | 284 | 284 | 1.01 | 146 | 143 | 0.99 |
| Householder Reduction | 151 | 246 | 1.96 | 85 | 170 | 2.21 | 52 | 125 | 2.60 | 35 | 106 | 3.17 |
| Accumulate | 90 | 109 | 1.74 | 50 | 85 | 1.72 | 29 | 50 | 1.71 | 19 | 33 | 1.69 |
| Diagonalize | 228 | 405 | 2.10 | 162 | 395 | 2.46 | 132 | 355 | 2.78 | 116 | 337 | 2.98 |
| Compute PC | 413 | 397 | 0.99 | 207 | 204 | 0.99 | 105 | 104 | 0.98 | 58 | 58 | 1.00 |
| DWT + ENERGY | 169 | 136 | 0.80 | 94 | 76 | 0.81 | 57 | 46 | 0.81 | 39 | 31 | 0.79 |
| SVM | 328 | 304 | 1.04 | 175 | 164 | 0.99 | 98 | 85 | 0.91 | 60 | 45 | 0.79 |
| TOTAL | 2400 | 2599 | 1.19 | 1326 | 1631 | 1.29 | 766 | 1053 | 1.45 | 475 | 756 | 1.68 |
| PULP 1 Core | PULP 2 Cores | PULP 4 Cores | PULP 8 Cores | |||||
|---|---|---|---|---|---|---|---|---|
| Kernel | E.Fl. (J) | E.Fx. (J) | E.Fl. (J) | E.Fx. (J) | E.Fl. (J) | E.Fx. (J) | E.Fl. (J) | E.Fx. (J) |
| PCA | ||||||||
| Mean + Covariance | 3206 | 4409 | 1495 | 1468 | 1100 | 789 | 886 | 471 |
| Householder Reduction | 475 | 1307 | 236 | 521 | 177 | 317 | 169 | 259 |
| Accumulate | 202 | 689 | 140 | 245 | 105 | 130 | 101 | 89 |
| Diagonalize | 720 | 2121 | 428 | 1068 | 394 | 759 | 480 | 629 |
| Compute PC | 1300 | 1850 | 601 | 596 | 407 | 286 | 353 | 190 |
| DWT + ENERGY | 533 | 191 | 259 | 117 | 188 | 81 | 173 | 63 |
| SVM | 1034 | 519 | 510 | 283 | 382 | 179 | 366 | 130 |
| TOTAL | 7576 | − | 3548 | 5201 | 2634 | 3295 | 2279 | 2351 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montagna, F.; Benatti, S.; Rossi, D. Flexible, Scalable and Energy Efficient Bio-Signals Processing on the PULP Platform: A Case Study on Seizure Detection. J. Low Power Electron. Appl. 2017, 7, 16. https://doi.org/10.3390/jlpea7020016
Montagna F, Benatti S, Rossi D. Flexible, Scalable and Energy Efficient Bio-Signals Processing on the PULP Platform: A Case Study on Seizure Detection. Journal of Low Power Electronics and Applications. 2017; 7(2):16. https://doi.org/10.3390/jlpea7020016
Chicago/Turabian StyleMontagna, Fabio, Simone Benatti, and Davide Rossi. 2017. "Flexible, Scalable and Energy Efficient Bio-Signals Processing on the PULP Platform: A Case Study on Seizure Detection" Journal of Low Power Electronics and Applications 7, no. 2: 16. https://doi.org/10.3390/jlpea7020016
APA StyleMontagna, F., Benatti, S., & Rossi, D. (2017). Flexible, Scalable and Energy Efficient Bio-Signals Processing on the PULP Platform: A Case Study on Seizure Detection. Journal of Low Power Electronics and Applications, 7(2), 16. https://doi.org/10.3390/jlpea7020016





