Abstract
This paper proposes a modified predictive direct torque control (PDTC) application-specific integrated circuit (ASIC) of a motor drive with a fuzzy controller for eliminating sampling and calculating delay times in hysteresis controllers. These delay times degrade the control quality and increase both torque and flux ripples in a motor drive. The proposed fuzzy PDTC ASIC calculates the stator’s magnetic flux and torque by detecting the three-phase current, three-phase voltage, and rotor speed, and eliminates the ripples in the torque and flux by using a fuzzy controller and predictive scheme. The Verilog hardware description language was used to implement the hardware architecture, and the ASIC was fabricated by the Taiwan Semiconductor Manufacturing Company through a 0.18-μm 1P6M CMOS process that involved a cell-based design method. The measurements revealed that the proposed fuzzy PDTC ASIC of the three-phase induction motor yielded a test coverage of 96.03%, fault coverage of 95.06%, chip area of 1.81 × 1.81 mm2, and power consumption of 296 mW, at an operating frequency of 50 MHz and a supply voltage of 1.8 V.
1. Introduction
The direct torque control (DTC) algorithm is based on the error between the reference and estimated values of torque and flux. Inverter states can be directly controlled by reducing the torque and flux errors within band limits [1]. The conventional proportional–integral–derivative (PID) control is still widely used as a speed regulator in DTC systems [2]. However, the induction motor (IM) has multivariable, strong coupling, nonlinear, and time-varying characteristics. A fuzzy PID motor speed regulator is used for adjusting the nonlinear control variable and for enhancing the speed, response, and stability of a DTC system [3]. Furthermore, the model predictive direct torque control (MPDTC) algorithm is used to maintain the motor torque, stator flux, and the inverter’s neutral point potential within the given hysteresis bounds by reducing the average switching frequency of the inverter, unlike the process in the conventional DTC method. Studies have reported that the MPDTC algorithm can achieve an average inverter switching frequency reduction of 16.5% [4,5].
In IM drive systems, the quick-response scheme is based on the limit cycle control of both flux and torque [6]. A low switching frequency is used in an inverter to achieve a rapid dynamic response. This is achieved by rapidly equaling the torque and flux to the reference values. The switching technique mainly contributes to large torque and flux errors, which generate additional torque and flux ripples in the motor control system [7]. To achieve a high IM control performance, decrease the variation in the torque and flux by applying the fuzzy theory, and lower the average inverter switching frequency with respect to the conventional DTC algorithm, a combination of fuzzy control and a predictive direct torque control (PDTC) algorithm has been proposed.
The model predictive control (MPC) algorithm has been used in various branches of automotive research. Borhan and Vahidi proposed an online optimization-based predictive controller to control power-split hybrid electric vehicles [8]. Suzuki et al. implemented an individual air-fuel estimation and control by using an MPC controller [9]. Bageshwar et al. computed the spacing-control laws for the transitional maneuvers of vehicles by using the MPC algorithm [10]. Saerens et al. presented the application of MPC in the control of conventional powertrains instead of hybrid powertrains [11]. He et al. illustrated an MPC-based torque demand control approach for the torque-based control of a parallel hybrid powertrain, which comprised a torque distributor, a nonlinear MPC controller, a linear MPC controller of the permanent-magnet synchronous motor, and a torque load observer [12]. According to the aforementioned review, the linear MPC algorithm is designed with current feedback. In other words, the MPC algorithm is implemented with closed-loop control, which results in a slow response from the controller. In the proposed PDTC algorithm, a modified predictive compensation circuit with open-loop control is used to speed up the controller’s response. Furthermore, subtracting the previous flux φs[k − 1] from the present flux φs[k] greatly reduces the ripples of the flux or torque.
Okumus proposed a torque control strategy in which the band is controlled by a fuzzy controller through an applied voltage vector and the slope of the torque to maintain a constant switching frequency in all operating conditions. Through the proposed technique, the switching frequency of the inverter can be kept nearly constant [13]. Siva et al. presented a direct torque-controlled IM drive system with a fuzzy variable structure controller (FVSC) and fuzzy state feedback controller (FSFC). The FVSC exhibited a slow response with noticeable overshoot. The ripples in the stator flux were lower in the FSFC compared with the PID and FVSC. The proposed controllers improved the performance and robustness of the drive system [14]. In addition, the PI control (PIC) of the IM exhibited more current ripples, high torque and flux distortions, a poor transient performance due to sudden disturbances, and poor sensitivity to control gains. To improve the performance of the IM, PIC was replaced by type-2 fuzzy logic control (TP2FLC), which resulted in an excellent dynamic performance of the IM with less harmonic distortion in the current, torque, and flux [15]. Dybkowski and Szabat presented an adaptive control structure while working with the online tuned neuro-fuzzy speed compensator. In the proposed fuzzy control system, a fuzzy controller and a fuzzy vector selection table were used to establish an appropriate voltage vector for achieving a high operating speed and stability [16,17].
In the PDTC algorithm, versatile and flexible control algorithms were developed for realizing electric motor drives with favorable performance characteristics [5]. The conventional direct torque control (CDTC) of an IM was improved using artificial intelligence to control the motor speed with a field-programmable gate array (FPGA). Fuzzy logic was used to improve the effectiveness of the conventional PI controller when it changed with time and operating conditions. In addition, the digital implementation of the CDTC with a fuzzy speed controller was based on the FPGA, which was used to overcome the limitations of software solutions (e.g., digital signal processors and microcontrollers) [18]. In this paper, we present an application-specific integrated circuit (ASIC) capable of fuzzy control and a PDTC for IM drives.
In this study, a fuzzy PDTC was fabricated using 0.18-µm 1P6M CMOS technology. Simulated and measured results were recorded at an operating frequency of 50 MHz and a supply voltage of 1.8 V. The remainder of this paper is organized as follows. Section 2 details the proposed topology of the fuzzy PDTC ASIC, implemented with 10 blocks. Section 3 presents the simulated and measured results. Section 4 presents our conclusions.
2. Proposed Topology of Fuzzy PDTC ASIC
Figure 1 presents the block diagram of the modified fuzzy PDTC for an IM drive, which comprises a Hall sensor, an analog-to-digital converter, an abc–dq transformation unit, a flux calculator, a voltage calculator, a torque calculator, a speed calculator, an angle selector, a predictive calculator, a fuzzy controller, a fuzzy voltage vector selector, and a short-circuit preventer. All blocks were designed using the Verilog hardware description language (HDL) and verified using an FPGA board. After the digital chip was implemented using the synthesis tool, auto place, routed tool, and verification tool, an ASIC was fabricated using a 0.18-μm 1P6M CMOS process for a three-phase IM control system.
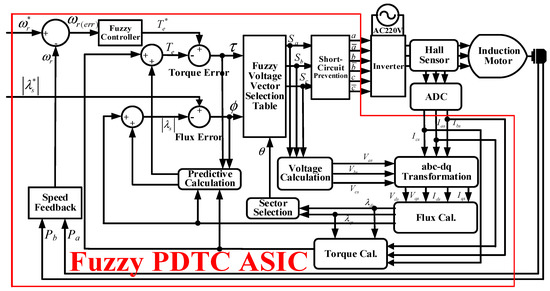
Figure 1.
Block diagram of the modified fuzzy PDTC ASIC for a three-phase IM control system.
As shown in Figure 1, the proposed fuzzy PDTC ASIC (red rectangle) comprises 10 blocks. In the design of these blocks, we focused on the voltage calculation, flux calculation, torque calculation, angle selection, modified predictive calculation, fuzzy control, fuzzy voltage vector selection, and short-circuit prevention.
2.1. Voltage Calculation
To calculate the voltage, an abc–dq transformation was performed to not only simplify the calculation process, but also accelerate the transformation. In general, the motor’s voltages were determined using three-phase switching states—Sa, Sb, and Sc—and the DC voltage Vdc of the inverter. The calculated three-phase output voltages, with respect to the central point, Van, Vbn, and Vcn, can be expressed as follows:
and
For the motor stator, the calculated Van, Vbn, and Vcn can be expressed as three-phase stator voltages—Vsas, Vsbs, and Vscs—which can be transformed into the two-phase stator voltages, Vsds and Vsqs, by using the following equations:
and
Table 1 presents the related voltage parameters with respect to various switching states. In addition, a Hall sensor was used to detect the three-phase stator currents—isas, isbs, and iscs—of the motor drive, and these currents were transformed into two-phase stator currents, isds and isqs, as follows:

Table 1.
Related voltage parameters with respect to various switching states.
If two stator currents, isas and isbs, are measured, the third parameter iscs can be calculated on the basis of the following equation:
2.2. Flux and Torque Calculations
After the two-phase stator currents and stator voltages are obtained, the two-phase magnetic fluxes φsds and φsqs can be calculated using the winding resistance Rs, which is the direct-current resistance in the single-phase winding of the stator. In other words, the magnetic fluxes in the ds–qs axis can be expressed as follows [16]:
If Rs is small, Equation (8) can be simplified using the sampling time T as follows [17]:
The magnetic torques Te in the ds–qs axis can then be expressed as follows [18]:
where p is the pole number of the motor. Note that the digital multiplier is implemented with the Booth multiplication algorithm [19], and the composite magnetic flux is completed with a square root operation, which is implemented in the shadow tree algorithm [20].
2.3. Angle Selection
The angle can be selected using the calculated two-phase stator fluxes and by determining the flux φsdqs. In general, the voltage space vector can be divided into six sectors, with each sector including an angle of 60°. To simplify the analysis, the first quadrant of the coordinate plane is depicted in Figure 2. Both φsds and φsqs are positive in this quadrant. In addition, Figure 2 presents two sectors, S1 and S2. The angle of the first sector, S1, extends from 0° to 30°, whereas that of the second sector, S2, extends from 30° to 90°. In trigonometry, a relational equation is expressed as follows:
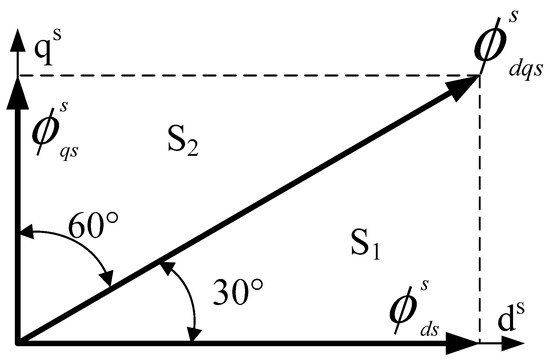
Figure 2.
First quadrant of the coordinate stator fluxes, φsds and φsqs.
Dividing |φsqs(t)| by |φsds(t)| gives the following:
When the two fluxes φsds(t) and φsqs(t) are positive and is negative, we select the first sector S1, whereas the output is the second sector S2 because the two fluxes φsds(t) and φsqs(t) are positive and is positive. The output is 1 if the value of φsds(t), φsqs(t), or is positive and is 0 otherwise. Table 2 is the sector selection table for the proposed fuzzy PDTC. The output sector can be easily selected using this table.

Table 2.
Sector selection table of the proposed fuzzy PDTC.
2.4. Modified Predictive Calculation
Figure 3 presents the modified compensation circuits of the present magnetic flux of the stator, φs[k], and the present torque of the motor, Te[k]. As shown in Figure 3a, the delay (z−1) block is completed using an edge-triggered D flipflop (DFF) circuit, the subtraction block (denoted by the symbol “−” in the figure) is used to obtain the deviation between the present flux φs[k] and the previous flux φs[k − 1], the absolute value block (Abs.) provides the magnitude of the deviation, and the multiplexer determines the output ∆kk + 1φs[k] according to the control signal Cφs[k]. Figure 3b presents the same function, but with the present torque Te[k] and previous torque Te[k − 1]. Unlike the conventional DTC, the predictive compensation circuit used in the current study can reduce the ripples in the flux and torque. Moreover, the proposed PDTC not only has the advantages of the conventional DTC, but also shortens the delay time and thus exhibits a high performance.
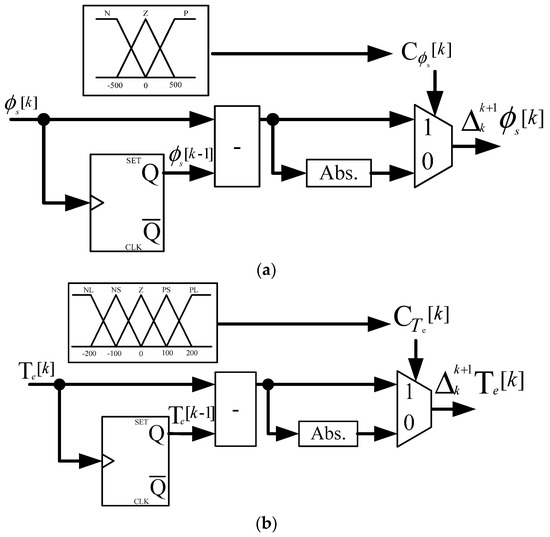
Figure 3.
Modified predictive compensation circuits of the proposed PDTC. (a) Magnetic flux of stator φs. (b) Torque of motor Te.
2.5. Fuzzy Controller
Figure 4 presents the membership functions of two input variables and an output variable. According to the analysis of the step response in a DTC system, three fields of the fuzzy variables can be defined as follows. The field of the motor speed feedback error e is [−100, 100], that of the speed error variation ∆e is [−10, 10], and that of the torque value u is [−2, 2]. The fuzzy subsets are {NB, NS, ZE, PS, PB} [3]. The abbreviations NB, NS, ZE, PS, and PB represent a negative big error, negative small error, zero error, positive small error, and positive big error, respectively [16].
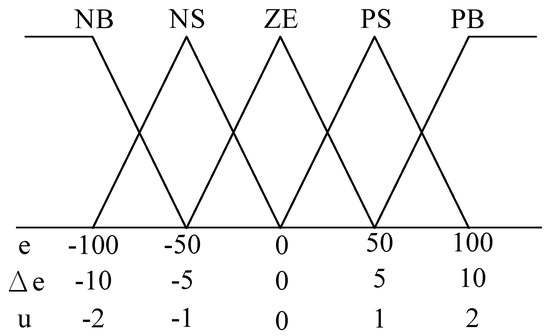
Figure 4.
Membership functions of two input variables and an output.
Each rule of the fuzzy controller can be described using e, ∆e, and u. As shown in Table 3, if e = NB and ∆e = NB, then u = PB. A total of 25 rules are presented for the two input variables. The fuzzy control rules are presented in Table 3.

Table 3.
Fuzzy control rules.
2.6. Fuzzy Voltage Vector Selector
To enhance the performance of the DTC system, the typical voltage vector selection table was modified. In the modified table, the input variables were the error in stator flux, error in the torque, and stator angle, and the output variable was the switching state selector. Figure 5 presents the membership function of the flux errors with three fuzzy subsets {N, Z, P}. The letters N, Z, and P represent a negative flux error, zero flux error, and positive flux error, respectively. Figure 6 presents the membership function of the torque error T with five fuzzy subsets {NL, NS, ZE, PS, PL}. The abbreviations NL, NS, ZE, PS, and PL represent a negative large error, negative small error, zero error, positive small error, and positive large error, respectively. ut is a fuzzy membership function and et is a fuzzy error. Figure 7 presents the membership function of the stator angle with six angular intervals, {θ1, θ2, θ3, θ4, θ5, θ6}. The angular intervals θ1, θ2, θ3, θ4, θ5, and θ6 extend from −29° to 30°, 31° to 90°, 91° to 150°, 151° to 210°, 211° to 270°, and 271° to 330°, respectively [21]. Table 4 is the fuzzy voltage vector selection table for the proposed PDTC with a fuzzy controller.
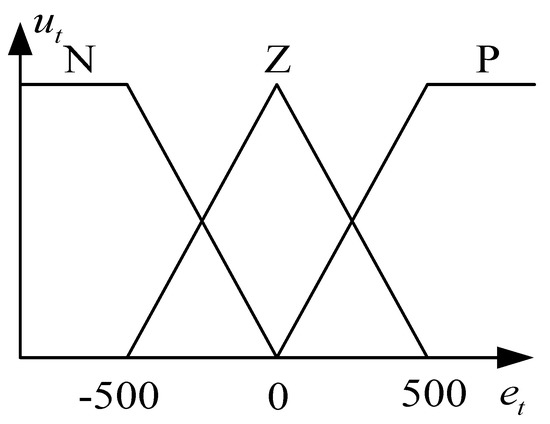
Figure 5.
Membership functions of flux error with three fuzzy subsets {N, Z, P}.
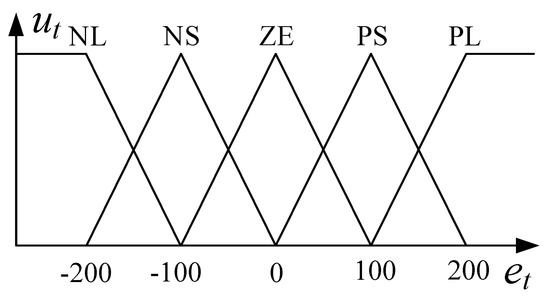
Figure 6.
Membership functions of torque error with five fuzzy subsets {NL, NS, ZE, PS, PL}.
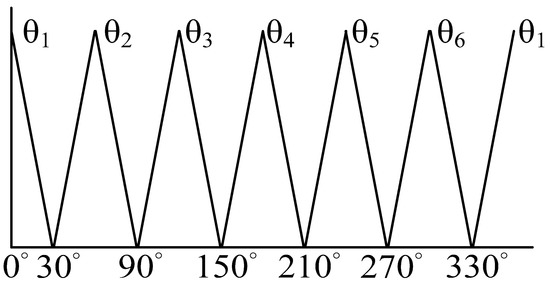
Figure 7.
Membership functions of the stator angle with six angular intervals {θ1, θ2, θ3, θ4, θ5, θ6}.

Table 4.
Fuzzy voltage vector selection table.
2.7. Short-Circuit Prevention
To prevent a short circuit in the inverter, dead time is used to protect the inverter from burning the motor control system. Figure 8 presents the proposed short-circuit prevention scheme, which comprises two states, 1→0 and 0→1, in the control signal. First, the “Up” signal is low (0) from high (1) when the control signal turns off (1→0); and the “Down” signal is high (1) from low (0) when the dead time (∆T) is up. Second, the “Down” signal is low (0) from high (1) when the control signal turns on (0→1); and the “Up” signal is high (1) from low (0) when the dead time (∆T) is up. The advantage of the proposed short-circuit prevention method is that it helps to easily adjust the dead-time interval (∆T) according to the specifications of the motor control system.
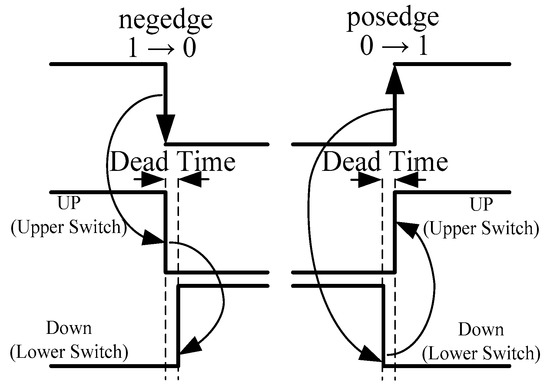
Figure 8.
Proposed short-circuit prevention scheme.
3. Simulation and Measurement Results
The proposed fuzzy PDTC was implemented using Verilog HDL, and ModelSim software was used to simulate and verify the operation of the designed hardware circuit. Figure 9 presents the simulation results for the six arms feeding the inverter. In this figure, Pa and Pb are the feedback signals of the speed encoder; the output signals Ua_out, Ub_out, and Uc_out are the output waveforms of the upper arms for the U-, V-, and W phases, respectively; and the output signals Da_out, Db_out, and Dc_out represent the output waveforms of the lower arms for the U-, V-, and W phases, respectively. In other words, three complementary switches, Ua_out and Da_out, Ub_out and Db_out, and Uc_out and Dc_out, were simulated to verify that the output waveforms of both the upper and lower arms worked as intended. Figure 10 presents the composite magnetic flux of the proposed fuzzy PDTC, and Figure 11 presents the composite magnetic flux of a conventional DTC. A comparison between Figure 10 and Figure 11 clearly reveals that the proposed architecture operated with smaller ripples. The performance of the proposed PDTC was superior to that of the conventional DTC [22]. Figure 12 presents the locus of the stator flux in the proposed fuzzy PDTC, which was superior to that in [23]. Figure 13 presents the simulated electromagnetic torque of the proposed fuzzy PDTC with respect to the change of speed from 0 to 1000 r/min in 1 s, which operated with small ripples, as shown in Figure 14. In comparison to [24], the proposed fuzzy PDTC performed smoothly by reducing the ripples generated in the indirect matrix converter. The ripples of the fuzzy controller occurred irrespective of the sampling frequency, whereas those of the hysteresis controller were dependent on the sampling frequency. Furthermore, a fuzzy voltage vector selection table (Table 4) was used to not only rapidly determine the six output waveforms, but also to protect the inverter from burning the motor control system with dead time.
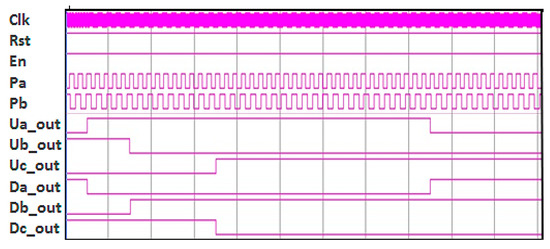
Figure 9.
Simulation of six arms through ModelSim software.
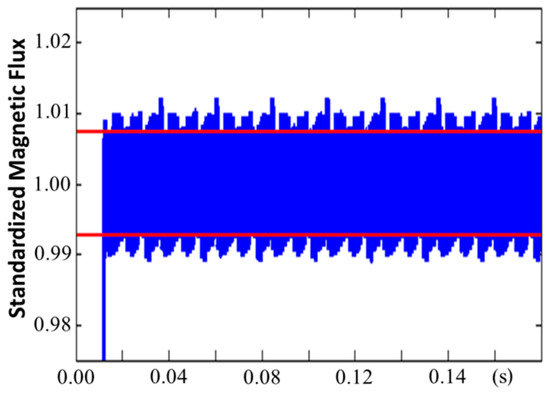
Figure 10.
Composite magnetic flux of the proposed fuzzy PDTC.
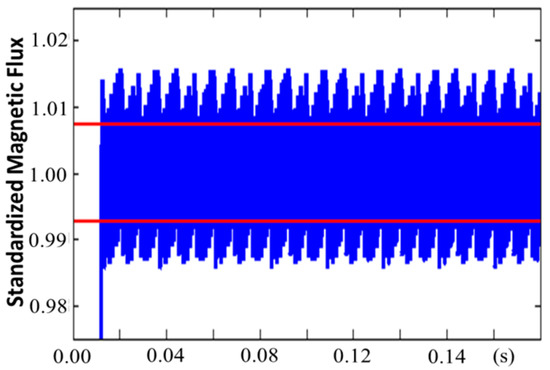
Figure 11.
Composite magnetic flux of the conventional DTC.
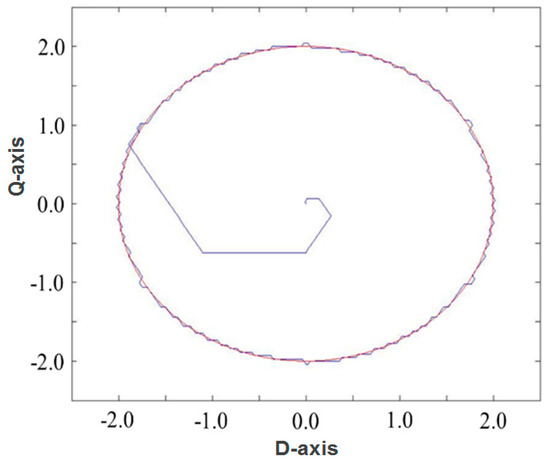
Figure 12.
Locus of the stator flux in the proposed fuzzy PDTC.
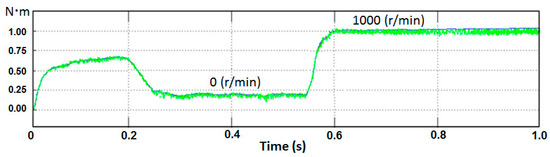
Figure 13.
Simulated electromagnetic torque with respect to the change of speed from 0 to 1000 r/min in 1 s for the proposed fuzzy PDTC.
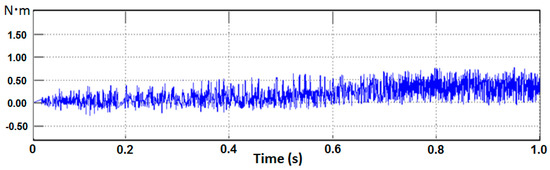
Figure 14.
Simulated torque error ripples with respect to the change of speed from 0 to 1000 r/min in 1 s.
An FPGA development board (Altera DE2-70) was used to verify the output waveforms of the six arms. Figure 15 presents the measured platform, which included an FPGA card, a switching board, an inverter, and an AC motor. The switching board was used for sensing the feedback signal and for accelerating the response between the FPGA card and inverter. Figure 16 presents the waveforms of the six arms measured using a logic analyzer. In Figure 16, three complementary switches, Ua_out and Da_out, Ub_out and Db_out, and Uc_out and Dc_out, work with a dead time of 3 μs to prevent a short circuit between the upper and lower arms. Figure 17 presents the measured dead time of the complementary switches.

Figure 15.
Measured platform, which includes an FPGA card, a switching board, an inverter, and an AC motor.
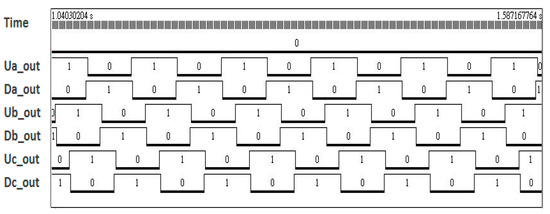
Figure 16.
Waveforms of six arms measured using a logic analyzer.
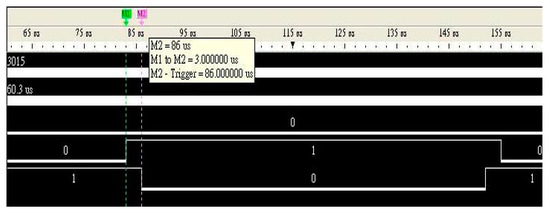
Figure 17.
Measured dead time of the complementary switches to prevent a short circuit between the upper and lower arms.
Figure 18 presents the measured feedback currents, ias and ibs, generated using the inverter (see Figure 1). Notably, the second output current of the inverter ibs was delayed by 120° from the first output current of the inverter ias. Figure 19 presents the experimental result of the torque response with a 1 N·m load torque and a 1000 rpm motor speed in 2 s for the proposed fuzzy PDTC. The torque error ripples varied from 0.12 N·m to 0.35 N·m and the average torque is about 0.2 N·m without a load torque, while the torque error ripples varied from 0.90 N·m to 1.18 N·m and the average torque is approximately 1.0 N·m at a 1 N·m load torque and 1000 rpm motor speed. The measured electromagnetic torques perform with small torque error ripples. Figure 20 presents the measured current response without torque load and Figure 21 shows the measured current response at a 1 N·m load torque in 2 s for the proposed fuzzy PDTC. In comparison to [24], the proposed fuzzy PDTC performs with small current error ripples and small torque error ripples. Figure 22 presents a microphotograph of the ASIC. Table 5 presents the system specifications of the proposed fuzzy PDTC ASIC.
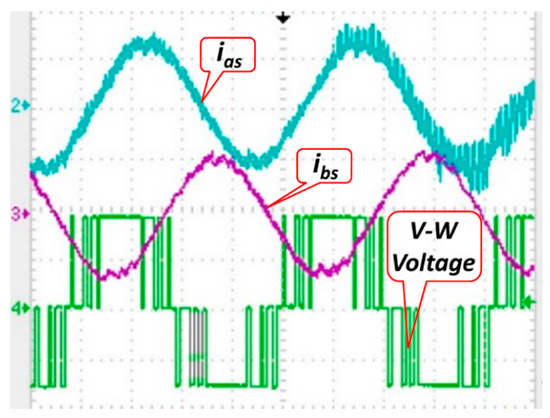
Figure 18.
Measured feedback currents, ias and ibs, of the inverter.
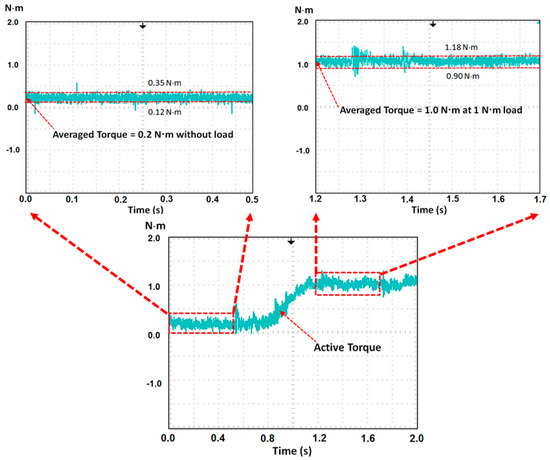
Figure 19.
Experimental result of the torque response at a 1 N·m load torque and 1000 rpm motor speed in 2 s for the proposed fuzzy PDTC.
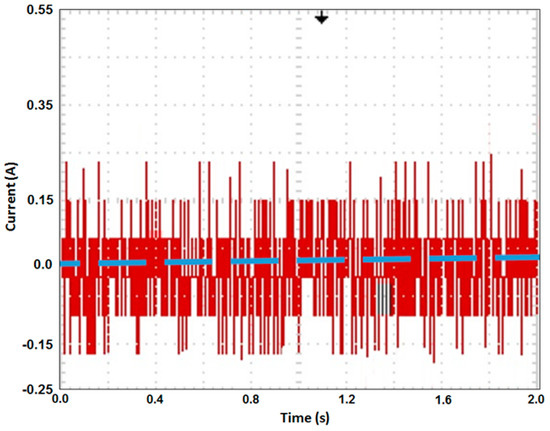
Figure 20.
Measured current response without torque load in 2 s.
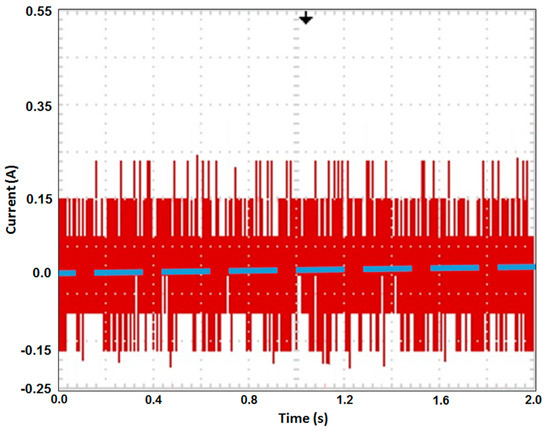
Figure 21.
Measured current response at a 1 N·m load torque in 2 s for the proposed fuzzy PDTC.

Figure 22.
Microphotograph of the proposed fuzzy PDTC ASIC.

Table 5.
System specifications of the proposed ASIC.
4. Conclusions
This study proposed an ASIC for fuzzy PDTC, which involves the conventional DTC, modified predictive calculation, and fuzzy control. All functional blocks were designed using Verilog HDL and were verified using an FPGA board. The proposed PDTC reduces ripples in the torque and flux hysteresis controllers by reducing the average switching time, and the fuzzy controller helps to achieve a high operating speed and high stability of motor control with a small delay time. The proposed fuzzy PDTC ASIC helps to not only calculate the stator’s magnetic flux and torque by detecting the three-phase currents, three-phase voltages, and rotor speed, but also to eliminate ripples in the torque and flux hysteresis controller by using the fuzzy controller and predictive scheme. According to the simulation results, the proposed fuzzy PDTC achieved a test coverage of 96.03%, fault coverage of 95.06%, and power consumption of 296 mW at an operating frequency of 50 MHz and a supply voltage of 1.8 V. The chip area of the proposed ASIC is 1.81 mm × 1.81 mm, and the chip contains pads.
Acknowledgments
The authors thank the National Science Council of the Republic of China, Taiwan, for financially supporting this research under Contract No. MOST 103-2221-E-027-048. We are also grateful to the Chip Implementation Center, Taiwan, for fabricating the test chip. We acknowledge Wallace Academic Editing for editing this manuscript.
Author Contributions
This study was completed by four authors. G.S. designed the fuzzy PDTC, completed the theoretical analysis, and wrote the paper; W.W. conceived and designed the experiments; W.L. analyzed the data and surveyed the references; and C.Y. completed the IC layout and simulation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lai, Y.S.; Chen, J.H. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction. IEEE Trans. Energy Convers. 2001, 16, 220–227. [Google Scholar]
- Li, Y.; Ang, K.H.; Chong, G.C.Y. PID control system analysis and design. IEEE Control Syst. Mag. 2006, 26, 32–41. [Google Scholar]
- Wei, W. Design of flux-weakening control system of PMSM based on the fuzzy self-tuning PID controller. In Proceedings of the International Conference on Consumer Electronics, Communications and Networks (CECNet), XianNing, China, 16–18 April 2011; pp. 226–229. [Google Scholar]
- Geyer, T.; Papafotiou, G.; Morari, M. Model predictive direct torque control—Part I: Concept, algorithm and analysis. IEEE Trans. Ind. Electron. 2009, 56, 1894–1905. [Google Scholar] [CrossRef]
- Papafotiou, G.; Kley, J.; Papadopoulos, K.G.; Bohren, P.; Morari, M. Model predictive direct torque control—Part II: Implementation and experimental evaluation. IEEE Trans. Ind. Electron. 2009, 56, 1906–1915. [Google Scholar] [CrossRef]
- Takahashi, I.; Noguchi, T. A new quick-response and high-efficiency control strategy of an induction motor. IEEE Trans. Ind. Appl. 1986, IA–22, 820–827. [Google Scholar] [CrossRef]
- Prakash, N.S.; Ramchand, R. Constant switching frequency DTC for induction motor fed from two level voltage source inverter. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Mumbai, India, 16–19 December 2014; pp. 1–5. [Google Scholar]
- Borhan, H.A.; Vahidi, A. Model predictive control of a power-split hybrid electric vehicle with combined battery and ultracapacitor energy storage. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5031–5036. [Google Scholar]
- Suzuki, K.; Shen, T.; Kako, J.; Yoshida, S. Individual A/F estimation and control with the fuel-gas ratio for multicylinder IC engines. IEEE Trans. Veh. Technol. 2009, 58, 4757–4768. [Google Scholar] [CrossRef]
- Bageshwar, V.L.; Jeanneret, W.L.; Rajamani, R. Model predictive control of transitional maneuvers for adaptive cruise control vehicle. IEEE Trans. Veh. Technol. 2004, 53, 1573–1585. [Google Scholar] [CrossRef]
- Saerens, B.; Diehl, M.; Swevers, J. Model predictive control of automotive powertrains—First experimental results. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 5692–5697. [Google Scholar]
- He, L.; Shen, T.; Yu, L.; Feng, N.; Song, J. A model-predictive-control-based torque demand control approach for parallel hybrid powertrains. IEEE Trans. Veh. Technol. 2013, 62, 1041–1052. [Google Scholar] [CrossRef]
- Okumus, H.I. A new torque controller for direct torque controlled induction machine drives. In Proceedings of the 12th International Middle-East Power System Conference, Aswan, Egypt, 12–15 May 2008; pp. 244–248. [Google Scholar]
- Siva Reddy, Y.V.; Vijaya Kumar, M.; Brahmananda Reddy, T.; Amarnath, J. Direct torque control of induction motor based on state feedback and variable structure fuzzy controllers. In Proceedings of the IEEE Power India Conference, New Delhi, India, 10–12 April 2006; pp. 1–5. [Google Scholar]
- Venkataramana Naik, N.; Singh, S.P. Improved dynamic performance of type-2 fuzzy based DTC induction motor using SVPWM. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, Karnataka, India, 16–19 December 2012; pp. 1–5. [Google Scholar]
- Mei, B.; Liu, H.; Zhang, J. Study of fuzzy control in direct torque control system. In Proceedings of the International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; pp. 129–132. [Google Scholar]
- Wahab, H.F.A.; Sanusi, H. Simulink model of direct torque control of induction machine. Am. J. Appl. Sci. 2008, 5, 1083–1090. [Google Scholar]
- Krim, S.; Gdaim, S.; Mtibaa, A.; Mimouni, M.F. Fuzzy speed controller for an induction motor associated with the direct torque control: Implementation on the FPGA. In Proceedings of the 4th International Conference on Systems and Control (ICSC), Sousse, Tunisia, 28–30 April 2015; pp. 492–497. [Google Scholar]
- Suriya, T.S.U.; Rani, A.A. Low power analysis of MAC using modified booth algorithm. In Proceedings of the 4th International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013; pp. 1–5. [Google Scholar]
- Wong, K.W.; Tsang, W.W. An efficient shadow algorithm for area light sources using BSP trees. In Proceedings of the 6th Pacific Conference on Computer Graphics and Application, Singapore, 26–28 October 1998; pp. 97–103. [Google Scholar]
- Benaicha, S.; Zidani, F.; Said, R.N.; Said, M.S.N. A novel direct torque fuzzy control of SVM-inverter-fed induction motor drive. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Istanbul, Turkey, 13–17 May 2013; pp. 340–345. [Google Scholar]
- Sutikno, T.; Idris, N.R.N.; Jidin, A.; Cirstea, M.N. An improved FPGA implementation of direct torque control for induction machines. IEEE Trans. Ind. Inf. 2013, 9, 1280–1290. [Google Scholar] [CrossRef]
- Ramasamy, S.; Venkataramani, B.; Jagadeeswara, S. FPGA implementation of direct torque control of induction motor. In Proceedings of the International Conference on Signal and Image Processing (ICSIP), Chennai, India, 15–17 December 2010; pp. 337–340. [Google Scholar]
- Singh, A.K.; Reddy, C.U.; Prabhakar, K.K.; Kumar, P. FPGA implementation of direct torque control of induction motor with reduced ripples in torque and flux. In Proceedings of the IEEE International Transportation Electrification Conference (ITEC), Chennai, India, 27–29 August 2015; pp. 1–7. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).