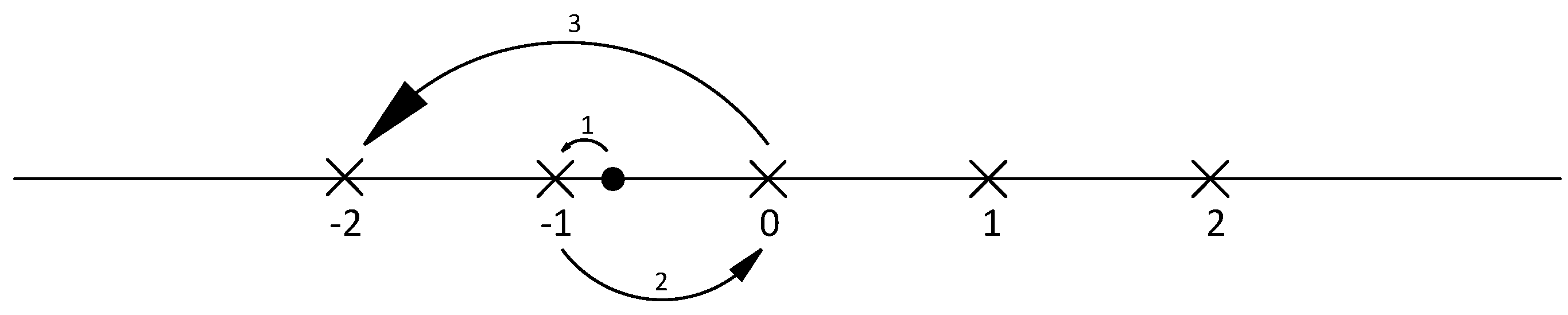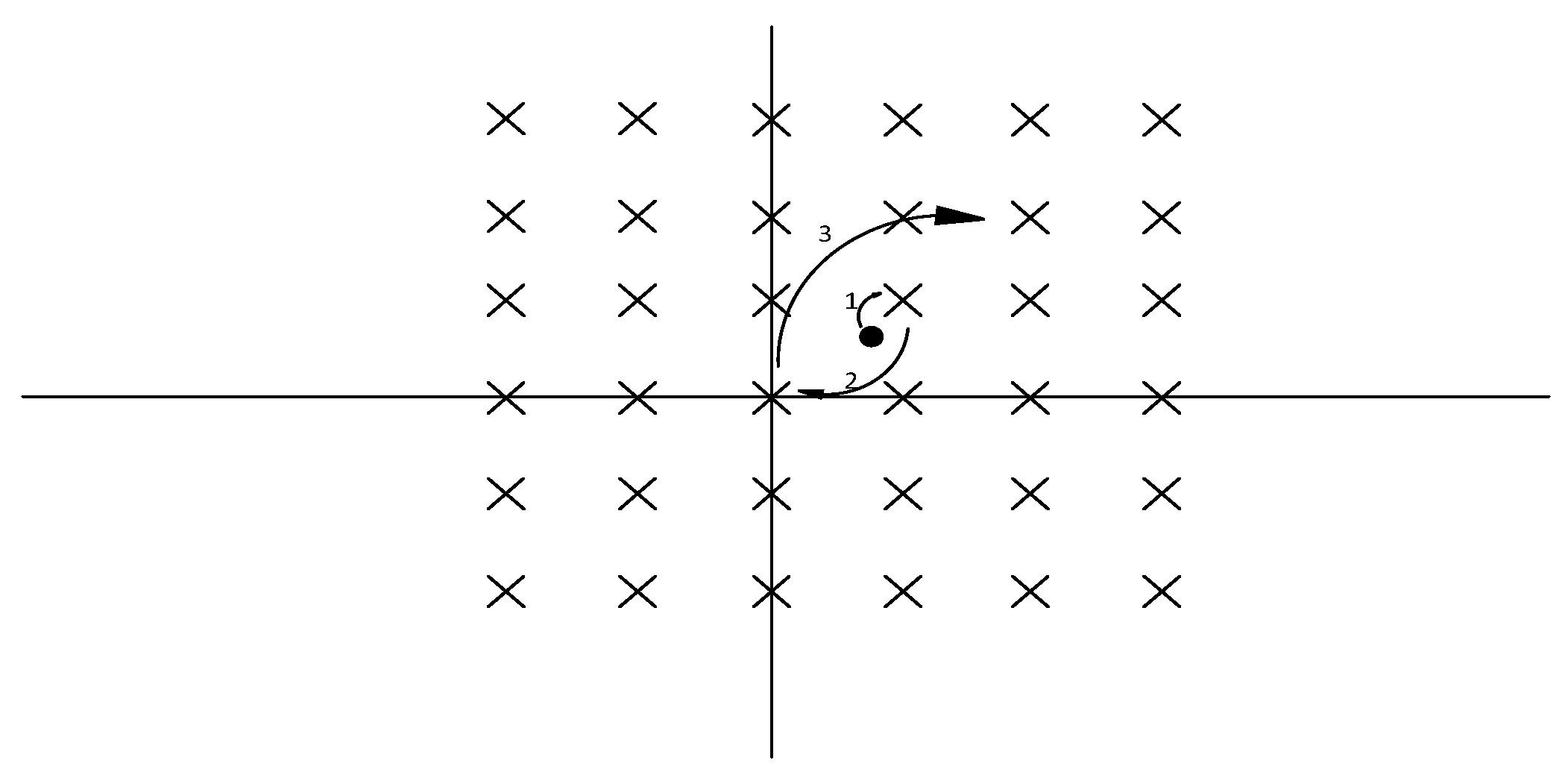Energy-Efficient Hardware Implementation of an LR-Aided K-Best MIMO Decoder for 5G Networks

Abstract

Energy efficiency is a primary design goal for future green wireless communication technologies. Multiple-input multiple-output (MIMO) schemes have been proposed in the literature to improve the throughput of communication systems, and they are expected to play a prominent role in the upcoming fifth generation (5G) standard. This paper presents a novel, high-efficiency MIMO decoder based on the K-Best algorithm with lattice reduction. We have designed a novel hardware architecture for this decoder, which was implemented using 32 nm standard CMOS technology. Our results show that the proposed decoder can achieve on average a four-fold reduction in the power costs compared to recently published designs for 5G networks. The throughput of the design is 506 Mbits/s, which is comparable to existing designs.

1. Introduction

With the escalating expansion of wireless network infrastructures and exponential growth in traffic rate, a considerable amount of worldwide energy is consumed by information and communication technologies (ICT) of which more than 70% is being used by radio access hardware and radio frequency [1] which, in turn, increases the overall energy consumption of the system and the production of CO₂ emissions that are threat to global warming. This has given rise to the concept of green communications, the latter is a new research trend which aims to develop innovative methods for the reduction of the total power needed to operate future mobile communication systems and to identify appropriate network architectures and radio technologies which facilitate the required power reduction [2]. The development of enabling technologies for green communications is currently a priority research area, in which there are several major international projects being carried out such as the European EARTH project [3], the international Green Touch consortium [4] and the Mobile VCE Green Radio (GR) [5]. Multiple-input multiple-output (MIMO) communication systems can allow higher data rates compared to single-antenna-aided systems, this is because they have greater spectral efficiency [6]. Hence, MIMO systems are expected to be a prominent part of the 5G standard [7,8]. However designing reliable and energy efficient MIMO detectors is a challenging task, because of the complexity of the implementation of the signal detection at the receiver due to the interfering sub-streams [9]. Sphere decoding (SD) is a popular MIMO detection scheme, thanks to its ability to achieve near-maximum likelihood (ML) performance. On the other hand, SD exhibits a variable complexity depending on the channel condition, which makes it not well suited for real-time hardware applications. Meanwhile, K-Best detectors exhibit a fixed complexity irrespective of channel conditions; therefore, they have received significant interest in recent years [10,11].

However, the relatively high complexity still required for K-best MIMO detectors imposes great demands on energy consumption and causes drainage of the battery, which may render its use unfeasible in green communication schemes [8]. A number of energy efficient hardware designs of K-best MIMO detector have been proposed [12,13,14]. Kim and Park in [13] employed a relaxed sorting operation technique to achieve a significant reduction in the power consumption of the MIMO detector. In [14], the authors adopted a sort-free approach to path extension in order to minimize energy costs. More recently, an adaptive hardware scheme was proposed in [12], where favorable channel conditions are exploited to reduce the energy consumption of the MIMO detection hardware, which was achieved through the use of reconfigurable MIMO detection architecture controlled by the signal to noise ratio (SNR).

Although these schemes proved to reduce power consumption of the MIMO detecting hardware, they may still not be suitable candidates for green communication networks, as they do not take into consideration the transmission power requirements. In fact, the transmission power accounts for more than 50% of the overall power consumed in wireless cellular networks [2], which is expected to rise significantly in 5G wireless networks because of the increase in signal frequencies [7,8]. In the context of this work, 5G networks refer to communication systems, which operate at frequencies higher than the conventional microwave frequencies, typically more than 6 GHz. At higher frequencies, the path losses and environment attenuation factors become significantly higher than those experienced in sub-6 GHz frequencies. Therefore, higher transmission power, as well as more sophisticated signal processing, are needed for 5G systems. Additionally, at higher carrier frequencies, 5G networks are expected to have significantly higher bandwidths than the currently operating systems such as 3G and 4G. Therefore, for green wireless communications there is a need for MIMO decoding schemes, which have low-power hardware implementation and minimal transmission power requirements.

Lattice reduction (LR) techniques [15] have received increasing attention for MIMO detection because of their potential to attain near-ML performance, while having a significantly lower complexity than the maximum likelihood detection (MLD), especially in large-scale MIMO systems [16]. In comparison with the conventional K-best detectors, the LR-aided K-best algorithm assumes no boundary information about the symbols in the lattice-reduced domain, which means possible children for each layer can be infinite. Therefore, to find the K-best partial candidates from the infinite children set, LR-aided K-best algorithms typically replace the infinite set with a finite subset of the children. The complexity of generating the subset may be reduced by using an on-demand child expansion based on the Schnorr-Euchner (SE) strategy [17].

This paper presents an energy-efficient LR-aided K-best detector targeting a 2 × 2 MIMO system with quadrature amplitude modulation (QAM) spatial multiplexing. We developed a new hardware architecture, which was implemented in 32 nm technology for verification and energy cost evaluation. Our results indicate that the proposed decoder reduces the overall power costs by four-fold, on average, compared to existing schemes, thanks to its better bit error rate BER performance. The throughput of the proposed decoder is comparable with existing approaches.

This paper is organised as follows: Section 2 outlines the main principles of sphere decoding and K-best algorithms; Section 3 explains how LR techniques can be combined with K-best decoding to enhance performance; Section 4 describes the proposed hardware architecture of the LR-aided K-best detection; Section 5 presents a framework to evaluate the overall power costs of a MIMO scheme, which takes into consideration its transmission power requirements; Section 6 explains the VLSI implementation details and compares the proposed design with recently-published energy efficient MIMO decoders; and, finally, conclusions are drawn in Section 7.

2. Sphere Decoding and the K-Best Algorithm

In this paper, we consider a MIMO system with ${\mathrm{N}}_{\mathrm{t}}$ transmit antennas and ${\mathrm{N}}_{\mathrm{r}}$ receive antennas. The maximum likelihood (ML) detector offers the best achievable BER performance; however, its complexity makes it impractical in terms of hardware implementation. On the other hand, the SD tries to decrease the complexity of ML and to achieve a sub-optimal performance by searching only through those points that fall inside a sphere of radius r, where the SD transforms the ML problem to a tree search [18]. There are many approaches to perform a tree search, where in this work we focus on Breadth-First Search (BFS) using the K-Best algorithm [8,9]. In the following we describe the original SD algorithm [18] in order to provide some background explanation of the idea of SD, then we describe the LR-aided SD algorithm in the next section, which forms the basis for our implementation.

The MIMO system is normally modeled using the following equation: y = Hx + n, where y represents the received MIMO signal, H represents the MIMO channel matrix, x represents the transmitted MIMO signal and n represents the additive white gaussian noise (AWGN). The ML algorithm for detecting the transmitted signal given the MIMO received signal model can be expressed as:

$$\underset{\mathrm{x}\in {\mathrm{X}}^{{\mathrm{N}}_{\mathrm{t}}}}{\widehat{\mathrm{x}}=\text{arg min}}{\Vert \mathrm{y}-\text{Hx}\Vert }^2,$$

(1)

Using the K-Best detector, the ML problem shown in Equation (1) is transformed to Equation (2) as:

$$\underset{\mathrm{x}\in {\mathrm{X}}^{2{\mathrm{N}}_{\mathrm{t}}}}{\widehat{\mathrm{x}}=\text{arg min}}{\Vert \check{\mathrm{y}}-\text{Rx}\Vert }^2.$$

(2)

The operation in Equation (2) is performed after performing QR-decomposition on the channel matrix H, which results in H = QR with R being an upper triangular matrix and Q a unitary matrix. In (2), $\begin{array}{c}\check{y}\end{array}=Q^{T}y$, and $x\in {\mathrm{X}}^{2{\mathrm{N}}_{\mathrm{t}}}$ represents the symbol vector of size $2{\mathrm{N}}_{\mathrm{t}}\times 1$, where the complex vector of size ${\mathrm{N}}_{\mathrm{t}}\times 1$ is transformed to a real vector of size $2{\mathrm{N}}_{\mathrm{t}}\times 1$. Equation (2) refers to a tree search due to the nature of $R$, where it normally starts from the last row towards the first row in the $R$ matrix. In each layer the K-Best algorithm will select the K candidates having the lowest partial Euclidean distance (PED) from $\check{y}$. The K-Best algorithm can be summarized as follows:

• Initialize the first layer $\mathrm{i}=2{\mathrm{N}}_{\mathrm{t}}$;
• Find the PEDs of all expanded nodes at layer $\mathrm{i}$ and select the K minimum PEDs;
• Expand the surviving nodes to their $\sqrt{\mathrm{M}}$ children and set $\mathrm{i}=\mathrm{i}-1$;
• If $\mathrm{i}\ne 1$ go to step 2, otherwise continue;
• Select the path with the lowest PEDs as the solution.

3. LR-Aided K-Best Decoder

The Lenstra–Lenstra–Lovász (LLL) algorithm is typically used to implement lattice reduction due to its relatively low complexity and good performance [5,6]. This section explains how the LR technique based on the LLL algorithm can be combined with the K-Best detector. Given the MIMO model of y = Hx + n, the received signal of the MIMO system can be transformed in LR form as [16]:

$$y=H T T^{\mathbf{-}\mathbf{1}} x+n=\tilde{H} \left(T^{\mathbf{-}\mathbf{1}} x\right)=\tilde{H} z+n$$

(3)

where $T$ is a unimodular matrix, which has a determinant of $\pm 1$ and all the entries of $T$ are integers [5,6]. The new channel matrix is represented as $\tilde{H}=H T$. Multiplying $T$ with $H$ gives a more orthogonal and better-conditioned matrix $\tilde{H}$ than the MIMO channel H [16]. By adopting Equation (3), the MIMO system model is transformed from $y=H x+n$ to $y=\tilde{H} z+n$. Therefore, the detector requires to detect $z=(T^{\mathbf{-}\mathbf{1}} x)$ from the reduced-lattice constellation and then recovers the original constellation point by $\widehat{x}=Tz$. Note that $z\in \mathbb{Z}$ integer set. Both $Hx$ and $\tilde{H}z$ produce the same point in the lattice but $\tilde{H}$ is more orthogonal than $H$ and gives more reliable estimation for the received signal $y$ at the receiver.

In order to perform K-Best detection, the decoder finds the $T$ matrix from $H$ by performing LLL algorithm [15]. Then, the orthogonal $\tilde{H}$ matrix is obtained by $\tilde{H}=HT$. Then, similarly to the conventional K-Best detector, QR decomposition is performed for $\tilde{H}$ so that $\tilde{H}=\tilde{Q}\tilde{R}$, where $\tilde{R}$ is an upper triangular matrix and $\tilde{Q}$ is a unitary matrix. The size of both $\tilde{Q}$ and $\tilde{R}$ is $2{\mathrm{N}}_{\mathrm{r}}\times 2{\mathrm{N}}_{\mathrm{t}}$, which is due to taking the real model into consideration. After QR decomposition, we can rewrite $y=\tilde{H} z+n$ as $y=\tilde{Q}\tilde{R} z+n$. Then, the ML process in Equation (1) is reshaped to represent the detected $\widehat{z}$ as:

$$\widehat{z}=\underset{\mathrm{z}\in {\mathbb{Z}}^{2{\mathrm{N}}_{\mathrm{t}}}}{\text{arg min}}{\Vert \check{y}-\tilde{R}z\Vert }^2$$

(4)

where z is computed as: $z=(T^{\mathbf{-}\mathbf{1}} x)$.

$\check{y}$ is a shifted and scaled version of y and it is computed as follows:

$$\check{y}={\tilde{Q}}^H \tilde{y}$$

(5)

$$\tilde{y}=\frac{\left(y-H 1_{2N_t\times 1}\right)}{2}$$

(6)

Afterwards, from Equation (4) the detector requires performing a tree search to detect $z$ and then recovers the original symbols by multiplying with T after rescaling and re-shifting $\widehat{z}$ as $\widehat{x}=2T\left(\widehat{z}\right)+1_{2N_t\times 1}$, which can be expressed as [17]:

$$\widehat{x}=2T\underset{\mathrm{z}\in {\mathbb{Z}}^{2{\mathrm{N}}_{\mathrm{t}}}}{\text{ arg min}}{\Vert \check{y}-\tilde{R}z\Vert }^2+{\mathbf{1}}_{2{\mathrm{N}}_{\mathrm{t}}\times 1},$$

(7)

where ${\mathbf{1}}_{2{\mathrm{N}}_{\mathrm{t}}\times 1}$ is a matrix of size $\left(2{\mathrm{N}}_{\mathrm{t}}\times 1\right)$ with all entries one.

To implement Equation (7) the breadth-first K-Best algorithm is used, where in the shift and scale of y transforms the points searched for into continuous numbers (−1, 0, 1, 2…) in each dimension. The detection of candidates in each layer exploits the on-demand child expansion the Schnorr-Euchner (SE) enumeration, hence there will be no fixed format of the candidates. The value of the candidates in the current layer is only based on the initial child ($chil{d}_i$) and steps obtained. The order of the detection in each layer can be presented in Figure 1.

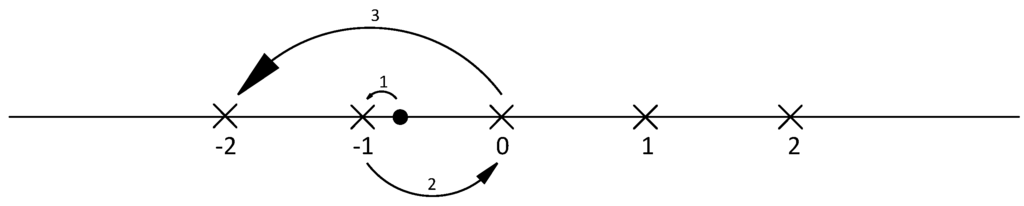
Figure 1. Schnorr-Euchner enumeration order in one dimension.

The crosses in Figure 1 represent the points in the lattice, while the black point is rounded to −1, which is the initial child in this example. The other candidates in the current layer will be based on the order as the Figure 1 shows. The constant k will determine the times of the jumping across the candidates. For the complex model used in this work, the order in two dimensions can be presented as Figure 2.

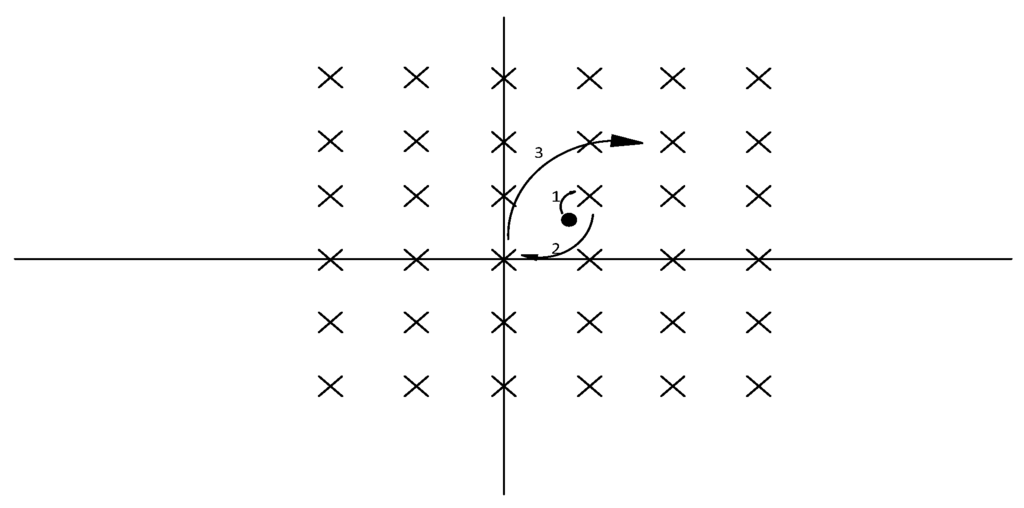
Figure 2. The SE enumeration order in two dimensions.

The removal of the fixed format of the candidates, combined with the on-demand child expansion method, significantly reduces the correlation among the candidates, which can improve the performance of the MIMO detection process and reduces its complexity.

4. System Architecture Design and Verification

We have developed and implemented a hardware architecture for an LR-aided K-Best detector targeting a 2 × 2 MIMO system with quadrature amplitude modulation (QAM) spatial multiplexing and K = 2. The word length is chosen to be 16 bits for all design variables after analyzing their expected range in the software model. More details are provided in the following sub-sections.

4.1. Software Implementation and Evaluation

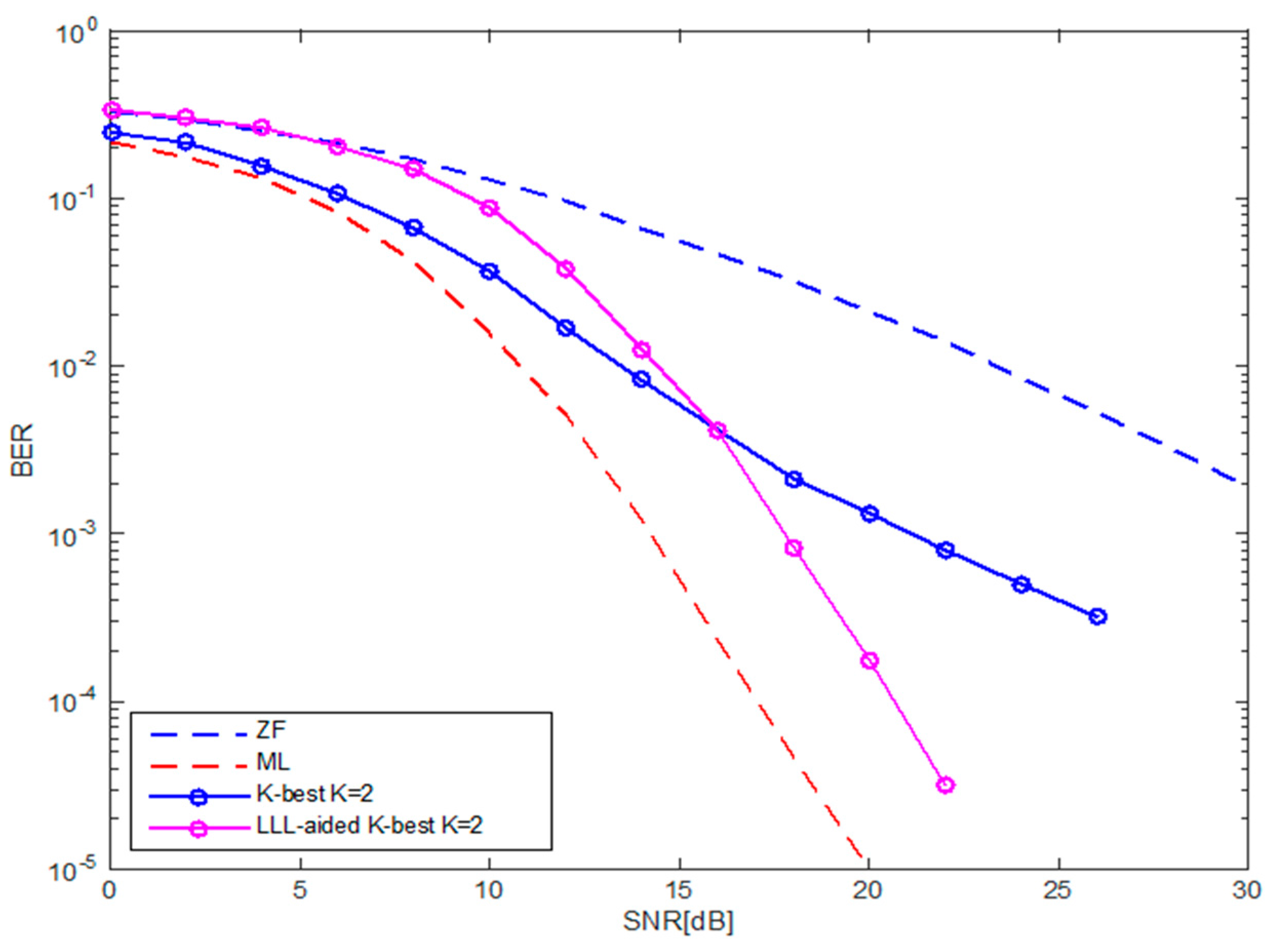
First we have built a software implementation of the proposed detector in MATLAB software provided by Mathworks. The BER performance of the design has been evaluated and compared with conventional MIMO schemes. The Rayleigh fading channel is used as a model of the communication medium. The results are shown in Figure 3. It can be seen that the performance improvement achieved by applying LR to the conventional K-Best is about 3.5 dB at a BER of ${10}^{-3}$. The performance of the LR-aided K-Best decoder approaches the ML performance as K increases. Furthermore, it is worth noting that the performance of LR-aided K-Best detector would have better performance at lower SNR compared to the conventional K-best decoder as the number of transmit and receive antennas increases [7].

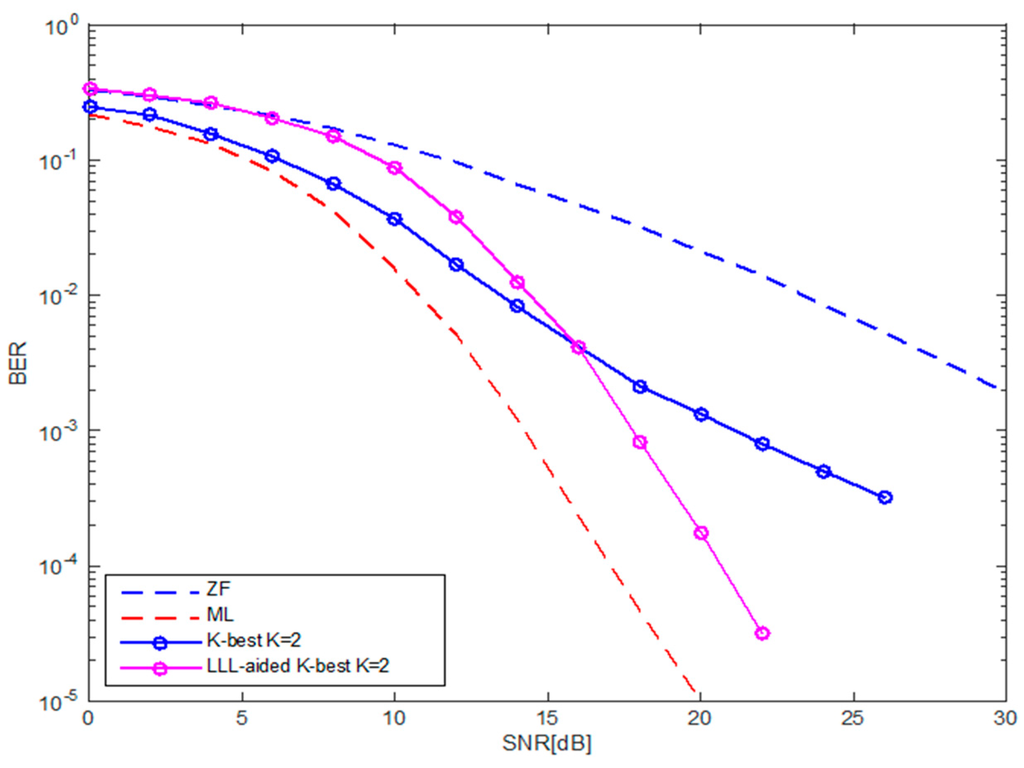
Figure 3. BER performance of 4-QAM over 2 × 2 MIMO system using LR-aided K-best and compared to the corresponding K-best.

4.2. Hardware Architecture

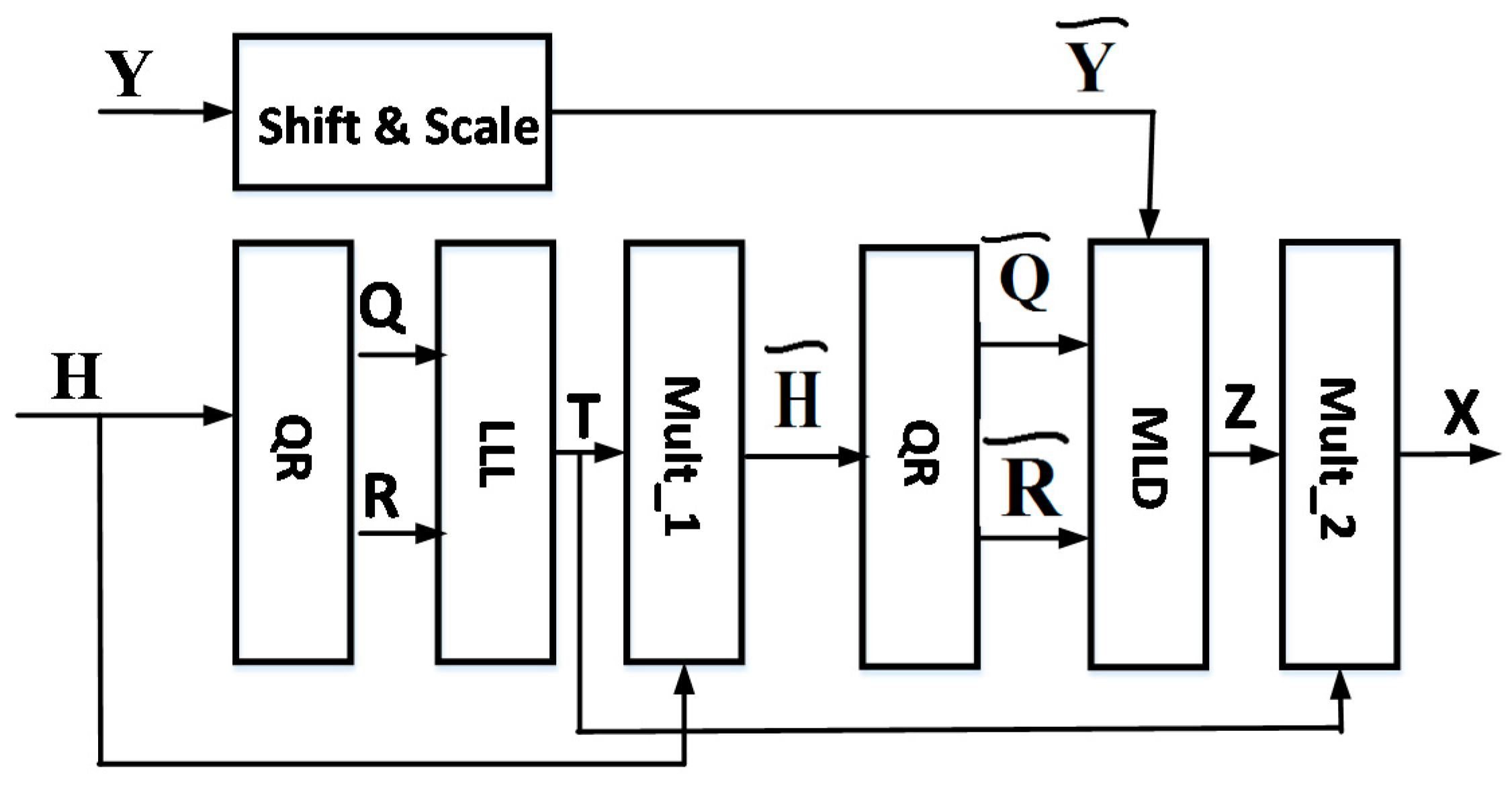
In the second stage of the design we have developed the hardware architecture as shown in Figure 4. This was modeled using System Verilog and implemented using 32 nm standard CMOS technology. The functionality of the design has been verified at each stage of the implementation by comparing it with the golden model as explained in the previous section. The functionality of each block of the system is explained below:

• The QR block decomposes the input H matrix into an orthonormal matrix Q and an upper triangular matrix R. The precision of the QR decomposition has a considerable effect on the performance of the symbol detection. Low-quality QR decomposition directly causes a bit error rate, especially in systems with large numbers of antennas and/or large signal constellation size. There are three common-used algorithms for the QR decomposition including Gram-Schmidt, householder reflections and given rotations. Among these, the given rotation method offer the best performance-hardware cost tradeoff. In this work, given rotations algorithm is chosen for QR decomposition.
• The LLL block implements the Lenstra–Lenstra–Lovász algorithm to compute the T matrix from Q and R matrixes. The CORDIC algorithm is used to implement all square root functions as it replaces multiplications with add and shift operations, which greatly simplifies the hardware.
• The MULT_1 block multiplies the T matrix with the H matrix to produce the orthogonal $\tilde{\mathrm{H}}$ matrix.
• The shift and scale block implements Equations (5) and (6) in order to extend the matrix for the received signal Y for the benefits of the following MIMO detection stage.
• The functionality of the MLD block is to detect z as described in Section 3, as $z=T^{\mathbf{-}\mathbf{1}} x$. To achieve this it needs to perform the search process described in Equation (7) using a breadth-first K-Best algorithm

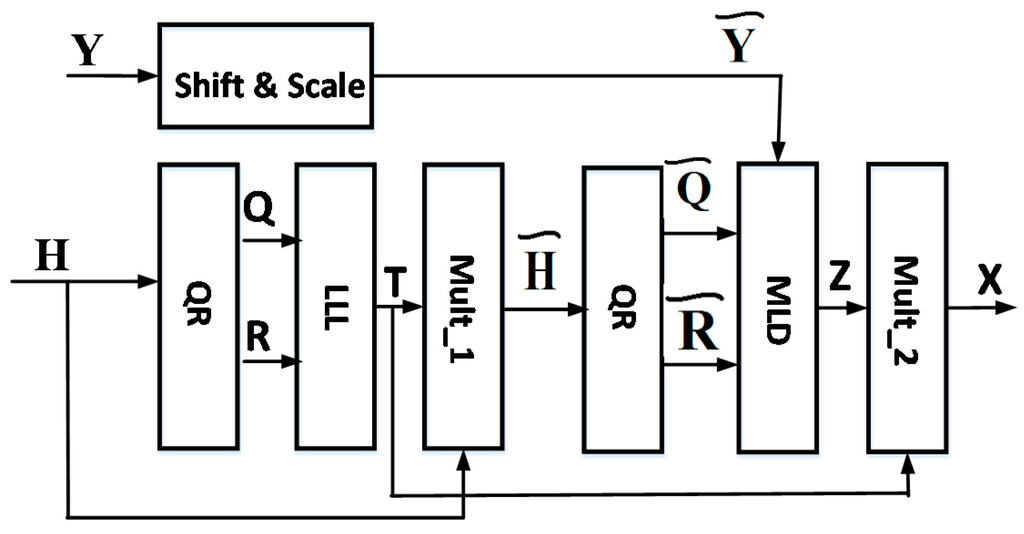
Figure 4. Hardware architecture of lr-aided k-best.

The MULT_2 block multiplies the output of the MLD block by the matrix T to recover the original constellation point x.

5. Evaluation of Energy Costs of MIMO Detectors

To design a green communication wireless system, it is important to reduce its overall power costs. Therefore, in order to analyse the energy efficiency of a MIMO decoding scheme in relation to a green wireless communication application, it is vital to consider both: the power consumption of the MIMO decoder hardware ($P_{hw}$) and also the minimum transmission power required for the decoder to work reliably ($P_{tr}$). Details on how each of these components can be evaluated are provided in the following two subsections:

a) Power Consumption Estimation of MIMO Decoder

The power dissipation of a hardware block ($P_{hw}$) is typically estimated as the sum of two components: dynamic and static. Dynamic power consumption ($P_{dynamic}$) is attributed to the charging and discharging of capacitances, it is dependent on the supply voltage (V), the operating frequency (f), the signals’ transition activities (δ), and the switching capacitances (C). Some of these factors are dependent on underlying CMOS technology used for implementation such as V, C, and f, whereas others depend on the application running on the hardware such as (δ). Dynamic power consumption can be computed as follows:

$$P_{dynamic}=\delta .f.C.V^2.$$

(8)

Static power consumption ($P_{static}$) is attributed to power dissipation caused by leakage currents and to short-circuit dissipation caused by current passing through the direct path between supply and ground during logical transitions in CMOS devices. Static power consumption is mainly a function of the implementation technology which determines the leakage currents and the supply voltage. The complexity of the circuit can affect static power dissipation, the more complex and the larger the design, the higher the amount of leakage power dissipation.

In this work, to estimate the power consumption we have implemented the proposed decoder using 32 nm standard CMOS technology, with a supply voltage of 1v. The operation frequency was set to 253 MHz. More details on this is provided in Section 6.

b) Estimation of Minimum Transmission Power Requirement

A MIMO decoder typically has a required minimum SNR below which it cannot operate reliably. This essentially means there is a minimum required transmission power which can be calculated using the formulae below [19]:

$$P_{tr}={10}^{\frac{RNF}{10}} kTB \left(\frac{S}{N}\right){\left(\frac{4\pi }{\lambda }\right)}^2 d^n$$

(9)

where:

S/N:	is the minimum signal to noise ratio required at the receiver.
RNF:	is a the receiver noise figure in dB, (e.g., for an ideal receiver (RNF = 0).
K:	is the Boltzmann constant.
T:	is the absolute temperature in K.
λ:	is the transmitted wavelength.
d:	is the distance between the transmitter and receiver
n:	is the path loss exponent which depends on the environment (e.g., for free space (n = 2)).

In this work, Equation (9) is used to estimate the minimum requirement for transmission power of MIMO detection schemes

6. VLSI Design and Comparative Analysis

A chip which implements an LR-aided K-Best detector targeting a 2 × 2 MIMO system was synthesized using 32 nm standard CMOS technology. The frequency of operation was set to 253 MHz at a supply voltage of 1 V. To estimate the power consumption of the MIMO decoder hardware ($P_{hw}$) under normal operation conditions, first we computed the channel matrix (H) based on free space medium. The latter was then applied to the MIMO decoder along with large number of typically received inputs (Y), the average power consumption has then been estimated for all test cases.

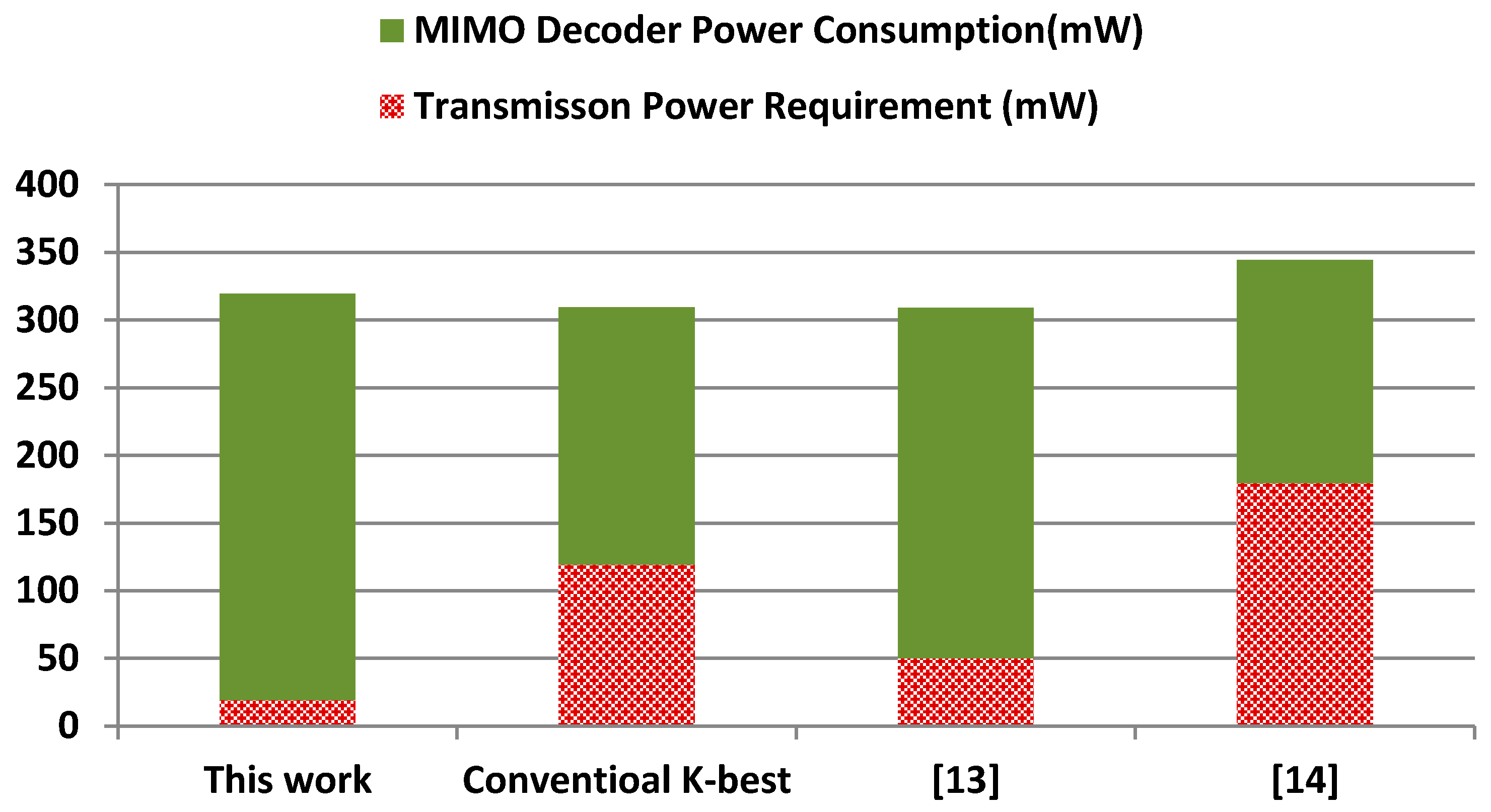
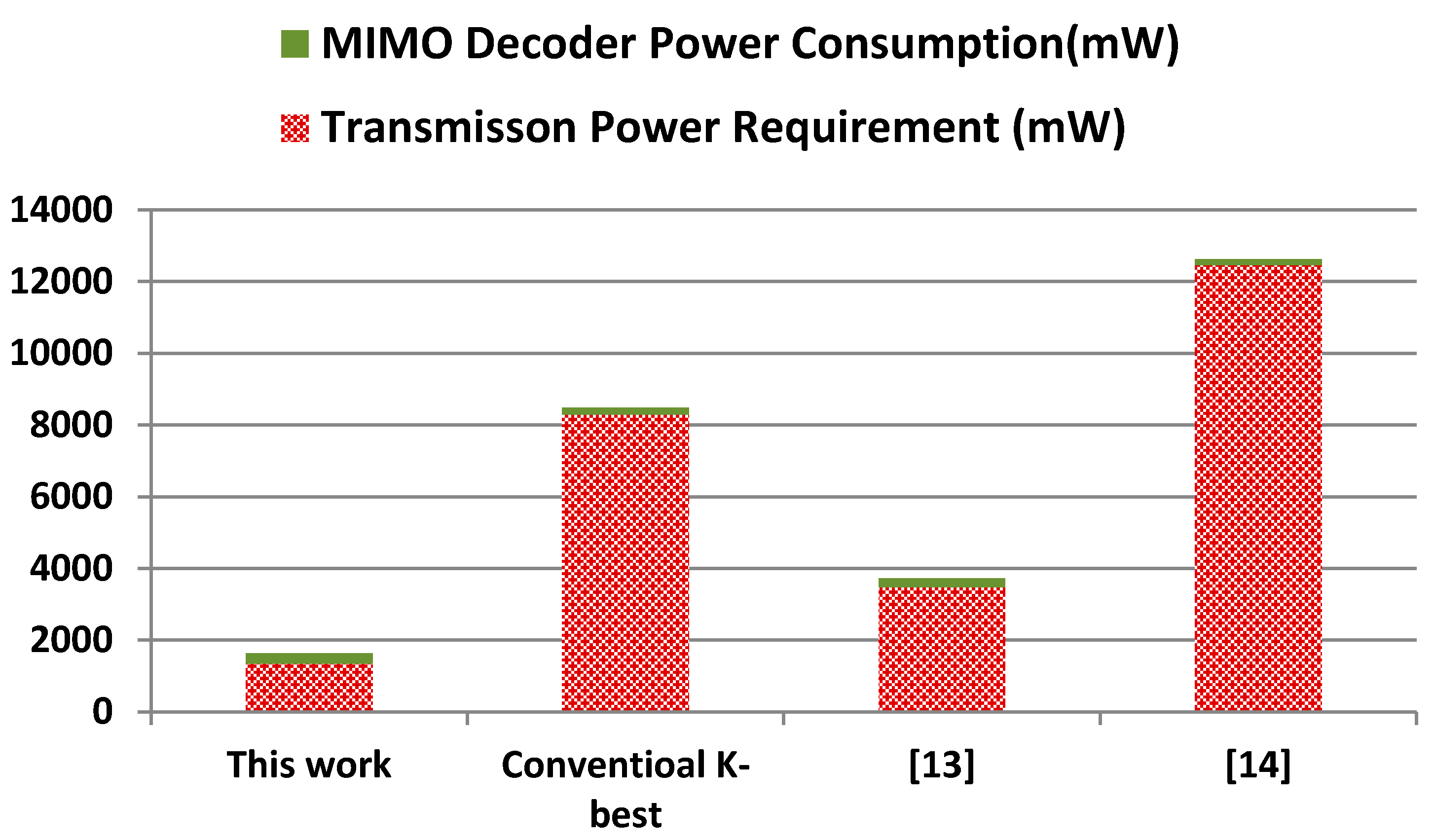
The minimum transmission power requirement is estimated using Equation (9) based on free space communication medium, where we have considered the minimum acceptable BER of 10⁻³, this is because received signals with BER higher than this figure may not be reliably detected [20]. We have considered two study cases: 4G and 5G wireless communication networks. The operation parameters of 4G systems are obtained from the third-generation partnership project which provide detailed information on the operating conditions of such networks [21], where we consider a 4G network transmission frequency of 1.8 GHz. The operation parameters of 5G networks are still in the development stage; initial estimates of the transmission frequencies indicate they are within the range 10–100 GHz [22]. For the purpose of this work we have considered the first successful implementation of a 5G wireless communication network recently announced by Ericsson [22], where in the transmission frequency was set to 15 GHz. In both of the above cases we consider the average distance between a mobile device and a base station around 200 m [20]. Figure 5 and Figure 6 illustrate the power costs of the proposed design in comparison with conventional K-best decoder and recently published energy efficient MIMO detection schemes. The two components of the power overheads: MIMO decoder power consumption and transmission power are illustrated separately. For completeness we have also included a comparison of the VLSI implementation in Table 1.

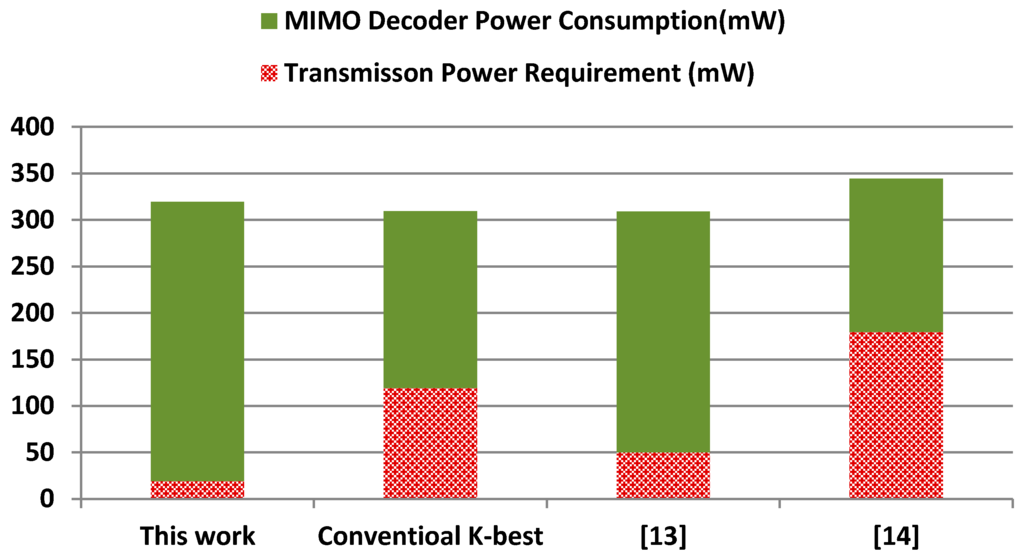
Figure 5. Comparative power costs of MIMO decoders for 4G wireless communication network (carrier frequency = 1.8 GHz).

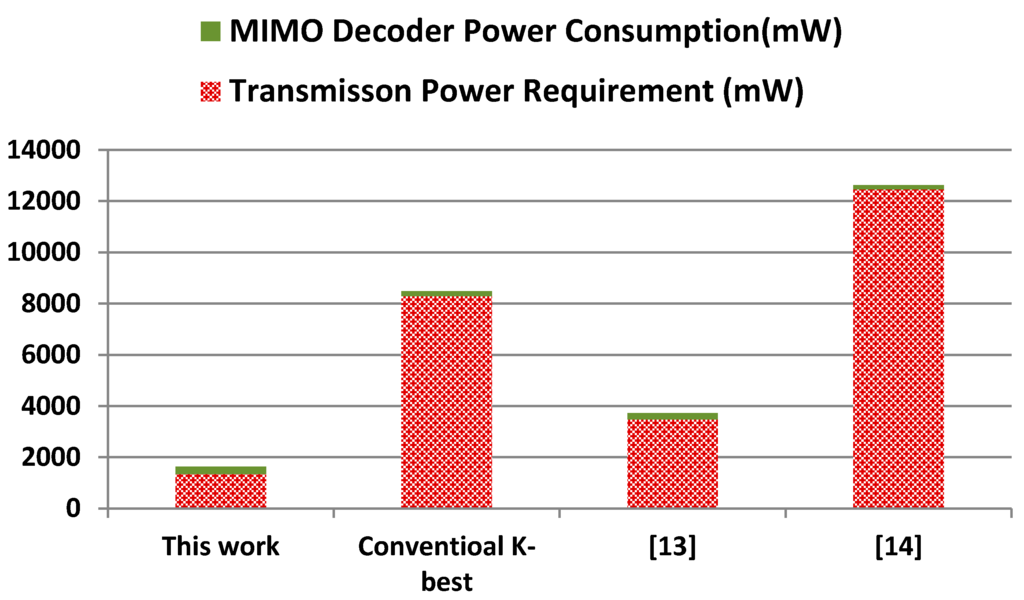
Figure 6. Comparative power costs of MIMO decoders for 5G wireless communication network (carrier frequency = 15 GHz).

Table 1. Comparison of VLSI implementations for MIMO detectors.

Reference	This Work	Conventional K Best	[13]	[14]
Configuration	2 × 2	2 × 2	4 × 4	4 × 4
	4-QAM	4-QAM	16-QAM	64-QAM
Technology	32 nm	32 nm	180 nm	65 nm
Operating Frequency (MHz)	253	253	146	158
Throughput (Mb/s)	506	506	584	463

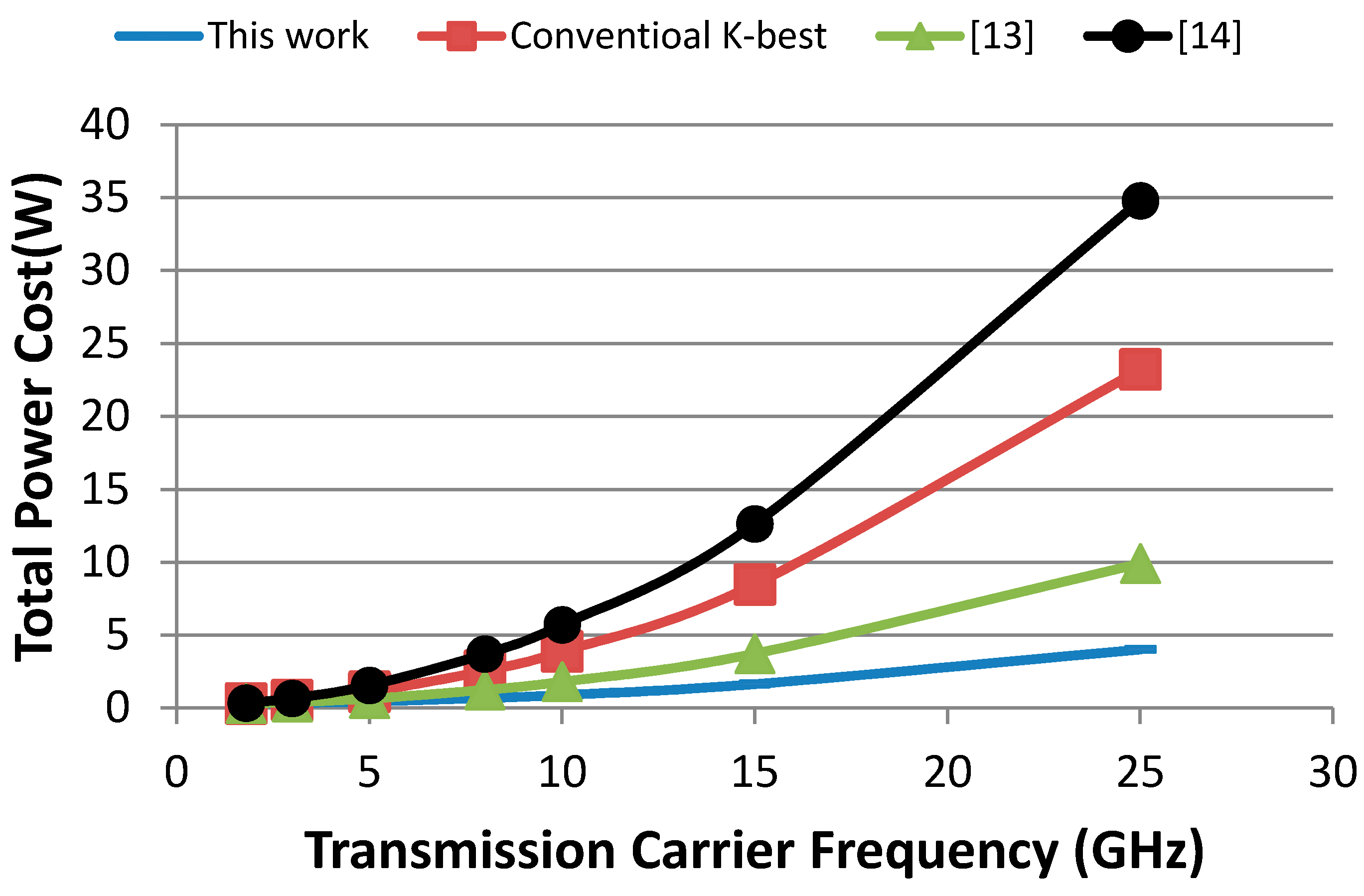
For the first case study, i.e., the 4G wireless mobile network, Figure 5 shows that the proposed MIMO can significantly reduce the transmission power requirements at the expense of increased power consumption of the MIMO decoder; therefore, its overall power costs is comparable to existing approaches. However for the second case study, i.e., the 5G wireless network, our decoder exhibits remarkably higher power efficiency, because it reduces the overall power cost: by two- and seven-fold, compared with conventional K-best implementations in [13,14], respectively. These large power saving are expected to be higher as the carrier frequency increases. Figure 7 show the relationship between the transmission carrier frequency and the overall power consumption costs for the four schemes.

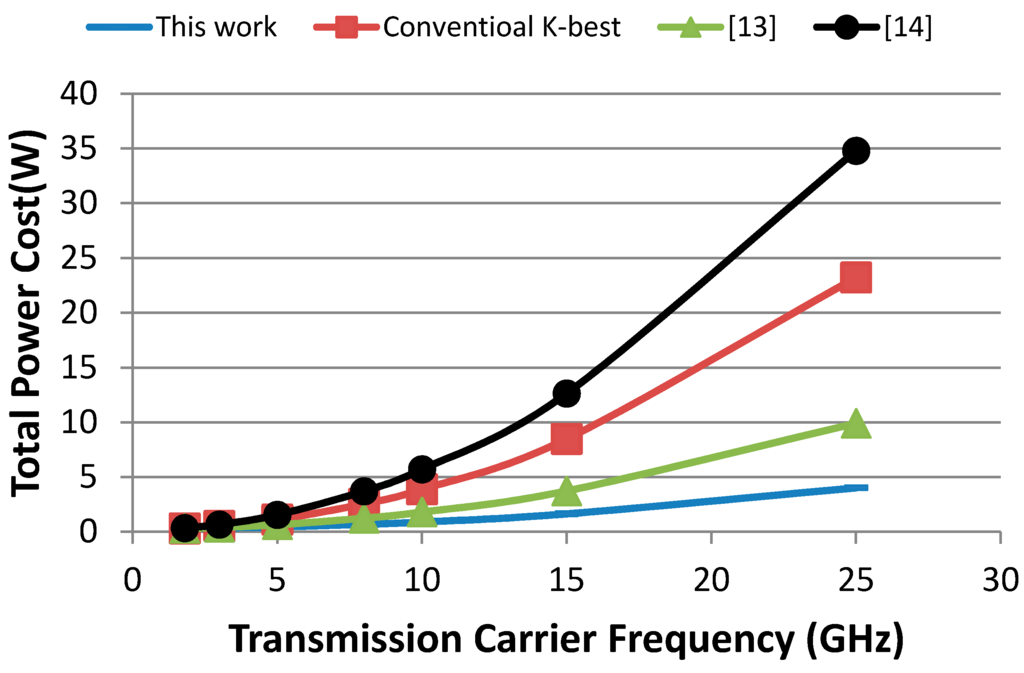
Figure 7. Comparative power costs of MIMO decoders for different transmission carrier frequencies.

Finally, it is worth noting that the throughput of the proposed design is comparable to existing approaches as outlined in Table 1.

7. Conclusions

The relentless rise in global demands for communication infrastructures has driven the continuous expansion of wireless communication mobile networks and an exponential growth in their traffic rates. This has led to a sharp increase of energy consumed by such systems, which has given rise to the concept of a green communication scheme. The latter aims to reduce the overall power needed to operate the future mobile communications systems. MIMO decodes are going to be an integral part of the 5G wireless communication networks. Therefore, in this work we introduced a novel energy efficient MIMO decoder which needs a fraction of the overall power requirement compared with recently published designs in 5G networks. The proposed design is based on an improved LR-aided K-Best MIMO detection algorithm. We have implemented the proposed decoder in 32 nm standard CMOS technology and verified its hardware implementation. In addition we have presented a framework to estimate the overall power costs of a MIMO system, which includes the power consumed by the decoder itself and the minimum transmission power required for a reliable operation. Our results indicate the proposed decoder reduces the overall power costs by four-fold on average compared to existing schemes for 5G communication network, thanks to its high BER performance. Our analysis also showed that the transmission power is going to be far more significant than that consumed by the MIMO decoder in future wireless networks. This is because of the continuous rise of transmission frequency (i.e., more transmission power), combined with scaling of semiconductor technology (i.e., a reduction in hardware dynamic power consumption), this observation should be noted by designers of future energy-efficient MIMO decoders.