An FSK and OOK Compatible RF Demodulator for Wake Up Receivers

Abstract

This work proposes a novel demodulation circuit to address the implementation of Wake-Up Receivers (Wu-Rx) in Wireless Sensor Nodes (WSN). This RF demodulator, namely Modulated Oscillator for envelOpe Detection (MOOD), is compatible with both FSK and OOK/ASK modulation schemes. The system embeds an LC oscillator, an envelope detector and a base-band amplifier. To optimize the trade-off between RF performances and power consumption, the cross-coupled based oscillator is biased in moderate inversion region. The proof of concept is implemented in a 65 nm CMOS technology and is intended for the 2.4 GHz ISM band. With a supply voltage of 0.5 V, the demodulator consumes 120 μW and demonstrates the demodulation of OOK and FSK at a data rate of 500 kbps.

1. Introduction

The so-called Internet Of Things (IOT) aims the development of a smart environment that supports people in their daily lives. Essential to the implementation of IOT is the deployment of inter-connected, and dense Wireless Sensor Networks (WSN). Among the taught challenge in the ubiquitous development of WSN is the management of energy. Specifically, the reduction of the power consumption in wireless nodes concentrates a lot of attention due to their small form factors.

In WSN, the energy consumption of wireless communications dominates the overall power budget. To cope with this pitfall the Radio-Frequency (RF) transceiver of wireless nodes, Figure 1, is only turned on during data broadcasting. Out of these periods of communications, the RF transceiver is in sleep mode, and an auxiliary RF receiver, namely wake-up receiver (WuRx) in Figure 1, monitors the wireless channel for potential incoming traffic [1]. Since the WuRx is continuously listening, its active power consumption must be very low compared to the RF transceiver. Typically a budget of 100 μW is allowed for WuRx [1]. To meet the requirement of ultra low power consumption, basic modulations such as OOK, FSK, or PSK, can be exploited for the wake up signals. Indeed the receiver architectures compatible with these modulation schemes are simple and allow power saving. The super-generative [2], tuned RF [3] or uncertain IF architectures [4] are popular solutions to demodulate an OOK modulated signal. In [3], the Wu Rx consumes 51 μW and achieves a sensitivity of −64 dBm at a data rate of 100 kbps to demodulate a 2400 MHz OOK modulated signal. For FSK demodulation, WuRx are based on frequency discrimination architecture. In [5], the Wu Rx consumes 126 μW and achieves a sensitivity of −65 dBm at a data rate of 20 kbps to demodulate a 900 MHz FSK modulated signal.

Figure 1. Radio module of a wireless sensor node.

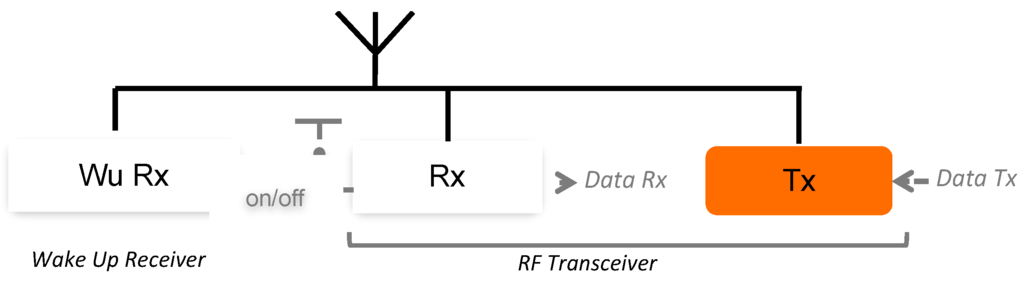
Figure 1. Radio module of a wireless sensor node.

The lack of regulation in WSN medium access opens up the choice for modulation in the wake up protocol. In practice, OOK and FSK signals are preferred but none of them really impose. The WuRx reported so far in the literature are compatible with only one of these two modulations. As a consequence, the WuRx architecture implemented in wireless nodes can limit the interoperability of WSNs. This work proposes a novel low power demodulator compatible with both OOK and FSK modulations. The principle of a dual mode demodulation is first exposed in Section 2. The proof of concept, detailed in Section 3, features an LC oscillator coupled with an envelope detector implemented in a 65 nm CMOS technology. The characterization of the MOdulated Oscillator for envelope Detection (MOOD) receiver is further presented in Section 4. The circuit consumes 120 μW, and properly demodulates OOK and FSK modulated signal at 2.4 GHz with data rate up to 500 kbps.

2. Principle of Frequency and Amplitude Demodulation with an LC Oscillator

The principle of frequency demodulation exploited in this work is first exposed. The response of a resonator oscillator in pulled and locked modes is analyzed the second time. It is demonstrated that an external frequency modulated signal is transformed into an amplitude-modulated signal when the oscillator is in pulled mode. In locked mode, an external amplitude modulated signal is transferred to the output with a maximum voltage swing.

2.1. Non-Coherent Demodulation of a Frequency Modulated Signal

The binary Frequency Shift Keying (FSK) is a frequency modulation commonly exploited in wireless sensor networks. The data are transmitted shifting the frequency of a continuous carrier between f₁ and f₂ as illustrated in Figure 2.

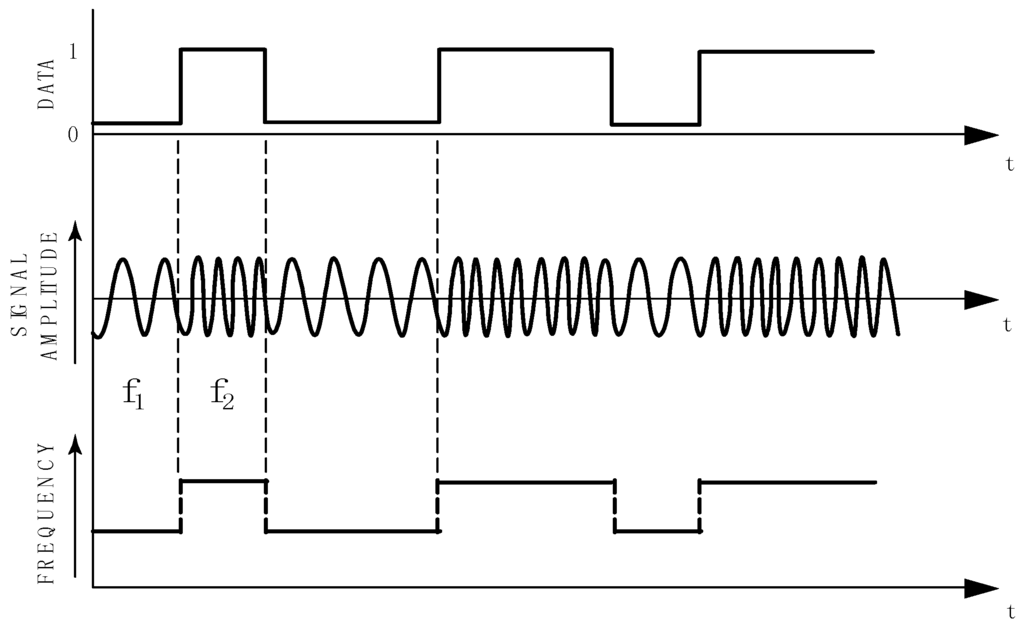
Figure 2. Principle of binary FSK modulations.

Figure 2. Principle of binary FSK modulations.

The non-coherent demodulation of a binary FSK modulated signal can be performed by frequency discrimination as depicted in Figure 3. This approach is interesting for power saving. Two parallel chains select one of the two frequencies, f₁ or f₂, and extract the amplitude of the signal by envelope detection. The data are then constructively generated by comparison of V_amp2(t) and V_amp1(t) signals. The frequency deviation, which is the shift between the two discrete frequencies f₁ and f₂, is usually in the range of few tens to few hundreds of kHz. As a consequence, the implementation of the circuits which perform the frequency selection is difficult, expensive and sensitive to process variations in the RF domain. For this reason, the FSK demodulation by frequency discrimination is not exploited in WSN applications.

Figure 3. Non-coherent FSK demodulator.

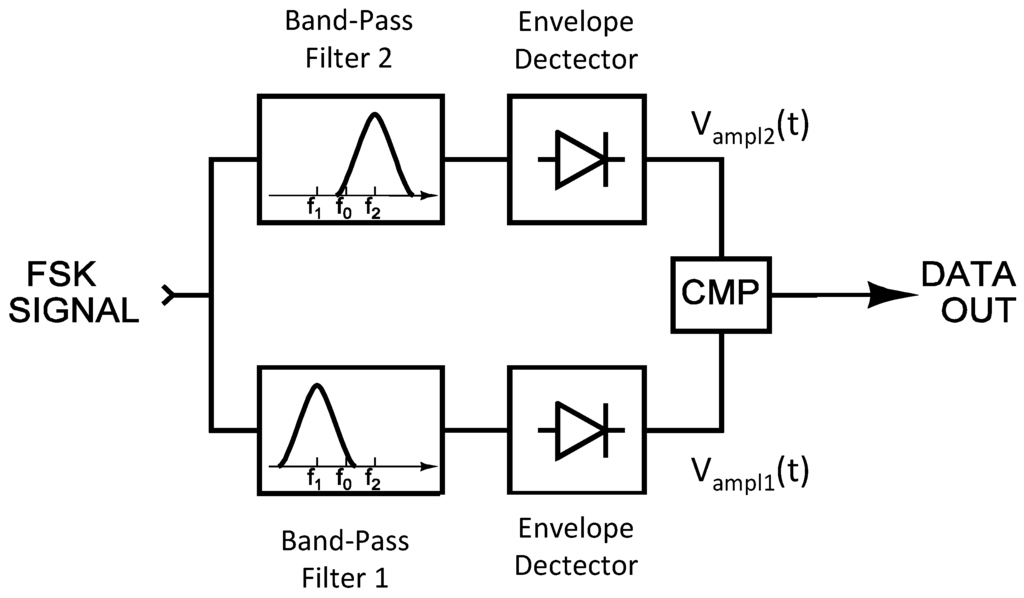
Figure 3. Non-coherent FSK demodulator.

We propose a new architecture for non-coherent demodulation that circumvents the selectivity limitation of the filter-type demodulator. It requires a frequency to amplitude conversion block and an envelope detector as illustrated in Figure 4.

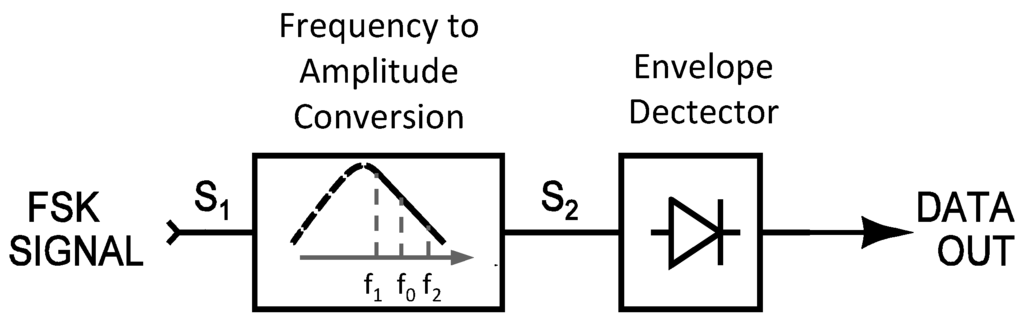
Figure 4. Proposed FSK demodulator.

Figure 4. Proposed FSK demodulator.

To limit the bandwidth of the receiver, it is convenient to use a frequency to amplitude conversion block with a frequency response of band-pass type as illustrated in Figure 4. The bandwidth of the band-pass block contains the carrier f₀, and the two frequencies f₁ and f₂. f₁ and f₂ are located in the roll-off response of the band-pass block which yields a different attenuation for each frequency. Hence, the frequency shift of the incoming FSK signal, S₁, is transformed into amplitude variations in S₂. The data are extracted from S₂ with an envelope detector. This signal processing of the FSK signal is illustrated in Figure 5. Since the proposed principle of demodulation is no longer based on frequency discrimination but frequency to amplitude conversion, the constrain on the filter selectivity is relaxed in comparison with the demodulator of Figure 3. One condition to perform the FM to AM transformation is to keep the frequency f₀, in Figure 4, different to the center frequency of the frequency to amplitude conversion block.

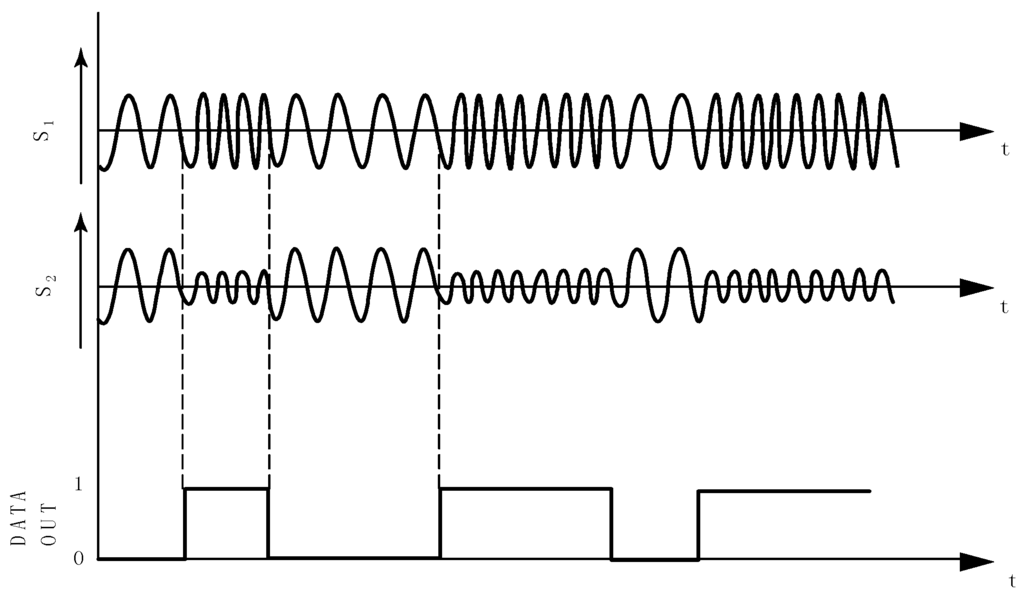
Figure 5. Time evolution of the received signal with the proposed architecture.

Figure 5. Time evolution of the received signal with the proposed architecture.

The relaxed selectivity for the band-pass filter and the single signal path processing of the proposed architecture significantly reduce the complexity, the power dissipation and the cost of implementation compared to a classical filter-type FSK demodulator. Another attractive aspect of the proposed demodulator is its compatibility with amplitude modulation. Indeed, an AM signal will be naturally demodulated by the system since the envelope of the incoming signal is already non-constant. Furthermore, this AM demodulation occurs with no condition on the signal carrier frequency until it is in the bandwidth of the frequency to amplitude conversion block.

2.2. AM-to-FM Conversion and AM-AM Transfer with an LC Oscillator

The critical block of the demodulation principle presented in Figure 3 is the frequency to amplitude converter. A band-pass filter with a steep slope rejection would be attractive, but it is not compatible with silicon integration. Another option is to perform the conversion with an LC Voltage Controlled Oscillator (LC-VCO). This popular block of RF transceivers exhibits a band-pass behavior and allows a center frequency tuning. Interestingly, the oscillating frequency of the LC-VCO can be adjusted to be different to the center frequency of the FSK modulated signal to ensure FM to AM conversion. However, in the presence of an injected signal, an LC oscillator can be either locked or pulled, depending on the magnitude of the perturbation. The response of an LC oscillator in these two modes of operation needs to be investigated to go further in the implementation of the concept proposed in Figure 4.

The phenomenon of injection [6], is a fundamental property of oscillators. Among the most famous contributions to its study are the theory of Adler [7], the theory of Kurokawa [8] and complementary study exposed in [9,10,11]. When an external periodic signal is mixed to an oscillator, the system can be locked or pulled. In locked mode, the oscillator tracks the injected signal. Depending on the ratio of the incident signal frequency to the oscillation frequency, different methods of injection locking are possible: fundamental, sub-harmonic and super-harmonic. In the first case, the injected frequency is the same as the oscillation frequency, in the other two cases the injected frequency is respectively a sub-harmonic or nth-harmonic of the oscillation frequency. If the injected signal frequency is out of the locking range, the oscillator is pulled (instead of locked) by the external signal. To further investigate the oscillator response in injection modes, we consider the behavioral model proposed in Figure 6. The tank Z(ω) resonates at a frequency ω₀, the ideal inverting amplifier, in the feedback path, ensures a close loop gain of unity and a total phase shift of 2π.

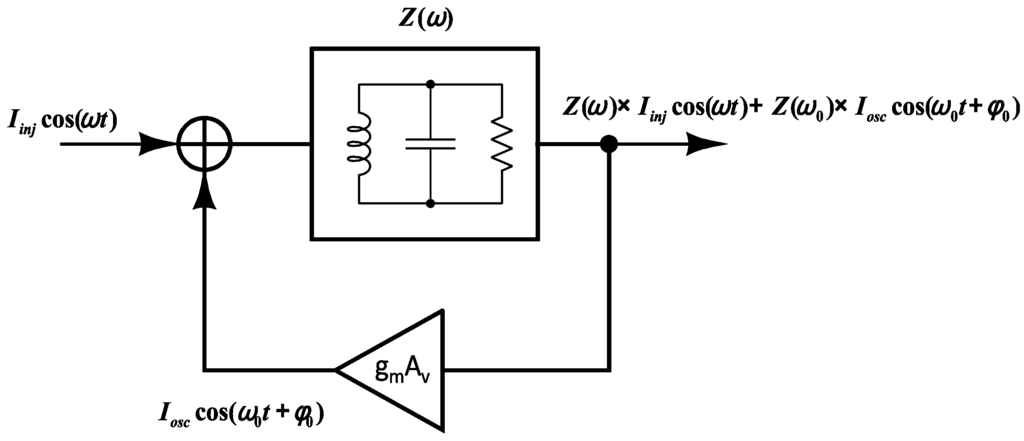
Figure 6. Simplified behavioral model for injection pulled oscillator.

Figure 6. Simplified behavioral model for injection pulled oscillator.

2.2.1. Injection of a FM Signal

If the amplitude and frequency of I_inj (Figure 6) are properly chosen, the circuit keeps on oscillating at ω₀ and injection pulling occurs. Under this condition, the output voltage contains both the injected signal and the free-running oscillation. To derive the analytic expressions of the output voltage under the injection of a modulated signal, we assume the simplified expression (Equation (1)) for the tank impedance.

$$\text{Z}(\mathsf{\omega })\cong \frac{{\text{R}}_{\text{p}}}{1+\text{j}2\text{Q}\frac{\mathsf{\omega }-{\mathsf{\omega }}_0}{{\mathsf{\omega }}_0}}$$

(1)

With (1/R_p) the tank losses and Q the tank quality factor. For the first case of study, we consider an injected FM signal I_FM Equation (2):

$${\text{I}}_{\text{Inj}}(\text{t})={\text{I}}_{\text{FM}}(\text{t})={\text{I}}_0\text{cos}\left[({\mathsf{\omega }}_{\text{c}}\text{t})+\mathsf{\beta }.\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})\right]$$

(2)

where ω_c and ω_m are respectively the carrier frequency and modulating frequency, β is the modulation index. The instantaneous phase and pulsation are derived as it follows:

$$\mathsf{\phi }(\text{t})=({\mathsf{\omega }}_{\text{c}}\text{t})+\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})$$

(3)

$$\mathsf{\phi }(\text{t})=\frac{\text{d}\mathsf{\phi }(\text{t})}{\text{dt}}={\mathsf{\omega }}_{\text{c}}+\mathsf{\beta }{\mathsf{\omega }}_{\text{m}}\text{cos}({\mathsf{\omega }}_{\text{m}}\text{t})$$

(4)

Combining Equations (1) and (2), the output voltage can be expressed as a superposition of the injected signal and the free-running oscillation:

$${\text{V}}_{\text{out}}(\text{t})={\text{V}}_{\text{Inj}}(\text{t})+{\text{V}}_{\text{osc}}(\text{t})$$

(5a)

$${\text{V}}_{\text{out}}(\text{t})=\text{Z}(\mathsf{\omega })\times {\text{I}}_0\text{cos}\left[({\mathsf{\omega }}_{\text{c}}\text{t})+\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})\right]+\text{Z}({\mathsf{\omega }}_0)\times {\text{I}}_{\text{osc}}\text{cos}\left[({\mathsf{\omega }}_0\text{t})+{\mathsf{\varphi }}_0\right]$$

(5b)

Let us focus now on the module of the output signal V_out:

$$\left|{\text{V}}_{\text{out}}\right|=\left|\text{Z}(\mathsf{\omega })\times {\text{I}}_0\text{cos}\left[({\mathsf{\omega }}_{\text{c}}\text{t})+\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})\right]+\text{Z}({\mathsf{\omega }}_0)\times {\text{I}}_{\text{osc}}\text{cos}\left[({\mathsf{\omega }}_0\text{t})+{\mathsf{\varphi }}_0\right]\right|$$

(6)

With respect to the triangular inequality, we have:

$$\left|{\text{V}}_{\text{out}}\right|\le \left|\text{Z}(\mathsf{\omega })\times {\text{I}}_0\text{cos}\left[({\mathsf{\omega }}_{\text{c}}\text{t})+\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})\right]\right|+\left|\text{Z}({\mathsf{\omega }}_0)\times {\text{I}}_{\text{osc}}\text{cos}\left[{\mathsf{\omega }}_0\text{t}+{\mathsf{\varphi }}_0\right]\right|$$

(7)

$$\left|{\text{V}}_{\text{out}}\right|\le \left|\text{Z}(\mathsf{\omega })\times {\text{I}}_0\right|+\left|\text{Z}({\mathsf{\omega }}_0)\times {\text{I}}_{\text{osc}}\right|$$

(8)

$$\left|{\text{V}}_{\text{out}}\right|\le {\text{R}}_{\text{p}}\left[{\text{I}}_{\text{osc}}+\frac{{\text{I}}_0}{\sqrt{1+4{\text{Q}}^2{\left(\frac{\mathsf{\omega }-{\mathsf{\omega }}_0}{{\mathsf{\omega }}_0}\right)}^2}}\right]$$

(9)

The second term in Equation (9) highlights that the module of the output voltage is modulated by the instantaneous frequency (or pulsation ω(t) in Equation (4)) of the injected FM signal. A pulled oscillator transforms a frequency modulated signal into an amplitude modulated signal. The signal’s envelope contains the data that will be further extracted by an envelope detector.

We consider now the situation of an injected FM signal locking the oscillator. The circuit oscillates at ω_c instead of ω₀ because the injection locking occurs. Under this condition, the output voltage (V_out) and the injected current (I_Inj) must bear a phase difference φ_out and satisfy the conditions of Equation (10):

$${\text{V}}_{\text{out}}\text{cos}({\mathsf{\omega }}_{\text{c}}\text{t}+{\mathsf{\varphi }}_{\text{out}})=\left[{\text{I}}_0\text{cos}\left[({\mathsf{\omega }}_{\text{c}}\text{t})+\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})\right]+{\text{I}}_{\text{osc}}\text{cos}\left[({\mathsf{\omega }}_{\text{c}}\text{t})+{\mathsf{\varphi }}_{\text{out}}\right]\right]\times \text{Z}(\mathsf{\omega })$$

(10)

With the complex exponential notation and after some simplifications, Equation (10) becomes:

$${\text{V}}_{\text{out}}(1+\text{j}2\text{Q}\frac{{\mathsf{\omega }}_{\text{c}}-{\mathsf{\omega }}_0}{{\mathsf{\omega }}_0})={\text{R}}_{\text{p}}({\text{I}}_{\text{osc}}+{\text{I}}_0{\text{e}}^{\text{j}[\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})-{\mathsf{\varphi }}_{\text{out}}]})$$

(11)

Equation (11) can be separated into real and imaginary parts leading to:

$$RealPart{\text{V}}_{\text{out}}={\text{R}}_{\text{p}}\left[{\text{I}}_{\text{osc}}+{\text{I}}_0\text{cos}(\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})-{\mathsf{\varphi }}_{\text{out}})\right]$$

(12a)

$$ImaginaryPart\text{ sin}\left[\mathsf{\beta }\text{sin}({\mathsf{\omega }}_{\text{m}}\text{t})-{\mathsf{\varphi }}_{\text{out}}\right]=\frac{2\text{Q}}{{\text{I}}_0}\frac{{\text{V}}_{\text{out}}}{{\text{R}}_{\text{p}}}\frac{{\mathsf{\omega }}_{\text{c}}-{\mathsf{\omega }}_0}{{\mathsf{\omega }}_0}$$

(12b)

The expression (Equation (12a)) provides the output amplitude where as Equation (12b) gives the output phase as a function of the injected signal frequency. Substituting V_out Equation (12a) in Equation (12b) the oscillator locking range can be derived according [6,9], it is reported in Equation (13).

$$\frac{\left|{\mathsf{\omega }}_{\text{c}}-{\mathsf{\omega }}_0\right|}{{\mathsf{\omega }}_0}\le \frac{1}{2\text{Q}}\frac{{\text{I}}_0}{{\text{I}}_{\text{osc}}}\text{ with }{\text{I}}_0\ll {\text{I}}_{\text{osc}}$$

(13)

Under locking conditions, the amplitude of V_out Equation (12a) is not modulated by the instantaneous frequency of the injected FM signal. As a consequence, the FM-to-AM conversion does not occur, and the demodulation of an FM signal is not possible.

2.2.2. Injection of an AM Signal

The expression of an amplitude-modulated signal is proposed in Equation (14). The behavior of the oscillator in pulled and locked mode is investigated under the injection of an AM signal.

$${\text{I}}_{\text{Inj}}(\text{t})={\text{I}}_{\text{AM}}(\text{t})={\text{I}}_0\left[1+\mathsf{\alpha }\text{cos}({\mathsf{\omega }}_{\text{m}}\text{t})\right]\text{sin}({\mathsf{\omega }}_{\text{c}}\text{t})$$

(14)

where ω_c and ω_m are respectively the carrier frequency and modulating frequency, α is the modulation index.

This study figures out the property of the AM modulated signal—i.e., the envelope variations—is naturally transferred to the output signal delivered by the oscillator. The maximum amplitude of the output voltage V_out is derived under pulling condition in Equation (15) and locking injection in Equation (16). A maximum amplitude is obviously achieved when the oscillator is locked.

$${\left|{\text{V}}_{\text{out}}\right|}_{\text{AM},\text{Pulling}}\le {\text{R}}_{\text{p}}\left[{\text{I}}_{\text{osc}}+\frac{{\text{I}}_0(1+\left|\mathsf{\alpha }\right|)}{\sqrt{1+4{\text{Q}}^2{\left(\frac{\mathsf{\omega }-{\mathsf{\omega }}_0}{{\mathsf{\omega }}_0}\right)}^2}}\right]$$

(15)

$${\left|{\text{V}}_{\text{out}}\right|}_{\text{AM},\text{Locking}}\le {\text{R}}_{\text{p}}\left[{\text{I}}_{\text{osc}}+{\text{I}}_0(1+\left|\mathsf{\alpha }\right|)\right]$$

(16)

To relax the constraint on filter selectivity in conventional non-coherent FSK demodulators (Figure 3), the principle of a novel demodulator has been proposed in Figure 4. To make it compatible with system on-chip integration, an LC oscillator is further studied to perform the frequency to amplitude conversion. These investigations on the behavior of a LC oscillator, in the presence of an external modulated signal, highlight the conditions of operation for FM and AM demodulation. In pulled mode, the LC oscillator converts an FM input signal, S₁ in Figure 4, into an AM output signal S₂. The data are transferred in the envelope of S₂, and extracted by an envelope detector. In locked mode, the frequency to amplitude conversion does not occur, the demodulation of an FM signal is not possible in such a mode. In the case of an AM injected signal S₁, it is transferred to S₂ with a maximum amplitude in locked mode, the data are then demodulated by envelope detection.

3. Implementation of a MOOD Demodulator

The demodulator architecture presented in Figure 7, namely Modulated Oscillator for Envelope Detection (MOOD), exploits the principle of demodulation proposed in Figure 4. It may be viewed as a Tuned RF receiver, where an LC oscillator is introduced before the envelope detector to perform an FM-to-AM conversion. It has been demonstrated this demodulation circuit is theoretically compatible with frequency and amplitude modulation schemes. As a proof of concept, this MOOD system is implemented in a 65 nm CMOS technology from ST Microelectronics, and is intended for 2.4 GHz ISM Band. This section further details the design strategy and the characterization of the main blocks featuring a MOOD receiver: the LC oscillator and the envelope detector.

Figure 7. Simplified behavioral model for injection pulled oscillator.

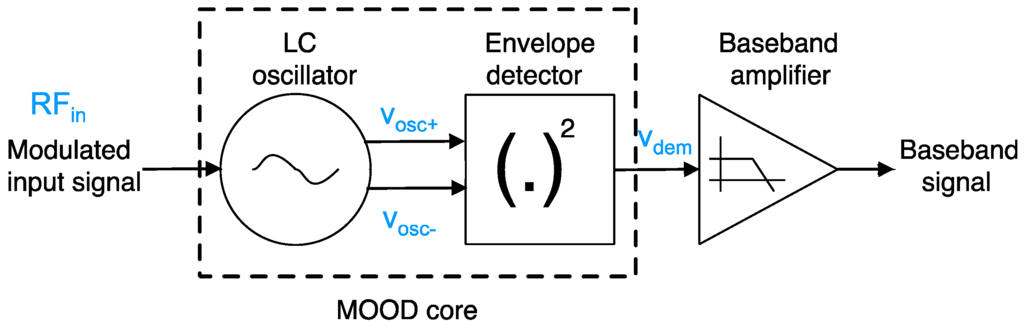
Figure 7. Simplified behavioral model for injection pulled oscillator.

3.1. Low Power LC Oscillator

LC oscillators are very popular in wireless transceivers as they achieve a low phase noise due to the high energy-storage capability of LC tanks. A standard cross-coupled architecture is selected here for its immunity to supply common-mode disturbances. The schematic of the oscillator is presented in Figure 8a and the device sizes are reported in Figure 8b. The tank, formed by L_tank and C_tank, sets the free running oscillation of the oscillator, which is fine tuned by C_var. The cross-coupled pair (M_2a, M_2b) compensates for the loss of the tank and sustains the oscillation. The transistors M_2i are sized to operate in moderate inversion region to achieve a best trade-off between performances and current consumption according [12]. The transistor M₁ steers the tail current and injects the external signal RF_in applied to its gate. The inductors L_g and L_s perform the 50 Ω input matching. A micrograph of the oscillator, implemented for a stand-alone characterization, is presented in Figure 8c.

Figure 8. Schematic of an LC cross-coupled oscillator with RF injection (a); device size (b); micrograph of the oscillator (c).

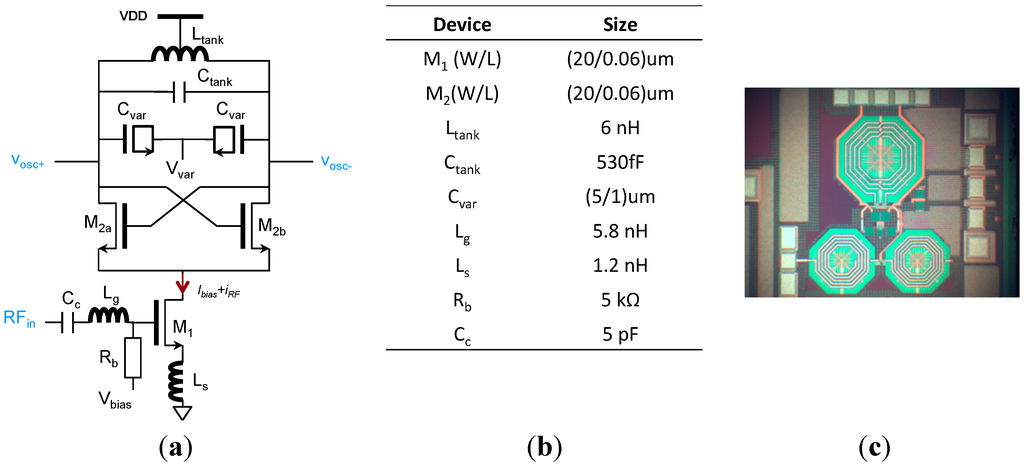
Figure 8. Schematic of an LC cross-coupled oscillator with RF injection (a); device size (b); micrograph of the oscillator (c).

The tuning range of the oscillator is presented in Figure 9a. The free running frequency is centered to 2.48 GHz, it can be adjusted from 2.43 GHz to 2.54 GHz. The phase noise (PN) is measured at 1 MHz from the carrier for different bias currents, Figure 9b. A minimum PN of −100 dBc/Hz is achieved at 400uA. Below this value, the oscillator operates in current limited mode, the PN increases with the decrease of the current. Above 400 μA, the PN regrows as the oscillator operates in voltage limited mode. The oscillator is further exploited in a low power mode, and the bias current is fixed to 248 μA. The performances of the oscillator are reported in Figure 9c for these conditions of operation.

Figure 9. Oscillator Tuning Range versus V_tune (a); Phase Noise at 1MHz versus bias current (b) Oscillator performances at VDD = 0.5 V; & I_bias = 248 μA (c).

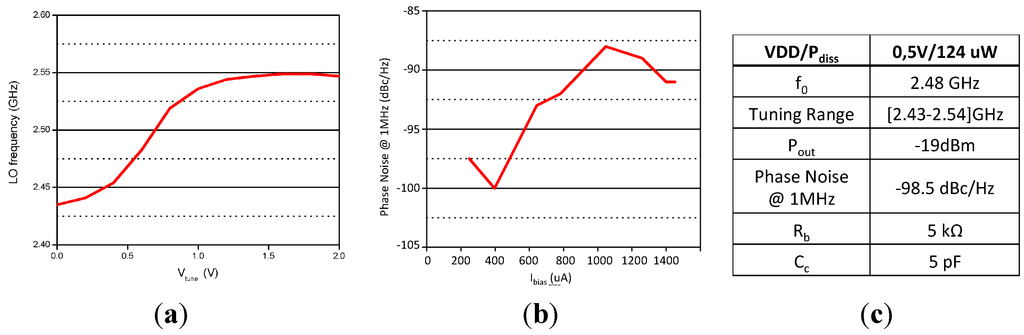
Figure 9. Oscillator Tuning Range versus V_tune (a); Phase Noise at 1MHz versus bias current (b) Oscillator performances at VDD = 0.5 V; & I_bias = 248 μA (c).

The two modes of operation, which will be further exploited in a MOOD receiver are pulled mode for FM to AM conversion and locked mode for AM to AM transfer. They are first characterized on the stand-alone 2.4 GHz LC-oscillator. To study the response in pulled mode, a continuous wave (CW) signal of −31 dBm is applied at the input node RF_in (Figure 8a). The output power of the oscillator, P_out, is represented in Figure 10a as a function of Δf, which is the deviation between the frequency of the CW signal and the free running frequency of the oscillator. For large frequency deviations, the output spectrum follows the free running response as it operates in pulled mode. Figure 10b represents the maximum FM to AL conversion gain (CG_FM-AM) of the oscillator in pulled mode. The figures, extracted from Figure 10a, are valid for a frequency shift of the FM signal equals to half of the corresponding frequency deviation Δf. CG_FM-AM strongly depends on the quality factor of the resonator, and it dramatically decreases when Δf exceeds 50 MHz. Within a frequency range of 2 MHz centered to the free running frequency, the oscillator is locked. The minimum power required to lock the oscillator is measured, and represented in Figure 10b for different Δf. We can note the smaller the frequency deviation, the lower is the power required to lock the oscillator. At a Δf = 20 MHz, a minimum power of −15 dBm is needed to lock the oscillator, for larger frequency deviations the locking power linearly increases with Δf with a slope of 0.25 dB/MHz. This analysis figures out that the sensitivity of a MOOD demodulator operating in locking mode is improved when the free running frequency of the oscillator is tuned to the carrier frequency of the incoming AM signal.

Figure 10. P_out in dBm versus Δf = |f_LO − f_RFin| with P_RFin = −31 dBm & f_LO = 2.48 GHz (a); FM to AM Conversion Gain (b); P_RFin to lock the oscillator versus Δf = |f_LO − f_RFin| (c).

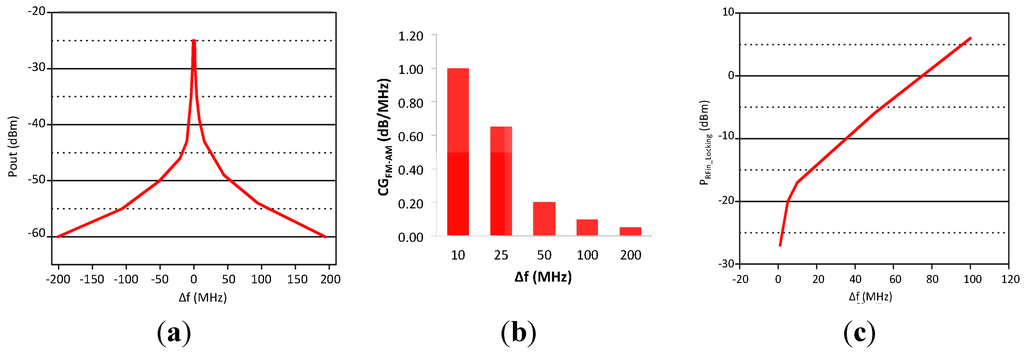
Figure 10. P_out in dBm versus Δf = |f_LO − f_RFin| with P_RFin = −31 dBm & f_LO = 2.48 GHz (a); FM to AM Conversion Gain (b); P_RFin to lock the oscillator versus Δf = |f_LO − f_RFin| (c).

3.2. Envelope Detector Design

An envelope detector (ED) provides a simple and very low power solution to extract the data embedded in the amplitude of a signal. This detection circuit can be implemented using any non-linear element, such as a diode. However, in the CMOS process, it is convenient to use MOS transistors to perform the detection. The schematic of the envelope detector, included in the MOOD demodulator of Figure 7, is presented in Figure 11a. A single-ended version of the circuit, Figure 11b,c, has been implemented for characterization.

The ED reported in Figure 11 is a CMOS version of the standard bipolar topology described in [13], and is basically a band-limited source follower. The operation of the circuit is similar to the bipolar version if the device M₁ is biased in weak inversion, as the drain current of a MOS transistor is an exponential function of gate-source voltage in this region. M₂ acts as a simple current source to bias M₁ with a constant current. A large capacitor C_f is connected to node V_out. The bandwidth at the output is derived in Equation (17). It is set by the pole f_p,det formed by C_f, and the output impedance of the detector which is approximately (1/g_m1) neglecting the body effect:

$${\text{f}}_{\text{p},\text{det}}=\frac{{\text{g}}_{\text{ml}}}{2\mathsf{\pi }{\text{C}}_{\text{f}}}$$

(17)

This pole is designed to be low enough to filter out any signal at the fundamental and higher harmonics but still affords enough bandwidth to avoid the attenuation of the baseband signal. For a typical OOK signal, the detected baseband waveform is a square wave, f_p,det is adjusted to twice the maximum data rate of the demodulated signal.

Figure 11. Differential ED implemented in the MOOD demodulator (a); single ED implemented as a standalone circuit for characterization (b); micrograph of the single ended ED in 65 nm CMOS (c).

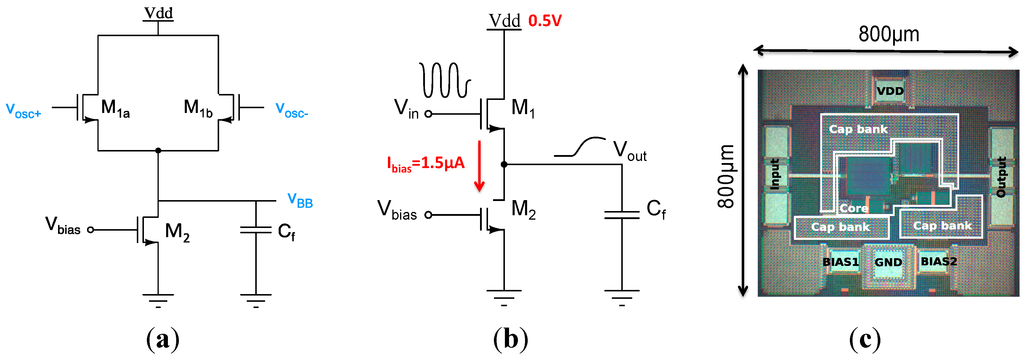
Figure 11. Differential ED implemented in the MOOD demodulator (a); single ED implemented as a standalone circuit for characterization (b); micrograph of the single ended ED in 65 nm CMOS (c).

An AC input signal is applied to the input, V_in in Figure 11b. Since the output bandwidth is much smaller than the input signal frequency, the full signal appears across the gate-source terminal V_GS of M₁. M₁, biased in WI region, generates an output current that is an exponential function of the input voltage. To further investigate the circuit of Figure 11b, an equivalent model is proposed in Figure 12. The exponential function, expanded with Taylor series and dropping terms above the second order, acts as a squaring function. It actually transforms the AC amplitude of V_in into a DC current i₀. The fundamental frequency, along with higher order harmonics, of V_in will be filtered out by C_f. Although higher order terms will also generate DC components, these contributions are small compared to the squaring term. The output impedance R_o is simply 1/g_m1.

Figure 12. Simple model of envelope detector to calculate conversion gain.

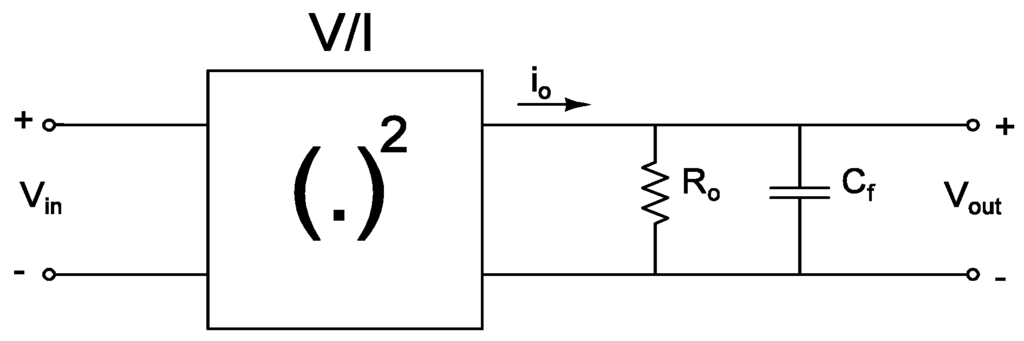
Figure 12. Simple model of envelope detector to calculate conversion gain.

Referring to Figure 11b, the large signal drain current of M₁ operating in weak inversion is modeled as [14]:

$${\text{I}}_{\text{D}}\approx {\text{I}}_0^{\text{'}}\text{exp}\left(\frac{{\text{V}}_{\text{GS}}-{\text{V}}_{\text{th}}}{\text{n}{\text{V}}_{\text{t}}}\right)$$

(18)

where I’₀ is a constant depending on process and device size, V_th is the threshold voltage, V_t is the thermal voltage (kT/q), and n is the subthreshold slope factor. Expanding Equation (18) in Taylor series and focusing on the second order term, the DC component i₀ of I_D is expressed in Equation (19):

$${\text{i}}_0=\frac{{\text{V}}_{\text{in}}^2}{2}\frac{{\text{I}}_{\text{D}}}{{(\text{n}{\text{V}}_{\text{t}})}^2}$$

(19)

Substituting for V_in, the expression of a sine wave (V_s sin(ω_st)) with g_m = I_D/nV_t, the DC component i₀, Figure 17, becomes:

$${\text{i}}_0=\frac{{\text{g}}_{\text{m}}}{2\text{n}{\text{V}}_{\text{t}}}{\text{V}}_{\text{s}}^2\left(\frac{1-\text{cos}(2{\mathsf{\omega }}_s\text{t})}{2}\right)$$

(20)

The second harmonic term in Equation (20) is filtered out by the detector output pole f_p,det, and the output voltage of the detector V_out is expressed as Equation (21):

$${\text{V}}_{\text{out}}={\text{i}}_0{\text{R}}_0=\frac{{\text{i}}_0}{{\text{g}}_{\text{m}}}=\frac{{\text{V}}_{\text{s}}^2}{4\text{n}{\text{V}}_{\text{t}}}$$

(21)

The conversion gain of the detector, GC_det, is finally the ratio of the output DC voltage V_out to the peak AC amplitude V_s of V_in:

$$\text{G}{\text{C}}_{\text{det}}=\frac{{\text{V}}_{\text{out}}}{{\text{V}}_{\text{s}}}=\frac{{\text{V}}_{\text{s}}}{4\text{n}{\text{V}}_{\text{t}}}$$

(22)

The measurement results of the single-ended detector are reported in Figure 13. The circuit consumes 2 μW for a VDD of 0.5 V. The frequency response of the detector, Figure 13a, exhibits a −3 dB bandwidth of 350 kHz, which allows a data rate demodulation up to 200 kb/s. According to Equation (22), the RF to DC conversion gain is a function of the input signal amplitude V_s. This analysis holds for small input signals where the response is dominated by the second order term and higher order effects are not significant. The measured conversion gain, GC_det, is illustrated in Figure 13b. If the amplitude of the input signal is kept below 200 mV, GC_det is close to 0dB and the expression (Equation (22)) gives a good approximation of it. If the amplitude is larger than 400 mV the conversion gain rolls off, and the small signal analysis is no longer correct. To preserve the dynamic of demodulated data, the amplitude of the AM signal at the input of envelope detector would not exceed 500 mV.

Figure 13. AC gain (a); AC to DC conversion gain CG_det versus the input amplitude V_s (b) of the envelope detector.

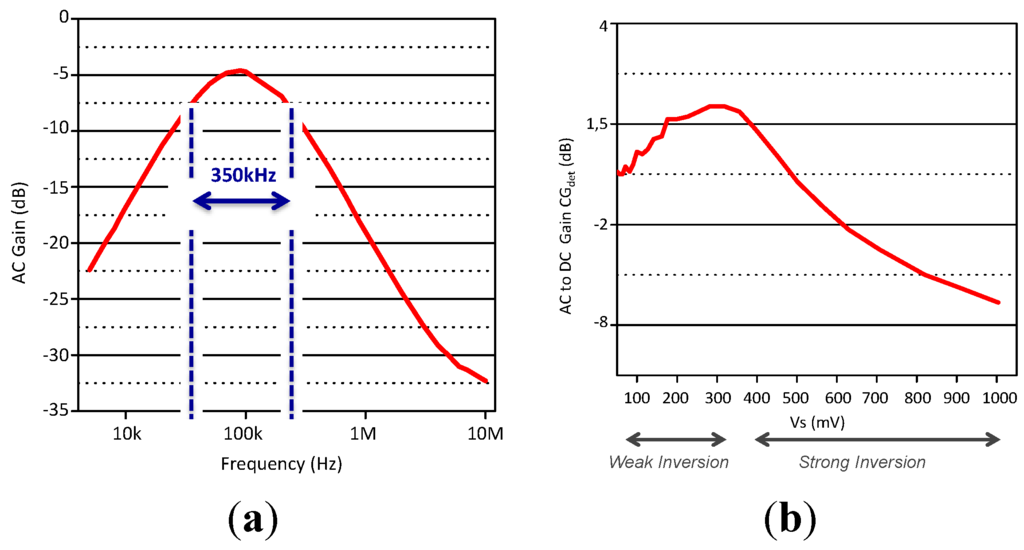
Figure 13. AC gain (a); AC to DC conversion gain CG_det versus the input amplitude V_s (b) of the envelope detector.

4. Characterization of MOOD Demodulator

A chip micrograph of the MOOD receiver proposed in Figure 7 is reported in Figure 14. The system was first tested with amplitude and frequency analog modulations. The measurement results are discussed in part 4.1. The response of MOOD receiver to a Frequency Shift Keying (FSK) modulated signal, and an On-Off Keying (OOK) modulated signal, is further exposed in part 4.2.

Figure 14. Chip micrograph of the MOOD receiver.

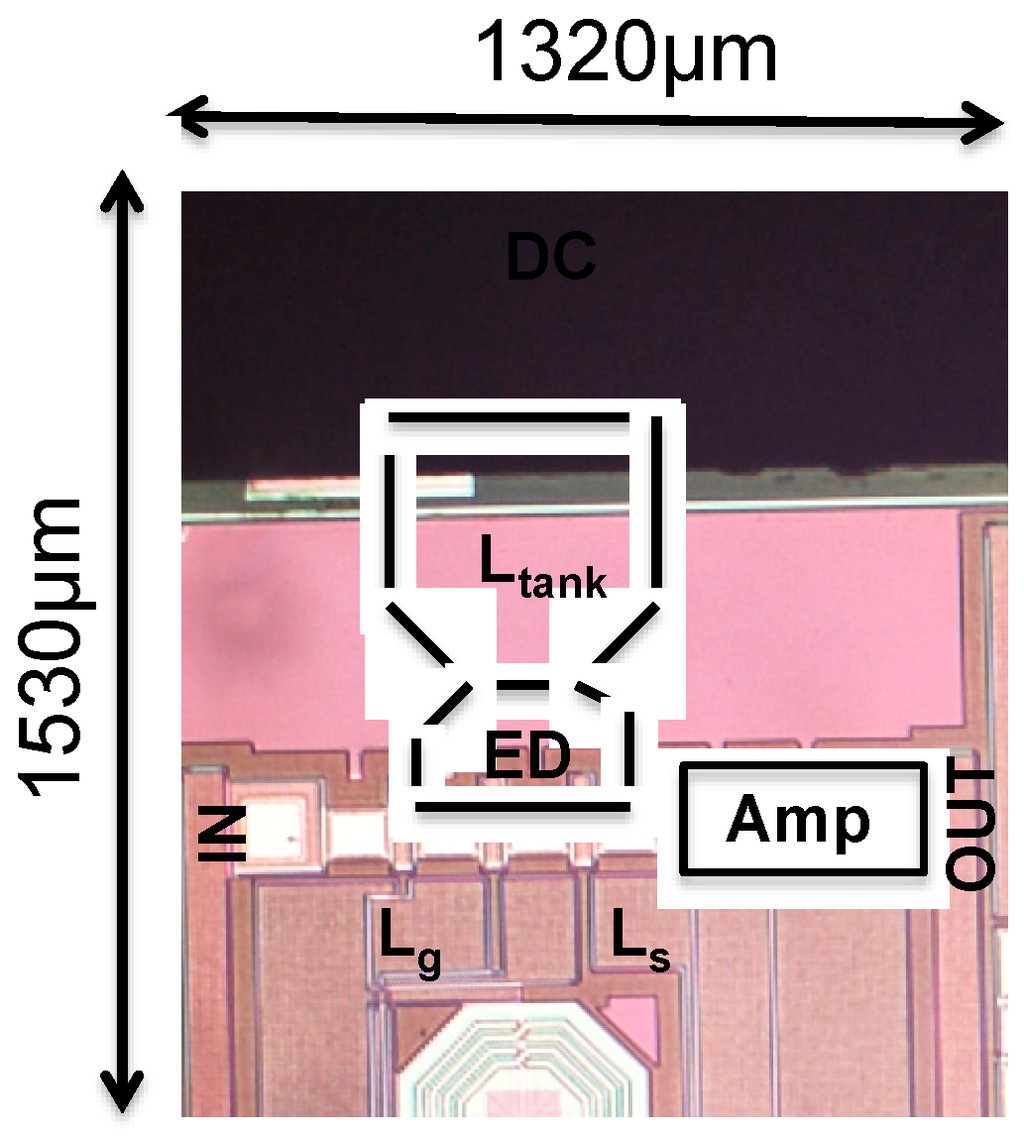
Figure 14. Chip micrograph of the MOOD receiver.

4.1. Demodulation of Amplitude and Frequency Modulated Signals

In the first set up, the modulating frequency f_m and the carrier power level P_carrier are respectively fixed to 200 kHz and −12 dBm. The free running frequency, f_OL, is set to 2.48 GHz. The measured peak-to-peak amplitude of the output voltage (V^PP) at base band is reported in Figure 15a, for an amplitude modulated (AM) input signal, in Figure 15b, for a frequency modulated (FM) input signal.

Figure 15. Peak-to-peak output voltage V^PP versus carrier frequency for modulation depth (m in %) with an AM input signal (a); an FM input signal (b).

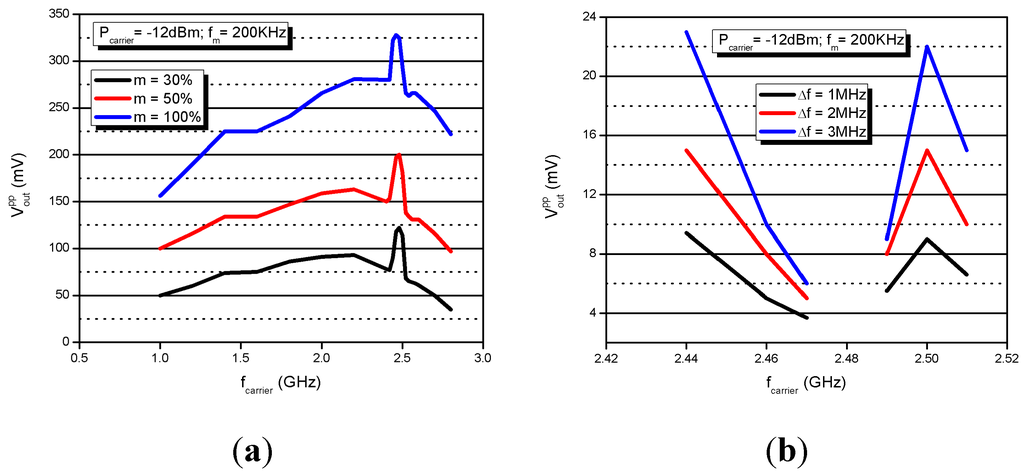
Figure 15. Peak-to-peak output voltage V^PP versus carrier frequency for modulation depth (m in %) with an AM input signal (a); an FM input signal (b).

In Figure 15, we observe the amplitude of the output voltage V^PP increases with the modulation depth for the two types of modulation. In the case of an AM signal, Figure 15a, the AM to AM conversion (V^PP) smoothly increases as the carrier frequency gets closer to the free running frequency f_OL. When the oscillator is locked, dashed box in Figure 15a, the AM to AM transfer is maximum, the best efficiency yields at m = 100% with a V^PP of 350 mV, which corresponds to a voltage gain of 6 dB. In the case of an FM input signal, Figure 15b, the frequency shift is converted into amplitude variation, we observe the amplitude of the output voltage V^PP decreases as the carrier frequency gets closer to the free running frequency f_OL. When the oscillator is locked, dash box in Figure 15b, the frequency to amplitude conversion does not occur and V^PP is zero, the FM signal is not demodulated.

The sensitivity of the receiver to the modulating frequency f_m is illustrated in Figure 16. The carrier frequency (f_carrier) and power (P_carrier) are fixed, the output amplitude V^PP is measured for different f_m. For the AM test, the oscillator is locked to achieve a maximum AM-to-AM transfer. According to Figure 16a, V^PP is maximum if the f_m frequency is kept below 300 kHz. Above this frequency the demodulated signal is attenuated by the bandwidth of envelope detector. For the FM test, Figure 16b, the oscillator is operated in pulled mode, and the sensitivity is maximum for a f_m of 380 kHz.

Figure 16. Peak-to-peak output voltage V^PP versus the modulating frequency f_m with an AM input signal (a); an FM input signal (b).

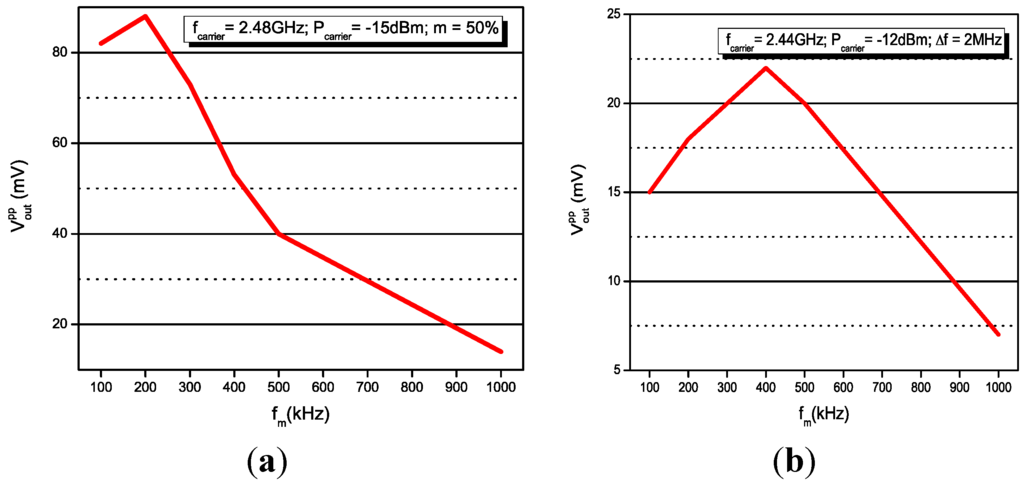
Figure 16. Peak-to-peak output voltage V^PP versus the modulating frequency f_m with an AM input signal (a); an FM input signal (b).

The test of the MOOD receiver with analog modulations confirms the investigations exposed in the Section 2. An AM signal is demodulated with a maximum efficiency when the oscillator is locked. A FM signal is demodulated on condition that the oscillator is in pulled mode.

4.2. FSK and OOK Demodulation

To complete the validation of the proposed demodulation concept, the MOOD receiver is tested with a pseudo random binary sequence. In Figure 17, the demodulated data are reported with the original data for different configurations of the AM input signal. In the two first test sets, Figure 17a,b, the data rate (D_b) and carrier power (P_carrier) are respectively fixed to 20 kbps and −18 dBm, only the carrier frequency f_RF changes. The amplitude of the demodulated data is larger in locked mode 8 mV, Figure 17a, compared to pulled mode 5 mV, Figure 17b. In Figure 17c the oscillator is locked, but the data rate is increased to 500 kbps. The wave form of the demodulated data is distorted by the cutoff frequency of the envelope detector. The bandwidth of the ED limits the maximum data rate in this case.

In Figure 18, the demodulated data are reported with the original data for different configurations of the FM input signal. Figure 18a illustrates the response of the receiver when the oscillator is locked. The FM signal is not demodulated. In Figure 18b,c, the oscillator is in pulled mode, and the FM frequency shift (Δf) is changed. For a small frequency shift, 100 kHz in Figure 18b, the shape of the demodulated data is distorted, and the amplitude is small (<1 mV). For a larger frequency shift, 1 MHz in Figure 18c, the demodulated data exhibit a steep slope transition and the amplitude reaches 2 mV. Indeed, a large frequency shift is transformed into a large output voltage swing by the roll-off response of the oscillator. This analysis highlights the frequency to amplitude conversion is dependent to the quality factor of the LC tank.

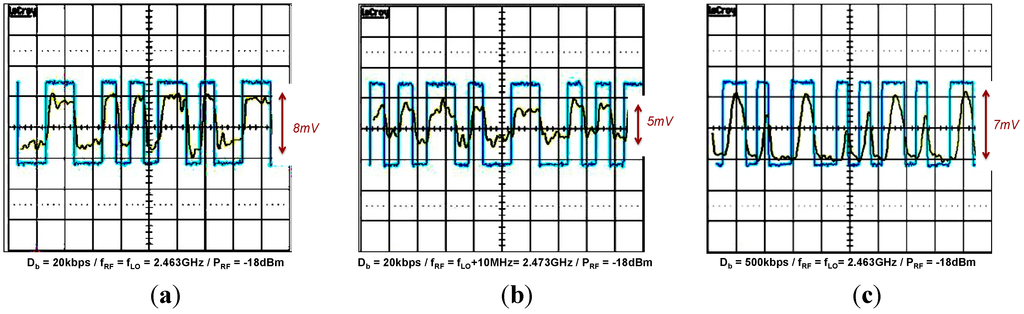
Figure 17. Demodulated data versus original data in locked mode at a data rate of 20 kbps (a); in pulled mode at a data rate of 20 kbps (b); in locked mode at a data rate of 500 kbps (c).

Figure 17. Demodulated data versus original data in locked mode at a data rate of 20 kbps (a); in pulled mode at a data rate of 20 kbps (b); in locked mode at a data rate of 500 kbps (c).

Figure 18. Demodulated data versus original data in locked mode (a); in pulled mode at a data rate of 100 kbps and frequency shift Δf = 100 kHz (b); in pulled mode at a data rate of 100 kbps and frequency shift Δf = 1 MHz (c).

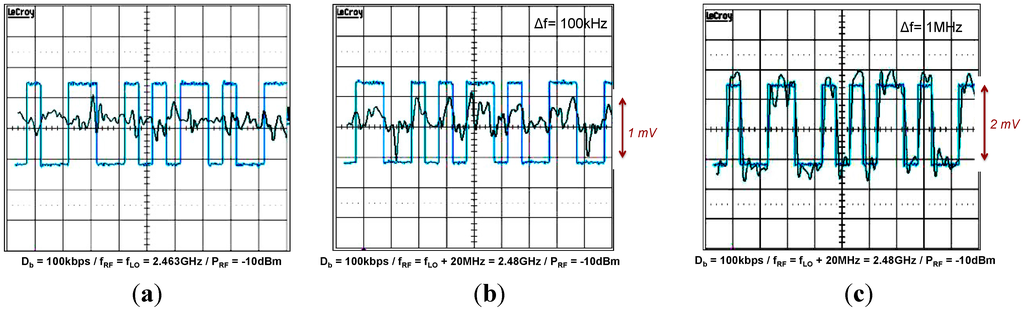
Figure 18. Demodulated data versus original data in locked mode (a); in pulled mode at a data rate of 100 kbps and frequency shift Δf = 100 kHz (b); in pulled mode at a data rate of 100 kbps and frequency shift Δf = 1 MHz (c).

The performances of the MOOD receivers are summarized in Table 1. The sensitivity, −36 dBm for OOK mode, and −27 dBm for FSK mode, is measured when the output Signal to Noise Ratio (SNR_out) reaches 12 dB. This sensitivity can be significantly improved with the introduction of a Low Noise Amplifier before the MOOD circuit. The demodulators presented in [15,16], Table 1, do not use any active RF function, which drastically reduces the power consumption to respectively 0.1 μW and 10 μW. To our knowledge, the demodulator presented in [15] exhibits the lowest power consumption reported in the literature. The introduction of a low noise amplification stage before the envelope detector, significantly improves the sensitivity as demonstrated in [4]. It also costs an extra power consumption of 40 μW. The receivers reported in [4,15,16] are based on envelope detectors, which limit the compatibility to OOK modulated signals. The reference [17] proposes a WuRx dedicated to the demodulation of FSK. It features a digitally controlled oscillator coupled with an envelope detector. The power consumption is 45 μW, which is large with respect to the operating frequency 80 MHz, and compared to OOK solutions. The demodulation of an FSK signal requires RF functions that burden the power budget of the receiver.

The MOOD receiver proposed in this work does not really compete with Wu-Rx based on an unique envelope detector, in terms of power consumption and sensitivity, for the demodulation of a OOK signal only. However it is a low power solution for the demodulation of an FSK signal, which is also compatible with an OOK signal.

Table 1. Modulated oscillator for envelope detection (MOOD) performances and comparison with the state of the art.

	This Work		[15]	[4]	[16]	[17]
Process	130 nm		130 nm	90 nm	180 nm	180 nm
Frequency	2.4 GHz		915 MHz	2 GHz	2.4 GHz	80 MHz
Power Consumption	120 μW		0.1 μW	52 μW	10 μW	45 μW
VDD	0.6 V		1.2 V	0.5 V	0.5 V	0.7 V
Modulation	OOK	FSK	OOK	OOK	OOK	FSK
Data rate	150 kbps	300 kbps	100 kbps	100 kbps	100 kbps	300 kbps
Sensitivity	−36 dBm	−27 dBm	−41 dBm	−72 dBm	−65 dBm	−62 dBm

Table 1. Modulated oscillator for envelope detection (MOOD) performances and comparison with the state of the art.

	This Work		[15]	[4]	[16]	[17]
Process	130 nm		130 nm	90 nm	180 nm	180 nm
Frequency	2.4 GHz		915 MHz	2 GHz	2.4 GHz	80 MHz
Power Consumption	120 μW		0.1 μW	52 μW	10 μW	45 μW
VDD	0.6 V		1.2 V	0.5 V	0.5 V	0.7 V
Modulation	OOK	FSK	OOK	OOK	OOK	FSK
Data rate	150 kbps	300 kbps	100 kbps	100 kbps	100 kbps	300 kbps
Sensitivity	−36 dBm	−27 dBm	−41 dBm	−72 dBm	−65 dBm	−62 dBm

5. Conclusions

The deployment of WSNs are critical for the development of IOT. Among the tough challenges in the implementation of dense WSNs are: the reduction of the power consumption dedicated to wireless communications, and the interoperability of the networks. To address these challenges, an ultra low power demodulator compatible with the two most common modulation schemes exploited in WSN—i.e., OOK and FSK—is proposed in this work.

The principle of demodulation is based on a frequency to amplitude conversion, performed by an LC oscillator optimized for low power consumption, and combined with an envelope detector, namely MOOD demodulators. The optimum conditions of operation of an MOOD demodulator are theoretically investigated and then verified with measurement results. Hence, the demodulation of an AM signal is improved when the oscillator is locked to the carrier frequency, where as the FM demodulation only occurs when the oscillator is in pulled mode. A proof of concept is implemented in a 65 nm CMOS technology and is intended for 2.4 GHz ISM Band. The measurement results of the MOOD demodulator demonstrate its ability to properly demodulate FSK and OOK modulated signals for a power budget of only 120 μW at a data rate of 100 kbps and a sensitivity close to −30 dBm.