39 fJ/bit On-Chip Identification ofWireless Sensors Based on Manufacturing Variation

Abstract

A 39 fJ/bit IC identification system based on FET mismatch is presented and implemented in a 130 nm CMOS process. ID bits are generated based on the $\Delta V_T$ between identically drawn NMOS devices due to manufacturing variation, and the ID cell structure allows for the characterization of ID bit reliability by characterizing $\Delta V_T$. An addressing scheme is also presented that allows for reliable on-chip identification of ICs in the presence of unreliable ID bits. An example implementation is presented that can address 1000 unique ICs, composed of 31 ID bits and having an error rate less than ${10}^{-6}$, with up to 21 unreliable bits.

1. Introduction

Recent advances in the design of wirelessly powered, millimeter-scale sensor tags will allow for the construction of increasingly small sensors for a variety of applications [1,2,3,4,5]. In the case of wirelessly powered sensors like RFID tags, however, decreasing size leads to decreased power delivery due to reduced antenna area. All sensor components must therefore be designed for minimum power consumption. A common component of such sensors is a non-volatile memory used to store a unique identification (ID) number. However, for very small sensors, implementation of such a memory is non-trivial because of the low supply voltage and available energy, which can be insufficient to program a conventional non-volatile (NV) memory such as Flash or EEPROM. An alternative would be to program each sensor at its time of manufacture, for example by a physical electrical connection that could supply the energy required for a NV memory, or by an array of laser-blown fuses. These approaches require extra masks or post-manufacturing steps, which raise the individual cost of the supposedly low-cost devices.

An alternative is an identification system based on the individual variation of ICs due to the CMOS manufacturing process [6]. A suitably designed circuit could be sensitive to these variations, and produce a string of bits that is random between chips, but temporally static, to be used as an ID number. This could be thought of as a particular type of NV memory that is “programmed” once at the time of manufacture with random data. Such variation sensitive circuits also have security and cryptographic applications, where they can be used to form Physical Unclonable Functions (PUFs) that allow for authentication and secret key generation [7,8].

In this paper, we present a circuit that generates random identification numbers based on manufacturing variation, with lower energy than reported in prior published work. We also present an addressing protocol that allows for reliable on-chip identification in the presence of unreliable bits. This reduces the amount of data that must be transmitted off-chip, lowering the energy consumption of the sensor. An analysis of the reliability of the system is also presented. While intended for the low-energy identification of wireless sensors, this same circuit could be used as part of a low-energy secret key generator for cryptographic applications [9].

2. System Overview and Design

The central element of the identification system is the ID generator, a circuit that produces an N-bit ID number based on small variations in the IC due to manufacturing. The number should be random, with each bit having equal likelihood of being “0” or “1”. The random event is the manufacture of the IC, which occurs only once.

Many circuits exhibit measurable differences due to manufacturing variation that could be used to generate random, unique data. These include memories, such as SRAM power-up state [10] and static noise margin [11], and DRAM retention fails [12]. Variations in delay lines and arbiters [13], ring-oscillators [9], scan-chain power-up state [14], and cross-coupled inverters [15,16,17], as well as direct measurements of the drain current of individual FETs [6] have also been examined for the generation of unique identification data and PUFs.

All random ID implementations have the property that not all of the random ID bits are necessarily reliable. The ID generator circuit should produce the same ID number every time it is activated, but in such systems some bits are more reliable than others, and unreliable bits may occasionally flip between successive ID generation events. Ultimately, this could cause errors in the identification process. Current literature solves this problem by requiring each sensor to transmit its generated ID number back to the external reader, which increases the amount of data that must be transmitted. However, for such systems, wireless communication is frequently the largest energy consumer, so any reduction in transmitted data directly improves system performance. It has been observed that prior knowledge of which bits are unreliable can be used to increase the accuracy of identification [15,18], and that the reliability of individual bits can be determined by examining the magnitude of the underlying variation [17].

Ideally, the ID generator bits would not be temporally random: successive reads or power-on cycles would always produce the same ID number for the lifetime of the IC. However, due to the nature of manufacturing variations and the presence of electrical noise, the value of individual bits may vary over multiple read operations. We can model the output of the ID generator, which we will call the generated code, G, as a discrete, N-bit random variable. For each bit, $G_i$ we can assign a probability, p, such that the probability of bit $G_i$ evaluating to “1” is p, and evaluating to “0” is $1-p$. An N-bit ID generator can then be completely described by a sequence of N probabilities $(p_0,p_1,...,p_{N-1})$.

Based on this ID generator, each IC can then be assigned an ID code C, where

$$C_i=\left\{\begin{array}{cc}1\hfill & p_i>1/2\hfill \\ 0\hfill & p_i\le 1/2\hfill \end{array}\right.$$

(1)

In other words, the chip code C is the most likely value of the random variable G, the output of one read of the ID generator. It is this number that will be used to identify the IC.

2.1. Remote Identification

When an external reader attempts to locate a particular IC among a population of ICs, variations in the output of the ID generators may cause errors. For example, consider an external reader that tries to locate IC A by transmitting the chip code for chip A, $C_A$. All chips in the population receive this code, and compare it to their generated codes, G. If $C_A=G_A$ then chip A concludes it is being addressed and can reply to the external reader. However, this may lead to false negative errors if unreliable bits in chip A’s ID generator result in $C_A\ne G_A$.

The common way to deal with this problem is to use a slightly different approach. To find chip A in a population of M chips, an external reader transmits an inquiry to all the chips, which all reply with their generated codes, $(G_0,G_1,...,G_{M-1})$. The external reader then computes the Hamming distance between all the received codes and chip code A, $H(C_A,G_i)$ for all i. The value of $G_i$ that has the smallest Hamming distance to $C_A$ is then concluded to have come from chip A.

We call this approach remote identification, since the target chip A is unable to positively conclude it is being addressed. Rather, identification happens remotely (from the perspective of the chip), at the external reader. The primary drawback of this approach is that the chip must transmit its generated code, increasing the energy consumed by the radio. This may also cause problems for systems involving large numbers of chips: some system for staggering their replies must be implemented to avoid collisions.

2.2. On-Chip Identification

By on-chip identification, we mean an addressing protocol by which chips are able to positively conclude they are being addressed. This can be accomplished with knowledge of the reliability of individual ID generator bits. Each bit of the ID generator can be classified as reliable or unreliable, based on each bit’s value of p. Although p is a continuous random variable, we can approximate it as a discrete random variable $p^{\prime }$, where

$$p^{\prime }=\left\{\begin{array}{cc}1-ϵ\hfill & 1-ϵ\le p\le 1\hfill \\ 1/2\hfill & ϵ<p<1-ϵ\hfill \\ ϵ\hfill & 0\le p\le ϵ\hfill \end{array}\right.$$

(2)

The variable ϵ is the threshold of reliability: reliable bits have a probability ϵ of flipping during read, and unreliable bits are treated as evaluating to either “0” or “1” with equal probability.

3. Circuit Implementation

Although there are many types of manufacturing variation that could serve as sources of entropy for a random ID generator, the type chosen for this application is the variation between the threshold voltage, $V_T$, of two identically drawn FETs. Because the variance of $V_T$ is inversely proportional to the device area [19], both devices are drawn as the minimum size available in the technology. A schematic of an N-bit random ID generator is shown in Figure 1.

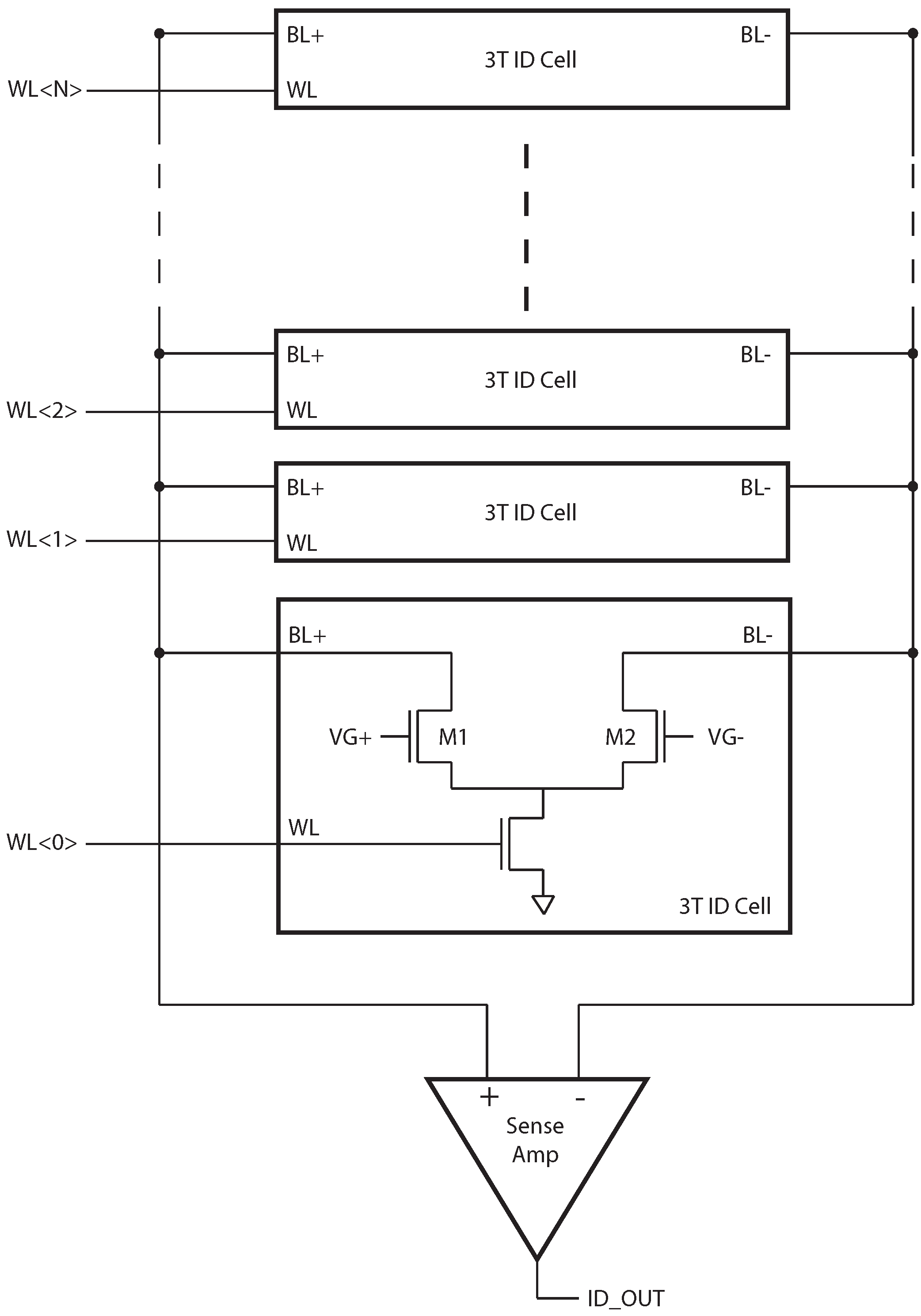
Figure 1. N-bit ID generator. The organization is similar to that of a memory, where multiple ID cells share a common set of bit-lines and a sense amplifier.

Figure 1. N-bit ID generator. The organization is similar to that of a memory, where multiple ID cells share a common set of bit-lines and a sense amplifier.

The organization of the ID generator is similar to that of a memory. Each ID cell produces one random bit, based on the $V_T$ difference between M1 and M2. When equal gate voltages are applied to M1 and M2, the $V_T$ difference creates a difference in drain currents, $\Delta I_D$, the polarity of which is detected by the sense amplifier (SA). A column of N ID cells is read sequentially to produce an N-bit random ID number. A simple shift register is used to drive the word-line signals rather than a row decoder, since random access is not necessary, and this requires less energy and area.

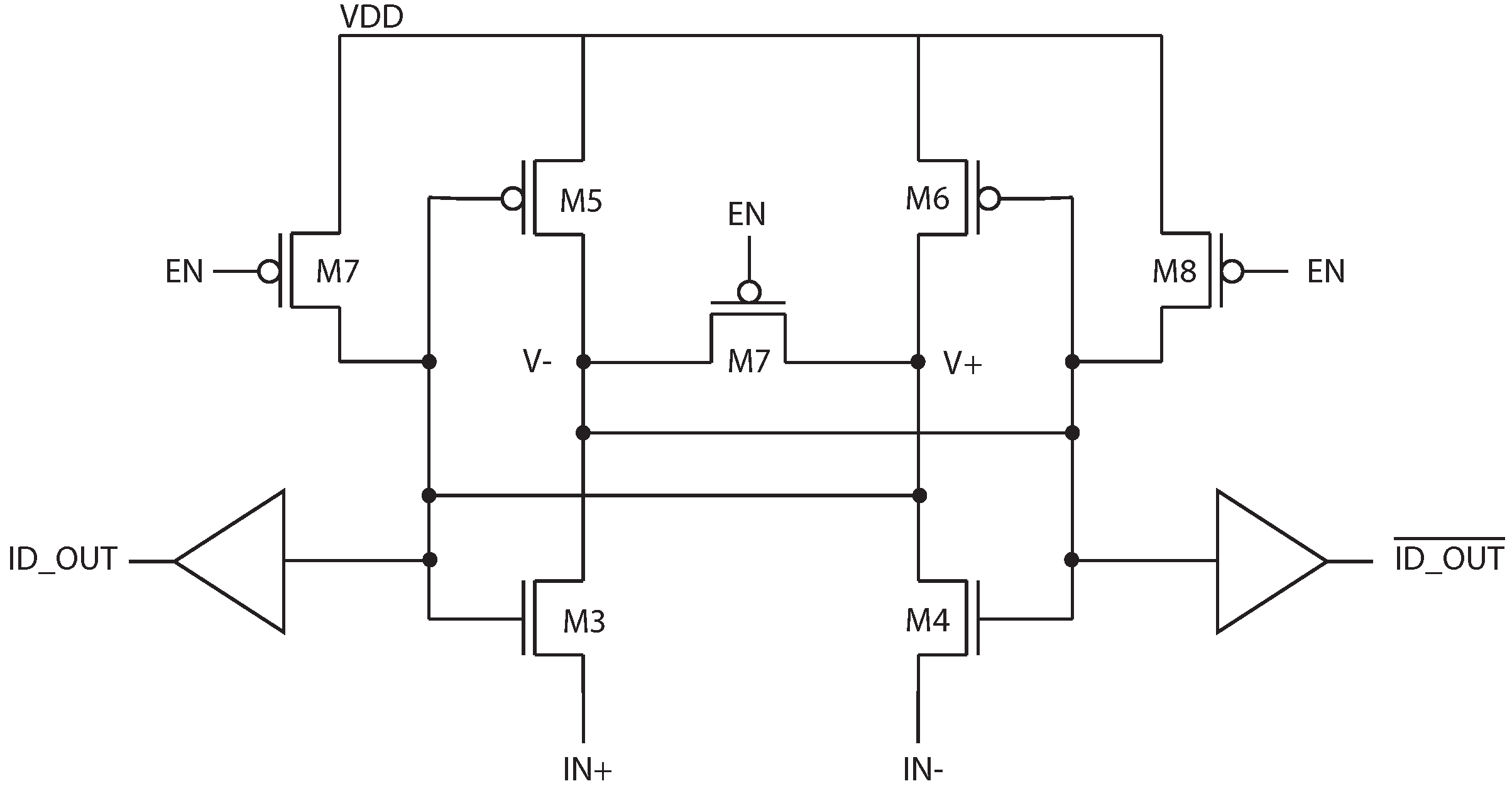
Because the SA should be constructed with negligible input referred offset, a single SA built from large devices is constructed, and shared by the column. A schematic of the latch-based sense amplifier is shown in Figure 2. This structure is preferred for low-energy operation since it draws no static current after it has settled to its final state. Sharing the SA among multiple bits also amortizes the SA leakage current.

Figure 2. Schematic of the latch-based sense amplifier in Figure 1.

Figure 2. Schematic of the latch-based sense amplifier in Figure 1.

3.1. Noise Analysis

In the absence of electrical noise, reading from a single ID cell would be entirely deterministic. However, when the sense amplifier is activated, the total difference between the ID cell currents is the combination of the inherent offset due to device mismatch and any electrical noise, such that

$$\Delta I=\Delta I_m+\Delta I_n$$

(3)

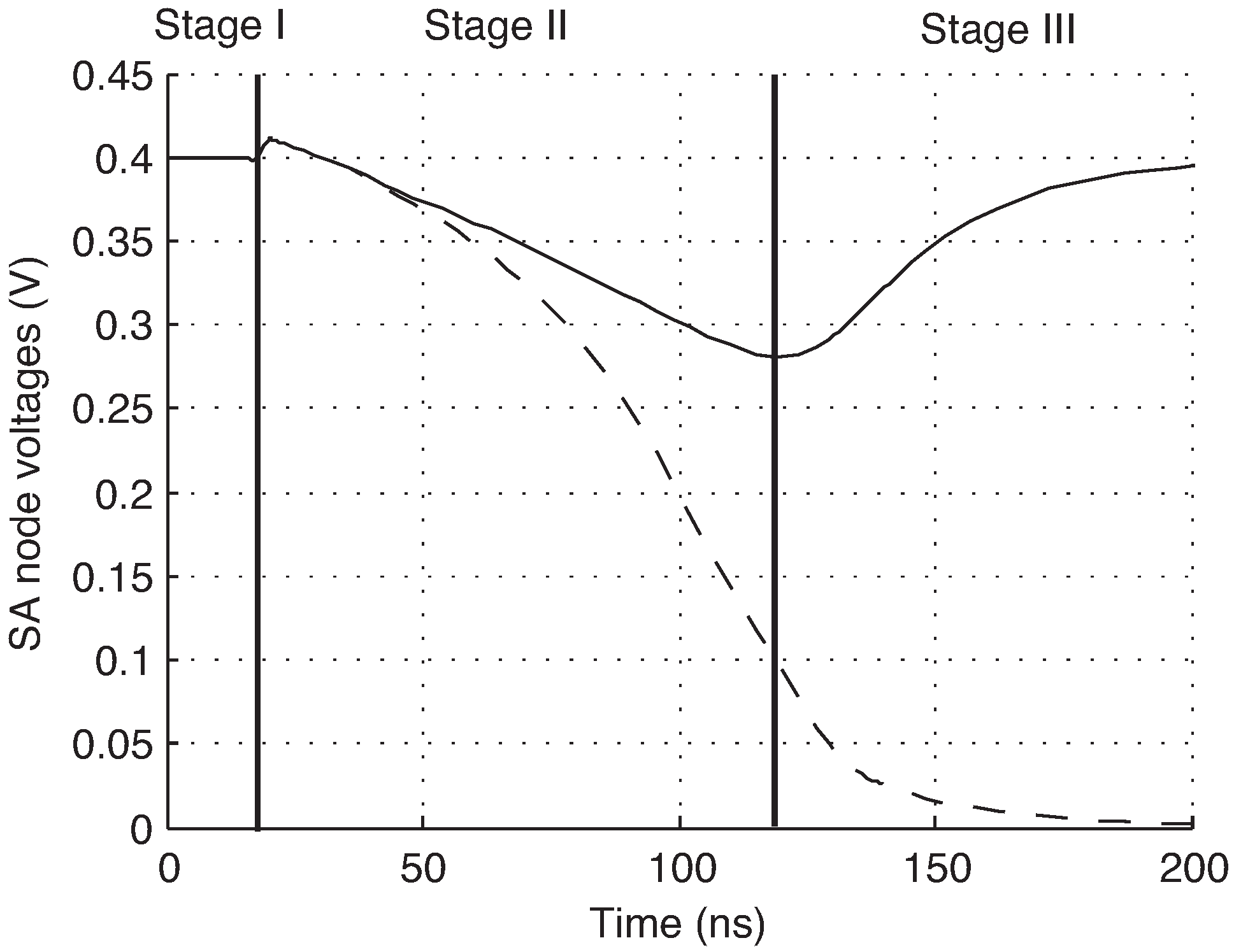
The internal nodes of the sense amplifier, $V_{+}$ and $V_{-}$, are pre-charged to VDD prior to sensing, and devices M5 and M6 are off at the start of a read operation. When the sense amplifier is activated, the internal nodes are discharged by the ID cell current. When one of the nodes discharges sufficiently to turn on M5 or M6, the positive feedback is engaged and the amplifier settles to a stable state. A simulation of this is shown in Figure 3, showing the three stages of operation.

The total difference voltage developed on the internal SA nodes, $\Delta V=V_{+}-V_{-}$, is the sum of the individual difference voltages due to mismatch and noise.

$$\Delta V=\Delta V_m+\Delta V_n$$

(4)

Figure 3. Simulated operation of SA. Stage I: pre-charge, Stage II: integration, Stage III: positive feedback.

Figure 3. Simulated operation of SA. Stage I: pre-charge, Stage II: integration, Stage III: positive feedback.

The effect of the mismatch and noise on the circuit output can be calculated. The probability of $\Delta V$ being positive at the time the SA feedback is activated is:

$$0<\Delta V_m+\Delta V_n$$

(5)

This is given by:

$$p=P\left(\Delta V_n>-\Delta V_m\right)$$

(6)

$$={\int }_{-\Delta V_m}^{\infty }{\Phi }_{\Delta V_n}\left(v\right)dv$$

(7)

$$=\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{\Delta V_m}{\sqrt{2}{\sigma }_{\Delta V_n}}\right)\right]$$

(8)

where ${\Phi }_{\Delta V_n}\left(v\right)$ is the probability density function of the normally distributed random variable $\Delta V_n$, with variance ${\sigma }_{\Delta V_n}$.

Finally, this can be rewritten in terms of the equivalent input noise, ${\sigma }_{V_{in}}$.

$$p=\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{\Delta V_T}{\sqrt{2}{\sigma }_{V_{in}}}\right)\right]$$

(9)

3.2. ID Cell Reliability

Knowing the relationship between p and $\Delta V_T$ allows for the reliability of each ID cell to be determined quickly. The magnitude of $\Delta V_T$ necessary for a given reliability threshold ϵ, $V_R$, can be calculated by inverting Equation (9) with $p=1-ϵ$.

$$V_R=\sqrt{2}{\sigma }_{V_{in}}{\mathrm{erf}}^{-1}(1-2ϵ)$$

(10)

As described in [17], two tests can then be performed on each ID cell, first by adding a difference voltage $V_R$ between the gates of M1 and M2 during read, such that $V_{G1}-V_{G2}=V_R$. If the result is a “0”, then $\Delta V_T<-V_R$. Next, a difference voltage $-V_R$ is applied. If the result is a “1”, then $\Delta V_T>V_R$. The ID cell can then be classified into one of three categories: reliable “1”, reliable “0”, or unreliable, based on the two tests. The classification system is shown in Table 1.

4. Masked Addressing

Because unreliable ID bits may lead to identification errors, some method for ensuring reliable identification is required. One obvious possibility would be to simply exclude all chips that have unreliable ID bits from use, but this would significantly reduce the yield, particularly in systems employing large numbers of ID bits.

Table 1. Classification of ID cells based on reliability tests, where $V_R$ is the magnitude of the threshold voltage difference required for reliable operation, C is ID code, and M is the ID mask.

$\Delta V_T<-V_R$	$\Delta V_T>V_R$	Classification	C	M
True	False	“0”	0	1
False	False	Unreliable	X	0
False	True	“1”	1	1

Table 1. Classification of ID cells based on reliability tests, where $V_R$ is the magnitude of the threshold voltage difference required for reliable operation, C is ID code, and M is the ID mask.

$\Delta V_T<-V_R$	$\Delta V_T>V_R$	Classification	C	M
True	False	“0”	0	1
False	False	Unreliable	X	0
False	True	“1”	1	1

An alternative is to record which ID bits of a particular chip are reliable, and then exclude the unreliable ID bits from use during identification. This is accomplished by recording two numbers for every chip: an N-bit ID code C, and an N-bit code mask M. Each bit $M_i$ is equal to “1” if the corresponding ID code bit $C_i$ is reliable, and equal to “0” if $C_i$ is unreliable. The values of $C_i$ and $M_i$ can be determined from the reliability tests as indicated in Table 1.

To identify a particular chip A, an external reader transmits both $C_A$ and $M_A$. Every chip receives this code and activates its ID generator, which produces a generated code, G, and then tests the following equality

$$C_A \& M_A=G \& M_A$$

(11)

If this equality is true, the chip can determine it is being addressed. Because the generated code, $G_A$, will only vary from $C_A$ among the bits excluded by the mask, $M_A$, this will ensure reliable identification. The protocols for initial chip characterization and subsequent chip identification are given below.

4.1. Chip Characterization

Chip characterization occurs once for each chip, recording C and M, which are necessary to identify the chip in the future.

(1)

A single chip A, to be characterized, is placed in range of the external reader. The external reader transmits a characterize signal.

(2)

The chip applies a voltage difference $\Delta V_R$ to the ID cells, activates the ID generator, and records the output $G_{+}$.

(3)

The chip applies a voltage difference $-\Delta V_R$ to the ID cells, activates the ID generator, and records the output $G_{-}$.

(4)

The chip transmits $G_{+}$ and $G_{-}$ to the external reader.

(5)

The external reader computes:

$$C_A=\overline{G_{+}} \& G_{-}$$

(12)

$$M_A=G_{+}\left|\right|G_{-}$$

(13)

(6)

The external reader stores $C_A$ and $M_A$ for chip A.

4.2. Chip Identification

Chip identification occurs when the system needs to locate a particular chip from a group of chips. Following identification, the chip can reply with a simple acknowledgement, and any other data to be collected.

(1)

To identify chip A, the external reader transmits $C_A \& M_A$ and $M_A$. All chips within range receive this message.

(2)

Each chip activates its ID generator, with zero voltage difference applied to the ID cells, producing a generated code G.

(3)

Each chip evaluates the statement

$$C_A \& M_A=G \& M_A$$

(14)

(4)

If the preceding step evaluates to true, the chip concludes it is being addressed.

4.3. Performance Metrics

An effect of this addressing scheme is that the maximum number of chips that can be addressed is reduced from the theoretical maximum of $2^N$. If only chips that have a number of unstable bits less than or equal to some maximum value, U, are selected for use, than the maximum number of chips that can be uniquely addressed is

$$S=2^{N-U}$$

(15)

For a chip with U unreliable bits, a false negative can only occur if there is an error among one of the $N-U$ reliable bits. If the probability of an error in one of the reliable bits is ϵ, then the false negative rate is

$$p_{FN}=1-{(1-ϵ)}^{N-U}$$

(16)

Errors among reliable bits could also cause false positive identifications. Calculating the combined probability of any false positive event is difficult, so we will restrict the calculation to single bit errors, since the probability of E bit errors is ${ϵ}^E$, which decreases rapidly for $E>1$. For $E=1$, only chips with codes within Hamming distance 1 of the target chip code can cause false positives. In the worst case, for an N bit code with U unreliable bits, there are $(N-U)2^U$ possible chip codes within a Hamming distance of 1. However, this number is usually much larger than the maximum number of uniquely addressable chips, S, given by Equation (15). In actual practice, therefore, there are at most $S-1$ other chips that could cause false positive errors. The probability of any of these chips causing a false positive is then

$$p_{FP}=1-{(1-ϵ)}^{2^{N-U}-1}$$

(17)

The total error rate, $p_E$ can then be found

$$p_E=1-(1-p_{FN})(1-p_{FP})$$

(18)

$$p_E=1-{(1-ϵ)}^{(N-U)(2^{N-U}-1)}$$

(19)

Restricting the use of chips to those that have a number of unreliable bits less than or equal to U reduces the yield. If the probability that a bit is unreliable is $p_U$, then the yield is given by

$$Y=\sum _{u=0}^U\left(\begin{array}{c}N\\ u\end{array}\right)p_U^u{(1-p_U)}^{N-u}$$

(20)

5. Experimental Results

The proposed circuit was fabricated in a 130 nm CMOS process. A photograph of the manufactured die is shown in Figure 4. As in Figure 1, one column of ID cells shared a single SA, with 32 ID cells per column. A shift register is used to generate the row select signal, and each shift register is shared by 32 columns to for a 32 × 32 array. Fifteen of these arrays are contained on each die, for a total of 15,360 ID bits per die. One 32-bit column, including the SA, occupies an area of 68.5 × 4.3 μm. For measurement, the value of $V_{DD}$ was 400 mV.

Figure 4. Photograph of random ID chip with 15,360 ID bits, fabricated in 130 nm CMOS process.

Figure 4. Photograph of random ID chip with 15,360 ID bits, fabricated in 130 nm CMOS process.

For each ID cell, the value of p was determined by reading from the cell 1000 times, and counting the number of results equal to “1”. To find the value of the threshold voltage mismatch, $\Delta V_T$ in the ID cell, the gate of M1 was held fixed, and the gate of M2 was swept in 1 mV increments. At each increment, the ID cell was read 100 times. From these two measurements, the relationship between p and $\Delta V_T$ was determined, and plotted in Figure 5. From this data, the value of the input referred voltage noise, ${\sigma }_{V_{in}}$, was determined to be 1.5 mV.

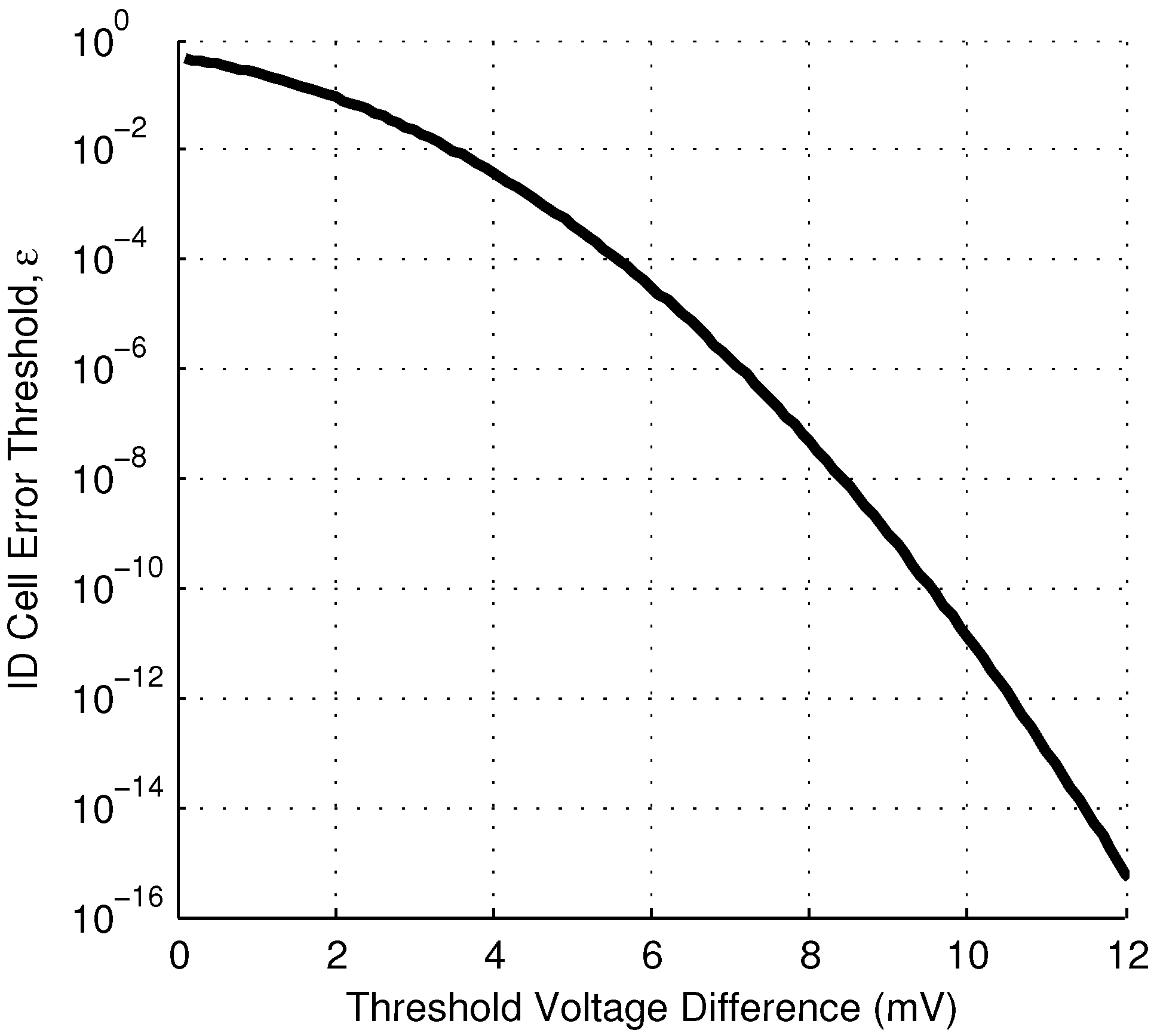
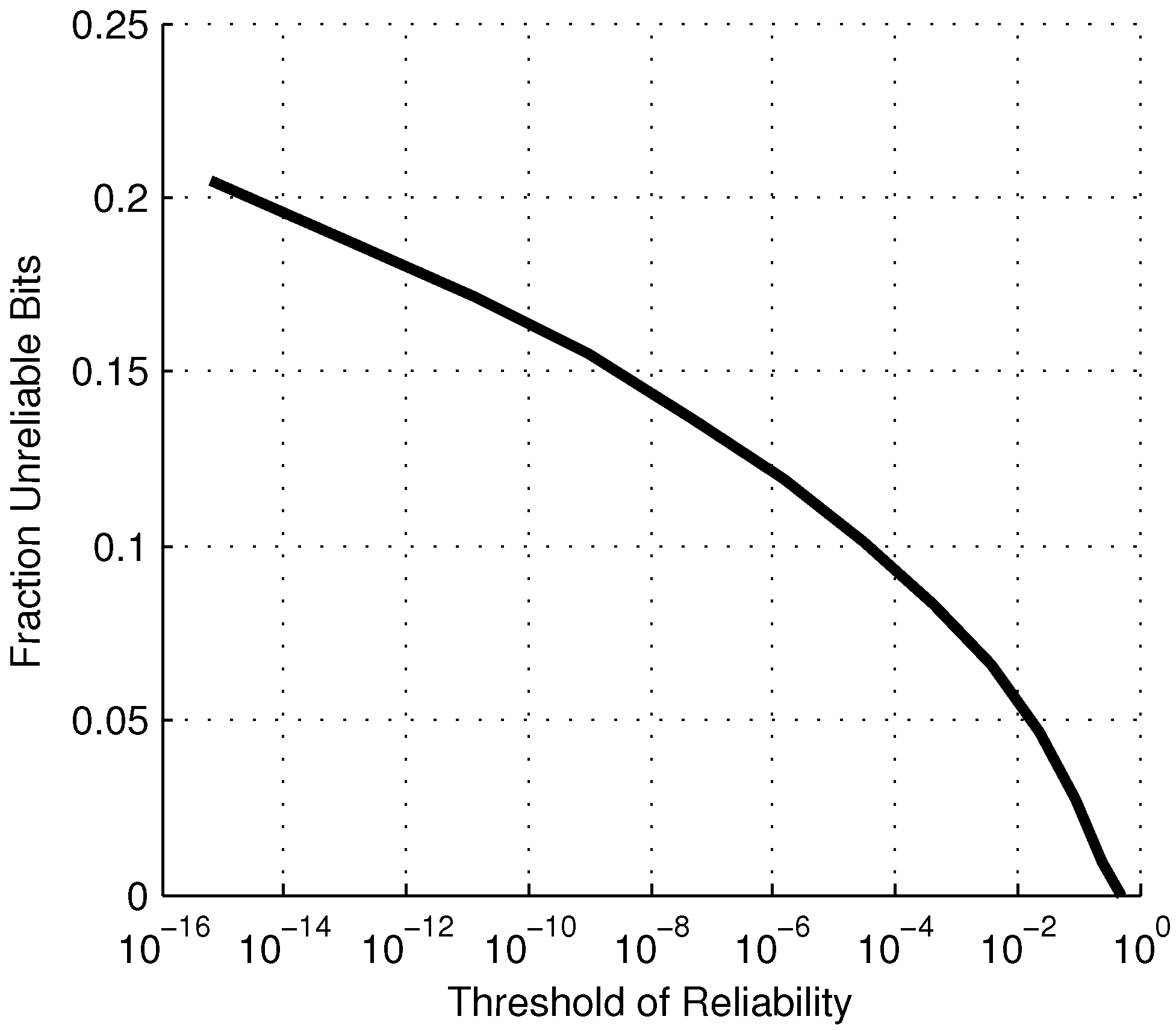
If a reliability threshold of $ϵ={10}^{-10}$ is chosen, Equation (10) indicates ID cells with $|\Delta V_T|>10$ mV will behave reliably. Of the fabricated ID cells examined, $82\%$ satisfy this inequality and can be classified as reliable ($p_U=0.18$). More generally, Figure 6 shows the relationship between $|\Delta V_T|$ and the reliability threshold, and Figure 7 shows the fraction of unreliable bits for a given reliability threshold.

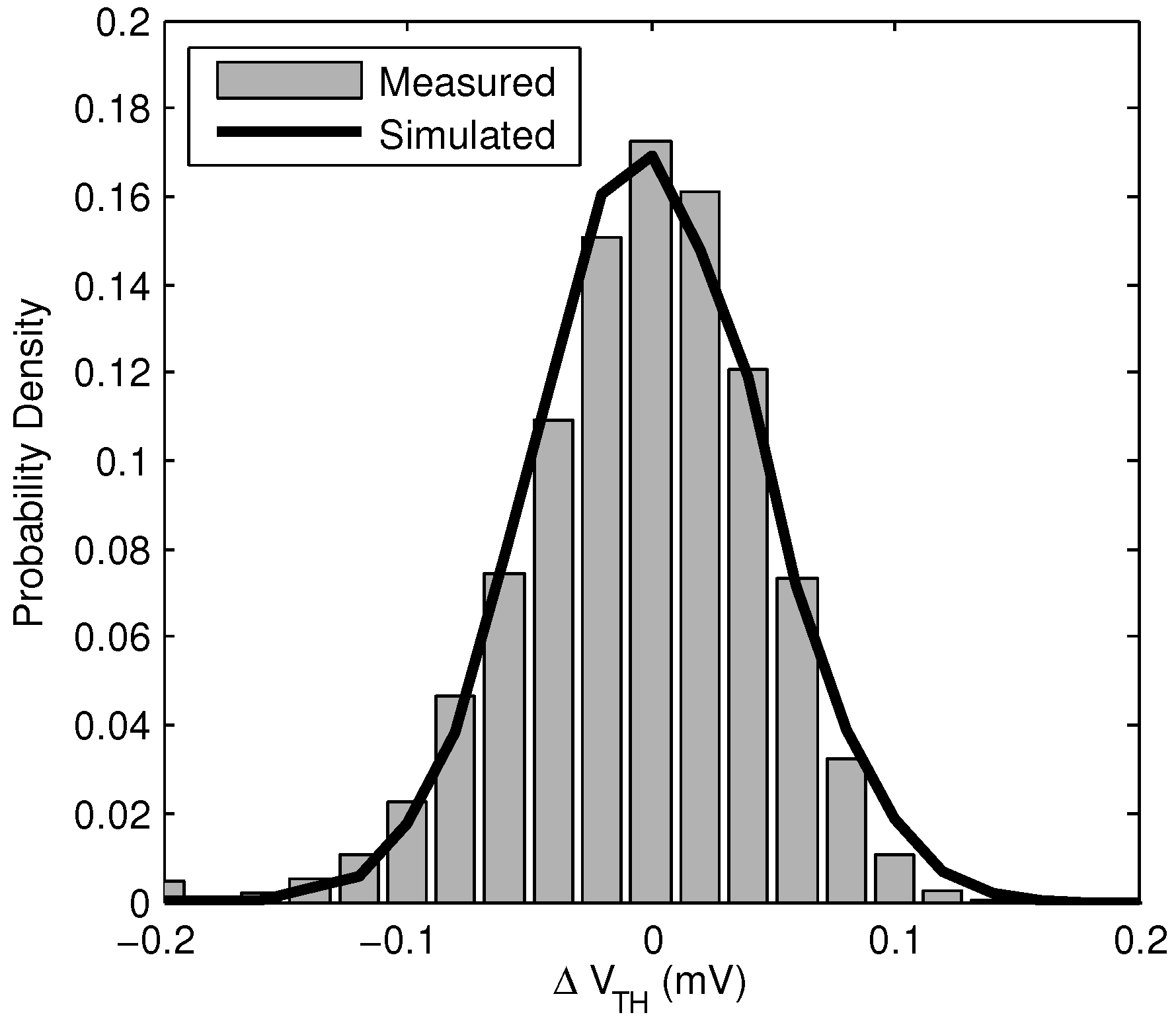
The location of unreliable cells for an arbitrarily chosen 32 × 32 array is shown in Figure 8. The unreliable cells are shown in black. The magnitude of $\Delta V_T$ is also shown for the same array. This indicates that unreliable bits have random spatial distribution in the array. The measured distribution of $\Delta V_T$ is shown in Figure 9, along with a Monte Carlo simulation of the same distribution. This shows the distribution of $\Delta V_T$ can be accurately predicted in advance for well modeled processes.

Figure 5. Relationship of ID cell probability, p, to threshold voltage mismatch $\Delta V_T$, measured over 15,360 bits. Equation (9) is also plotted with ${\sigma }_{V_{in}}$ = 1.5 mV.

Figure 5. Relationship of ID cell probability, p, to threshold voltage mismatch $\Delta V_T$, measured over 15,360 bits. Equation (9) is also plotted with ${\sigma }_{V_{in}}$ = 1.5 mV.

Figure 6. Relationship between ID cell error rate, ϵ, and the magnitude of the threshold voltage mismatch in the ID cell, $|\Delta V_T|$.

Figure 6. Relationship between ID cell error rate, ϵ, and the magnitude of the threshold voltage mismatch in the ID cell, $|\Delta V_T|$.

The relationship between $|\Delta V_T|$ and the reliability threshold depends on the value of ${\sigma }_{V_{in}}$, which will vary in different technologies. Equation (9) shows that the required $|\Delta V_T|$ is linearly related to ${\sigma }_{V_{in}}$, i.e., a 10× increase in ${\sigma }_{V_{in}}$ would require a 10× increase in the difference threshold $|\Delta V_T|$ to maintain the same error threshold. This may reduce the yield, if the standard deviation of the threshold voltage is not also higher in the alternate technology.

The energy consumption was measured to be 39 fJ/bit at a readout rate of 40 kBps. This is 23× less than the next lowest published value of 930 fJ/bit [16]. The decreased energy consumption is likely due to the lower supply voltage, sharing of a single SA (which amortizes the SA leakage current), and the use of a shift register for sequential access rather than a row decoder. The effective area per bit (32-bit column and sense amplifier divided by 32), is 9.2 μm${}^2$.

Figure 7. Fraction of manufactured bits that can be expected to be unreliable for a given threshold of reliability, ϵ.

Figure 7. Fraction of manufactured bits that can be expected to be unreliable for a given threshold of reliability, ϵ.

Figure 8. (A) Location of unreliable bits ($|\Delta V_T|<10$ mV), shown in black, in a 32 × 32 array of random ID cells. (B) Magnitude of $|\Delta V_T|$ in the same array, where black is 0 mV and white is 50 mV.

Figure 8. (A) Location of unreliable bits ($|\Delta V_T|<10$ mV), shown in black, in a 32 × 32 array of random ID cells. (B) Magnitude of $|\Delta V_T|$ in the same array, where black is 0 mV and white is 50 mV.

Figure 9. Normalized histogram showing measured and simulated distribution of $\Delta V_T$. Measured sample size is 15,360 bits, and simulated sample size is 10,000 bits.

Figure 9. Normalized histogram showing measured and simulated distribution of $\Delta V_T$. Measured sample size is 15,360 bits, and simulated sample size is 10,000 bits.

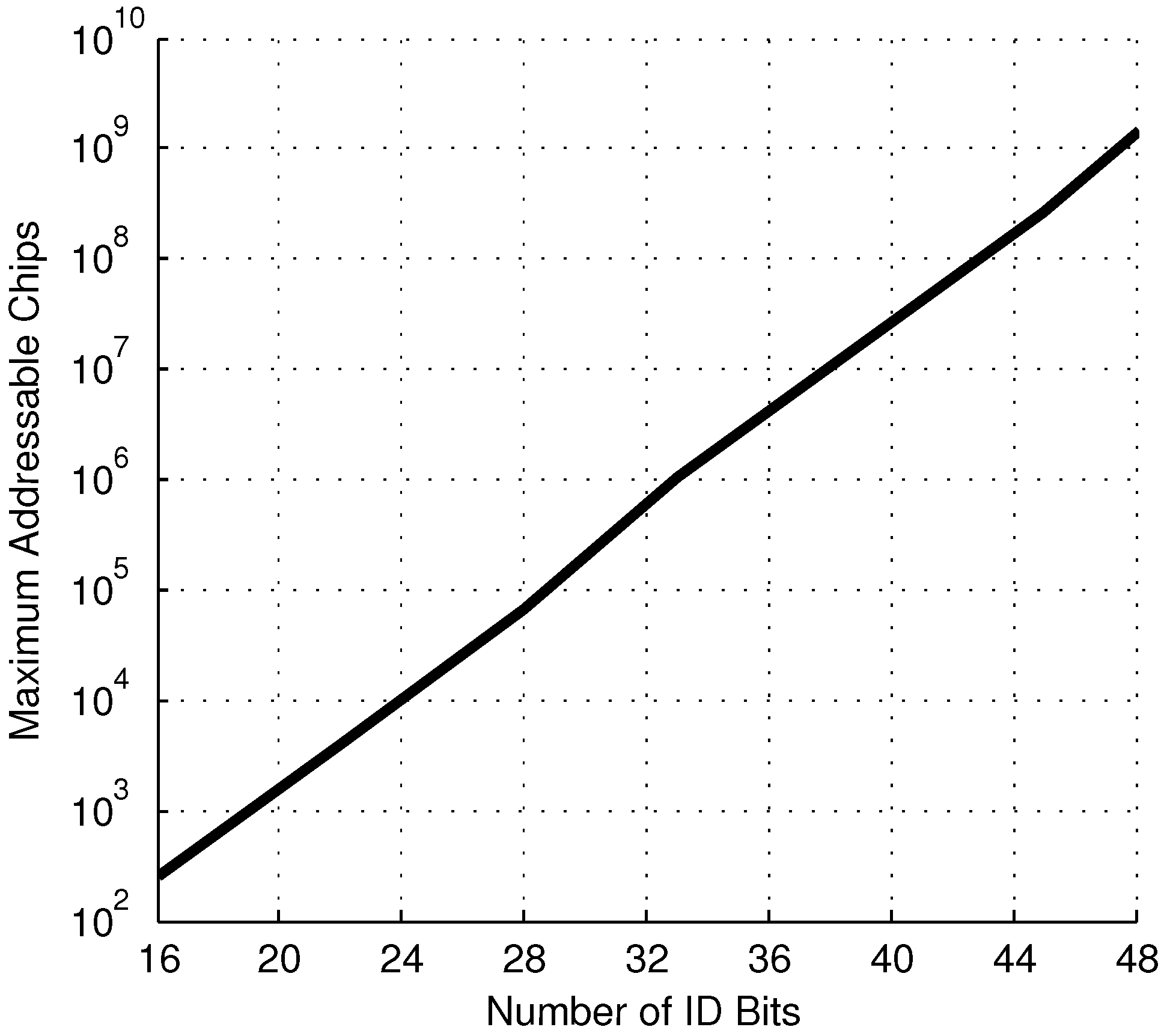
As previously noted, having a non-zero number of unreliable bits, U, reduces the maximum number of addressable chips from the theoretical maximum of $2^N$. For this system, with ${\sigma }_{V_{in}}$ = 1.5 mV, a chosen reliability threshold of $ϵ={10}^{-10}$ and $p_U=0.18$, and a 99.9% yield, the maximum number of addressable chips versus the number of ID bits is shown in Figure 10. This shows reasonable performance as the addressing scheme is scaled up to large systems.

Figure 10. Maximum number of addressable chips under the masked addressing system for a given number of random ID bits, N.

Figure 10. Maximum number of addressable chips under the masked addressing system for a given number of random ID bits, N.

5.1. Temperature Dependence

To evaluate the reliability of the random ID system over temperature, the change in $\Delta V_T$ was measured for all the ID cells over 30 ${}^{\circ }$C and 50 ${}^{\circ }$C increases in temperature. We observed that for each ID cell, the temperature dependence of $\Delta V_T$ varies, in part proportionally to $\Delta V_T$, and in part randomly between cells. The change in $\Delta V_T$ over the observed range is roughly linear with temperature, and so can be expressed as

$$\frac{d\Delta V_T}{dT}=K$$

(21)

where K is a random variable, with mean value proportional to $\Delta V_T$:

$${\mu }_K=a\Delta V_T$$

(22)

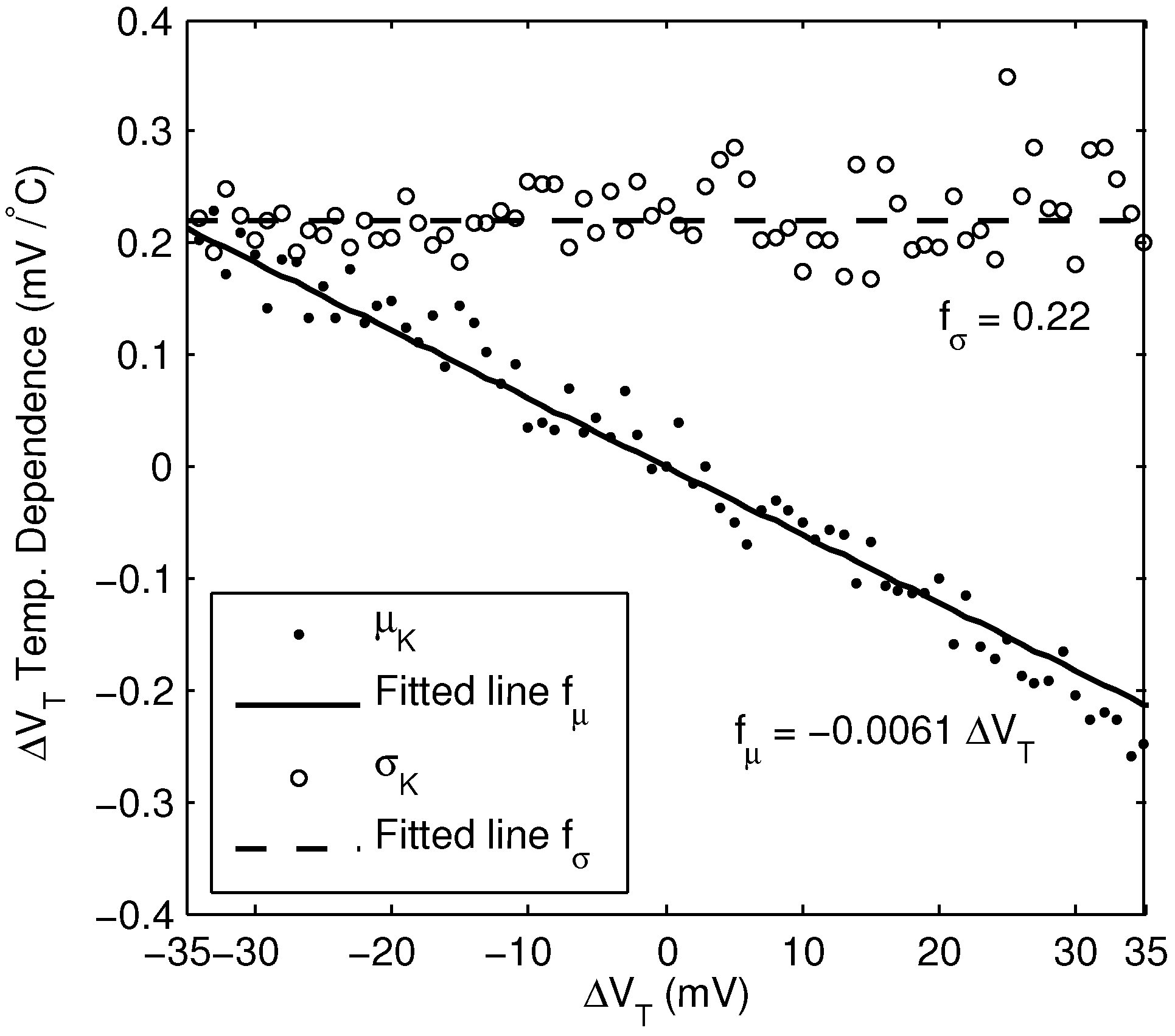
The temperature coefficient, a, was found to be −6.1 × 10${}^{-3}$${}^{\circ }$C${}^{-1}$. Because a is negative, the magnitude of $\Delta V_T$ tends to decrease as temperature increases. The standard deviation of K was found to be ${\sigma }_K=0.22$ mV/${}^{\circ }$C. A plot of the mean and standard deviation of the temperature dependence is shown in Figure 11, over a range of $\Delta V_T$ values.

A possible explanation for the apparent randomness of the temperature dependence is that the devices M1 and M2 in Figure 1 are assumed to differ only in their values of $V_T$, when in fact other device parameters such as the mobility ${\mu }_n$, gate oxide capacitance $C_{ox}$, and effective dimensions W and L will vary as well [19]. For example, in the preceding characterization scheme, if devices M1 and M2 are determined to have equal drain currents when driven with equal gate voltages, it is assumed that their values of $V_T$ are equal. However, it could also be that their values of $V_T$ are unequal, and other devices parameters are unequal in such a way that the drain currents remain equal. These other device parameters will then have their own, unequal temperature dependence [20], resulting in the apparent random temperature dependence. A possible improvement to this work would be a more elaborate characterization scheme in which the mismatch between devices M1 and M2 could be more completely determined, although this would increase the complexity of the characterization scheme.

Figure 11. Mean and standard deviation of the change in $\Delta V_T$ per 1 ${}^{\circ }$C change in temperature, derived from measurement of 15,360 bits of a single chip.

Figure 11. Mean and standard deviation of the change in $\Delta V_T$ per 1 ${}^{\circ }$C change in temperature, derived from measurement of 15,360 bits of a single chip.

The practical effect of this is that a larger value of $V_R$ must be selected for reliable operation, due to the combined effects of electronic noise and temperature dependence. For positive values of $\Delta V_T$, and if all temperature dependencies are assumed to fall within $6\sigma$, then the worst case temperature shift from $\Delta V_T$ to $\Delta V_T^{\prime }$ over an increase in temperature $\Delta T$ is

$$\Delta V_T^{\prime }-\Delta V_T=(a\Delta V_T-6{\sigma }_K)\Delta T$$

(23)

Rearranging Equation (23) and substituting $\Delta V_T^{\prime }=V_R$ and $\Delta V_T=V_R^{\prime }$ gives the value of $V_R^{\prime }$ measured at nominal temperature that is required to ensure $|\Delta V_T^{\prime }|\ge V_R$ after a temperature increase of $\Delta T$.

$$\Delta V_R^{\prime }=\frac{V_R+6\sigma \Delta T}{1+a\Delta T}$$

(24)

That is, by only selecting ID cells with $|\Delta V_T|\ge V_R^{\prime }$, it is ensured that after a $\Delta T$ increase in temperature, the new threshold voltage difference will satisfy the original reliability requirement, $|\Delta V_T^{\prime }|\ge V_R$. For example, using the previously determined value of $V_R=10$ mV, and assuming a possible temperature increase of 10 ${}^{\circ }$C, Equation (24) indicates that $V_R^{\prime }=25$ mV. This increases the fraction of unreliable bits to $p_U=0.41$.

This method could be employed by determining the parameters a and σ of Equation (24) once for a particular manufacturing process. The characterization of individual chips would then not require any extra measurements beyond the two already required by the characterization scheme, and these measurements do not have to be taken at a particular temperature. This method is, however, inefficient due to the constraint imposed by Equation (23), which assumes the worst case temperature dependence. This is highly unlikely for any given ID cell; a large fraction of cells characterized in this way as unreliable would in fact behave reliably. An obvious alternative would be simply to characterize each cell twice, once at each extreme of the expected operating temperature range, and only select cells that have the same classification at both extremes as reliable. This is more efficient, in the sense that the fraction of unreliable bits will be smaller, but requires a temperature controlled environment for characterizing each chip, which is frequently expensive and time-consuming to employ.

5.2. Addressing Parameter Selection

The selection of the particular parameters of the addressing scheme depends heavily on the particular application. In most cases, the specifications will require the selection of three minimum requirements: (1) address space size (S); (2) yield (Y); and (3) error rate ($p_E$). After these requirements are specified, the other parameters of the masked addressing scheme can be determined. The parameters of a hypothetical system are determined here using experimentally derived data, to give an indication of the performance of this work.

Consider a system with the specifications $S=1000$, $Y=99.9\%$, $p_E={10}^{-6}$, and a possible $\Delta T=10$ ${}^{\circ }$C. Given the requirement $S=1000$ and Equation (15), the following constraint is imposed

$$N-U\ge 10$$

(25)

Given this constraint, a lower limit for N can be found using Equation (20), with $Y=0.999$ and $p_U=0.41$. The smallest value that satisfies these conditions is $N=31$, setting $U=21$. Finally the total error rate can be found using Equation (19) to be $p_E=1.03\times {10}^{-7}$.

6. Conclusions

This work presents a circuit and addressing scheme that can be used to remotely identify integrated circuits using their inherent manufacturing variation. Unlike other identification techniques based on manufacturing variation, identification can be done on-chip, which reduces the amount of data that must be transmitted by the chip. This is made possible by characterizing the reliability of the random ID bits, and then developing an addressing scheme that is insensitive to errors among the unreliable bits. Our approach uses 39 fJ/bit per bit, which is 23× less energy than prior art, and includes a mathematical treatment of the reliability of such a system. Additionally, this circuit could be used as part of a low-energy secret key generator for cryptographic applications.