The Impact of Process Scaling on Scratchpad Memory Energy Savings †
Abstract
:1. Introduction
2. Background
3. Motivation
4. Conceptual Framework
4.1. Models
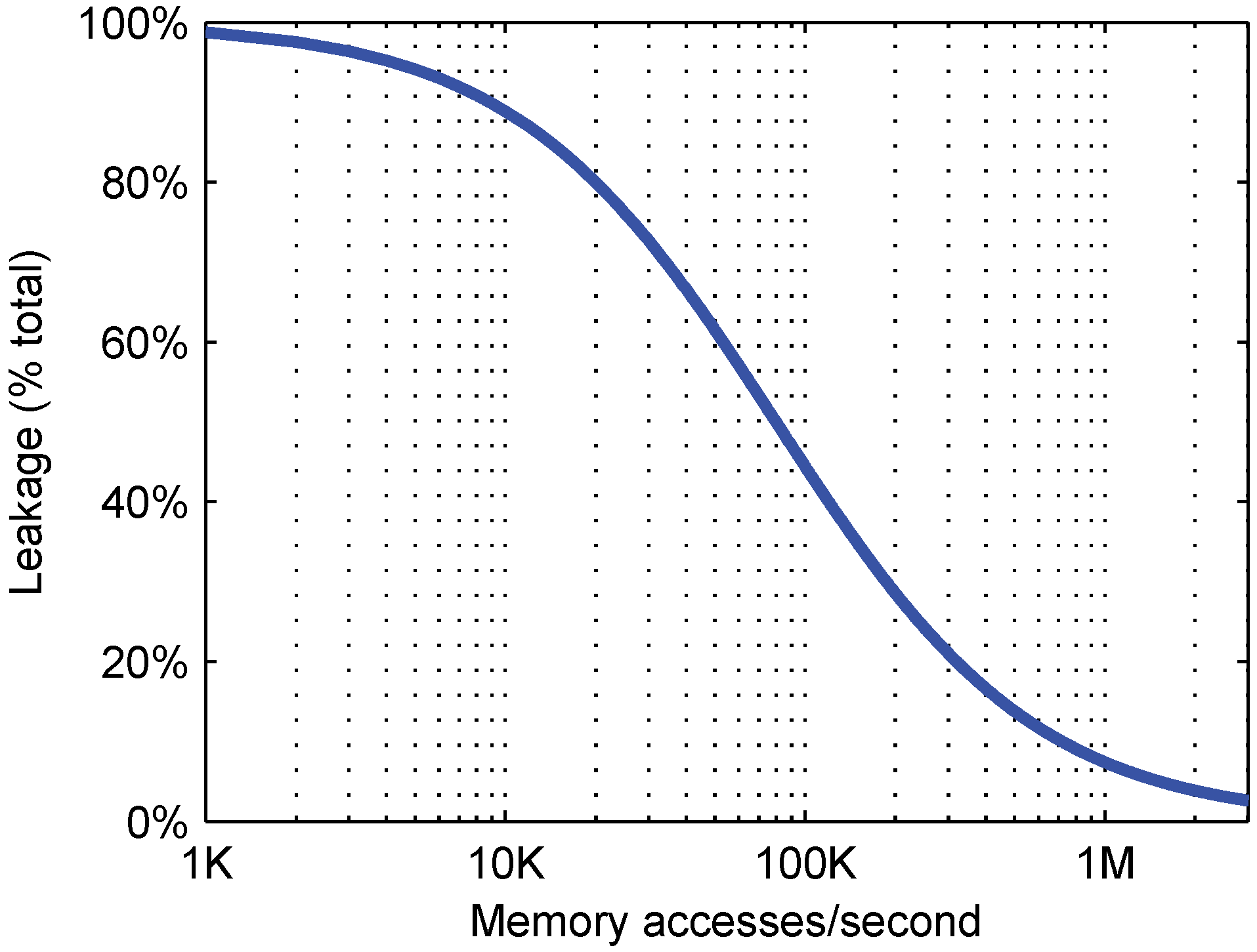
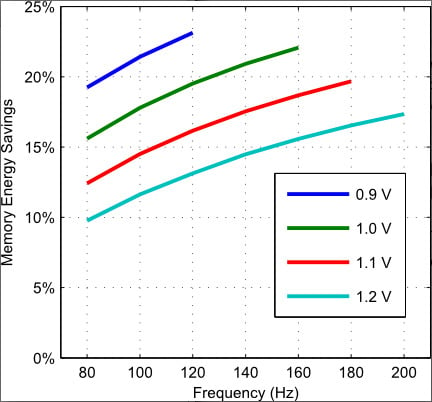
4.2. Relative Importance of Active and Leakage Energy
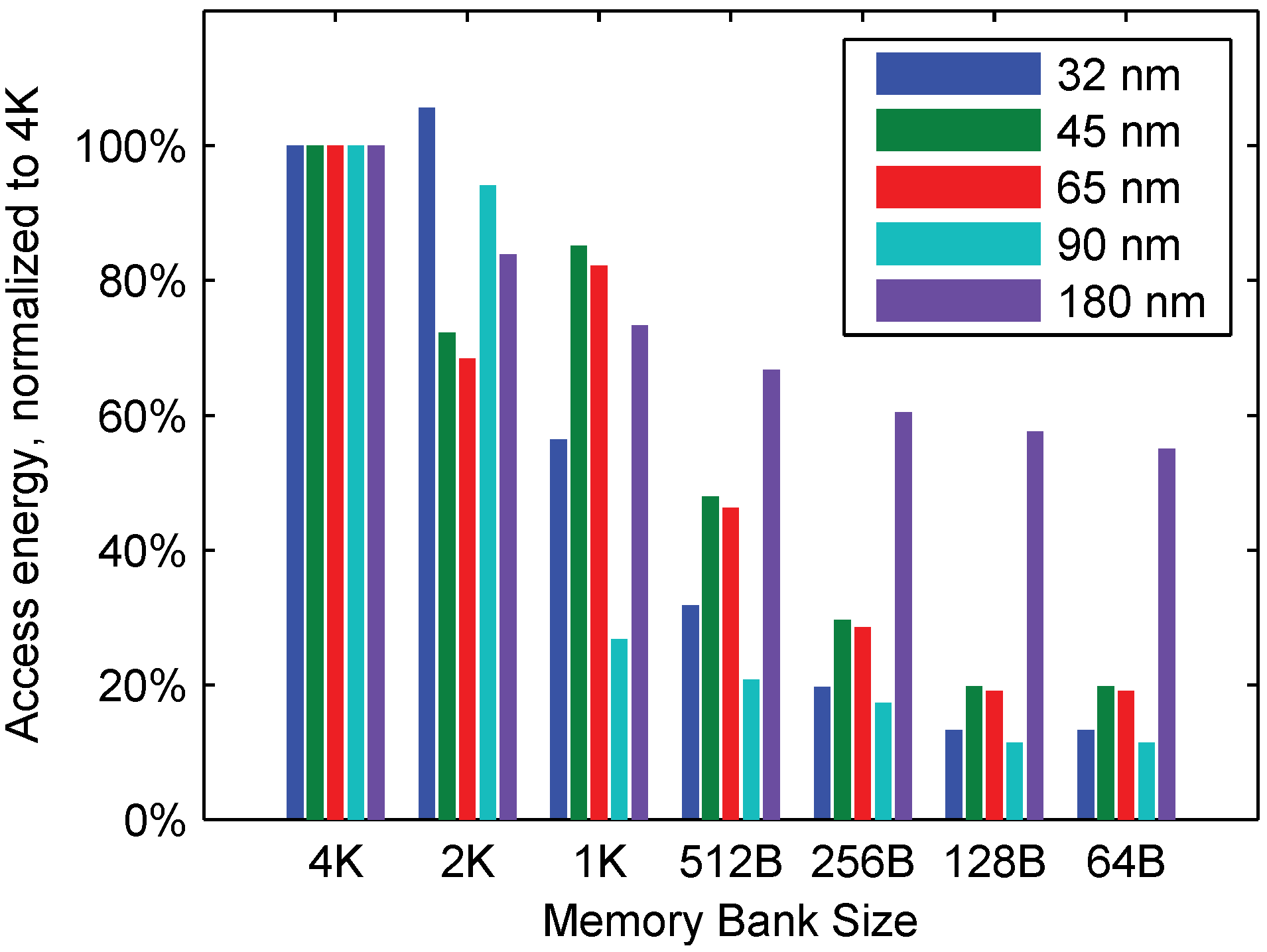
4.3. Access Energy and Memory Size
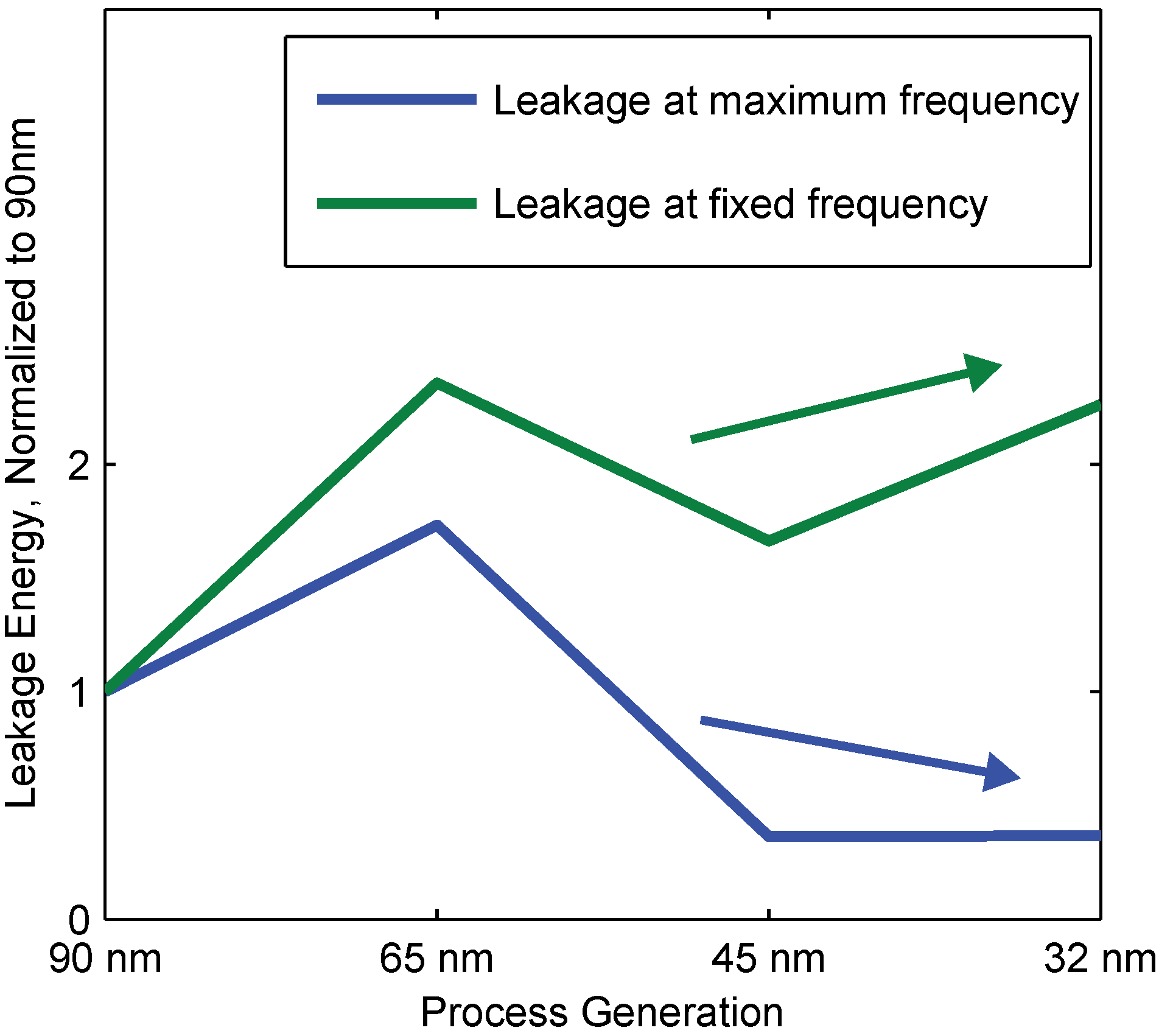
4.4. Leakage Energy and Process Scaling
5. Scaling Trends
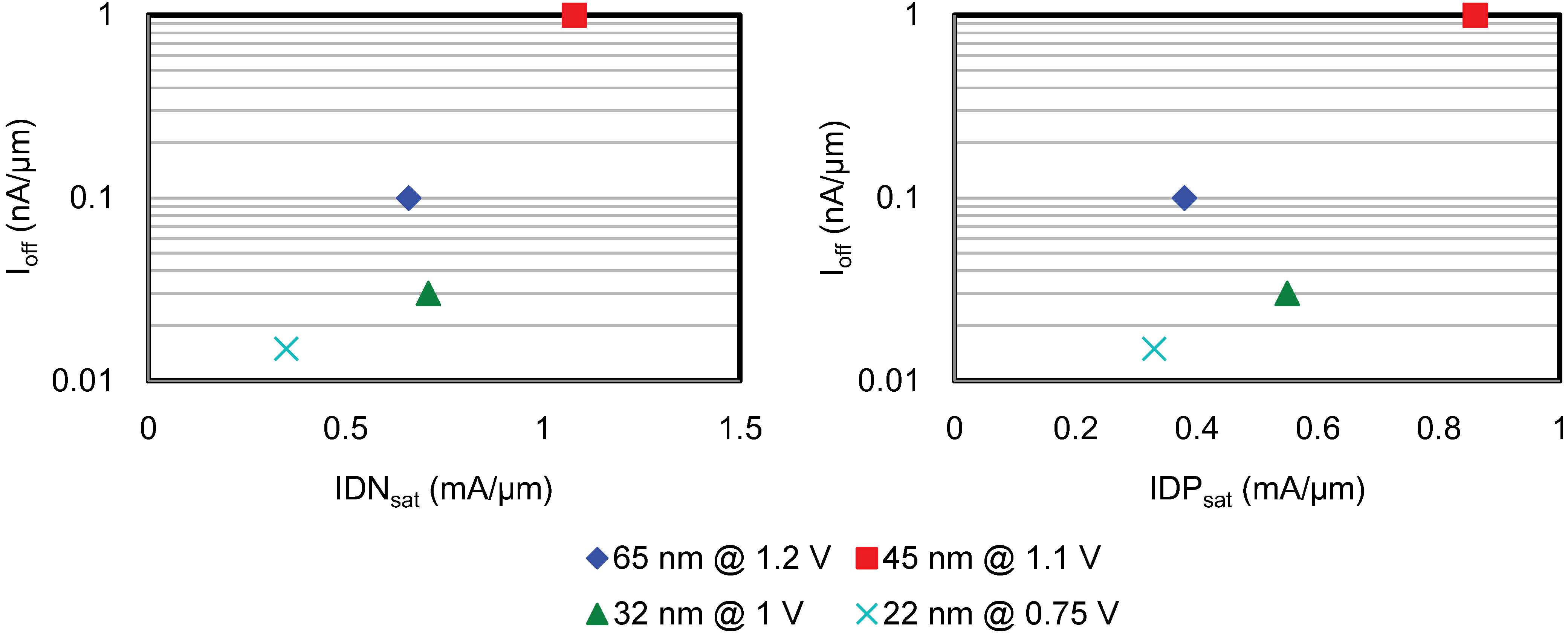
5.1. Process Innovations
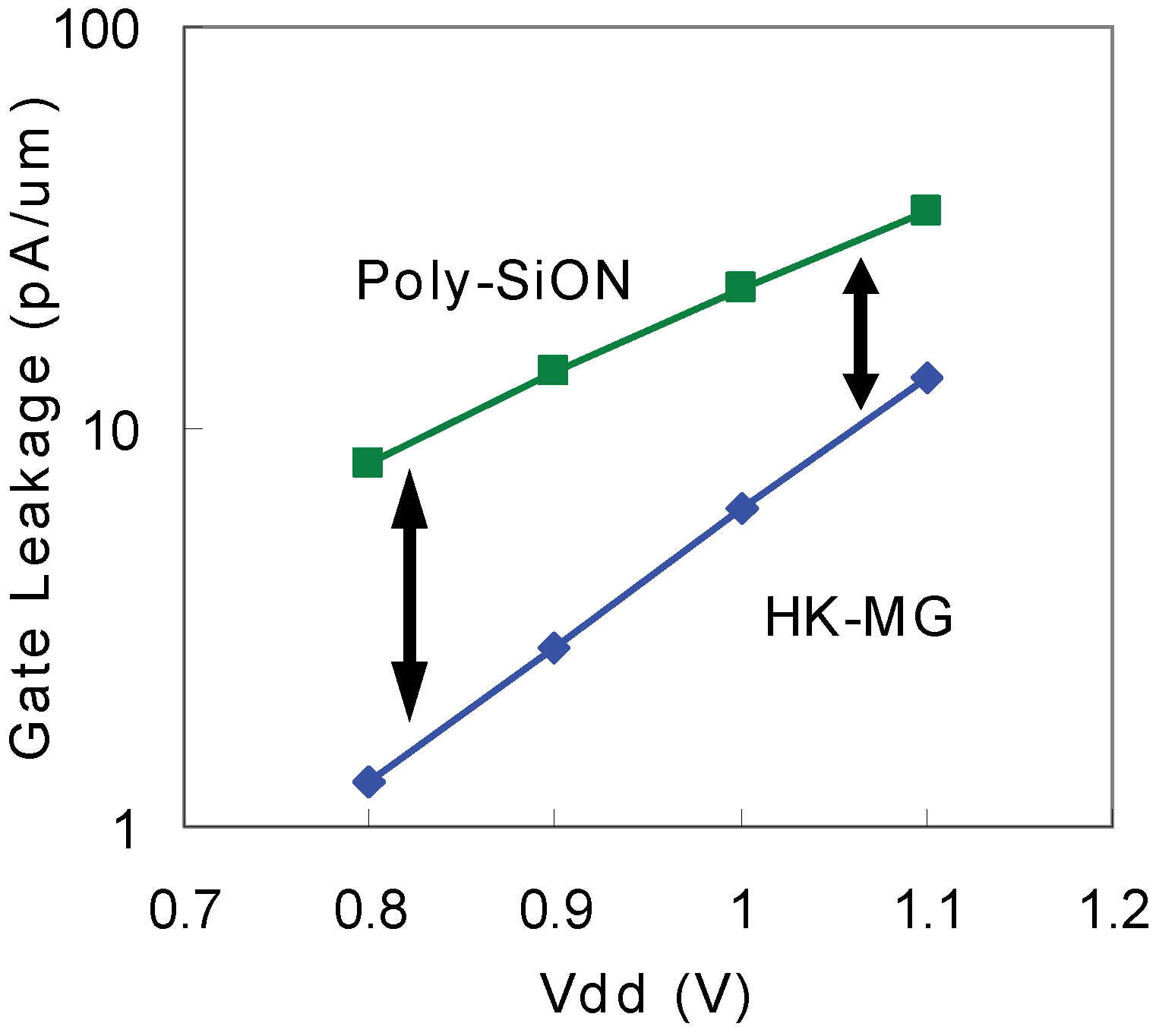
5.2. SRAM Cell Design
6. WIMS Microcontroller

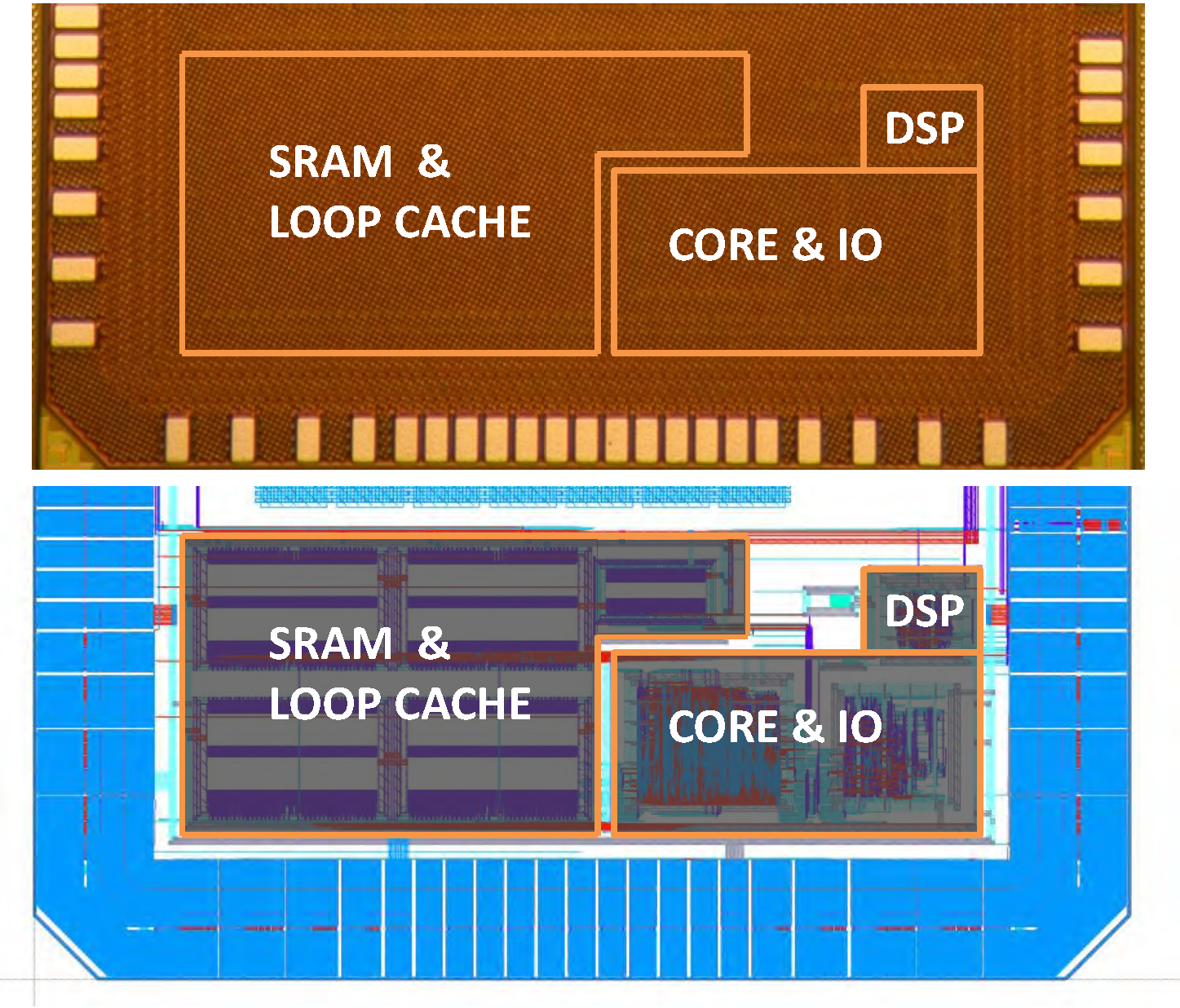
6.1. Measured Data
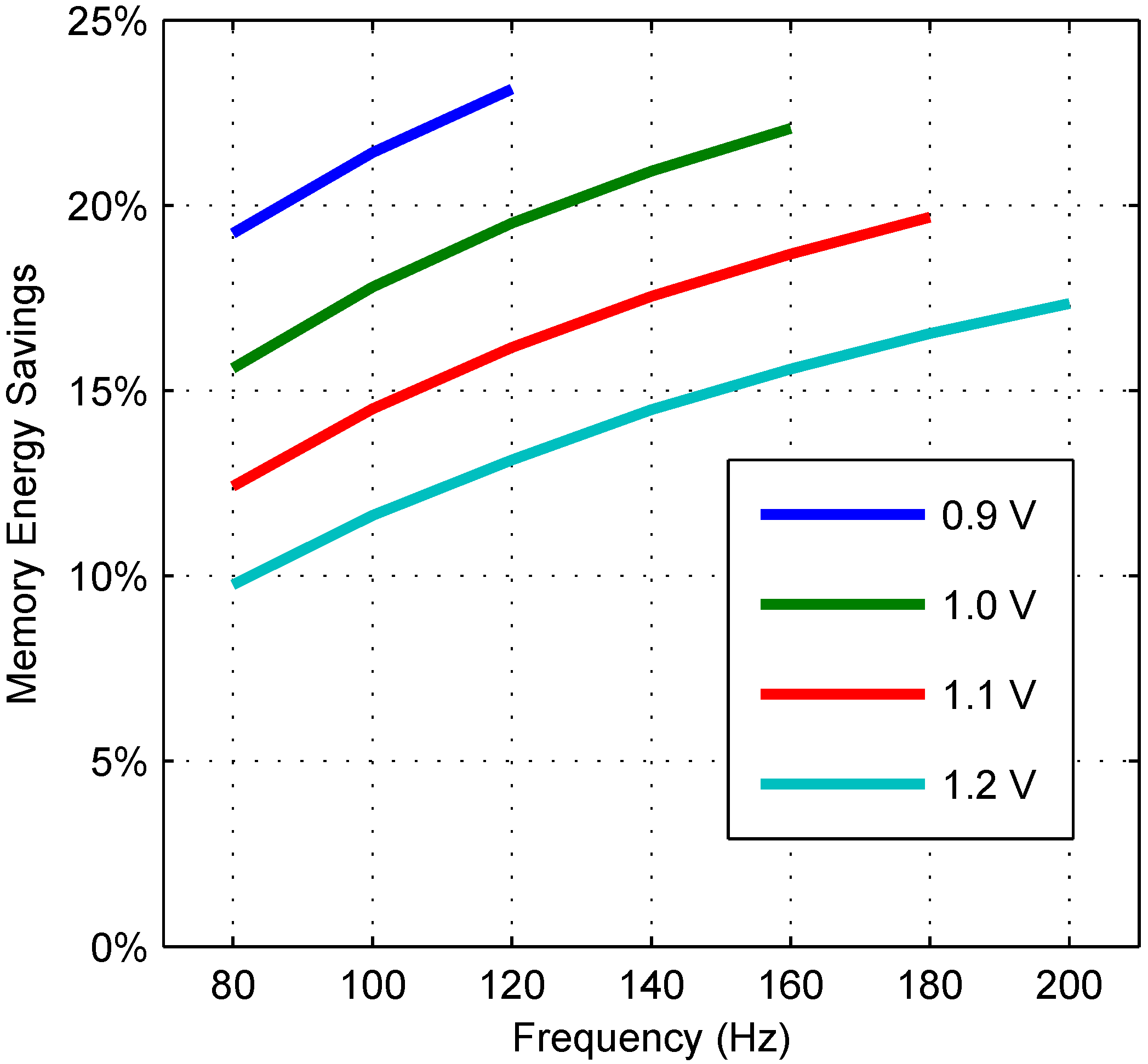
6.2. 32-nm Projections
6.3. WIMS Scratchpad Memory Approach
- Identify the most executed blocks of code.
- Assign these blocks of code, in the order of the most used first, to the scratchpad memory, until it is full.
- Redirect instruction fetch (when entering code block), subroutine calls and references to these blocks to the new locations in the scratchpad memory.
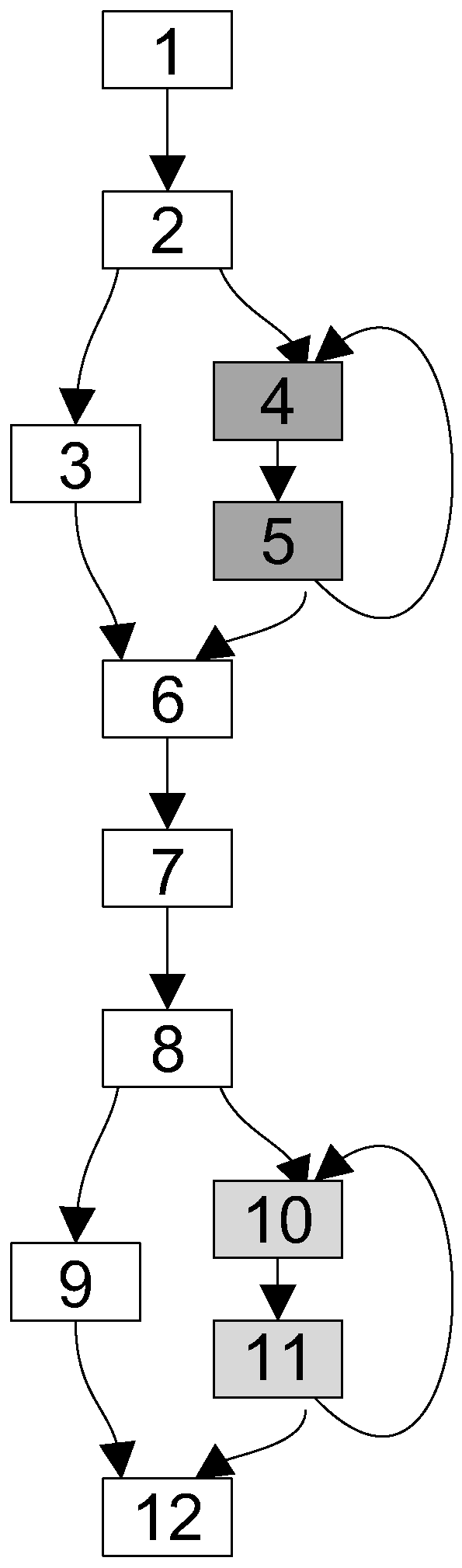
- Identify blocks of code, such that the energy to copy the code to the scratchpad memory is less than the energy saved by executing the code from the scratchpad memory.
- Assign these blocks of code addresses in the scratchpad memory and redirect references to them to their new addresses.
- Insert copy instructions immediately prior to each of these blocks, so that the block will be in the scratchpad memory prior to its execution or prior to its being called if it is a subroutine.
- Consolidate copy instructions to avoid unnecessary copying.
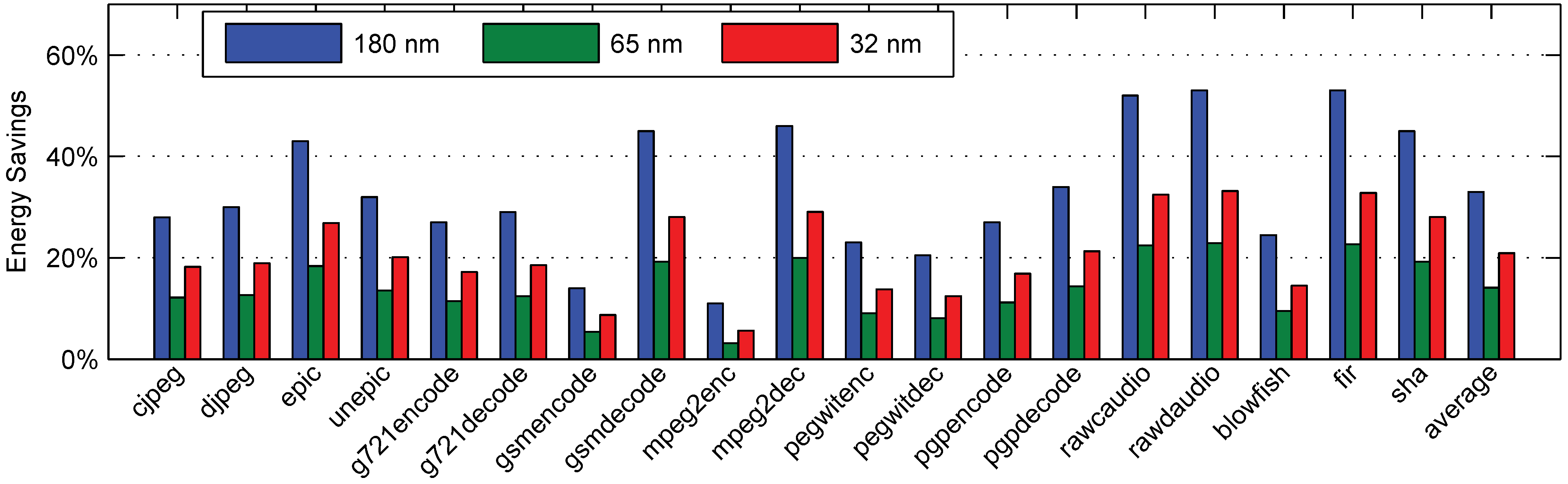
6.4. Static Benchmarks
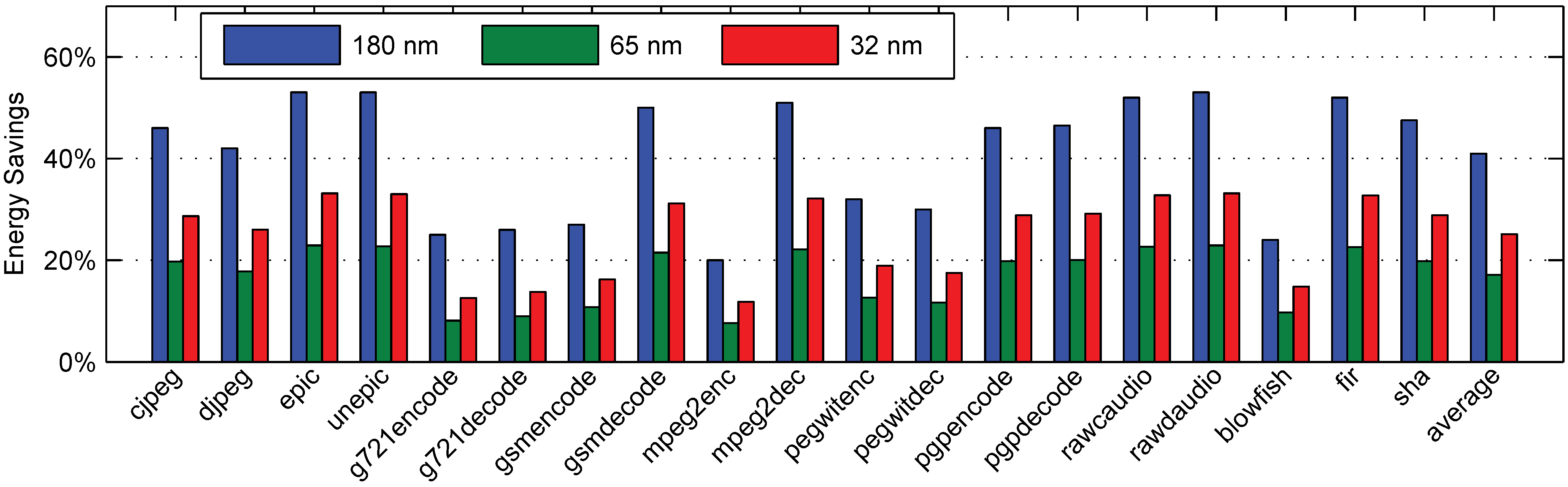
6.5. Dynamic Benchmarks
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Redd, B.; Kellis, S.; Gaskin, N.; Brown, R. Scratchpad Memories in the Context of Process Scaling. In Proceedings of the IEEE 54th International Midwest Symposium on the Circuits and Systems (MWSCAS), Seoul, Korea, 7–10 August 2011.
- Kellis, S.; Gaskin, N.; Redd, B.; Campbell, J.; Brown, R. Energy Profile of a Microcontroller for Neural Prosthetic Application. In Proceedings of the IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 3841–3844.
- Steinke, S.; Wehmeyer, L.; Bo-Sik, L.; Marwedel, P. Assigning Program and Data Objects to Scratchpad for Energy reduction. In Proceedings of the Design, Automation and Test in Europe Conference and Exhibition, Paris, France, 4–8 March 2002; pp. 409–415.
- Kin, J.; Gupta, M.; Mangione-Smith, W.H. The Filter Cache: An Energy Efficient Memory Structure. In Proceedings of the 30th Annual ACM/IEEE International Symposium Microarchitecture, Washington, DC, USA, 1–3 December 1997; pp. 184–193.
- Bellas, N.; Hajj, I.; Polychronopoulos, C.; Stamoulis, G. Energy and Performance Improvements in Microprocessor Design Using a Loop Cache. In Proceedings of the International Conference on Computer Design (ICCD ’99), Austin, TX, USA, 10–13 October 1999; pp. 378–383.
- Lea Hwang, L.; Moyer, B.; Arends, J. Instruction Fetch Energy Reduction Using Loop Caches for Embedded Applications with Small Tight Loops. In Proceedings of the Low Power Electronics and Design, San Diego, CA, USA, 17 August 1999; pp. 267–269.
- Gordon-Ross, A.; Cotterell, S.; Vahid, F. Exploiting fixed programs in embedded systems: A loop cache example. IEEE Comp. Archit. Lett. 2002, 1, 2. [Google Scholar] [CrossRef]
- Egger, B.; Lee, J.; Shin, H. Scratchpad Memory Management for Portable Systems with a Memory Management Unit. In Proceedings of the 6th ACM & IEEE International Conference on Embedded Software (EMSOFT ’06), Seoul, Korea, 22–25 October 2006; ACM: New York, NY, USA, 2006; pp. 321–330. [Google Scholar]
- Verma, M.; Wehmeyer, L.; Marwedel, P. Cache-Aware Scratchpad Allocation Algorithm. In Proceedings of the Design, Automation and Test in Europe Conference and Exhibition, Washington, DC, USA, 16–20 February 2004; pp. 1264–1269.
- Ravindran, R.A.; Nagarkar, P.D.; Dasika, G.S.; Marsman, E.D.; Senger, R.M.; Mahlke, S.A.; Brown, R.B. Compiler Managed Dynamic Instruction Placement in a Low-Power Code cache. In Proceedings of the International Symposium on Code Generation and Optimization (CGO), Washington, DC, USA, 20–23 March 2005; pp. 179–190.
- Borkar, S. Design challenges of technology scaling. Micro IEEE 1999, 19, 23–29. [Google Scholar] [CrossRef]
- Guangyu, C.; Feihui, L.; Ozturk, O.; Guilin, C.; Kandemir, M.; Kolcu, I. Leakage-Aware SPM Management. In Proceedings of the IEEE Computer Society Annual Symposium on Emerging VLSI Technologies and Architectures, Karlsruhe, Germany, 2–3 March 2006.
- Kandemir, M.; Irwin, M.J.; Chen, G.; Kolcu, I. Compiler-guided leakage optimization for banked scratch-pad memories. IEEE Trans. Larg. Scale Integr. (VLSI) Syst. 2005, 13, 1136–1146. [Google Scholar] [CrossRef]
- Huangfu, Y.; Zhang, W. Compiler-based approach to reducing leakage energy of instruction scratch-pad memories. In Proceedings of the 2013 IEEE 31st International Conference on Computer Design (ICCD), Asheville, NC, USA, 6–9 October 2013; pp. 439–442.
- Takase, H.; Tomiyama, H.; Zeng, G.; Takada, H. Energy efficiency of scratch-pad memory in deep submicron domains: An empirical study. IEICE Electron. Express 2008, 5, 1010–1016. [Google Scholar] [CrossRef]
- Thoziyoor, S.; Muralimanohar, N.; Ahn, J.; Jouppi, N. CACTI 5.1. Available online: http://www.hpl.hp.com/techreports/2008/HPL-2008-20.html (accessed on 5 June 2014).
- 2005 International Technology Roadmap for Semiconductors. Available online: http://www.itrs.net/reports.html (accessed on 5 June 2014).
- Wilton, S.; Jouppi, N. CACTI: An enhanced cache access and cycle time model. IEEE J. Solid-State Circuits 1996, 31, 677–688. [Google Scholar] [CrossRef]
- Jan, C.H.; Bai, P.; Choi, J.; Curello, G.; Jacobs, S.; Jeong, J.; Johnson, K.; Jones, D.; Klopcic, S.; Lin, J.; et al. A 65 nm Ultra Low Power Logic Platform Technology Using Uni-Axially Strained-Silicon Transistors. In Proceedings of the 2005 IEEE International Electron Devices Meeting (IEDM) Technical Digest, Washington, DC, USA, 5 December 2005; pp. 60–63.
- Jan, C.H.; Bai, P.; Biswas, S.; Buehler, M.; Chen, Z.P.; Curello, G.; Gannavaram, S.; Hafez, W.; He, J.; Hicks, J.; et al. A 45 nm Low Power System-on-Chip Technology with Dual Gate (Logic and I/O) High-k/Metal Gate Strained Silicon Transistors. In Proceedings of the 2008 IEEE International Electron Devices Meeting (IEDM 2008), San Francisco, CA, USA, 15–17 December 2008.
- Jan, C.H.; Agostinelli, M.; Buehler, M.; Chen, Z.P.; Choi, S.J.; Curello, G.; Deshpande, H.; Gannavaram, S.; Hafez, W.; Jalan, U.; et al. A 32 nm SoC Platform Technology with 2nd Generation High-k/Metal Gate Transistors Optimized for Ultra Low Power, High Performance, and High Density Product Applications. In Proceedings of the 2009 IEEE International Electron Devices Meeting (IEDM), Baltimore, MD, USA, 7–9 December 2009.
- Jan, C.H.; Bhattacharya, U.; Brain, R.; Choi, S.J.; Curello, G.; Gupta, G.; Hafez, W.; Jang, M.; Kang, M.; Komeyli, K.; et al. A 22 nm SoC Platform Technology Featuring 3-D Tri-gate and High-k/metal gate, optimized for ultra low power, high performance and high density SoC applications. In Proceedings of the 2012 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 10–13 December 2012; pp. 3.1.1–3.1.4.
- Dennard, R.; Gaensslen, F.; Rideout, V.; Bassous, E.; LeBlanc, A. Design of ion-implanted MOSFET’s with very small physical dimensions. Solid-State Circuits IEEE J. 1974, 9, 256–268. [Google Scholar] [CrossRef]
- Yang, H.S.; Wong, R.; Hasumi, R.; Gao, Y.; Kim, N.S.; Lee, D.H.; Badrudduza, S.; Nair, D.; Ostermayr, M.; Kang, H.; et al. Scaling of 32 nm Low Power SRAM with High-K Metal Gate. In Proceedings of the 2008 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 15–17 December 2008.
- Fujita, K.; Torii, Y.; Hori, M.; Oh, J.; Shifren, L.; Ranade, P.; Nakagawa, M.; Okabe, K.; Miyake, T.; Ohkoshi, K.; et al. Advanced Channel Engineering Achieving Aggressive Reduction of VT Variation for Ultra-Low-Power Applications. In Proceedings of the 2011 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 5–7 December 2011; pp. 32.3.1–32.3.4.
- Athe, P.; Dasgupta, S. A Comparative Study of 6T, 8T and 9T Decanano SRAM Cell. In Proceedings of the 2009 IEEE International Symposium on Industrial Electronics Applications (ISIEA 2009), Kuala Lumpur, Malaysia, 4–6 October 2009; Volume 2, pp. 889–894.
- Calhoun, B.H.; Chandrakasan, A. A 256kb Sub-threshold SRAM in 65 nm CMOS. In Proceedings of the 2006 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC 2006), San Francisco, CA, USA, 6–9 February 2006; pp. 2592–2601.
- Lin, S.; Kim, Y.B.; Lombardi, F. A Low Leakage 9T Sram Cell for Ultra-Low Power Operation. In Proceedings of the 18th ACM Great Lakes Symposium on VLSI, Orlando, FL, USA, 4–6 May 2008; ACM Press: New York, NY, USA, 2008; pp. 123–126. [Google Scholar]
- Marsman, E.; Senger, R.; McCorquodale, M. A 16-bit Low-Power Microcontroller with Monolithic MEMS-LC Clocking. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems (ISCAS 2005), Kobe, Japan; 2005; pp. 624–627. [Google Scholar]
- Magen, N.; Kolodny, A.; Weiser, U.; Shamir, N. Interconnect-Power Dissipation in a Microprocessor. In Proceedings of the 2004 International Workshop on System Level Interconnect Prediction (SLIP ’04), Paris, France, 14–15 February 2004; ACM: New York, NY, USA, 2004; pp. 7–13. [Google Scholar]
- Predictive Technology Model. Available online: http://ptm.asu.edu/interconnect.html (accessed on 5 June 2014).
- 2011 International Technology Roadmap for Semiconductors. Available online: http://www.itrs.net/reports.html (accessed on 5 June 2014).
- Lee, C.; Potkonjak, M.; Mangione-Smith, W. MediaBench: A Tool for Evaluating and Synthesizing Multimedia and Communications Systems. In Proceedings of the 30th Annual IEEE/ACM International Symposium on Microarchitecture, Research Triangle Park, NC, USA, 1–3 December 1997; pp. 330–335.
- Guthaus, M.; Ringenberg, J.; Ernst, D.; Austin, T.; Mudge, T.; Brown, R. MiBench: A Free, Commercially Representative Embedded Benchmark Suite. In Proceedings of the 2001 IEEE International Workshop on Workload Characterization (WWC-4 2001), Washington, DC, USA, 2 December 2001; pp. 3–14.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Redd, B.; Kellis, S.; Gaskin, N.; Brown, R. The Impact of Process Scaling on Scratchpad Memory Energy Savings. J. Low Power Electron. Appl. 2014, 4, 231-251. https://doi.org/10.3390/jlpea4030231
Redd B, Kellis S, Gaskin N, Brown R. The Impact of Process Scaling on Scratchpad Memory Energy Savings. Journal of Low Power Electronics and Applications. 2014; 4(3):231-251. https://doi.org/10.3390/jlpea4030231
Chicago/Turabian StyleRedd, Bennion, Spencer Kellis, Nathaniel Gaskin, and Richard Brown. 2014. "The Impact of Process Scaling on Scratchpad Memory Energy Savings" Journal of Low Power Electronics and Applications 4, no. 3: 231-251. https://doi.org/10.3390/jlpea4030231
APA StyleRedd, B., Kellis, S., Gaskin, N., & Brown, R. (2014). The Impact of Process Scaling on Scratchpad Memory Energy Savings. Journal of Low Power Electronics and Applications, 4(3), 231-251. https://doi.org/10.3390/jlpea4030231