Study of Back Biasing Schemes for ULV Logic from the Gate Level to the IP Level
Abstract
:1. Introduction
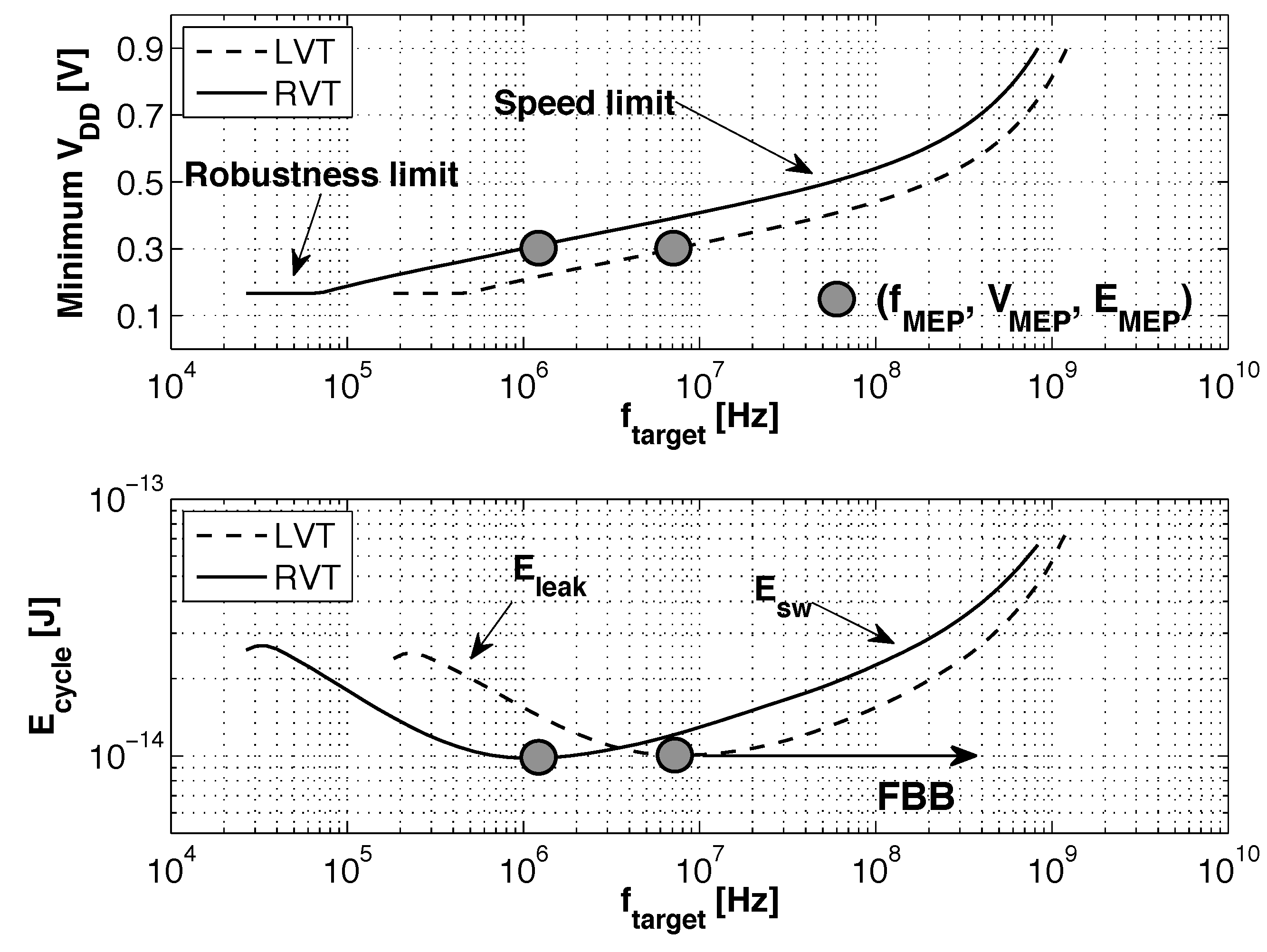
- At the gate level, we evaluate the impact of back gate biasing and several schemes of back gate biasing on key factor of merit of a test bench circuit simulated at gate level. Technology scaling of bulk CMOS leads to increased variability, drain-induced barrier lowering (DIBL) and gate leakage that are harmful to the minimum energy level [9]. MEP reduction with technology scaling is limited by short channel effects in advanced bulk nodes, calling for FDSOI technologies to keep reducing MEP, while improving the corresponding . In this work, the 28-nm FDSOI technology MEP is compared to 130-nm to 28-nm bulk technology MEP to quantify the high potential of FDSOI for ultra-low power and ultra-low voltage anticipated in [11,12,13]. Section 3.1 illustrates the effect of scaling and back biasing in the ULV domain. In addition to its use for trading the performance for energy efficiency, body biasing has already been proposed on bulk technology to mitigate random mismatch under process variation (PV) in [14]. In [15], the authors proposed an analytical framework to analyze the PMOS/NMOS ratio variation with supply voltage and an adaptive scheme to optimize this ratio while compensating for PV. In this work, we use BB to control systematic PMOS/NMOS mismatch over the range without resorting to sizing modifications, allowing the use of standard cell libraries sized at nominal voltage. Systematic mismatch cancellation results in both energy and robustness improvement. We show that such adaptive BB can save of energy per cycle at MEP and improve the gate count for a functional die yield by a factor of six. Mismatch compensation schemes are described in Section 3.2, and energy efficiency and robustness results are shown in Section 3.3 and Section 3.4;
- At the library level, we recharacterized a standard cell library when applying different BB voltages and investigate the obtained performances, as shown in Section 4;
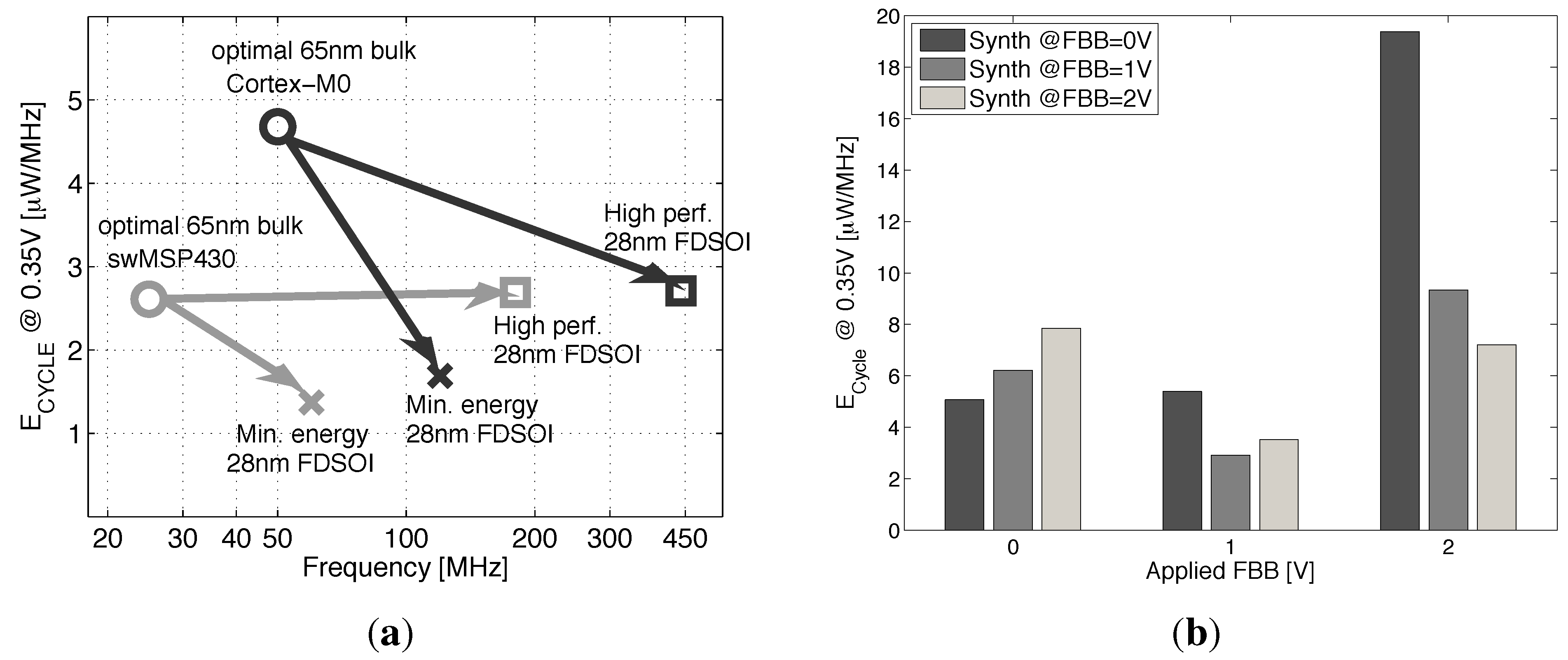
- At the IP level, we study the scaling perspective of ULV microcontrollers cores towards a 28-nm implementation by using the recharacterized libraries. We validate the conclusions made at the gate and library levels based on the synthesis results of two microcontroller cores at 0.35 V in 28 nm FDSOI, as compared to the latest best-in-class results in 65-nm CMOS bulk [4]. Energy efficiency depending on BB use at the synthesis or during the operation of the microcontroller is discussed in Section 5.
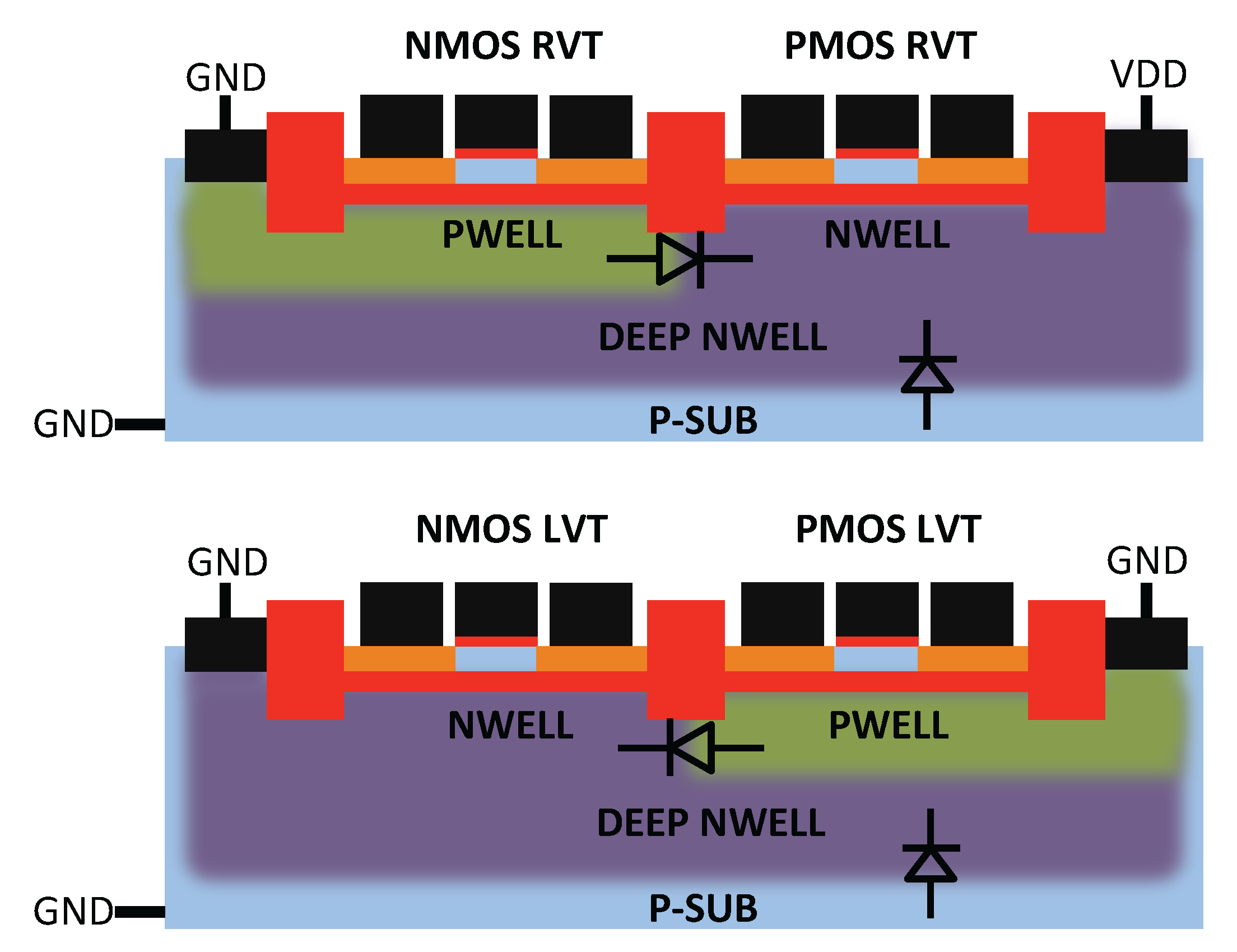
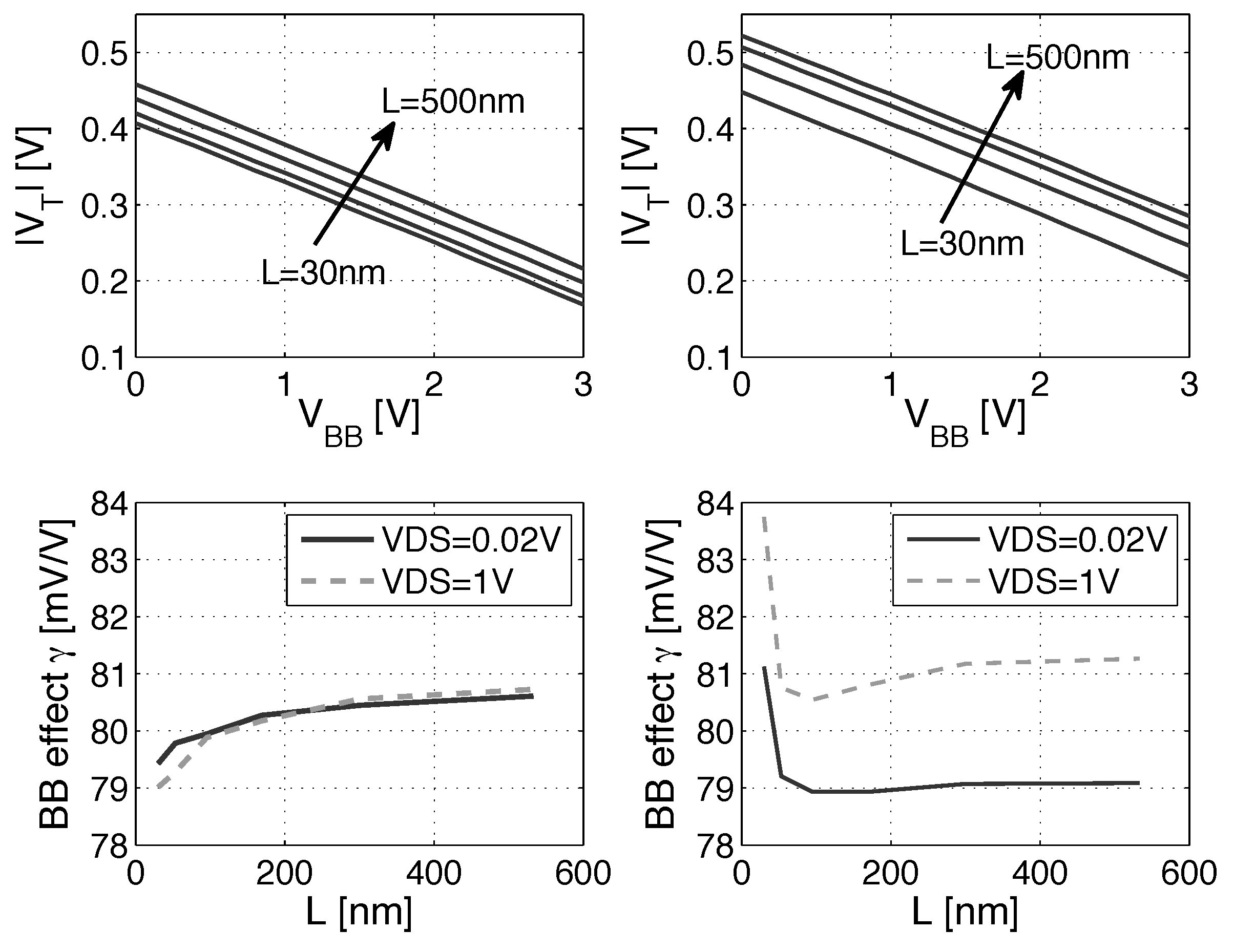
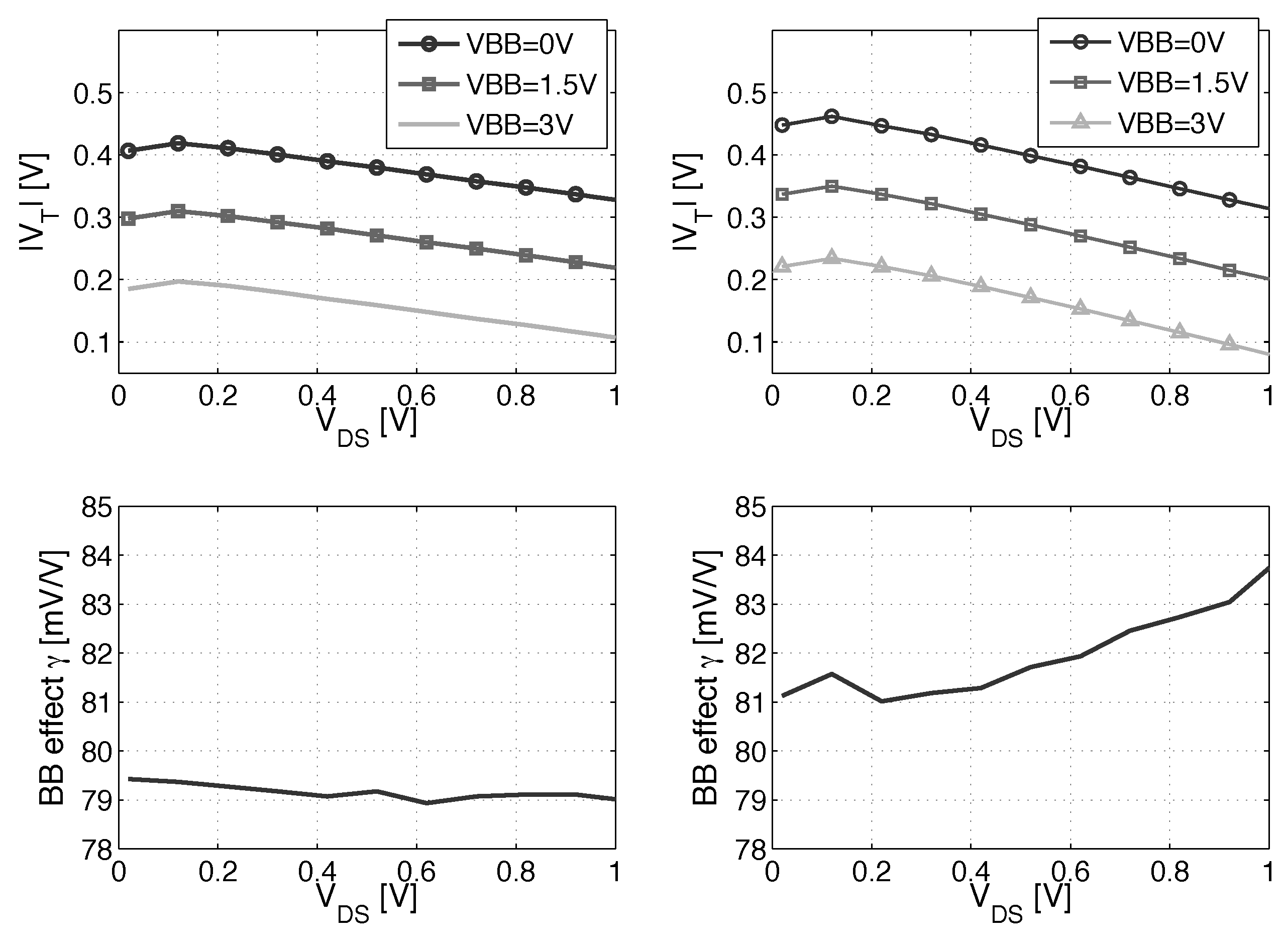
2. Back Biasing at the Device Level
3. Back Biasing Analysis at the Gate Level
3.1. Scaling and Back Biasing Impact on Frequency and Energy Efficiency
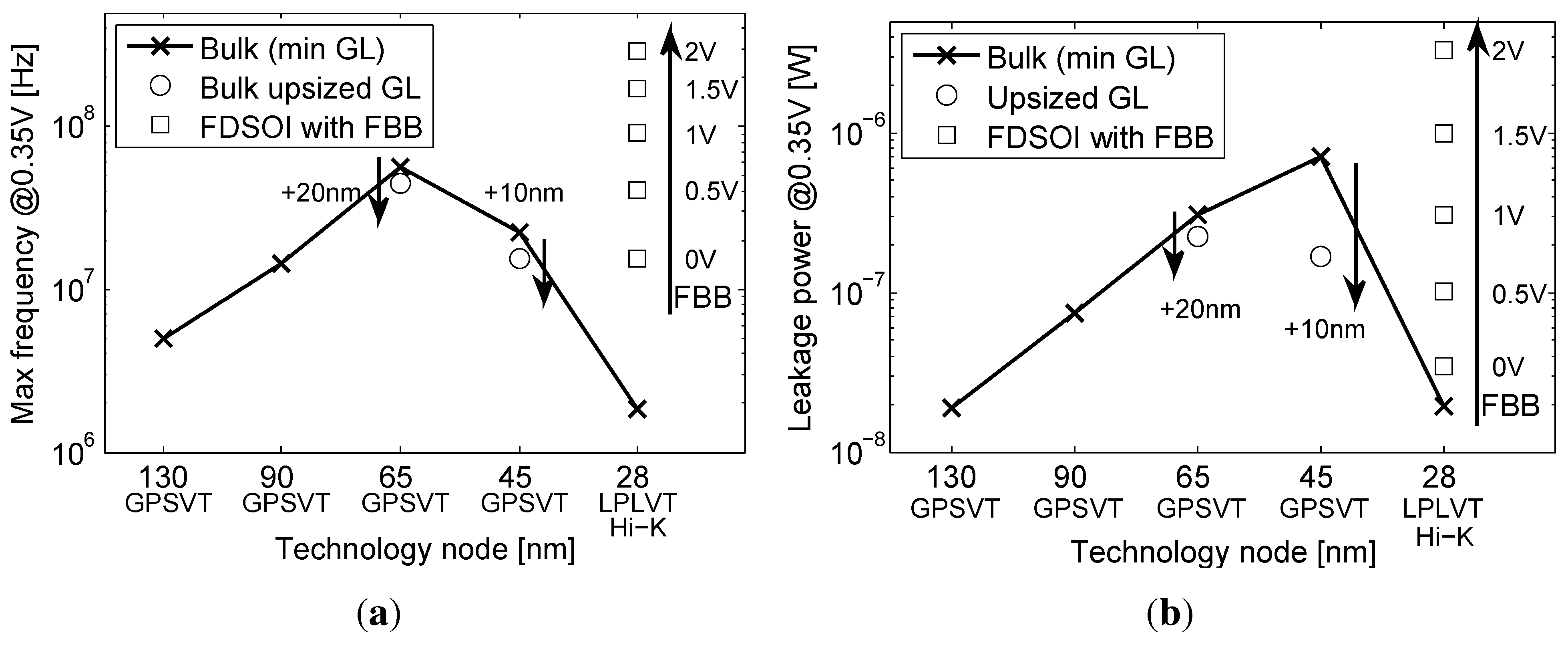
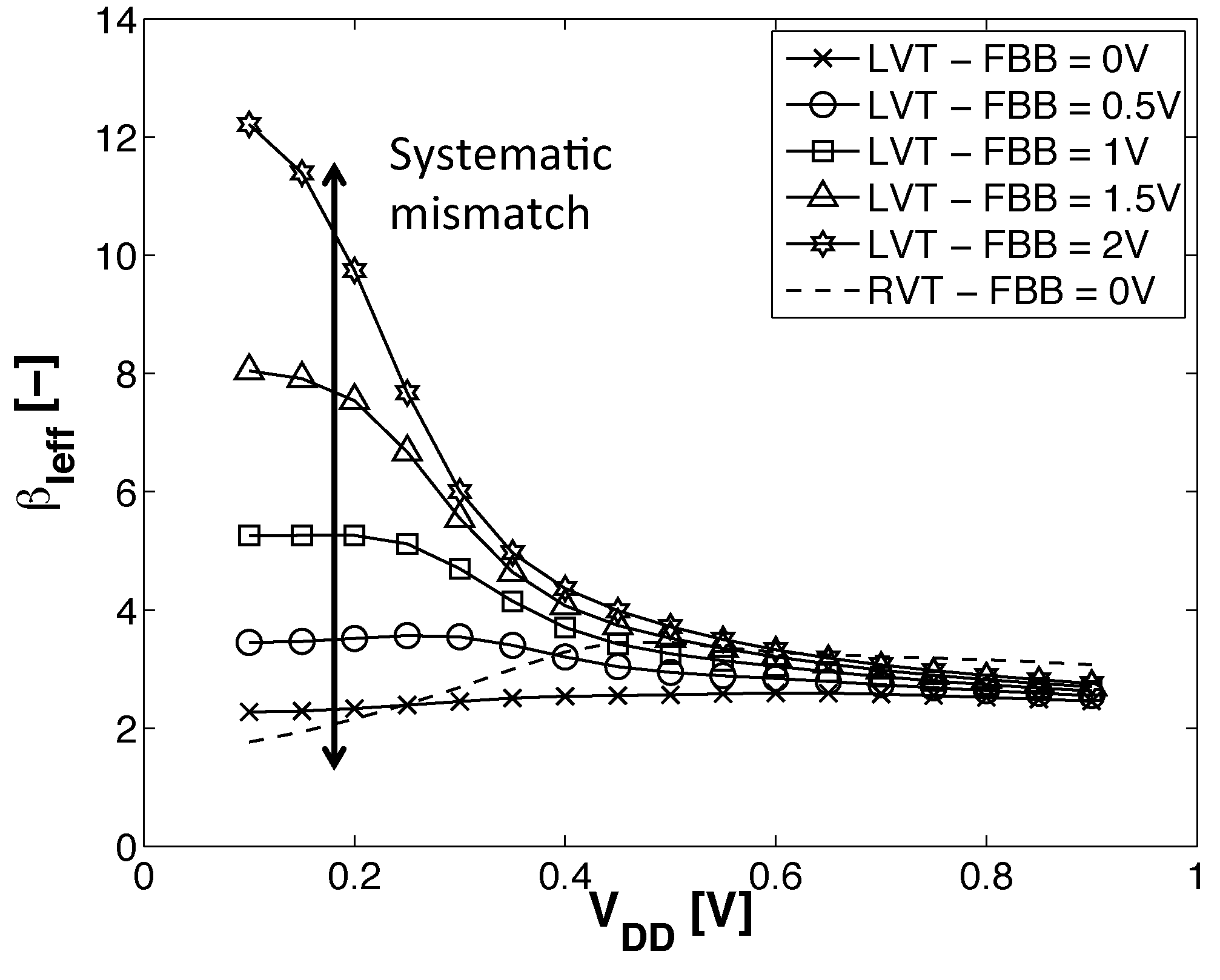
3.2. Delay Equalization and Back Biasing Compensation Schemes
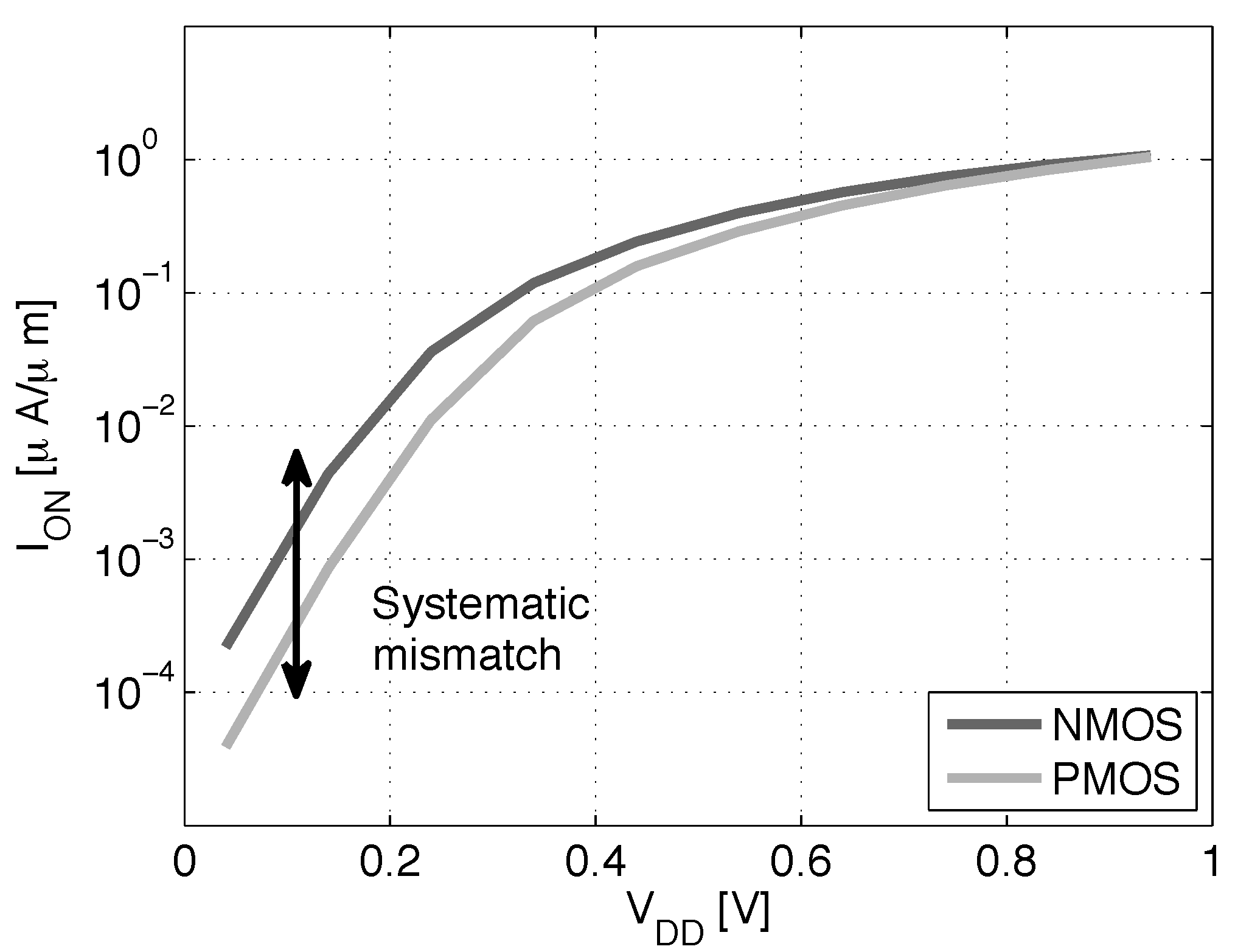
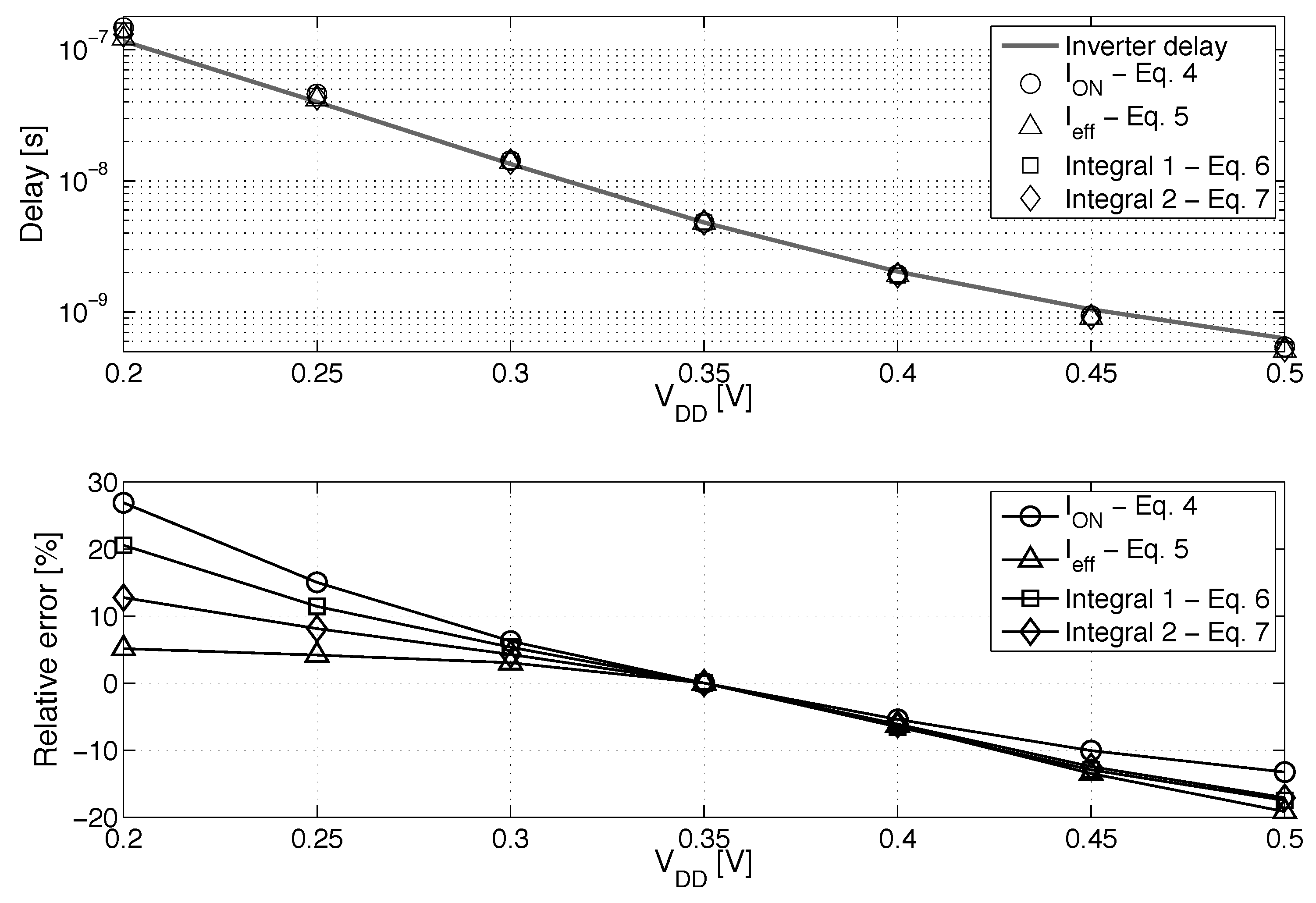
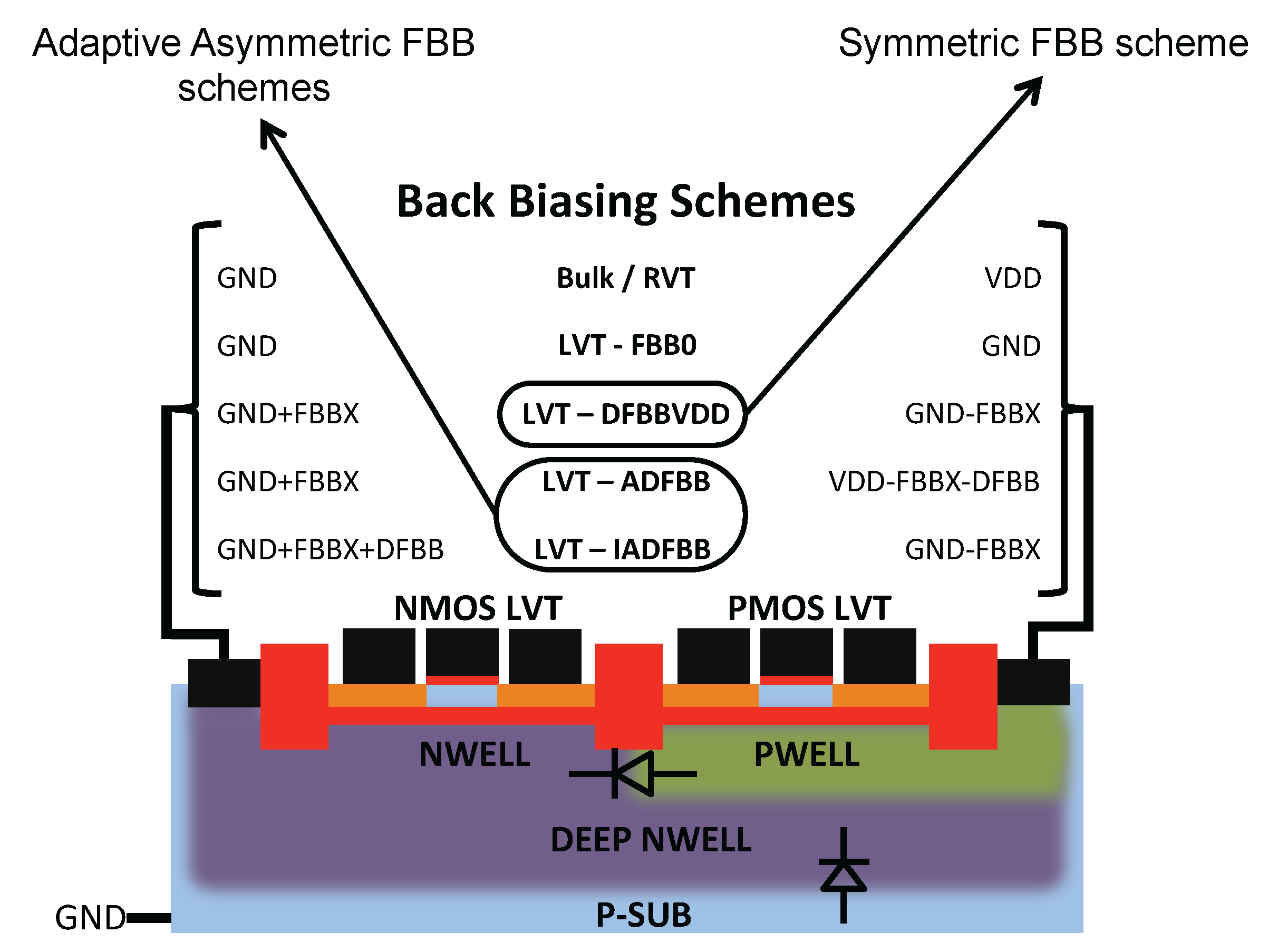
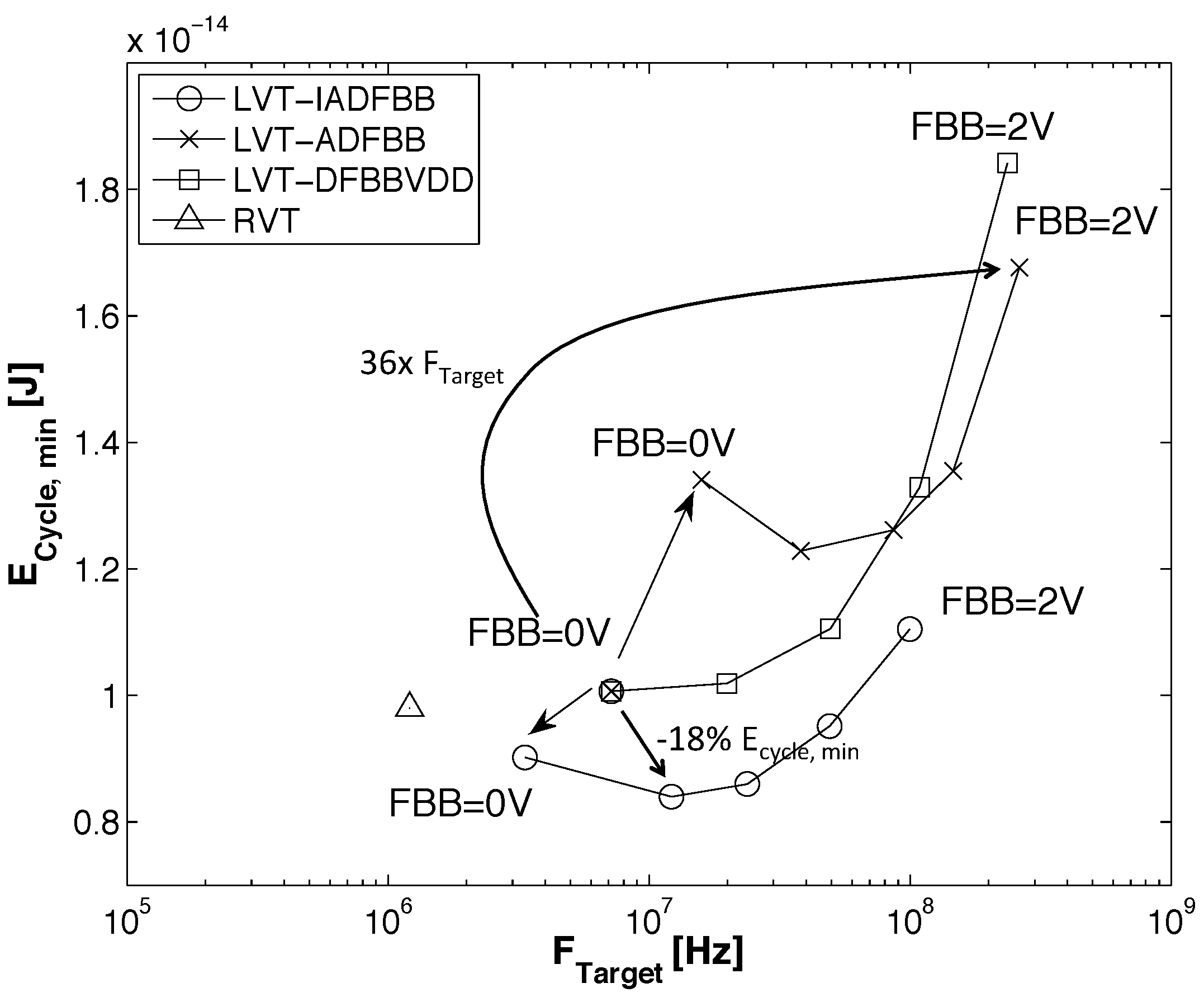
- DFBBVDD: The PMOS back gate is connected to GND instead of , as in bulk technology or for RVT devices. The DFBB is equal to (DFBBVDD). In this technology, the PMOS is weaker than the NMOS, and a straightforward way to roughly compensate for the systematic mismatch is to apply a differential FBB equal to the nominal 0.9 − 1 V on the PMOS. This scheme is a simple extrapolation of this rule, where the supply voltage of a super-threshold standard cell-based design is scaled down and no other modifications are made;
- ADFBB: As shown in Figure 9, the PMOS boost with DFBBVDD compensation is not strong enough at low , and diverges from its value in the super-threshold domain, where standard cells are designed. In this scheme, the optimal adaptive DFBB (ADFBB) at each is applied to the PMOS device to equalize rising and falling delays for an inverter;
- IADFBB: The goal of this scheme is to achieve the same delay equalization as with ADFBB by reducing the NMOS with a negative BB instead of boosting the PMOS .
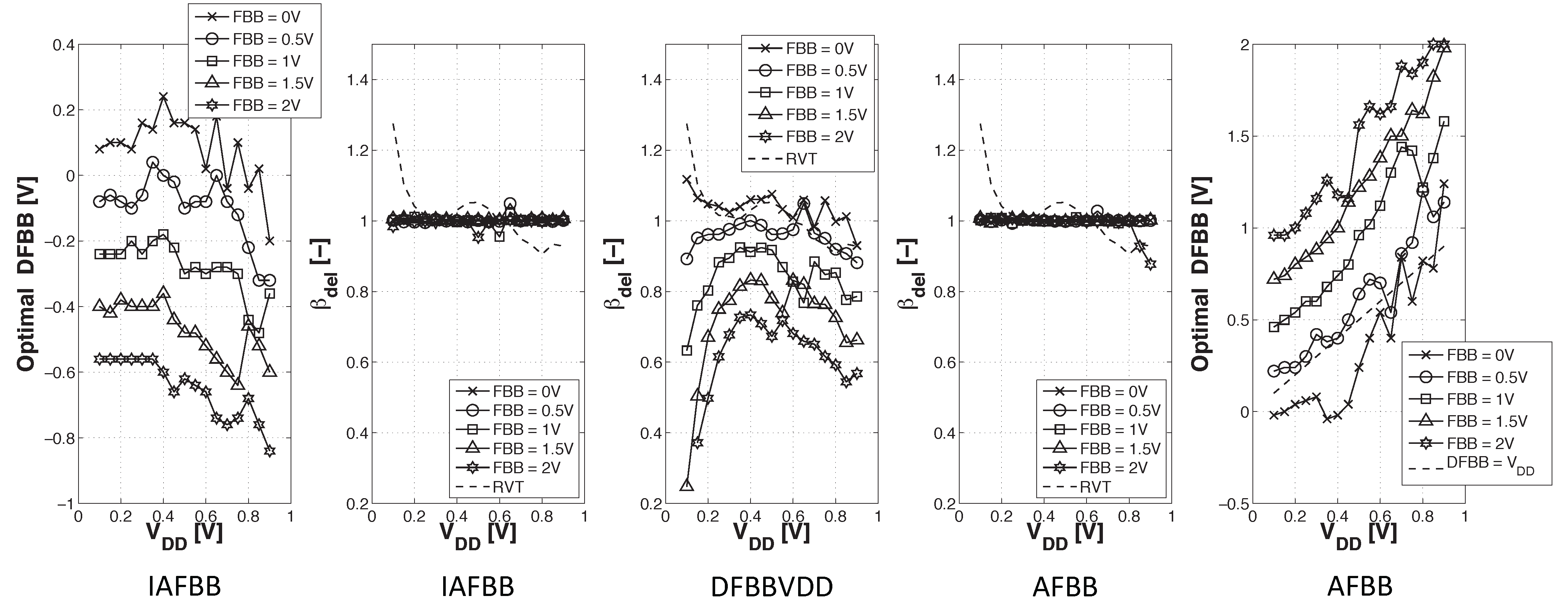
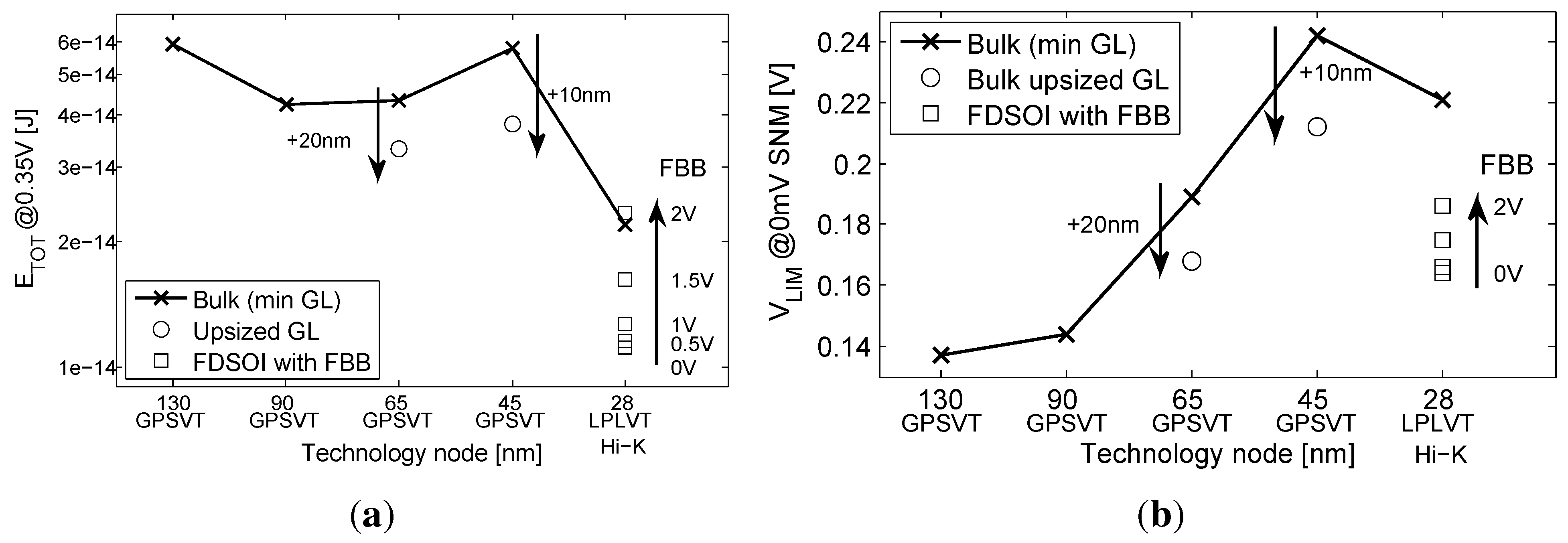
3.3. Impact of Back Biasing Compensation Schemes on the Minimum Energy Point
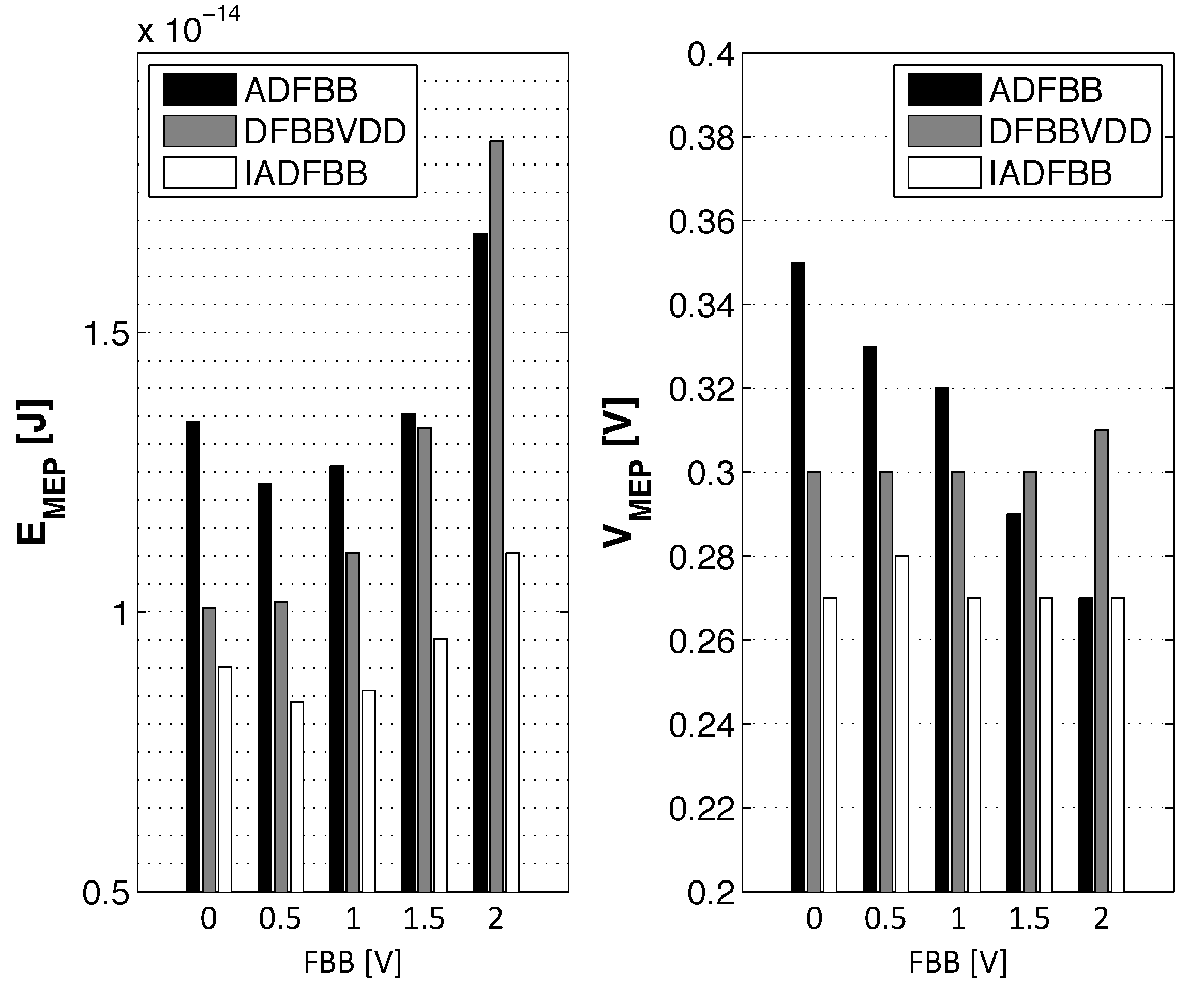
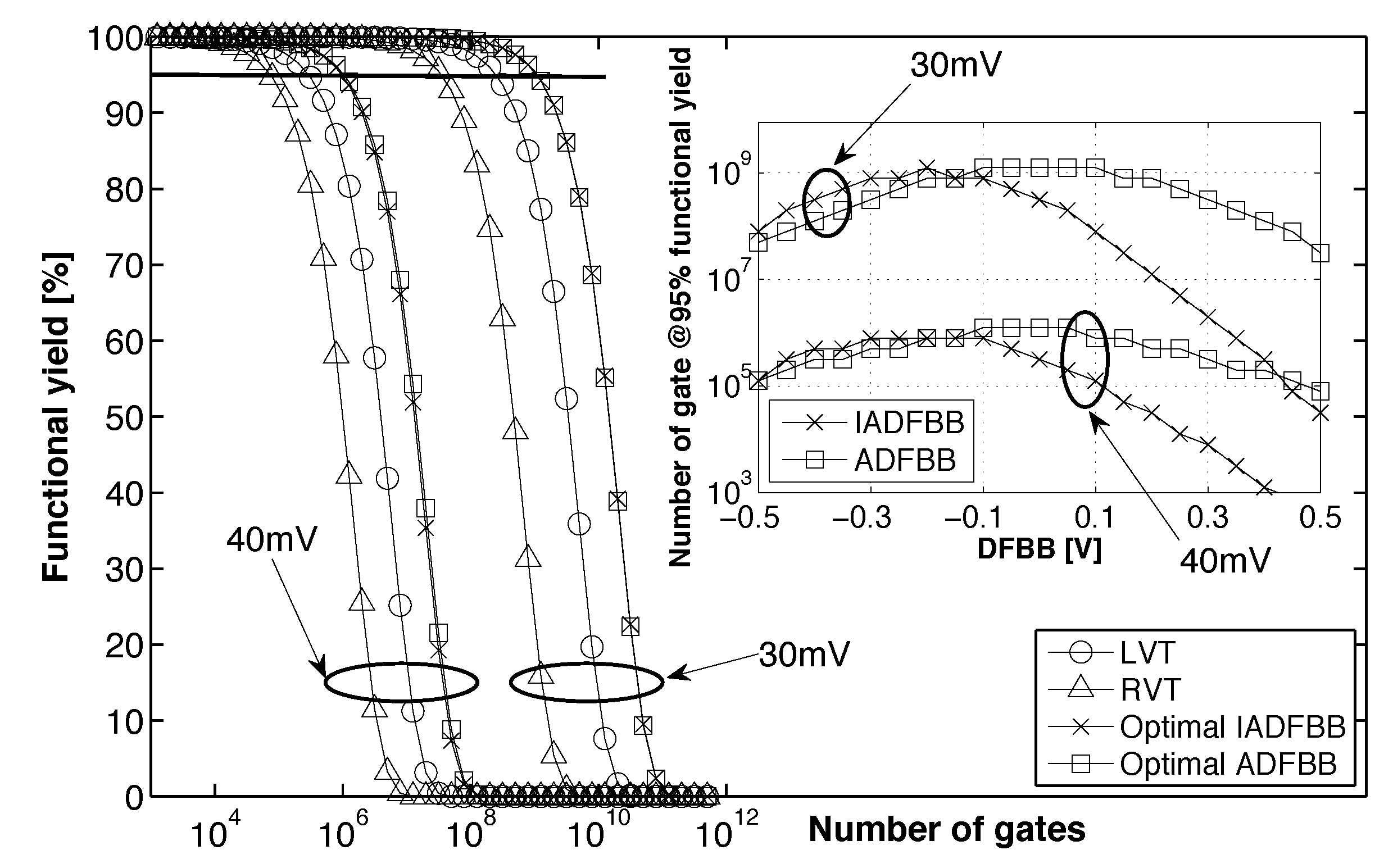
3.4. Impact of Back Biasing Compensation Schemes on Robustness
- :
- As the two ratios depend linearly on and , having will favor one noise margin over the other and lead to a decreased global noise margin. Indeed, the gate noise margin is defined as ;
- S:
- If , the ratio will be reduced, as it can be written as . A subthreshold swing mismatch will then lead to favoring one noise margin over the other;
- η:
- In the subthreshold domain, the DIBL effect increases both NMOS and PMOS currents in the same proportions. If the DIBL effect between the two devices is different, one drive current will be increased, but when the high DIBL device does not drive, the high leakage and low drive device will lead to reduced robustness.
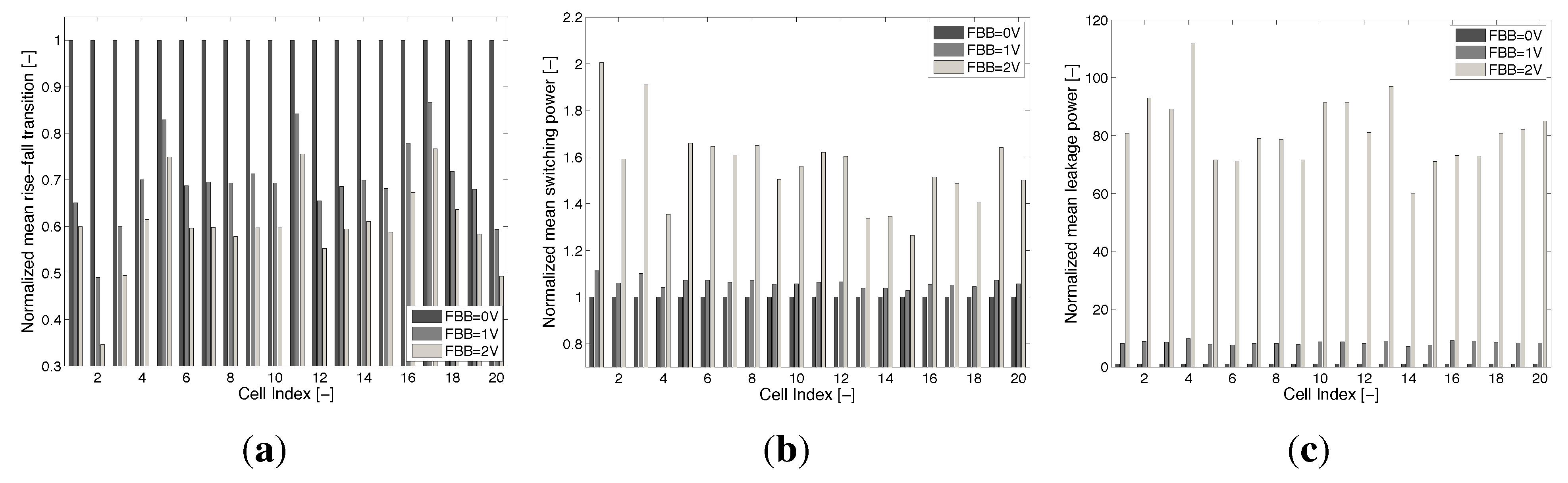
4. Back Biasing Analysis at the Standard Cell Library Level
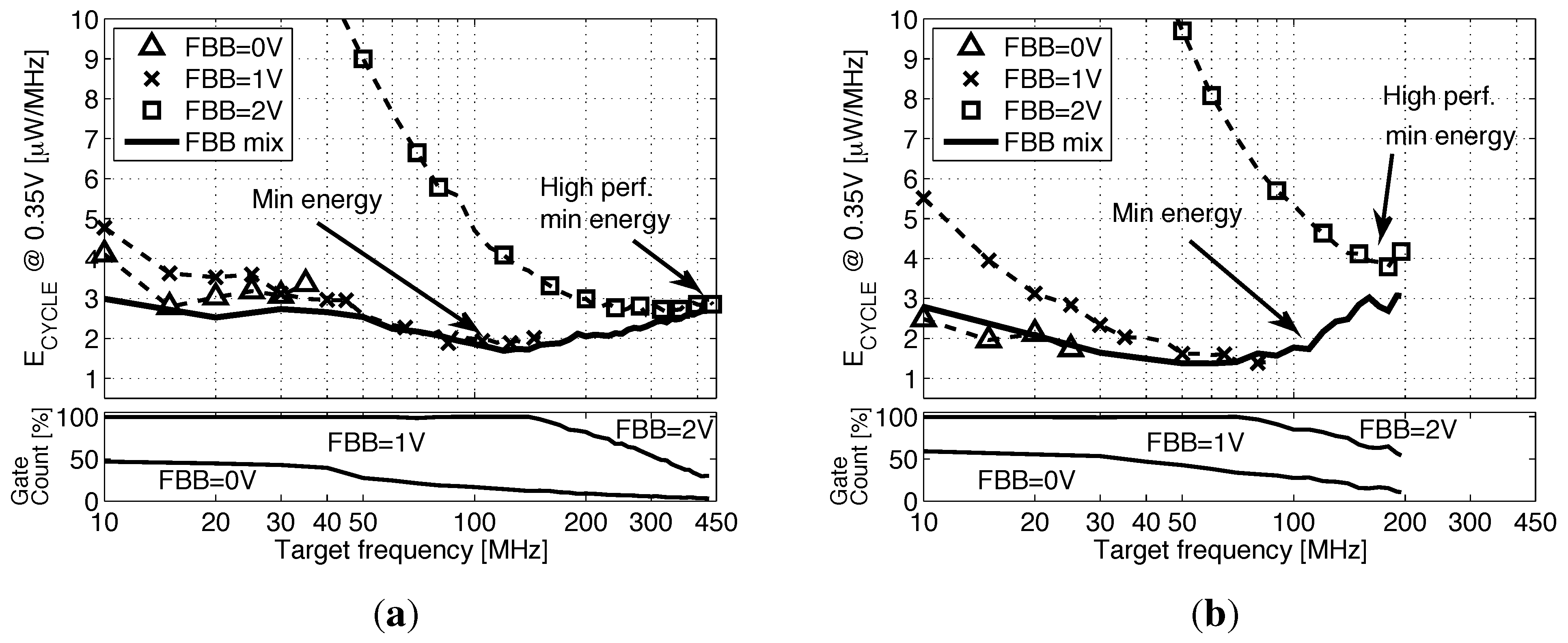
5. Back Biasing Analysis at the IP Level
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bol, D.; de Vos, J.; Botman, F.; de Streel, G.; Bernard, S.; Flandre, D.; Legat, J.-D. Green SoCs for a Sustainable Internet-of-Things. In Proceedings of the IEEE Faible Tension Faible Consommation (FTFC), Paris, France, 20–21 June 2013.
- Wang, A.; Chandrakasan, A.P.; Kosonocky, S.V. Optimal Supply and Threshold Scaling for Subthreshold CMOS Circuits. In Proceedings of the IEEE Computer Society Annual Symposium on VLSI Proceedings, Pittsburgh, PA, USA, 25–26 April 2002; pp. 5–9.
- Calhoun, B.H.; Wang, A.; Chandrakasan, A. Device Sizing for Minimum Energy Operation for Subthreshold Circuits. In Proceedings of the IEEE Custom Integrated Circuits Conference, City, Country, 3–6 October 2004; pp. 90–95.
- Bol, D.; de Vos, J.; Hocquet, C.; Botman, F.; Durvaux, F.; Boyd, S.; Flandre, D.; Legat, J. SleepWalker: A 25-MHz 0.4-V Sub-mm2 7-μW/MHz microcontroller in 65-nm LP/GP CMOS for low-carbon wireless sensor nodes. IEEE J. Solid-State Circuits 2013, 48, 20–32. [Google Scholar] [CrossRef]
- Abouzeid, F.; Clerc, S.; Pelloux-Prayer, B.; Argoud, F.; Roche, P. 28 nm CMOS, Energy Efficient and Variability Tolerant, 350 mV-to-1.0V, 10 MHz/700 MHz, 252 Bits Frame Error-Decoder. In Proceedings of the ESSCIRC, Bordeaux, France, 17–21 September 2012; pp. 153–156.
- Bol, D. Robust and energy-efficient ultra-low-voltage circuit design under timing constraints in 65/45 nm CMOS. J. Low-Power Electron. Appl. 2011, 1, 1–19. [Google Scholar] [CrossRef]
- Kwong, J.; Chandrakasan, A. Variation-Driven Device Sizing for Minimum Energy Sub-Threshold Circuits. In Proceedings of the International Symposium on Low Power Electronics and Design (ISLPED’06), Tegernsee, Germany, 4–6 October 2006; pp. 8–13.
- Alioto, M. Ultra-low power VLSI circuit design demystified and explained: A tutorial. IEEE Trans. Circuits Syst. I 2012, 59, 3–29. [Google Scholar] [CrossRef]
- Bol, D.; Flandre, D.; Legat, J.-D. Technology Flavor Selection and Adaptive Techniques for Timing-Constrained 45 nm Subthreshold Circuits. In Proceedings of the 14th ACM/IEEE International Symposium on Low Power Electronics and Design (ISLPED ’09), San Fancisco, CA, USA, 19–21 August 2009; pp. 21–26.
- Flatresse, P. Product Vision on Planar Fully Depleted Technology FD28 nm for Mobile Applications. In Proceedings of the IEEE International SOI Conference, Napa, CA, USA, 1–4 October 2012.
- Bol, D.; Flandre, D.; Legat, J.-D. Nanometer MOSFET effects on the minimum-energy point of sub-45 nm subthreshold logic—Mitigation at technology and circuit levels. ACM Trans. Des. Autom. Electron. Syst. 2010, 16, 1–26. [Google Scholar] [CrossRef]
- Bol, D.; Ambroise, R.; Flandre, D.; Legat, J.-D. Sub-45 nm Fully-Depleted SOI CMOS Subthreshold Logic for Ultra-Low-Power Applications. In Proceedings of the IEEE International SOI Conference (SOI), New Paltz, NY, USA, 6–9 October 2008.
- Bol, D.; Bernard, S.; Flandre, D. Pre-Silicon 22/20 nm Compact MOSFET Models for Bulk vs. FD SOI Low-Power Circuit Benchmarks. In Proceedings of the IEEE International SOI Conference (SOIC), Tempe, AZ, USA, 3–6 October 2011.
- Pu, Y.; de Gyvez, J.P.; Corporaal, H.; Ha, Y. Vt Balancing and Device Sizing toward High Yield of Sub-Threshold Static Logic Gates. In Proceedings of the 2007 International Symposium on Low Power Electronics and Design (ISLPED), Portland, OR, USA, 27–29 August 2007; pp. 355–358.
- Hwang, M.E.; Roy, K. ABRM: Adaptive β-ratio modulation for process-tolerant ultradynamic voltage scaling. IEEE Trans. VLSI Syst. 2010, 18, 281–290. [Google Scholar] [CrossRef]
- De Streel, G.; Bol, D. Impact of Back Gate Biasing Schemes on Energy and Robustness of ULV Logic in 28 nm UTBB FDSOI Technology. In Proceedings of the IEEE International Symposium on Low Power Electronics and Design (ISLPED), Beijing, China, 4–6 September 2013; pp. 255–260.
- De Streel, G.; Bol, D. Scaling Perspectives of ULV Microcontroller Cores to 28 nm UTBB FDSOI CMOS. In Proceedings of the IEEE SOI-3D-Subthreshold Microelectronics Technology Unified Conference (S3S), Monterey, CA, USA, 7–10 October 2013; pp. 1–2.
- Calhoun, B.H.; Wang, A.; Chandrakasan, A. Modeling and sizing for minimum energy operation in subthreshold circuits. IEEE J. Solid-State Circuits 2005, 40, 1778–1786. [Google Scholar] [CrossRef]
- Bol, D.; Ambroise, R.; Flandre, D.; Legat, J. Interests and limitations of technology scaling for subthreshold logic. IEEE Trans. VLSI Syst. 2009, 17, 1508–1519. [Google Scholar] [CrossRef]
- Na, M.H.; Nowak, E.J.; Haensch, W.; Cai, J. The Effective Drive Current in CMOS Inverters. In Proceedings of the International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 8–11 December 2002; pp. 121–124.
- Ono, G.; Miyazaki, M. Threshold-voltage balance for minimum supply operation. IEEE J. Solid-State Circuits 2003, 38, 830–833. [Google Scholar] [CrossRef]
- Thomas, O.; Noel, J.-P.; Fenouillet-Beranger, C.; Jaud, M.-A.; Dura, J.; Perreau, P.; Boeuf, F.; Andrieu, F.; Delprat, D.; Boedt, F.; et al. 32 nm and beyond Multi-VT Ultra-Thin Body and BOX FDSOI: From Device to Circuit. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Paris, France, 30 May–2 June 2010; pp. 1703–1706.
- Kilchytska, V.; Flandre, D.; Andrieu, F. On the UTBB SOI MOSFET Performance Improvement in Quasi-Double-Gate Regime. In Proceedings of the European Solid-State Device Research Conference (ESSDERC), Bordeaux, France, 17–21 September 2012; pp. 246–249.
- Pu, Y.; de Gyvez, J.P.; Corporaal, H.; Yajun, H. Statistical Noise Margin Estimation for Sub-Threshold Combinational Circuits. In Proceedings of the Asia and South Pacific Design Automation Conference (ASPDAC), Seoul, Korea, 21–24 March 2008; pp. 176–179.
- Girard, O. OpenMSP430 Project, 2010: Opencore.org.
- Weber, O.; Faynot, O.; Andrieu, F.; Buj-Dufournet, C.; Allain, F.; Scheiblin, P.; Foucher, J.; Daval, N.; Lafond, D.; Tosti, L.; et al. High Immunity to Threshold Voltage Variability in Undoped Ultra-Thin FDSOI MOSFETs and Its Physical Understanding. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 15–17 December 2008; pp. 1–4.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
De Streel, G.; Bol, D. Study of Back Biasing Schemes for ULV Logic from the Gate Level to the IP Level. J. Low Power Electron. Appl. 2014, 4, 168-187. https://doi.org/10.3390/jlpea4030168
De Streel G, Bol D. Study of Back Biasing Schemes for ULV Logic from the Gate Level to the IP Level. Journal of Low Power Electronics and Applications. 2014; 4(3):168-187. https://doi.org/10.3390/jlpea4030168
Chicago/Turabian StyleDe Streel, Guerric, and David Bol. 2014. "Study of Back Biasing Schemes for ULV Logic from the Gate Level to the IP Level" Journal of Low Power Electronics and Applications 4, no. 3: 168-187. https://doi.org/10.3390/jlpea4030168
APA StyleDe Streel, G., & Bol, D. (2014). Study of Back Biasing Schemes for ULV Logic from the Gate Level to the IP Level. Journal of Low Power Electronics and Applications, 4(3), 168-187. https://doi.org/10.3390/jlpea4030168




