A Non-Isolated High Gain Step-Up DC/DC Converter Based on Coupled Inductor with Reduced Voltage Stresses

Abstract

Hybrid electric vehicles (HEVs) have gained significant attention for their superior energy efficiency and are becoming a predominant mode of urban transportation. The DC/DC converter plays a critical role in HEV energy management systems, especially in matching the voltage levels between the battery and DC bus. This paper proposes a novel high-gain DC/DC converter with a wide input voltage range based on coupled inductors. The innovation lies in the integration of a resonant cavity and the simultaneous realization of zero-voltage switching (ZVS) and zero-current switching (ZCS), effectively reducing both voltage/current stresses on the power switches and switching losses. Compared with conventional topologies, the proposed design achieves higher voltage gain without extreme duty cycles, improved conversion efficiency, and enhanced reliability. Detailed operating principles are analyzed, and design conditions for voltage stress reduction, gain extension, and soft switching are derived. The simulation model has been conducted in a PSIM environment, and a 300 W experimental prototype, implemented using a dsPIC33FJ64GS606 digital controller, has been established and demonstrates 93% peak efficiency at a 10 times voltage gain. The performance and practical feasibility of the proposed topology have been evaluated by both simulation and experiments.

1. Introduction

The deep damage caused by fossil fuel burning to ecosystems and public health has become a major global challenge that needs to be addressed urgently. To address these negative impacts, a systematic shift to renewable energy systems is not only a key initiative to mitigate climate change, but it has also become a core strategy for the international community to jointly promote [1,2,3]. DC microgrids are often integrated with renewable energy systems such as solar and wind. However, the output voltage level of these power generation systems is low, making it difficult to meet the DC bus voltage requirements of microgrids [4,5,6]. In the field of hybrid electric vehicles (HEVs), due to the low output voltage of new energy sources such as fuel cells, it is often necessary to connect multiple battery cells in series [7,8,9]. This increases system cost and efficiency, so DC-DC converters with high voltage gain and high efficiency have become the focus of current research [10,11,12,13].

Current research on high-gain converters has two main technical routes: isolated and non-isolated [14,15]. For example, isolated DC-DC converters with push-pull, half-bridge, full-bridge, and forward-flyback are used to realize high-voltage gain by adjusting the number of turns of the transformer [16,17,18,19]. However, due to the unavoidable leakage inductance of the transformer, these converters often have high power losses and are prone to high spikes in switching voltage [20]. In order to minimize the impact of voltage spikes on converter stability, additional active clamping techniques and buffer circuits are often used [21]. However, the use of drivers increases the cost and complexity of the circuit.

Even if the conventional Boost converter operates under higher duty cycle conditions, its actual voltage gain still finds it difficult to meet the high gain requirements, and there is a technical problem of low efficiency [22,23]. Ref. [24] designed the Boost converter and Cuk converter together using switched capacitor doubling units with magnetic coupling of the input and output inductors. This approach reduces the current ripple and decreases the size of the converter. Although the article analyzes the peak diode current caused by capacitor imbalance and selects appropriate devices accordingly. However, a capacitor imbalance still occurs during actual operation, affecting the stability and reliability of the circuit. In [25], a novel high-boost converter suitable for fuel cell systems is proposed. The interleaving structure reduces input and output ripples, and the addition of additional capacitors as voltage dividers reduces the voltage stress of active switches and diodes, enabling the use of lower-rated voltage devices to reduce switching and conduction losses. However, the structure of the new converter is complex, including multiple parts such as the interleaving structure and an additional capacitor voltage divider. Ref. [26] proposes a modularly expandable high-gain boost converter, which can flexibly adjust the voltage gain by increasing the number of booster modules, and all its switches can realize Zero Voltage Switching (ZVS) opening in the entire load range. The conversion efficiency of this converter is higher, but the average current of the input inductance is larger. Ref. [27] presents an improved Y-source DC-DC converter. It utilizes resonance to realize the ZVS of the switch, so the circuit structure is simple and requires fewer devices. Magnetic coupling between the coupled inductors can reduce inductor current fluctuation, lower the switch voltage drop, and reduce the conduction loss, thus improving the efficiency of the system. However, the leakage of the transformer causes voltage spikes, increasing losses and electromagnetic interference. Reference [28] addresses this problem. It designs a passive absorption circuit by combining a multi-winding coupled inductor and a voltage-multiplying capacitor unit to recover leakage energy and suppress voltage spikes. Ref. [29] uses a lossless passive clamping circuit to reduce the voltage stress of the main switch. Therefore, the large voltage spikes on the main switch are alleviated and efficiency is improved. However, the circuit design is complicated and the stability performance of the converter needs to be improved. Reference [30] effectively reduces the current ripple by series coupling the input inductor. The high voltage gain is realized by adjusting the turn ratio of the coupled inductor.

In conclusion, high-gain converters generally suffer from high energy loss and limited conversion efficiency. There are various parasitic parameters in the circuit, such as the resistance of the inductor and the on-resistance of the switch. As a result, energy is lost in large amounts during high-gain conversion, reducing the overall efficiency of the converter. It is difficult for the converter to maintain high conversion efficiency at high power outputs or with a wide range of input voltage variations. Its conversion efficiency may decrease significantly with changes in load or input conditions.

In this paper, an integrated high-gain DC/DC converter topology based on coupled inductors with a voltage multiplier unit is proposed to match the battery voltage and DC bus voltage in the energy conversion system of a hybrid vehicle. The capacitors at both ends of the coupled inductor can be used as energy-exchange capacitors to improve the circuit voltage gain. It also absorbs peak voltages caused by leakage inductance to reduce the voltage stress on the switches. The voltage multiplier unit allows for higher output voltages to be achieved without adding additional components. The voltage multiplier inductor is involved in constructing the resonant cavity to realize the soft switching characteristics of the power tube, resulting in lower switching losses. The main contributions of this paper can be summarized as follows:

(1) This paper presents a high-gain DC/DC converter based on a coupled inductor with a wide input voltage range. As the required power interface, it implements ZVS and Zero Current Switching (ZCS) to reduce the voltage/current stress on the power switch. It also matches the voltage level between the battery and the DC bus.

(2) Capacitors at the ends of coupled inductors can be used as energy exchange capacitors to increase the voltage gain of the circuit. Peak voltages caused by leakage inductance can also be absorbed, thereby reducing the voltage stress on the switching tube.

(3) The voltage multiplier unit allows for higher output voltages to be realized without adding additional components. The voltage-multiplying inductor is involved in the construction of the resonator, which realizes the soft-switching characteristics of the power tubes and reduces the switching losses.

(4) According to the experimental results, the high efficiency of 90% can be achieved at a voltage gain of 10 times.

The rest of this manuscript is arranged as follows: Section 2 introduces in detail the system topology and operation principle. The voltage and current performance of the system is analyzed in Section 3. In Section 4, the realization condition of the soft switch. Section 5 shows the closed-loop simulation and experimental verification results. Finally, a brief conclusion is given in Section 6.

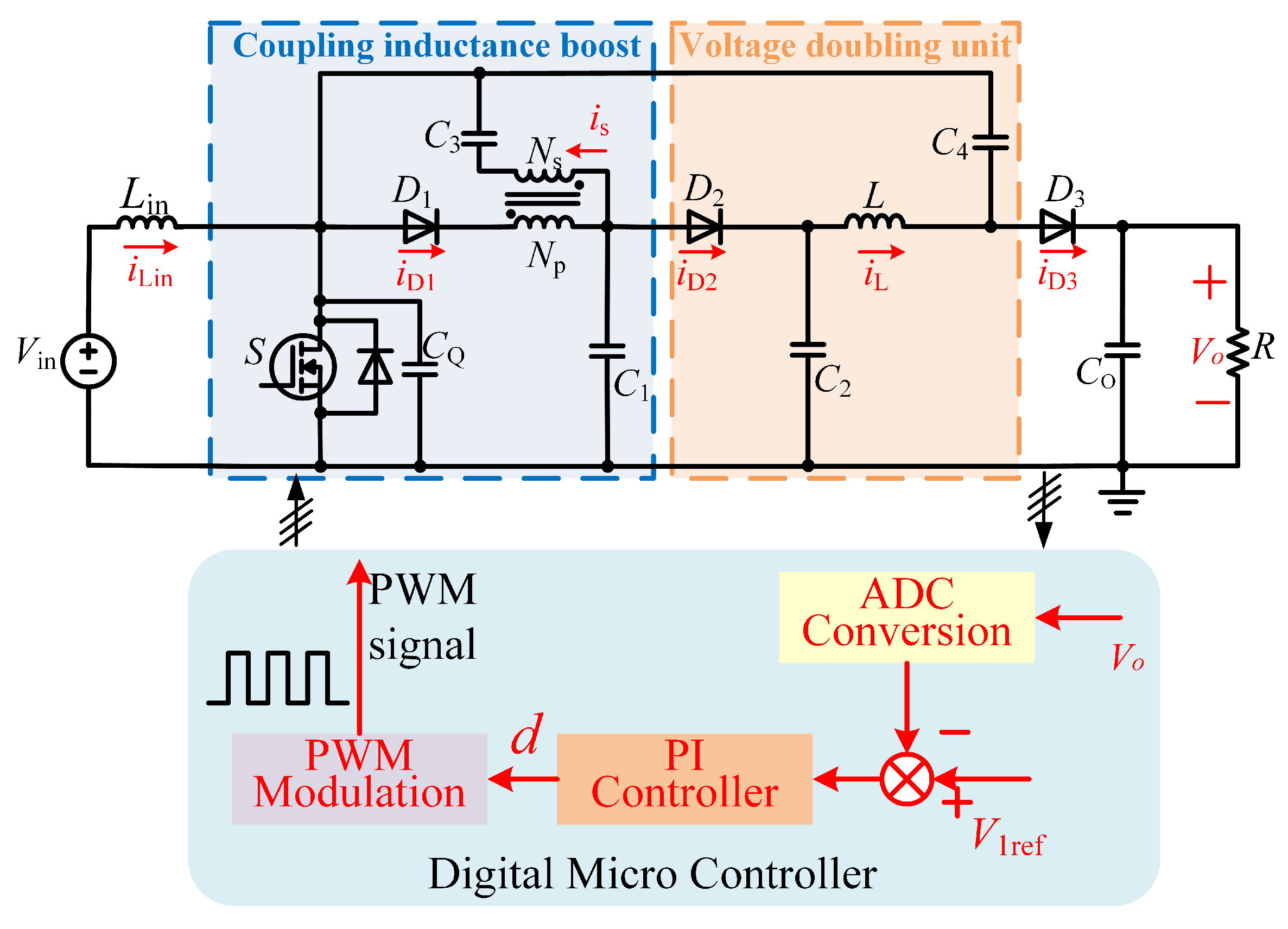
2. Coupled Inductance-Based High-Gain DC/DC Conversion System Configuration

2.1. System Configuration

In this paper, a coupled-inductor-based high-gain DC-DC converter topology is proposed, which focuses on the establishment of a two-stage energy modulation architecture. The high voltage gain is realized through the series connection structure of the coupled inductor and the voltage doubling unit. Among them, the latter voltage-doubling unit is composed of an interleaved LC resonant network. Specifically, the coupled inductor is used first to improve the voltage gain through the magnetic coupling effect. Then the voltage gain is further improved by the voltage doubling unit in series in the back stage. The main switch performs zero-voltage turn-on by connecting the resonant capacitors in parallel at both ends to reduce converter losses. The topology realizes efficient energy transfer through the dynamic coupling of the magnetic energy-electric field. This structure provides a low-ramp and high-efficiency power supply to the load.

The circuit topology of the proposed is shown in Figure 1. The converter consists of two parts: the coupling inductance boost structure and the later stage voltage doubling unit, including the input inductance $L_{in}$, the switch (Q), three diodes ($D_1$, $D_2$, $D_3$), and five capacitors ($C_1$, $C_2$, $C_3$, $C_4$, $C_o$), a rear inductor (L), and a double-winding coupled inductor (the winding turns are $N_p$, $N_s$, respectively). $V_{in}$ and $V_o$ are input and output voltages, respectively. Diode $D_1$ and the Q switching transistor enable the input inductor to operate in continuous current mode. Capacitor $C_4$ and the inductor exchange energy to enhance the output voltage, while also absorbing the leakage energy of the coupled inductor to suppress voltage spikes. The rear inductor L, winding $N_s$, and capacitors $C_Q$, $C_1$, $C_2$, $C_3$, $C_4$ form a resonant cavity. $C_Q$ includes a parasitic switch capacitor and an external capacitor.

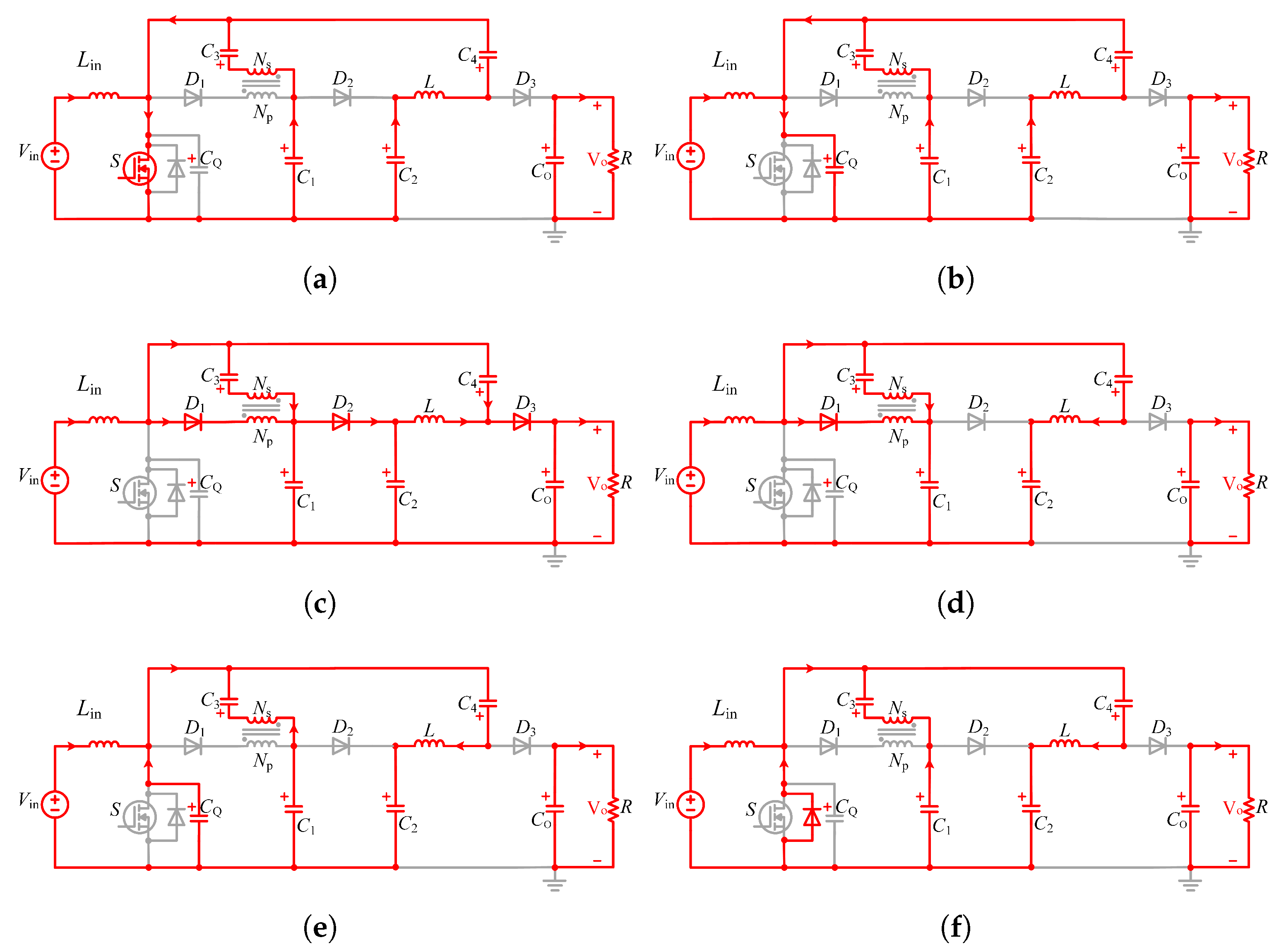
2.2. Operation Principle of the Proposed Converter

The proposed single-switch converter topology employs a single active power device. Its operation mechanism is controlled by the interaction of the gate drive signal with the polarity of the current in the coupled inductor. In steady-state operation, the switching cycle consists of six distinct phases (Figure 2). Each operating phase has a corresponding equivalent circuit configuration (Figure 3).

State 1 [t₀–t₁]: The switch achieves ZVS in this state, and the diodes $D_1$, $D_2$, $D_3$ are reverse cutoff. The equivalent power conversion circuit is shown in Figure 3a. The input voltage $V_{in}$ charges the input inductor $L_{in}$, which serves as the input energy storage. The coupled inductor front stage winding $N_p$ transfers energy to the rear stage winding $N_s$. The voltage-doubling unit inductor L and capacitors $C_3$ and $C_4$ form a loop. The input inductor voltage is equal to the input voltage, and the input inductor current $i_{Lin}$ rises linearly with the rate of change.

$$i_{L_{in}}\left(t\right)=i_{L_{in}}\left(t_0\right)+{\displaystyle \frac{1}{L_{in}}}{\int }_{t_0}^{t_1}{V}_{in}dt$$

(1)

The inductor L of the voltage doubling unit is boosted in series with the capacitors $C_3$ and $C_4$. The current and voltage expressions for the rear inductor L are as follows:

$$i_L\left(t\right)=i_L\left(t_0\right)+{\displaystyle \frac{1}{L}}{\int }_{t_0}^{t_1}\left(V_{in}-v_{C_2}\left(t\right)+v_{C_4}\left(t\right)\right)dt$$

(2)

$$V_L\left(t\right)=V_{in}-v_{C_2}\left(t\right)+v_{C_4}\left(t\right)$$

(3)

$C_1$ and $C_2$ are charged by the input inductor current. $C_3$ and $C_4$ are charged by the inductor current of the doubling unit. $C_o$ does not participate in the charging and discharging of the preceding circuit and releases energy by supplying power to the load.

State 2 [$t_1$–$t_2$]: In this state, the switching diode renews the current and the capacitor network is charged. The equivalent power conversion circuit is shown in Figure 3b. At this point, the main switch Q is cut off, and the diode remains cut off due to reverse bias. At this time, the input voltage is charged to the resonant capacitor $C_Q$ through the input inductor $L_{in}$. The input inductor current decreases linearly:

$$i_{L_{in}}\left(t\right)=i_L\left(t_1\right)+{\displaystyle \frac{1}{L}}{\int }_{t_1}^{t_2}(v_{C_2}\left(t\right)+v_{C_1}\left(t\right)-V_o)dt$$

(4)

The voltage of the input inductor is the following:

$$V_{L_{in}}=V_{in}-V_{C_Q}$$

(5)

The input inductor $L_{in}$ transfers energy to the back stage inductor L and the capacitor network. The current and voltage of the rear inductor L are as follows:

$$i_L\left(t\right)=i_L\left(t_1\right)+{\displaystyle \frac{1}{L}}{\int }_{t_1}^{t_2}(v_{C_2}\left(t\right)+v_{C_4}\left(t\right)-V_o)dt$$

(6)

$$V_L=V_{in}-v_{C_1}\left(t\right)-v_{C_2}\left(t\right)$$

(7)

State 3 [$t_2$–$t_3$]: This state is the phase of inductor energy release and fast charging of the capacitor network. The equivalent power circuit is shown in Figure 3c. The main switch Q stays off and the charging of the resonant capacitor $C_Q$ is complete. Diodes $D_1$, $D_2$, $D_3$ naturally conduct due to forward bias. At this time, the input inductor current expression is as follows:

$$i_{L_{in}}\left(t\right)=i_L\left(t_2\right)+{\displaystyle \frac{1}{L}}{\int }_{t_2}^{t_3}(v_{C_2}\left(t\right)+v_{C_4}\left(t\right)-V_o)dt$$

(8)

The voltage of the input inductor is the following:

$$V_{L_{in}}=V_{in}-v_{C_1}\left(t\right)-v_{C_2}\left(t\right)$$

(9)

In this state, the current $i_{LP}$ of the front-stage coupled inductor increases linearly and the back-stage coupled inductor current $i_{Ls}$ decays linearly. The input inductor $L_{in}$. and the coupled inductors together perform energy injection to the capacitor networks $C_1$, $C_2$, and $C_o$. The formula for the back-stage inductor current is the same as that of state 2, which still maintains a linear decrease. The voltage of the rear inductor can be expressed as follows.

$$V_L\left(t\right)=V_o-v_{C_3}\left(t\right)-v_{C_4}\left(t\right)$$

(10)

State 4 [t₃–t₄]: This state is the stage of energy redistribution of the capacitor network in the voltage-doubling unit. The equivalent power conversion circuit is shown in Figure 3d. The main switch Q continues to be off. Diode D₁ is on, D₂ and D₃ are off. The energy of the system is redistributed through magnetic coupling with the capacitor network. C₃ and C₄ discharge to C₂ through the rear inductor. The input inductor charges C₁. At this point, the input inductor current can be expressed as follows.

$$i_{L_{in}}\left(t\right)=i_{L_{in}}\left(t_3\right)+{\displaystyle \frac{1}{L_{in}}}{\int }_{t_3}^{t_4}(V_{in}-v_{C_1}\left(t\right))dt$$

(11)

The voltage of the input inductor is the following:

$$V_{L_{in}}=V_{in}-v_{C_1}\left(t\right)$$

(12)

The voltage expression for the rear inductor is the same as for state 3. The current grows linearly in the reverse direction, and its rate of change is with leakage inductance neglected:

$$i_L\left(t\right)=i_L\left(t_3\right)+{\displaystyle \frac{1}{L}}{\int }_{t_3}^{t_4}(V_o-v_{C_3}\left(t\right)-v_{C_4}\left(t\right))dt$$

(13)

State 5 [t₄–t₅]: This state is the reset phase of the cycle and the balance of energy. The equivalent power conversion circuit is shown in Figure 3e. The main switch Q is continuously turned off and all diodes are turned off due to reverse bias. The input inductor current expression is as follows:

$$i_{L_{in}}\left(t\right)=i_{L_{in}}\left(t_4\right)+{\displaystyle \frac{1}{L_{in}}}{\int }_{t_4}^{t_5}(V_{in}-v_{C_Q}\left(t\right))dt$$

(14)

The voltage of the input inductor is as follows:

$$V_{L_{in}}=V_{in}-v_{C_Q}\left(t\right)$$

(15)

The final transfer of energy from the converter in this state is accomplished through the load. The inductor current and voltage expressions of the voltage doubling unit are as follows:

$$i_L\left(t\right)=i_L\left(t_5\right)-{\displaystyle \frac{1}{L}}{\int }_{t_5}^{t_6}{V}_{o}dt$$

(16)

$$V_L=V_{C_4}-V_{C_2}+V_{C_Q}$$

(17)

At the completion of this state, a cycle has been completed without considering the ZVS of the main switch in the next cycle.

State 6 [t₅–t₆]: This state prepares for the ZVS of the main switch in the next cycle. The equivalent power conversion circuit is shown in Figure 3f. The main switch Q remains off and all diodes are cut off in reverse. The resonant capacitor $C_Q$ energy is fully discharged in state 5. The drain source voltage of switch Q is reduced to near zero due to resonance. The current in the rear inductor decays to the soft-switching boundary condition.

The operating cycle of this converter is characterized by a multistage energy cycle. The base gain boost is realized by a coupled inductor and a capacitor storage. Then, the voltage-doubling unit is utilized for energy redistribution and soft switching transition. Finally, the ZVS preparation is realized by resonance and diode renewal.

3. System Performance Analysis

The winding turn ratio is specified as n = $N_s$/$N_p$ (where in this proposal n = 1), and the influence of leakage induction on the circuit is ignored. The coupling inductance voltage has the following relationship:

$$\left\{\begin{array}{c}{\displaystyle \frac{V_{N_p}}{N_p}=\frac{V_{N_s}}{N_s}}\\ V_{N_p}+V_{N_s}=V_{C_p}\end{array}\right.$$

(18)

$V_{CP}$ is the total voltage of the induced coupled voltage in the circuit, represented as the sum of the voltages of the primary and secondary windings. $V_{NP}$ is the voltage of the primary winding and $V_{NS}$ is the voltage of the secondary winding.

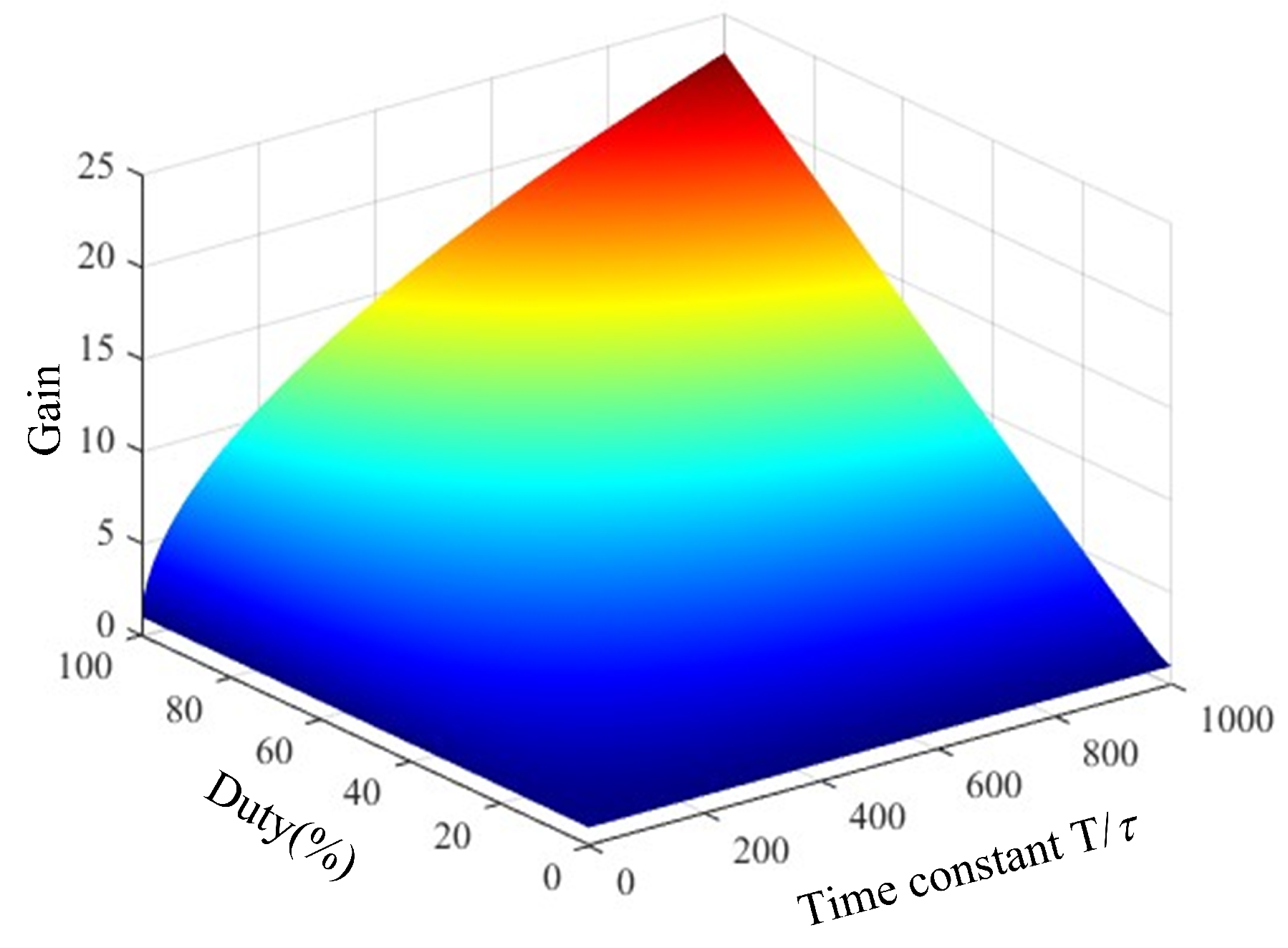
3.1. Output Voltage Gain of the System

The voltage gain characteristic of this DC-DC converter exhibits a two-mode segmentation characteristic with the level of duty cycle D. In the low duty cycle mode, the voltage doubling unit inductor enters a quasi-steady state at the end of state 5. Neglecting the transient process of state 6, its stored energy is temporarily stored until the next cycle. At this time, the inductor current will remain unchanged and the voltage across the input inductor $L_{in}$ is zero. The volt-second balance equation for $L_{in}$ in this mode can thus be listed as follows:

$$V_{in}D{T}_s+{\displaystyle \frac{n}{3n+1}}(V_{in}-V_o)(t_3+t_4)=0$$

(19)

The voltage gain expression of this mode can be solved as follows:

$$G=1+{\displaystyle \frac{D{T}_s}{\frac{n}{3n+1}(t_3+t_4)}}=1+{\displaystyle \frac{T_s{D}^2{V}_{in}R}{2\tau V_o}}$$

(20)

The expression for voltage gain in this mode is obtained by simplifying Formula (20):

$$G={\displaystyle \frac{1+\sqrt{1+2D^2\frac{T}{\tau }}}{2}}$$

(21)

$\tau$ in the above equation is the time constant. The relationship between the gain of voltage and duty cycle and time constant is shown in Figure 4. It can be seen that the voltage gain is a combination of duty cycle and time constant. The time constant $\tau$ depends on $L_{eq}$ and $C_{eq}$, which are the equivalent inductance and capacitance of the resonant network. The equivalent inductance can be changed by changing the coupled inductor turn ratio n or the core air gap $\delta$ to change the time constant to select the optimum time constant to improve the gain of the converter:

$$L_{eq}={\displaystyle \frac{N_p^2{\mu }_0{A}_e}{l_e+\delta (1+n^2)}}$$

(22)

where ${\mu }_0$ represents the vacuum conductivity, $A_e$ is the cross-sectional area of the core, and $l_e$ is the magnetic circuit length.

The transient process of the state and the energy feedback effect are further considered in the low-duty cycle mode. The volt-second balance equations are again written for both ends of the input inductor $L_{in}$:

$$\begin{array}{cc}\hfill {\int }_0^T{V}_{in}dt& =V_{in}D{T}_s+{\displaystyle \frac{n}{3n+1}}(V_{in}-V_o)(t_3+t_4)\hfill \\ \hfill & +{\int }_0^{t_s}{\displaystyle \frac{n}{3n+1}}(V_{in}-V_o)cos\omega tdt=0\hfill \end{array}$$

(23)

In the high duty cycle mode, when the switch-off time in one cycle is less than the time duration of states 3 and 4, the capacitive network energy redistribution process continues to affect the inductor current. Time-varying energy exchange must be considered when calculating the gain. The volt-second balance equation is written for the input inductor $L_{in}$ to obtain the following:

$$V_{in}D{T}_s+{\displaystyle \frac{n}{3n+1}}(V_{in}-V_o)(1-D{T}_s)=0$$

(24)

The gain expression in high duty cycle mode can be solved from Equation (24):

$$G=1+\left({\displaystyle \frac{1}{n}}+3\right){\displaystyle \frac{D}{1-D}}$$

(25)

The converter proposed in this paper realizes a non-linear jump in gain characteristics by magnetic coupling and a series voltage doubling unit. The voltage gain is switched from the quasi-linear region to the exponential growth mode when the duty cycle $D>0.4$. The disadvantage of low gain at low duty cycle of the conventional high-gain converter is compensated.

3.2. Analysis of Voltage Stress on Capacitors and Inductors

Voltage stress is a key indicator for evaluating the reliability and system economy of power electronic devices. Accurate analysis and optimal design of voltage stress are significant for single-switch high-gain DC-DC converters. In this paper, the voltage stress of the main devices is limited by the leakage inductance energy circulation of the coupled inductor and the voltage clamping effect of the capacitor network. This makes the proposed converter have less voltage stress when realizing a higher voltage gain.

According to the principle of volt-second equilibrium of the input inductor $L_{in}$, it can be seen that the average value of the inductor voltage is zero during the entire switching cycle. The relationship between the input inductor voltage and the capacitor voltage contained in the energy transfer network can be obtained:

$$\left\{\begin{array}{c}{V}_{in}=-V_{C_4}+V_{C_2}\hfill \\ V_{in}=-V_{C_3}+V_{C_1}\hfill \end{array}\right.$$

(26)

When analyzing the voltage stress, it is assumed that the circuit is in a steady state and the capacitor voltage remains constant. The expression for the capacitive voltage stress in the converter can be solved by combining Equations (6), (10) and (17):

$$\left\{\begin{array}{c}{V}_{C_1}={\displaystyle \frac{(n+1)V_o+2n{V}_{in}}{3n+1}}\hfill \\ V_{C_2}={\displaystyle \frac{(2n+1)V_o+n{V}_{in}}{3n+1}}\hfill \\ V_{C_3}={\displaystyle \frac{n+1}{3n+1}}(V_o-V_{in})\hfill \\ V_{C_4}={\displaystyle \frac{2n+1}{3n+1}}(V_o-V_{in})\hfill \end{array}\right.$$

(27)

The voltage stress on capacitors $C_3$ and $C_4$ of the capacitor network in the voltage-doubling unit is only half of the input/output voltage difference. The symmetrical structure of the voltage-doubling unit significantly reduces the voltage stress of the capacitors. Through the capacitor network and magnetic coupling, the capacitor voltage is effectively controlled. The problem of linear growth of the capacitor voltage with gain is avoided in the single-switch boost topology.

3.3. Analysis of Voltage Stress on Power Switches

When the circuit is in steady state, the voltage stress of the switch is the same in each cycle. For state 3, diode $D_3$ is switched on, and the expression of the power switch voltage can be obtained from the Kirchoff voltage law as follows:

$$V_s=-V_{C_4}+V_o={\displaystyle \frac{(2n+1)V_{in}+n{V}_o}{3n+1}}$$

(28)

The diode voltage stress can be expressed as follows:

$$\left\{\begin{array}{c}{V}_{D_1}=V_{Np}+V_{C_1}\hfill \\ V_{D_2}=V_{C_2}-V_{C_3}\hfill \\ V_{D_3}=V_o-V_{C_4}\hfill \end{array}\right.$$

(29)

The voltage stress of the switch Q is not linearly related to the gain G and the duty cycle D. However, voltage stress can be significantly reduced by optimizing the turn ratio n of the coupled inductor. Meanwhile, the capacitor $C_Q$ absorbs the leakage inductance energy under soft-switching conditions, which can further suppress the voltage spike and the switching voltage stress.

3.4. Performance Comparison of Different Converters

Table 1. Performance parameters of different converters.

Converter	Number of Switches	Number of Diodes	Switching Voltage Stress	Voltage Gain
Ref. [16]	1	4	${\displaystyle \frac{V_o(1+D)}{D(3+D)}}$	${\displaystyle \frac{D(3+D)}{1-D}}$
Ref. [18]	2	8	${\displaystyle \frac{(n+1)V_{in}+V_o}{n+2}}$	${\displaystyle \frac{1+(n+1)D}{1-D}}$
Ref. [20]	2	4	${\displaystyle \frac{V_{in}}{1-D}}$	${\displaystyle \frac{n+2}{1-D}}$
Ref. [21]	1	3	${\displaystyle \frac{V_o}{n+2}}$	${\displaystyle \frac{n+2}{1-D}}$
Proposed converter	1	3	${\displaystyle \frac{(2n+1)V_{in}+n{V}_o}{3n+1}}$	${\displaystyle \frac{1+\sqrt{1+2D^2\frac{T}{\tau }}}{2}}$

shows the comparison of various parameters of different converters. By comparing the performance of different converters, the following table can be obtained. n represents the number of expansion modules from Ref. [18] and the rest is the turn ratio of the coupled inductors.

Figure 5 shows the comparison curves of the voltage gains of different converters. The voltage gain is obtained for turns ratio n = 2 and coupling factor k = 1, although the gain of Ref. [20] and Ref. [21] is higher than the proposed converter in the higher and lower duty cycles. However, in practical applications, the lower duty cycle cannot meet the need for a high gain. A higher duty cycle often means an increase in losses and a decrease in efficiency. The proposed converter has a higher gain in the duty cycle range of 30% to 72% compared with other converters. It realizes the ZVS conduction of the switch, which reduces the losses.

3.5. Soft Switching Condition

In order to facilitate analysis, the rear inductance L, input inductance $L_{in}$ and the secondary side winding $L_{Ns}$ are equivalent to an inductance $L_{eq}$, and the capacitors $C_1$ and $C_2$ can be treated as voltage sources.

When the capacitor $C_Q$ starts to discharge, the equivalent inductance $L_{eq}$ resonates with $C_Q$. Taking t₄ as the time origin analysis, the expression of $C_Q$ voltage between t₄ and t₅ can be obtained as follows:

$$V_{C_Q}={\displaystyle \frac{(V_o-V_{in})n}{3n+1}}cos\omega t+V_{in}$$

(30)

In Formula (30), $\omega$ is the resonant angular frequency. From the above formula, the expression of angular frequency and resonant period can be obtained as follows:

$$\omega ={\displaystyle \frac{1}{\sqrt{L_{eq}{C}_Q}}}$$

(31)

$$T_r=2\pi \sqrt{L_{eq}{C}_Q}$$

(32)

The resonance ends when the capacitor $C_Q$ voltage drops to zero, from which the resonance duration can be calculated as follows:

$$t_{m5}={\displaystyle \frac{1}{\omega }}arccos\left[{\displaystyle \frac{3n+1}{(1-G)n}}\right]$$

(33)

In Formula (33), G is the voltage gain. During state 6, the switch body diode conducts a continuous current, and the current decreases linearly. When reduced to zero, the resonance will occur again and the maximum diode conduction time can be obtained, that is, $t_{m6}$.

$$t_{m6}={\displaystyle \frac{1}{\omega }}\sqrt{{\left[{\displaystyle \frac{(G-1)n}{3n+1}}\right]}^2-1}$$

(34)

The durations of states 3 and 4 can be expressed as follows:

$$t_{m3}+t_{m4}={\displaystyle \frac{2L_{eq}{V}_o(3n+1)}{V_{in}DRn}}$$

(35)

From the definition of soft switch, it can be seen that the drain source voltage of the switch $V_{DS}$ must be zero when the circuit conduction signal comes, and the $V_{DS}$ will rise again after the switch diode current drops to zero. Figure 6 shows the waveforms at both ends of the switch when resonance occurs.

In Figure 6, $t_x$ is the time period from the beginning of resonance to the time when the circuit conduction signal arrives and $i_{DQ}$ is the current of the switch diode. As can be seen in the figure above, to achieve zero-voltage switching, $t_x$ must meet the following relations:

$$t_{m5}<t_x<t_{m5}+t_{m6}$$

(36)

By solving Formula (36), it can be concluded that the conditions for the switch to achieve ZVS are as follows:

$$1-{\displaystyle \frac{t_{m3}+t_{m4}+t_{m5}+t_{m6}}{T}}<D<1-{\displaystyle \frac{t_{m3}+t_{m4}+t_{m5}}{T}}$$

(37)

Figure 7 shows the simulation waveform of the drive signal and the switching voltage. When the duty cycle changes, the soft switching of the switch can be realized by properly adjusting the resonant capacitance, which greatly reduces the switching loss.

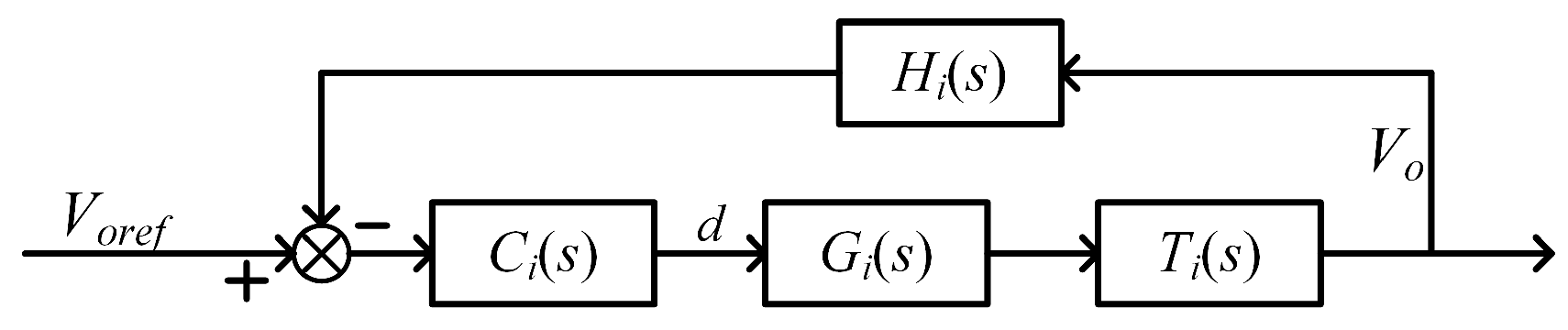
4. Control System Design

Output voltage control aims to regulate the magnitude of the converter’s output voltage and enhance the converter’s dynamic response characteristics. Its control block diagram is shown in Figure 8. Here $V_{oref}$ represents the reference value of the output voltage. $G_i\left(s\right)$ is the transfer function of the main switch control signal duty cycle d to the average value of the output voltage, $T_i\left(s\right)$ is the transfer function of the voltage sensor and $H_i\left(s\right)$ is the transfer function of the feedback loop.

In Figure 8, $V_o$ is the actual value of the output voltage and $C_i\left(s\right)$ is the transfer function of the PI controller. The transfer function of the average output voltage with respect to the duty cycle of the main switch control signal is derived using the small signal modeling method, as shown in Equation (38).

$$G_{vd}\left(s\right)={\displaystyle \frac{{\widehat{V}}_{o\left(s\right)}}{\widehat{d}\left(s\right)}}={\displaystyle \frac{\frac{(3n+1)V_{\mathrm{in}}}{{(1-d)}^2}·(1+SdR{C}_1)}{\left(1+\frac{L_{\mathrm{in}}S}{{(1-d)}^2}\right)(1+SR{C}_1)}}$$

(38)

By incorporating the converter parameters, the Bode plot of the system’s open-loop transfer function before PI controller compensation can be plotted in MATLAB 2022b, as shown in Figure 9.

As can be seen in Figure 9, the open-loop system exhibits a small slope in the characteristic amplitude-frequency curve in the low-frequency band, resulting in a slow dynamic response. The crossover frequency of the system is 215.85 kHz, and the phase margin is −${90}^{\circ }$, so the system is unstable. The compensation design of control parameters for the PI controller stabilizes the system and improves its dynamic performance. The Bode plot of the compensated system transfer function is shown in Figure 10.

The compensated system has an infinite gain margin and a phase margin of ${55}^{\circ }$, satisfying the stability criteria of the control system and validating the correctness of the controller designed in this paper.

5. Analysis of Simulation Results

The PSIM simulation software (PSIM 2023) is simulated according to the parameters in

Table 2. Main circuit parameters of experimental prototype.

Mods	Model Number
$V_{in}$	12 V
$f_s$	100 kHz
$D_1,D_2,D_3$	DPF30I300PA
$C_1,C_2$	$2\mathsf{\mu }\mathrm{F}/630\mathrm{V}\times 5$, $2\mathsf{\mu }\mathrm{F}/630\mathrm{V}\times 5$
$C_3,C_4$	$2\mathsf{\mu }\mathrm{F}/630\mathrm{V}\times 5$, $2\mathsf{\mu }\mathrm{F}/630\mathrm{V}\times 5$
$C_o$	$820\mathsf{\mu }\mathrm{F}/400\mathrm{V}\times 4$
$L_{in},L$	1 mH, $6.5\mathsf{\mu }\mathrm{F}$
n	$N_s/N_p=1:1$
Load R	$50\Omega$

. Because the duty cycle range of the soft switch realized by resonance is not large, the scheme of a non-parallel resonant capacitor is used to collect the voltage gain under each duty cycle when verifying the correctness of the voltage gain. The coupling inductance turn ratio n is 1, and the circuit parameters are not changed during the simulation. That is, when the time constant is fixed, only the variation in the voltage gain is considered with the duty cycle.

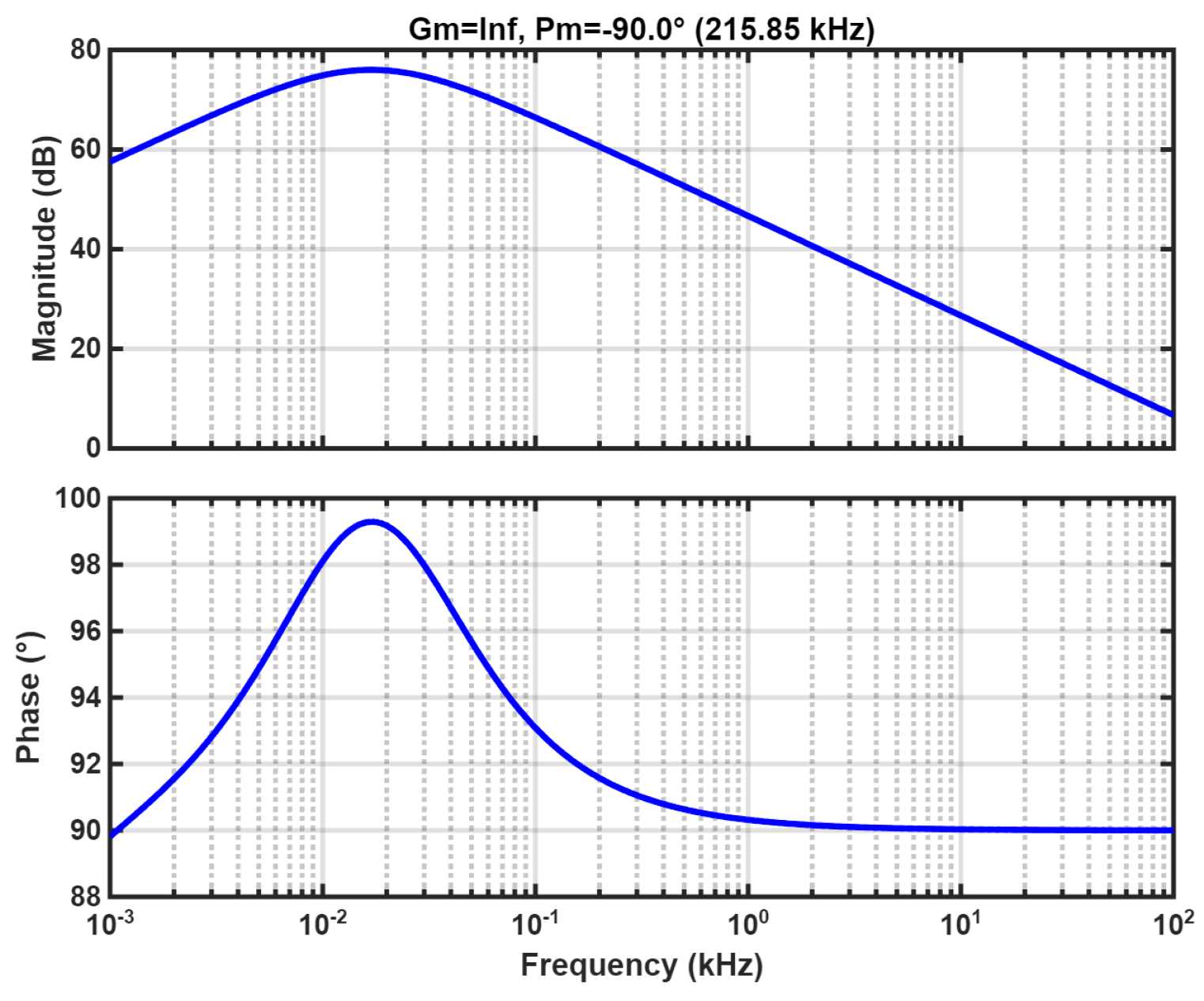
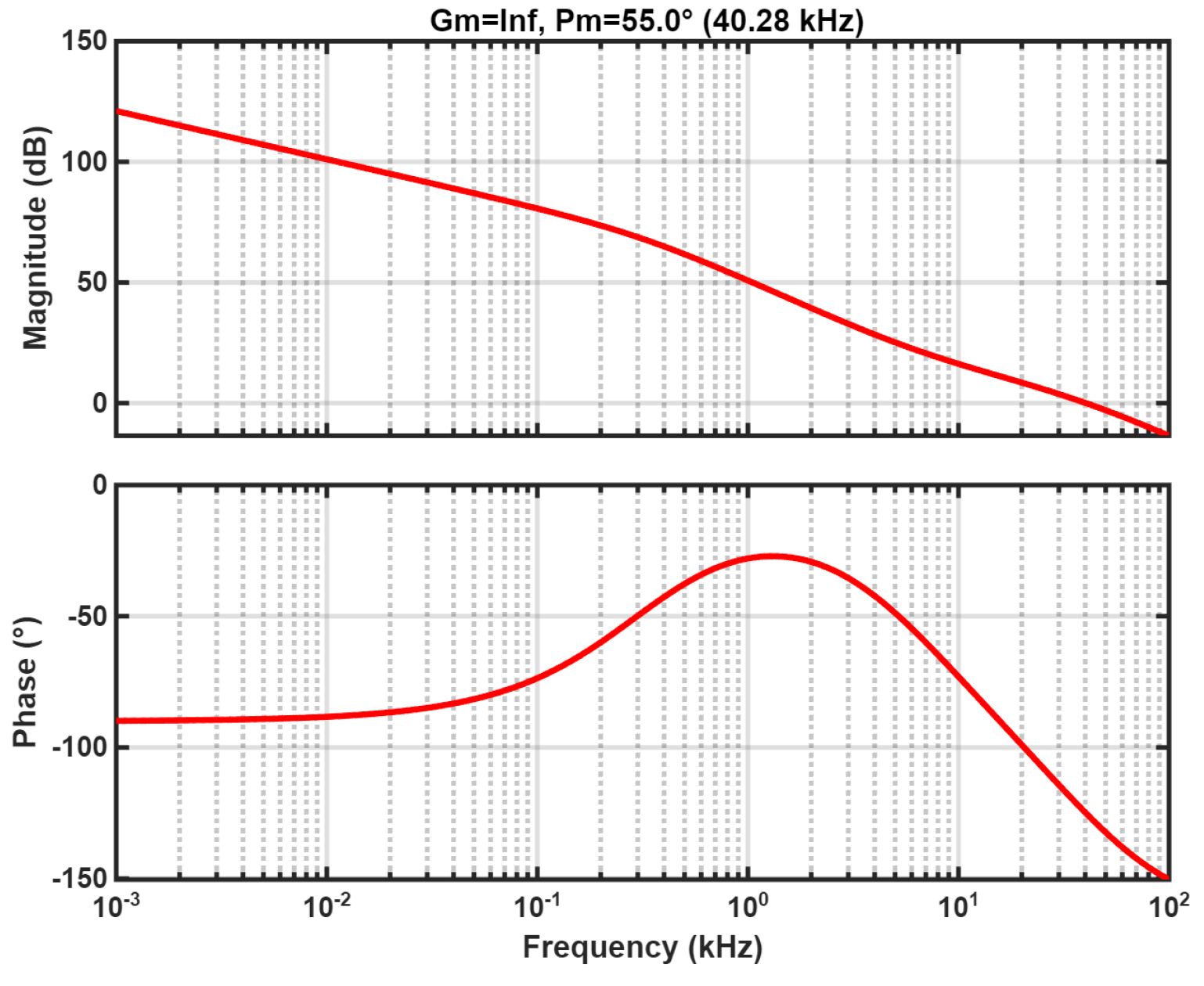
5.1. Open-Loop Scanning

From the theoretical analysis, it can be seen that when the input voltage of the converter is constant, the output voltage is positively correlated with the duty cycle of the main switching control signal. Under the condition of 12 V input voltage and 50 $\Omega$ load, open-loop scanning of the output voltage and voltage gain is carried out under different duty cycles.

The output voltage and voltage gain curves obtained from the open-loop scan are shown in Figure 11. The correctness of the theoretical analysis is verified.

5.2. Closed-Loop Simulation

Closed-loop control is incorporated in the simulation. The validation of the effectiveness of the closed-loop controller is carried out under the condition of a sudden change in voltage at the energy input port and a sudden change in load. The input voltage at the energy input port is varied from 12 V to 18 V and the load is 50 $\Omega$. The output voltage is set to 80 V and the closed-loop simulation results are shown in Figure 12.

The input voltage is constant at 12 V and the load is changed from 50 $\Omega$ to 25 $\Omega$. The output voltage is set to 90 V. The closed-loop simulation results are shown in Figure 13.

From Figure 12 and Figure 13, it can be seen that the controller achieves the preset values under the conditions of dynamic changes in input voltage and sudden changes in load.

6. Analysis of Experimental Results

In order to verify the feasibility of the proposed coupled inductor high-gain converter, an experimental prototype is fabricated based on the parameters of Table 2 under the existing conditions in the laboratory, as shown in Figure 14. The system uses the DSPIC33F development board as the main control unit. A half-bridge driver circuit is used to drive the MOSFET to generate the control signal. The RXLG resistor is used as the load unit. The voltage output port is fed back to the ADC interface of the DSP through a parallel voltage acquisition board to form a closed loop.

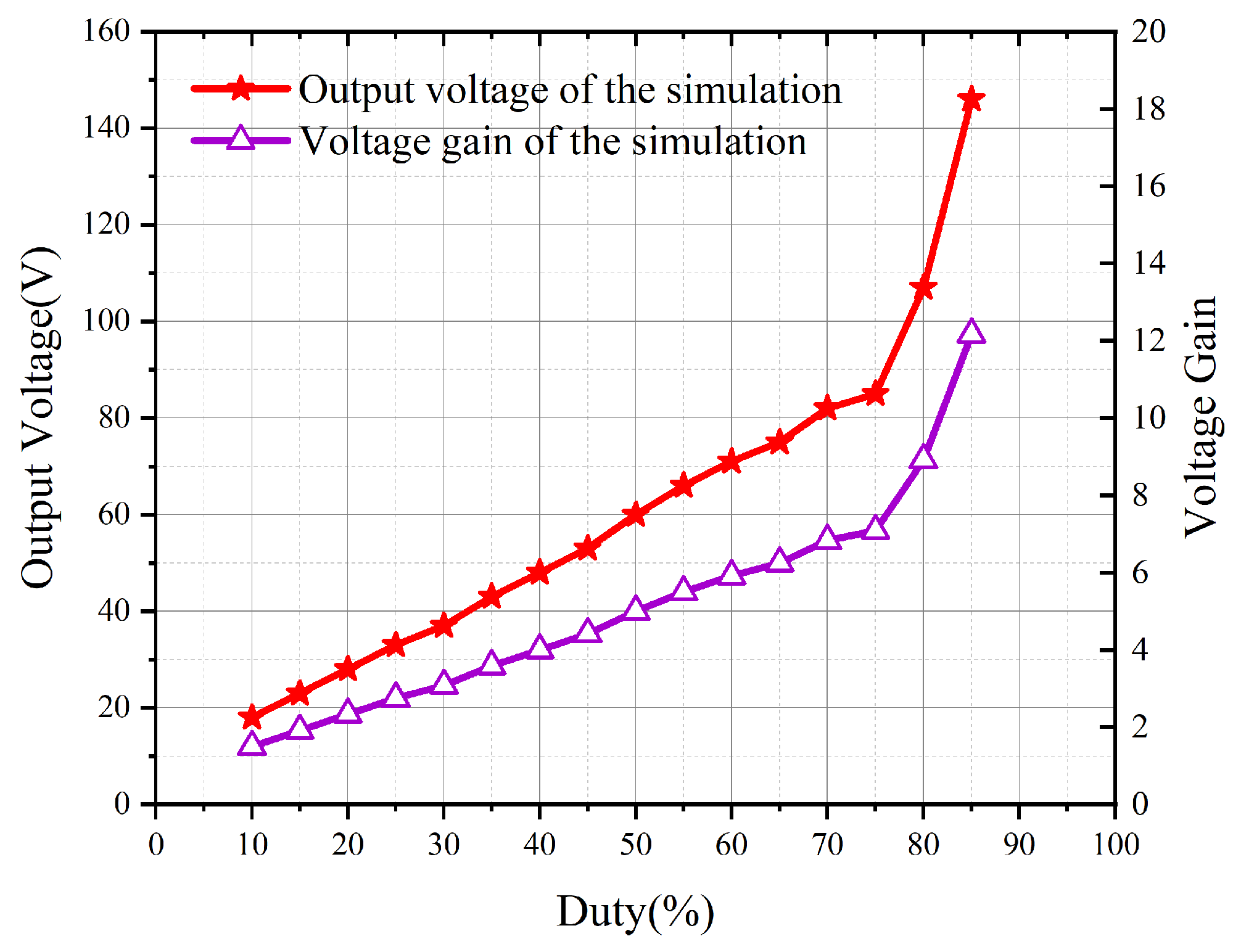
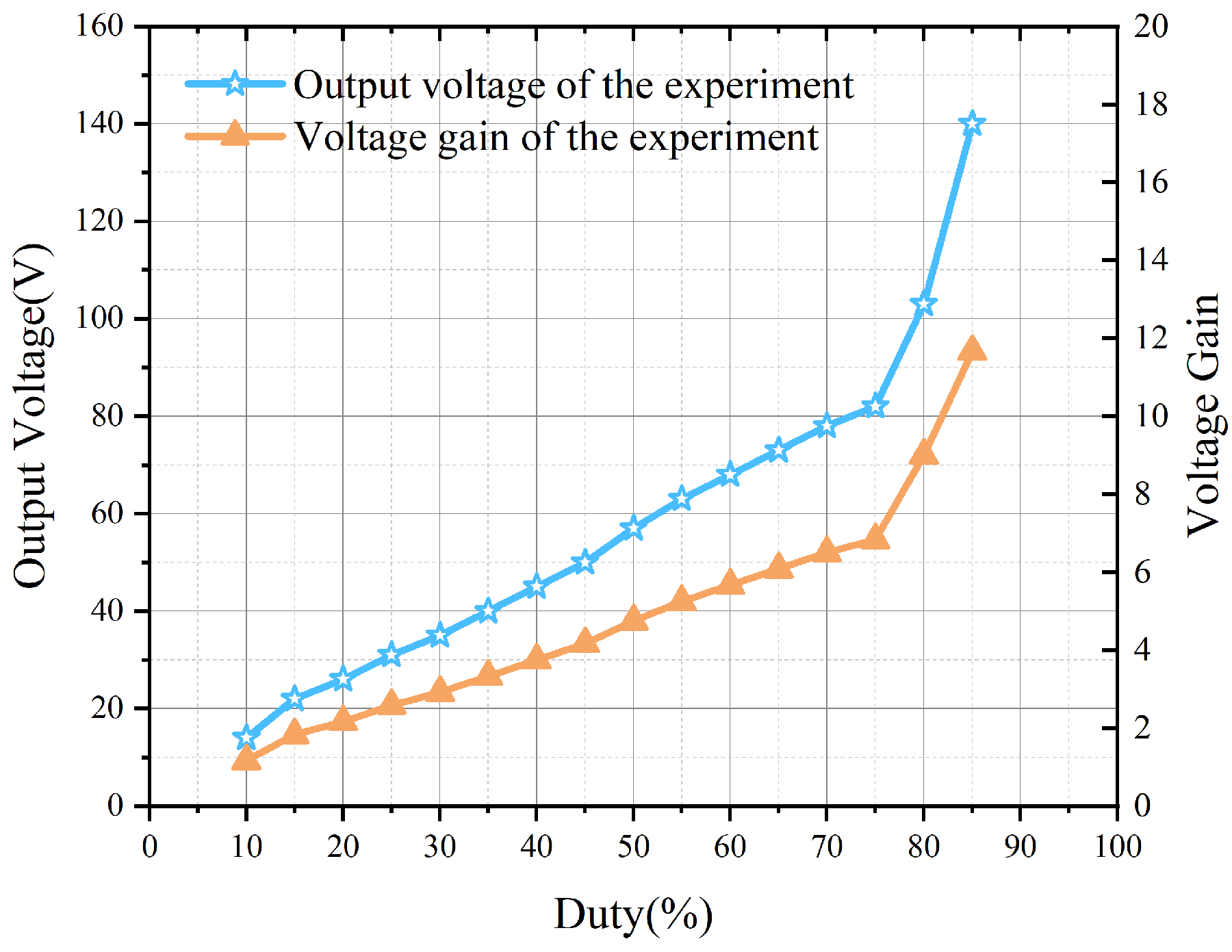
6.1. Open-Loop Scanning

Experimental verification is carried out to verify the reasonableness of the theoretical analysis and simulation results. The fixed load resistance is 50 ohms, and the energy input port voltage is set to 12 V. The duty cycle of the control switch is varied in the interval [0.1, 0.85] in steps of 0.05. The open-loop scanning results of the actual gain of the converter and the output voltage with the variation in the switching duty cycle are obtained as shown in Figure 15.

When the duty cycle of the control signal is in the interval [0.1, 0.85], the load power is provided by the output port. Energy flows from the input port to the output port. When the duty cycle of the control signal reaches 0.8, the open-loop gain reaches 11.7 times. The open-loop scan curve of the converter efficiency is shown in Figure 16. The efficiency of the converter is at a high level throughout the operating range. It reaches a maximum of 93% at a switching duty cycle of 0.65.

The comparison of simulation and experimental open-loop scanning is shown in Figure 17. The output voltage and gain in the finite duty cycle range are basically consistent with the simulation results. The correctness of the converter theory is verified.

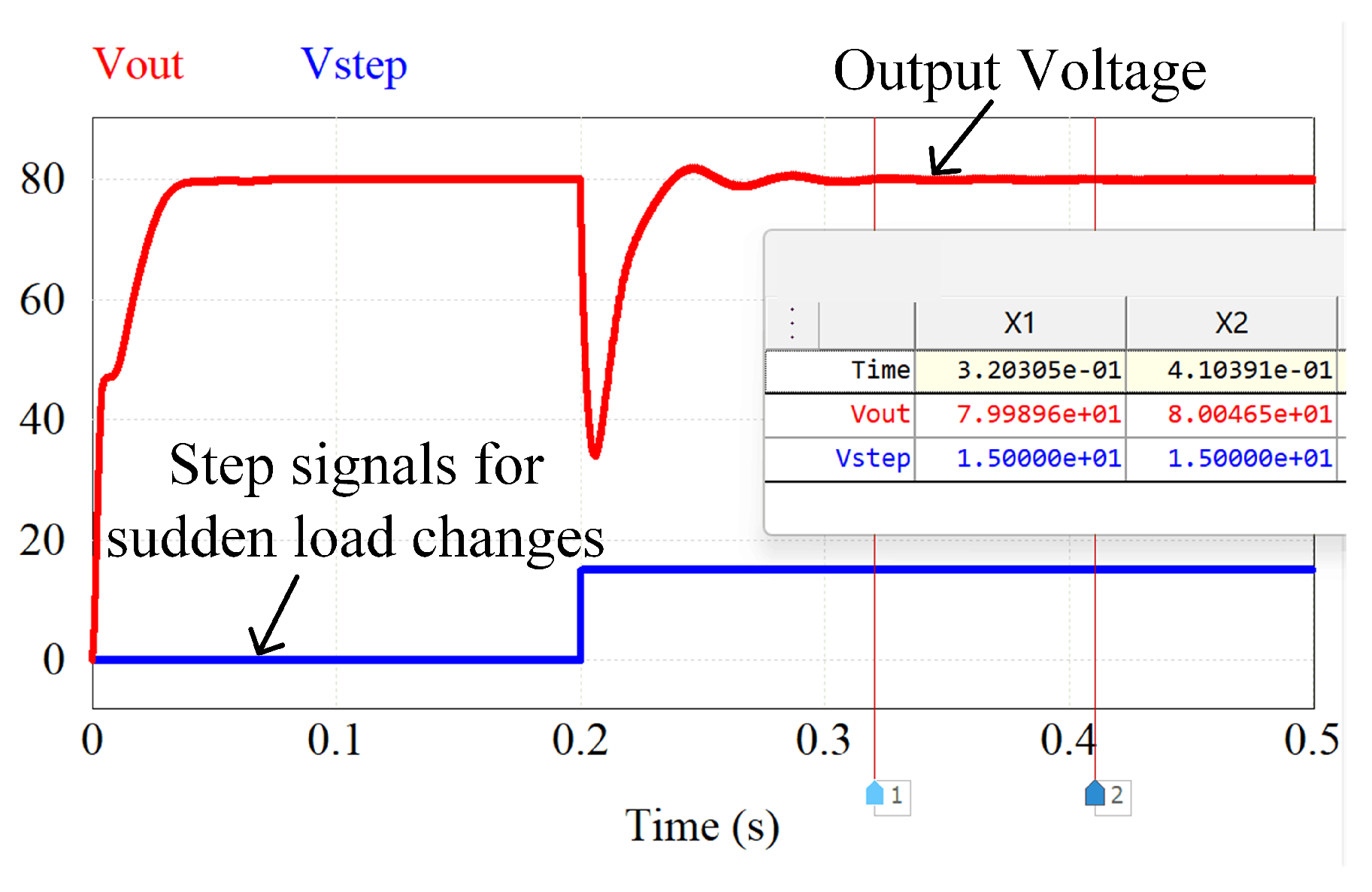
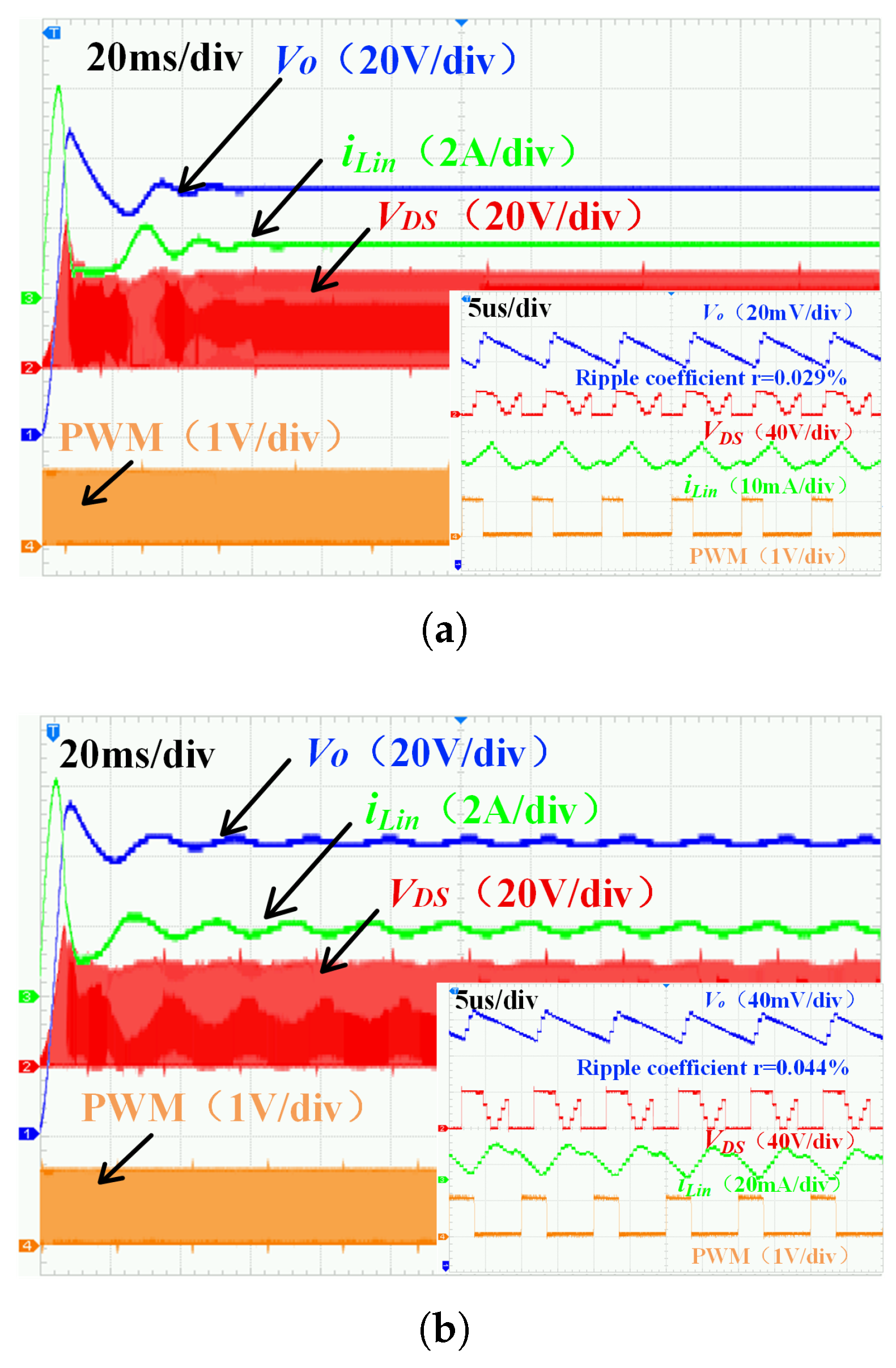
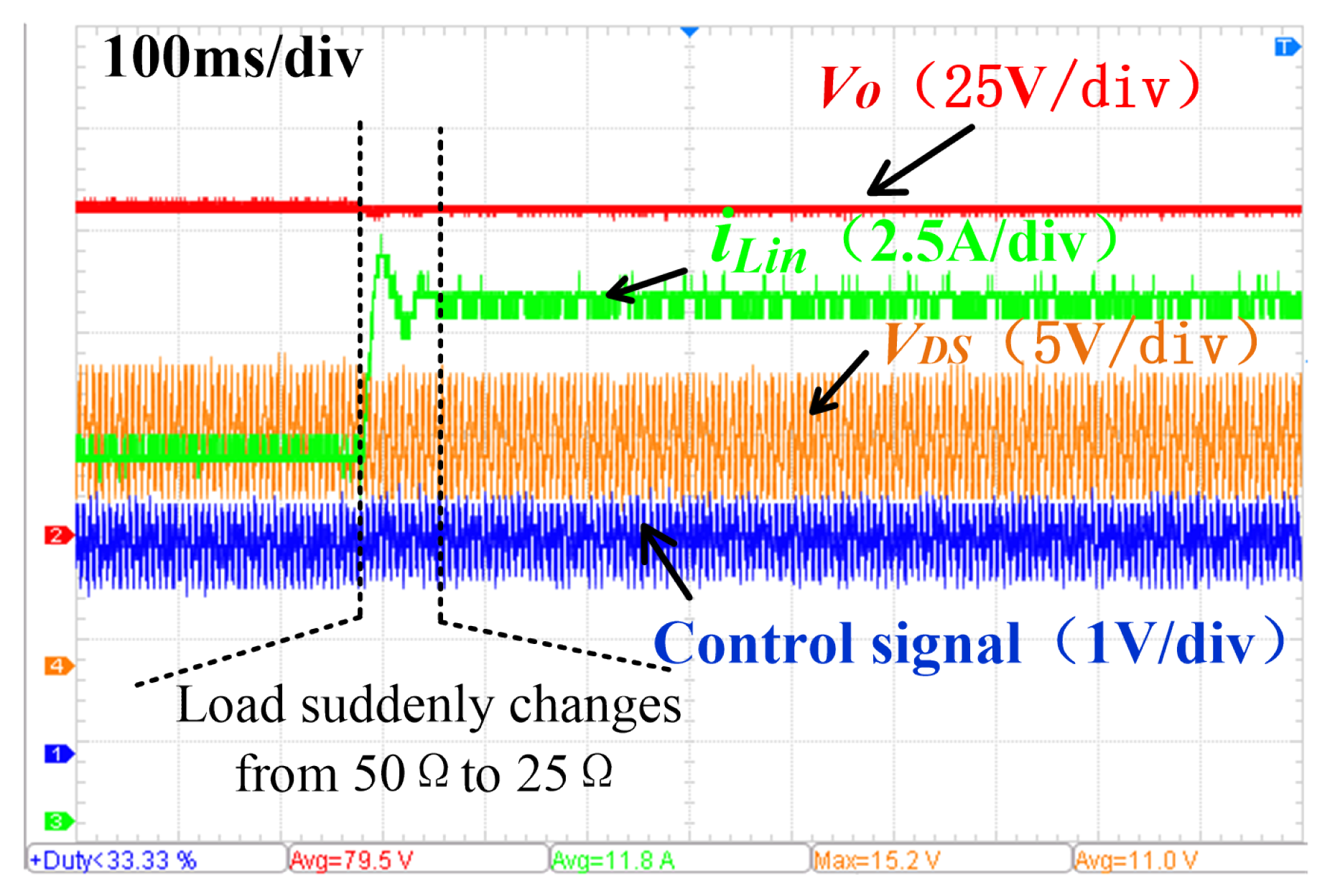
6.2. Closed-Loop Scanning of the Converter

Based on the previous section, the feasibility of the closed-loop system is verified next. The reference values for the output voltage are set to 70 V, 80 V, and 100 V, respectively. The waveforms of the trigger and steady state, and the duty cycle in steady state, are measured. The results are shown in Figure 18.

The output voltage is fed back to the DSP through the distributor for PID closed-loop control. Reasonable adjustment parameters can basically achieve a rapid voltage response. It can be seen that the output voltage is basically the same as the given voltage in the steady state.

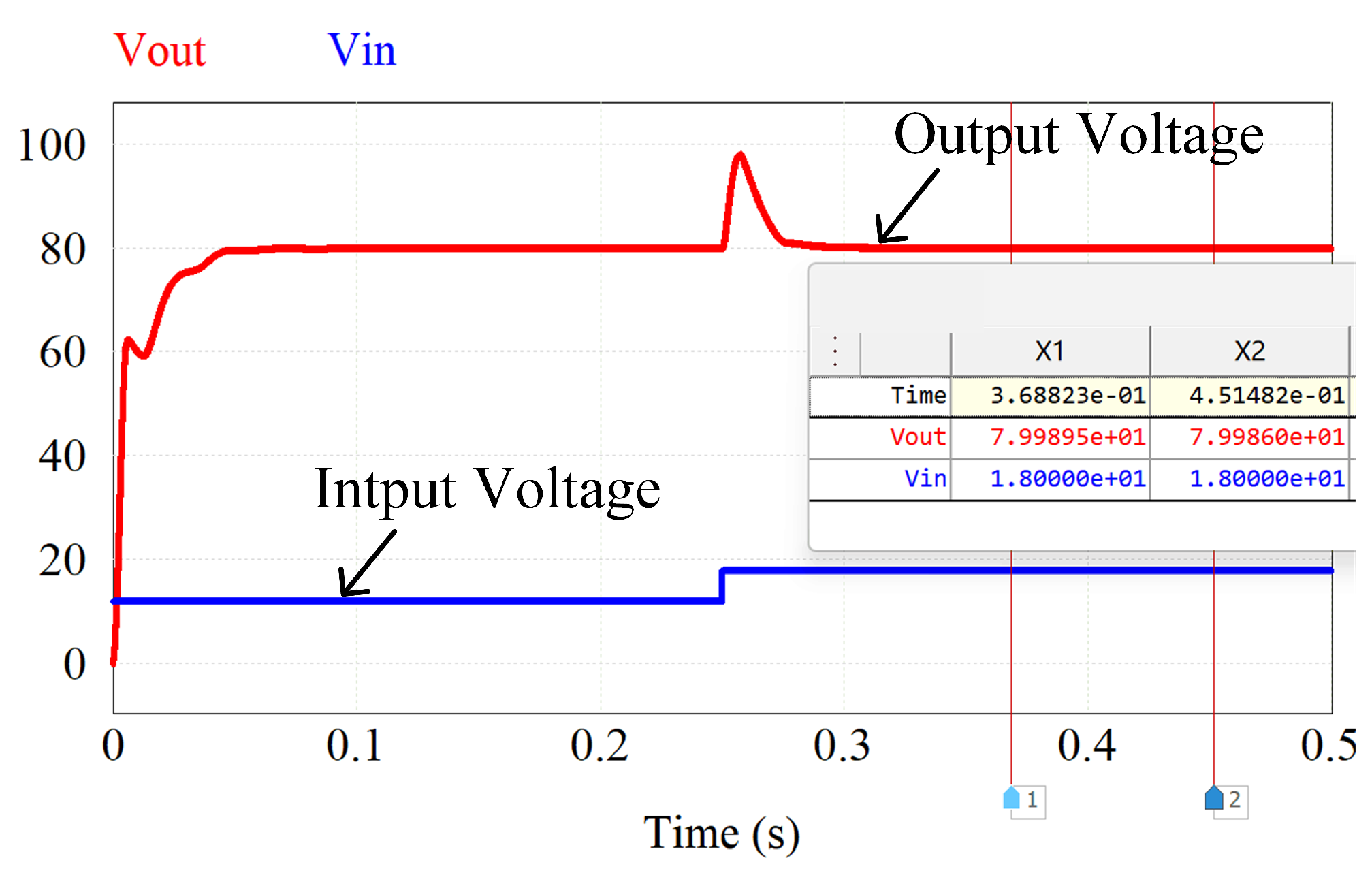
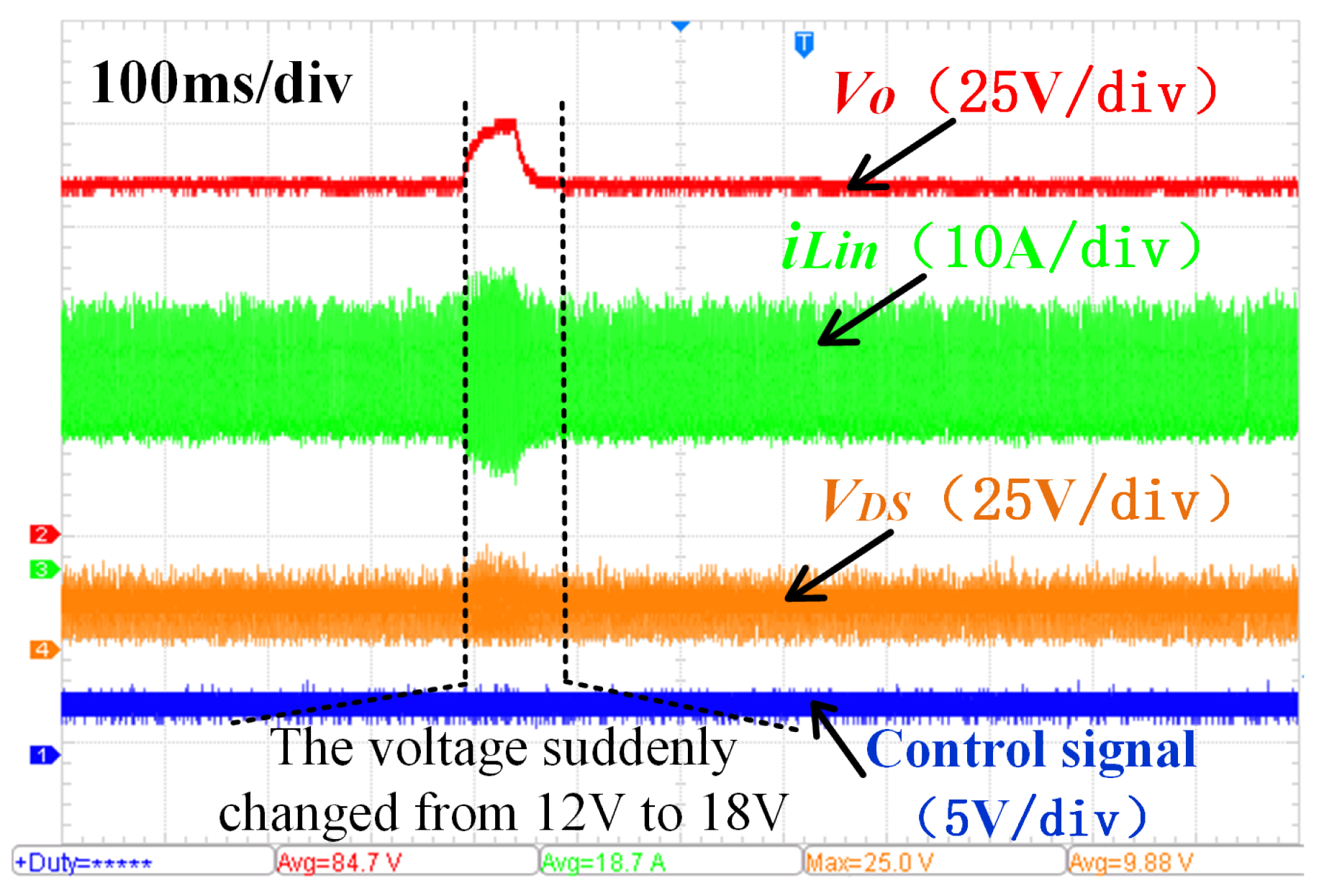
6.3. Transformer Dynamic Response Performance Experiment

To verify the dynamic performance and robustness of the designed converter under sudden changes in input voltage levels and load conditions, a system dynamic response performance test was designed, which mainly includes (1) dynamic response test of the converter under sudden changes in energy input port voltage levels; (2) dynamic response test of the converter under sudden changes in load conditions.

In the sudden voltage-level change experiment at the energy input port, the fixed load resistance is 50 $\Omega$, and the energy input port is connected to a 24 V DC regulated power supply. The response parameters are set, and the voltage at the energy input port connected to the regulated power supply suddenly changes from 12 V to 18 V. The experimental results of the system’s response performance at this time are shown in Figure 19.

As shown in the experimental waveform in Figure 19, before the sudden change in voltage level, the load voltage was 85 V and the power output on the load side was stable. After sudden voltage changes, the input inductance current increased to a new equilibrium point and the average output voltage stabilized. During this process, the change in load voltage was negligible and the power output on the load side remained stable. The dynamic response time of the system was less than 100 ms, and the load voltage remained stable before and after the sudden voltage change.

In the load step response performance experiment, the energy input port voltage level was 12 V. A switch was used to change the load resistance from 50 $\Omega$ to 25 $\Omega$. The results of the system dynamic response experiment are shown in Figure 20.

As shown in Figure 20, before the load change, the resistance value was 50 $\Omega$, and the output voltage was 80 V. The converter operated stably while maintaining a stable power output. During the change in load step, the amplitude of the input inductor current increases to a new steady-state point, while the output voltage remains constant. The dynamic response process lasts approximately 100 ms. The results indicate that the designed controller exhibits good robustness and dynamic response performance in response to load step changes, maintaining a constant output voltage under such conditions.

The results of the system dynamic response performance experiments show that the designed controller can maintain a constant output voltage under sudden changes in the energy input port voltage level and load resistance, demonstrating excellent robustness and dynamic response performance.

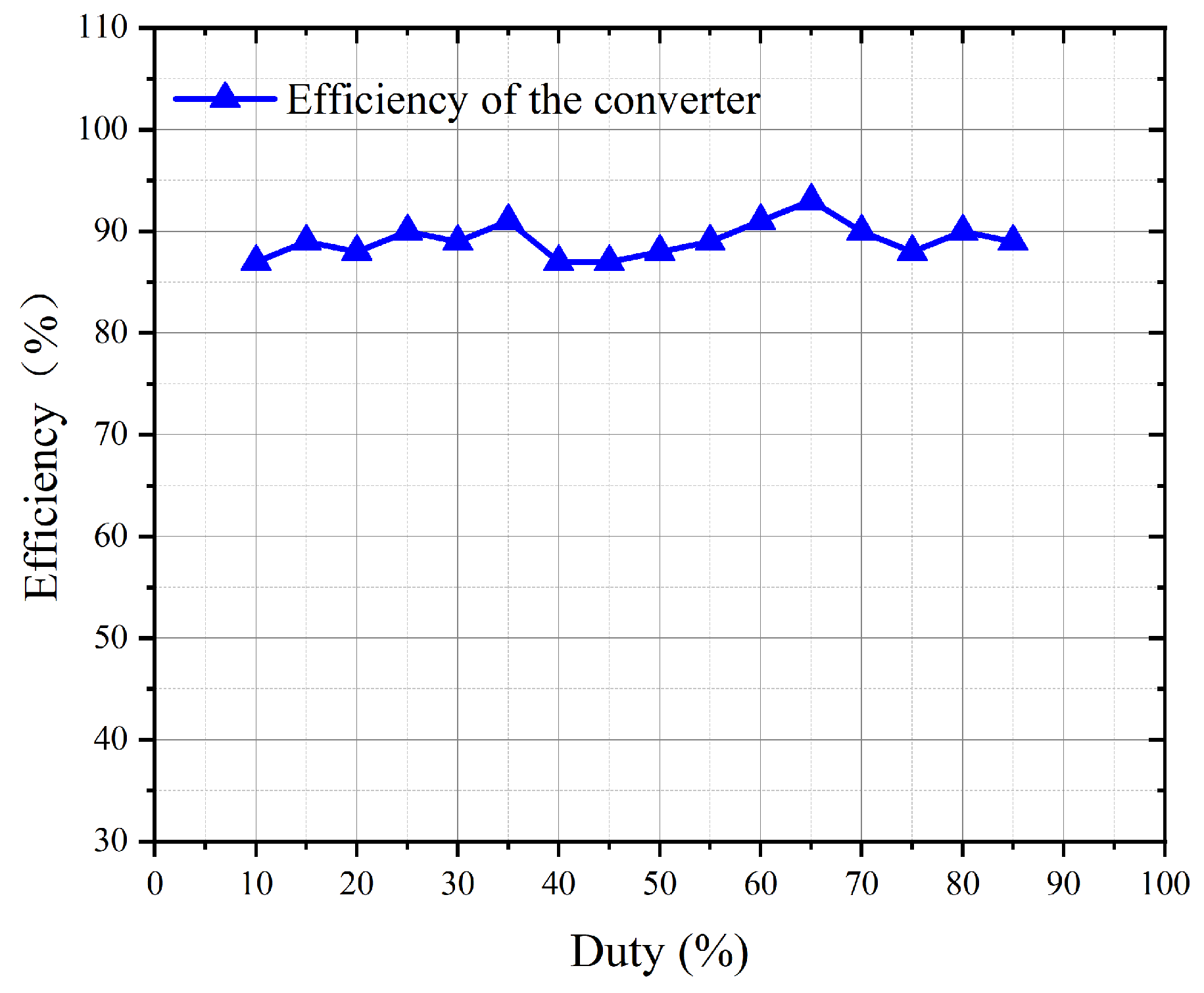
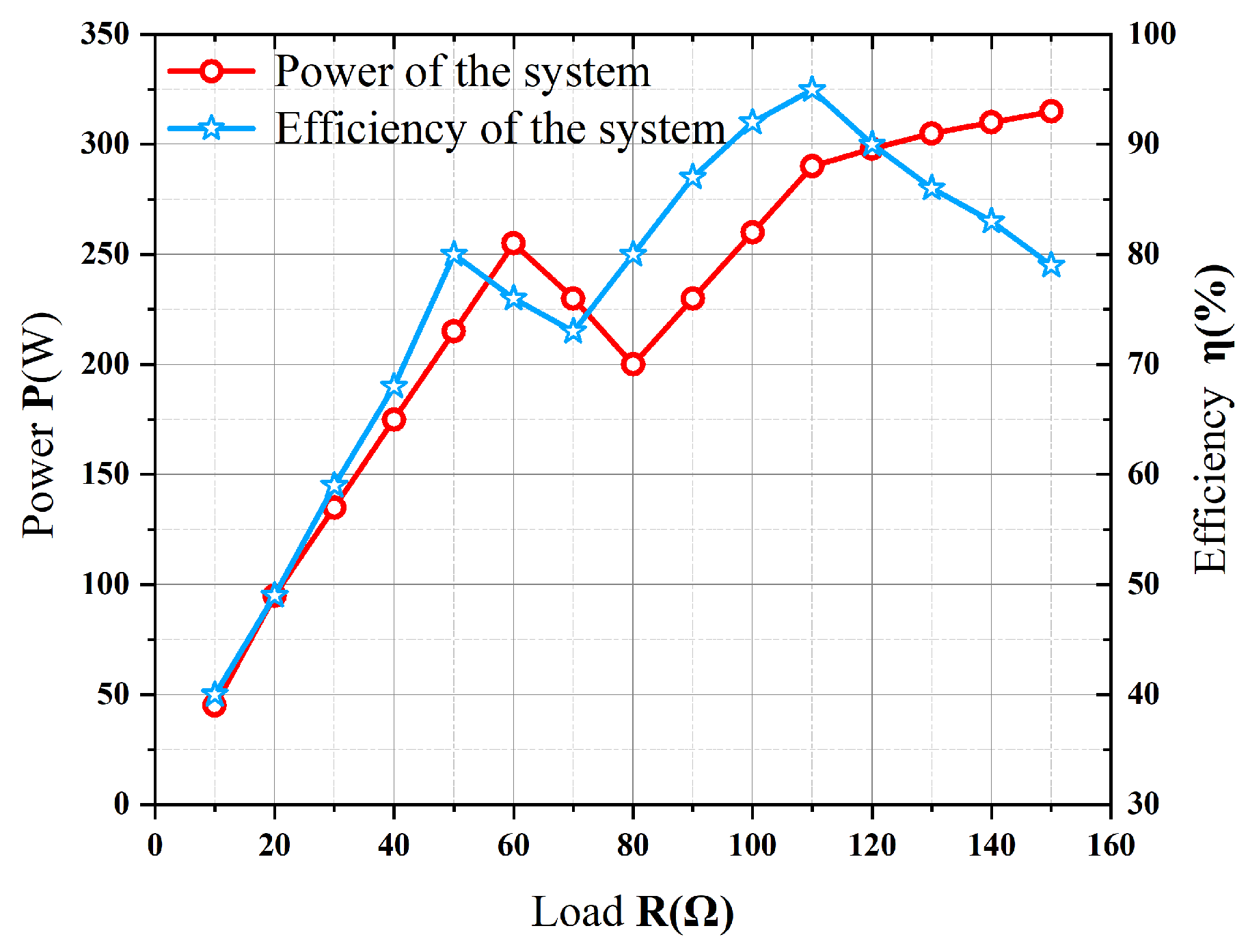
6.4. Full Load Range Efficiency Test

From the theoretical analysis, it can be seen that the output voltage is mainly dependent on the duty cycle of the main switch control signal. The fixed duty cycle is 0.5 and the input voltage is 12 V. The power and efficiency of the system with different load resistances are scanned as shown in Figure 21. The maximum efficiency of the system reaches 94% at a load of 110 $\Omega$.

7. Conclusions

In this paper, a high-gain DC-DC converter based on coupled inductance with soft-switching characteristics is proposed. The feasibility is verified by a 300 W prototype built by experiments. The switch can work in ZVS using a parallel resonant capacitor, and the switching voltage stress is reduced. All diodes can be ZCS turned off, so the converter has low losses. At the same time, the voltage gain of the converter is greatly improved in the duty cycle range. The tight wounds of the primary and secondary winding of the coupling inductor make the coupling coefficient of the converter very high, which is conducive to reducing leakage induction and improving overall efficiency. The common ground of input and output can reduce the ground impedance and improve the anti-interference ability of the converter.