Low-Voltage Ride Through Capability Analysis of a Reduced-Size DFIG Excitation Utilized in Split-Shaft Wind Turbines
Abstract
1. Introduction
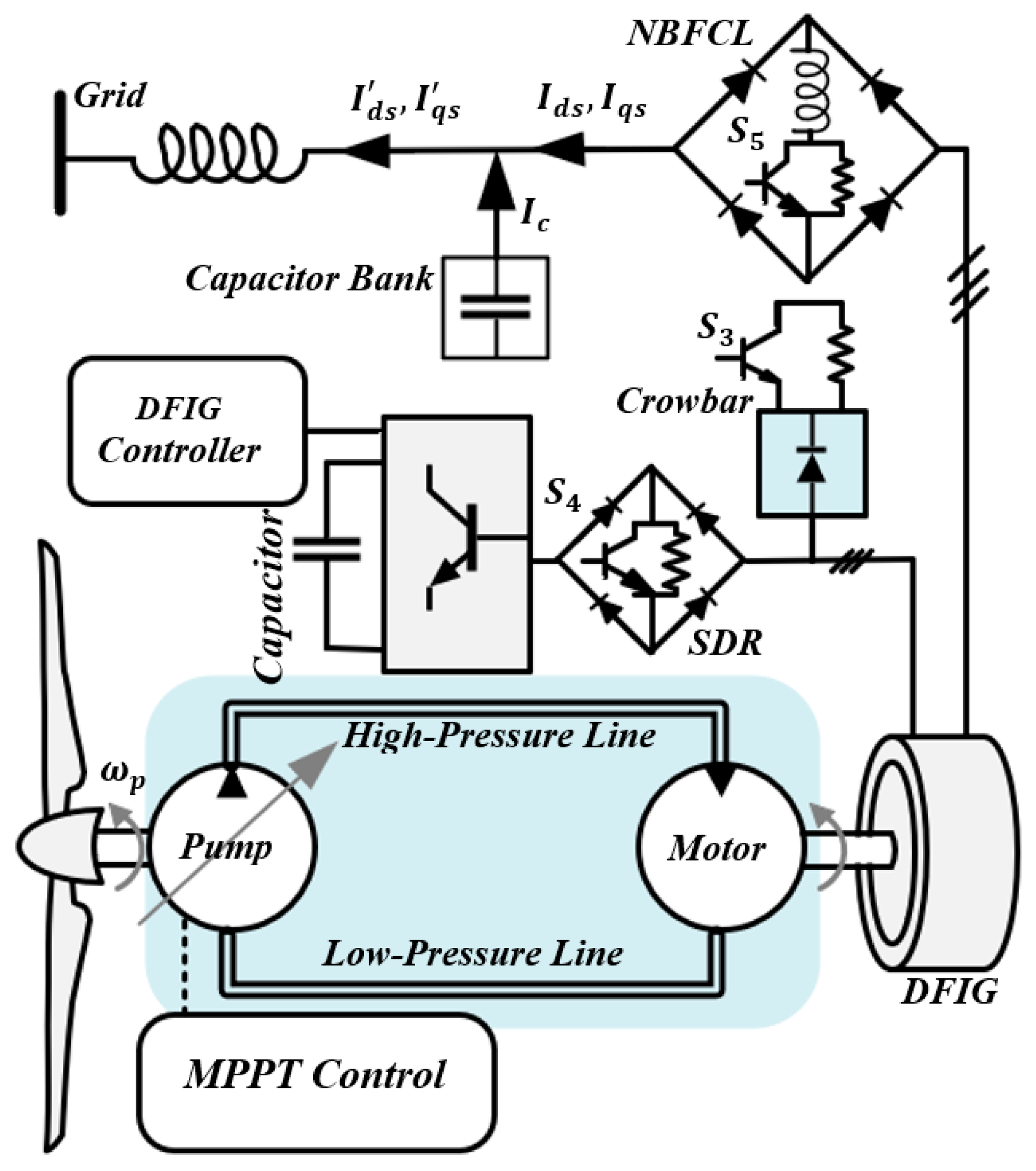
2. Split-Shaft Drivetrain Model
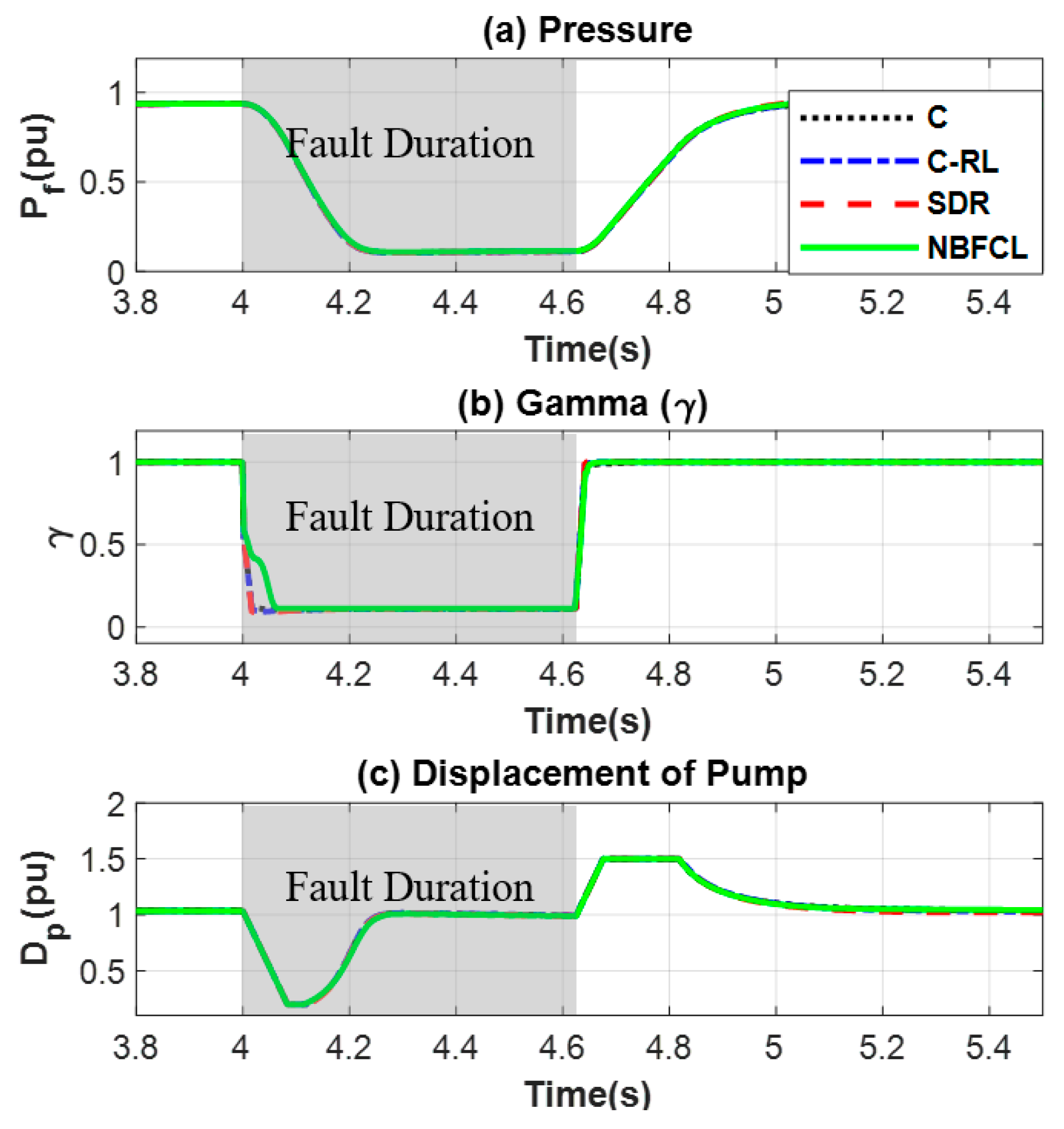
2.1. Hydraulic Transmission System Model
2.2. Energy Conversion Efficiency and Power Flow
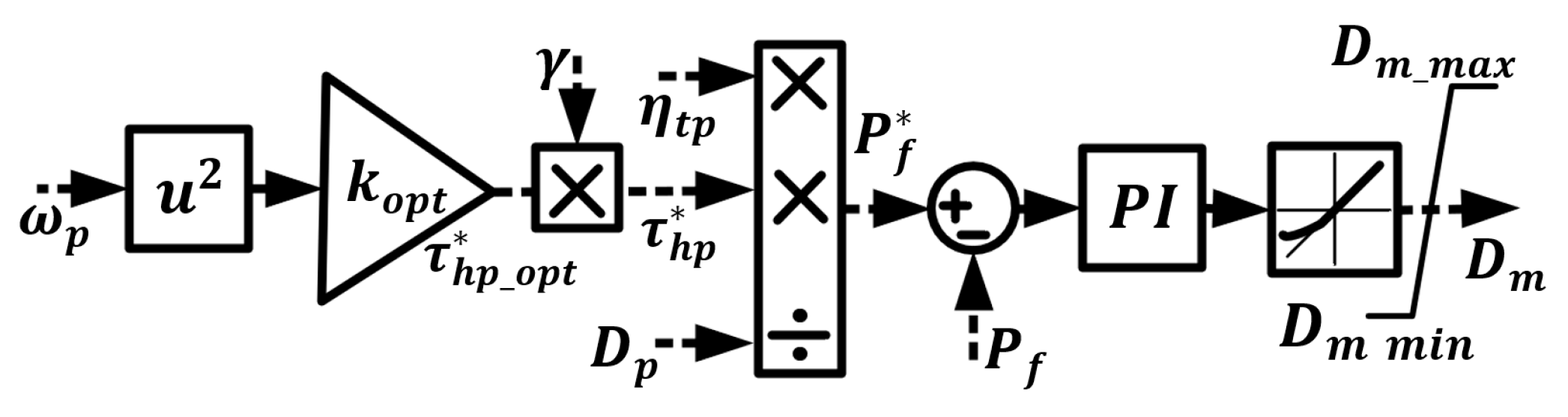
2.3. Optimal Hydraulic Motor Displacement Control
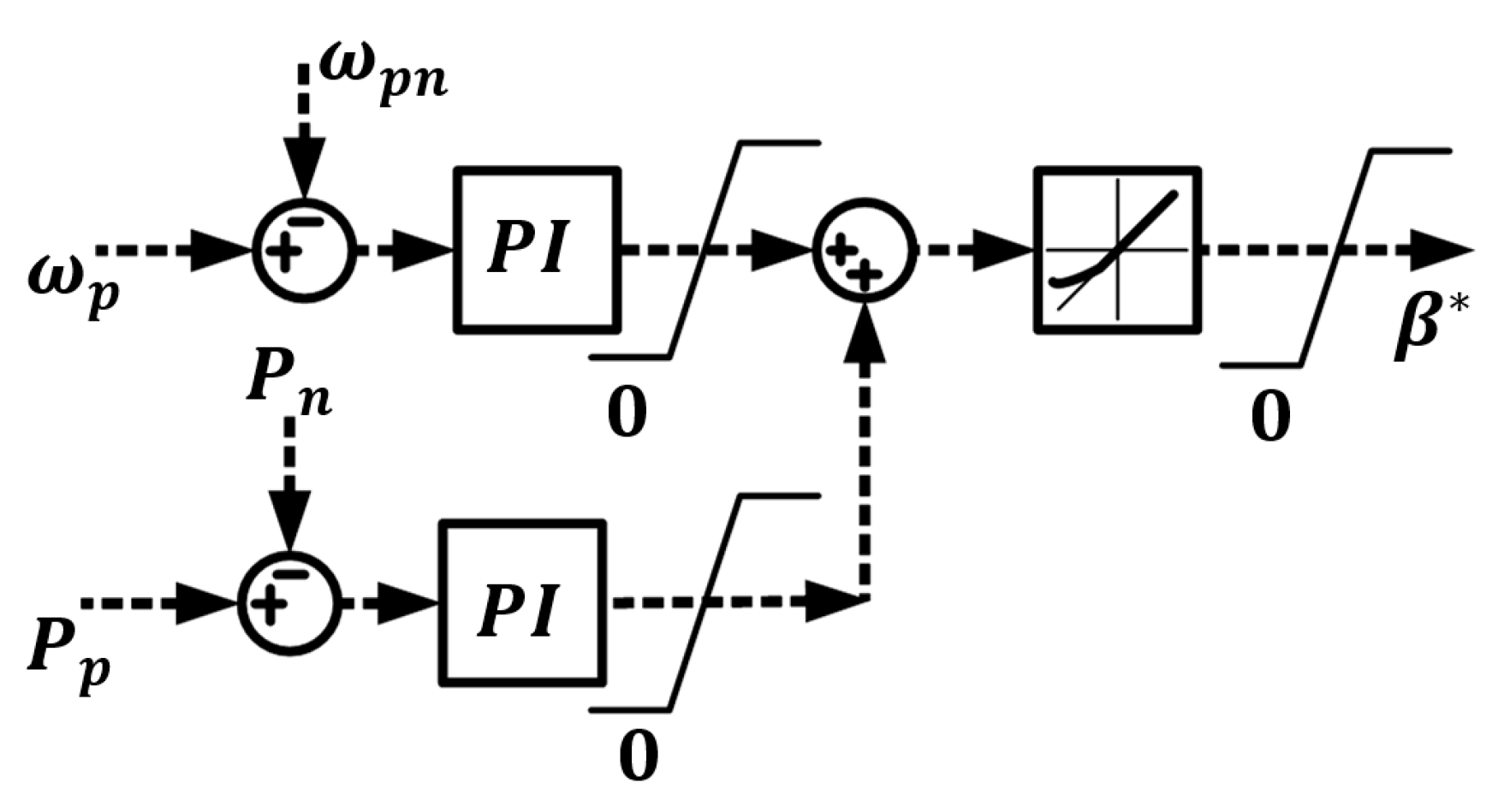
2.4. Optimal Pump Displacement Control (OPDC)
3. Quasi-Self-Excited Hydraulic WECS
4. LVRT Challenges for DFIG
4.1. Grid Code Requirements
4.2. Protection Measures
5. Proposed LVRT for Hydraulic Wind Turbine
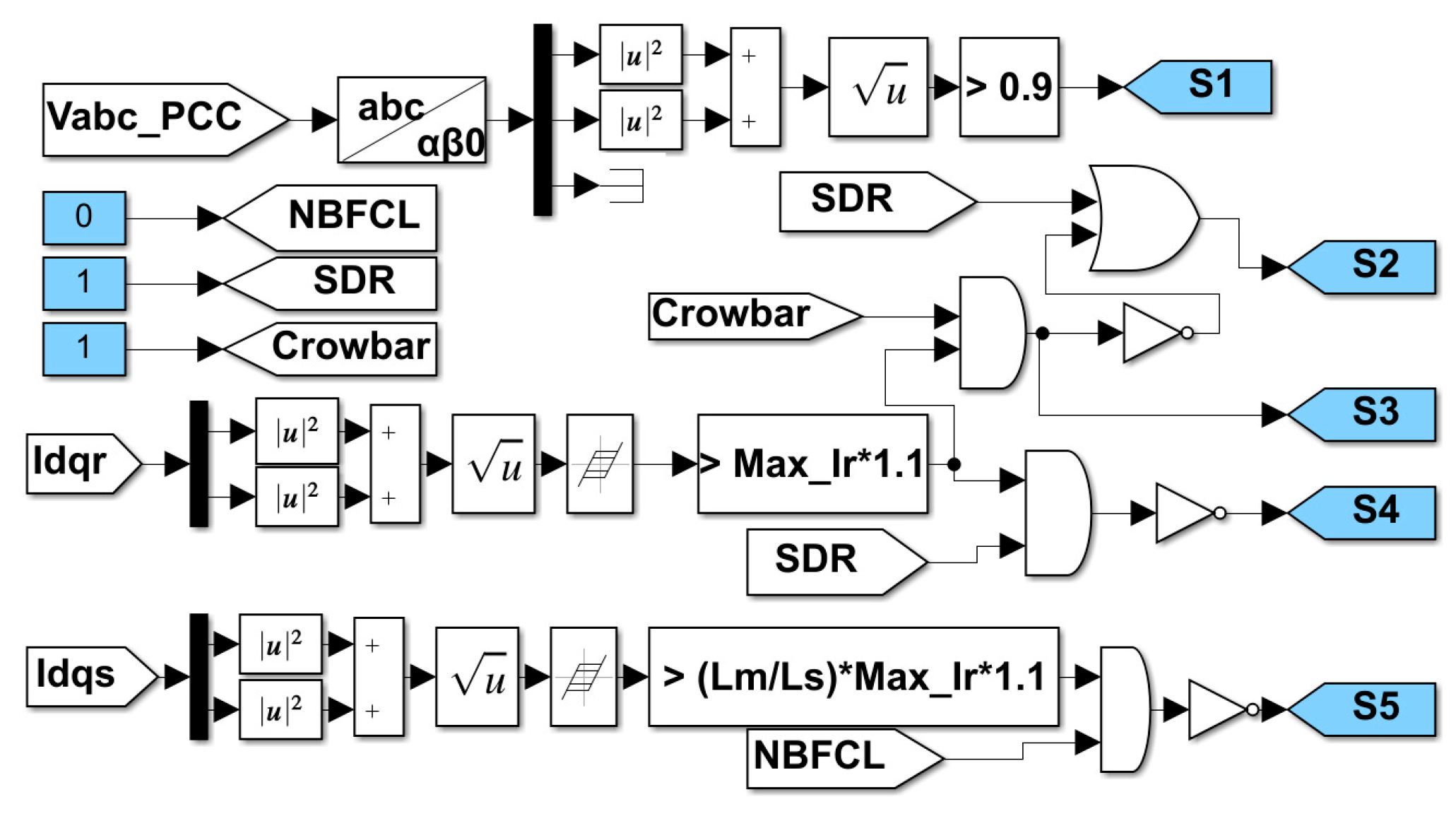
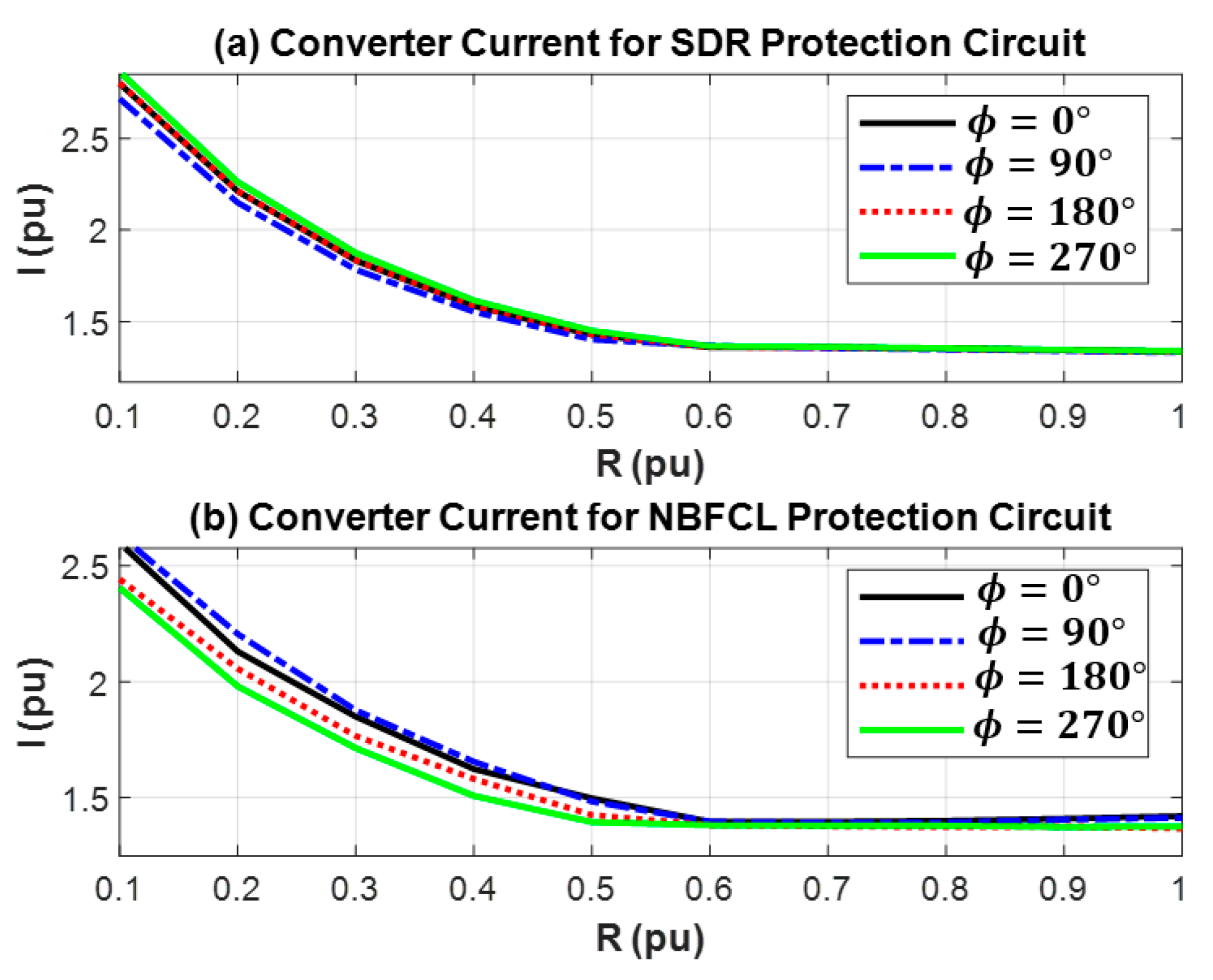
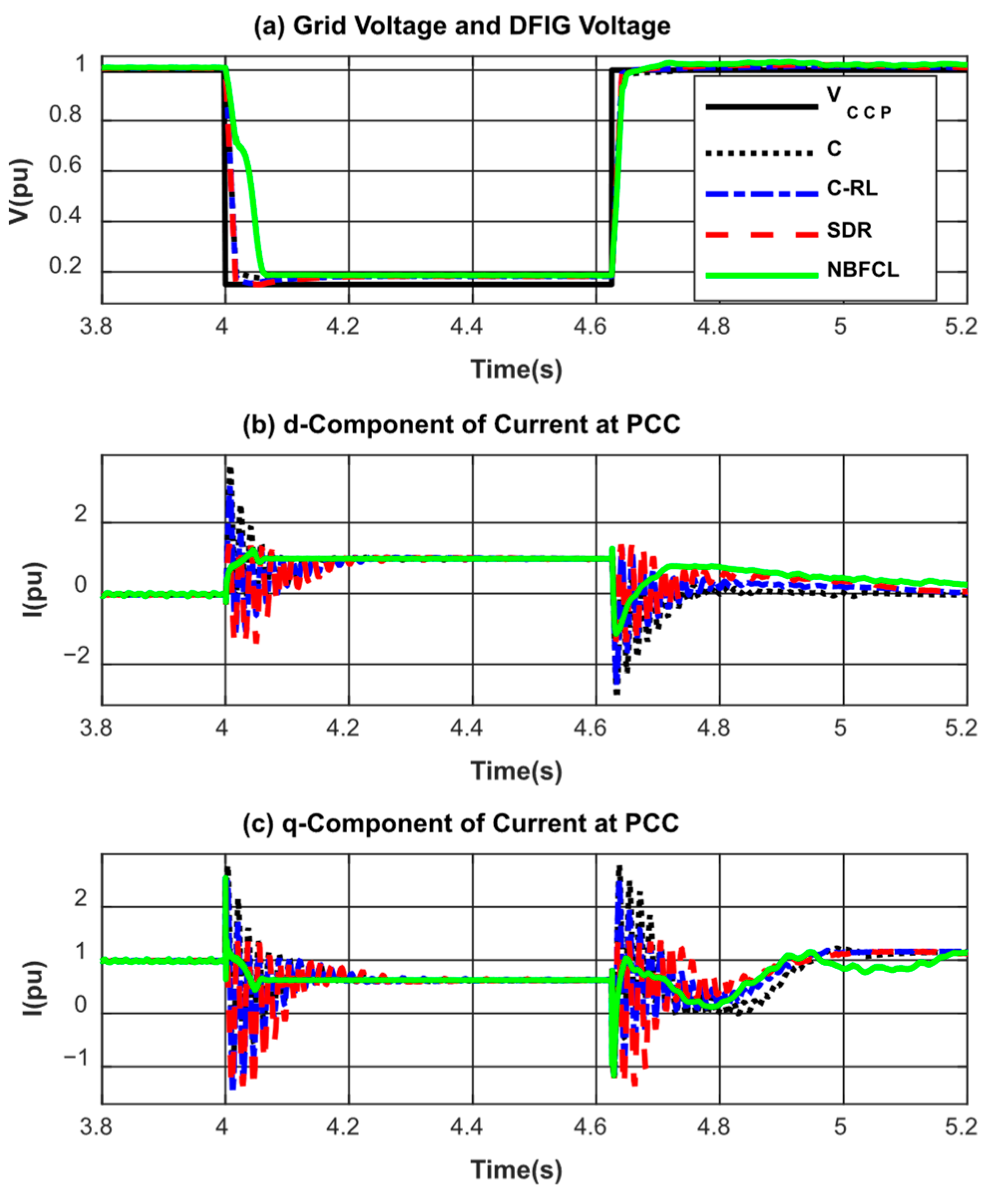
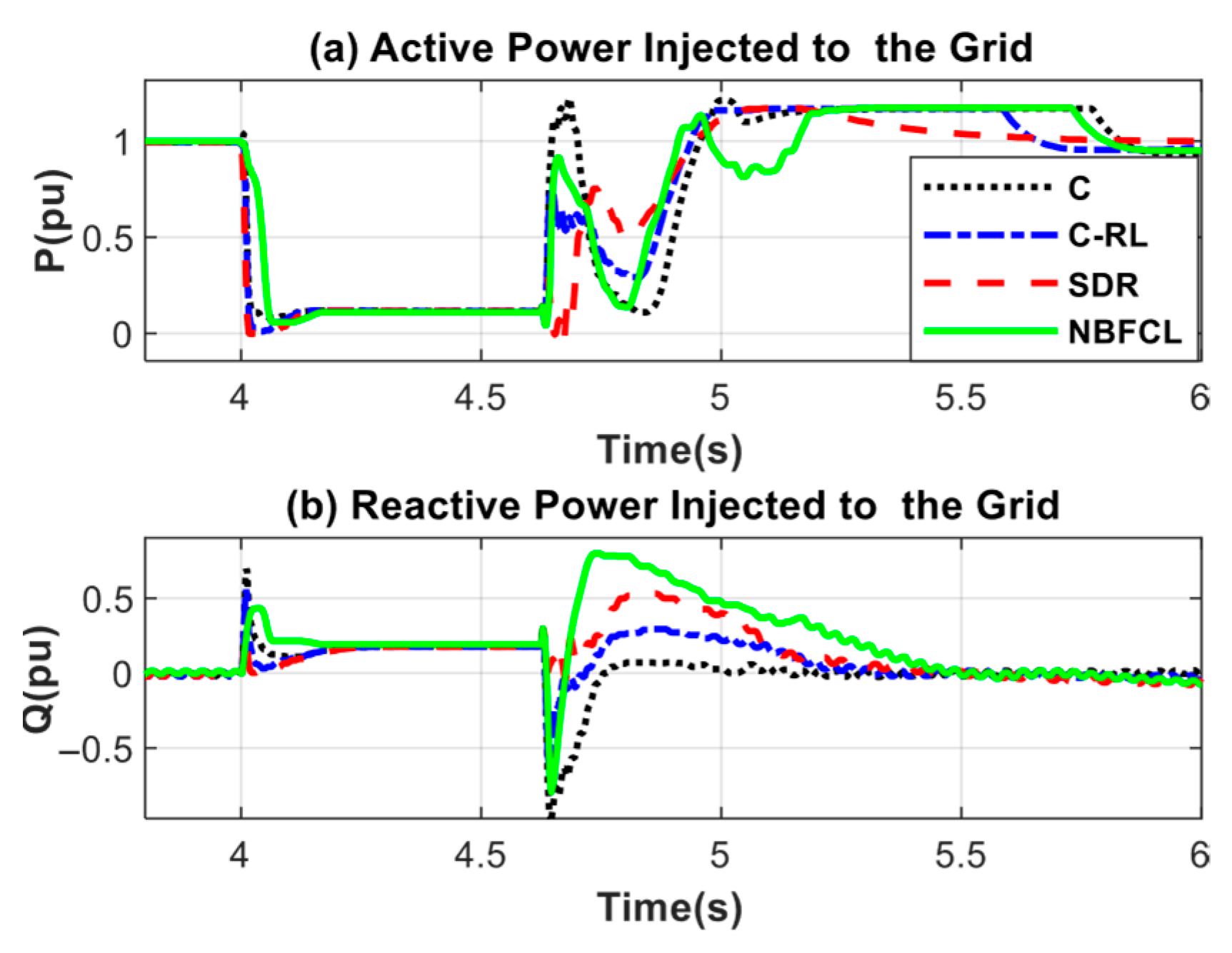
5.1. Overcurrent and Overvoltage Protection
- (1)
- Active Crowbar (C)
- (2)
- Crowbar and RL (C-RL)
- (3)
- SDR
- (4)
- NBFCL
5.2. Reactive Current Reference Calculations
5.3. Active Power Reference Calculation
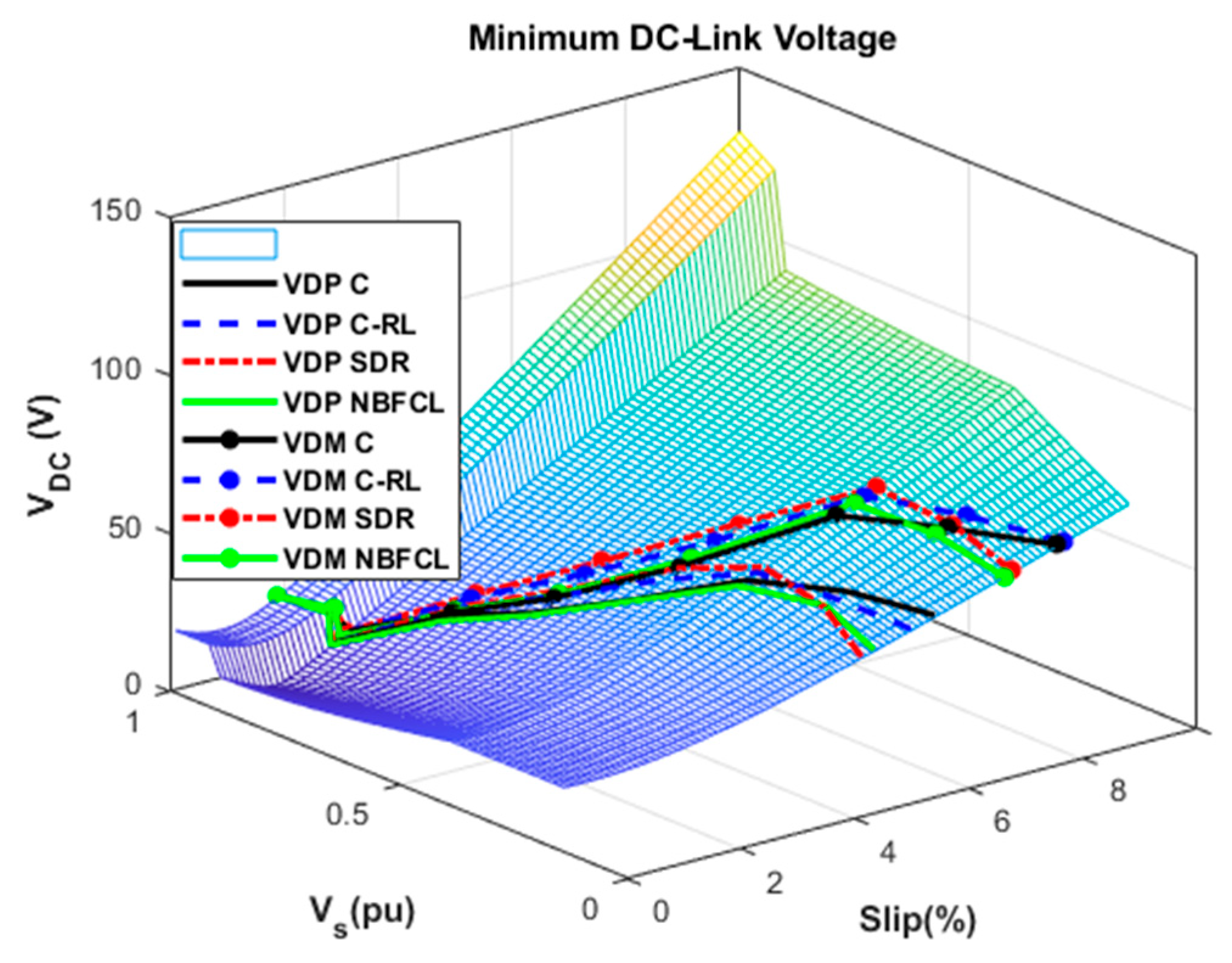
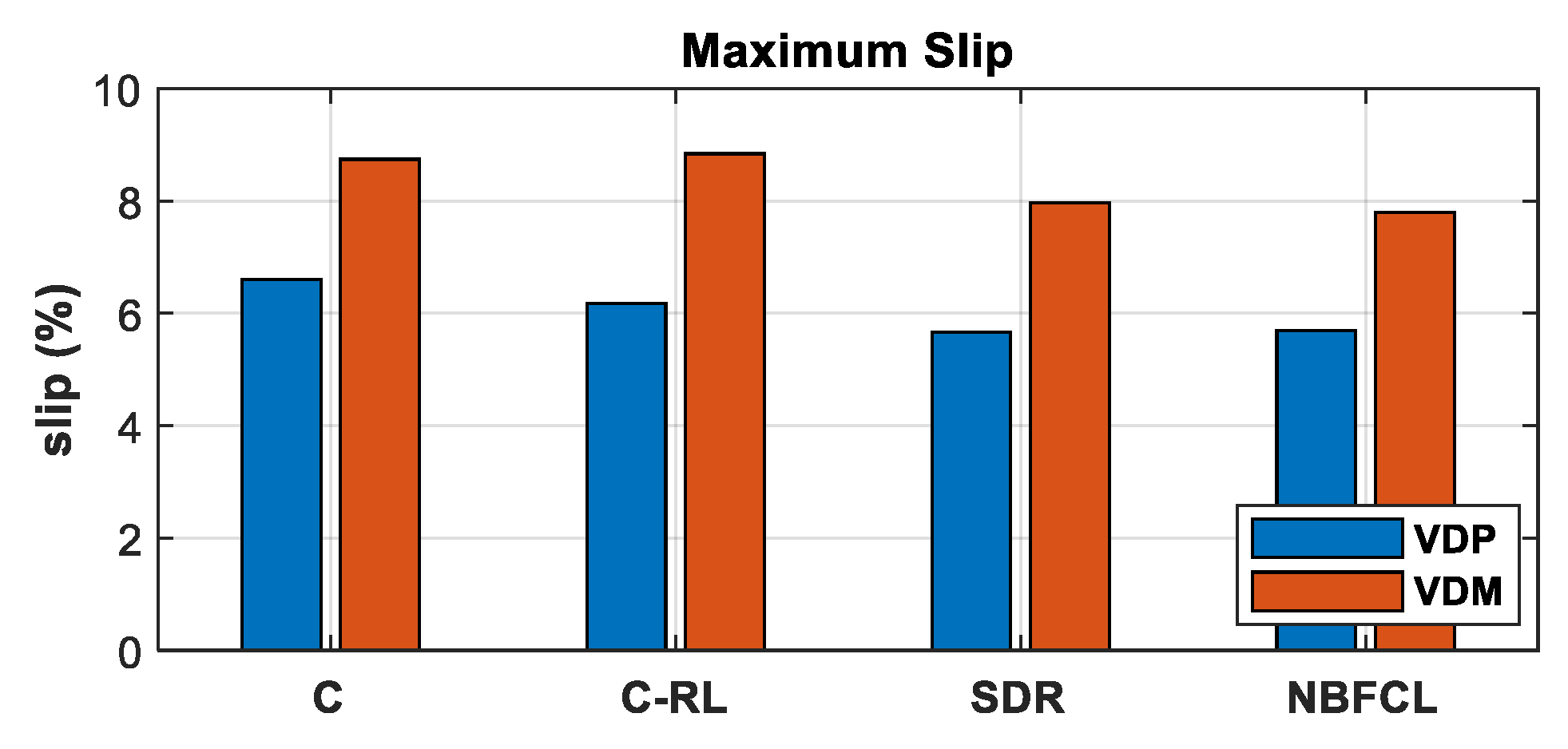
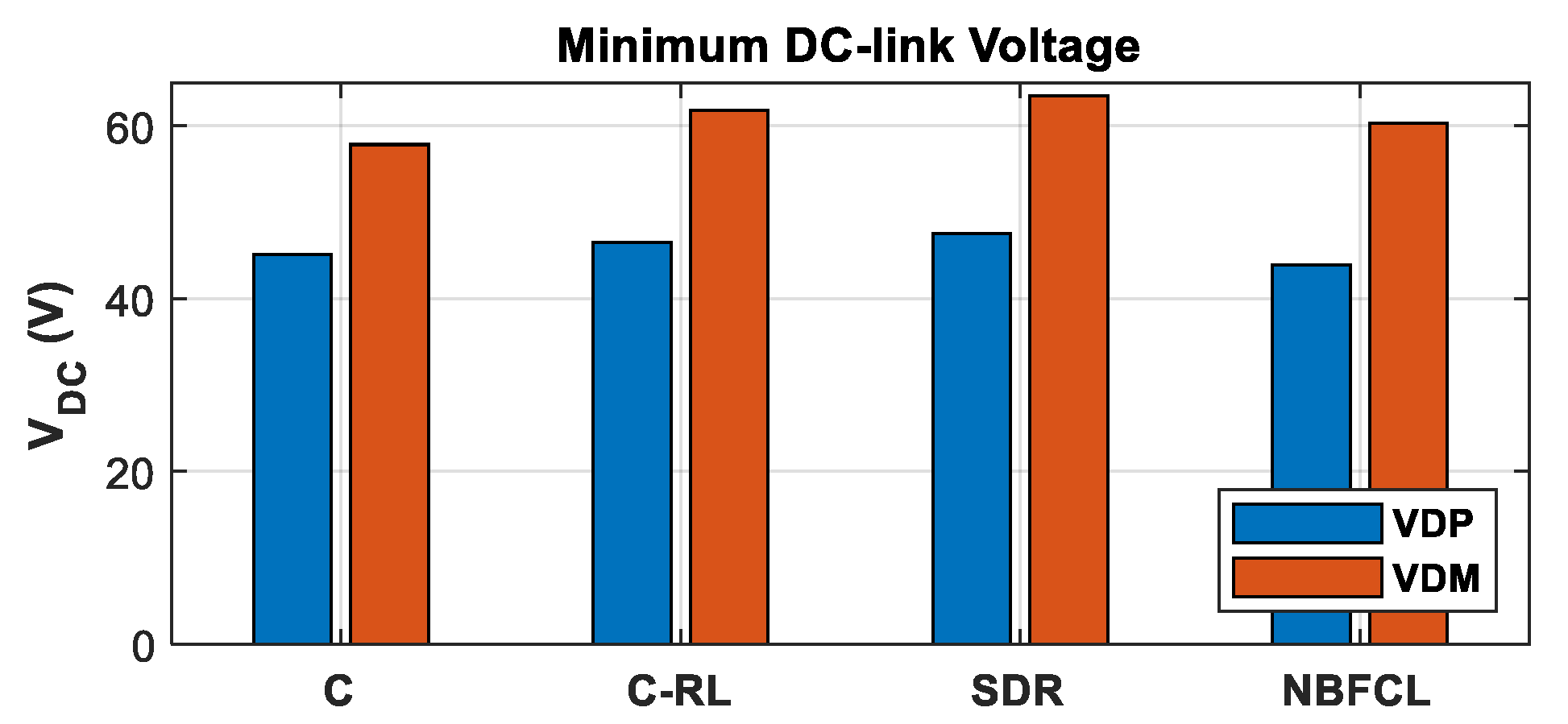
6. Design of Experiment and Simulation Results
6.1. Variable-Displacement Pump (VDP) Configuration
6.2. Variable-Displacement Motor (VDM) Configuration
7. Converter Size Determination
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Greek symbols: | |
| Pitch angle reference | |
| Bulk modulus of the fluid | |
| Torque efficiency of hydraulic pump and motor | |
| Volumetric efficiency of hydraulic pump and motor | |
| Volumetric efficiency of the hydraulic drivetrain | |
| Direct and quadrature components of stator flux | |
| Optimal tip speed ratio | |
| Dynamic viscosity of the fluid | |
| Air density | |
| Electrical and wind turbine torques | |
| Torque of hydraulic pump | |
| Breakaway torque of hydraulic pump and motor | |
| Pump and motor angular velocities | |
| Synchronous angular velocity of the DFIG | |
| Latin symbols: | |
| Maximum power capacity of the wind turbine | |
| Coulomb friction coefficient of the hydraulic pump and motor | |
| Slippage coefficient of the hydraulic pump and motor | |
| Viscous drag coefficient of the hydraulic pump and motor | |
| Hydraulic pump and motor displacements | |
| Optimal pump displacement | |
| Direct and quadrature components of the rotor current | |
| Direct and quadrature components of the stator current | |
| Nominal rotor current | |
| Wind rotor–hydraulic pump inertia | |
| Generator–hydraulic motor inertia | |
| Stator, rotor, and magnetizing inductances | |
| Pressure of the fluid | |
| Pole number of the DFIG | |
| Converter and rotor losses | |
| Aerodynamic power of the wind turbine | |
| Air gap power of stator | |
| Mechanical power of the hydraulic motor | |
| Electrical power of the DFIG | |
| Flow of hydraulic pump and motor | |
| Stator and magnetizing reactive power of the DFIG | |
| Reactive power of the capacitor bank | |
| Radius of the rotor of the wind turbine | |
| Stator and rotor resistance | |
| Target DFIG slip | |
| DFIG slip | |
| Volume of the fluid | |
| Direct and quadrature components of the rotor voltage | |
| Direct and quadrature components of the stator voltage | |
| Wind velocity | |
References
- Artigao, E.; Martín-Martínez, S.; Honrubia-Escribano, A.; Gómez-Lázaro, E. Wind turbine reliability: A comprehensive review towards effective condition monitoring development. Appl. Energy 2018, 228, 1569–1583. [Google Scholar] [CrossRef]
- Tazi, N.; Châtelet, E.; Bouzidi, Y. Using a hybrid cost-FMEA analysis for wind turbine reliability analysis. Energies 2017, 10, 276. [Google Scholar] [CrossRef]
- Taherian-Fard, E.; Sahebi, R.; Niknam, T.; Izadian, A.; Shasadeghi, M. Wind Turbine Drivetrain Technologies. IEEE Trans. Ind. Appl. 2020, 56, 1729–1741. [Google Scholar] [CrossRef]
- Henderson, G.; Gevorgian, V.; Yan, W.; Flynn, D.; Mendieta, W.; Alam, S.M.S. Type 5 wind turbine technologies: Three main candidates compared. In Proceedings of the 23rd Wind & Solar Integration Workshop (WIW 2024), Helsinki, Finland, 8–11 October 2024. [Google Scholar]
- Deldar, M.; Izadian, A.; Anwar, S. A decentralized multivariable controller for hydrostatic wind turbine drivetrain. Asian J. Control 2019, 22, 1038–1051. [Google Scholar] [CrossRef]
- Deldar, M.; Izadian, A.; Anwar, S. Reconfiguration of a wind turbine with hydrostatic drivetrain to improve annual energy production. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 6660–6666. [Google Scholar]
- Jarquin Laguna, A. Steady-State Performance of the Delft Offshore Turbine. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Rajabhandharaks, D.; Hsu, P. Optimal aerodynamic energy capture strategies for hydrostatic transmission wind turbine. In Proceedings of the 2014 IEEE Conference on Technologies for Sustainability (SusTech), Portland, OR, USA, 24–26 July 2014; pp. 140–147. [Google Scholar]
- Do, H.T.; Dang, T.D.; Truong, H.V.A.; Ahn, K.K. Maximum Power Point Tracking and Output Power Control on Pressure Coupling Wind Energy Conversion System. IEEE Trans. Ind. Electron. 2018, 65, 1316–1324. [Google Scholar] [CrossRef]
- Chen, M.; Santos, S.M.; Izadian, A. Torque-Assisting compressed air energy storage hydraulic wind drivetrains. In Proceedings of the 2016 IEEE Power and Energy Conference at Illinois (PECI), Urbana, IL, USA, 19–20 February 2016; pp. 1–5. [Google Scholar]
- Wei, L.; Liu, Z.; Zhao, Y.; Wang, G.; Tao, Y. Modeling and Control of a 600 kW Closed Hydraulic Wind Turbine with an Energy Storage System. Appl. Sci. 2018, 8, 1314. [Google Scholar] [CrossRef]
- Liu, Z.; Tao, Y.; Wei, L.; Zhan, P.; Yue, D. Analysis of Dynamic Characteristics of a 600 kW Storage Type Wind Turbine with Hybrid Hydraulic Transmission. Processes 2019, 7, 397. [Google Scholar] [CrossRef]
- Ai, C.; Zhou, G.; Gao, W.; Guo, J.; Jie, G.; Han, Z.; Kong, X. Research on Quasi-Synchronous Grid-Connected Control of Hydraulic Wind Turbine. IEEE Access 2020, 8, 126092–126108. [Google Scholar] [CrossRef]
- Akbari, R.; Izadian, A.; Weissbach, R. An Approach in Torque Control of Hydraulic Wind Turbine Powertrains. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 979–982. [Google Scholar]
- Akbari, R.; Izadian, A. Reduced-Size Converter in DFIG-Based Wind Energy Conversion System. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4217–4223. [Google Scholar]
- Akbari, R.; Izadian, A.; Weissbach, R. Quasi Self-Excited DFIG-Based Wind Energy Conversion System. IEEE Trans. Ind. Appl. 2021, 57, 2816–2824. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, W.; Nian, H.; Li, J. Improved vector control of DFIG based wind turbine during grid dips and swells. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2010; pp. 511–515. [Google Scholar]
- Lima, F.K.; Luna, A.; Rodriguez, P.; Watanabe, E.H.; Blaabjerg, F. Rotor voltage dynamics in the doubly fed induction generator during grid faults. IEEE Trans. Power Electron. 2009, 25, 118–130. [Google Scholar] [CrossRef]
- Xiang, D.; Ran, L.; Tavner, P.J.; Yang, S. Control of a doubly fed induction generator in a wind turbine during grid fault ride-through. IEEE Trans. Energy Convers. 2006, 21, 652–662. [Google Scholar] [CrossRef]
- Xiao, S.; Yang, G.; Zhou, H.; Geng, H. An LVRT control strategy based on flux linkage tracking for DFIG-based WECS. IEEE Trans. Ind. Electron. 2012, 60, 2820–2832. [Google Scholar] [CrossRef]
- Hu, S.; Lin, X.; Kang, Y.; Zou, X. An improved low-voltage ride-through control strategy of doubly fed induction generator during grid faults. IEEE Trans. Power Electron. 2011, 26, 3653–3665. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, X.; Zhang, X.; Yang, S.; Wang, L. Improved ride-through control of DFIG during grid voltage swell. IEEE Trans. Ind. Electron. 2014, 62, 3584–3594. [Google Scholar] [CrossRef]
- Zhu, D.; Zou, X.; Deng, L.; Huang, Q.; Zhou, S.; Kang, Y. Inductance-emulating control for DFIG-based wind turbine to ride-through grid faults. IEEE Trans. Power Electron. 2016, 32, 8514–8525. [Google Scholar] [CrossRef]
- Suppioni, V.P.; Grilo, A.P.; Teixeira, J.C. Improving network voltage unbalance levels by controlling DFIG wind turbine using a dynamic voltage restorer. Int. J. Electr. Power Energy Syst. 2018, 96, 185–193. [Google Scholar] [CrossRef]
- Sitharthan, R.; Sundarabalan, C.; Devabalaji, K.; Nataraj, S.K.; Karthikeyan, M. Improved fault ride through capability of DFIG-wind turbines using customized dynamic voltage restorer. Sustain. Cities Soc. 2018, 39, 114–125. [Google Scholar] [CrossRef]
- Guo, W.; Xiao, L.; Dai, S. Enhancing low-voltage ride-through capability and smoothing output power of DFIG with a superconducting fault-current limiter–magnetic energy storage system. IEEE Trans. Energy Convers. 2012, 27, 277–295. [Google Scholar] [CrossRef]
- Ananth, D.; Kumar, G.N. Fault ride-through enhancement using an enhanced field oriented control technique for converters of grid connected DFIG and STATCOM for different types of faults. ISA Trans. 2016, 62, 2–18. [Google Scholar] [CrossRef]
- Morren, J.; De Haan, S.W. Ridethrough of wind turbines with doubly-fed induction generator during a voltage dip. IEEE Trans. Energy Convers. 2005, 20, 435–441. [Google Scholar] [CrossRef]
- Morren, J.; De Haan, S.W. Short-circuit current of wind turbines with doubly fed induction generator. IEEE Trans. Energy Convers. 2007, 22, 174–180. [Google Scholar] [CrossRef]
- Li, D.; Zhang, H. A combined protection and control strategy to enhance the LVRT capability of a wind turbine driven by DFIG. In Proceedings of the 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010; pp. 703–707. [Google Scholar]
- Döşoğlu, M.K. Crowbar hardware design enhancement for fault ride through capability in doubly fed induction generator-based wind turbines. ISA Trans. 2020, 104, 321–328. [Google Scholar] [CrossRef]
- Liang, J.; Howard, D.F.; Restrepo, J.A.; Harley, R.G. Feedforward transient compensation control for DFIG wind turbines during both balanced and unbalanced grid disturbances. IEEE Trans. Ind. Appl. 2013, 49, 1452–1463. [Google Scholar] [CrossRef]
- Yang, J.; Fletcher, J.E.; O’Reilly, J. A series-dynamic-resistor-based converter protection scheme for doubly-fed induction generator during various fault conditions. IEEE Trans. Energy Convers. 2010, 25, 422–432. [Google Scholar] [CrossRef]
- Justo, J.J.; Mwasilu, F.; Jung, J.-W. Enhanced crowbarless FRT strategy for DFIG based wind turbines under three-phase voltage dip. Electr. Power Syst. Res. 2017, 142, 215–226. [Google Scholar] [CrossRef]
- Soliman, H.; Wang, H.; Zhou, D.; Blaabjerg, F.; Marie, M.I. Sizing of the series dynamic breaking resistor in a doubly fed induction generator wind turbine. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 1842–1846. [Google Scholar]
- Hossain, M.E. A non-linear controller based new bridge type fault current limiter for transient stability enhancement of DFIG based Wind Farm. Electr. Power Syst. Res. 2017, 152, 466–484. [Google Scholar] [CrossRef]
- Firouzi, M.; Gharehpetian, G.B. LVRT performance enhancement of DFIG-based wind farms by capacitive bridge-type fault current limiter. IEEE Trans. Sustain. Energy 2017, 9, 1118–1125. [Google Scholar] [CrossRef]
- Fereidouni, A.; Masoum, M.A.; Hosseinimehr, T.; Moghbel, M. Performance of LR-type solid-state fault current limiter in improving power quality and transient stability of power network with wind turbine generators. Int. J. Electr. Power Energy Syst. 2016, 74, 172–186. [Google Scholar] [CrossRef]
- Hossain, M.E. Low voltage ride-through capability improvement methods for DFIG based wind farm. J. Electr. Syst. Inf. Technol. 2018, 5, 550–561. [Google Scholar] [CrossRef]
- Mahela, O.P.; Gupta, N.; Khosravy, M.; Patel, N. Comprehensive overview of low voltage ride through methods of grid integrated wind generator. IEEE Access 2019, 7, 99299–99326. [Google Scholar] [CrossRef]
- Deldar, M. Decentralized Multivariable Modeling and Control of Wind Turbine with Hydrostatic Drive-Train. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2016. Available online: https://docs.lib.purdue.edu/dissertations/AAI10182440 (accessed on 30 December 2020).
- Herbert, E.M. Hydraulic Control Systems; John Willy and Sons Inc.: Hoboken, NJ, USA, 1967. [Google Scholar]
- Al-Shetwi, A.Q.; Sujod, M.Z. Grid-connected photovoltaic power plants: A review of the recent integration requirements in modern grid codes. Int. J. Energy Res. 2018, 42, 1849–1865. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Chang, S.-M.; Mandal, P. Grid-connected wind power plants: A survey on the integration requirements in modern grid codes. IEEE Trans. Ind. Appl. 2019, 55, 5584–5593. [Google Scholar] [CrossRef]
- Tarafdar Hagh, M.; Khalili, T. A review of fault ride through of PV and wind renewable energies in grid codes. Int. J. Energy Res. 2019, 43, 1342–1356. [Google Scholar] [CrossRef]
- Ahmed, S.D.; Al-Ismail, F.S.; Shafiullah, M.; Al-Sulaiman, F.A.; El-Amin, I.M. Grid integration challenges of wind energy: A review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- Dicorato, M.; Forte, G.; Trovato, M. Wind farm stability analysis in the presence of variable-speed generators. Energy 2012, 39, 40–47. [Google Scholar] [CrossRef]
- Zin, A.A.B.M.; HA, M.P.; Khairuddin, A.B.; Jahanshaloo, L.; Shariati, O. An overview on doubly fed induction generators′ controls and contributions to wind based electricity generation. Renew. Sustain. Energy Rev. 2013, 27, 692–708. [Google Scholar] [CrossRef]
- Huang, P.-H.; El Moursi, M.S.; Xiao, W.; Kirtley, J.L. Fault ride-through configuration and transient management scheme for self-excited induction generator-based wind turbine. IEEE Trans. Sustain. Energy 2013, 5, 148–159. [Google Scholar] [CrossRef]





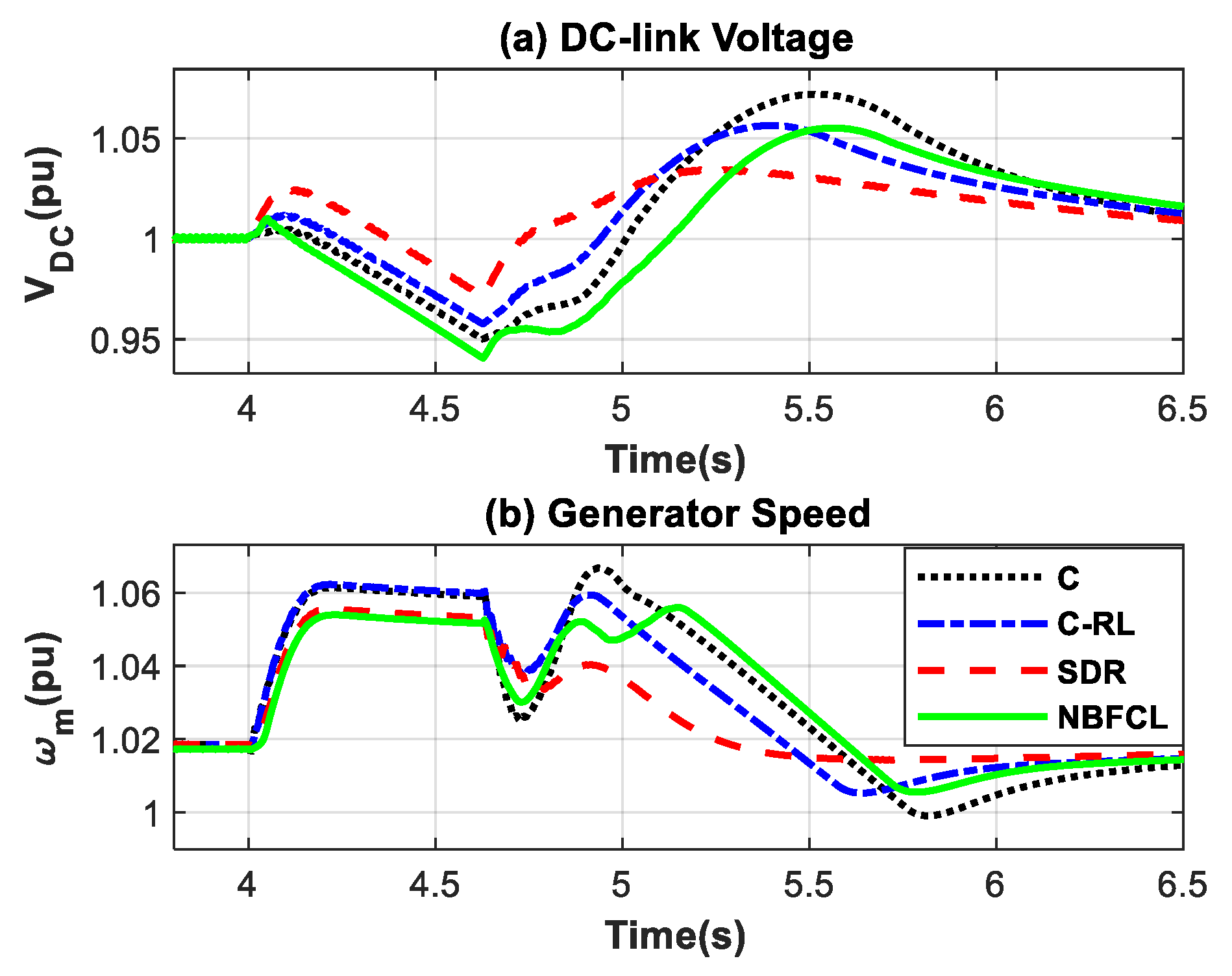
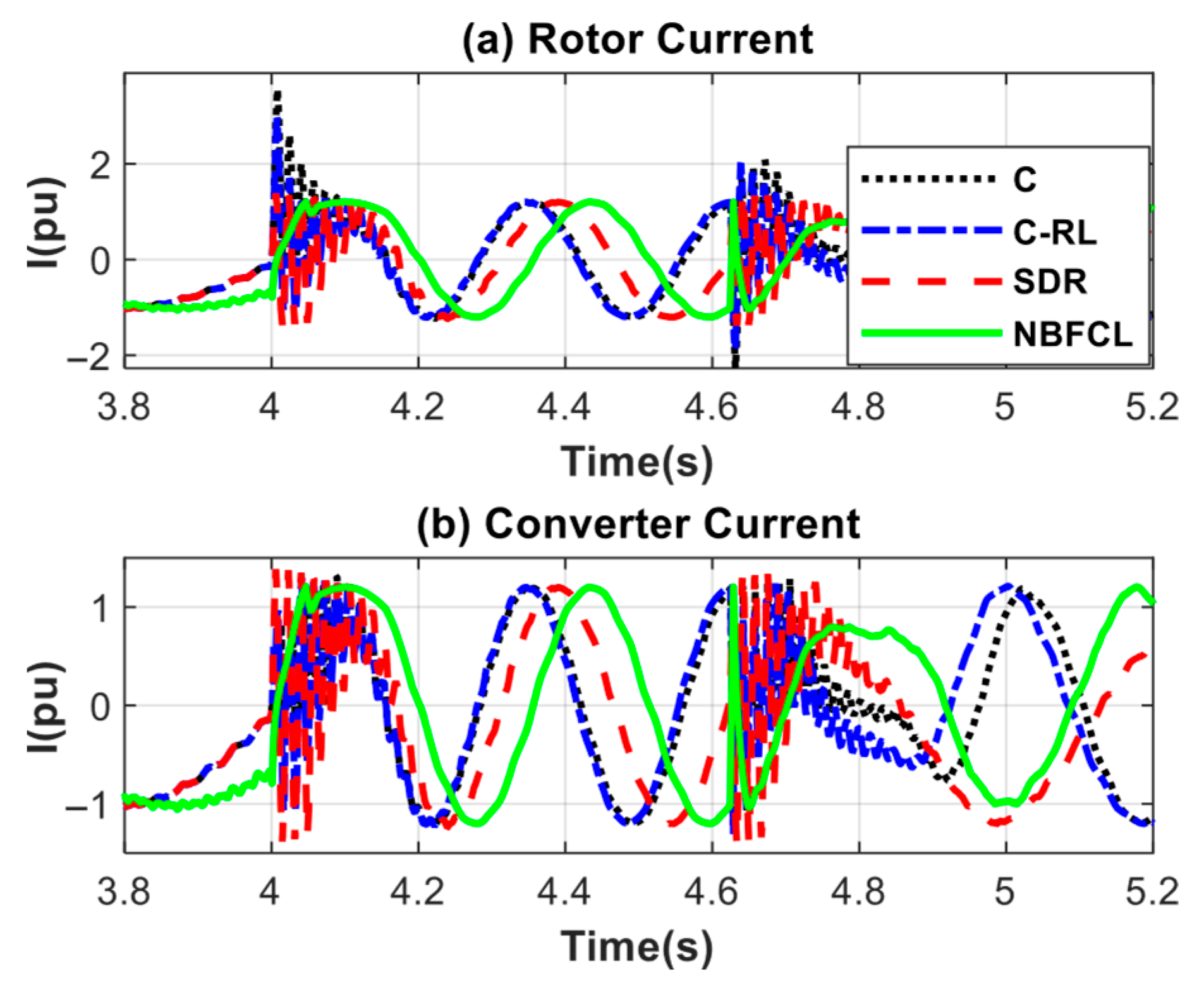
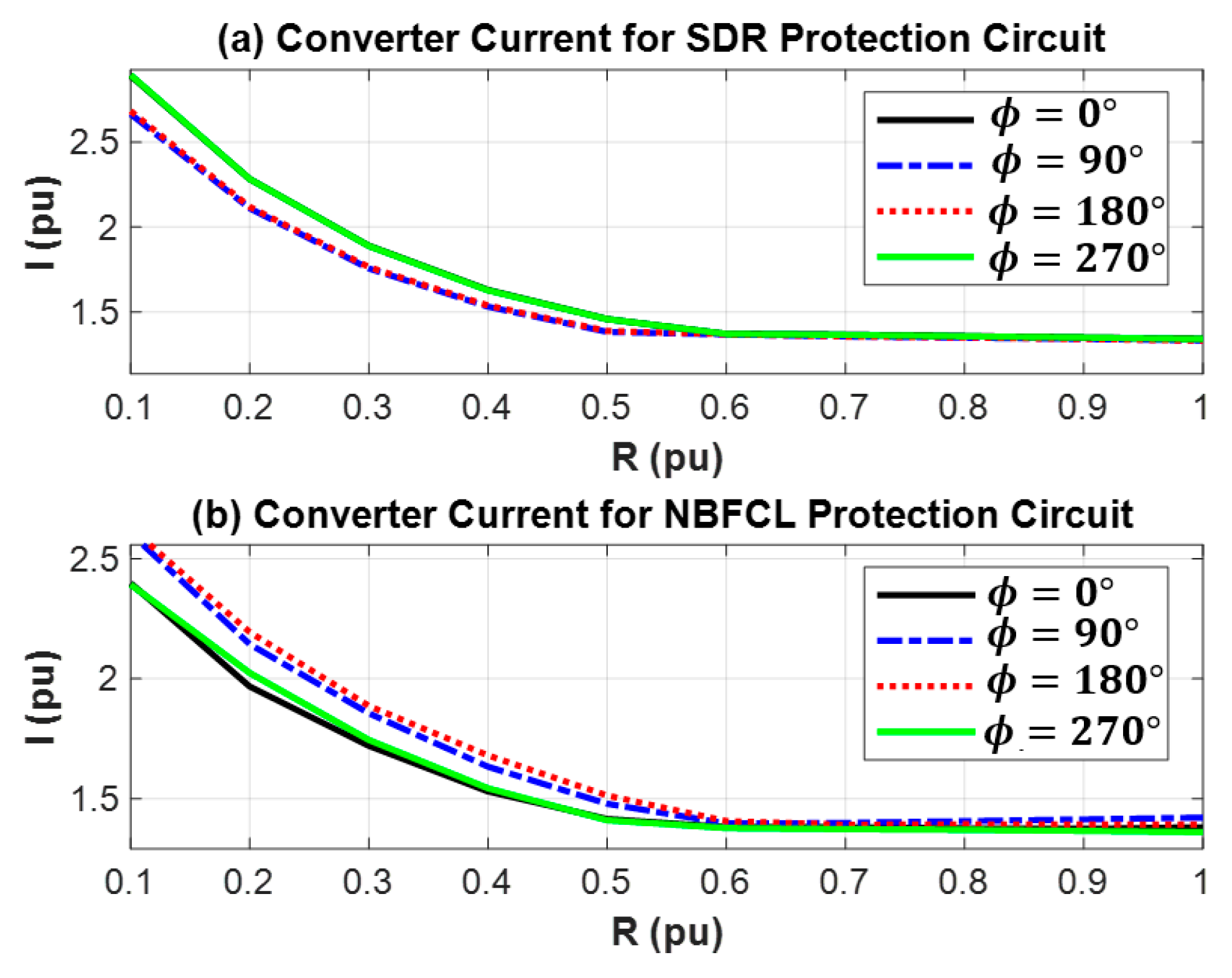
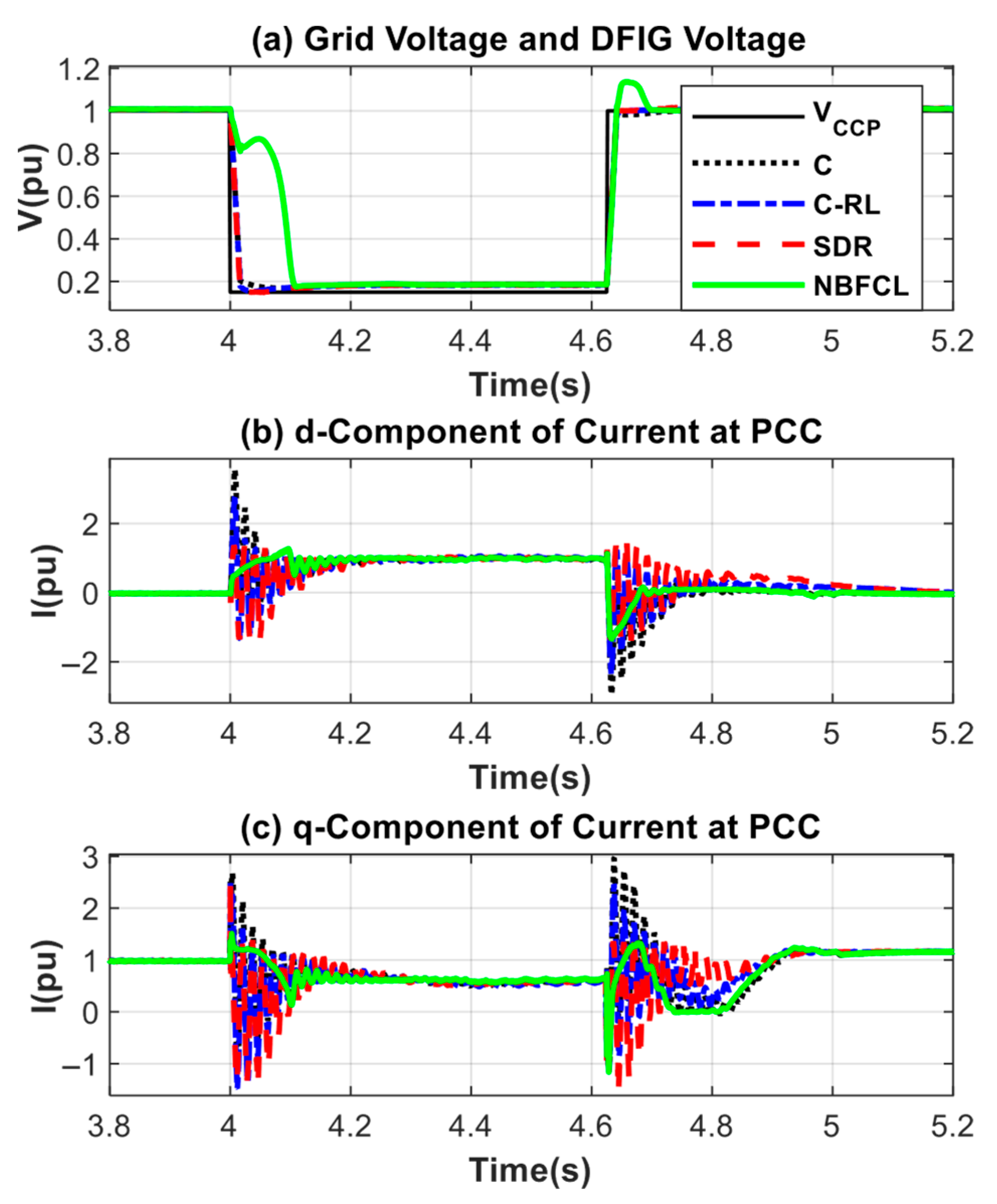
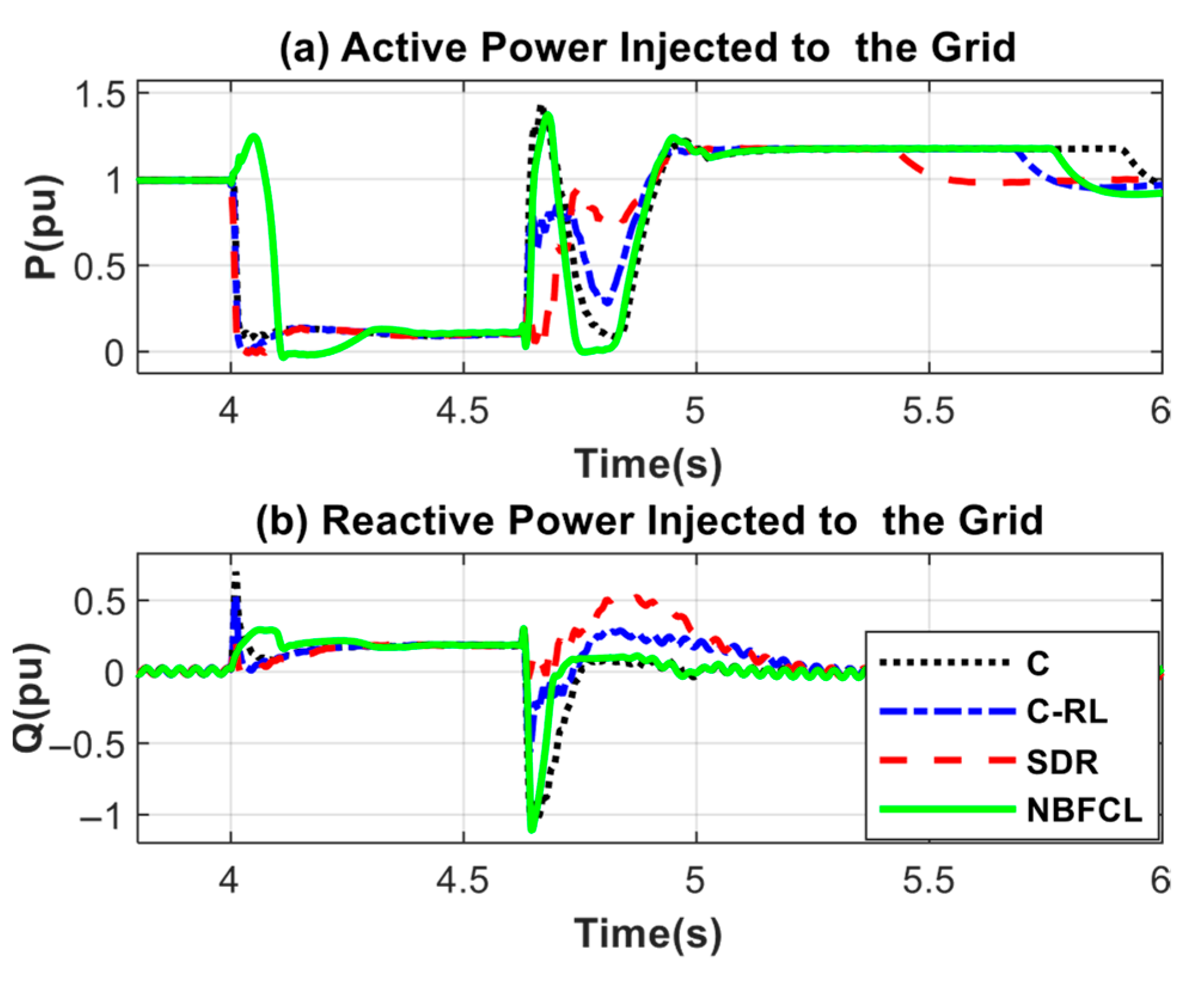
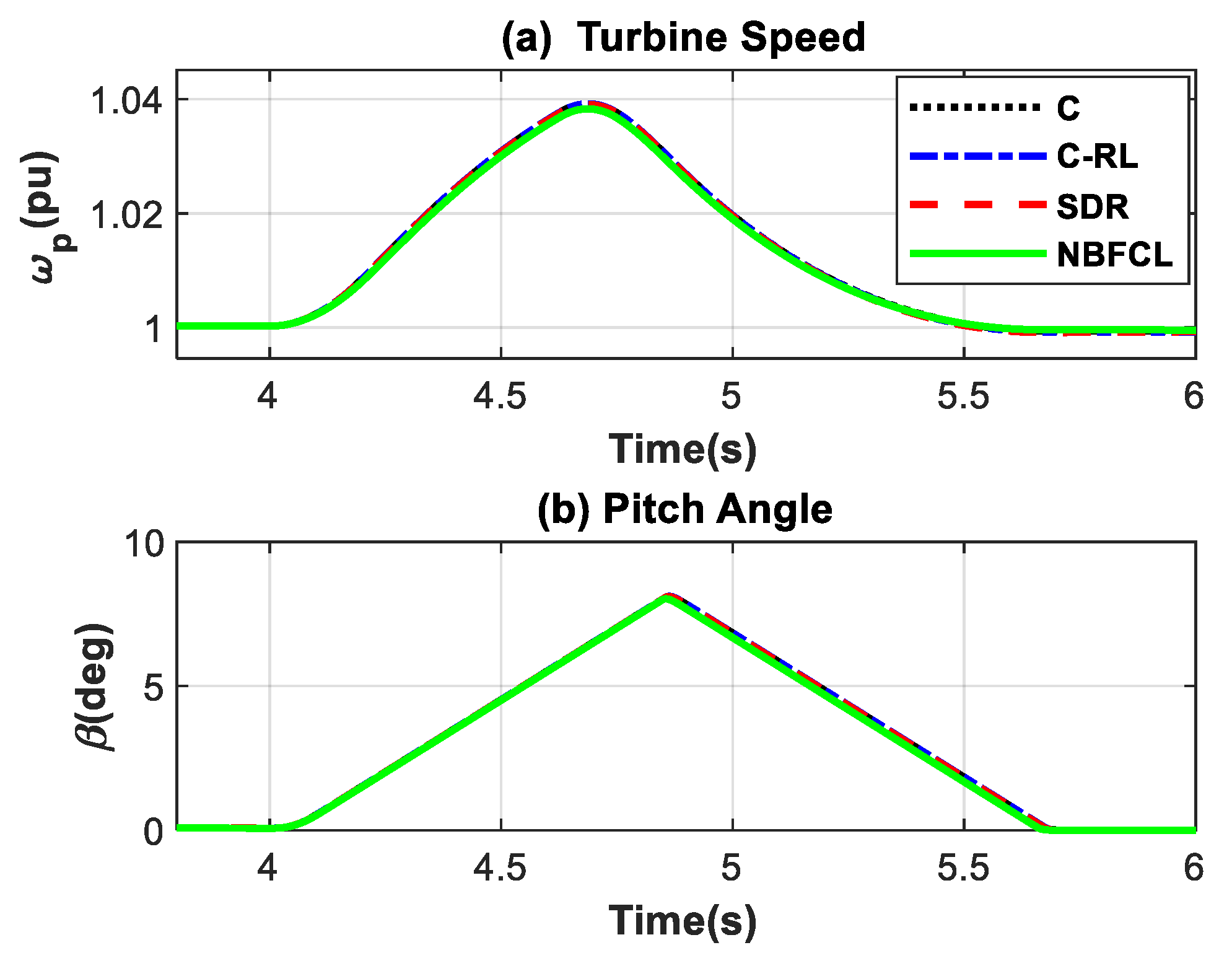
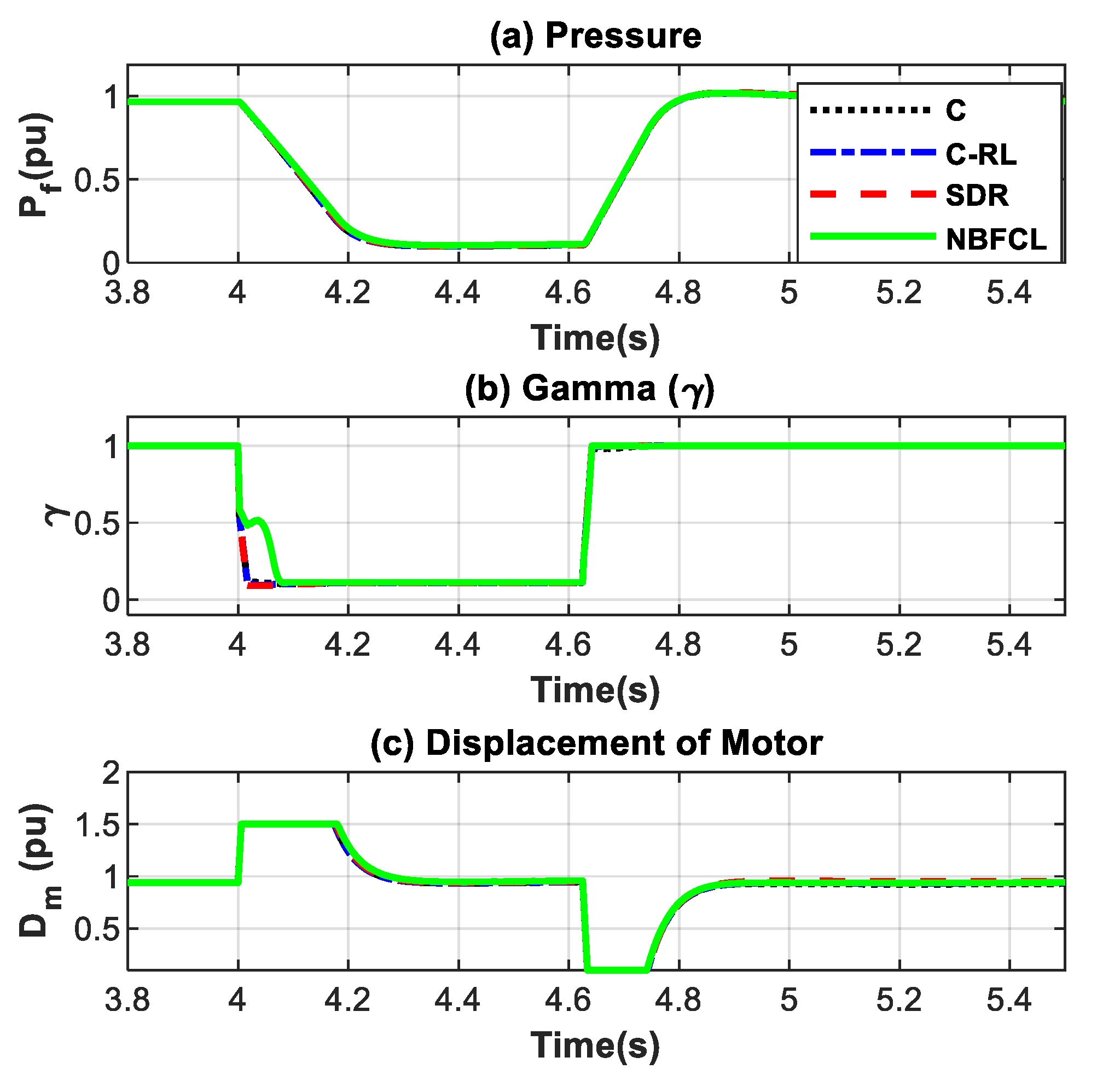

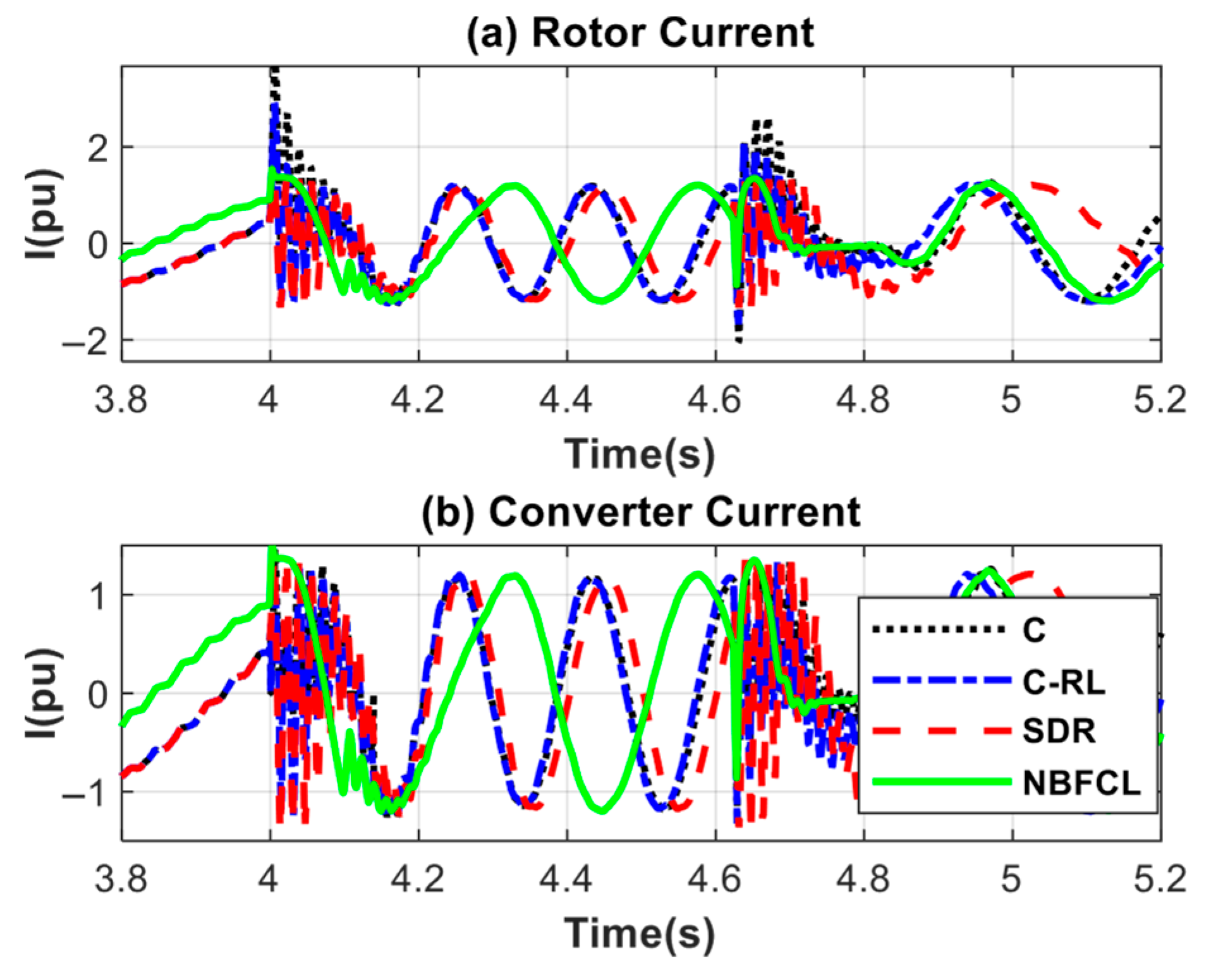

| Switches with a Constant State | Switches That Are Activated or Deactivated During a Fault | |
|---|---|---|
| SDR | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbari, R.; Izadian, A. Low-Voltage Ride Through Capability Analysis of a Reduced-Size DFIG Excitation Utilized in Split-Shaft Wind Turbines. J. Low Power Electron. Appl. 2025, 15, 41. https://doi.org/10.3390/jlpea15030041
Akbari R, Izadian A. Low-Voltage Ride Through Capability Analysis of a Reduced-Size DFIG Excitation Utilized in Split-Shaft Wind Turbines. Journal of Low Power Electronics and Applications. 2025; 15(3):41. https://doi.org/10.3390/jlpea15030041
Chicago/Turabian StyleAkbari, Rasoul, and Afshin Izadian. 2025. "Low-Voltage Ride Through Capability Analysis of a Reduced-Size DFIG Excitation Utilized in Split-Shaft Wind Turbines" Journal of Low Power Electronics and Applications 15, no. 3: 41. https://doi.org/10.3390/jlpea15030041
APA StyleAkbari, R., & Izadian, A. (2025). Low-Voltage Ride Through Capability Analysis of a Reduced-Size DFIG Excitation Utilized in Split-Shaft Wind Turbines. Journal of Low Power Electronics and Applications, 15(3), 41. https://doi.org/10.3390/jlpea15030041






