Microstrip Line Modeling Taking into Account Dispersion Using a General-Purpose SPICE Simulator
Abstract
1. Introduction
- Qucsator is an open-source simulation backend that supports the simulation of microstrip lines and advanced RF features [17,18]. The main disadvantage of this simulator is its very poor SPICE compatibility. It uses an unique netlist syntax and supports only a limited subset of the SPICE model. This makes difficult to integrate Qucsator into open PDKs.
- Scikit-RF [19] is an extension package for the Python programming language. It enables the calculation of RF circuits using Python scripts and allows us to define the transmission line structure and more complex schematics. This tool does not allow us to import SPICE models.
- The Ngspice [20] simulation backend introduces RF simulation features, including scattering matrix (S-parameter) analysis. Ngspice has good compatibility with SPICE models provided by electronic component vendors. This simulation backend may be used from Qucs-S [21] or KiCAD GUI. However, the transmission line models in Ngspice are represented only by lossy and lossless lines, as well as the URC line.
- Using a parametrized subnetlist (macromodel) is the most obvious strategy [26]. This device representation method may have performance issues for complex models. The frequency dependency may be not allowed in subnetlist parameters for some SPICE backends because of netlist syntax restrictions.
- The Verilog-A [27] hardware description language (HDL) is the preferred method for adding a model for modern circuit simulators. Verilog-A allows researchers to compile model as a binary shared module and attach it to the simulator. Recompiling and patching the simulation backend itself is not required. Ngspice supports Verilog-A using the OpenVAF compiler [28]. However, Verilog-A cannot be used to the represent transmission line model. Verilog-A describes an electronics device as its current–voltage (IV) curve. In fact, this device is represented as a network of controlled current and voltage sources. This does not allow researchers to define a model in the frequency domain using the two-port circuit matrices, which is required for transmission line representation.
- XSPICE CodeModels [29,30] could be an alternative to Verilog-A models. The XSPICE models could be defined separately for the frequency and time domains. This allows researchers to define frequency-domain models as the impedance or admittance matrix of a two-port circuit. The disadvantage of XSPICE is that it requires researchers to have C programming language knowledge for model design.
2. Model Equations
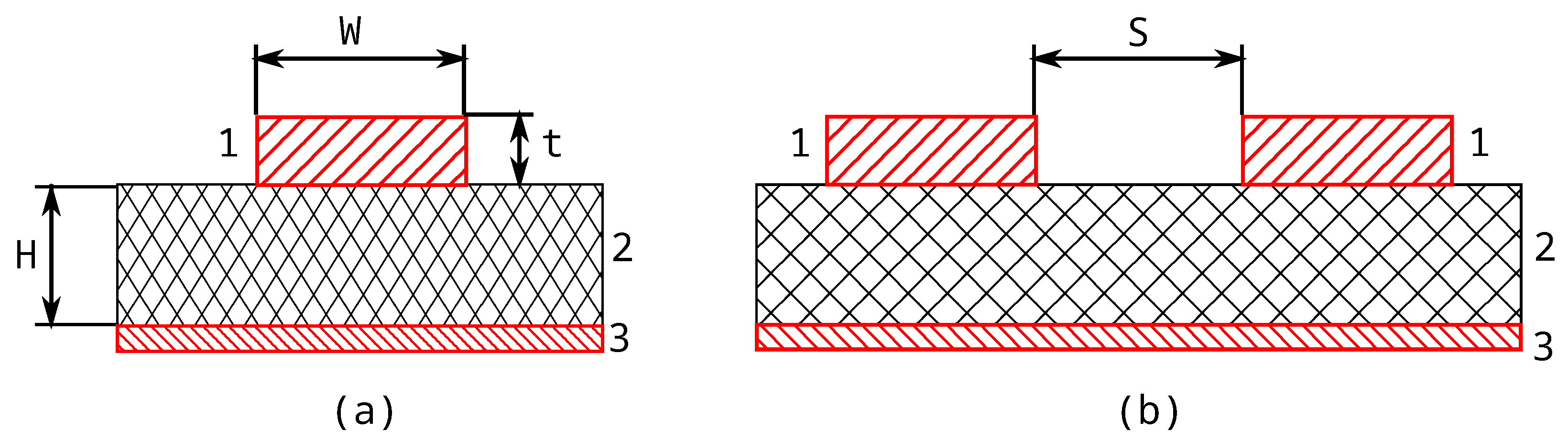
2.1. Microstrip Line and Coupled Microstrips
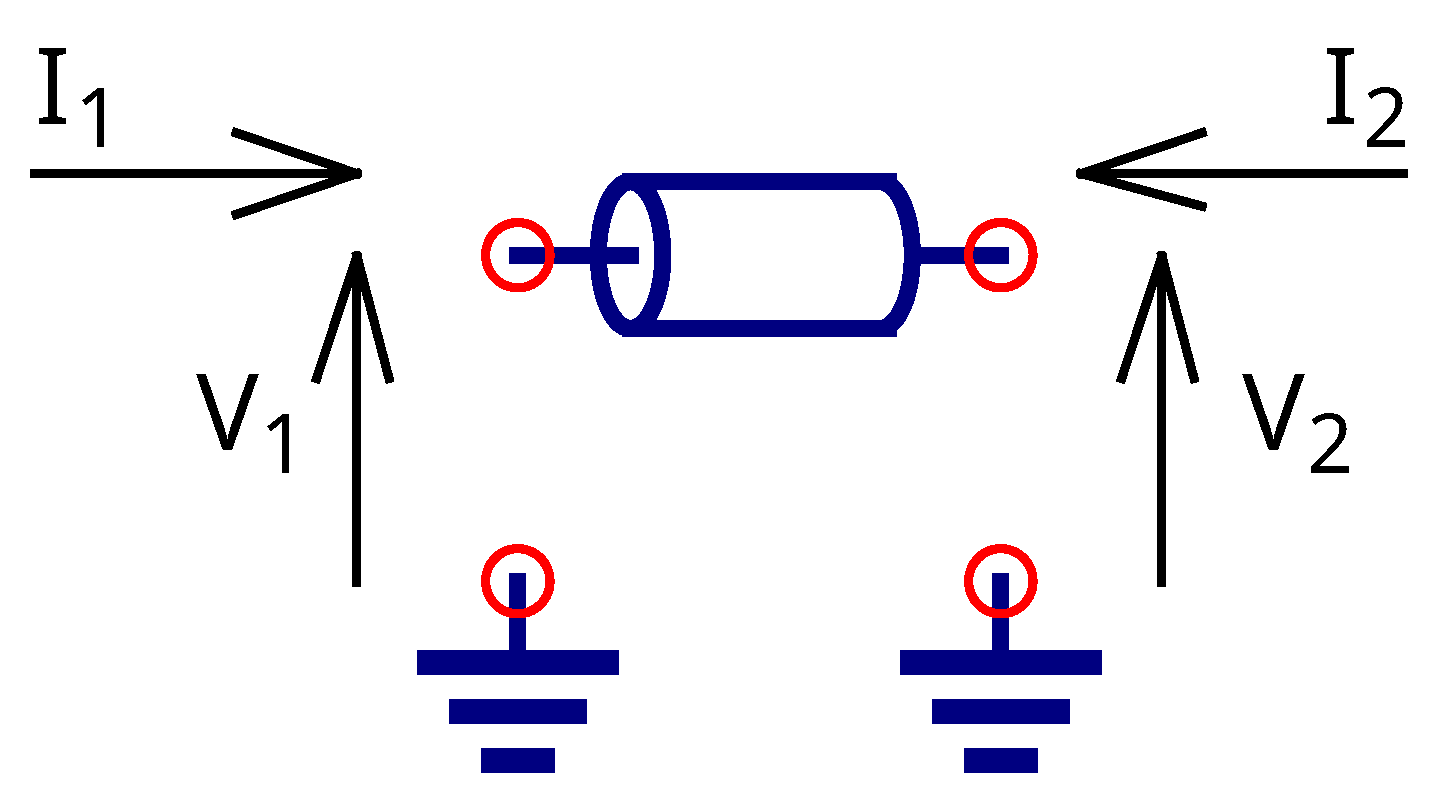
2.2. Generic Transmission Line
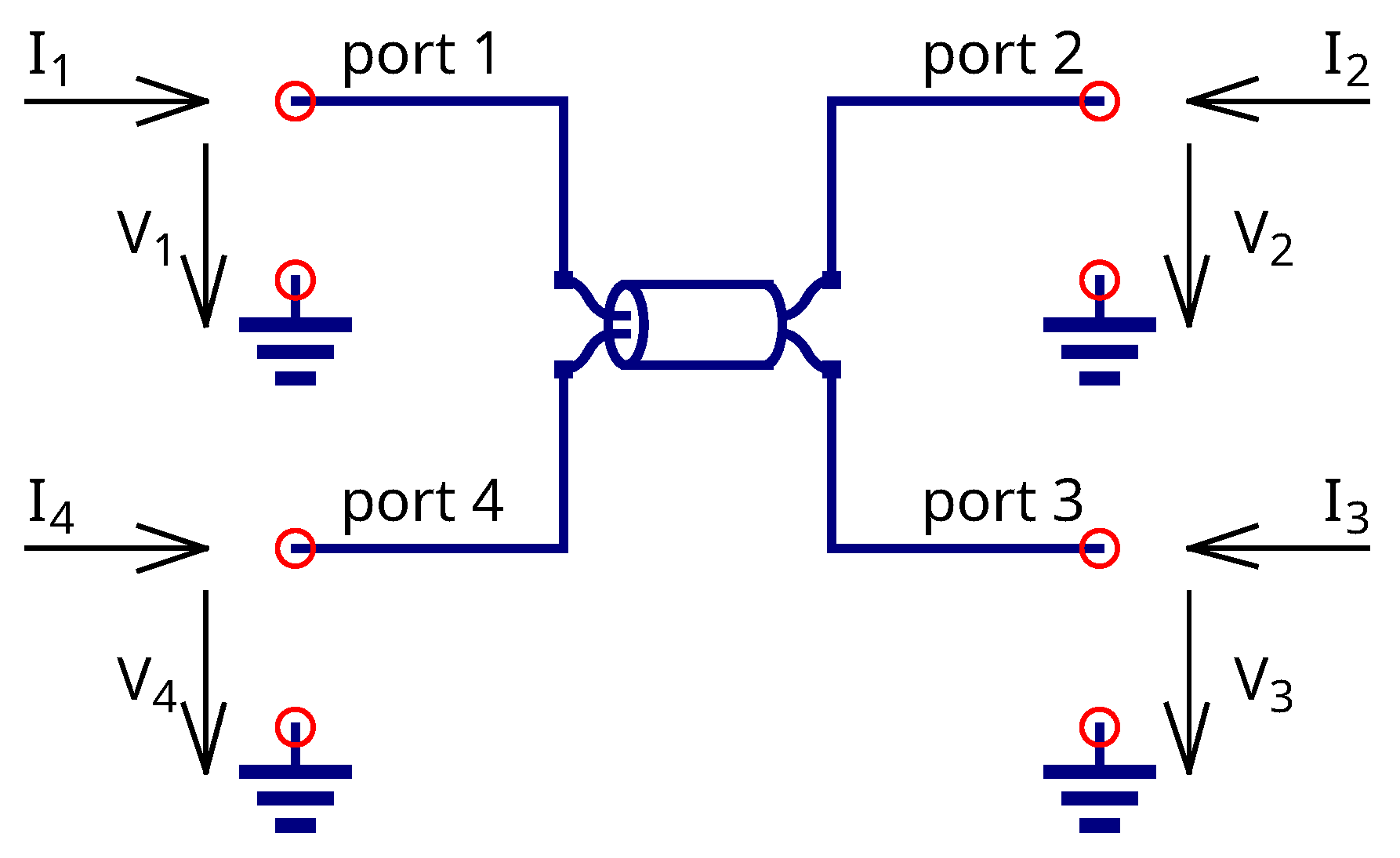
2.3. Generic Coupled Transmission Lines
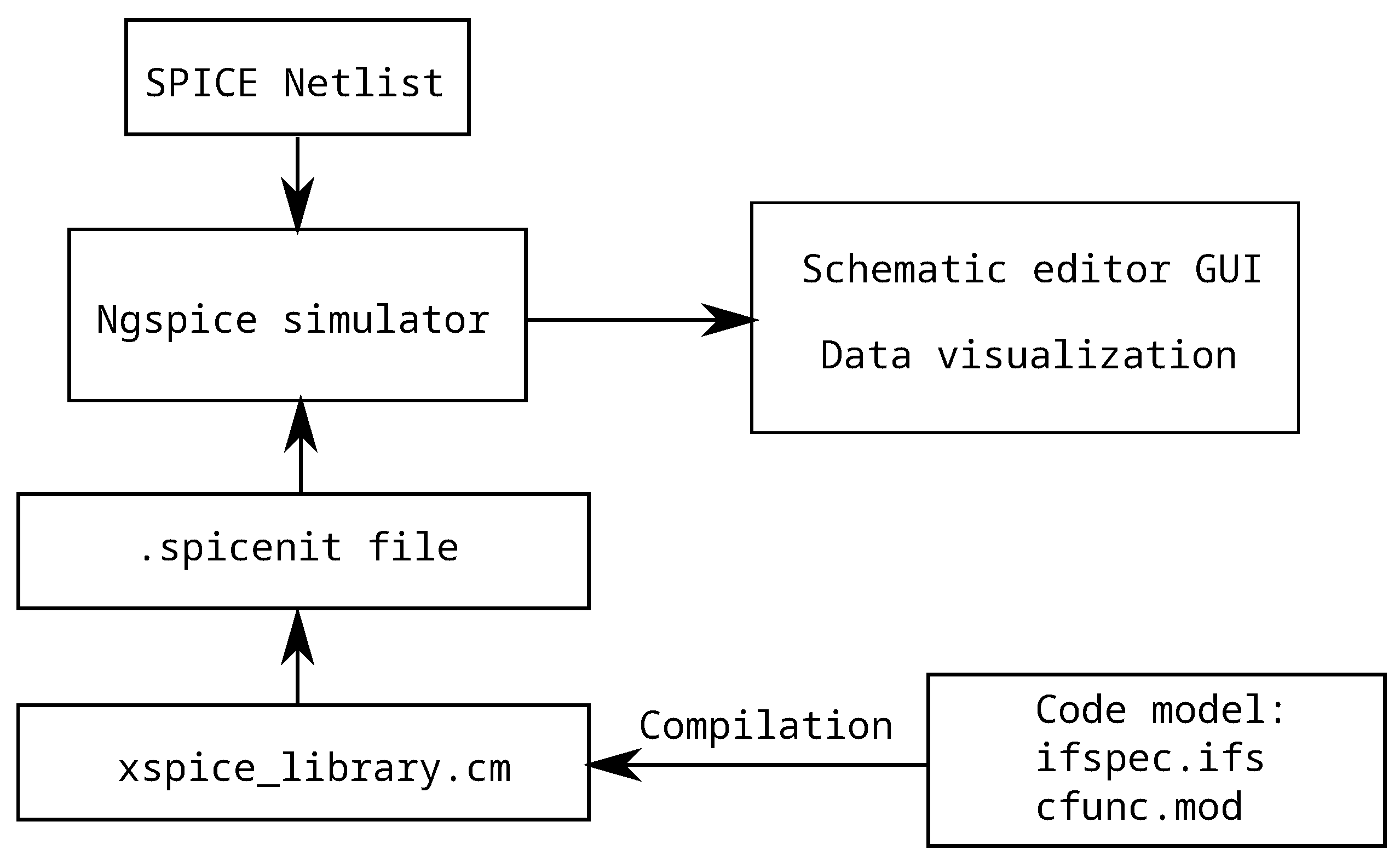
3. XSPICE Model Generation
3.1. Common XSPICE Model Structure
- 1.
- ifspec.ifs, which contains the model interface description, i.e., port and parameter descriptions, including allowed boundaries.
- 2.
- cfunc.mod, which contains model source code and internal logic. Here, we place one or more equations that describe component static current–voltage curves and other non-linear dynamic properties.
3.2. Transmission Line Models Structure
| Listing 1. The pseudocode of the transmission line XSPICE model. |
 |
| Listing 2. The implementation of the transmission line XSPICE model. |
| * Microstrip line instance A_MS1 %hd(p1 0) %hd(p2 0) %vd(p1 0) %vd(p2 0) MODEL_MS1 * Microstrip modelcard .MODEL MODEL_MS1 MLIN(l=100E-3 w=1E-3 model=0 disp=0 + er=4.5 h=1.55E-3 t=35u tand=0.0167 rho=1.7E-8 d=0.15E-6 ) * Coupled microstrips instance A_MS2 %hd(p1 0) %hd(p2 0) %hd(p3 0) %hd(p4 0) + %vd(p1 0) %vd(p2 0) %vd(p3 0) %vd(p4 0) MODEL_MS2 * Coupled microstrip modelcard .MODEL MODEL_MS2 CPMLIN(L=20e-3 W=1e-3 S=0.3e-3 model=0 disp=0 + er=4.5 h=1.55E-3 t=35u tand=0.0167 rho=1.7E-8 d=0.15E-6 ) |
4. Simulation Results
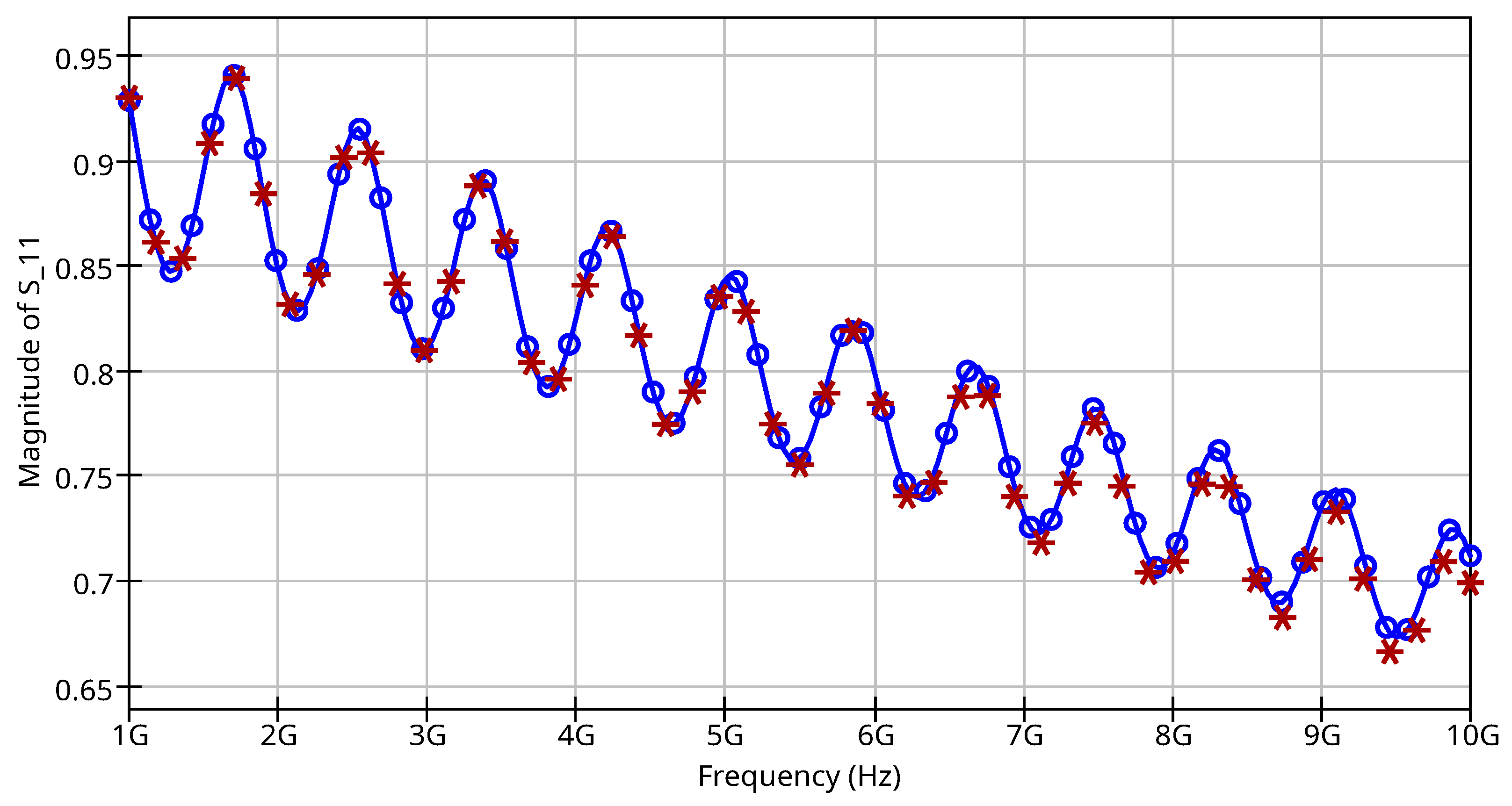
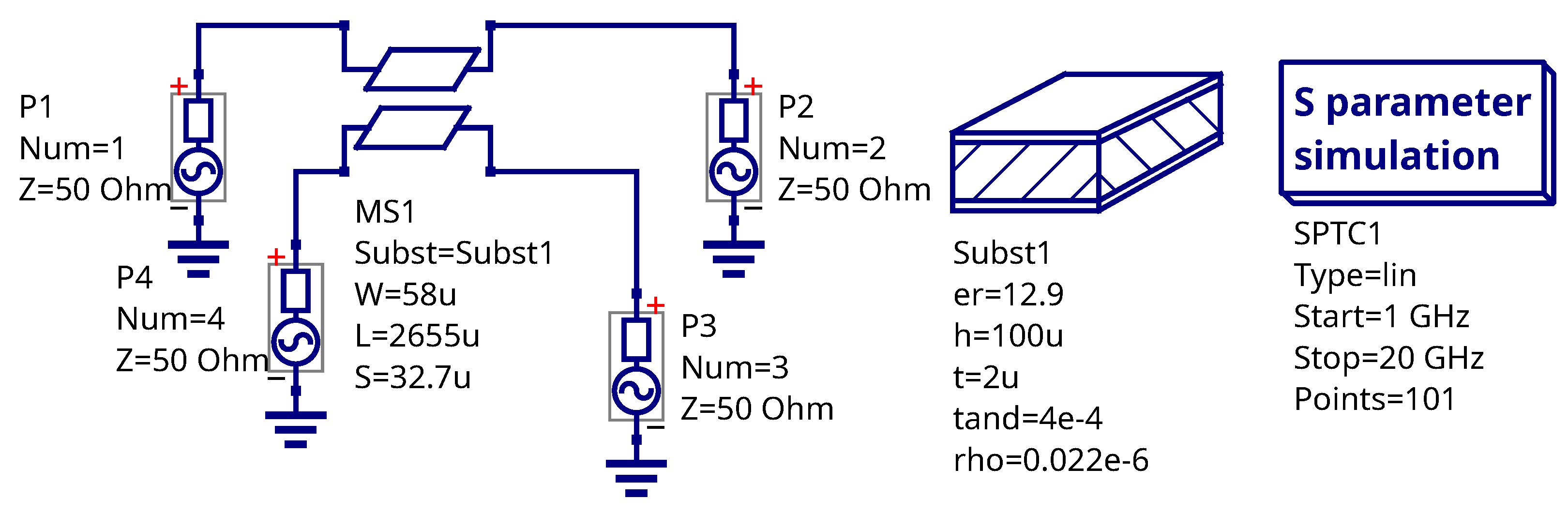
4.1. XSPICE Model Verification
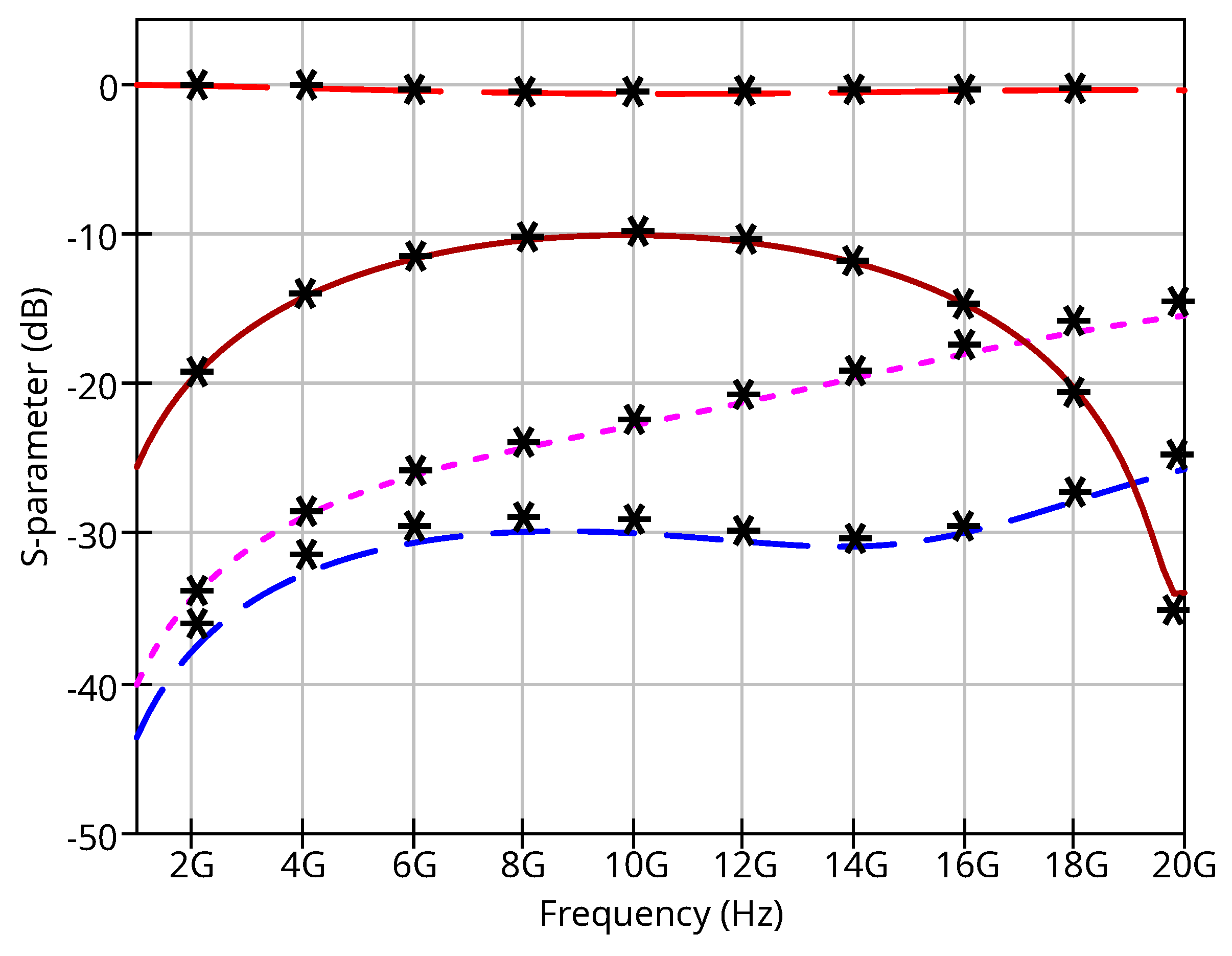
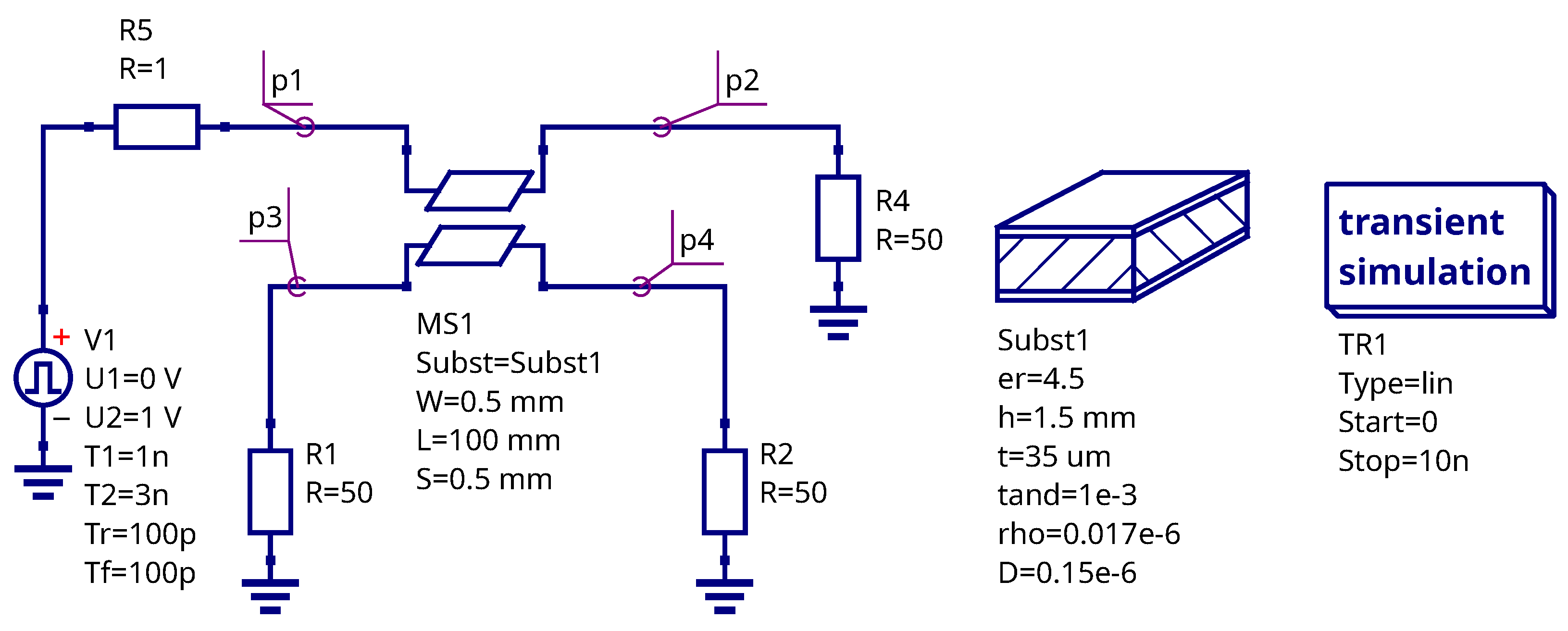
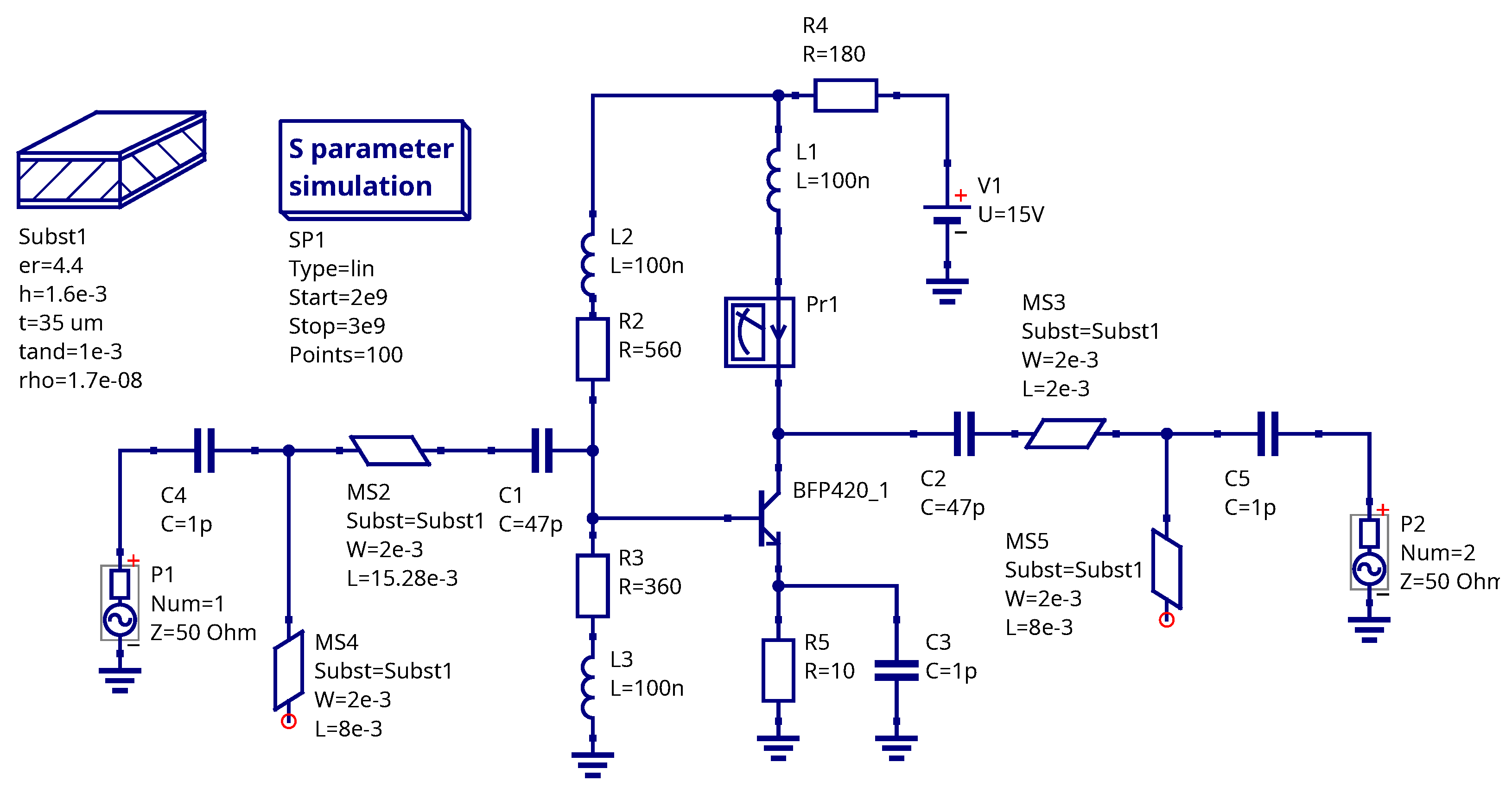
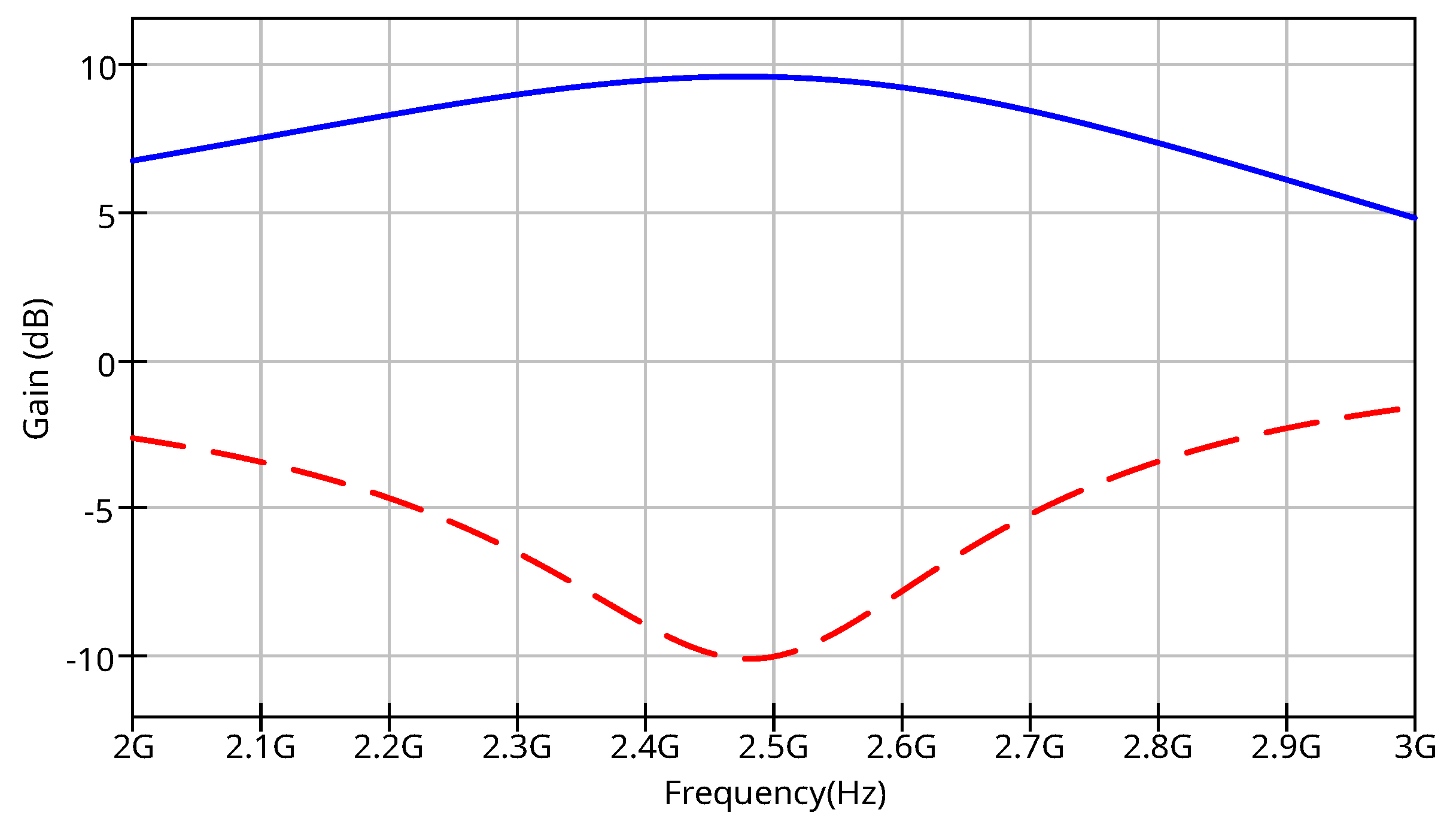
4.2. LNA Simulation Example
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vendelin, G.D.; Pavio, A.M.; Rohde, U.L.; Rudolph, M. Microwave Circuit Design Using Linear and Nonlinear Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Harikirubha, S.; Baranidharan, V.; Saranya, S.; Keerthana, K.; Nandhini, M. Different shapes of microstrip line design using FR4 substrate materials—A comprehensive review. Mater. Today Proc. 2021, 45, 3404–3408. [Google Scholar] [CrossRef]
- Shaban, M. Design and Modeling of a Reconfigurable Multiple Input, Multiple Output Antenna for 24 GHz Radar Sensors. Modelling 2025, 6, 2. [Google Scholar] [CrossRef]
- Li, C.; Ma, Z.H.; Chen, J.X.; Wang, M.N.; Huang, J.M. Design of a Compact Ultra-Wideband Microstrip Bandpass Filter. Electronics 2023, 12, 1728. [Google Scholar] [CrossRef]
- Colaiuda, D.; Ulisse, I.; Ferri, G. Rectifiers’ Design and Optimization for a Dual-Channel RF Energy Harvester. J. Low Power Electron. Appl. 2020, 10, 11. [Google Scholar] [CrossRef]
- Pirouznia, P.; Ganji, B.A. Analytical optimization of high performance and high quality factor MEMS spiral inductor. Prog. Electromagn. Res. M 2014, 34, 171–179. [Google Scholar] [CrossRef]
- Kimionis, J.; Georgiadis, A.; Daskalakis, S.N.; Tentzeris, M.M. A printed millimetre-wave modulator and antenna array for backscatter communications at gigabit data rates. Nat. Electron. 2021, 4, 439–446. [Google Scholar] [CrossRef]
- Dobush, I.M.; Sheyerman, F.I.; Babak, L.I.; Svetlichnyi, Y.A. A 0.1–4.5 GHz MMIC Controlled Digital Step Attenuator Based on SiGe. Instruments Exp. Tech. 2019, 62, 175–184. [Google Scholar] [CrossRef]
- Grabinski, W.; Scholz, R.; Verley, J.; Keiter, E.R.; Vogt, H.; Warning, D.; Nenzi, P.; Lannutti, F.; Salfelder, F.; Davis, A.; et al. FOSS CAD for the Compact Verilog—A Model Standardization in Open Access PDKs. In Proceedings of the 2024 8th IEEE Electron Devices Technology & Manufacturing Conference (EDTM), Bangalore, India, 3–6 March 2024; pp. 1–3. [Google Scholar] [CrossRef]
- Herman, K.; Herfurth, N.; Henkes, T.; Andreev, S.; Scholz, R.; Müller, M.; Krattenmacher, M.; Pretl, H.; Grabinski, W. On the Versatility of the IHP BiCMOS Open Source and Manufacturable PDK: A step towards the future where anybody can design and build a chip. IEEE Solid-State Circuits Mag. 2024, 16, 30–38. [Google Scholar] [CrossRef]
- Ozdol, A.B.; Kandis, H.; Burak, A.; Ozkan, T.A.; Kaynak, M.; Gurbuz, Y. A High Linearity 6 GHz LNA in 130 nm SiGe Technology. In Proceedings of the 2022 17th European Microwave Integrated Circuits Conference (EuMIC), Milan, Italy, 26–27 September 2022; pp. 68–71. [Google Scholar] [CrossRef]
- Herman, K.; Scholz, R.; Andreev, S. Reflections on the First European Open Source PDK by IHP—Experiences After One Year and Future Activities. In Proceedings of the 2024 31st International Conference on Mixed Design of Integrated Circuits and System (MIXDES), Gdansk, Poland, 27–28 June 2024; pp. 19–22. [Google Scholar] [CrossRef]
- Kaynak, M.; Wietstruck, M.; Zhang, W.; Drews, J.; Scholz, R.; Knoll, D.; Korndörfer, F.; Wipf, C.; Schulz, K.; Elkhouly, M.; et al. RF-MEMS switch module in a 0.25 um BiCMOS technology. In Proceedings of the 2012 IEEE 12th Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems, Virtual, 16–18 January 2012; pp. 25–28. [Google Scholar] [CrossRef]
- Vladirmirescu, A. Shaping the History of SPICE. IEEE Solid-State Circuits Mag. 2011, 3, 36–39. [Google Scholar] [CrossRef]
- Nałęcz, M. SPICE-Compatible Circuit Models of Multiports Described by Scattering Parameters with Arbitrary Reference Impedances. Electronics 2024, 13, 2260. [Google Scholar] [CrossRef]
- Abu Qahouq, J.A.; Al-Smadi, M.K. Modeling and Simulation of a Planar Permanent Magnet On-Chip Power Inductor. Modelling 2024, 5, 339–351. [Google Scholar] [CrossRef]
- Zonca, A.; Roucaries, B.; Williams, B.; Rubin, I.; D’Arcangelo, O.; Meinhold, P.; Lubin, P.; Franceschet, C.; Jahn, S.; Mennella, A.; et al. Modeling the frequency response of microwave radiometers with QUCS. J. Instrum. 2010, 5, T12001. [Google Scholar] [CrossRef]
- Suana, J.A.R.; Montoya, J.J.M.; Alarcon, O.C.; Navarro, E.A. Using Open-Source Software QucsStudio to Design a Microwave Amplifier for SDR Applications. In Proceedings of the 2021 IEEE URUCON, Montevideo, Uruguay, 24–26 November 2021; pp. 177–181. [Google Scholar] [CrossRef]
- Arsenovic, A.; Hillairet, J.; Anderson, J.; Forsten, H.; Rieß, V.; Eller, M.; Sauber, N.; Weikle, R.; Barnhart, W.; Forstmayr, F. Scikit-rf: An Open Source Python Package for Microwave Network Creation, Analysis, and Calibration [Speaker’s Corner]. IEEE Microw. Mag. 2022, 23, 98–105. [Google Scholar] [CrossRef]
- Lannutti, F.; Nenzi, P.; Olivieri, M. KLU sparse direct linear solver implementation into NGSPICE. In Proceedings of the Proceedings of the 19th International Conference Mixed Design of Integrated Circuits and Systems-MIXDES 2012, Rzeszow, Poland, 24–26 May 2012; pp. 69–73. [Google Scholar]
- Brinson, M.; Kuznetsov, V. Qucs-0.0.19S: A new open-source circuit simulator and its application for hardware design. In Proceedings of the 2016 International Siberian Conference on Control and Communications (SIBCON), Moscow, Russia, 12–14 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Hammerstad, E.; Jensen, O. Accurate Models for Microstrip Computer-Aided Design. In Proceedings of the 1980 IEEE MTT-S International Microwave symposium Digest, San Antonio, TX, USA, 28–30 May 1980; pp. 407–409. [Google Scholar] [CrossRef]
- Kirschning, M.; Jansen, R. Accurate Wide-Range Design Equations for the Frequency-Dependent Characteristics of Parallel Coupled Microstrip Lines (Corrections). IEEE Trans. Microw. Theory Tech. 1985, 33, 288. [Google Scholar] [CrossRef]
- Hu, X.; Qiu, Y.; Xu, Q.L.; Tian, J. A Hybrid FDTD–SPICE Method for Predicting the Coupling Response of Wireless Communication System. IEEE Trans. Electromagn. Compat. 2021, 63, 1530–1541. [Google Scholar] [CrossRef]
- Fregonese, S.; Cabbia, M.; Yadav, C.; Deng, M.; Panda, S.R.; De Matos, M.; Céli, D.; Chakravorty, A.; Zimmer, T. Analysis of High-Frequency Measurement of Transistors Along With Electromagnetic and SPICE Cosimulation. IEEE Trans. Electron Devices 2020, 67, 4770–4776. [Google Scholar] [CrossRef]
- Kuznetsov, V.V.; Andreev, V.V.; Lomakin, S.A. Semiconductor Device Compact Simulation Taking Into Account the ESD Effect and Using the Free Circuit Simulation Software. In Proceedings of the 2025 7th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 8–10 April 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Fino, M.H. Verilog-A compact model of integrated tapered spiral inductors. In Proceedings of the 2016 MIXDES-23rd International Conference Mixed Design of Integrated Circuits and Systems, Łodź, Poland, 23–25 June 2016; pp. 58–61. [Google Scholar] [CrossRef]
- Kuthe, P.; Müller, M.; Schröter, M. VerilogAE: An Open Source Verilog-A Compiler for Compact Model Parameter Extraction. IEEE J. Electron Devices Soc. 2020, 8, 1416–1423. [Google Scholar] [CrossRef]
- Cox, F.; Kuhn, W.; Murray, J.; Tynor, S. Code-level modeling in XSPICE. In Proceedings of the 1992 IEEE International Symposium on Circuits and Systems (ISCAS), San Diego, CA, USA, 10–13 May 1992; IEEE: New York, NY, USA, 1992; Volume 2, pp. 871–874. [Google Scholar] [CrossRef]
- Kasprowicz, D. Table-Based Model of a Dual-Gate Transistor for Statistical Circuit Simulation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2019, 38, 1493–1500. [Google Scholar] [CrossRef]
- Lock, C.; Greeff, J.; Joubert, S. Modelling of telegraph equations in transmission lines. In Proceedings of the TIME2008 Conference, Buffelspoort, South Africa, 22–26 September 2008; pp. 138–148. [Google Scholar] [CrossRef]
- Ali, S.Z.; Ahsan, K.; ul Khairi, D.; Alhalabi, W.; Anwar, M.S. Advancements in FR4 dielectric analysis: Free space approach and measurement validation. PLoS ONE 2024, 19, e0305614. [Google Scholar] [CrossRef]
- Chen, L.; Kim, C.; Batra, R.; Lightstone, J.P.; Wu, C.; Li, Z.; Deshmukh, A.A.; Wang, Y.; Tran, H.D.; Vashishta, P.; et al. Frequency-dependent dielectric constant prediction of polymers using machine learning. npj Comput. Mater. 2020, 6, 61. [Google Scholar] [CrossRef]
- Brinson, M.; Kuznetsov, V. Improvements in Qucs-S equation-defined modelling of semiconductor devices and IC’s. In Proceedings of the 2017 MIXDES-24th International Conference "Mixed Design of Integrated Circuits and Systems, Bydgoszcz, Poland, 22–24 June 2017; pp. 137–142. [Google Scholar] [CrossRef]
- Brinson, M.; Tomaszewski, D. Advances in Qucs-S Schematic Capture for SPICE and Verilog-A Device Modelling and Circuit Simulation. In Proceedings of the 2022 29th International Conference on Mixed Design of Integrated Circuits and System (MIXDES), Wrocław, Poland, 23–24 June 2022; pp. 27–32. [Google Scholar] [CrossRef]
- Chukhraev, I.V.; Drach, V.E. Parameter Optimization of Broadband Interference-Suppressing Filters of Hi-Performance Power Supplies. In Proceedings of the 2023 5th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 16–18 March 2023; Volume 5, pp. 1–5. [Google Scholar] [CrossRef]
- Krupka, J.; Mouneyrac, D.; Hartnett, J.G.; Tobar, M.E. Use of Whispering-Gallery Modes and Quasi-TE0np Modes for Broadband Characterization of Bulk Gallium Arsenide and Gallium Phosphide Samples. IEEE Trans. Microw. Theory Tech. 2008, 56, 1201–1206. [Google Scholar] [CrossRef]
- Fedorov, E.; Issakov, V. A compact low-loss Ku-Band 90° Hybrid Coupler for Front-End Modules in 45 nm SOI CMOS. In Proceedings of the 2024 IEEE BiCMOS and Compound Semiconductor Integrated Circuits and Technology Symposium (BCICTS), Lauderdale, FL, USA, 27–30 October 2024; pp. 111–114. [Google Scholar] [CrossRef]
- Solomko, V.; Tanc, B.; Kehrer, D.; Ilkov, N.; Bakalski, W.; Simbürger, W. Tunable directional coupler for RF front-end applications. Electron. Lett. 2015, 51, 2012–2014. [Google Scholar] [CrossRef]
- Wang, Q.; Huang, X.; Yin, B. Crosstalk analysis and suppression of microstrip lines on PCB board. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Singapore, 16–18 December 2022; Volume 5, pp. 875–879. [Google Scholar] [CrossRef]
- Song, K.; Kim, J.; Kim, H.; Lee, S.; Ahn, J.; Brito, A.; Kim, H.; Park, M.; Ahn, S. Modeling, Verification, and Signal Integrity Analysis of High-Speed Signaling Channel with Tabbed Routing in High Performance Computing Server Board. Electronics 2021, 10, 1590. [Google Scholar] [CrossRef]
- Kuznetsov, V.V.; Andreev, V.V. Transmission Line Pulse Setup for Electrostatic Discharge Robustness Testing of the Semiconductor Devices. Instruments Exp. Tech. 2024, 67, 268–273. [Google Scholar] [CrossRef]
- Mahadik, S.R.; Bombale, U.L. Amplifier type active antenna at 2.45 GHz for wireless applications. Analog. Integr. Circuits Signal Process. 2019, 101, 89–97. [Google Scholar] [CrossRef]





| Core Model | XSPICE | Verilog-A | |
|---|---|---|---|
| Time (s) | 0.143 | 0.156 | 2.58 |
| Model Parameter | Default Value | Unit | Description |
|---|---|---|---|
| 50.0 | Ohm | line impedance | |
| A | 0 | dB | line attenuation |
| L | 1.0 | m | line length |
| 50.0 | Ohm | even mode impedance | |
| 50.0 | Ohm | odd mode impedance | |
| 0 | dB | even mode attenuation | |
| 0 | dB | odd mode attenuation | |
| 1.0 | even mode relative dielectric permittivity | ||
| 1.0 | odd mode relative dielectric permittivity | ||
| L | 1.0 | m | Line length |
| Model Parameter | Default Value | Unit | Description |
|---|---|---|---|
| 4.5 | Relative dielectric permittivity | ||
| h | m | Substrate dielectric thickness | |
| t | m | Substrate conductor thickness | |
| Ohm · m | Substrate conductor resistance | ||
| 0 | Dielectric loss tangent | ||
| D | 0 | RMS substrate roughness |
| Frequency (GHz) | difference, ADS Mode (%) | difference, ADS Mode (%) | Difference, Qucs Mode (%) | Difference, Qucs Mode (%) |
|---|---|---|---|---|
| 1 | 0.03 | 0.14 | 0.01 | 0.11 |
| 5 | 1.29 | 0.3 | 0.01 | 0.13 |
| 10 | 3.7 | 1.7 | 0.01 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, V. Microstrip Line Modeling Taking into Account Dispersion Using a General-Purpose SPICE Simulator. J. Low Power Electron. Appl. 2025, 15, 42. https://doi.org/10.3390/jlpea15030042
Kuznetsov V. Microstrip Line Modeling Taking into Account Dispersion Using a General-Purpose SPICE Simulator. Journal of Low Power Electronics and Applications. 2025; 15(3):42. https://doi.org/10.3390/jlpea15030042
Chicago/Turabian StyleKuznetsov, Vadim. 2025. "Microstrip Line Modeling Taking into Account Dispersion Using a General-Purpose SPICE Simulator" Journal of Low Power Electronics and Applications 15, no. 3: 42. https://doi.org/10.3390/jlpea15030042
APA StyleKuznetsov, V. (2025). Microstrip Line Modeling Taking into Account Dispersion Using a General-Purpose SPICE Simulator. Journal of Low Power Electronics and Applications, 15(3), 42. https://doi.org/10.3390/jlpea15030042






