Analytical Implementation of Electron–Phonon Scattering in a Schottky Barrier CNTFET Model
Abstract
:1. Introduction
- It adopts a fully analytical approach, which significantly enhances runtime performance.
- The model encompasses critical factors such as non-ballistic transport and transmission through Schottky barrier (SB) contacts.
- It employs specific and detailed formulations for both acoustic phonon (A-Ph) and optical phonon (O-Ph) electron scattering processes.
2. Transport Model
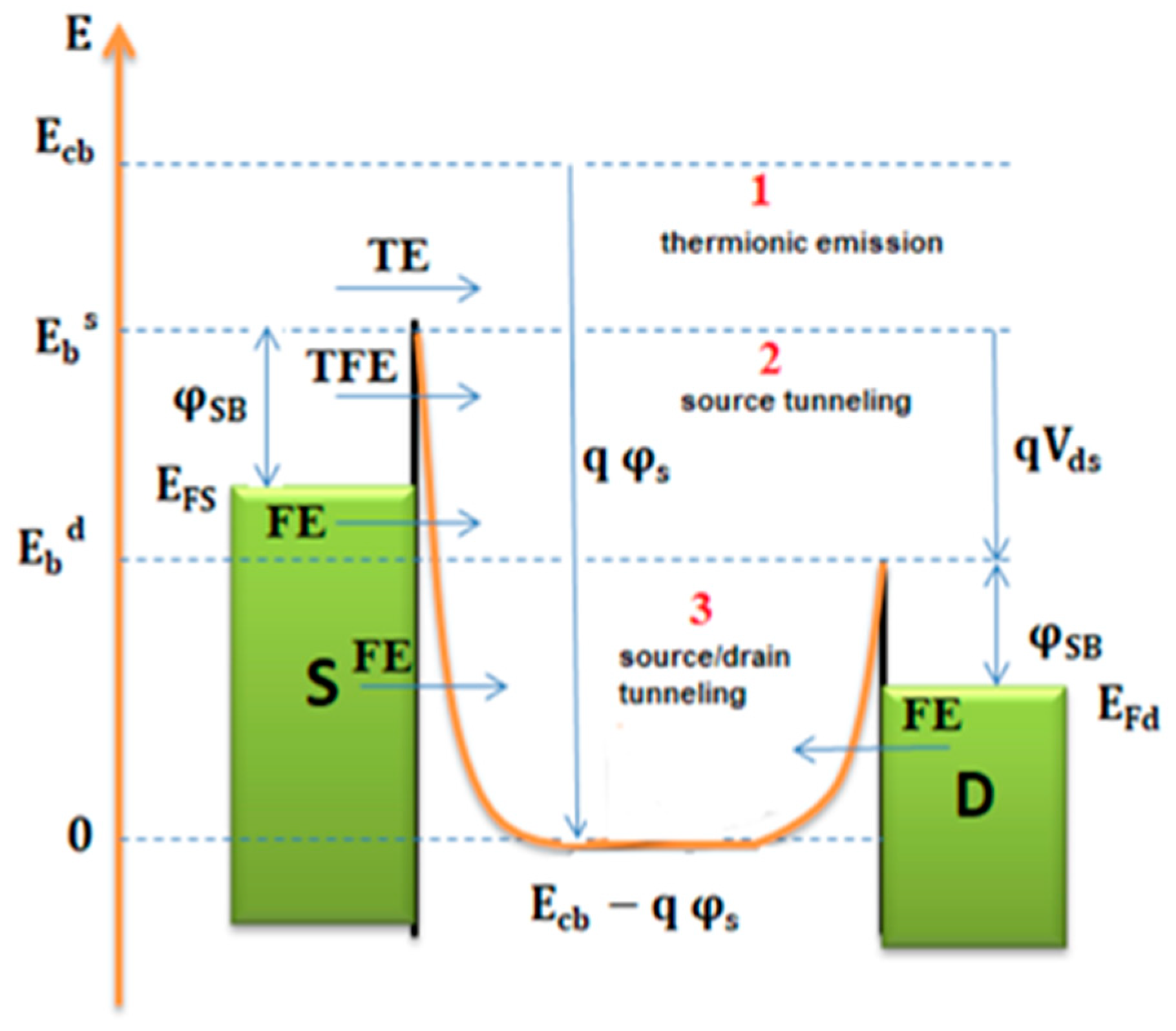
2.1. SB-CNTFET Physical Model
2.2. Electron–Phonon Scattering
2.2.1. Acoustic Phonon Scattering (A-Ph)
2.2.2. Optical Phonon Scattering (O-Ph)
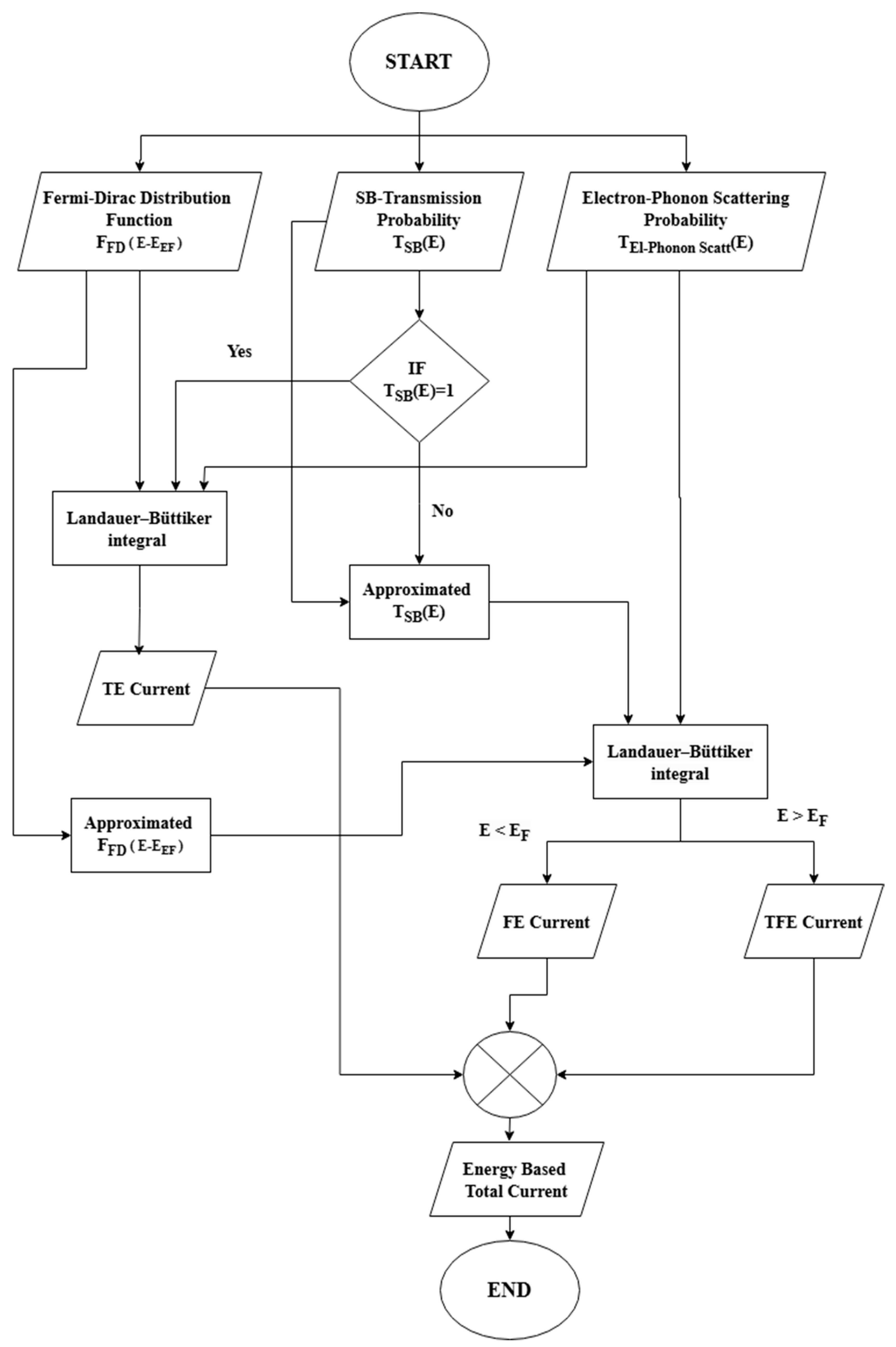
2.3. SB-CNTFET Current Equation
2.4. Mathematical Model
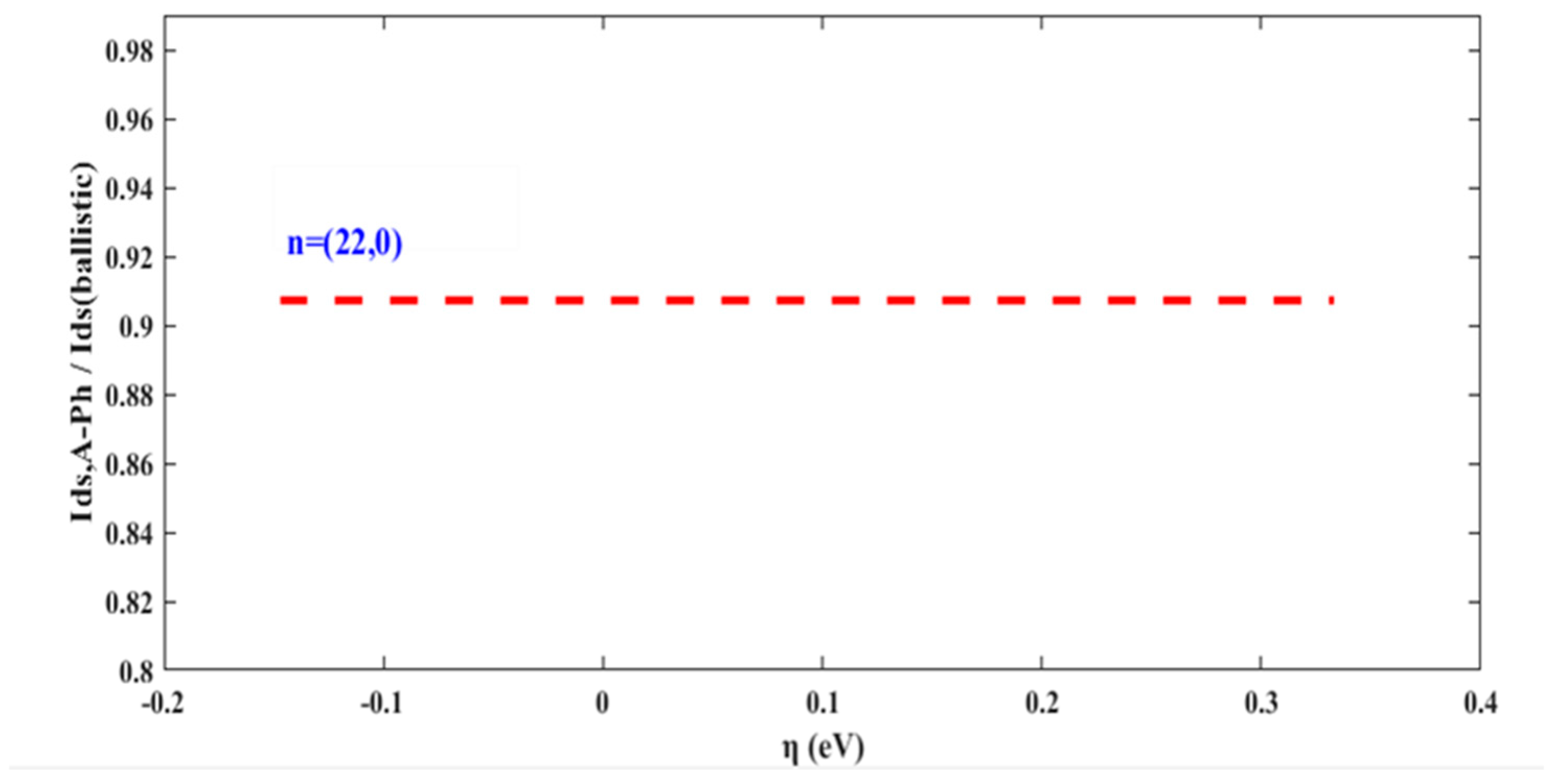
2.4.1. Effect of Acoustic Phonon Only (A-Ph)
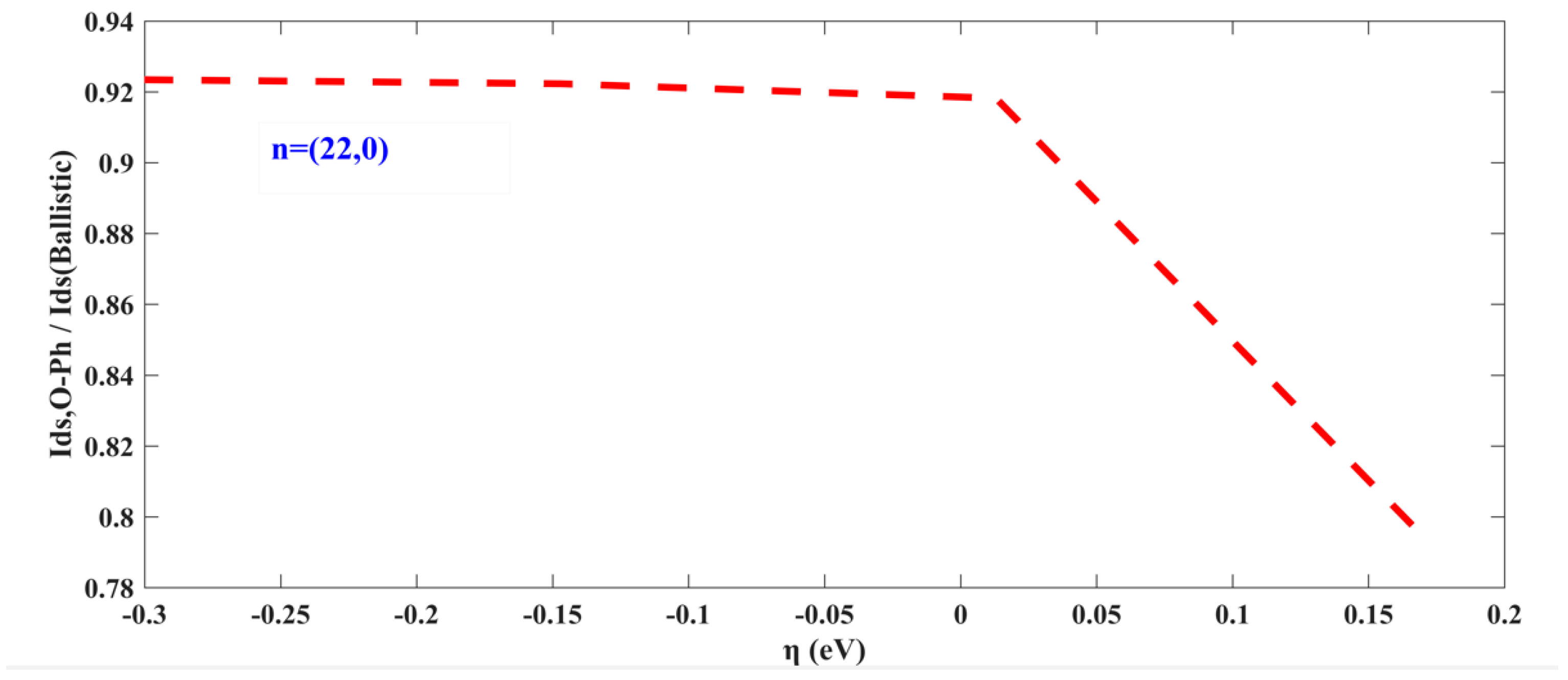
2.4.2. Effect of Optical Phonon Only (O-Ph)
2.4.3. Effect of Both Acoustic and Optical Phonons
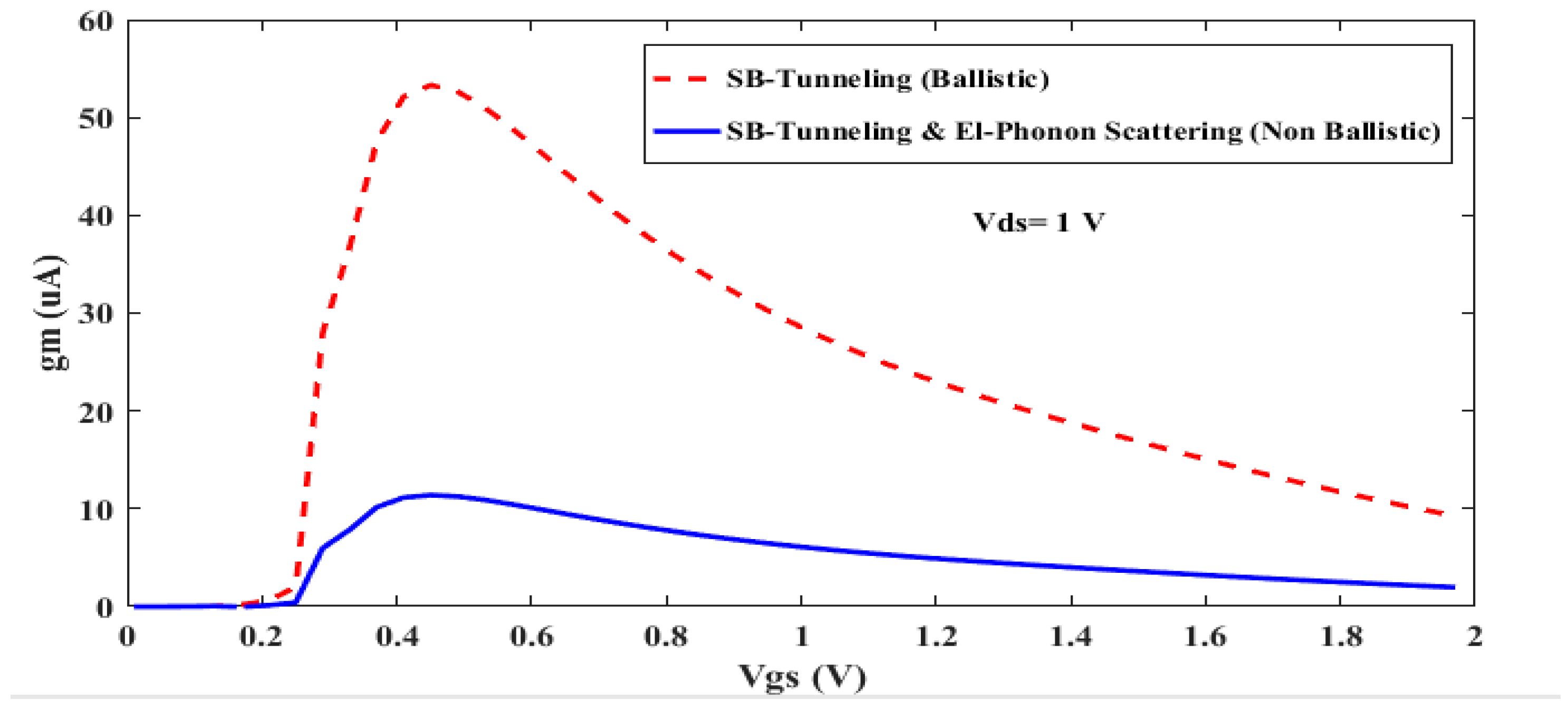
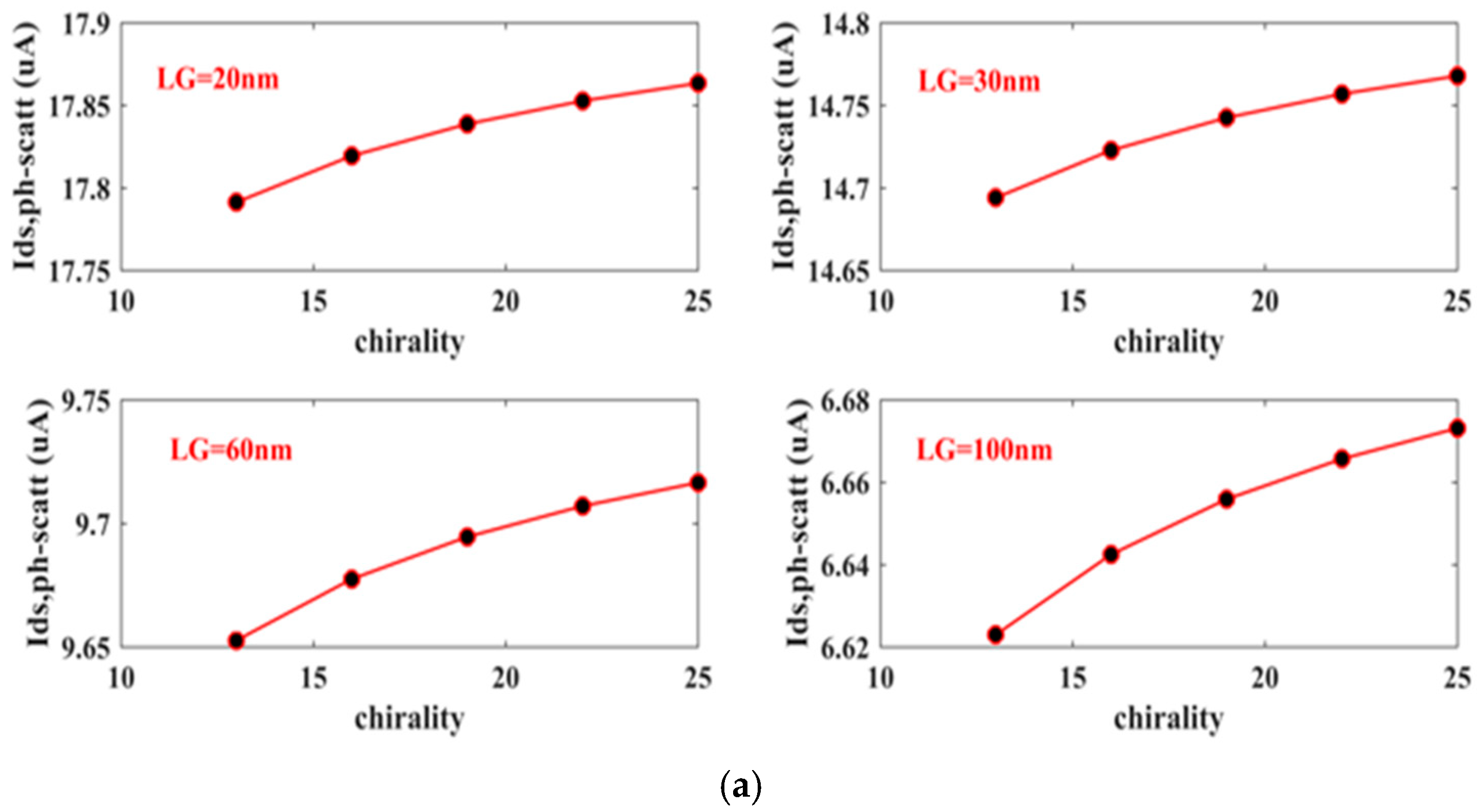
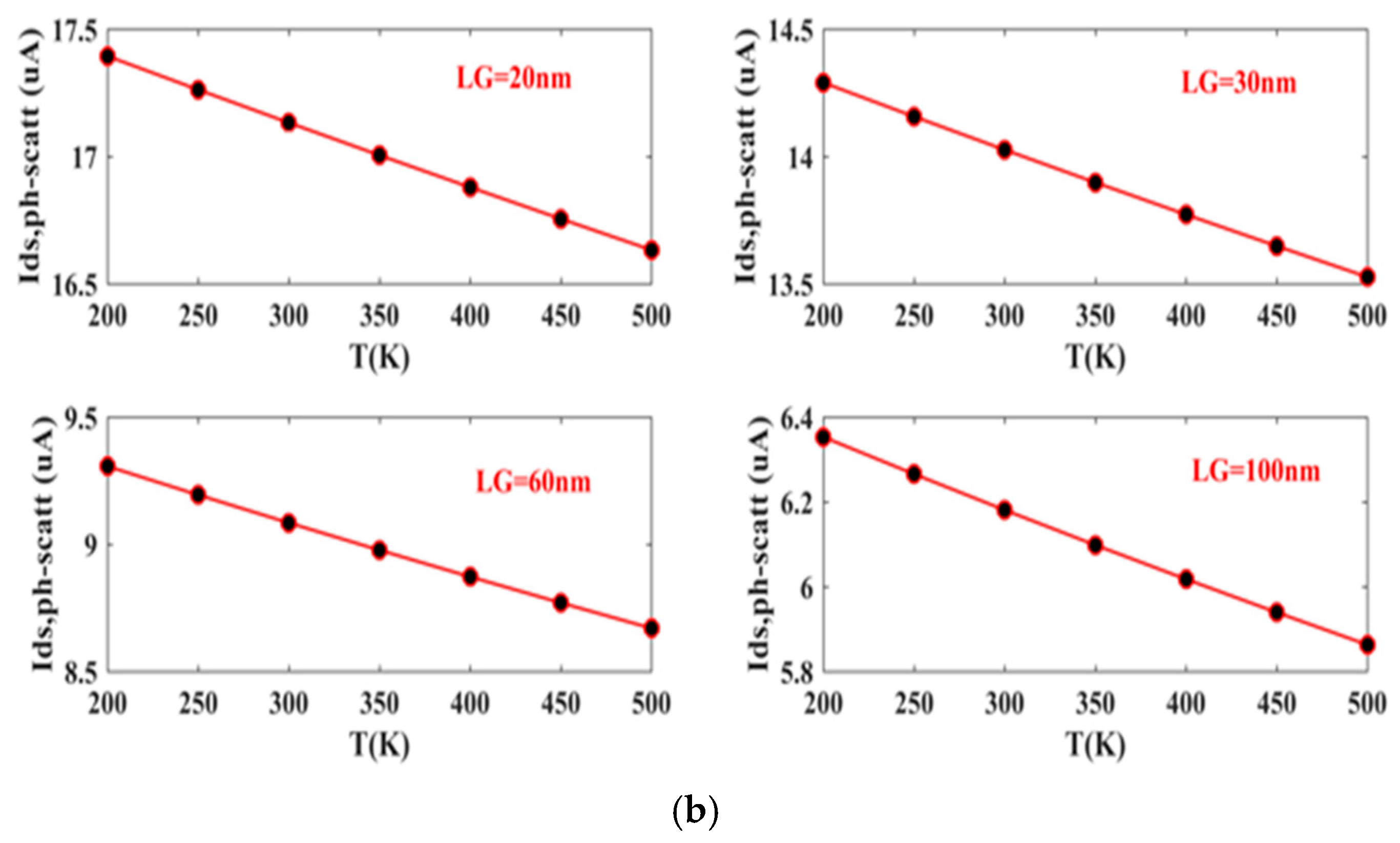
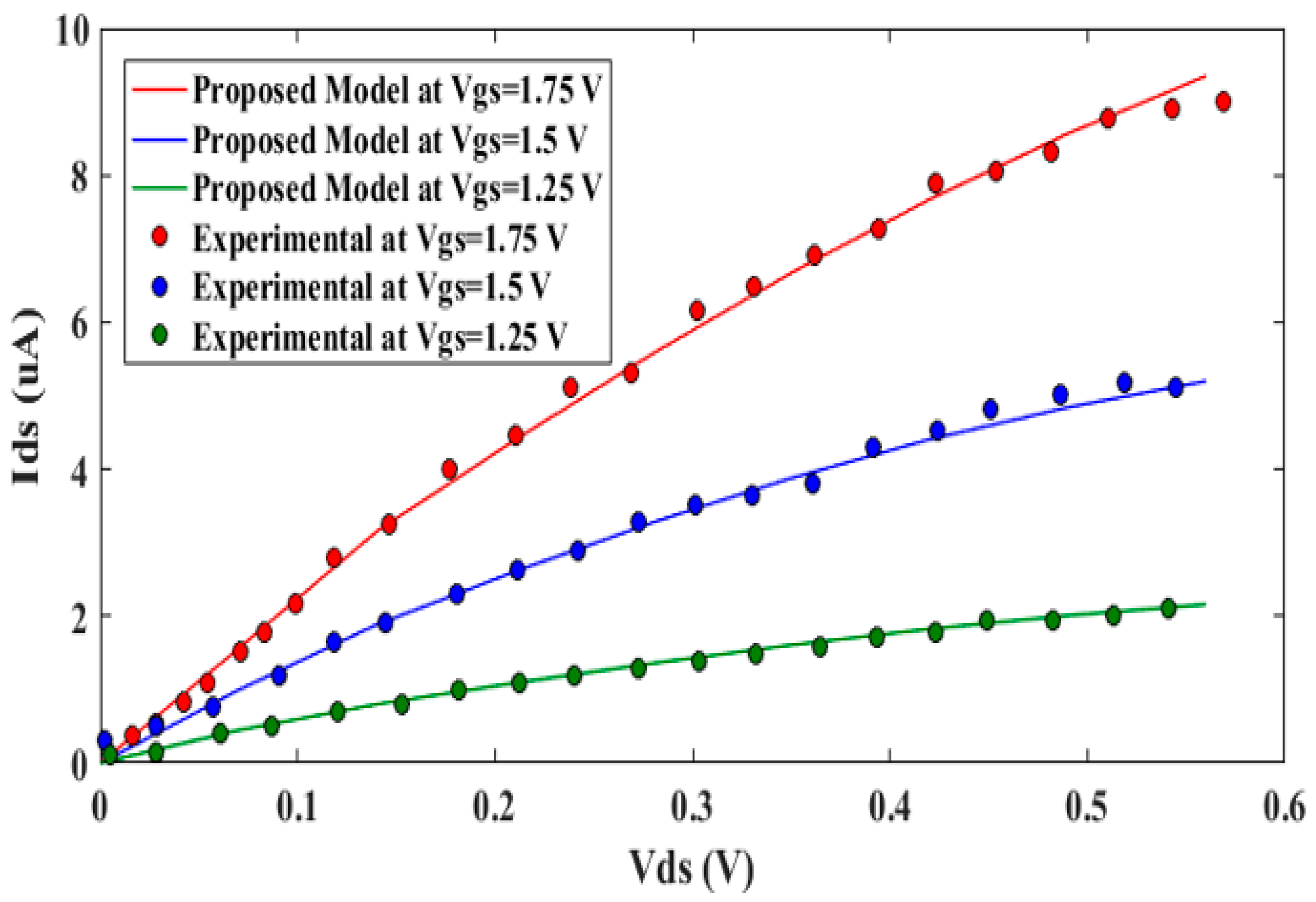
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bu, W.; Wang, W. The Evolution of IC Manufacturing Technology. In Handbook of Integrated Circuit Industry; Springer: Berlin/Heidelberg, Germany, 2023; pp. 863–870. [Google Scholar]
- Gargini, P.A. The IRDS is paving the way for chips acts around the world. In Proceedings of the International Conference on Extreme Ultraviolet Lithography 2023, Monterey, CL, USA, 2–5 October 2023; SPIE: Bellingham, WA, USA, 2023. [Google Scholar]
- Gargini, P.A. Overcoming Semiconductor and Electronics Crises With IRDS: Planning for the Future. IEEE Electron Devices Mag. 2023, 1, 32–47. [Google Scholar] [CrossRef]
- Song, S.; Qin, L.; Wang, Z.; Lyu, J.; Gong, J.; Yang, S. Improving the Performance of Arsenene Nanoribbon Gate-All-Around Tunnel Field-Effect Transistors Using H Defects. Nanomaterials 2024, 14, 1960. [Google Scholar] [CrossRef]
- Choi, W.C.; Jo, S.-H. Radiation Hardened Read-Stability and Speed Enhanced SRAM for Space Applications. Appl. Sci. 2024, 14, 9015. [Google Scholar] [CrossRef]
- Tamersit, K. WS2 Nanosheet-Based Ultrascaled Field-Effect Transistor for Hydrogen Gas Sensing: Addressing the Sensitivity-Downscaling Trade-Off. Sensors 2024, 24, 6730. [Google Scholar] [CrossRef]
- Deng, X.; Kang, N.; Zhang, Z.J.C. Carbon-based cryoelectronics: Graphene and carbon nanotube. Chip 2023, 2, 100064. [Google Scholar] [CrossRef]
- Raja, G.B. Future Prospective Beyond-CMOS Technology: From Silicon-Based Devices to Alternate Devices. In Advanced Field-Effect Transistors; CRC Press: Boca Raton, FL, USA, 2023; pp. 1–22. [Google Scholar]
- Zahoor, F.; Hanif, M.; Bature, U.I.; Bodapati, S.; Chattopadhyay, A.; Hussin, F.A.; Abbas, H.; Merchant, F.; Bashir, F. Carbon nanotube field effect transistors: An overview of device structure, modeling, fabrication and applications. Phys. Scr. 2023, 98, 082003. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, J.; Liao, W.; Zhao, Y.; Jiang, J.; Chen, C. Progress on a Carbon Nanotube Field-Effect Transistor Integrated Circuit: State of the Art, Challenges, and Evolution. Micromachines 2024, 15, 817. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Chen, Z.; Chen, J.; Chen, H.; Jiang, J.; Chen, C. Full-custom 90 nm cntfet process design kit: Characterization, modeling, and implementation. Electronics 2024, 13, 605. [Google Scholar] [CrossRef]
- Chen, J.; Hu, B.; Wang, Z. Interfacial Thermal Transport of Carbon Nanotube on the Substrate. Int. J. Thermophys. 2023, 44, 136. [Google Scholar] [CrossRef]
- Khorsand, V.; Yousefi, R.; Ghoreishi, S.S.; Afzalian, A. Role of Phonon Scattering in a Junctionless Carbon Nanotube Field-Effect Diode. J. Electron. Mater. 2023, 52, 2449–2457. [Google Scholar] [CrossRef]
- Rudderham, C.; Maassen, J. Analysis of simple scattering models on the thermoelectric performance of analytical electron dispersions. J. Appl. Phys. 2020, 127, 065105. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Jiang, J.; Chen, C. An Improved Dual-Gate Compact Model for Carbon Nanotube Field Effect Transistors with a Back-Gate Effect and Circuit Implementation. Electronics 2024, 13, 620. [Google Scholar] [CrossRef]
- Tripathy, S.; Kumari, A.; Bhattacharyya, T.K. A Comprehensive Physics-Based Compact Model for CNT Thin Film Transistors—Part I: Schottky Contact. IEEE Trans. Electron Devices 2024, 71, 5709–5716. [Google Scholar] [CrossRef]
- Laird, E.A.; Kuemmeth, F.; Steele, G.A.; Grove-Rasmussen, K.; Nygård, J.; Flensberg, K.; Kouwenhoven, L.P. Quantum transport in carbon nanotubes. Rev. Mod. Phys. 2015, 87, 703–764. [Google Scholar] [CrossRef]
- Chin, H.C.; Hamzah, A.; Alias, N.E.; Tan, M.L.P. Modeling the impact of phonon scattering with strain effects on the electrical properties of MoS2 field-effect transistors. Micromachines 2023, 14, 1235. [Google Scholar] [CrossRef]
- Park, J. Thermal transport study in a strained carbon nanotube and graphene junction using phonon wavepacket analysis. J. Carbon Res. 2023, 9, 21. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Wang, J.; Zhao, Z. A New Analytical Large-Signal Model for Quasi-Ballistic Transport in InGaAs HEMTs Accommodating Dislocation Scattering. Micromachines 2023, 14, 1023. [Google Scholar] [CrossRef]
- Akhoundi, E.; Houssa, M.; Afzalian, A. The impact of electron phonon scattering, finite size and lateral electric field on transport properties of topological insulators: A first principles quantum transport study. Materials 2023, 16, 1603. [Google Scholar] [CrossRef]
- d’Honincthun, H.C.; Galdin-Retailleau, S.; Sée, J.; Dollfus, P. Electron-phonon scattering and ballistic behavior in semiconducting carbon nanotubes. Appl. Phys. Lett. 2005, 87, 172112. [Google Scholar] [CrossRef]
- Guo, J.; Lundstrom, M. Role of phonon scattering in carbon nanotube field-effect transistors. Appl. Phys. Lett. 2005, 86, 193103. [Google Scholar] [CrossRef]
- Koswatta, S.O.; Hasan, S.; Lundstrom, M.S.; Anantram, M.P.; Nikonov, D.E. Nonequilibrium green’s function treatment of phonon scattering in carbon-nanotube transistors. IEEE Trans. Electron Devices 2007, 54, 2339–2351. [Google Scholar] [CrossRef]
- Pourfath, M.; Kosina, H.; Selberherr, S. Numerical study of quantum transport in carbon nanotube transistors. Math. Comput. Simul. 2008, 79, 1051–1059. [Google Scholar] [CrossRef]
- Frégonèse, S.; Goguet, J.; Maneux, C.; Zimmer, T. Implementation of electron–phonon scattering in a CNTFET compact model. IEEE Trans. Electron Devices 2009, 56, 1184–1190. [Google Scholar] [CrossRef]
- Perebeinos, V.; Tersoff, J.; Avouris, P. Electron-Phonon Interaction and Transport in Semiconducting Carbon Nanotubes. Phys. Rev. Lett. 2005, 94, 086802. [Google Scholar] [CrossRef]
- Wong, H.-S.P.; Akinwande, D. Carbon Nanotube and Graphene Device Physics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Bejenari, I.; Schröter, M.; Claus, M. Analytical drain current model for non-ballistic Schottky-Barrier CNTFETs. In Proceedings of the 2017 47th European Solid-State Device Research Conference (ESSDERC), Leuven, Belgium, 11–14 September 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Bhardwaj, A.K.; Gupta, S.; Raj, B. Development and Analysis of Compact Model for Double Gate Schottky Barrier Carbon Nano Tube Field Effect Transistor. J. Nanoelectron. Optoelectron. 2020, 15, 1199–1208. [Google Scholar]
- Bejenari, I.; Schröter, M.; Claus, M. Analytical drain current model of 1-D ballistic Schottky-barrier transistors. IEEE Trans. Electron Devices 2017, 64, 3904–3911. [Google Scholar] [CrossRef]
- Franklin, A.D.; Chen, Z. Length scaling of carbon nanotube transistors. Nat. Nanotechnol. 2010, 5, 858–862. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, S.; Ding, L.; Liang, X.; Pei, T.; Shen, J.; Xu, H.; Chen, Q.; Cui, R.; Li, Y.; et al. Self-Aligned Ballistic n-Type Single-Walled Carbon Nanotube Field-Effect Transistors with Adjustable Threshold Voltage. Nano Lett. 2008, 8, 3696–3701. [Google Scholar] [CrossRef]
- Yao, Z.; Kane, C.L.; Dekker, C. High-field electrical transport in single-wall carbon nanotubes. Phys. Rev. Lett. 2000, 84, 2941. [Google Scholar] [CrossRef]

| Symbol | Description | Value |
|---|---|---|
| Gate, drain to source voltage | Bias dependent | |
| Energy gap | Chirality dependent | |
| Schottky barrier height | Fitting parameter | |
| The source and drain Fermi level | Bias dependent | |
| Carbon–carbon atom distance | 2.49 A° | |
| bond energy | eV | |
| Characteristic length | Fitting parameter | |
| Surface potential | Bias dependent | |
| CNT diameter | Chirality dependent | |
| Gate insulator thickness | 8 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdalla, I.L.; Matter, F.A.; Afifi, A.A.; Ibrahem, M.I.; Hamed, H.F.A.; El-Mokadem, E.S. Analytical Implementation of Electron–Phonon Scattering in a Schottky Barrier CNTFET Model. J. Low Power Electron. Appl. 2025, 15, 28. https://doi.org/10.3390/jlpea15020028
Abdalla IL, Matter FA, Afifi AA, Ibrahem MI, Hamed HFA, El-Mokadem ES. Analytical Implementation of Electron–Phonon Scattering in a Schottky Barrier CNTFET Model. Journal of Low Power Electronics and Applications. 2025; 15(2):28. https://doi.org/10.3390/jlpea15020028
Chicago/Turabian StyleAbdalla, Ibrahim L., Fatma A. Matter, Ahmed A. Afifi, Mohamed I. Ibrahem, Hesham F. A. Hamed, and Eslam S. El-Mokadem. 2025. "Analytical Implementation of Electron–Phonon Scattering in a Schottky Barrier CNTFET Model" Journal of Low Power Electronics and Applications 15, no. 2: 28. https://doi.org/10.3390/jlpea15020028
APA StyleAbdalla, I. L., Matter, F. A., Afifi, A. A., Ibrahem, M. I., Hamed, H. F. A., & El-Mokadem, E. S. (2025). Analytical Implementation of Electron–Phonon Scattering in a Schottky Barrier CNTFET Model. Journal of Low Power Electronics and Applications, 15(2), 28. https://doi.org/10.3390/jlpea15020028







