Design of Ultra-Low-Power Rail-to-Rail Input Common Mode Range Standard-Cell-Based Comparators
Abstract
:1. Introduction
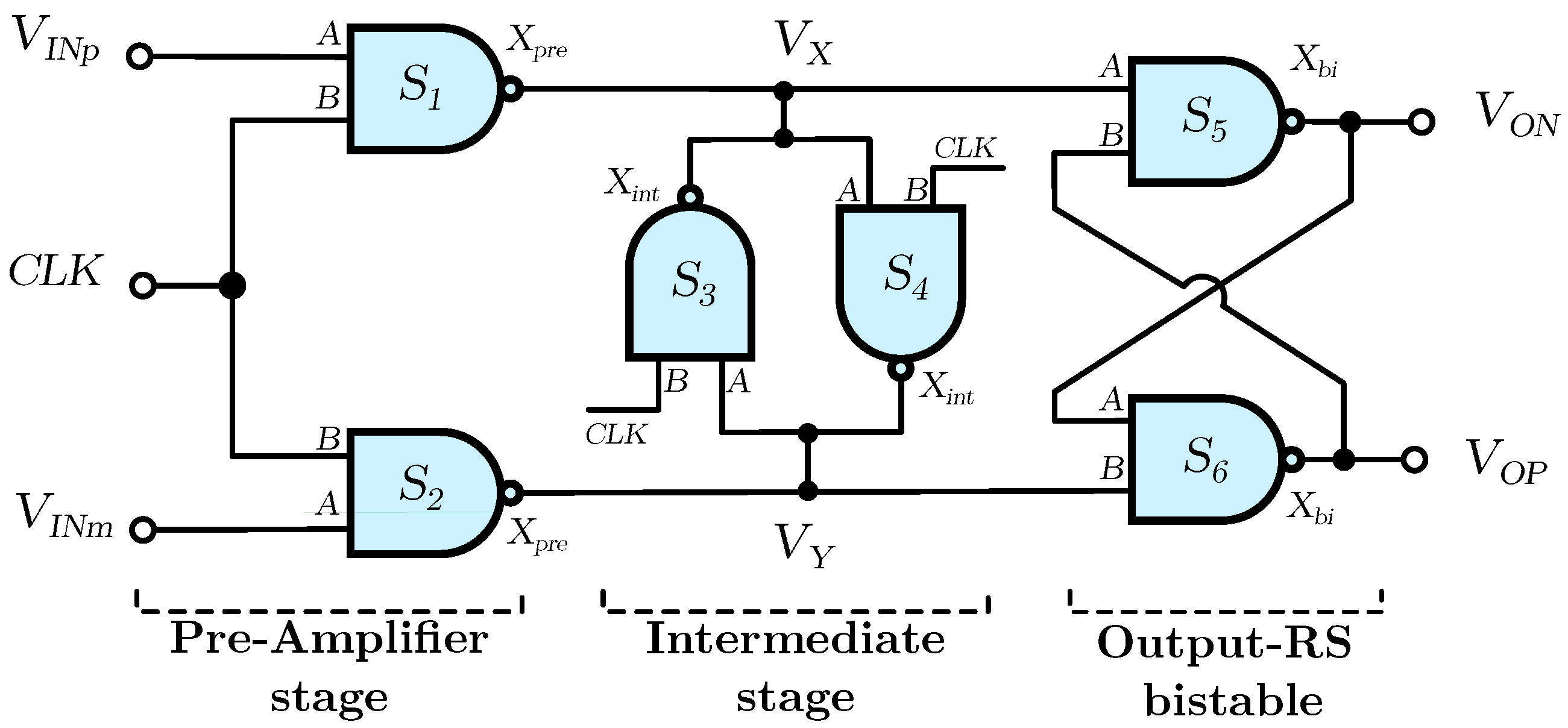
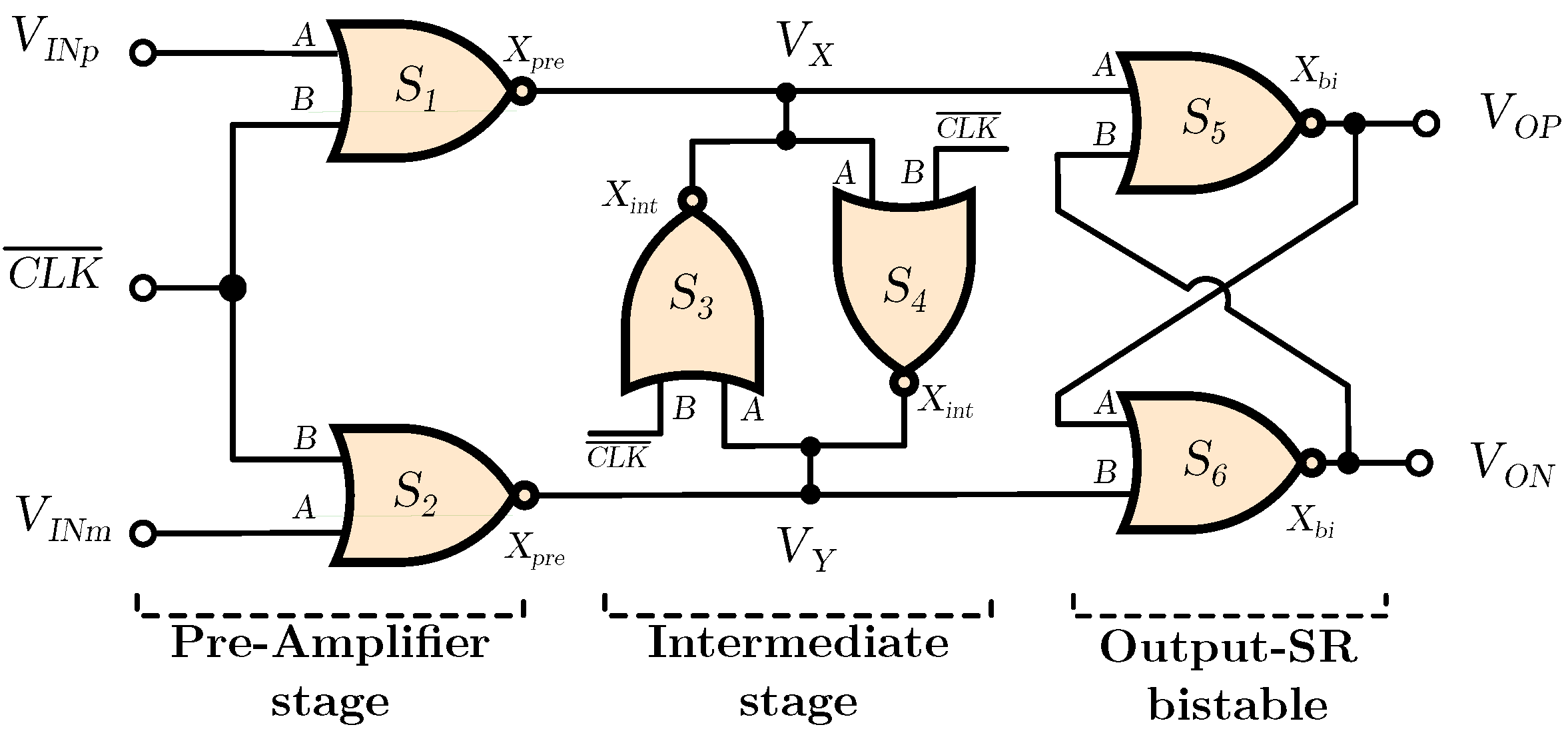
2. Rail-to-Rail ICMR Standard Cell-Based DVCs
2.1. NAND2 SCB-DVC
2.2. NOR2 Proposed SCB-DVC
3. Standard-Cell Oriented Design
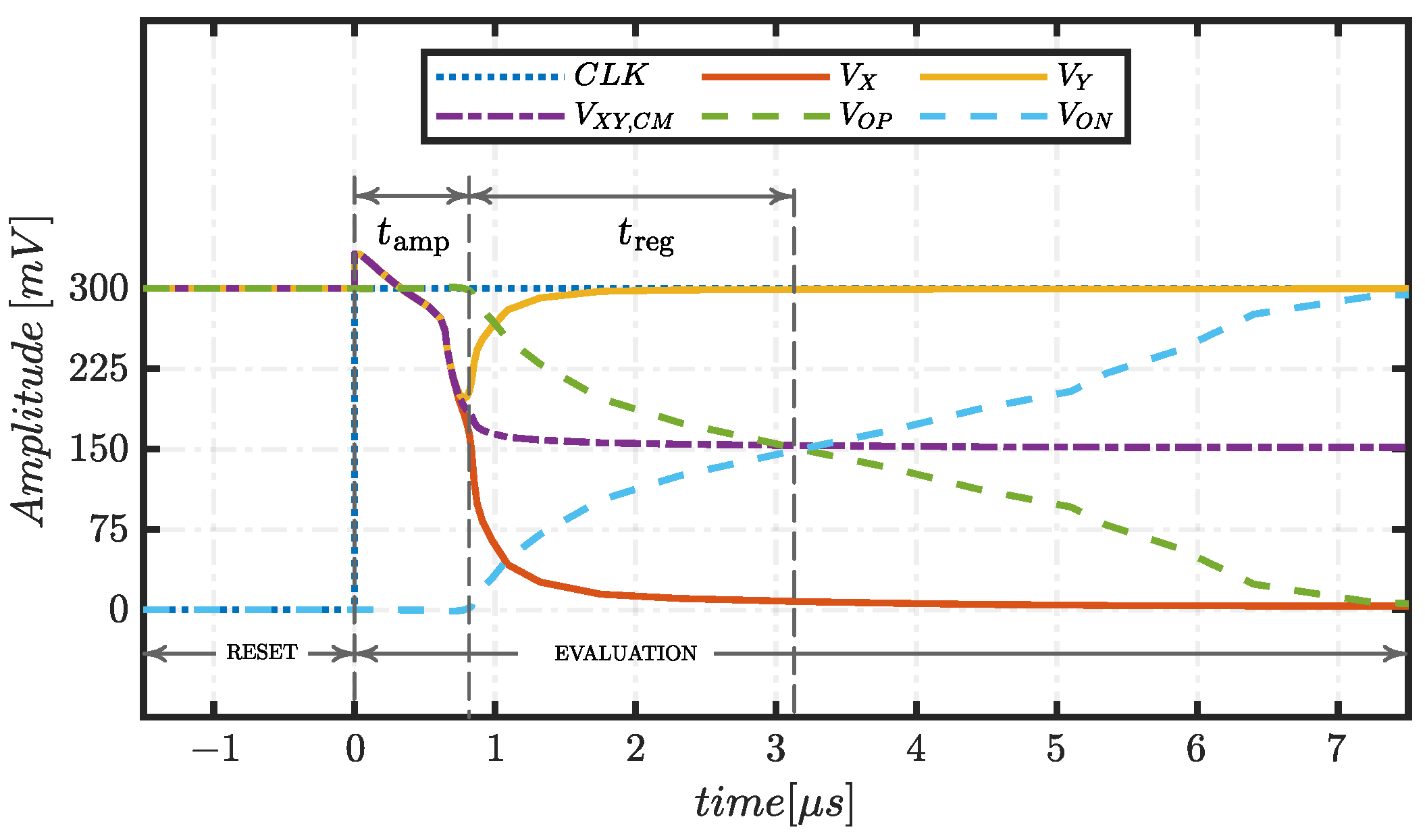
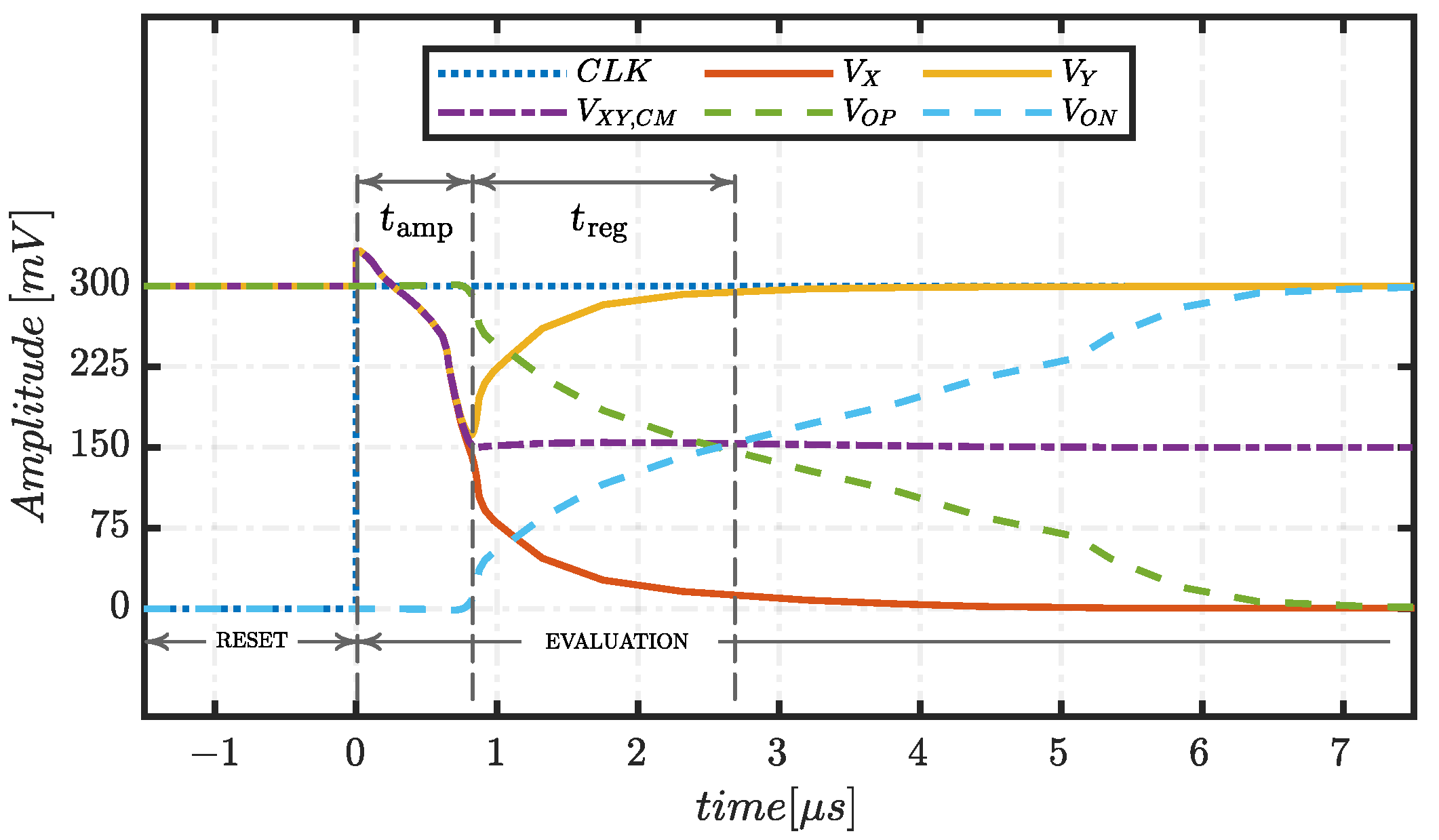
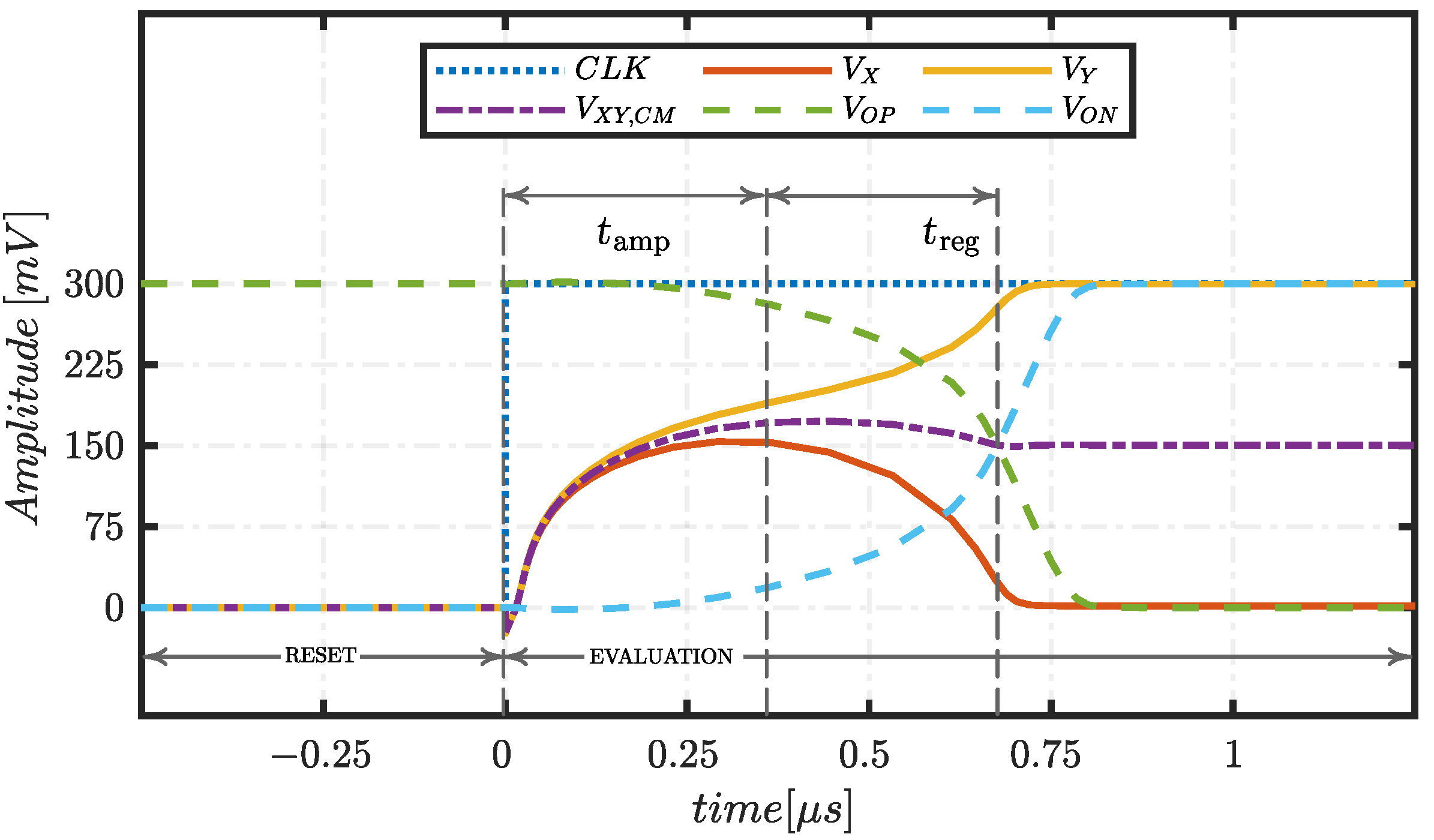
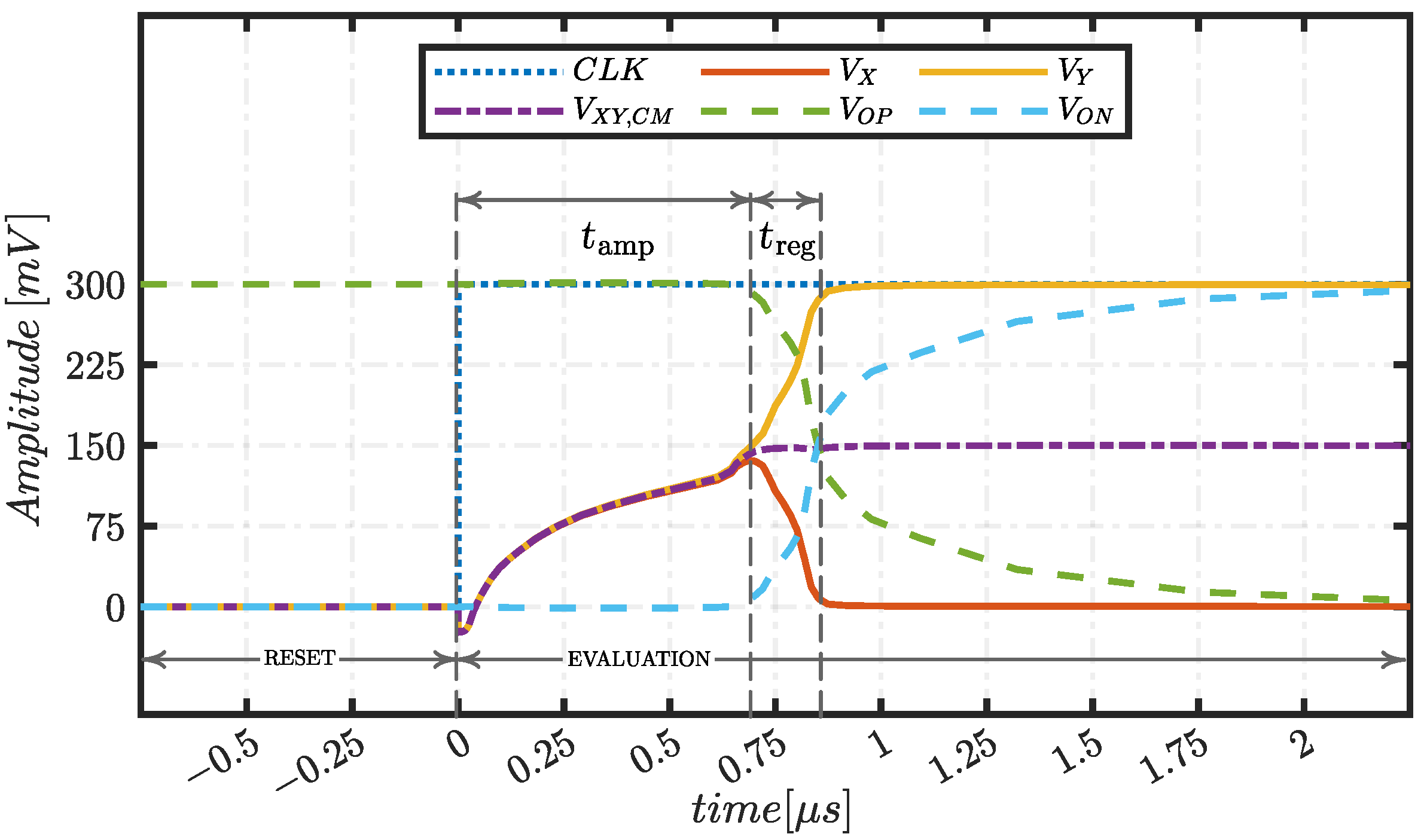
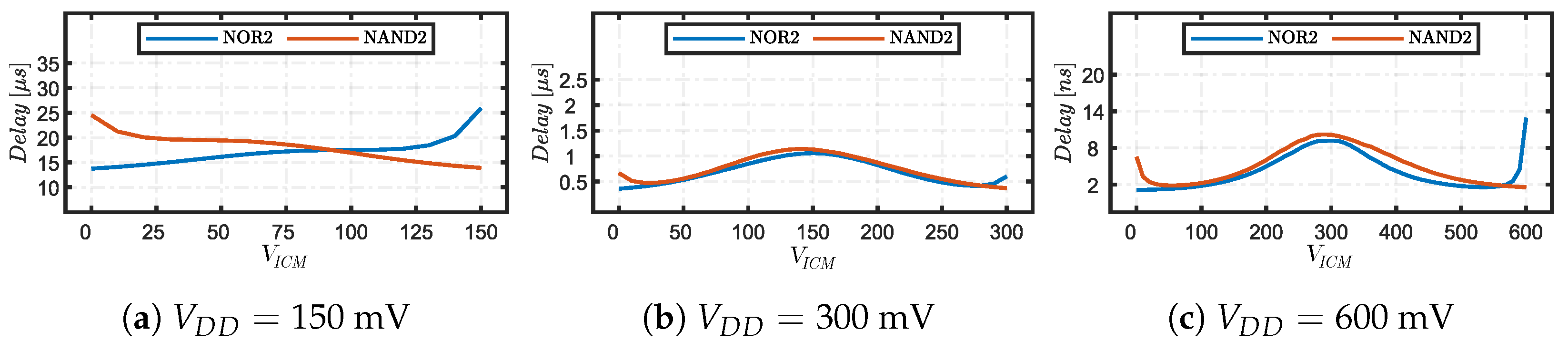
3.1. Delay
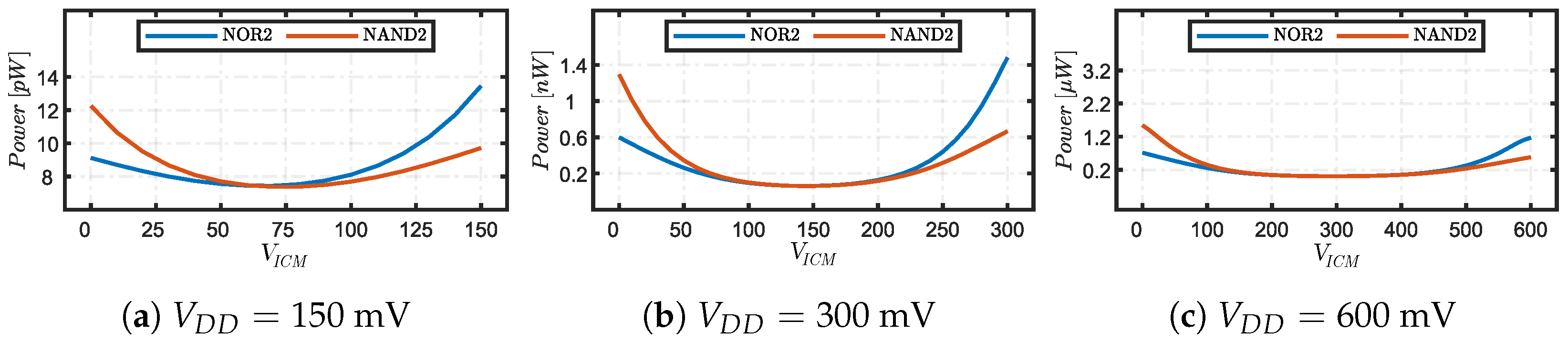
3.2. Power Consumption
3.3. Input Common Mode Range (ICMR)
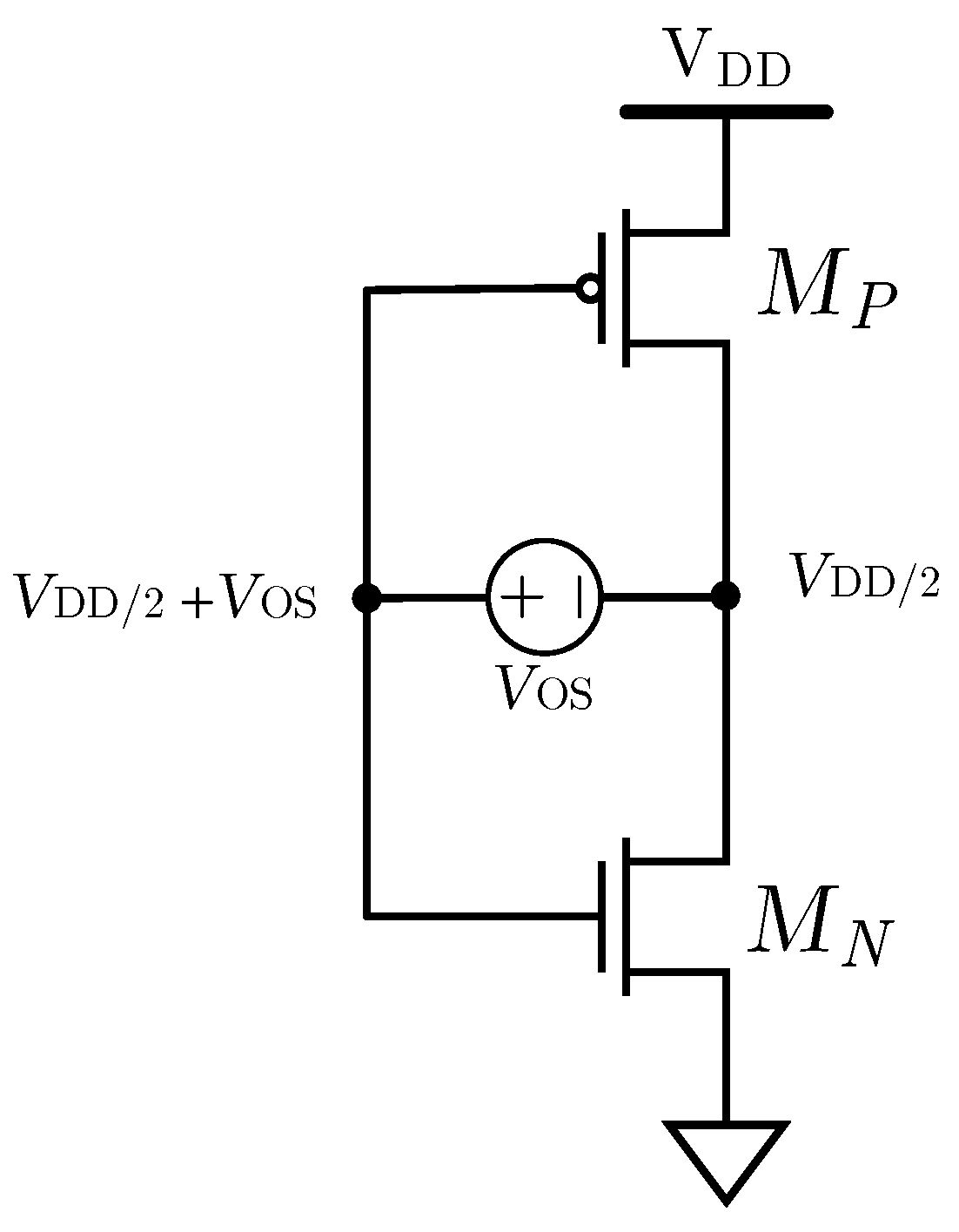
3.4. Offset
4. Comparison
4.1. Rail-to-Rail ICMR with Minimum Offset Design
4.2. Rail-to-Rail ICMR with Minimum Power Consumption Design
4.3. Comparison with the State-of-the-Art of Rail-to-Rail Topologies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Volkmann, J. Deep Brain Stimulation for the Treatment of Parkinson’s Disease. J. Clin. Neurophysiol. 2004, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Hannan, M.A.; Mutashar, S.; Samad, S.A.; Hussain, A. Energy harvesting for the implantable biomedical devices: Issues and challenges. BioMed Eng. Online 2014, 13, 79. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.J.; Jeong, H.; Cho, K.W.; Lu, N.; Kim, D.H. Wearable and Implantable Devices for Cardiovascular Healthcare: From Monitoring to Therapy Based on Flexible and Stretchable Electronics. Adv. Funct. Mater. 2019, 29, 1808247. [Google Scholar] [CrossRef]
- Karthick, R.; Ramkumar, R.; Akram, M.; Vinoth Kumar, M. Overcome the challenges in bio-medical instruments using IOT–A review. Mater. Today Proc. 2021, 45, 1614–1619. [Google Scholar] [CrossRef]
- Aledhari, M.; Razzak, R.; Qolomany, B.; Al-Fuqaha, A.; Saeed, F. Biomedical IoT: Enabling Technologies, Architectural Elements, Challenges, and Future Directions. IEEE Access 2022, 10, 31306–31339. [Google Scholar] [CrossRef]
- Privitera, M.; Ballo, A.; Ali, K.; Grasso, A.D.; Alioto, M. Sub-μW Battery-Less and Oscillator-Less Wi-Fi Backscattering Transmitter Reusing RF Signal for Harvesting, Communications, and Motion Detection. IEEE J. Solid-State Circuits 2024, 1–12. [Google Scholar] [CrossRef]
- Catania, A.; Gagliardi, F.; Piotto, M.; Bruschi, P.; Dei, M. Ultralow-Power Inverter-Based Delta-Sigma Modulator for Wearable Applications. IEEE Access 2024, 12, 80009–80019. [Google Scholar] [CrossRef]
- Van Elzakker, M.; Van Tuijl, E.; Geraedts, P.; Schinkel, D.; Klumperink, E.A.M.; Nauta, B. A 10-bit Charge-Redistribution ADC Consuming 1.9 μW at 1 MS/s. IEEE J. Solid-State Circuits 2010, 45, 1007–1015. [Google Scholar] [CrossRef]
- Majidzadeh, V.; Silay, K.M.; Schmid, A.; Dehollain, C.; Leblebici, Y. A fully on-chip LDO voltage regulator with 37 dB PSRR at 1 MHz for remotely powered biomedical implants. Analog Integr. Circ. Signal Process. 2011, 67, 157–168. [Google Scholar] [CrossRef]
- Wang, S.H.; Hung, C.C. A 0.3V 10b 3MS/s SAR ADC with Comparator Calibration and Kickback Noise Reduction for Biomedical Applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 558–569. [Google Scholar] [CrossRef]
- Di Patrizio Stanchieri, G.; Aiello, O.; De Marcellis, A. A 0.4 V 180 nm CMOS Sub-μW Ultra-Compact and Low-Effort Design PWM-Based ADC. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024; pp. 1–5, ISSN 2158-1525. [Google Scholar] [CrossRef]
- Toledo, P.; Rubino, R.; Musolino, F.; Crovetti, P. Re-Thinking Analog Integrated Circuits in Digital Terms: A New Design Concept for the IoT Era. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 816–822. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Klimach, H.; Bampi, S. A 300mV-Supply, 2nW-Power, 80pF-Load CMOS Digital-Based OTA for IoT Interfaces. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 170–173. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Aiello, O.; Alioto, M. Fully Digital Rail-to-Rail OTA with Sub-1000- μm² Area, 250-mV Minimum Supply, and nW Power at 150-pF Load in 180 nm. IEEE Solid-State Circuits Lett. 2020, 3, 474–477. [Google Scholar] [CrossRef]
- Palumbo, G.; Scotti, G. A Novel Standard-Cell-Based Implementation of the Digital OTA Suitable for Automatic Place and Route. J. Low Power Electron. Appl. 2021, 11, 42. [Google Scholar] [CrossRef]
- Centurelli, F.; Giustolisi, G.; Pennisi, S.; Scotti, G. A Biasing Approach to Design Ultra-Low-Power Standard-Cell-Based Analog Building Blocks for Nanometer SoCs. IEEE Access 2022, 10, 25892–25900. [Google Scholar] [CrossRef]
- Privitera, M.; Crovetti, P.; Grasso, A.D. A Novel Digital OTA Topology With 66-dB DC Gain and 12.3-kHz Bandwidth. IEEE Trans. Circuits Syst. II 2023, 70, 3988–3992. [Google Scholar] [CrossRef]
- Weaver, S.; Hershberg, B.; Moon, U.K. Digitally Synthesized Stochastic Flash ADC Using Only Standard Digital Cells. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 84–91. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Fully Synthesizable, Rail-to-Rail Dynamic Voltage Comparator for Operation down to 0.3 V. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5, ISSN 2379-447X. [Google Scholar] [CrossRef]
- Li, X.; Zhou, T.; Ji, Y.; Li, Y. A 0.35 V-to-1.0 V synthesizable rail-to-rail dynamic voltage comparator based OAI&AOI logic. Analog Integr. Circ. Signal Process. 2020, 104, 351–357. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Toledo, P.; Alioto, M. Rail-to-Rail Dynamic Voltage Comparator Scalable Down to pW-Range Power and 0.15-V Supply. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2675–2679. [Google Scholar] [CrossRef]
- Della Sala, R.; Centurelli, F.; Scotti, G.; Palumbo, G. Rail to Rail ICMR and High Performance ULV Standard-Cell-Based Comparator for Biomedical and IoT Applications. IEEE Access 2024, 12, 4642–4659. [Google Scholar] [CrossRef]
- Della Sala, R.; Centurelli, F.; Scotti, G.; Palumbo, G. Standard-Cell-Based Comparators for Ultra-Low Voltage Applications: Analysis and Comparisons. Chips 2023, 2, 173–194. [Google Scholar] [CrossRef]
- Pelgrom, M.; Duinmaijer, A.; Welbers, A. Matching properties of MOS transistors. IEEE J. Solid-State Circuits 1989, 24, 1433–1439. [Google Scholar] [CrossRef]
- Croon, J.; Rosmeulen, M.; Decoutere, S.; Sansen, W.; Maes, H. An easy-to-use mismatch model for the MOS transistor. IEEE J. Solid-State Circuits 2002, 37, 1056–1064. [Google Scholar] [CrossRef]
- Yuan, X.; Shimizu, T.; Mahalingam, U.; Brown, J.S.; Habib, K.Z.; Tekleab, D.G.; Su, T.C.; Satadru, S.; Olsen, C.M.; Lee, H.; et al. Transistor Mismatch Properties in Deep-Submicrometer CMOS Technologies. IEEE Trans. Electron Devices 2011, 58, 335–342. [Google Scholar] [CrossRef]
- Sheikholeslami, A. Process Variation and Pelgrom’s Law [Circuit Intuitions]. IEEE Solid-State Circuits Mag. 2015, 7, 8–9. [Google Scholar] [CrossRef]
- T Hart, P.A.; Babaie, M.; Charbon, E.; Vladimirescu, A.; Sebastiano, F. Subthreshold Mismatch in Nanometer CMOS at Cryogenic Temperatures. IEEE J. Electron Devices Soc. 2020, 8, 797–806. [Google Scholar] [CrossRef]
- ’T Hart, P.A.; Babaie, M.; Charbon, E.; Vladimirescu, A.; Sebastiano, F. Characterization and Modeling of Mismatch in Cryo-CMOS. IEEE J. Electron Devices Soc. 2020, 8, 263–273. [Google Scholar] [CrossRef]
- Borgmans, J.; Rombouts, P. The Mismatch Performance of Pseudo Digital Ring Oscillators Used in VCO ADCs: PSRR and CMRR. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 579–592. [Google Scholar] [CrossRef]










| 30–300 | 10–300 | 0–300 | 0–300 | 0–300 | |
| 40–300 | 30–300 | 10–300 | 0–300 | 0–300 | |
| 70–280 | 50–300 | 30–300 | 20–300 | 10–300 | |
| 80–260 | 70–290 | 50–300 | 40–300 | 30–300 | |
| 90–250 | 80–270 | 60–300 | 50–300 | 40–300 |
| 0–270 | 0–280 | 0–300 | 0–300 | 0–300 | |
| 0–250 | 0–270 | 0–290 | 0–300 | 0–300 | |
| 20–230 | 0–250 | 0–270 | 0–290 | 0–300 | |
| 40–220 | 20–230 | 0–260 | 0–270 | 0–280 | |
| 60–210 | 40–230 | 0–250 | 0–270 | 0–280 |
| Topology | Supply [mV] | Power [pW] | Delay [ns] | PDP [aJ] | [mV] | [mV] | FOM1 [V·pW] | FOM2 [V·aJ] | ||
|---|---|---|---|---|---|---|---|---|---|---|
| NOR2 | 12.9 | 16,100 | 207.6 | 14.6 | 9.73% | 0.419 | 0.188 | 3.03 | ||
| 156.1 | 1020 | 159 | 45.3 | 15.1% | −0.674 | 7.07 | 7.21 | |||
| 29,200 | 9.36 | 273.3 | 95.4 | 15.9% | −0.727 | 2780 | 26.07 | |||
| NAND2 [22] | 9.32 | 19,070 | 177 | 18.3 | 12.2% | 0.947 | 0.17 | 3.25 | ||
| 90.3 | 1150 | 103.8 | 50.8 | 16.9% | 0.66 | 4.59 | 5.29 | |||
| 14,590 | 11.04 | 161 | 105.2 | 17.5% | −1.4 | 1540 | 16.94 |
| Topology | Supply [mV] | Power [pW] | Delay [ns] | PDP [aJ] | [mV] | [mV] | FOM1 [V·pW] | FOM2 [V·aJ] | ||
|---|---|---|---|---|---|---|---|---|---|---|
| NOR2 | 7.48 | 17,200 | 128 | 29.6 | 19.7% | 0.942 | 0.22 | 3.82 | ||
| 62.7 | 1050 | 65.8 | 75.4 | 25.1% | 0.108 | 4.72 | 4.96 | |||
| 8770 | 9.18 | 80.58 | 145.3 | 24.2% | 4.2 | 1270 | 11.7 | |||
| NAND2 [22] | 7.37 | 18,600 | 137 | 24.6 | 16.4% | 0.986 | 0.18 | 3.38 | ||
| 62 | 1130 | 70 | 62.6 | 20.8% | 0.133 | 3.88 | 4.39 | |||
| 8760 | 10.1 | 88.4 | 119.7 | 19.95% | −2.7 | 1040 | 10.59 |
| Topology | Supply [mV] | Power [pW] | Delay [ns] | PDP [aJ] | [mV] | [mV] | FOM1 [V·pW] | FOM2 [V·aJ] | |
|---|---|---|---|---|---|---|---|---|---|
| NOR2 | 12.9 | 16,100 | 207.6 | 14.6 | 9.73% | 0.419 | 0.188 | 3.03 | |
| 156.1 | 1020 | 159 | 45.3 | 15.1% | −0.674 | 7.07 | 7.21 | ||
| 29,200 | 9.36 | 273.3 | 95.4 | 15.9% | −0.727 | 2780 | 26.07 | ||
| NAND2 [22] | 9.32 | 19,070 | 177 | 18.3 | 12.2% | 0.947 | 0.17 | 3.25 | |
| 90.3 | 1150 | 103.8 | 50.8 | 16.9% | 0.66 | 4.59 | 5.29 | ||
| 14,590 | 11.04 | 161 | 105.2 | 17.5% | −1.4 | 1540 | 16.94 | ||
| [19] | 7.9 | 134,000 | 1060 | 12.1 | 8.06% | 18.6 | 0.175 | 23.5 | |
| 30.3 | 8530 | 258.8 | 10.3 | 3.43% | 1.2 | 0.31 | 2.68 | ||
| 8290 | 152.1 | 1260 | 10.21 | 1.7% | 0.53 | 80 | 12.89 | ||
| [20] | 15.2 | 50,600 | 770 | 13.83 | 9.22% | 6.49 | 0.23 | 11.75 | |
| 99.1 | 4460 | 442 | 11.9 | 3.87% | 1.98 | 1.19 | 5.33 | ||
| 8300 | 70.8 | 587 | 11.61 | 1.93% | 2.01 | 97 | 6.92 |
| Topology | Supply [mV] | Power [pW] | Delay [ns] | PDP [aJ] | [mV] | [mV] | FOM1 [V·pW] | FOM2 [V·aJ] | |
|---|---|---|---|---|---|---|---|---|---|
| NOR2 | 7.48 | 17,200 | 128 | 29.6 | 19.7% | 0.942 | 0.22 | 3.82 | |
| 62.7 | 1050 | 65.8 | 75.4 | 25.1% | 0.108 | 4.72 | 4.96 | ||
| 8770 | 9.18 | 80.58 | 145.3 | 24.2% | 4.2 | 1270 | 11.7 | ||
| NAND2 [22] | 7.37 | 18,600 | 137 | 24.6 | 16.4% | 0.986 | 0.18 | 3.38 | |
| 62 | 1130 | 70 | 62.6 | 20.8% | 0.133 | 3.88 | 4.39 | ||
| 8760 | 10.1 | 88.4 | 119.7 | 19.95% | −2.7 | 1040 | 10.59 | ||
| [19] | 7.9 | 134,000 | 1060 | 12.1 | 8.06% | 18.6 | 0.175 | 23.5 | |
| 30.3 | 8530 | 258.8 | 10.3 | 3.43% | 1.2 | 0.31 | 2.68 | ||
| 8290 | 152.1 | 1260 | 10.21 | 1.7% | 0.53 | 80 | 12.89 | ||
| [20] | 15.2 | 50,600 | 770 | 13.83 | 9.22% | 6.49 | 0.23 | 11.75 | |
| 99.1 | 4460 | 442 | 11.9 | 3.87% | 1.98 | 1.19 | 5.33 | ||
| 8300 | 70.8 | 587 | 11.61 | 1.93% | 2.01 | 97 | 6.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manno, A.; Scotti, G.; Palumbo, G. Design of Ultra-Low-Power Rail-to-Rail Input Common Mode Range Standard-Cell-Based Comparators. J. Low Power Electron. Appl. 2025, 15, 14. https://doi.org/10.3390/jlpea15010014
Manno A, Scotti G, Palumbo G. Design of Ultra-Low-Power Rail-to-Rail Input Common Mode Range Standard-Cell-Based Comparators. Journal of Low Power Electronics and Applications. 2025; 15(1):14. https://doi.org/10.3390/jlpea15010014
Chicago/Turabian StyleManno, Antonio, Giuseppe Scotti, and Gaetano Palumbo. 2025. "Design of Ultra-Low-Power Rail-to-Rail Input Common Mode Range Standard-Cell-Based Comparators" Journal of Low Power Electronics and Applications 15, no. 1: 14. https://doi.org/10.3390/jlpea15010014
APA StyleManno, A., Scotti, G., & Palumbo, G. (2025). Design of Ultra-Low-Power Rail-to-Rail Input Common Mode Range Standard-Cell-Based Comparators. Journal of Low Power Electronics and Applications, 15(1), 14. https://doi.org/10.3390/jlpea15010014








