A Power-Efficient 16-bit 1-MS/s Successive Approximation Register Analog-to-Digital Converter with Digital Calibration in 0.18 μm Complementary Metal Oxide Semiconductor
Abstract
1. Introduction
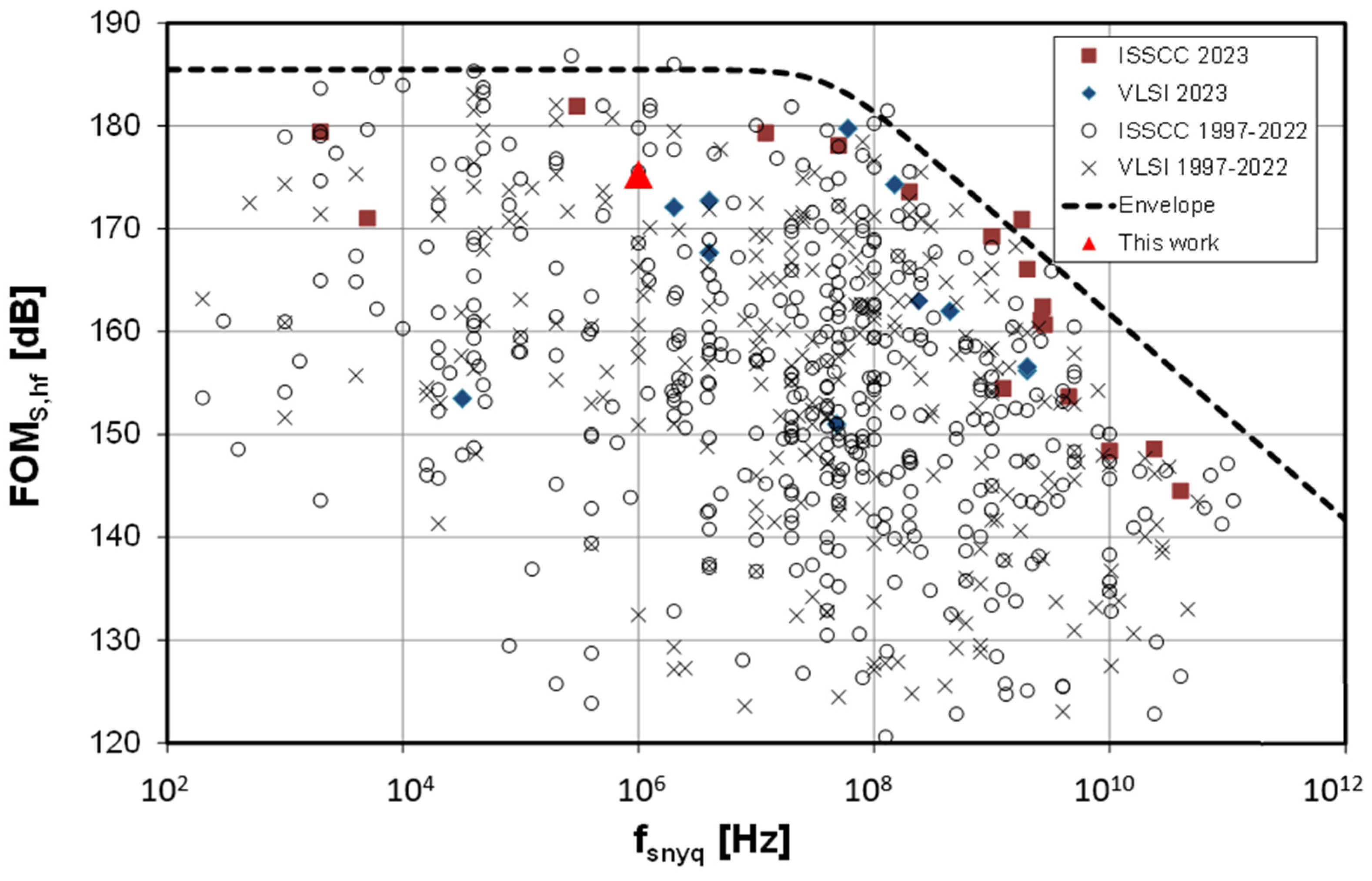
2. Simulation Results
3. SAR ADC Architecture and Digital Calibration
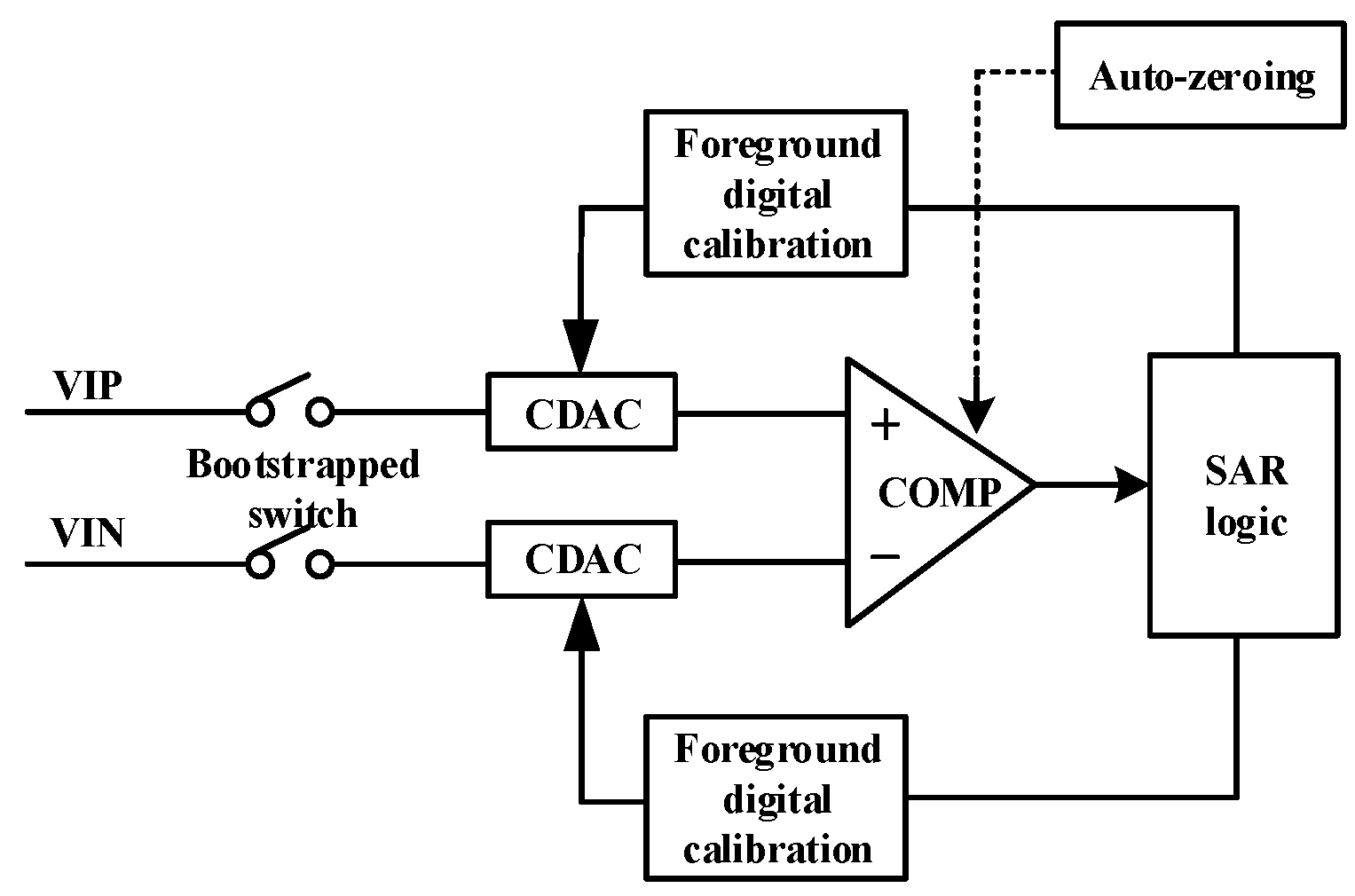
3.1. SAR ADC Architecture
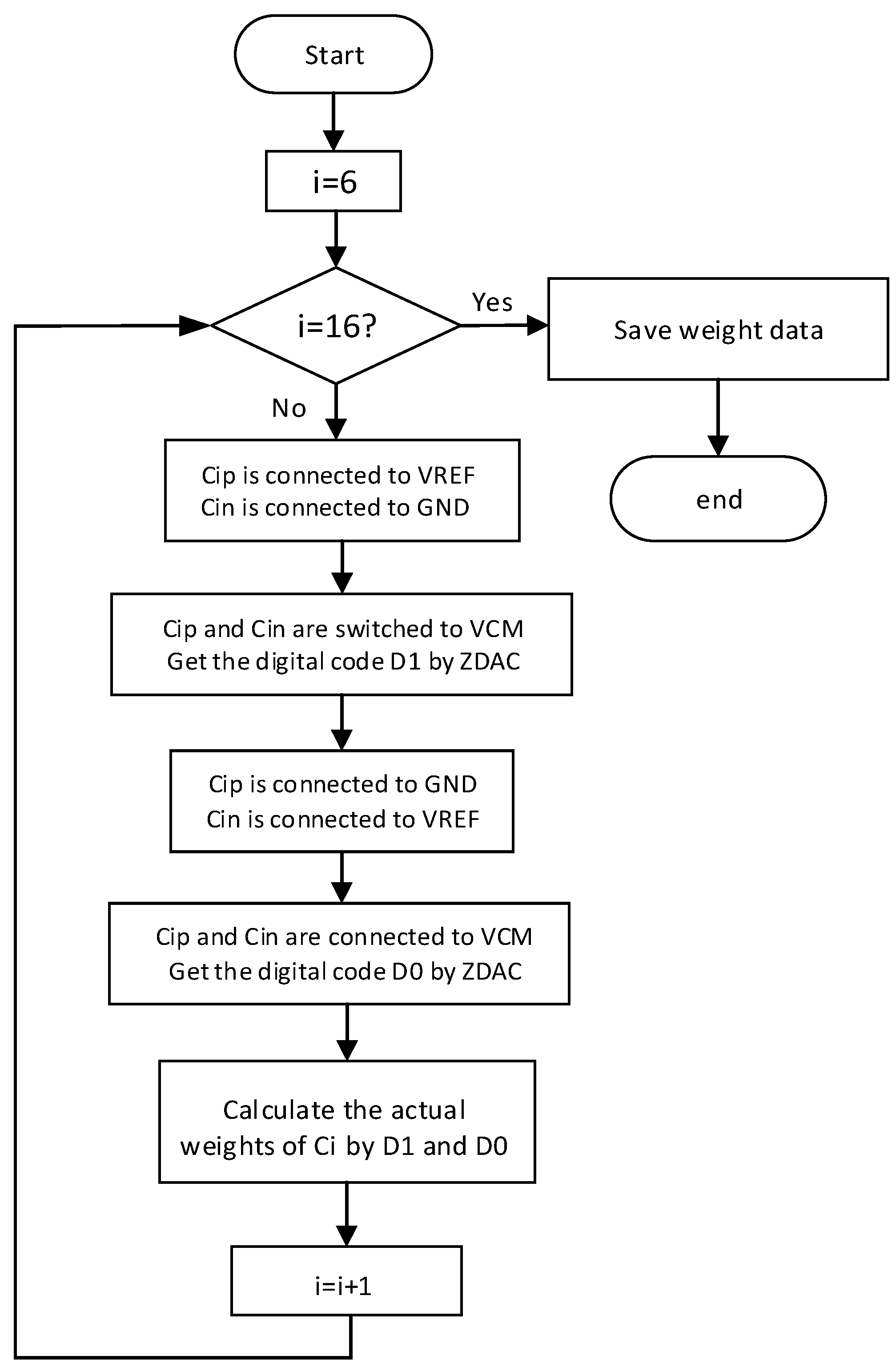
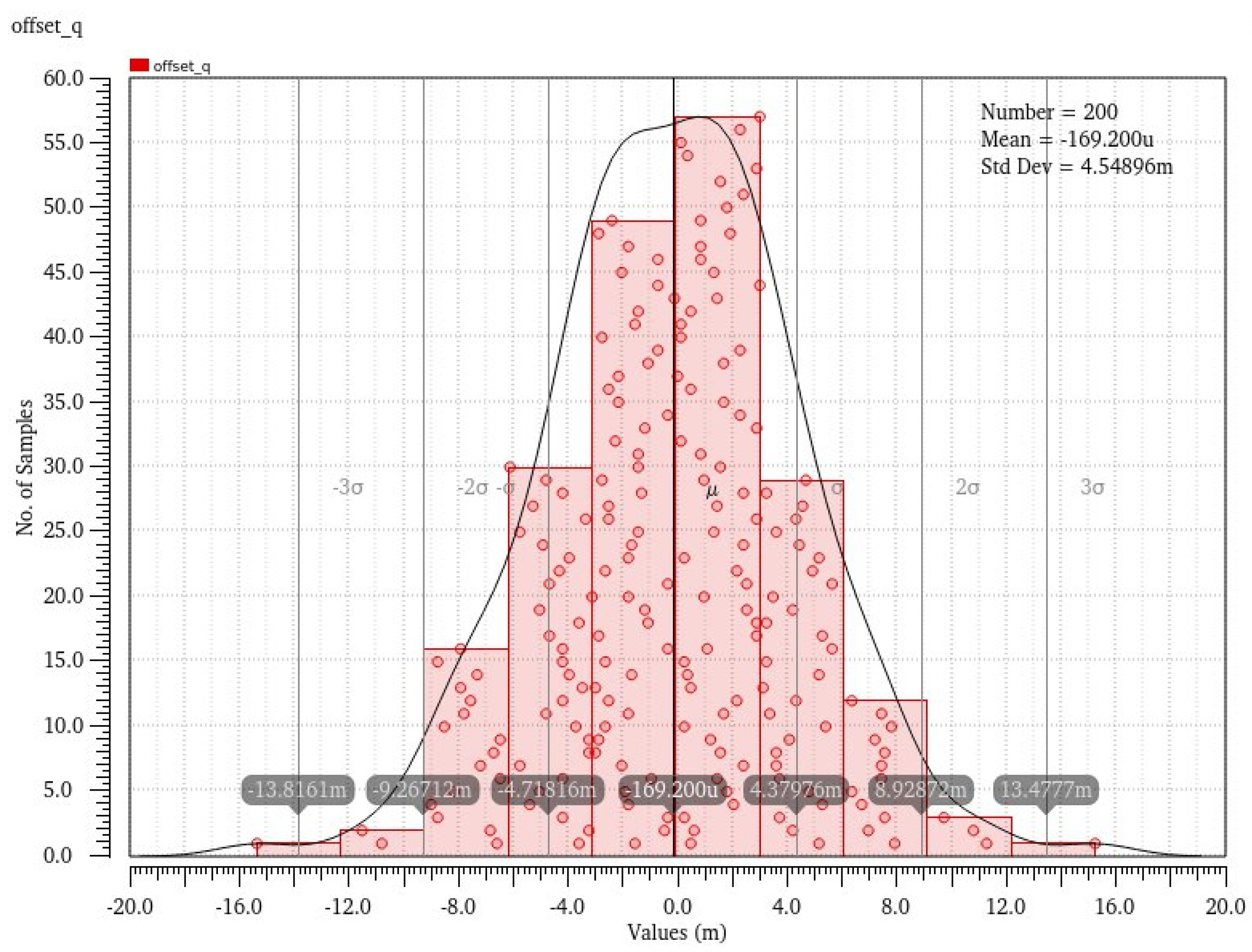
3.2. DAC Foreground Calibration
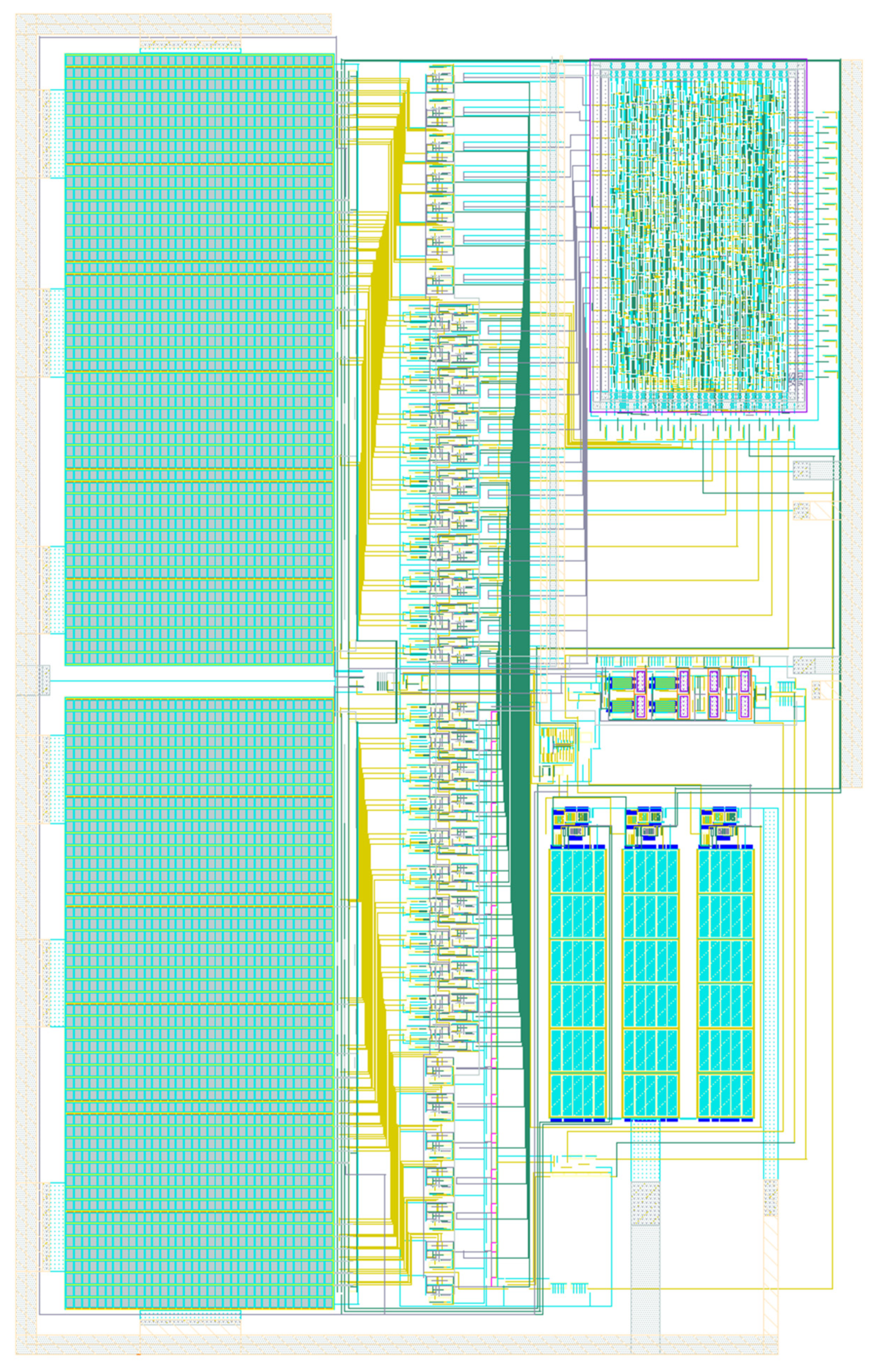
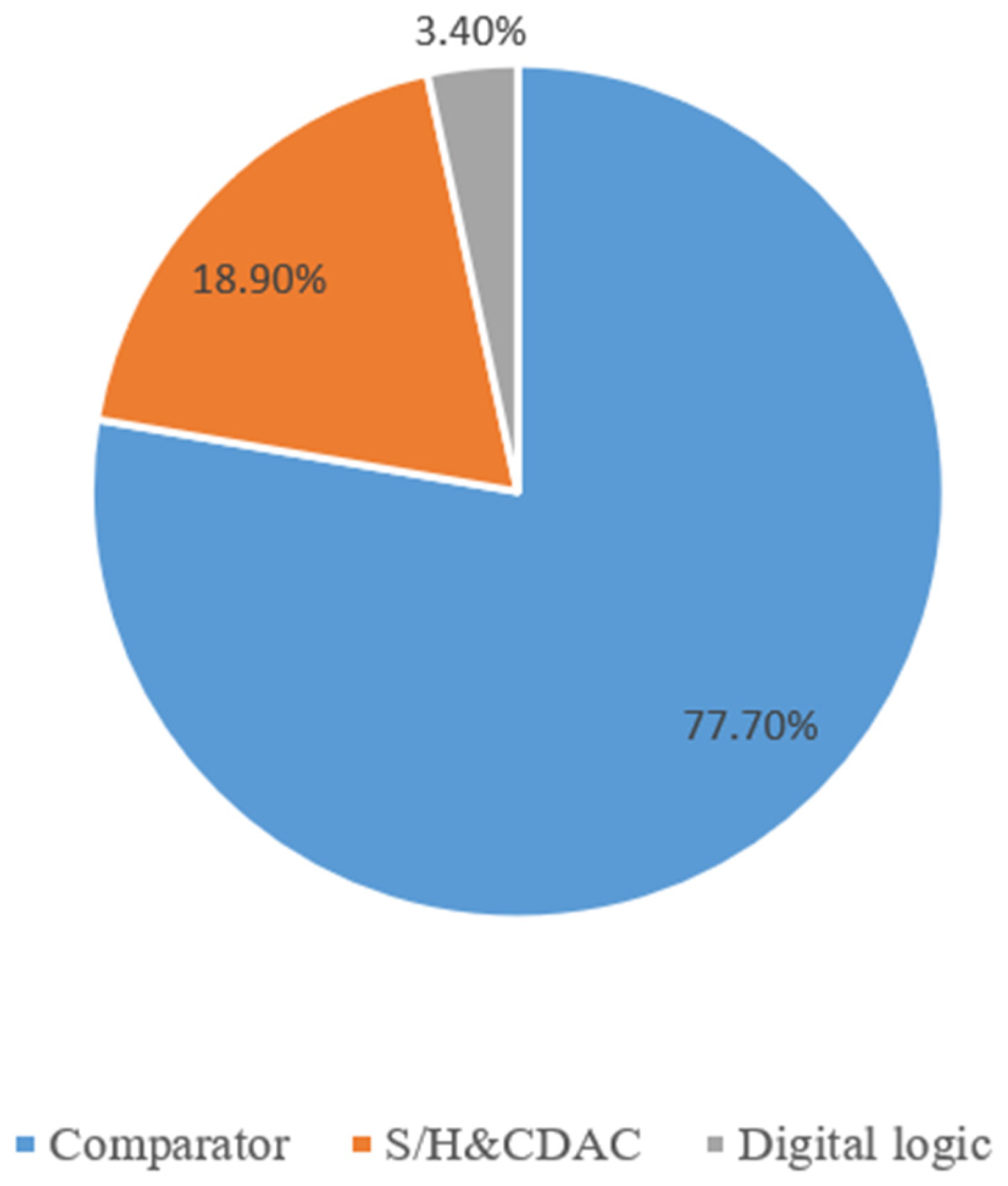
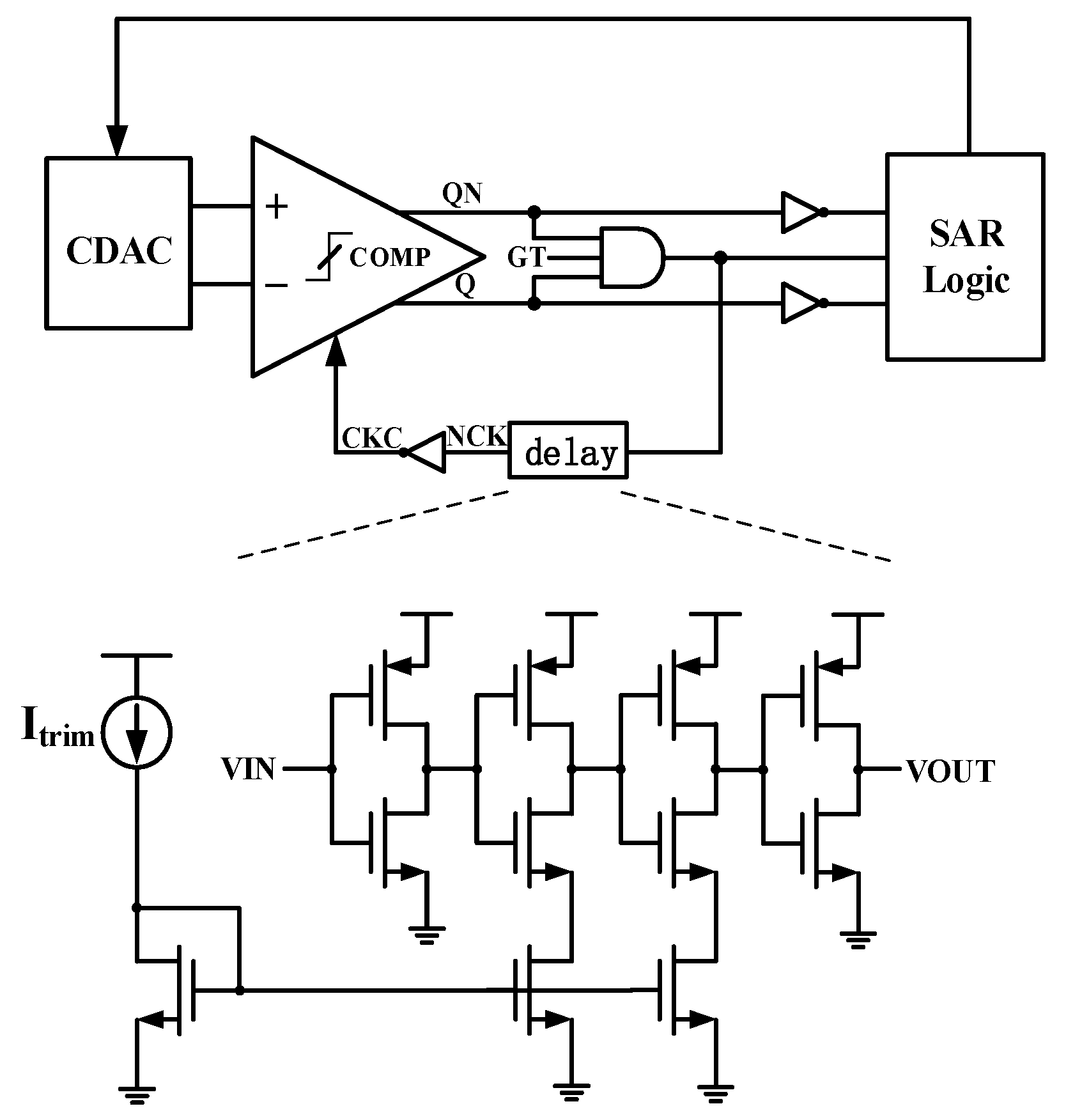
4. SAR ADC Circuit Implementation
4.1. Bootstrapped Switch
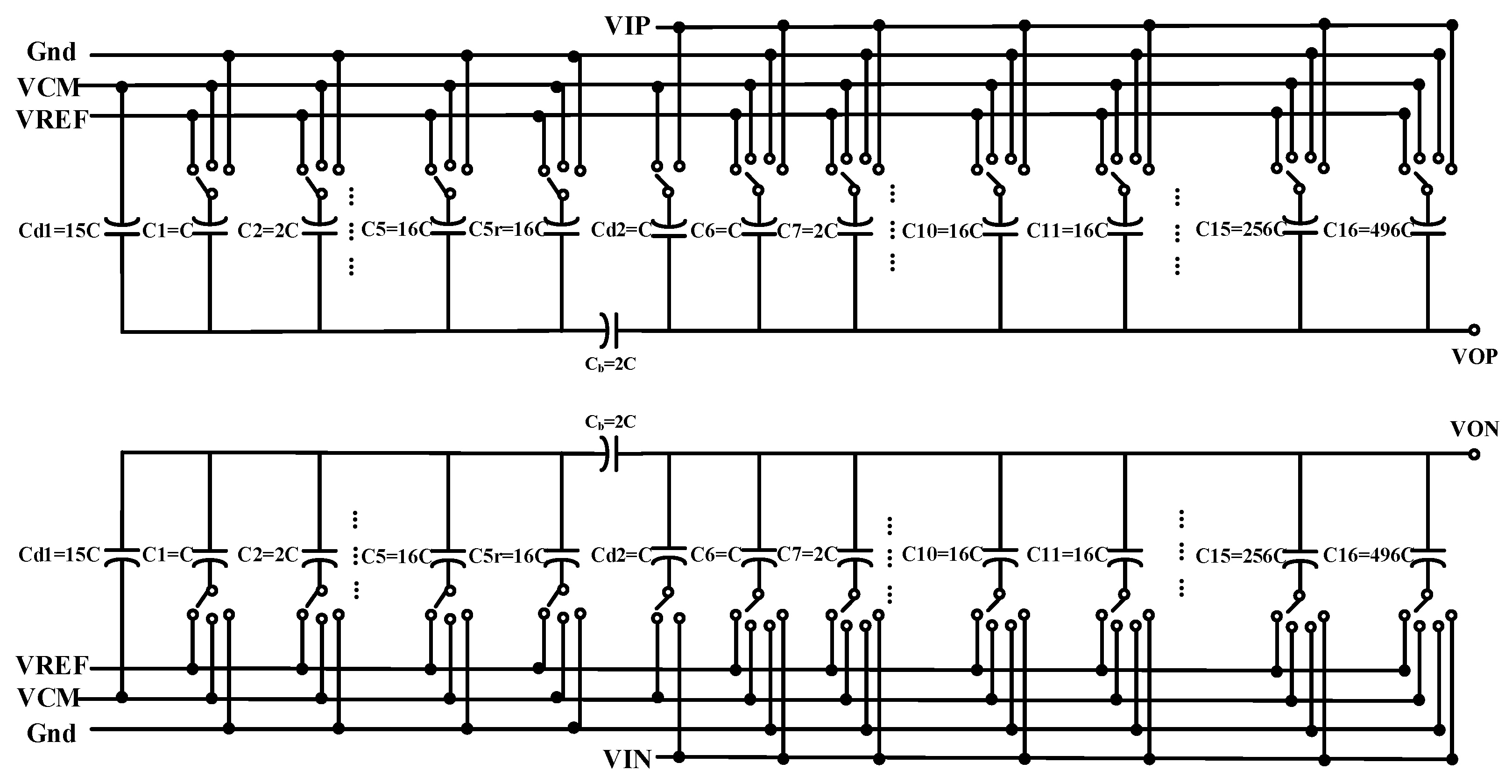
4.2. Capacitive DAC
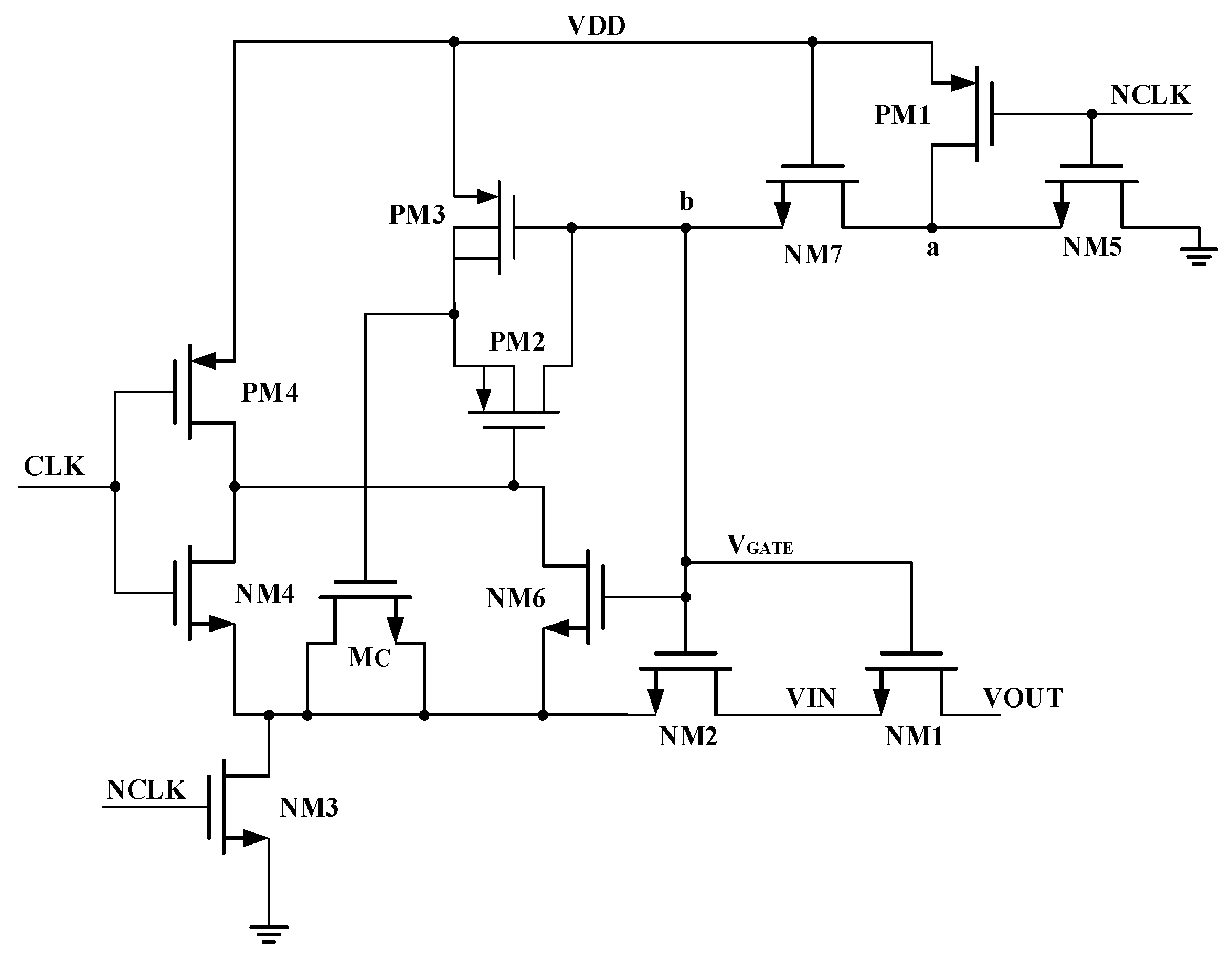
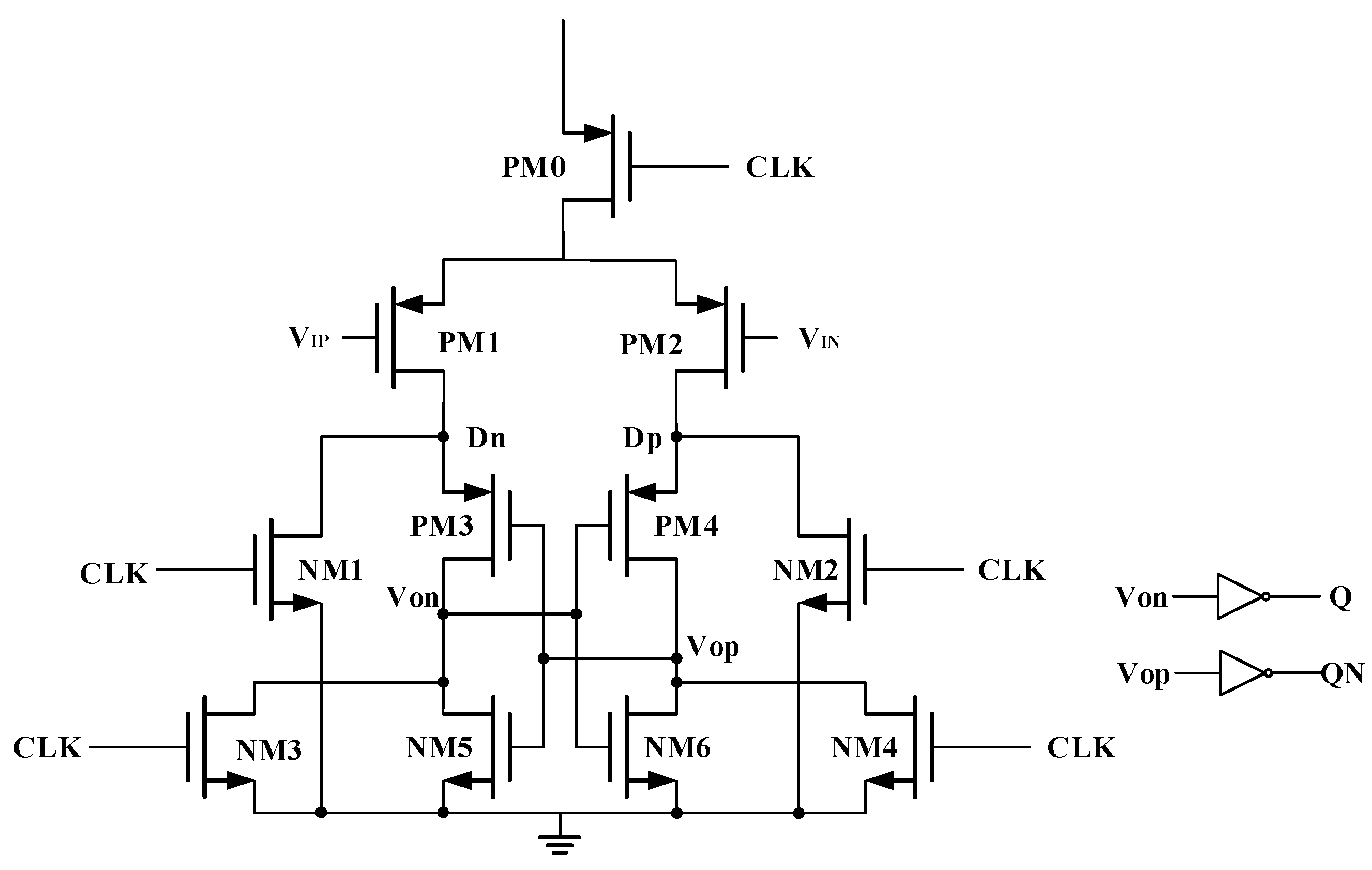
4.3. Comparator
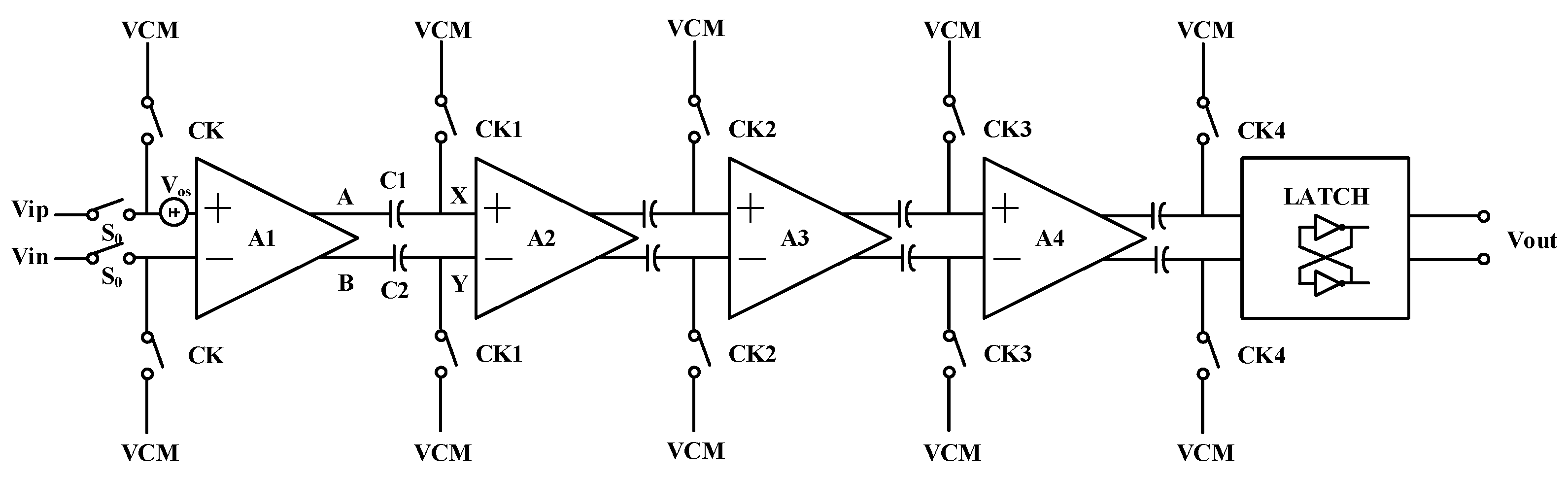
4.4. SAR Logic
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Wang, X.; Gao, Z.; Zhan, M.; Tang, X.; Sun, N. 9.3 A 40kHz-BW 90dB-SNDR Noise-Shaping SAR with 4× Passive Gain and 2nd-Order Mismatch Error Shaping. In Proceedings of the 2020 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 158–160. [Google Scholar]
- Zhu, Y.; Chan, C.H.; Chio, U.F.; Sin, S.W.; Seng-Pan, U.; Martins, R.P.; Maloberti, F. A 10-bit 100-MS/s Reference-Free SAR ADC in 90 nm CMOS. IEEE J. Solid-State Circuits 2010, 45, 1111–1121. [Google Scholar] [CrossRef]
- Bindra, H.S.; Annema, A.J.; Louwsma, S.M.; Nauta, B. A 0.2–8 MS/s 10b flexible SAR ADC achieving 0.35–2.5 fJ/conv-step and using self-quenched dynamic bias comparator. In Proceedings of the 2019 Symposium on VLSI Circuits, Kyoto, Japan, 9–14 June 2019; pp. C74–C75. [Google Scholar]
- Maddox, M.; Chen, B.; Coln, M.; Kapusta, R.; Shen, J.; Fernando, L. A 16 bit linear passive-charge-sharing SAR ADC in 55nm CMOS. In Proceedings of the 2016 IEEE Asian Solid-State Circuits Conference (A-SSCC), Toyama, Japan, 7–9 November 2016; pp. 153–156. [Google Scholar]
- Konno, S.; Miyahara, Y.; Sobue, K.; Hamashita, K. A 16b 1.62MS/s Calibration-free SAR ADC with 86.6dB SNDR utilizing DAC Mismatch Cancellation Based on Symmetry. In Proceedings of the 2020 IEEE Asian Solid-State Circuits Conference (A-SSCC), Hiroshima, Japan, 9–11 November 2020; pp. 1–2. [Google Scholar]
- Cao, C.; Ye, Q.; Zhu, Z.; Yang, Y. A background digital calibration of split-capacitor 16-bit SAR ADC with sub-binary architecture. Microelectron. J. 2015, 46, 795–800. [Google Scholar] [CrossRef]
- Verma, N.; Chandrakasan, A.P. An Ultra Low Energy 12-bit Rate-Resolution Scalable SAR ADC for Wireless Sensor Nodes. IEEE J. Solid-State Circuits 2007, 42, 1196–1205. [Google Scholar] [CrossRef]
- Choi, S.; Ku, H.S.; Son, H.; Kim, B.; Park, H.J.; Sim, J.Y. An 84.6-dB-SNDR and 98.2-dB-SFDR Residue-Integrated SAR ADC for Low-Power Sensor Applications. IEEE J. Solid-State Circuits 2018, 53, 404–417. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, S.J.; Huang, C.P.; Chang, L.J.; Shyu, Y.T.; Hou, C.H.; Tseng, H.A.; Kung, C.Y.; Hu, H.J. A 12-b 40-MS/s Calibration-Free SAR ADC. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 881–890. [Google Scholar] [CrossRef]
- Miki, T.; Morie, T.; Matsukawa, K.; Bando, Y.; Okumoto, T.; Obata, K.; Sakiyama, S.; Dosho, S. A 4.2 mW 50 MS/s 13 bit CMOS SAR ADC With SNR and SFDR Enhancement Techniques. IEEE J. Solid-State Circuits 2015, 50, 1372–1381. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, L.; Tang, K.; Zheng, Y. A 98.6 dB SNDR SAR ADC With a Mismatch Error Shaping Technique Implemented With Double Sampling. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 774–778. [Google Scholar] [CrossRef]
- McNeill, J.; Coln, M.C.W.; Larivee, B.J. “Split ADC” architecture for deterministic digital background calibration of a 16-bit 1-MS/s ADC. IEEE J. Solid-State Circuits 2005, 40, 2437–2445. [Google Scholar] [CrossRef]
- Enz, C.C.; Temes, G.C. Circuit techniques for reducing the effects of op-amp imperfections: Autozeroing, correlated double sampling, and chopper stabilization. Proc. IEEE 1996, 84, 1584–1614. [Google Scholar] [CrossRef]
- Razavi, B.; Wooley, B.A. Design techniques for high-speed, high-resolution comparators. IEEE J. Solid-State Circuits 1992, 27, 1916–1926. [Google Scholar] [CrossRef]
- Hesener, M.; Eicher, T.; Hanneberg, A.; Herbison, D.; Kuttner, F.; Wenske, H. A 14b 40 MS/s Redundant SAR ADC with 480 MHz Clock in 0.13 pm CMOS. In Proceedings of the 2007 IEEE International Solid-State Circuits Conference, Digest of Technical Papers, San Francisco, CA, USA, 11–15 February 2007; pp. 248–600. [Google Scholar]
- Allstot, D.J. A precision variable-supply CMOS comparator. IEEE J. Solid-State Circuits 1982, 17, 1080–1087. [Google Scholar] [CrossRef]
- Lee, H.S.; Hodges, D.A.; Gray, P.R. A self-calibrating 15 bit CMOS A/D converter. IEEE J. Solid-State Circuits 1984, 19, 813–819. [Google Scholar] [CrossRef]
- Tseng, W.H.; Lee, W.L.; Huang, C.Y.; Chiu, P.C. A 12-bit 104-MS/s SAR ADC in 28 nm CMOS for digitally-assisted wireless transmitters. In Proceedings of the 2015 IEEE Asian Solid-State Circuits Conference (A-SSCC), Xiamen, China, 9–11 November 2015; pp. 1–4. [Google Scholar]
- Kapusta, R.; Shen, J.; Decker, S.; Li, H.; Ibaragi, E.; Zhu, H. A 14b 80 MS/s SAR ADC With 73.6 dB SNDR in 65 nm CMOS. IEEE J. Solid-State Circuits 2013, 48, 3059–3066. [Google Scholar] [CrossRef]
- Liu, W.; Huang, P.; Chiu, Y. A 12b 22.5/45 MS/s 3.0 mW 0.059 mm2 CMOS SAR ADC achieving over 90 dB SFDR. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 7–11 February 2010; pp. 380–381. [Google Scholar]
- Li, H.; Maddox, M.; Coin, M.C.W.; Buckley, W.; Hummerston, D.; Naeem, N. A signal-independent background-calibrating 20b 1 MS/S SAR ADC with 0.3 ppm INL. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 242–244. [Google Scholar]
- Murmann, B. ADC Performance Survey 1997–2023. Available online: https://github.com/bmurmann/ADC-survey (accessed on 1 May 2024).
- Shen, J.; Shikata, A.; Fernando, L.D.; Guthrie, N.; Chen, B.; Maddox, M.; Mascarenhas, N.; Kapusta, R.; Coln, M.C.W. A 16-bit 16-MS/s SAR ADC With On-Chip Calibration in 55-nm CMOS. IEEE J. Solid-State Circuits 2018, 53, 1149–1160. [Google Scholar] [CrossRef]
- Xu, H.; Huang, H.; Cai, Y.; Du, L.; Zhou, Y.; Xu, B.; Gong, D.; Ye, J.; Chiu, Y. A 78.5-dB SNDR Radiation- and Metastability-Tolerant Two-Step Split SAR ADC Operating Up to 75 MS/s With 24.9-mW Power Consumption in 65-nm CMOS. IEEE J. Solid-State Circuits 2019, 54, 441–451. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, Y.; Zhu, Y.; Chan, C.H.; Martins, R.P. A 79.5 dB-SNDR Pipelined-SAR ADC with a Linearity-Shifting 32× Dynamic Amplifier and Mounted-Over-Die Bypass Capacitors. In Proceedings of the 2023 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Kyoto, Japan, 11–16 June 2023; pp. 1–2. [Google Scholar]
- Bannon, A.; Hurrell, C.P.; Hummerston, D.; Lyden, C. An 18 b 5 MS/s SAR ADC with 100.2 dB dynamic range. In Proceedings of the 2014 Symposium on VLSI Circuits Digest of Technical Papers, Honolulu, HI, USA, 10–13 June 2014; pp. 1–2. [Google Scholar]
- Chung, Y.H.; Tien, C.H.; Zeng, Q.F. A 16-Bit Calibration-Free SAR ADC With Binary-Window and Capacitor-Swapping DAC Switching Schemes. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 88–99. [Google Scholar] [CrossRef]
- Fiorelli, R.; Guerra, Ó.; Río, R.D.; Rodríguez-Vázquez, Á. Effects of capacitors non-idealities in un-even split-capacitor array SAR ADCs. In Proceedings of the 2015 Conference on Design of Circuits and Integrated Systems (DCIS), Estoril, Portugal, 25–27 November 2015; pp. 1–4. [Google Scholar]
- Srinivasan, C.; Godbole, K.M. Error Correction Architecture to Increase Speed and Relax Current Drive Requirements of SAR ADC. U.S. Patent US6747589B2, 8 June 2004. [Google Scholar]
- Liu, C.C.; Chang, S.J.; Huang, G.Y.; Lin, Y.Z.; Huang, C.M.; Huang, C.H.; Bu, L.; Tsai, C.C. A 10b 100 MS/s 1.13 mW SAR ADC with binary-scaled error compensation. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 7–11 February 2010; pp. 386–387. [Google Scholar]
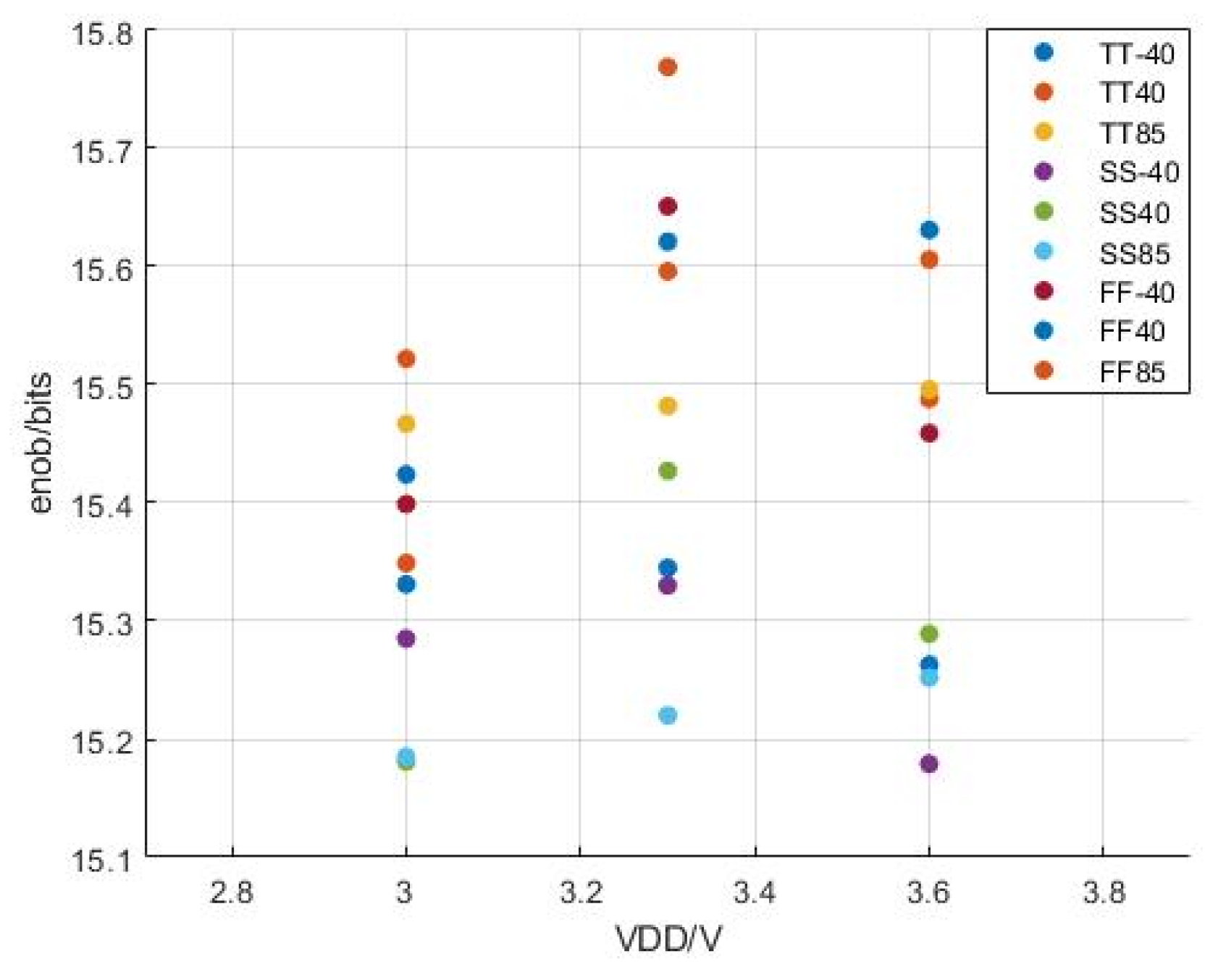
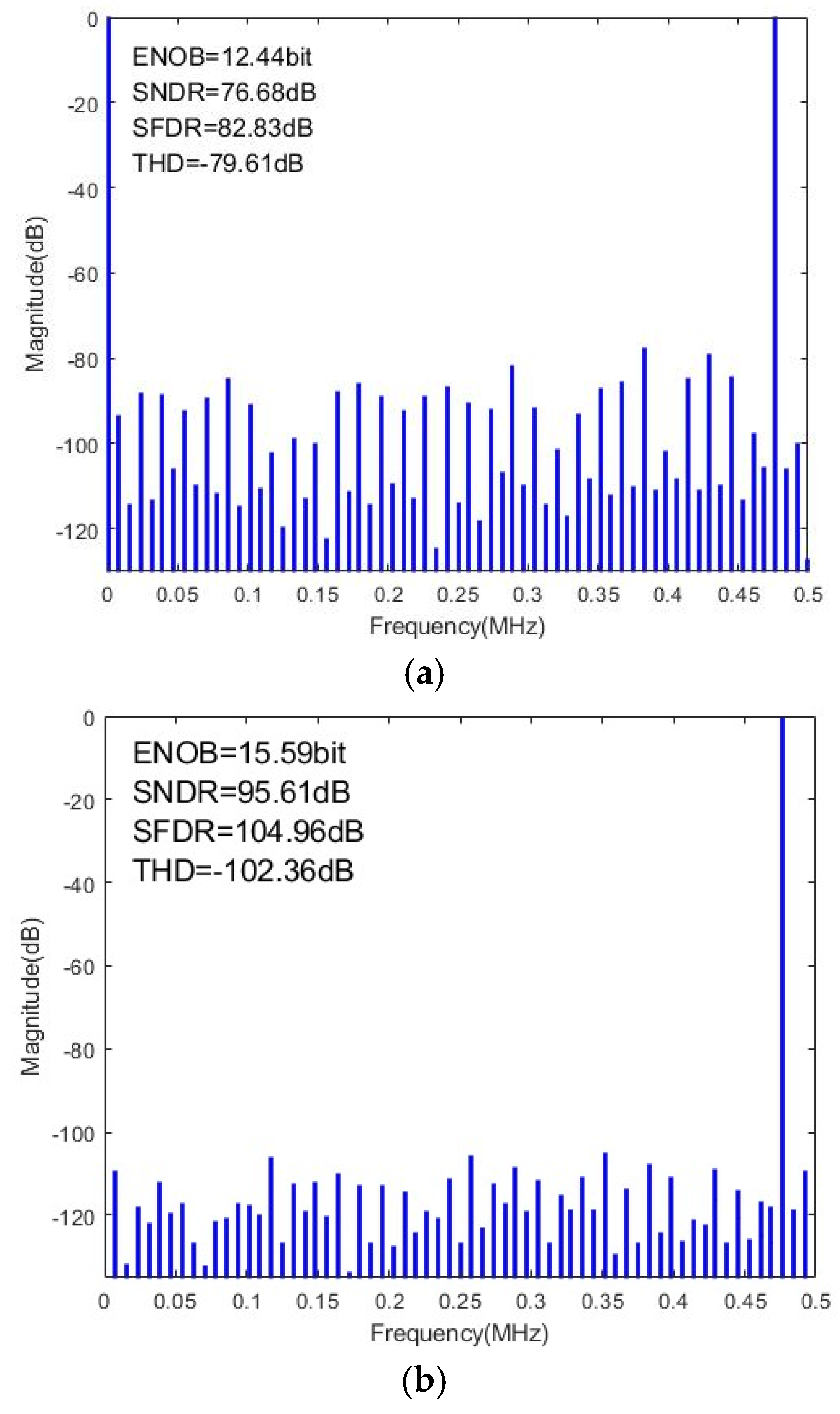

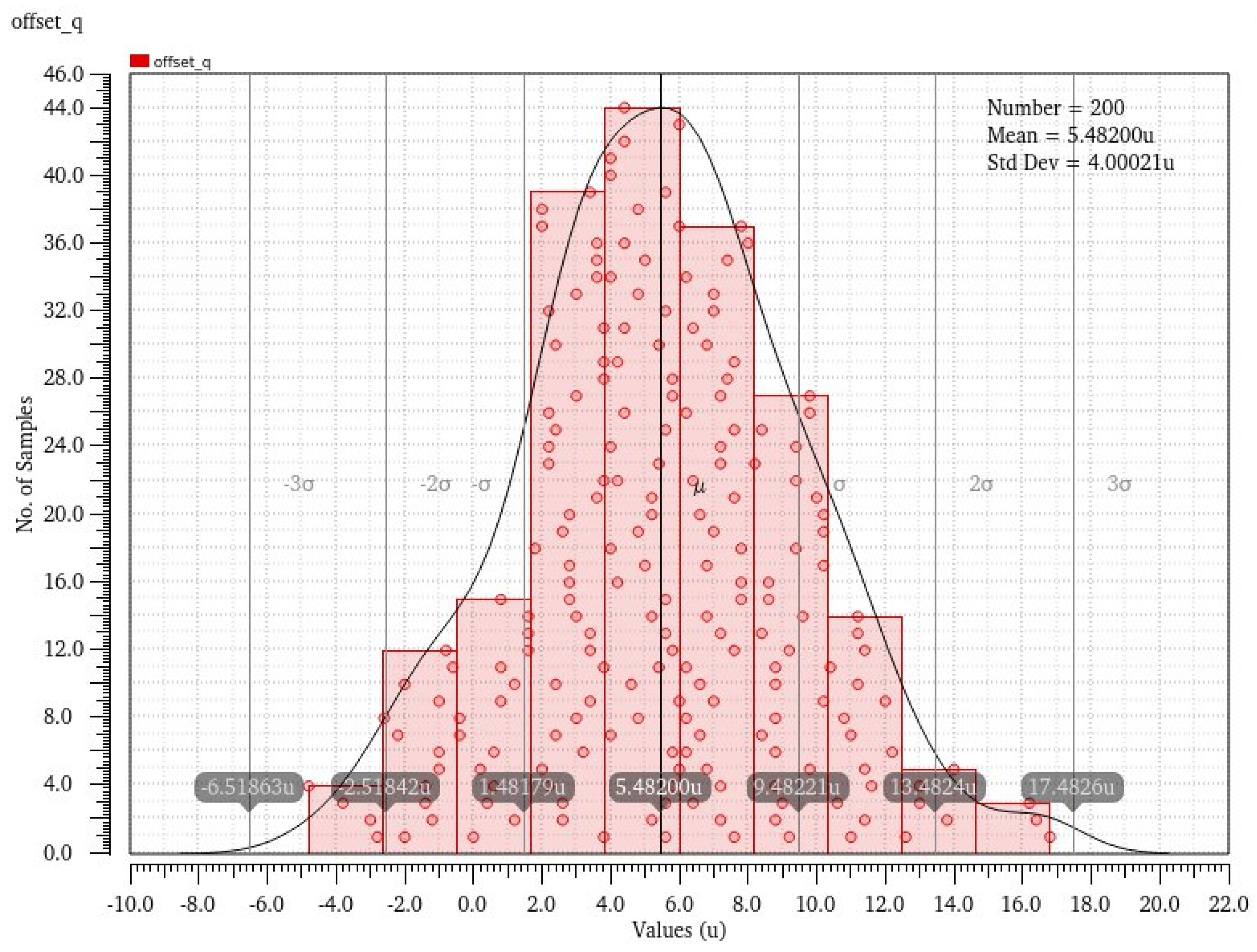
| Corner | Supply Voltage (V) | Temperature (°C) | ENOB (bits) with/without Calibration | SNDR (dB) with/without Calibration | SFDR (dB) with/without Calibration |
|---|---|---|---|---|---|
| TT | 3.3 | 40 | 15.50/12.50 | 95.06/77.01 | 105.00/83.49 |
| FF | 3.3 | 85 | 15.11/12.46 | 92.73/76.76 | 100.97/83.35 |
| FF | 3 | −40 | 15.23/12.50 | 93.46/76.99 | 99.79/83.74 |
| SS | 3.6 | −40 | 14.98/12.56 | 91.97/77.40 | 99.99/84.60 |
| SS | 3 | 85 | 15.42/12.40 | 94.62/76.44 | 105.36/83.05 |
| This Work * | [23] | [26] | [4] | [24] | [25] | [27] | |
|---|---|---|---|---|---|---|---|
| Type | SAR | SAR | Pipe SAR | SAR | Pipe SAR | Pipe SAR | BW-SAR |
| Resolution (bits) | 16 | 16 | 18 | 16 | 14 | 15 | 16 |
| Speed (MS/s) | 1 | 16 | 5 | 1 | 75 | 60 | 1 |
| Power (mW) | 5.4 | 16.3 | 30.5 | 6.95 | 24.9 | 1.55 | 1.05 |
| SNDR (dB) | 95.61 | 78 | 99 | 91 | 70.8 | 76.9 | 83 |
| SFDR (dB) | 104.96 | 98 | 100 | 100 | 89.6 | 87.3 | 100 |
| VDD (V) | 3.3 | 3.3/1.2 | 5/1.8 | 1.2 | 1.8 | 1.1 | 1.8/3.3 |
| Calibration | On chip | On chip | Off chip | Off chip | On chip | On chip | No |
| FoM (dB) | 175.3 | 165 | 177.7 | 159.6 | 165.6 | 179.8 | 169.8 |
| Process (nm) | 180 | 55 | 180 | 55 | 65 | 65 | 180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Qiao, W.; Xing, X.; Feng, H. A Power-Efficient 16-bit 1-MS/s Successive Approximation Register Analog-to-Digital Converter with Digital Calibration in 0.18 μm Complementary Metal Oxide Semiconductor. J. Low Power Electron. Appl. 2024, 14, 32. https://doi.org/10.3390/jlpea14020032
He X, Qiao W, Xing X, Feng H. A Power-Efficient 16-bit 1-MS/s Successive Approximation Register Analog-to-Digital Converter with Digital Calibration in 0.18 μm Complementary Metal Oxide Semiconductor. Journal of Low Power Electronics and Applications. 2024; 14(2):32. https://doi.org/10.3390/jlpea14020032
Chicago/Turabian StyleHe, Xinyuan, Weifeng Qiao, Xinpeng Xing, and Haigang Feng. 2024. "A Power-Efficient 16-bit 1-MS/s Successive Approximation Register Analog-to-Digital Converter with Digital Calibration in 0.18 μm Complementary Metal Oxide Semiconductor" Journal of Low Power Electronics and Applications 14, no. 2: 32. https://doi.org/10.3390/jlpea14020032
APA StyleHe, X., Qiao, W., Xing, X., & Feng, H. (2024). A Power-Efficient 16-bit 1-MS/s Successive Approximation Register Analog-to-Digital Converter with Digital Calibration in 0.18 μm Complementary Metal Oxide Semiconductor. Journal of Low Power Electronics and Applications, 14(2), 32. https://doi.org/10.3390/jlpea14020032






