A Simple, Robust, and Versatile MATLAB Formulation of the Dynamic Memdiode Model for Bipolar-Type Resistive Random Access Memory Devices
Abstract
1. Introduction
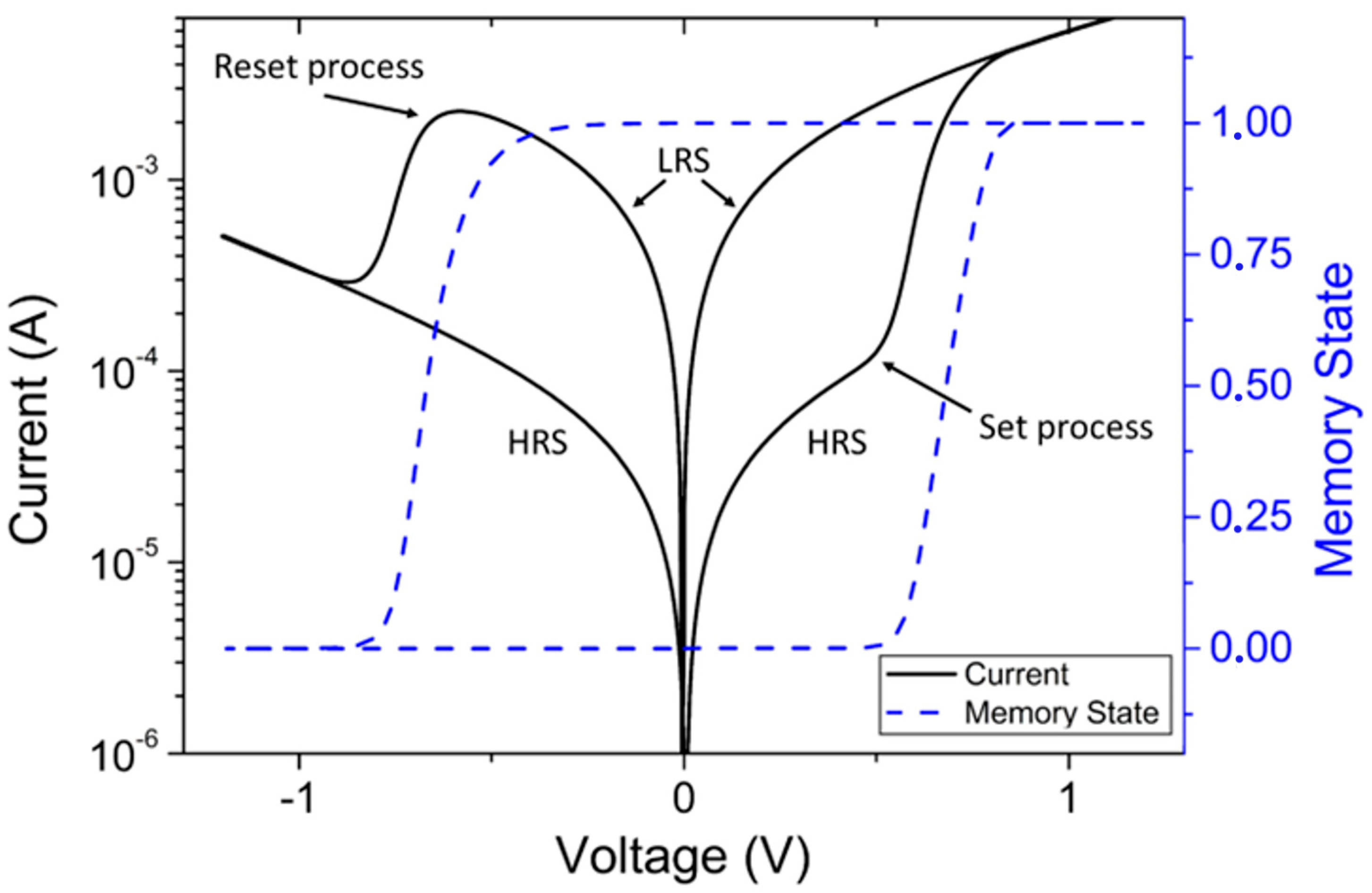
2. Dynamic Memdiode Model
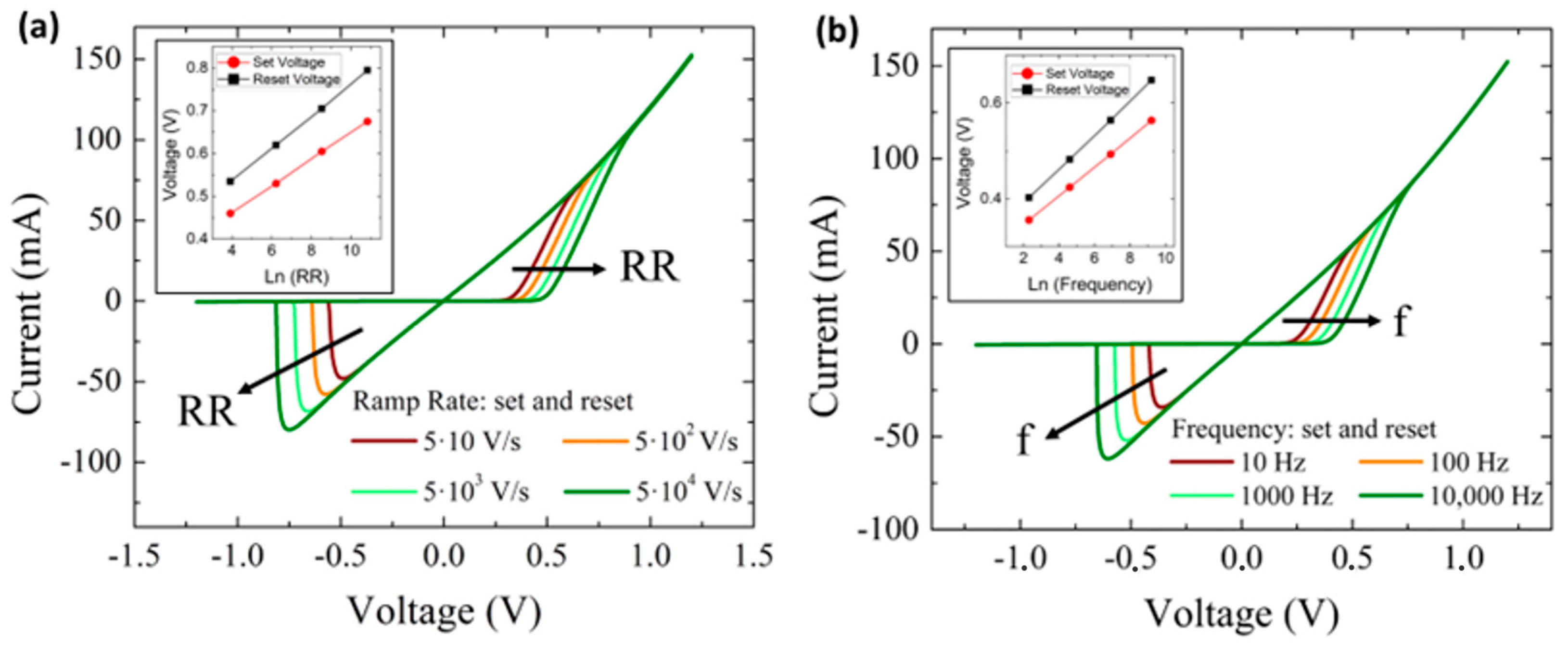
3. First Case Study: Modeling of Frequency and Ramp Rate Effects
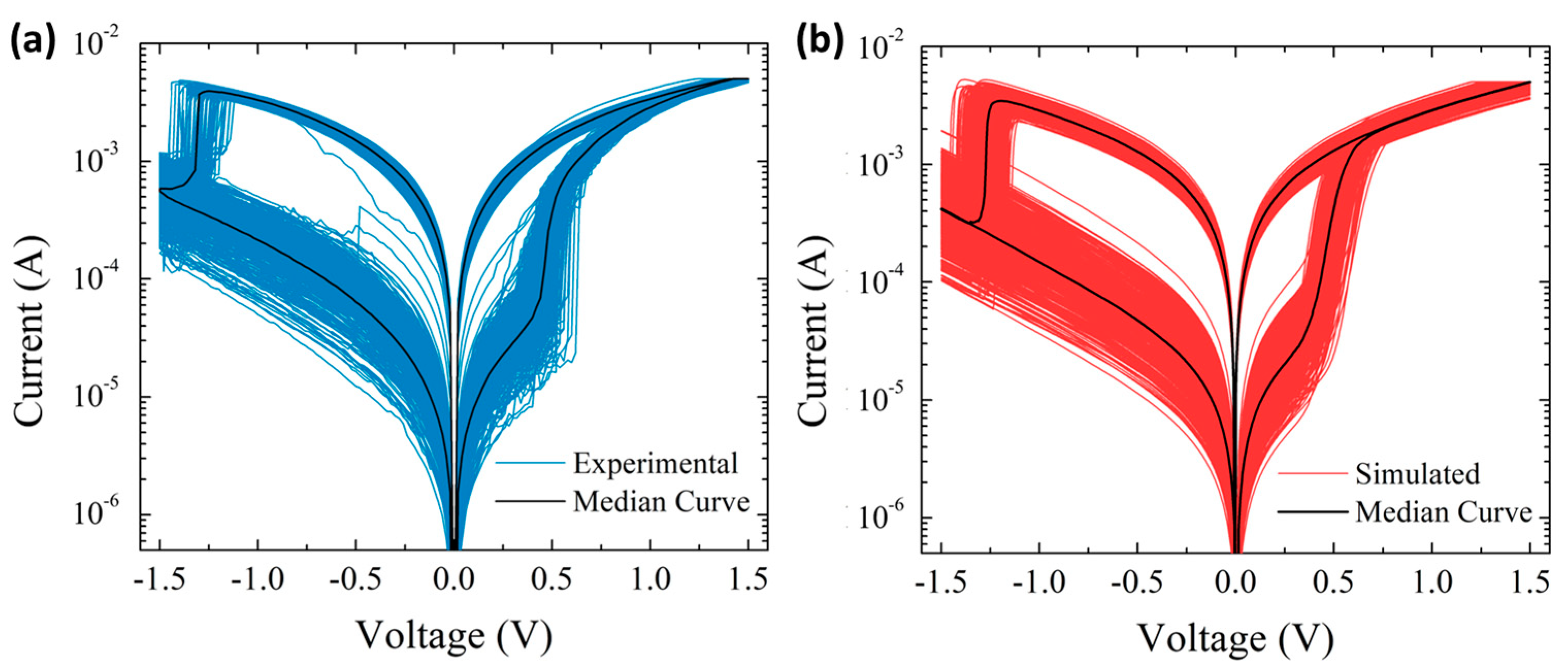
4. Second Case Study: Modeling Cycle-to-Cycle Variability
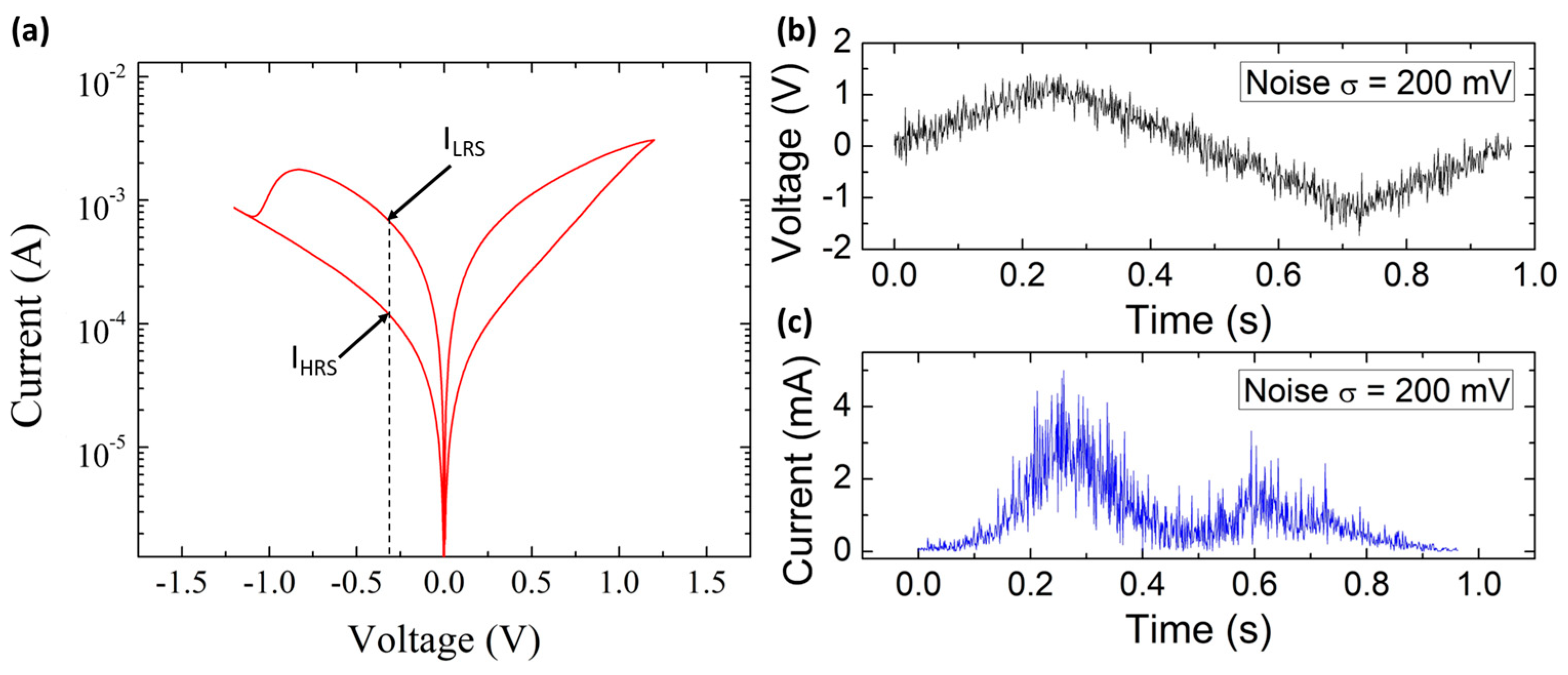
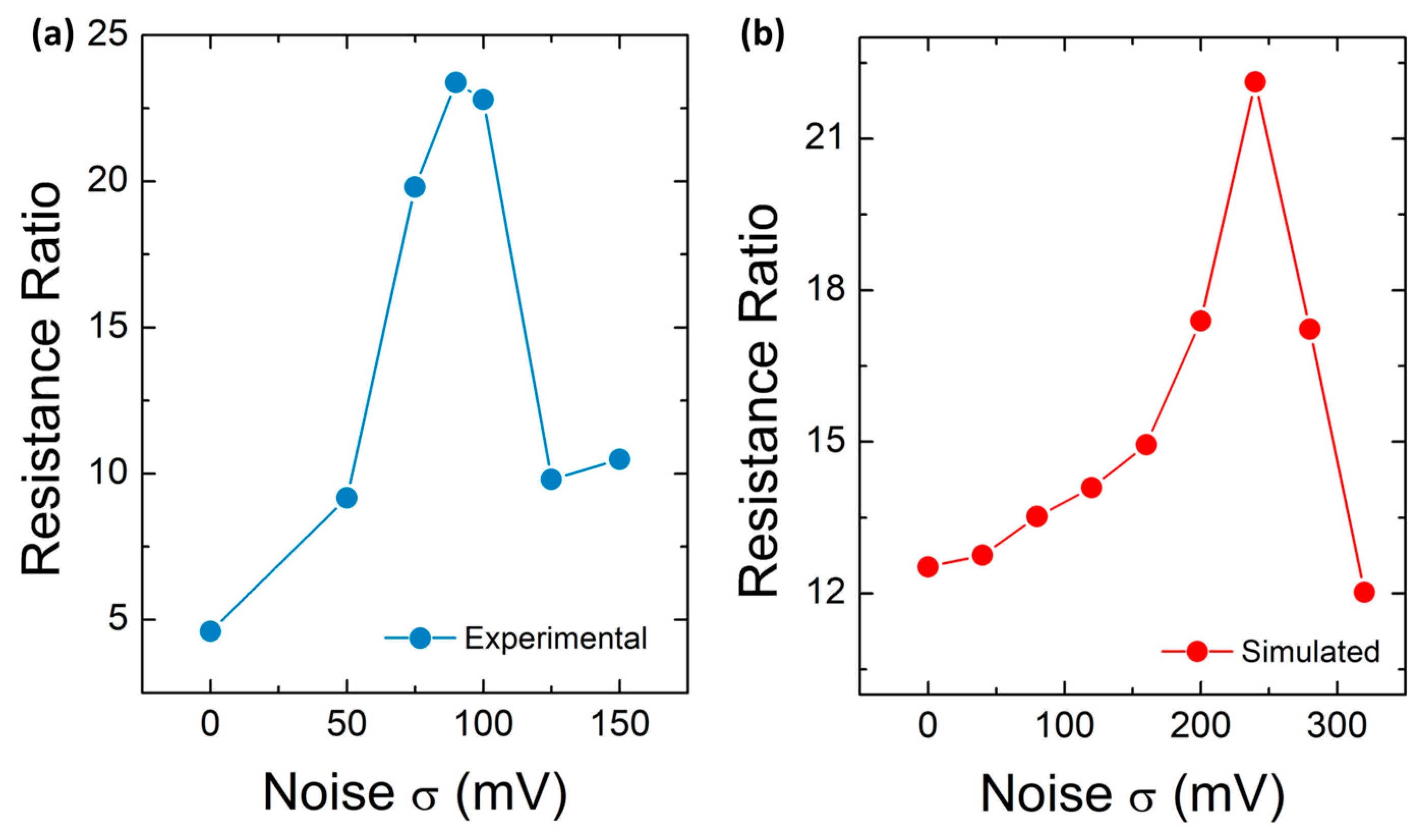
5. Third Case Study: Modeling the Stochastic Resonance Impact on RRAM Devices
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Frequency Effect—DMM in MATLAB |
|---|
|
ncyc=4; for n=1:ncyc V= 1.2 * sin(linspace(0, 2*pi, 10000));%Frequency % step=0.005; V1=0:step:1.2; V2=0:-step:-1.2; V=[V1 flip(V1) V2 flip(V2)];%Ramp Rate aoff=2; aon=2; Ri=3; Roff=30; Ron=10; Ioff=10E-5; Ion=150E-3; etas=40; etar=-40; gam=0; Vs=0.35; Vr=-0.35; l(1)=0; I(1)=0; RR(n)=1; At(n)=1/(10^n); f(n)=1/At(n);%Frequency % At(n)=1; RR(n)=5*10^(n); %Ramp Rate for t=1:length(V) Vi=V(t)-(Ri)*I(t); I0=(Ion-Ioff)*l(t)+Ioff; a=(aon-aoff)*l(t)+aoff; R=(Ron-Roff)*l(t)+Roff; Tsr=exp(-etas*(Vi-(Vs+log(RR(n))/etas)))*(V(t)>0)+exp(-etar*l(t)^gam*(Vi-(Vr+log(RR(n))/etar)))*(V(t)<=0); I(t+1)=(1/(a*R))*(lambertw((a*R*I0)/2).*exp(a*Vi)-lambertw((a*R*I0)/2).*exp(-a*Vi)); l(t+1)=(l(t)-heaviside(Vi))*exp(-(At(n)/Tsr))+heaviside(Vi); Vm(t,n)=V(t); Im(t,n)=I(t);lm(t,n)=l(t); end pos=find(lm(:,n) >=0.5); reset(n)=Vm(pos(end),n); set(n)=Vm(pos(1)); end subplot(2, 1, 1); plot(Vm,(Im)); title('I-V - Frequency effect');%Frequency subplot(2, 1, 2); plot(log(f),set,log(f),abs(reset)); title('Log F VS |S/R Voltage|'); %Frequency % subplot(2, 1, 1); plot(Vm,(Im)); title('I-V - Ramp Rate effect'); %Ramp Rate % subplot(2, 1, 2); plot(log(RR),set,log(RR),abs(reset)); title('Log RR VS |S/R Voltage|'); %Ramp Rate |
Appendix B
| Cycle-to-Cycle Variability—DMM in MATLAB |
| ncyc=450; for n=1:ncyc step=0.005; V1=0:step:1.5; V2=0:-step:-1.5; V=[V1 flip(V1) V2 flip(V2)];%for applied voltage Maoff=2.1; Saoff=0.13; aoff=Maoff+Saoff*randn;%M=mean S=standard deviation Maon=1.25; Saon=0.06; aon=Maon+Saon*randn; MIoff=3.7E-5;IoffLN=log(MIoff);SIoff=0.6; Ioff=exp(IoffLN+SIoff*randn);%lognormal MIon=2.4E-3; IonLN=log(MIon);SIon=0.12; Ion=exp(IonLN+SIon*randn); MVs=0.38;VsLN=log(MVs);SVs=0.12; Vs=exp(VsLN+SVs*randn);%lognormal MVr=-0.86; SVr=0.035; Vr=MVr+SVr*randn; Metas=32; Setas=3.1; etas=Metas+Setas*randn; etar=-27; Ri=60; gam=0; At=1E-3; Roff=50; Ron=20; IC=5E-3; l(1)=0; I(1)=0; for t=1:length(V) Vi=V(t)-(Ri)*I(t); I0=(Ion-Ioff)*l(t)+Ioff; a=(aon-aoff)*l(t)+aoff; R=(Ron-Roff)*l(t)+Roff; Tsr=exp(-etas*(Vi-Vs))*(V(t)>0)+exp(-etar*l(t)^gam*(Vi-Vr))*(V(t)<=0); if I(t)>IC I(t)=IC; % Compliance current end I(t+1)=(1/(a*R))*(lambertw(a*R*I0/2)*exp(a*Vi)-lambertw(a*R*I0/2*exp(-a*Vi))); l(t+1)=(l(t)-heaviside(Vi))*exp(-At/Tsr)+heaviside(Vi); Vm(t,n)=V(t); Im(t,n)=I(t);lm(t,n)=l(t); end pos=find(lm(:,n) >=0.5); posI=find(Vm(:,n)>=0.2); ihrs(n)=Im(posI(1),n); reset(n)=Vm(pos(end),n); end subplot(2, 1, 1); semilogy(Vm,abs(Im),'r'); title('I-V + C2C Variability'); subplot(2, 2, 3); hist(ihrs,15) ; title('Histogram Ihrs'); subplot(2, 2, 4); hist(reset,15) ; title('Histogram VReset'); |
Appendix C
| Stochastic Resonance—DMM in MATLAB |
|---|
| for g=1:9 %g iterates the noise sigma ncyc=200; for n=1:ncyc step=0.005; V1=0:step:1.2; V2=0:-step:-1.2; V=[V1 flip(V1) V2 flip(V2)];%applied voltage aoff=1.9;aon=1.3;Roff=30; Ron=50;Ioff=19E-5;Ion=6.5E-3; %Parameters Vs=0.55;Vr=-0.45; etas=4; etar=-9; Ri=0; gam=0; L0=0; At=1E-3;l(1)=0; I(1)=0; for t=1:length(V)%calculating current ampn=((g-1)*40)*1E-3; V(t)=V(t)+ampn*randn;%noise inclusion Vi=V(t)-(Ri)*I(t); I0=(Ion-Ioff)*l(t)+Ioff; a=(aon-aoff)*l(t)+aoff; R=(Ron-Roff)*l(t)+Roff; Tsr=exp(-etas*(Vi-Vs))*(V(t)>0)+exp(-etar*l(t)^gam*(Vi-Vr))*(V(t)<=0); I(t+1)=(1/(a*R))*(lambertw(a*R*I0/2)*exp(a*Vi)-lambertw(a*R*I0/2*exp(-a*Vi))); l(t+1)=(l(t)-heaviside(Vi))*exp(-At/Tsr)+heaviside(Vi); Im(t,n,g)=I(t); Vm(t,n,g)=V(t); %Saving I and V variables end nn=1; pos=find(Vm(:,1,1)>=0.3);%Data analysis Rl=mean((Im(pos(end)-nn:pos(end)+nn,:,g))); Rh=mean((Im(pos(1)-nn:pos(1)+nn,:,g))); rat=(Rl./Rh); RRatio(g,1)=mean(rat); end end subplot(2,1,1); semilogy(Vm(:,:,1),abs(Im(:,:,1)), 'r'); title('I-V without noise'); subplot(2,1,2); plot(RRatio); title('RRatio VS Noise sigma'); |
References
- Im, I.H.; Kim, S.J.; Jang, H.W. Memristive Devices for New Computing Paradigms. Adv. Intell. Syst. 2020, 2, 2000105. [Google Scholar] [CrossRef]
- Nagashima, K.; Yanagida, T.; Oka, K.; Taniguchi, M.; Kawai, T.; Kim, J.; Park, B.H. Resistive Switching Multistate Nonvolatile Memory Effects in a Single Cobalt Oxide Nanowire. Nano Lett. 2010, 10, 1359–1363. [Google Scholar] [CrossRef] [PubMed]
- Ishibea, T.; Maeda, Y.; Terada, T.; Naruse, N.; Mera, Y.; Kobayashi, E.; Nakamura, Y. Resistive switching memory performance in oxide hetero-nanocrystals with well-controlled interfaces. Sci. Technol. Adv. Mater. 2020, 21, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Shu, F.; Chen, X.; Yu, Z.; Gao, P.; Liu, G. Metal–Organic Frameworks–Based Memristors: Materials, Devices, and Applications. Molecules 2022, 27, 8888. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Zhu, X.; Lu, W.D. Nanoscale resistive switching devices for memory and computing applications. Nano Res. 2020, 13, 1228–1243. [Google Scholar] [CrossRef]
- Ielmini, D.; Wong, S.H.P. In-memory computing with resistive switching devices. Nat. Electron. 2018, 1, 333–343. [Google Scholar] [CrossRef]
- Pedretti, G.; Milo, V.; Ambrogio, S.; Carboni, R.; Bianchi, S.; Calderoni, A.; Ramaswamy, N.; Spinelli, A.S.; Ielmini, D. Stochastic learning in neuromorphic hardware via spike timing dependent plasticity with RRAM synapses. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 77–85. [Google Scholar] [CrossRef]
- Li, C.; Hu, M.; Li, Y.; Jiang, H.; Ge, N.; Montgomery, E.; Zhang, J.; Song, W.; Dávila, N.; Graves, C.E.; et al. Analogue signal and image processing with large memristor crossbars. Nat. Electron. 2018, 7, 52–59. [Google Scholar] [CrossRef]
- Aziza, H.; Postel-Pellerin, J.; Bazzi, H.; Canet, P.; Moreau, M.; Della Marca, V.; Harb, A. True Random Number Generator Integration in a Resistive RAM Memory Array Using Input Current Limitation. IEEE Trans. Nanotechnol. 2020, 19, 214–222. [Google Scholar] [CrossRef]
- Ielmini, D.; Milo, V. Physics-based modeling approaches of resistive switching devices for memory and in-memory computing applications. J. Comput. Electron. 2017, 16, 1121–1143. [Google Scholar] [CrossRef]
- Elgabra, H.; Farhat, I.A.H.; Hosani, A.S.A.; Homouz, D.; Mohammad, B. Mathematical modeling of a memristor device. In Proceedings of the 2012 International Conference on Innovations in Information Technology (IIT), Abu Dhabi, United Arab Emirates, 18–20 March 2012; pp. 156–161. [Google Scholar] [CrossRef]
- Huang, L.; Mosleh, A. A Physics of Failure, Kinetic Simulation Model for Reliability of RRAM. In Proceedings of the 2023 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 23–26 January 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Mladenov, V.; Kirilov, S. A Memristor Neural Network Based on Simple Logarithmic-Sigmoidal Transfer Function with MOS Transistors. Electronics 2024, 13, 893. [Google Scholar] [CrossRef]
- Aguirre, F.L.; Suñé, J.; Miranda, E. SPICE Implementation of the Dynamic Memdiode Model for Bipolar Resistive Switching Devices. Micromachines 2022, 13, 330. [Google Scholar] [CrossRef] [PubMed]
- Karpov, V.; Niraula, D.; Karpov, I. Thermodynamic analysis of conductive filaments. Appl. Phys. Lett. 2016, 109, 093501. [Google Scholar] [CrossRef]
- Wouters, D.J.; Menzel, S.; Rupp, J.A.J.; Hennen, T.; Waser, R. On the universality of the I–V switching characteristics in non-volatile and volatile resistive switching oxides. Faraday Discuss. 2019, 213, 183–196. [Google Scholar] [CrossRef] [PubMed]
- Miranda, E.; Piros, E.; Aguirre, F.L.; Kim, T.; Schreyer, P.; Gehrunger, J.; Oster, T.; Hofmann, K.; Suñé, J.; Hochberger, C.; et al. Simulation of Bipolar-Type Resistive Switching Devices Using a Recursive Approach to the Dynamic Memdiode Model. IEEE Electron Device Lett. 2023, 44, 1551–1554. [Google Scholar] [CrossRef]
- Ostrovskii, V.; Fedoseev, P.; Bobrova, Y.; Butusov, D. Structural and parametric identification of Knowm memristors. Nanomaterials 2022, 12, 63. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, A.; Cagli, C.; Perniola, L.; Suñé, J.; Miranda, E. Effect of the voltage ramp rate on the set and reset voltages of ReRAM devices. Mic. Eng. 2017, 178, 61–65. [Google Scholar] [CrossRef]
- Chen, A.; Lin, M.R. Variability of resistive switching memories and its impact on crossbar array performance. In Proceedings of the 2011 International Reliability Physics Symposium, Monterey, CA, USA, 10–14 April 2011; pp. 843–846. [Google Scholar] [CrossRef]
- Piccolboni, G.; Molas, G.; Garbin, D.; Vianello, E.; Cueto, O.; Cagli, C.; Traore, B.; De Salvo, B.; Ghibaudo, G.; Perniola, L. Investigation of Cycle-to-Cycle Variability in HfO2-Based OxRAM. IEEE Electron Device Lett. 2016, 37, 721–723. [Google Scholar] [CrossRef]
- García-Redondo, F.; López-Vallejo, M.; Barrio, C.L. Advanced integration of variability and degradation in RRAM SPICE compact models. In Proceedings of the 2017 14th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Taormina, Italy, 12–15 June 2017. [Google Scholar]
- Roldán, J.B.; Miranda, E.; Maldonado, D.; Mikhaylov, A.N.; Agudov, N.V.; Dubkov, A.A.; Koryazhkina, M.N.; González, M.B.; Villena, M.A.; Poblador, S.; et al. Variability in resistive memories. Adv. Intell. Syst. 2023, 5, 2200338. [Google Scholar] [CrossRef]
- Reuben, J.; Biglari, M.; Fey, D. Incorporating Variability of Resistive RAM in Circuit Simulations Using the Stanford–PKU Model. IEEE Trans. Nanotechnol. 2020, 19, 508–518. [Google Scholar] [CrossRef]
- Salvador, E.; Gonzalez, M.B.; Campabadal, F.; Martin-Martinez, J.; Rodriguez, R.; Miranda, E. Assessment of the variability of the I-V characteristic of HfO2-based resistive switching devices and its simulation using the quasi-static memdiode model. Solid State Electron. 2023, 206, 108667. [Google Scholar] [CrossRef]
- Poblador, S.; Gonzalez, M.B.; Campabadal, F. Investigation of the multilevel capability of TiN/Ti/HfO2/W resistive switching devices by sweep and pulse programming. Microelectron. Eng. 2018, 187–188, 148–153. [Google Scholar] [CrossRef]
- Delignette-Muller, M.L.; Dutang, C. fitdistrplus: An R Package for Fitting Distributions. J. Stat. Softw. 2015, 64, 1–34. [Google Scholar] [CrossRef]
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, L453. [Google Scholar] [CrossRef]
- Wiesenfeld, K.; Moss, F. Stochastic resonance and the benefits of noise: From ice ages to crayfish and SQUIDs. Nature 1995, 373, 33–36. [Google Scholar] [CrossRef]
- Harmer, G.P.; Davis, B.R.; Abbot, D. A review of stochastic resonance: Circuits and measurement. IEEE Trans. Instrum. Meas. 2002, 31, 299–309. [Google Scholar] [CrossRef]
- Kasai, S. Stochastic resonance and related phenomena in nonlinear electron nanodevices. In Proceedings of the IEEE International Nanoelectronics Conference (INEC), Sapporo, Japan, 28–31 July 2014. [Google Scholar]
- Scotland, A.; Di Ventra, M. Stochastic memory: Memory enhancement due to noise. Phys. Rev. E 2012, 85, 011116. [Google Scholar] [CrossRef] [PubMed]
- Patterson, G.A.; Fierens, P.I.; Grosz, D.F. On the beneficial role of noise in resistive switching. Appl. Phys. Lett. 2013, 103, 074102. [Google Scholar] [CrossRef]
- Roldán, J.B.; Cantudo, A.; Torres, J.J.; Maldonado, D.; Shen, Y.; Zhen, W.; Yuan, Y.; Lanza, M. Stochastic resonance in 2D materials based memristors. npj 2D Mater. Appl. 2024, 8, 7. [Google Scholar] [CrossRef]
- Mikhaylov, A.N.; Guseinov, D.V.; Belov, A.I.; Korolev, D.S.; Shishmakova, V.A.; Koryazhkina, M.N.; Filatov, D.O.; Gorshkov, O.N.; Maldonado, D.; Alonso, F.J.; et al. Stochastic resonance in a metal-oxide memristive device. Chaos Solitons Fractals 2021, 144, 110723. [Google Scholar] [CrossRef]
- Rodriguez, R.; Martin-Martinez, J.; Salvador, E.; Crespo-Yepes, A.; Miranda, E.; Nafria, M.; Rubio, A.; Ntinas, V.; Sirakoulis, G.C. Beneficial Role of Noise in Hf-based Memristors. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 27 May–1 June 2022. [Google Scholar]



| Dynamic Memdiode Model in MATLAB |
|---|
| step=5E-3; V1=0:step:1.2; V2=0:-step:-1.2; V=[V1 flip(V1) V2 flip(V2)]; %Voltage input aoff=2; aon=2; Ri=40; Roff=30; Ron=30; Ioff=10E-5; Ion=3E-3; %Parameter definition etas=40; etar=-15; gam=0.1; At=1E-3; Vs=0.5; Vr=-0.3; l(1)=0; I(1)=0; for t=1:length(V) %Auxiliary functions Vi=V(t)-Ri*I(t); I0=(Ion-Ioff)*l(t)+Ioff; a=(aon-aoff)*l(t)+aoff; R=(Ron-Roff)*l(t)+Roff; Tsr =exp(-etas*(Vi-Vs))*(V(t)>0)+exp(-etar*l(t)^gam*(Vi-Vr))*(V(t)<=0); I(t+1)=(1/(a*R))*(lambertw(a*R*I0/2) *exp(a*Vi)-lambertw(a*R*I0/2*exp(-a*Vi)));% Model equations l(t+1)=(l(t)-heaviside(Vi))*exp(-At/Tsr)+heaviside(Vi); Vm(t)=V(t); Im(t)=I(t); lm(t)=l(t); %Saving variables and plotting end semilogy(Vm,abs(Im),’black’) xlabel(‘Voltage (V)’); ylabel(‘Current (A)’); title(‘Current-Voltage Characteristics’); |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salvador, E.; Rodriguez, R.; Miranda, E. A Simple, Robust, and Versatile MATLAB Formulation of the Dynamic Memdiode Model for Bipolar-Type Resistive Random Access Memory Devices. J. Low Power Electron. Appl. 2024, 14, 30. https://doi.org/10.3390/jlpea14020030
Salvador E, Rodriguez R, Miranda E. A Simple, Robust, and Versatile MATLAB Formulation of the Dynamic Memdiode Model for Bipolar-Type Resistive Random Access Memory Devices. Journal of Low Power Electronics and Applications. 2024; 14(2):30. https://doi.org/10.3390/jlpea14020030
Chicago/Turabian StyleSalvador, Emili, Rosana Rodriguez, and Enrique Miranda. 2024. "A Simple, Robust, and Versatile MATLAB Formulation of the Dynamic Memdiode Model for Bipolar-Type Resistive Random Access Memory Devices" Journal of Low Power Electronics and Applications 14, no. 2: 30. https://doi.org/10.3390/jlpea14020030
APA StyleSalvador, E., Rodriguez, R., & Miranda, E. (2024). A Simple, Robust, and Versatile MATLAB Formulation of the Dynamic Memdiode Model for Bipolar-Type Resistive Random Access Memory Devices. Journal of Low Power Electronics and Applications, 14(2), 30. https://doi.org/10.3390/jlpea14020030






