An Experimental Study on Step-Up DC–DC Converters for Organic Photovoltaic Cells
Abstract
:1. Introduction
2. The Organic Photovoltaic Cell
3. Step-Up Voltage Inductive DC–DC Converters
3.1. Problem Statement
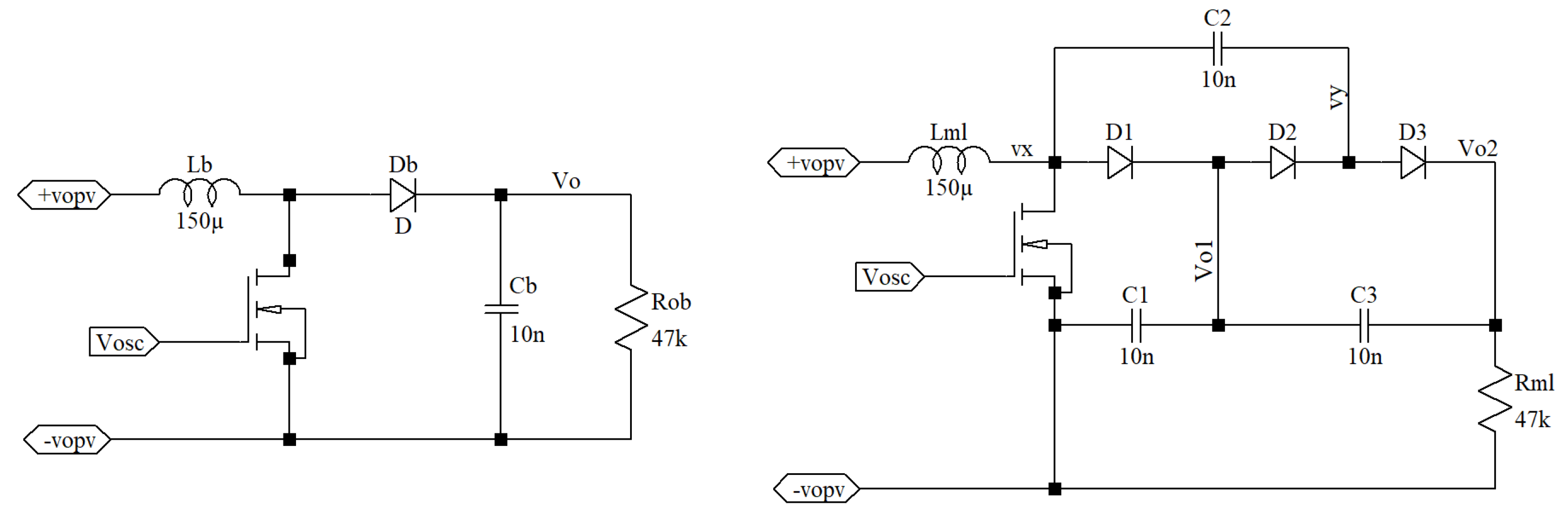
3.2. The Hard Switching Boost Converter
3.3. Multi-Level Boost Converter
3.4. Design Challenges for the Proposed Solutions
3.4.1. Semiconductor Devices
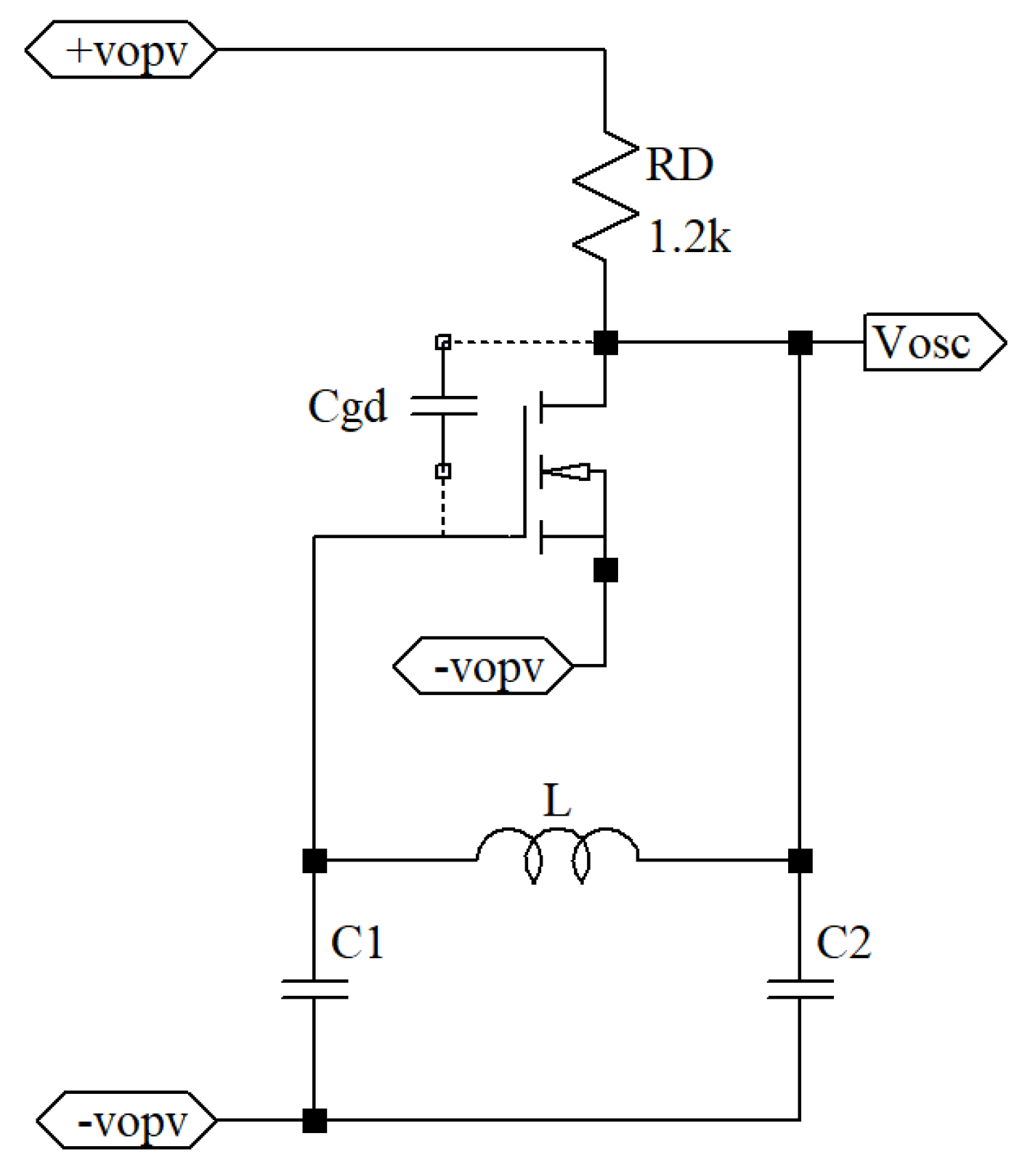
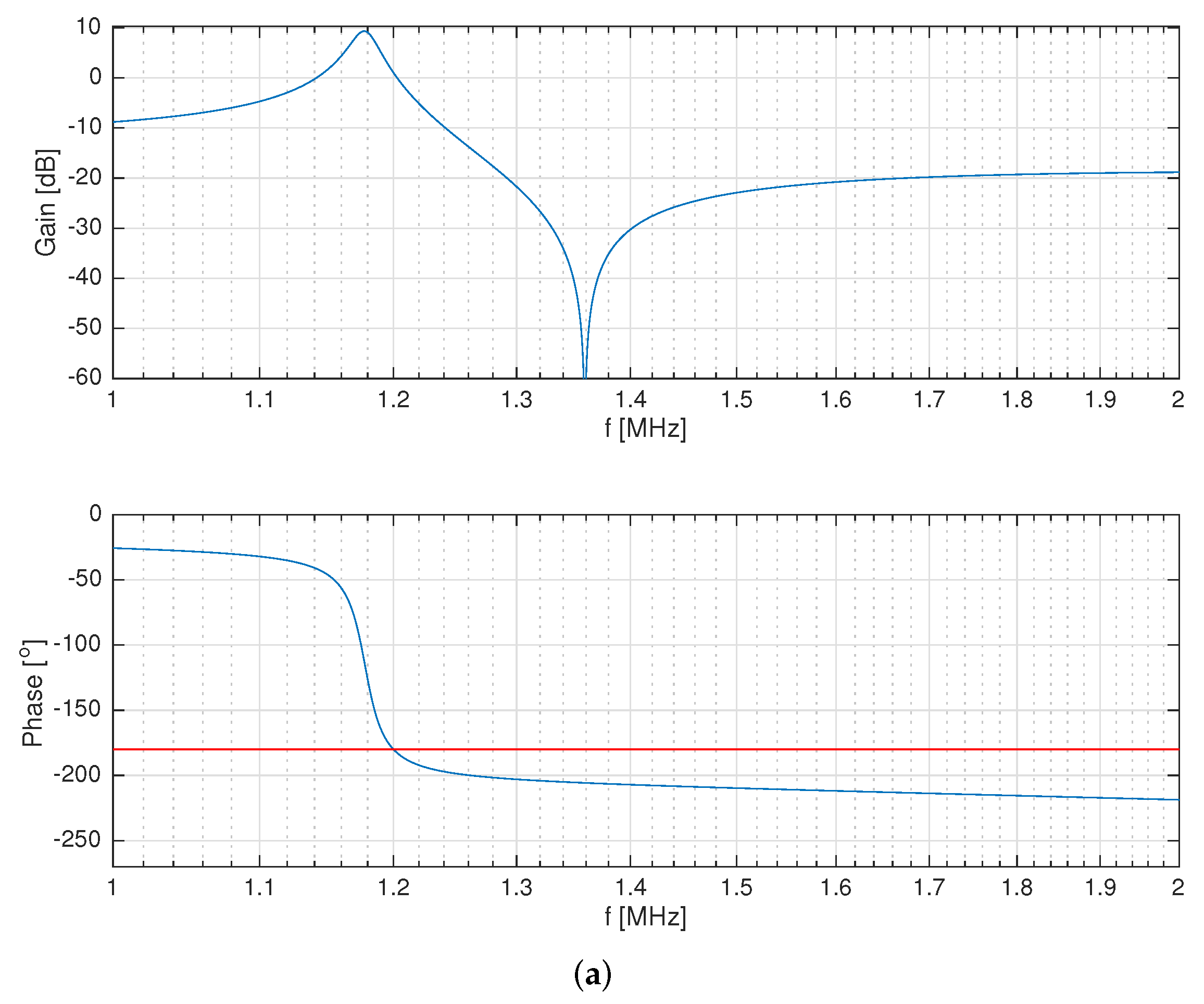
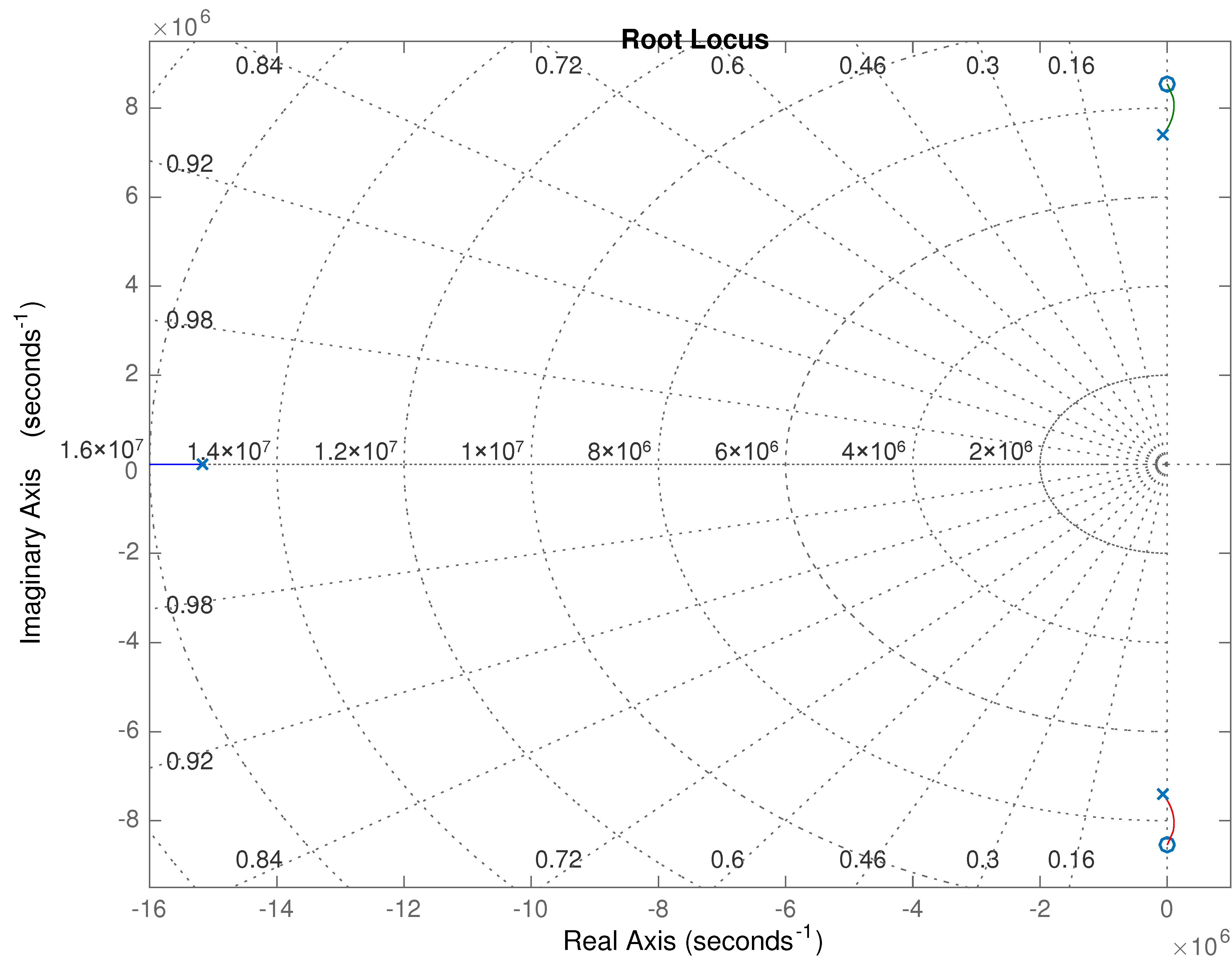
3.4.2. MOSFET Driving Oscillator
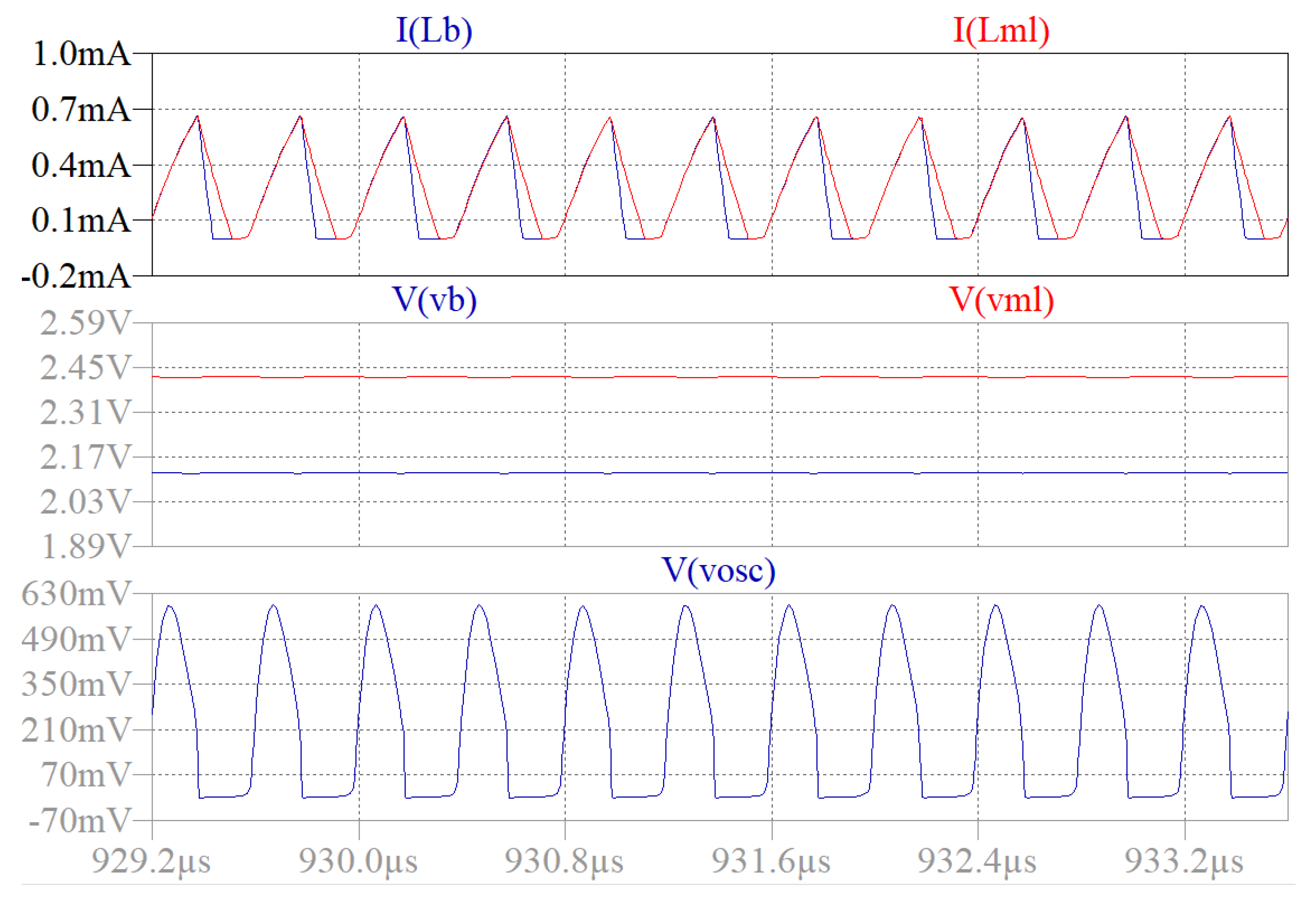
3.5. System Evaluation and Design Assessment
4. Prototypes and Experimental Results
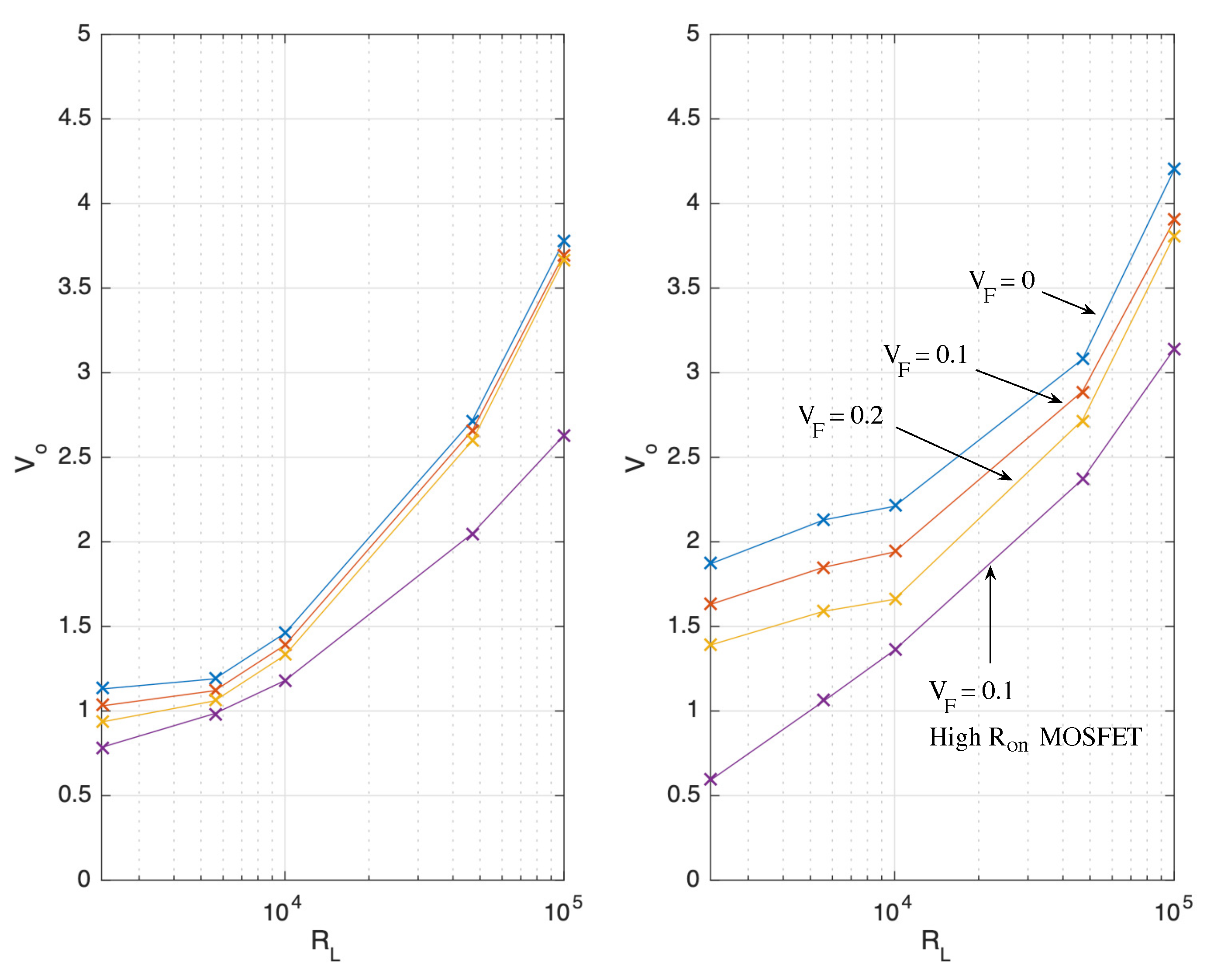
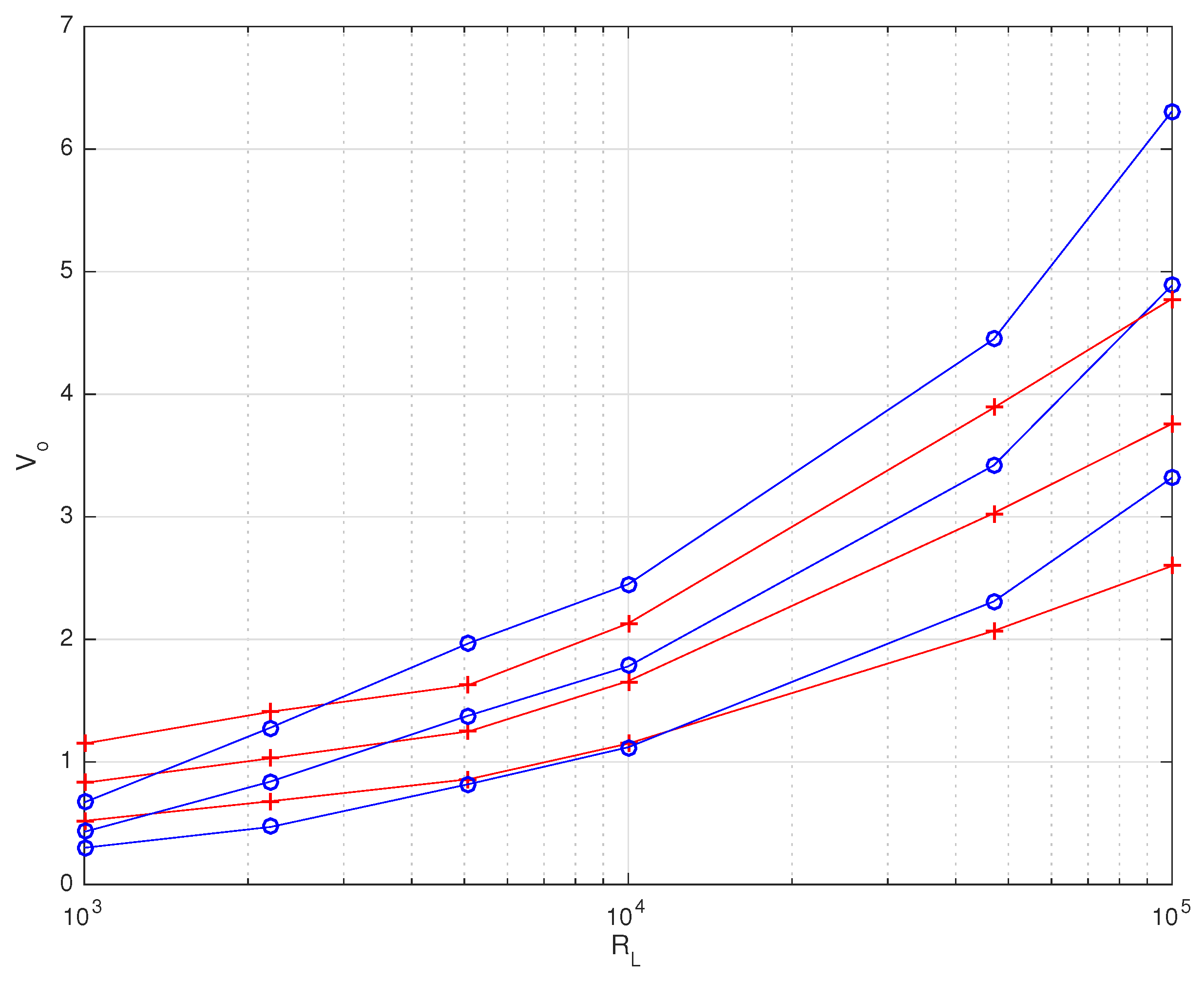
4.1. Systems Supplied by a Voltage Source
4.2. Systems Supplied by the OPV
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Newell, D.; Duffy, M. Review of Power Conversion and Energy Management for Low-Power, Low-Voltage Energy Harvesting Powered Wireless Sensors. IEEE Trans. Power Electron. 2019, 34, 9794–9805. [Google Scholar] [CrossRef]
- Richelli, A.; Salem, M.; Colalongo, L. A Review of Fully Integrated and Embedded Power Converters for IoT. Energies 2021, 14, 5419. [Google Scholar] [CrossRef]
- Mansour, M.M.; Torigoe, S.; Yamamoto, S.; Kanaya, H. Compact and Simple High-Efficient Dual-Band RF-DC Rectifier for Wireless Electromagnetic Energy Harvesting. Electronics 2021, 10, 1764. [Google Scholar] [CrossRef]
- Edla, M.; Lim, Y.Y.; Mikio, D.; Padilla, R.V. Non-Linear Switching Circuit for Active Voltage Rectification and Ripples Reduction of Piezoelectric Energy Harvesters. Energies 2022, 15, 709. [Google Scholar] [CrossRef]
- Oh, T.; Islam, S.K.; Mahfouz, M.; To, G. A Low-Power CMOS Piezoelectric Transducer Based Energy Harvesting Circuit for Wearable Sensors for Medical Applications. J. Low Power Electron. Appl. 2017, 7, 33. [Google Scholar] [CrossRef] [Green Version]
- Tabesh, A.; Fréchette, L.G. A Low-Power Stand-Alone Adaptive Circuit for Harvesting Energy From a Piezoelectric Micropower Generator. IEEE Trans. Ind. Electron. 2010, 57, 840–849. [Google Scholar] [CrossRef] [Green Version]
- Churchill, K.K.; Chong, G.; Ramiah, H.; Ahmad, M.Y.; Rajendran, J. Low-Voltage Capacitive-Based Step-Up DC-DC Converters for RF Energy Harvesting System: A Review. IEEE Access 2020, 8, 186393–186407. [Google Scholar] [CrossRef]
- Adami, S.E.; Degrenne, N.; Vollaire, C.; Allard, B.; Costa, F. Ultra-low power, low voltage, autonomous resonant DC-DC converter for low power applications. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013. [Google Scholar] [CrossRef] [Green Version]
- Ayaz, M.; Farjah, E.; Ghanbari, T. A novel self-starting ultra low-power and low-voltage two-stage DC-DC boost converter for microbial energy harvesting. In Proceedings of the 6th Power Electronics, Drive Systems & Technologies Conference (PEDSTC2015), Tehran, Iran, 3–4 February 2015; pp. 498–502. [Google Scholar] [CrossRef]
- Lin, Y.; Wu, T.; Zeng, Y.; Yang, J.; Chen, W.; Li, Z. A 15 mV-input and 71%-efficiency boost converter with 22 mV output ripple for thermoelectric energy harvesting application. Microelectron. J. 2022, 121, 105353. [Google Scholar] [CrossRef]
- Dillersberger, H.; Deutschmann, B.; Tham, D. A Bipolar ±13 mV Self-Starting and 85% Peak Efficiency DC/DC Converter for Thermoelectric Energy Harvesting. Energies 2020, 13, 5501. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, X.; Zhao, M.; Wang, L.; Shen, X. 30–300mV input, ultra-low power, self-startup DC-DC boost converter for energy harvesting system. In Proceedings of the 2012 IEEE Asia Pacific Conference on Circuits and Systems, Kaohsiung, Taiwan, 2–5 December 2012; pp. 432–435. [Google Scholar] [CrossRef]
- Gujrati, T.; Mani, P.G. Ultra Low Power Self- Resonating Boost Converter. In Proceedings of the 2019 International Conference on Computing, Power and Communication Technologies (GUCON), New Delhi, India, 27–28 September 2019; pp. 21–24. [Google Scholar]
- Rastmanesh, M.; El-Masry, E.; El-Sankary, K. Low Power Photo-Voltaic Harvesting Matrix Based Boost DC–DC Converter with Recycled and Synchro-Recycled Scheme. J. Low Power Electron. Appl. 2020, 10, 39. [Google Scholar] [CrossRef]
- de Carvalho, M.R.S.; Neto, R.C.; Barbosa, E.J.; Limongi, L.R.; Bradaschia, F.; Cavalcanti, M.C. An Overview of Voltage Boosting Techniques and Step-Up DC-DC Converters Topologies for PV Applications. Energies 2021, 14, 8230. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Wu, H.; Xing, Y.; Batarseh, I. Overview of High-Step-Up Coupled-Inductor Boost Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 689–704. [Google Scholar] [CrossRef]
- Ravi, D.; Letha, S.S.; Samuel, P.; Reddy, B.M. An Overview of Various DC-DC Converter Techniques used for Fuel Cell based Applications. In Proceedings of the 2018 International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018; pp. 16–21. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Ramirez, J.M.; Peng, F.Z.; Valderrabano, A. A DC–DC multilevel boost converter. IET Power Electron. 2010, 3, 129–137. [Google Scholar] [CrossRef]
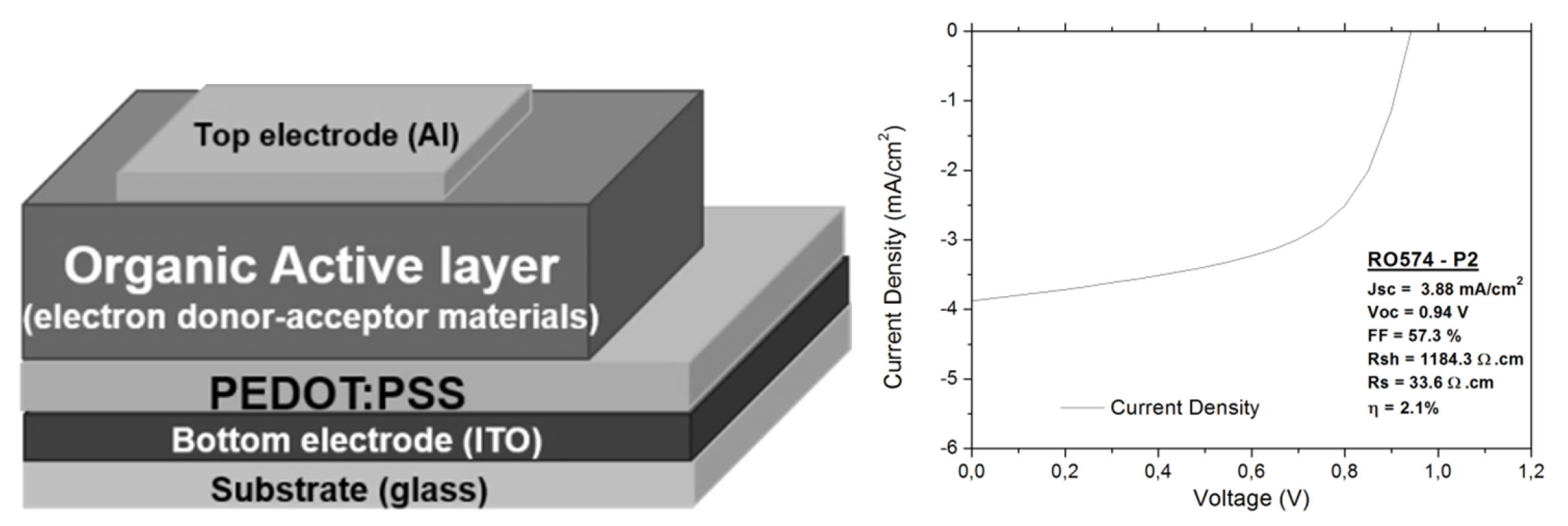
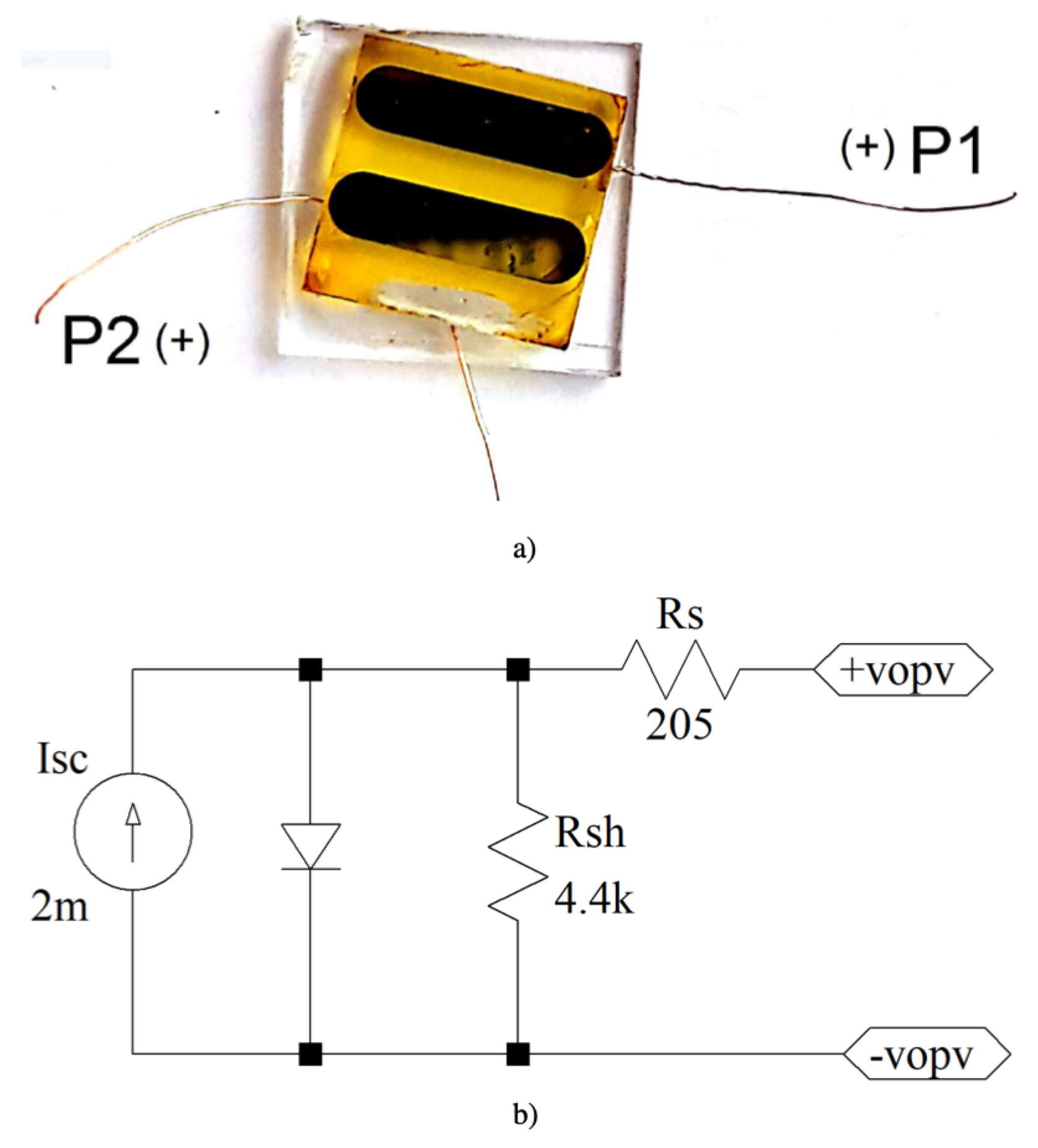

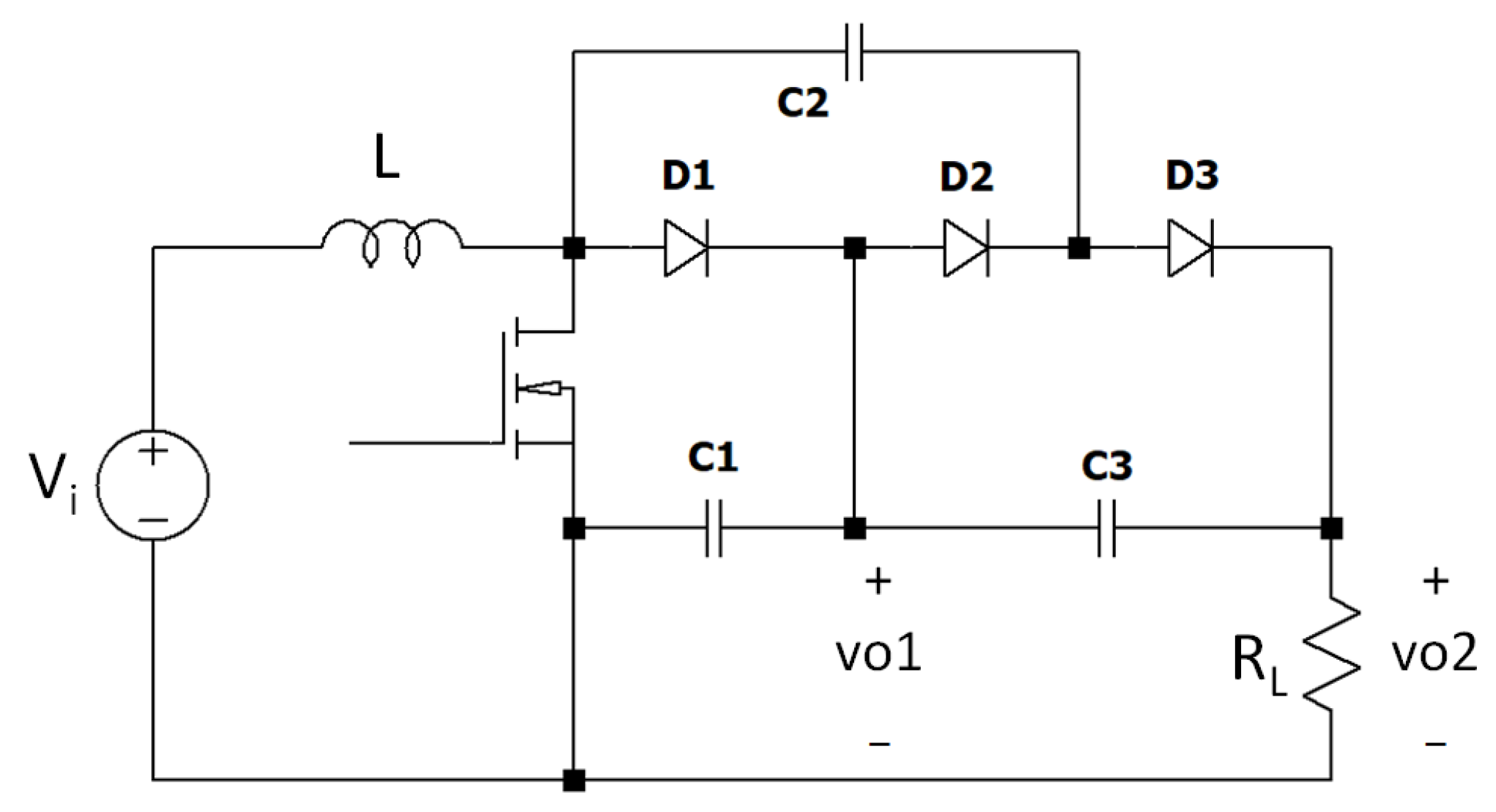
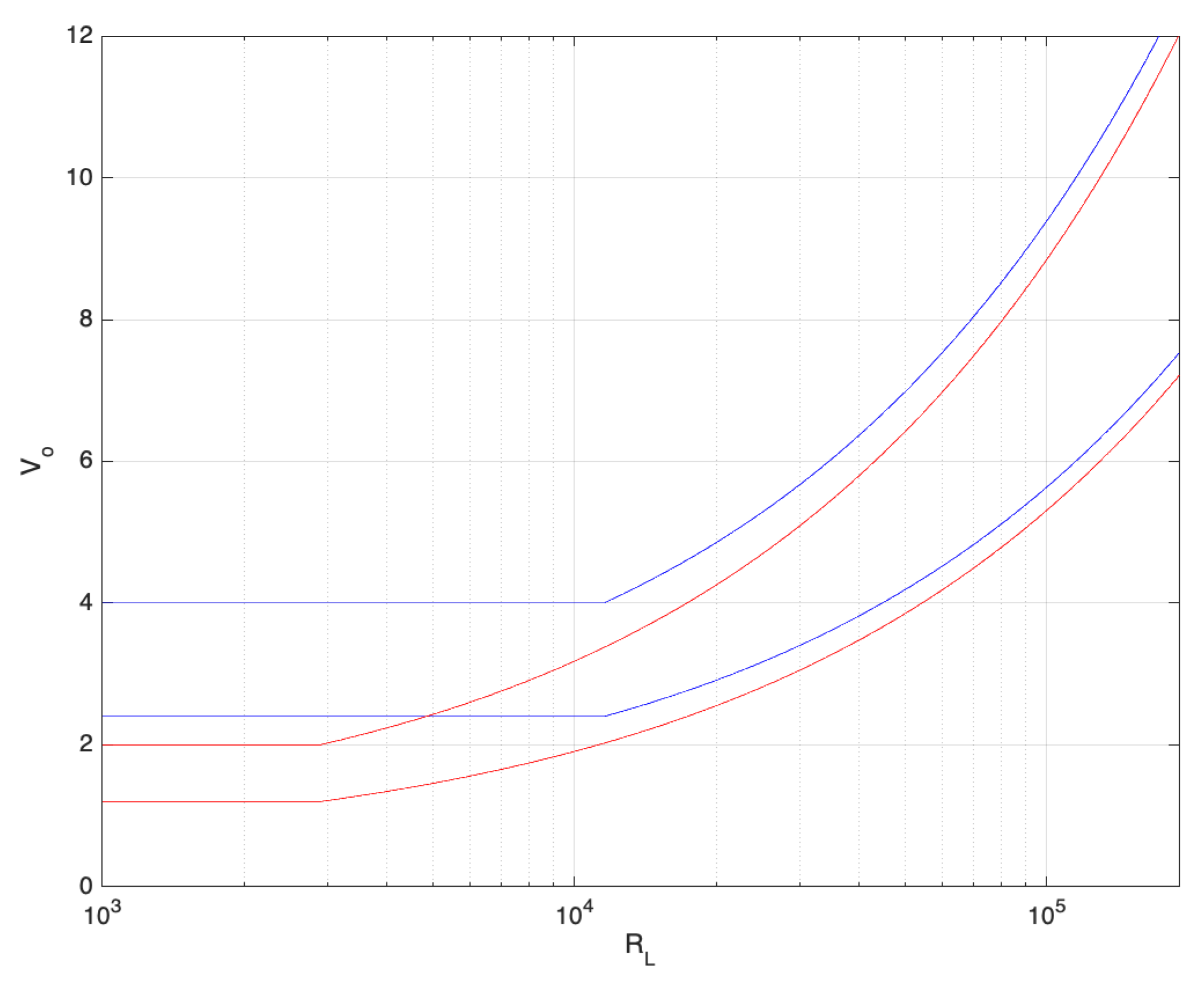

| Jsc | Isc | Voc | Rs | Rsh | FF | PCE |
|---|---|---|---|---|---|---|
| (mA/cm) | (mA) | (V) | () | () | (%) | |
| −4.17 | 1.00 | 0.96 | 205.55 | 4420.10 | 0.49 | 2.05 |
| ±0.22 | ±0.05 | ±0.01 | ±18.32 | ±649.28 | ±0.02 | ±0.13 |
| (V) | Area | # | ||||
|---|---|---|---|---|---|---|
| Topology | (V) | 10 k | 100 k | ∞ | (cm) | Components |
| Boost | 0.65 | 1.4 | 2.7 | 4.2 | 2.35 | 8 |
| Multilevel | 0.65 | 1.4 | 3.4 | 7.4 | 2.35 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos, P.M.; Serralheiro, A.J.; Borges, B.; Torres, J.P.N.; Charas, A. An Experimental Study on Step-Up DC–DC Converters for Organic Photovoltaic Cells. J. Low Power Electron. Appl. 2022, 12, 20. https://doi.org/10.3390/jlpea12020020
dos Santos PM, Serralheiro AJ, Borges B, Torres JPN, Charas A. An Experimental Study on Step-Up DC–DC Converters for Organic Photovoltaic Cells. Journal of Low Power Electronics and Applications. 2022; 12(2):20. https://doi.org/10.3390/jlpea12020020
Chicago/Turabian Styledos Santos, P. Mendonça, António J. Serralheiro, Beatriz Borges, João Paulo N. Torres, and Ana Charas. 2022. "An Experimental Study on Step-Up DC–DC Converters for Organic Photovoltaic Cells" Journal of Low Power Electronics and Applications 12, no. 2: 20. https://doi.org/10.3390/jlpea12020020
APA Styledos Santos, P. M., Serralheiro, A. J., Borges, B., Torres, J. P. N., & Charas, A. (2022). An Experimental Study on Step-Up DC–DC Converters for Organic Photovoltaic Cells. Journal of Low Power Electronics and Applications, 12(2), 20. https://doi.org/10.3390/jlpea12020020








