Abstract
In this paper, we introduce a novel tree-based architecture which allows the implementation of Ultra-Low-Voltage (ULV) amplifiers. The architecture exploits a body-driven input stage to guarantee a rail-to-rail input common mode range and body-diode loading to avoid Miller compensation, thanks to the absence of high-impedance internal nodes. The tree-based structure improves the CMRR of the proposed amplifier with respect to the conventional OTA architectures and allows achievement of a reasonable CMRR even at supply voltages as low as 0.3 V and without tail current generators which cannot be used in ULV circuits. The bias currents and the static output voltages of all the stages implementing the architecture are accurately set through the gate terminals of biasing transistors in order to guarantee good robustness against PVT variations. The proposed architecture and the implementing stages are investigated from an analytical point of view and design equations for the main performance metrics are presented to provide insight into circuit behavior. A 0.3 V supply voltage, subthreshold, ultra-low-power (ULP) OTA, based on the proposed tree-based architecture, was designed in a commercial 130 nm CMOS process. Simulation results show a dc gain higher than 52 dB with a gain-bandwidth product of about 35 kHz and reasonable values of CMRR and PSRR, even at such low supply voltages and considering mismatches. The power consumption is as low as 21.89 nW and state-of-the-art small-signal and large-signal FoMs are achieved. Extensive parametric and Monte Carlo simulations show the robustness of the proposed circuit to PVT variations and mismatch. These results confirm that the proposed OTA is a good candidate to implement ULV, ULP, high performance analog building blocks for directly harvested IoT nodes.
1. Introduction
The continuous evolution of electronic systems and the ever increasing symbiotic relationship between humans and electronic devices characterize the era of Internet of Things (IoT) [1,2]. Smart and portable devices, such as laptops, smartphones, smartwatches, fit-trackers and so on, are used more and more often for checking emails, banking management, counter services and the like. Indeed, most of these electronic apparatuses have changed the way we work, study or play.
This IoT revolution has also driven the development of body area networks [3], which exploit implantable and wearable devices, and are widely used in healthcare monitoring and in the study of neurodegenerative diseases such as Parkinson’s, Alzheimer’s and so on [4,5,6,7].
The growing popularity of these electronic devices is also due to their increasing capability to work with low power consumption and low supply voltage in order to maximize battery life or employ energy harvesting techniques.
The stringent requirements in terms of ultra-low-power (ULP) and ultra-low-voltage (ULV) operation set by the above applications have brought about a revolution also in the approach to the design of analog integrated circuits (ICs). In fact, the latter have to be reinvented to enhance the autonomy of smart devices and find a balance between performance, area footprint and power consumption at supply voltages of a few hundreds of millivolts. As such, analog interfaces are among the most challenging building blocks for IoT applications [1,8,9,10,11].
The Operational Transconductance Amplifier (OTA) stands out, among the analog building blocks, for its design complexity, especially if ULP and ULV operation are key requirements. In the last few years, there has been a growing trend in the design of ULP OTAs and a plenty of solutions have been proposed in the literature [12,13,14]. Most of the low voltage OTAs reported in the last decade operate with supply voltages ranging from 0.5 V to about 1 V, and are based on the conventional cascode, folded cascode, multi-stage or gain-boosting approaches, which have been successfully exploited in the past to implement high-performance amplifiers for several application scenarios [15,16,17,18,19]. A novel OTA architecture based on current gain stages to improve bandwidth and slew rate has been recently proposed in [20]. The OTA reported in [20] operates with a supply voltage of 1 V and exhibits state of the art small-signal and large-signal figures of merit. Unfortunately, most of these conventional amplifier topologies are not suited for applications requiring supply voltages lower than 0.5 V, and inverter-based [21,22,23,24,25,26] and pseudo-differential [27,28] architectures are preferred. However, an aggressive supply voltage scaling severely limits the swing of the control voltage, thus strongly limiting the effectiveness of body bias approaches to set the bias or the common mode current. Therefore, gate-driven amplifiers operating at supply voltages lower than 0.5 V are not able to guarantee either rail-to-rail input common mode range (ICMR) or well-defined bias currents.
The bulk-driven technique [29,30,31] allows rail-to-rail ICMR in ULV amplifiers at the cost of reduced gain and a resistive input impedance component. Bulk-driven amplifiers are surely one of the best alternatives to attain rail-to-rail input–output swing when a well-defined bias or common mode current is required to increase the robustness against process, supply voltage, and temperature (PVT) variations [32,33,34,35,36,37,38,39,40,41,42]. Indeed, the signal-free gate terminals can be used to accurately set the bias current of the different OTA stages. The bulk-driven technique combined with inverter-based topologies has also been exploited in recent papers to design ULV amplifiers [33,36,39].
A completely novel approach based on fully digital operation to the design of analog differential circuits has been introduced in [43]. Several papers dealing with the fully digital implementation of OTAs for IoT applications have been recently published [44,45,46]. The digital OTAs in [44,45] are based on the C-Muller element and do not require any passive component. Such digital OTAs are able to operate at supply voltages lower than 0.3 V and are very interesting from the viewpoint of the area footprint and power consumption. However, the operation of this kind of circuits can be sensitive to PVT variations and mismatch and may require suitable calibration strategies to achieve high production yield [47].
Indeed, even if bulk-driven OTAs exhibit some drawbacks with respect to gate-driven ones (higher noise, larger area and lower bandwidth) and to digital OTAs (larger area and power consumption), they can be designed to be robust against PVT and mismatch variations and still represent the best solution to attain rail-to-rail ICMR at supply voltages of the order of 0.3 V.
In this work, we present a novel OTA architecture based on a tree-like structure. This can be viewed as the ULV implementation of the OTA reported in [20], previously proposed by the authors to enhance the bandwidth efficiency. The current gains obtained by means of conventional current mirrors in [20] are not feasible in ULV conditions and have to be implemented by means of other solutions such as the one presented in [48]. In the ULV architeture proposed in this paper, the current gains are implemented by using a different approach which is based on the body-to-gate (B2G) interfaces as will be detailed in the following. The proposed architecture exploits a body-driven input stage to guarantee a rail-to-rail input common mode range and body-diode loading to avoid Miller compensation, thanks to the absence of high-impedance internal nodes. The bias currents and the static output voltages of all the stages implementing the proposed architecture are accurately set through the gate terminals of biasing transistors in order to guarantee a good robustness against PVT variations. However, this biasing strategy results in pseudo-differential stages and therefore has a negative impact on CMRR performance. The proposed tree-like structure improves the CMRR of the OTA with respect to conventional pseudo-differential amplifiers and allows achievement of a reasonable CMRR even in ULV conditions. A 0.3 V supply voltage ULP OTA based on this architecture was designed in a 130 nm CMOS process, and simulation results show state of the art small-signal and large-signal figures of merit (FoMs).
2. Proposed Topology
The block scheme of the proposed OTA architecture is depicted in Figure 1. This architecture of ULV OTA was derived from the OTA introduced by the authors in [20] and is a three stage, tree-like OTA, made up of the cascade of differential-to-single-ended converter stages, to maximize CMRR. Three different topologies are exploited in the three stages of the OTA to optimize the tradeoff between performance and efficiency. Each one of these stages was extensively investigated and their behavior is discussed in the next subsections. It has to be remarked that the proposed ULV OTA makes extensive use of the body terminals of MOS devices and thus it can be implemented only in CMOS technologies (such as triple-well-bulk or FDSOI), where both NMOS and PMOS transistors have available body connections. However, this is not a strong limitation, since most modern processes have available body connections for both PMOS and NMOS transistors.
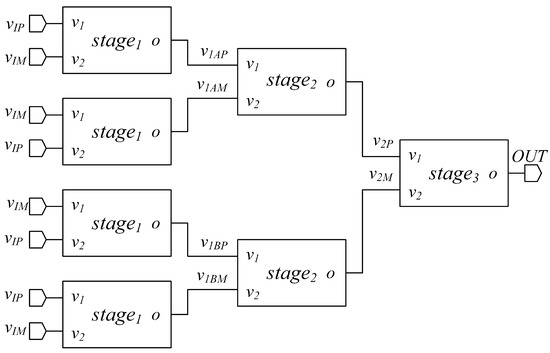
Figure 1.
Proposed tree-like architecture of the OTA.
2.1. Stage
The topology of the blocks denoted as stage in Figure 1 is reported in Figure 2, and is made up of transistors and . This input stage has the same topology adopted for the OTA in [40]. It is a bulk-driven stage in which the bias current is accurately set through the voltage applied to the gate of transistor . The bias voltage is generated by the biasing circuit reported in Figure 3. The current flowing in is mirrored through and , so that the standby current of all MOS devices is accurately set. The body terminals of transistors and are connected to the input voltages, and respectively. The output of stage is loaded through a body–diode connection on the transistor whose gate voltage is connected to the bias voltage , and results in an output impedance lower than the one of conventional input stages. This stage thus provides limited gain, but allows achievement of a rail-to-rail input common mode range and improvement of the bandwidth. As a consequence, noise and mismatch of the second stage contributes to the total input referred noise and offset. However, even if noise and offset performance are suboptimal, the OTA can still be designed to exhibit acceptable noise and offset, while achieving very good bandwidth efficiency.
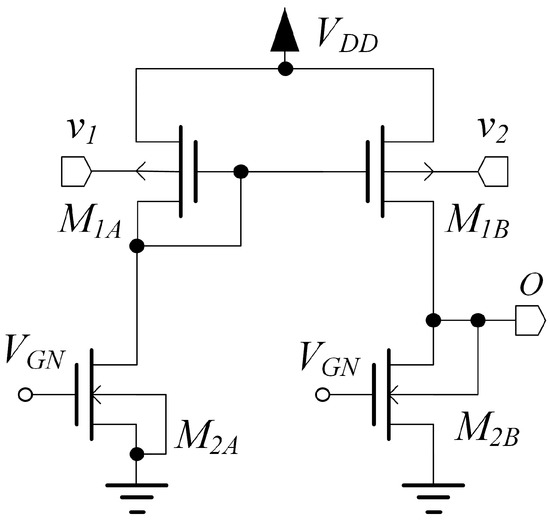
Figure 2.
Stage used in the proposed OTA architecture.
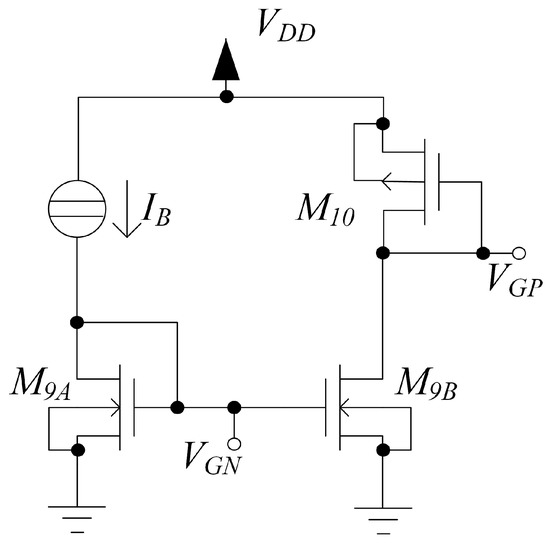
Figure 3.
Biasing circuit used in the proposed OTA architecture.
2.2. Stage
The topology of stage is shown in Figure 4. This stage converts the input differential signal to single-ended providing some gain, a well defined bias point and contributing to the overall CMRR. The input signal is applied to the gates of and , and the bias current is set through the gates of and connected to the bias voltage generated by the circuit in Figure 3. The current cancellation given by the body-to-body (B2B) (Appendix B) current mirror , allows to attain good common mode rejection ratio as will be better shown in the next sections. Since the output is body-loaded, also this stage doesn’t show any high-impedance internal node and thus does not require any internal compensation.
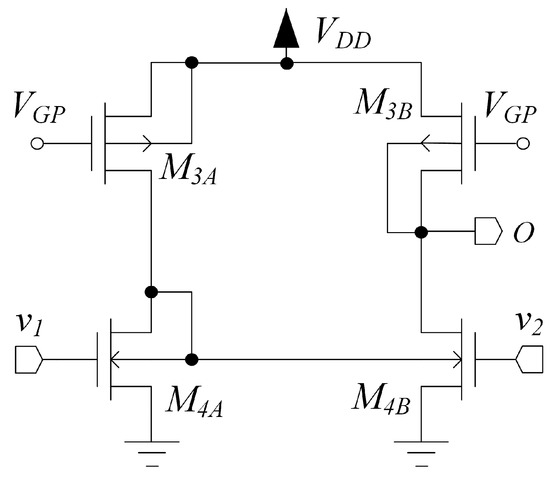
Figure 4.
Stage used in the proposed OTA architecture.
2.3. Stage
The topology of stage is shown in Figure 5. This stage combines the signal behavior of an inverter-based pseudo-differential pair (Arbel topology) with differential-to-single-ended conversion through the body current mirror and robust biasing, and is composed by an n-input and a p-input stage similar to that of Figure 4, but without diode loading, connected together. The signal is applied to the gates of two PMOS and two NMOS devices, respectively and , and the body-diode connections in and implement body-driven current mirrors performing differential-to-single-ended conversion and common mode current cancellation. Transistors , and and act as current sources and are exploited to set the bias current in all the branches of the third stage through and , respectively; thus, each transistor has a well-defined bias point.
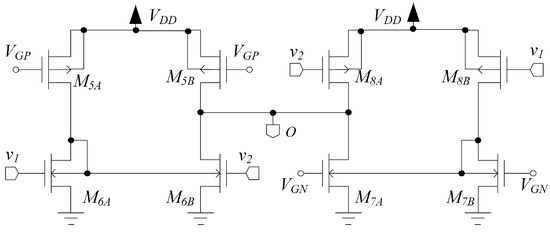
Figure 5.
Stage used in the proposed OTA architecture.
2.4. Architectural Considerations
It has to be noted that, referring to the proposed architecture, at the interfaces between stage and stage and between stage and stage, we have a body-to-gate (B2G) connection. These B2G connections result in lower voltage gain with respect to the conventional drain-to-gate connections, but the lower gain allows avoidance of high-impedance internal nodes, and therefore compensation capacitors. In fact, even if each B2G interface generates a pole (as shown in Appendix A), it is placed at a much higher frequency than the one given by the output stage, which provides the dominant pole.
3. Circuit Analysis
In this section, the small-signal and large-signal performances of the proposed architecture are analyzed from an analytical point of view, and design equations for the main performance parameters, such as gain, frequency response, slew-rate and noise, are presented to provide insight into circuit behavior.
3.1. Differential Gain
Referring to the small-signal equivalent circuits of stage, stage and stage, the differential mode gain of the different stages was computed. Using the standard notation for small-signal parameters of MOS devices, the differential gain of the first stage can be expressed as:
where:
According to usual approximations, the pole-zero doublet in Equation (1) can be neglected.
Thereafter, the differential gain of stage can be derived to be:
where:
Moreover, in this case, the pole-zero doublet in Equation (3) can be neglected.
Finally, the stage differential gain can be computed by neglecting the pole-zero doublets given by body–diode connections of and ; hence, it can be expressed as:
where it is denoted with:
considering that and .
The overall gain of the amplifier can then be expressed as:
and rewritten as:
It is evident from Equation (8) that the output capacitance sets the dominant pole since the poles of stage and stage are at higher frequencies due to the body–diode connected loads and the smaller load capacitances.
Starting from the above results, the gain-bandwidth product (GBW) of the proposed OTA can be computed as:
where:
The phase margin of the whole OTA can then be expressed as:
3.2. Common Mode Gain
The common mode gain of stage was found to be:
where:
therefore, the CMRR of stage can be expressed as:
The common mode gain of stage is:
where:
whereas its CMRR amounts to:
Stage shows a common mode gain of:
where:
and its CMRR results:
Due to the body current mirror, the CMRR of these stages is reduced with respect to stage. Combining the above results, the common mode gain of the proposed tree-like architecture can be derived as:
Finally, the CMRR of the overall OTA can be expressed as:
therefore, the total CMRR is about:
By looking at Equation (22), it is evident that the CMRR in typical conditions is high, due both to the cascade of several stages and to the scaling factor of the tree architecture, and that it can be enhanced by further iterating the tree-like structure of the proposed OTA architecture. However, in ULV conditions, PVT variations and mismatch may impact on the stability of the operating point, especially in the presence of a B2G interface, and significantly degrade the of the OTA. As a consequence, the CMRR of this architecture is more sensitive to PVT variations and mismatch than other architectures which adopt higher supply voltages and/or a more stable operating point. Anyway, to cope with this problem, design centering techniques are exploited in this work in order to increase the overall CMRR in a given range of PVT and mismatch conditions achieving a reasonable robustness. The above reported frequency analysis shows that the common mode gain presents some zeros that could appear before the unity-gain frequency (depending on the ratio), thus reducing the CMRR at high frequency. A large load capacitance is usually required to achieve stability, therefore the resulting CMRR reduction is often limited.
3.3. Large-Signal Performances
The large-signal performance of the proposed OTA has been investigated by assuming that the load capacitance is much larger than the other circuit capacitances. The slew-rate is thus determined by the output stage, and it can be assumed that the output voltage of stage, which drives stage, is a rail-to-rail signal.
With reference to Figure 5, the output current is given by ; positive and negative slew-rates are given by and , where and are the maximum positive and negative values of .
For the current, we use the standard relationship for sub-threshold current:
where is the thermal voltage and .
For the positive slew-rate, we have = and = 0, and we can assume that the body voltages of and are approximately 0. By denoting with , the quiescent current of the devices of stage, we obtain:
where: , with and the quiescent voltage at body and gate terminals of the NMOS and PMOS devices.
For the negative slew-rate, we have , = and in this case we derive:
where: and with as the quiescent voltage at gate terminals of NMOS devices. In this case, we assume that the body terminals of and are approximately . Equations (25) and (26) show that, in general, positive and negative slew-rates give different results.
3.4. Noise Analysis
The noise analysis has been carried out assuming that each transistor can be modelled with only one noise current generator, which includes both thermal and flicker noise. The power spectral density of the modelled current generator can be expressed as follows:
where:
Taking into account that the noise sources due to stage can be neglected due to the high gain of the preceding stages (considering also the contribution of the tree structure), the equivalent input noise mainly results from the first two stages and can be expressed as follows:
As it can be observed from Equation (30), the noise performance of the amplifier is worsened by body driving, which shows a transconductance gain (i.e., ) which is n-times lower than . Consequently, in order to reduce the equivalent input noise, larger transistors are required. The result in Equation (30) can be written in a less concise form as:
where
and
are the input-referred noise spectra for the first and second stage (contribution of the single cell). Factor 16 in the denominator of (31) accounts for the gain contribution of a N-level tree architecture, whereas the factors 4 and 2 in the numerator consider how many identical cells are present.
4. Amplifier Design and Simulation Results
The proposed OTA has been designed and simulated in a 130 nm CMOS process from STMicroelectronics. Small-signal and large-signal figures of merit (FoMs) were used to compare it against recently published OTAs with supply voltages lower than 0.5 V. Extensive parametric and Monte Carlo simulations were carried out in order to assess the robustness of the amplifier to PVT variations and mismatch referring to both open-loop and closed-loop simulation test benches.
4.1. Sizing
The transistors in the stages implementing the architecture in Figure 1 were sized as reported in Table 1. The bias voltages and in Figure 2, Figure 4 and Figure 5, are generated by the biasing circuit shown in Figure 3. Moreover, the sizing of the NMOS transistors and and of the PMOS transistor () of the biasing circuit are reported in Table 1. The voltages and propagate the bias current, nA, through body-mirroring or gate-mirroring.

Table 1.
Transistors’ sizing.
4.2. Circuit Simulations
The proposed OTA was simulated within the Cadence Virtuoso environment assuming a supply voltage of 0.3 V and an output load capacitance of 50 pF.
Referring to the open-loop simulation test bench the differential gain (magnitude and phase) was evaluated as reported in Figure 6. As can be observed from the figure, the phase margin is about 52.40°, whereas the gain-bandwidth product is about 35.16 kHz. Figure 6 also shows the common mode gain in typical conditions.
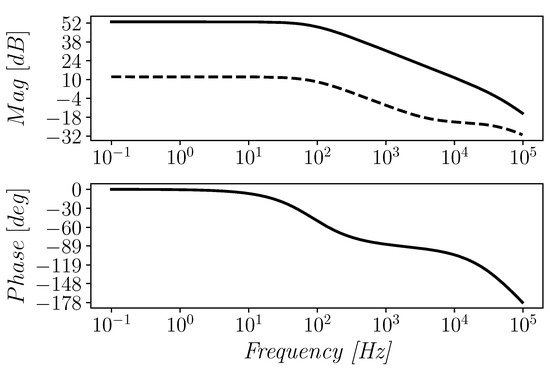
Figure 6.
Differential (solid) and common mode (dashed) gain of the proposed OTA.
Figure 7 confirms that the bias currents of all the three stages of the OTA are accurately set and are also very stable for an input signal amplitude going rail-to-rail in closed-loop unity-gain configuration.
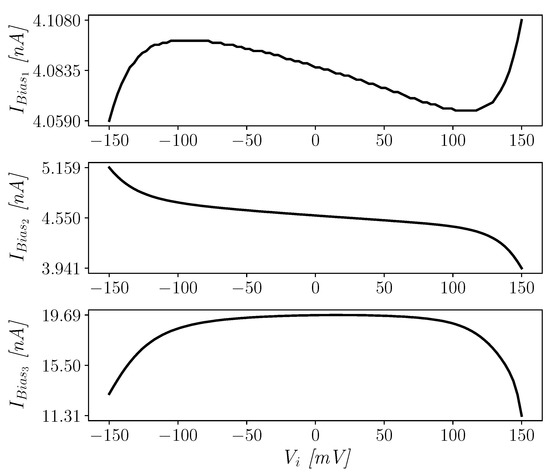
Figure 7.
Biasing currents of the three stages vs. input common mode level.
The amplifier was then tested in unity-gain configuration and its transfer characteristic is reported in Figure 8, highlighting the rail-to-rail capabilities of the OTA.
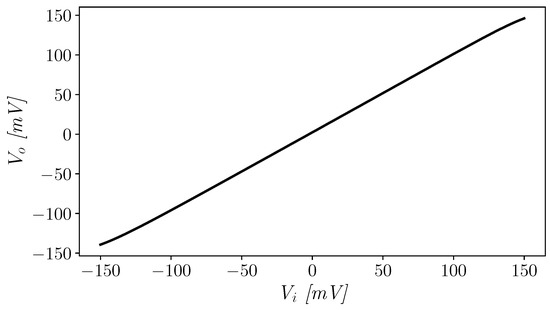
Figure 8.
Unity-gain amplifier transcharacteristic.
Sinusoidal waves at different amplitudes and with a frequency of 200 Hz were used to excite the unity-gain amplifier and evaluate distortions. The OTA exhibits very good total harmonic distortion (THD), also with an input signal swing equal to the supply voltage (as depicted in Figure 9). As can be observed from Figure 9, when a 90% signal swing is considered, the THD is about 0.673%, whereas when a full-swing signal is used the THD is still good and equal to about 1.38%. Furthermore, to assess the slew-rate (SR) performance of the amplifier, a full range square wave was used, and results are shown in Figure 10. The amplifier shows positive and negative slew-rate (SR and SR) equal to 18.61 and 11.51 V/ms, respectively. Though not symmetrical, the worst-case slew-rate is not much worse than the best one, hence large-signal performance is good on both signal edges.
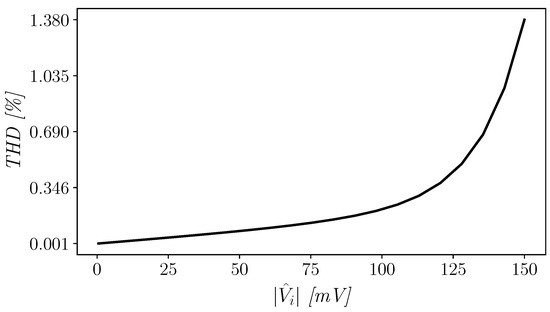
Figure 9.
THD vs. amplitude of the input signal in unity-gain configuration.
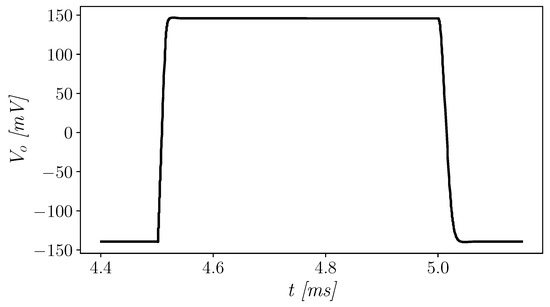
Figure 10.
Response to square input wave.
The input-referred noise spectrum of the proposed OTA is reported in Figure 11 and shows a value of about 1.60 at 1 kHz.
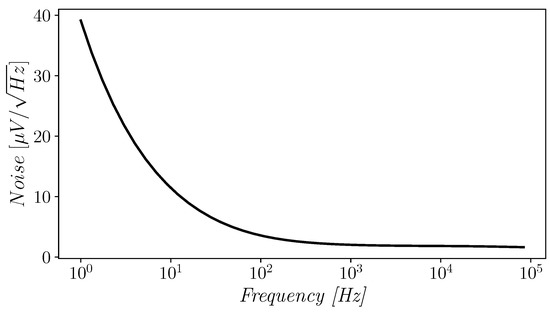
Figure 11.
Input-referred noise of the proposed OTA.
4.3. Robustness to Mismatch and PVT Variations
The OTA was then extensively tested by means of parametric and Monte Carlo simulations to demonstrate its robustness to PVT and mismatch variations. Table 2 reports the results of 200 Monte Carlo iterations. Power dissipation (P) has a standard deviation lower than the 10% of the mean value. Large-signal performance (i.e., and ) is close to the nominal value, whereas the attained mean value of the phase margin is about 53°. The standard deviation of the offset is relatively large, confirming the suboptimal performance in terms of noise and offset of the proposed OTA. Its value is however similar to other ULV OTAs reported in the literature.

Table 2.
Performance under mismatch variations.
Figure 12
reports the histogram of the CMRR that clearly shows a log-normal distribution, probably due to the sub-threshold operating condition of the circuit. The architecture exhibits a CMRR up to 98dB for some iterations (as expected from theoretical results in Section 3.2), and remains relatively high under mismatch variations, with a mean value of about 42 dB.
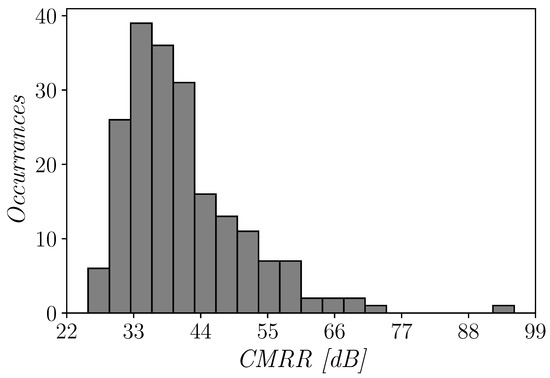
Figure 12.
Histogram of the common mode rejection ratio (CMRR) of the proposed OTA for 200 Monte Carlo mismatch iterations.
The power supply rejection ratio (PSRR) of the proposed OTA is also quite good despite the very low supply voltage. Figure 13 reports the histogram of the PSRR, that shows a mean value of about 56.13 dB with a limited variation under mismatch.
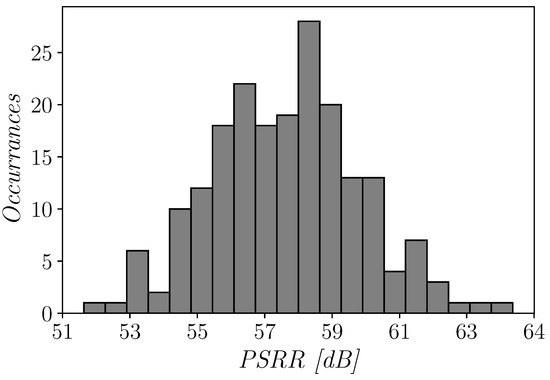
Figure 13.
Histogram of the power supply rejection ratio (PSRR) of the proposed OTA for 200 Monte Carlo mismatch iterations.
The performance under PVT variations was investigated taking into account a supply voltage variation and a [0, 70] °C temperature range. In Table 3, the performance under temperature variations is summarized. Total power consumption, the gain-bandwidth product as well as noise and total harmonic distortion are adequately stable across the considered temperature range. However, it is evident from Table 3 that the differential gain and CMRR degrade at high temperatures; this is probably due to variations in the bias point of and in particular in transistors and entering the triode region. A temperature-dependent current biasing approach would probably allow achievement of better results, but this has not been considered in this work. Furthermore it has to be noted that an ideal constant current source was considered: while such generator can be devised (e.g., see [49], or using a higher supply voltage for the current reference), this clearly remains a critical issue, dependent on the application environment of the OTA.

Table 3.
Performance vs. temperature variations.
Table 4 shows that the amplifier is stable under power supply variations, with power dissipation and slew-rate increasing significantly with the supply voltage, whereas CMRR improves at lower supply voltages due to the following design centering approach.

Table 4.
Performance vs Voltage Variations.
The OTA was then tested under different process corners and results are reported in Table 5. As is evident from Table 5, the proposed OTA shows good performance, even assuming the worst case process conditions.

Table 5.
Performance vs. corners.
4.4. Discussion and Comparison with the Literature
In order to compare the amplifier with the literature, we employ the two standard figures of merit (FOMs) for small and large-signal performance, namely and . The is defined as:
where is the load capacitance; the is defined as:
where is the average (between the positive and negative edge) slew-rate.
However, since most works presented in the literature show an asymmetric slew-rate, it is more meaningful to consider the worst case slew-rate. Consequently, as in [40], we define the as:
where is the worst case slew-rate between the positive and negative signal edges.
The proposed amplifier exhibits the largest small-signal among the comparable ULV literature, with a approaching 80.29 k against the previously reported record of about 20.16 k attained by [42]. The proposed OTA outperforms gate-driven, body-driven and also digital OTAs. Large-signal performance is also very good, especially if the worst-case is considered: the proposed amplifier is the best in the literature. Indeed, the is about 34.40 k; furthermore, the worst case also is very good, approximately 26.30 k, which is an awesome result, also given that previous works attained in the best case k and in the worst case k. The proposed amplifier has a small area occupation with respect to comparable body-driven designs, though the area is larger than digital and gate-driven designs (Table 6).

Table 6.
Comparison table.
5. Conclusions
In this work, we propose a novel tree-based OTA architecture that exploits body-driven stages to achieve rail-to-rail ICMR, and body-diode loads to avoid Miller compensation, improving the bandwidth efficiency. A ULV ULP OTA exploiting this approach was designed in a 130 nm CMOS process from STMicroelectronics. Simulation results show a dc gain higher than 52 dB, a gain-bandwidth product of about 35.16 kHz with nominal CMRR and PSRR, respectively, equal to 42.11 dB and 56.13 dB. Large-signal characteristics are also very good both in terms of THD and slew-rate. Due to the very limited power consumption of about 21.89 nW, the OTA exhibits state-of-the-art small-signal and large-signal FoMs. Summarizing, the overall performance of the proposed OTA shows record-breaking small-signal and large-signal performance, relatively large DC gain and reasonable PSRR and CMRR performance. The OTA exhibits good stability and robustness against PVT and mismatch variations.
Author Contributions
Conceptualization, F.C., R.D.S. and G.S.; data curation, R.D.S.; investigation, F.C., R.D.S., P.M. and G.S.; software, R.D.S.; validation, R.D.S.; supervision, F.C. and G.S.; writing—original draft preparation, R.D.S. and P.M.; writing—review and editing, F.C. and G.S.; funding acquisition, A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Body-to-Gate (B2G) Interface
This section aims to explain the body-to-gate (B2G) interface which is exploited in each stage ith−1, ith interface. Following the notation in Figure A1a, the current gain can be expressed as:
where derives from Miller approximation on and can be therefore expressed as:
where load conductance and as a consequence it could be equal to or (respectively, for stage and stage). It is possible thereafter to conclude that the interface behaves as a small signal current-mirror with gain.
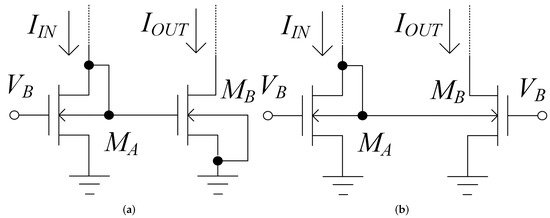
Figure A1.
(a) Body-to-gate (B2G) interface; (b) body-to-body (B2B) mirror.
Appendix B. Body-to-Body (B2B) Mirror
This section aims at explaining the body-to-body (B2B) interface which is exploited in each stage. Following the notation in Figure A1b, the current gain can be expressed as:
where also in this case denotes the Miller approximation and can be derived as:
Finally, it can be concluded that the interface could be considered as a B2B mirror that enables a small-signal current mirror whose gain is fixed by properly sizing and .
References
- Alioto, M. Enabling the Internet of Things—From Integrated Circuits to Integrated Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Sobin, C.C. A survey on architecture, protocols and challenges in IoT. Wirel. Pers. Commun. 2020, 112, 1383–1429. [Google Scholar] [CrossRef]
- Wu, T.; Wu, F.; Redouté, J.M.; Yuce, M.R. An autonomous wireless Body Area Network implementation towards IoT connected healthcare applications. IEEE Access 2017, 5, 11413–11422. [Google Scholar] [CrossRef]
- Lee, J.; Johnson, M.; Kipke, D. A tunable biquad switched-capacitor amplifier-filter for neural recording. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 295–300. [Google Scholar] [CrossRef] [PubMed]
- Della Sala, R.; Monsurrò, P.; Scotti, G.; Trifiletti, A. Area-efficient low-power bandpass Gm-C filter for epileptic seizure detection in 130 nm CMOS. In Proceedings of the 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 298–301. [Google Scholar]
- Liu, Z.; Tan, Y.; Li, H.; Jiang, H.; Liu, J.; Liao, H. A 0.5-V 3.69-nW complementary source-follower-C based low-pass filter for wearable biomedical applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4370–4381. [Google Scholar] [CrossRef]
- Swaroop, K.N.; Chandu, K.; Gorrepotu, R.; Deb, S. A health monitoring system for vital signs using IoT. Internet Things 2019, 5, 116–129. [Google Scholar] [CrossRef]
- Toledo, P.; Rubino, R.; Musolino, F.; Crovetti, P. Re-thinking analog integrated circuits in digital terms: A new design concept for the IoT era. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 816–822. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Ultra-low power and minimal design effort interfaces for the Internet of Thing. In Proceedings of the ICSyS19IEEE International Circuits and Systems Symposium (ICSyS), Kuantan, Malaysia, 18–19 September 2019; pp. 1–4. [Google Scholar]
- Harpe, P.; Gao, H.; Dommele, R.; Cantatore, E.; van Roermund, A.H.M. A 0.20 mm2 3 nW signal acquisition IC for miniature sensor nodes in 65 nm CMOS. IEEE J. Solid-State Circuits 2016, 51, 240–248. [Google Scholar] [CrossRef] [Green Version]
- Chi, Q.; Yan, H.; Zhang, C.; Pang, Z.; Xu, L.D. A reconfigurable smart sensor interface for industrial WSN in IoT environment. IEEE Trans. Ind. Inform. 2014, 10, 1417–1425. [Google Scholar] [CrossRef]
- Grasso, A.D.; Pennisi, S. Ultra-low power amplifiers for IoT nodes. In Proceedings of the ICECS18 IIEEE International Conference on Electronics, Circuits and Systems (ICECS), Bordeaux, France, 9–12 December 2018; pp. 497–500. [Google Scholar]
- Richelli, A.; Colalongo, L.; Kovacs-Vajna, Z.; Calvetti, G.; Ferrari, D.; Finanzini, M.; Pinetti, S.; Prevosti, E.; Savoldelli, J.; Scarlassara, S. A survey of low voltage and low power amplifier topologies. J. Low Power Electron. Appl. 2018, 8, 22. [Google Scholar] [CrossRef] [Green Version]
- Khateb, F.; Dabbous, S.B.A.; Vlassis, S. A survey of non-conventional techniques for Low-voltage Low-power analog circuit design. Radioengineering 2013, 22, 415–427. [Google Scholar]
- Cabrera-Bernal, E.; Pennisi, S.; Grasso, A.D.; Torralba, A.; Carvajal, R.G. 0.7-V three-stage class-AB CMOS operational transconductance amplifier. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1807–1815. [Google Scholar] [CrossRef]
- Taherzadeh-Sani, M.; Hamoui, A.A. A 1-V process-insensitive current-scalable two-stage opamp with enhanced DC gain and settling behavior in 65-nm digital CMOS. IEEE J. Solid-State Circuits 2011, 46, 660–668. [Google Scholar] [CrossRef]
- Paul, A.; Ramirez-Angulo, J.; Lopez-Martin, A.J.; Carvajal, R.G.; Rocha-Perez, J.M. Pseudo-three-stage Miller op-amp with enhanced small-signal and large-signal performance. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 2246–2259. [Google Scholar] [CrossRef]
- Riad, J.; Estrada-López, J.J.; Padilla-Cantoya, I.; Sánchez-Sinencio, E. Power-scaling output-compensated three-stage OTAs for wide load range applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2180–2192. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Yu, S.S.; Zhao, X.; Trinh, H.; Shi, P. A robust local positive feedback based performance enhancement strategy for non-recycling folded cascode OTA. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2897–2908. [Google Scholar] [CrossRef]
- Centurelli, F.; Della Sala, R.; Monsurrò, P.; Scotti, G.; Trifiletti, A. A novel OTA architecture exploiting current gain stages to Boost bandwidth and slew-rate. Electronics 2021, 10, 1638. [Google Scholar] [CrossRef]
- Aguirre, P.C.D.; Susin, A.A. PVT compensated inverter-based OTA for low-voltage CT sigma-delta modulators. Electron. Lett. 2018, 54, 1264–1266. [Google Scholar] [CrossRef]
- Braga, R.A.; Ferreira, L.H.; Coletta, G.D.; Dutra, O.O. A 0.25-V calibration-less inverter-based OTA for low-frequency Gm-C applications. Microelectron. J. 2019, 83, 62–72. [Google Scholar] [CrossRef]
- Lv, L.; Zhou, X.; Qiao, Z.; Li, Q. Inverter-based subthreshold amplifier techniques and their application in 0.3-V ΣΔ-modulator. IEEE J. Solid-State Circuits 2019, 54, 1436–1445. [Google Scholar] [CrossRef]
- Manfredini, G.; Catania, A.; Benvenuti, L.; Cicalini, M.; Piotto, M.; Bruschi, P. Ultra-low-voltage inverter-based amplifier with novel common-mode stabilization loop. Electronics 2020, 9, 1019. [Google Scholar] [CrossRef]
- Rodovalho, L.H.; Aiello, O.; Rodrigues, C.R. Ultra-low-voltage inverter-based operational transconductance amplifiers with Voltage gain enhancement by improved composite transistors. Electronics 2020, 9, 1410. [Google Scholar] [CrossRef]
- Rodovalho, L.H.; Rodrigues, C.R.; Aiello, O. Self-biased and supply-voltage scalable inverter-based operational transconductance amplifier with improved composite transistors. Electronics 2021, 10, 935. [Google Scholar] [CrossRef]
- Baghtash, H.F. A 0.4 V, body-driven, fully differential, tail-less OTA based on current push-pull. Microelectron. J. 2020, 99, 104768. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhadauria, V. An ultra-low-power near rail-to-rail pseudo-differential subthreshold gate-driven OTA with improved small and large signal performances. Analog. Integr. Circuits Signal Process. 2021, 109, 345–366. [Google Scholar] [CrossRef]
- Allen, P.E.; Blalock, B.J.; Rincon, G.A. 1 V CMOS opamp using bulk-driven MOSFETs. In Proceedings of the ISSCC’95-International Solid-State Circuits Conference, San Francisco, CA, USA, 15–17 February 1995; pp. 192–193. [Google Scholar] [CrossRef]
- Blalock, B.J.; Allen, P.E.; Rincon-Mora, G.A. Designing 1-V op amps using standard digital CMOS technology. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1998, 45, 769–780. [Google Scholar] [CrossRef] [Green Version]
- Stockstad, T.; Yoshizawa, H. A 0.9-V 0.5-/spl mu/A rail-to-rail CMOS operational amplifier. IEEE J. Solid-State Circuits 2002, 37, 286–292. [Google Scholar] [CrossRef]
- Ferreira, L.; Sonkusale, S. A 60-dB gain OTA operating at 0.25-V power supply in 130-nm digital CMOS process. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 1609–1617. [Google Scholar] [CrossRef]
- Colletta, G.D.; Ferreira, L.H.; Pimenta, T.C. A 0.25-V 22-nS symmetrical bulk-driven OTA for low-frequency G_m G m-C applications in 130-nm digital CMOS process. Analog. Integr. Circuits Signal Process. 2014, 81, 377–383. [Google Scholar] [CrossRef]
- Abdelfattah, O.; Roberts, G.W.; Shih, I.; Shih, Y.C. An ultra-low-voltage CMOS process-insensitive self-biased OTA with rail-to-rail input range. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2380–2390. [Google Scholar] [CrossRef]
- Akbari, M.; Hashemipour, O. A 63-dB gain OTA operating in subthreshold with 20-nW power consumption. Int. J. Circuit Theory Appl. 2017, 45, 843–850. [Google Scholar] [CrossRef]
- Veldandi, H.; Shaik, R.A. A 0.3-V pseudo-differential bulk-input OTA for low-frequency applications. Circuits Syst. Signal Process. 2018, 37, 5199–5221. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. A 0.3-V 98-dB Rail-to-Rail OTA in 0.18 μm CMOS. IEEE Access 2020, 8, 27459–27467. [Google Scholar] [CrossRef]
- Woo, K.C.; Yang, B.D. A 0.25-V rail-to-rail three-stage OTA with an enhanced DC gain. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1179–1183. [Google Scholar] [CrossRef]
- Centurelli, F.; Della Sala, R.; Scotti, G.; Trifiletti, A. A 0.3 V, rail-to-rail, ultralow-power, non-tailed, body-driven, sub-tThreshold amplifier. Appl. Sci. 2021, 11, 2528. [Google Scholar] [CrossRef]
- Centurelli, F.; Della Sala, R.; Monsurrò, P.; Scotti, G.; Trifiletti, A. A 0.3 V rail-to-rail ultra-low-power OTA with improved bandwidth and slew rate. J. Low Power Electron. Appl. 2021, 11, 19. [Google Scholar] [CrossRef]
- Fortes, A.; Quirino, F.A.; da Silva, L.A.; Girardi, A. Low power bulk-driven OTA design optimization using cuckoo search algorithm. Analog. Integr. Circuits Signal Process. 2021, 106, 99–109. [Google Scholar] [CrossRef]
- Centurelli, F.; Della Sala, R.; Monsurró, P.; Tommasino, P.; Trifiletti, A. An ultra-low-voltage class-AB OTA exploiting local CMFB and body-to-gate interface. AEU Int. J. Electron. Commun. 2022, 145, 154081. [Google Scholar] [CrossRef]
- Crovetti, P.S. A digital-based analog differential circuit. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3107–3116. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Aiello, O.; Alioto, M. Fully digital rail-to-rail OTA with sub-1000-μm² area, 250-mV minimum supply, and nW power at 150-pF load in 180 nm. IEEE Solid-State Circuits Lett. 2020, 3, 474–477. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Aiello, O.; Alioto, M. Design of digital OTAs with operation down to 0.3 V and nW power for direct harvesting. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3693–3706. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Klimach, H.; Bampi, S.; Aiello, O.; Alioto, M. 300mV-supply, sub-nW-power digital-based operational transconductance amplifier. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3073–3077. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Klimach, H.; Bampi, S. Dynamic and static calibration of ultra-low-voltage, digital-based operational transconductance amplifiers. Electronics 2020, 9, 983. [Google Scholar] [CrossRef]
- Fiorelli, R.; Arnaud, A.; Galup-Montoro, C. Series-parallel association of transistors for the reduction of random offset in non-unity gain current mirrors. In Proceedings of the ISCAS04 IEEE International Symposium on Circuits and Systems, Vancouver, BC, Canada, 23–26 May 2004; Volume 1, pp. 881–884. [Google Scholar]
- Narasimman, N.; Kim, T.T. A 0.3 V, 49 fJ/conv.-step VCO-based delta sigma modulator with self-compensated current reference for variation tolerance. In Proceedings of the ESSCIRC Conference 2016: 42nd European Solid-State Circuits Conference, Lausanne, Switzerland, 12–15 September 2016; pp. 237–240. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. A compact 0.3-V class AB bulk-driven OTA. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 224–232. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. Design and implementation of sub 0.5-V OTAs in 0.18-μm CMOS. Int. J. Circuit Theory Appl. 2018, 46, 1129–1143. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).