Abstract
The elliptic curve cryptosystem (ECC) has been proven to be vulnerable to non-invasive side-channel analysis attacks, such as timing, power, visible light, electromagnetic emanation, and acoustic analysis attacks. In ECC, the scalar multiplication component is considered to be highly susceptible to side-channel attacks (SCAs) because it consumes the most power and leaks the most information. In this work, we design a robust asynchronous circuit for scalar multiplication that is resistant to state-of-the-art timing, power, and fault analysis attacks. We leverage the genetic algorithm with multi-objective fitness function to generate a standard Boolean logic-based combinational circuit for scalar multiplication. We transform this circuit into a multi-threshold dual-spacer dual-rail delay-insensitive logic () circuit. We then design point-addition and point-doubling circuits using the same procedure. Finally, we integrate these components together into a complete secure and dependable ECC processor. We design and validate the ECC processor using Xilinx ISE and implement it in a Xilinx Kintex-7 field-programmable gate array (FPGA).
1. Introduction and Motivation
As edge computing on resource-constrained edge devices is gaining momentum, the need for a low-cost cryptosystem for these devices is also increasing. For public-key cryptography, elliptic curve cryptography (ECC) is regarded as a better solution in terms of security per bit, computation, and memory/storage requirements as compared to other public-key cryptographic approaches, such as RSA [1]. This is mainly due to ECC’s shorter key length as compared to RSA under comparable security levels. The ECC’s shorter key length also leads to a reduction in computing complexity and storage cost. These characteristics make ECC more attractive to resource-constrained systems (e.g., edge devices), which require acceptably high security levels with performance and resource constraints [2].
Although cracking ECC has proven to be a mathematically difficult problem, the advent of cryptanalytic attacks on implementations, also known as side-channel attacks (SCAs), has overturned this traditional concept through a fine-grained analysis of sensitive leakages, such as timing, power, visible light, electromagnetic emanations, and acoustic side-channel information [3]. Various hardware-based countermeasures to resist SCAs have been proposed in [4,5]. In [4], Liao et al. applied binary randomized montgomery operation (RMO) to modular arithmetic to design an ECC coprocessor that is resistant to non-invasive SCAs. In [5], Lee et al. proposed a power-analysis-resistant dual-field ECC processor using heterogeneous dual-processing-element architecture. The authors implemented priority-oriented scheduling of right-to-left double-and-add-always elliptic curve scalar multiplication with a randomized processing technique to achieve a power-analysis-resistant dual-field ECC processor.
Many of the existing ECC processors are based on sequential circuits (or synchronous circuits) (e.g., [4,5]). This is mainly because of the ease of design and verification of synchronous sequential circuits as compared to asynchronous circuits. However, from a security perspective, the synchronous sequential circuits consume more power and energy (due to the increased clock rates and clock generation/distribution circuits), which in turn make these circuits more susceptible to power-/energy-analysis attacks. Furthermore, an attacker can easily isolate the operation time of a certain logic-switching activity by referring to the clock signals, making the side-channel analysis much easier than the asynchronous circuits. Additionally, almost all of the state-of-the-art SCAs are targeted for sequential circuits. These attack methodologies are, however, not always appropriate to attack combinational circuits. For example, hamming weight- and hamming distance-based power models used in differential power analysis (DPA) and correlated power analysis (CPA) attacks are only suitable for power characterization of registers and buses (note that here we focus only on hardware security attacks and not on the software/algorithmic vulnerabilities of ECC). Yet, neither of these models are suitable for large-scale, multi-input combinational circuits [6,7]. Hence, we propose to design an ECC processor as a pure asynchronous combinational circuit.
SCAs against combinational circuits have not been extensively explored but, from recent research works, we know that they are not immune to such attacks [8,9]. Zheng [6] proposed an SCA called a power template match attack that is effective against combinational circuits. This attack is able to crack the S-box (implemented as a combinational circuit) of PRINTcipher. To mount this attack, first, the authors built a power model template based on the input transitions of the combinational circuit (i.e., S-box). Using this power model template, they estimated the average power consumption of the modeled combinational circuit. Then, they implemented the combinational circuit in hardware and measured the actual power consumption. By correlating the average power consumption values obtained from the power model template with the average values of actual power consumption, they were able to recover the secret key. This attack works on combinational circuits designed using the standard-cell libraries based on forward application-specific integrated circuit (ASIC) design flow with a synchronous design style. Therefore, it is apparent that security risks exist in the standard-cell-based design flow because it has no special consideration for protection of combinational circuit design.
To prevent SCAs against combinational circuits, it is necessary to migrate the design approach to non-conventional combinational logic. We leverage this principle in the design of our secure and robust ECC processor, wherein we employ a genetic algorithm (GA) to evolve a non-conventional combinational circuit. GA is a pseudo-random algorithm that can generate multiple, functionally equivalent circuits. We can randomly select a circuit from the pool of functionally equivalent circuits generated by our GA as our ECC processor. This makes power template match attacks (e.g., those illustrated in [6]) inaccurate against our ECC processor because power template match attacks require an attacker to design the same circuit to generate the power model template. Moreover, Zheng [6] was successful at mounting an attack on an S-box of PRINTcipher which has 5-bit input and 3-bit output. The small input length (5-bit) made the design of a power model template feasible because the circuit has only possible input transitions. However, our elliptic curve cryptosystem will have a 160-bit input, which will have possible input transitions. It is apparent that it will be infeasible to take into account all of these input transitions to build an effective power model template to mount the power template match attack proposed in [6]. Although GAs have been used for constructing the security components of cryptosystems, such as AES S-Boxes in [10,11], prior works have not applied GA for designing combinational circuits for ECC. Furthermore, our GA employs a multi-objective fitness function, which has not been used in prior works [10,11].
Apart from power-analysis, there are several other attack surfaces that can be employed for SCA in combinational circuits. An SCA on combinational circuits may be performed using information leaked through glitches, early propagation, unstable power traces, and dependencies of circuit delays on input data. Glitches in a combinational circuit (caused by toggling of gates before final values are settled) can potentially leak information through the side-channels [12]. In addition, the early propagation phenomenon, in which logic gates evaluate their outputs before all inputs have settled, can also leak important information via side-channels [13]. As a countermeasure for these attack surfaces, we transform the non-conventional combinational circuit design of our ECC processor to a multi-threshold dual-spacer dual-rail delay-insensitive logic () paradigm [14] (see Section 5). This work is an extension of our earlier work [15], in which we used a GA to address the vulnerability of ECC to SCAs by evolving combinational logic circuits that correctly implemented ECC hardware that was resistant to timing and power analysis attacks. However, our earlier work [15] did not utilize for GA-based evolving combinational circuits. Furthermore, our earlier work [15] did not propose a secure and dependable ECC processor that utilized the proposed GA-based evolving combinational circuits.
In this work, we transform the GA-based evolving combinational circuits to the paradigm to provide stronger resilience against SCAs, as compared to prior works. removes the dependency on clock signals and implements a delay-insensitive hand-shake protocol to perform operations asynchronously within the circuit. This allows designers to mask the start times and end times of operations of different sub-blocks of the circuit or instruction-processing, thus providing flatter power traces and more constant energy consumption. Additionally, circuits possess benefits of delay-insensitive asynchronous circuits, such as having no clock tree, high energy efficiency, robust circuit operation under process/voltage/temperature variations, and low noise/electromagnetic emission. These characteristics enhance the robustness of the circuits against SCAs [13,14,16].
In summary, we make the following contributions.
- We propose the design of a side-channel attack-resistant asynchronous circuit for scalar multiplication in an elliptic curve over the prime field. We leverage the genetic algorithm with a multi-objective fitness function to generate a standard Boolean logic-based combinational circuit for scalar multiplication. We transform this circuit into a circuit by replacing the standard Boolean logic gates of the combinational circuit with gates and adding a register interface and early completion detection logic. We then design point-addition and point-doubling circuits using the same procedure.
- We integrate scalar multiplication, point-addition, and point-doubling circuits to design a secure, dependable, and robust ECC processor using a system-on-chip field-programmable gate array (SoC FPGA). Dependability is provided by using our novel fault tolerance using self-reconfiguration in dual modular redundant system (FT-SR-DMR) scheme.
- We perform functional verification of the proposed circuit using Xilinx ISE and implement it on a Xilinx Kintex-7 FPGA.
- We analyze the resilience of our proposed circuit against timing analysis, power analysis, and fault analysis attacks.
The remainder of this article is organized as follows. Section 2 describes the security threat model assumed for this work. Section 3 presents the SCA vulnerabilities of ECC and existing countermeasures. Section 4 illustrates the generation of combinational circuits for scalar multiplication in ECC using a genetic algorithm. Section 5 elaborates the conversion of combinational circuit for scalar multiplication generated by our proposed genetic algorithm into an -based design that is resilient to both power- and timing-based SCAs. The high-level architecture of our proposed secure and dependable ECC processor is described in Section 6. Section 7 analyzes the security of the proposed elliptic curve cryptosystem against various types of attacks mentioned in our threat model. Experimental results and analyses are presented in Section 8. Finally, Section 9 concludes this work.
2. Threat Model and Assumptions
In this article, we assume a skilled and determined attacker who aims to extract secret information from ECC hardware by exploiting information leaked via side-channels. We assume that the attacker is well-equipped with all the necessary tool-sets, such as hardware with ECC implementation, a robust power model, physical measurement, and analysis tools (like oscilloscopes, logic analyzers, signal generators, FPGA boards, etc.), for launching state-of-the-art non-invasive timing analysis, power analysis, and electromagnetic emanation analysis attacks. We further suppose that the attacker is capable of mounting a differential fault analysis attack [17] by introducing soft-errors in the ECC hardware, thus causing the hardware to behave abnormally (or malfunction). Under this threat model, the attacker can employ a number of strategies, such as timing analysis, (simple/differential) power analysis, template attacks, and differential fault analysis, to extract secret information via side-channels [17,18]. Later in this article, we propose a secure and dependable ECC processor that is resilient to non-invasive SCAs and fault attack strategies.
3. SCA Vulnerability of ECC Scalar Multiplication and Existing Countermeasures
SCAs have proven to be extremely effective as a practical means for attacking implementations of cryptographic algorithms, especially in constrained devices, such as chip-cards, where straightforward implementations of cryptographic algorithms can be broken with minimal units. In this section, we provide a digest of existing attacks and countermeasures.
Timing and simple power analysis SCAs: Timing attacks can be mounted by exploiting the timing variance for different input values [18]. Timing variations can be caused by cache (e.g., time for instruction execution in case of cache hit and miss are different) or conditional branches. Simple power analysis attacks on cryptographic implementations can be performed if the power traces show distinctive key-dependent patterns [18]. For example, difference in power consumption of point-doubling and point addition in double-and-add algorithms can reveal the value of secret keys.
Differential side-channel analysis attacks: Differential side-channel analysis attacks (DPA, short for differential power analysis, and DEMA, short for differential electromagnetic analysis) pry out secret information from measurements of power or electromagnetic emanations by using statistical techniques [19]. Differential SCAs require leakage from side-channels to be larger than noise. Leakage is distinguished from noise by averaging samples of leaked data generated from a large number of same key operations.
Refined power analysis and zero-value analysis attack: Refined power analysis (RPA) attacks infer secret information by using search algorithms to find special points on the elliptic curve, having one coordinate as zero (e.g., ). The attacker assumes some specific bits of the secret key and uses an algorithm to search for , by feeding guess points P to the system. When the search algorithm succeeds in finding the special points, the intermediate results of the algorithm can be analyzed to speculate the correctness of the assumed bits of the secret key [20]. Zero-value point attacks (ZPAs) are a special case of RPA. ZPAs work even if the search algorithm fails to find special points on the elliptic curve. In ZPAs, the attacker can extract secret information from cases when the values in the auxiliary registers of elliptic curve point addition and point-doubling operations in Jacobian coordinates become zero [21].
Template attack: Template attacks determine secret information through precise multivariate characterization of signals and noise of a target system by using detailed profiles of signals and noise of identical experimental systems [22]. Template attacks are the strongest form of SCAs possible in an information theoretic sense because they utilize all possible information (both signal and noise) available in each sample of leaked information. Template attacks are thus in sharp contrast with other statistical methods (e.g., DPA, CPA, RPA, etc.) which consider noise as a hindrance and focus on eliminating noise by averaging over a large number of samples of leakage data.
Fault attacks: Fault attacks are carried out by actively disturbing the cryptographic devices by inducing faults and exploiting the abnormal behavior of the victim device to derive secret information [23]. Faults can be injected using different methods, such as changing a bit in memory with laser, violating the setup time with glitches in the clock, or abnormally lowering the supply voltage. The precision of the time and location of fault injections has a significant impact on the success rate of fault attacks. Fault attacks can be classified into three categories: safe-error-based analysis, weak-curve-based analysis, and differential fault analysis. Differential fault analysis attacks analyze the difference between correct and erroneous outputs to retrieve the secret bit-by-bit [24].
There are multiple possible methods proposed to thwart most of the attacks discussed above. The attacks and their existing countermeasures are listed in Table 1. In this article, we propose a new cryptographic circuit design paradigm based on a genetic algorithm and logic to thwart simple and differential side-channel analysis attacks.

Table 1.
SCAs in elliptic curve scalar multiplication and their existing countermeasures.
4. Generation of Combinational Circuit for Scalar Multiplication Using Genetic Algorithm
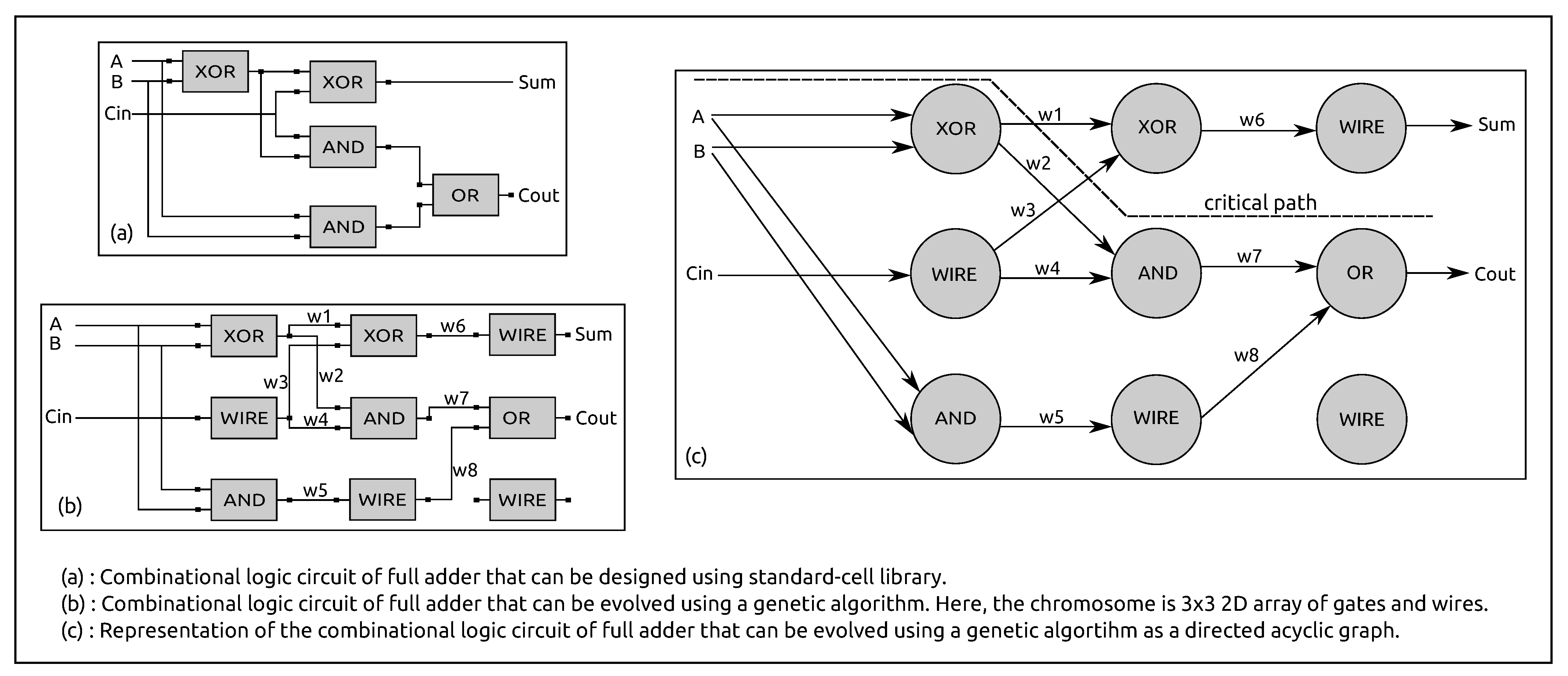
GAs are widely used algorithms, which can be applied to various applications. For security and cryptography, GAs have been used to construct components for cryptographic algorithms (e.g., S-boxes in AES [10,11]). Other than these applications, the GAs can also be used as an engine to discover new designs of digital circuits because they allow one to explore a much larger space of possible designs [33,34,35,36]. In addition to digital circuit designs, designs generated by GA are often different from those created by top-down, human, rule-based design approaches (such as designing digital circuits using standard cell libraries based on forward ASIC design flow). Figure 1a shows the design of a full adder circuit using the Boolean algebra, truth table, and K-map. The same full adder circuit is generated by using GA with circuit configurations which has nine gates, connected as shown in Figure 1b. In order to compute the propagation delay of the critical path of our evolved circuit, we represent the evolved combinational circuit as a directed acyclic graph, as shown in Figure 1c. The potential advantage of using non-conventional combinational circuits designed using GA is that it can improve the resistance of the circuit against certain SCAs for which an attacker needs to build an exact prototype of the circuit. In addition, usually the evolved circuits are found to be more efficient (in terms of size and propagation delay) than those created using traditional design methods [35]. In this work, we use a GA to generate combinational circuits that perform scalar multiplication in an elliptic curve over the prime field. We chose scalar multiplication because it is the most critical operation in ECC and there are numerous SCAs performed on scalar multiplication [34]. In this work, we fix the size of a secret key to 6-bit, and base point to 5-bit. Our future plan is to design a full-sized combinational circuit that supports 160-bit key length.
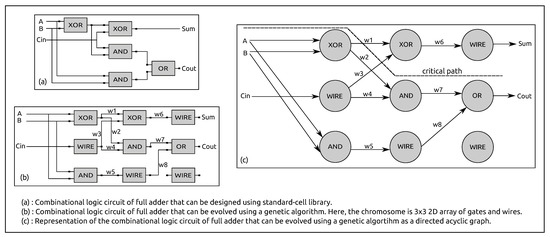
Figure 1.
Illustration of differences in a full adder circuit generated by a conventional circuit design method and proposed genetic algorithm method.
In this section, we first delineate the fundamentals of ECC. Then, we describe the representation of a combinational circuit for scalar multiplication as a chromosome in our GA. Next, we elaborate on the multi-objective fitness function used in our GA. Finally, we explain the core genetic algorithm used to generate the combinational circuit for scalar multiplication.
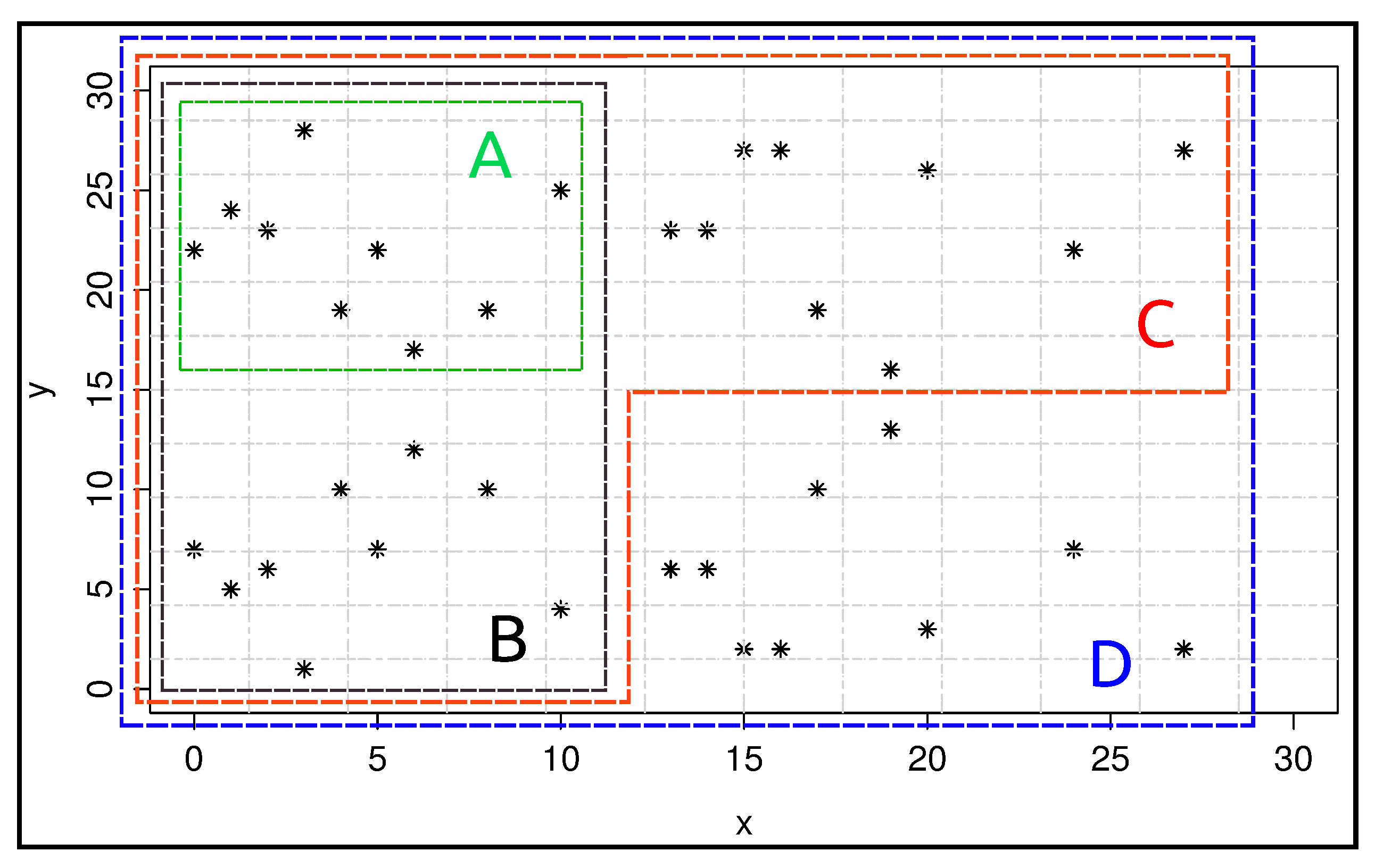
Elliptic Curve Cryptosystem and Scalar Multiplication: ECC [37] is based on the algebraic structure of elliptic curves over finite fields. For our work, we use an elliptic curve over prime field , where the prime number . Equation (1) shows the elliptic curve we employ for our ECC. The coefficients and are set to 4 and 20, respectively. Figure 2 shows the points in the elliptic curve of Equation (1).
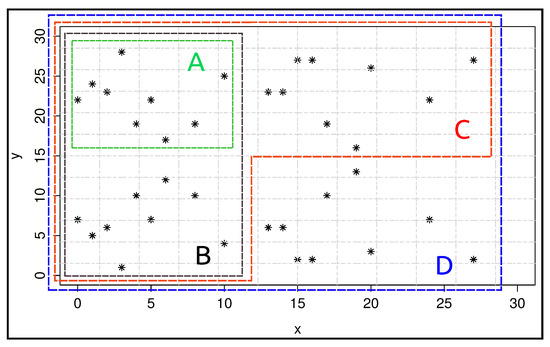
Figure 2.
Points in elliptic curve over prime field [15].
In the public key generation step of ECC, the scalar multiplication involving the base point on the elliptic curve is the critical operation. The base point is a point chosen from the points in Figure 2. The scalar value used in the scalar multiplication operation is the secret key or private key. In this work, we used a secret key with 6-bit length. The security of elliptic curve-based security applications and protocols relies on an elliptic curve discrete logarithm problem—the inability to compute the secret scalar value given the base point and public key.
Scalar multiplication between a point and a scalar k is denoted by and is computed using a Double-and-Add algorithm (Algorithm 1) [18]. We implement the Double-and-Add algorithm for computing the functional correctness (one of the objectives in a multi-objective fitness function of our GA) of the evolved circuit.
| Algorithm 1 Double-and-Add algorithm for scalar multiplication in ECC [15]. |
| Input: Elliptic curve , an elliptic curve point N, and scalar k of bits. |
| Output:M = kN |
| t = number of bits of k |
| = prime number |
| Initialization: |
| Core Algorithm: |
| for downto 0 do |
| if then |
| end if |
| return (M) |
| end for |
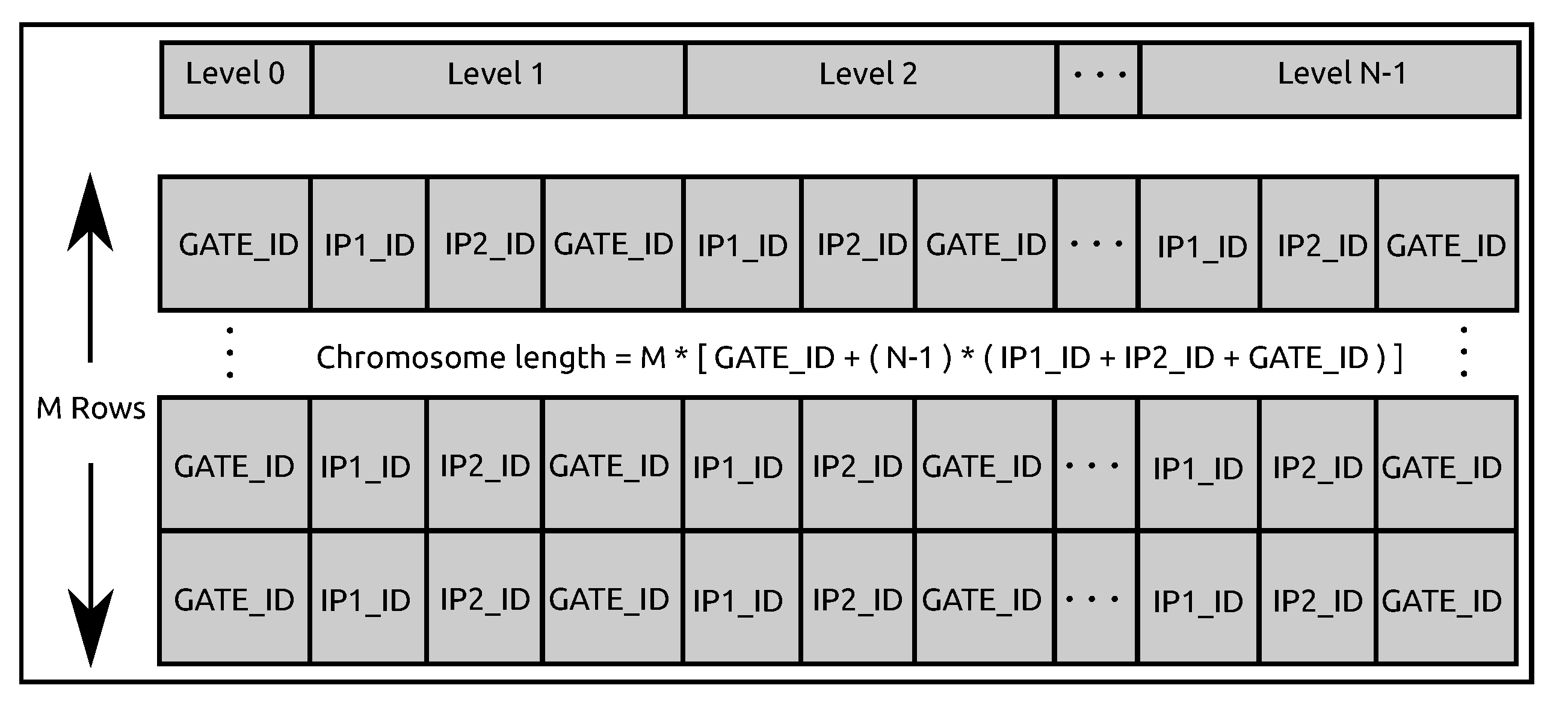
Encoding a Combinational Circuit as a Binary Chromosome: In GA, a solution is represented by a chromosome and a fitness value associated with the chromosome. A chromosome is usually represented as a string of binary values, 0’s and 1’s. In our digital circuit design problem, the solution is a combinational circuit. Thus, we use a 2D binary chromosome for encoding the combinational circuit into a genotype (Figure 3). The 2D binary chromosome has a size N×M, where N is the number of vertical levels (numbered from 0 to N − 1) and M is the number of logic gates in each level. We use eight different types of Boolean logic gates which are shown in Table 2. In that account, three bits are used to represent a gate in binary. Thus, the GATE_ID in Figure 3 is three bits wide. The logic gates in Level 0 have two functions. First, these gates act as input interface which take input signals from external sources. Second, these gates group with gates in Level 1 to level N-1 to form a functional combinational circuit that performs scalar multiplication. The outputs from gates at level N produce the overall circuit output values which is the product of the scalar value and base point.
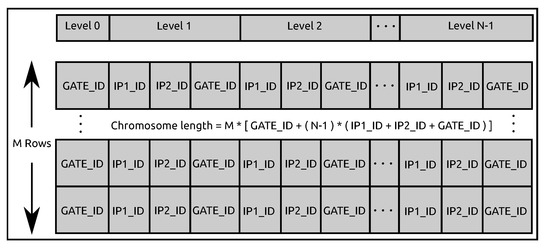
Figure 3.
Chromosome representing a combinational circuit for point arithmetic [15].

Table 2.
The gate equivalent and propagation delay of standard Boolean logic gates [15].
As shown in Figure 3, each gate has two inputs and one output. The outputs of the gates at each level are indexed by numbers from 0 to M. These outputs are connected to inputs of the gates at the next level. Hence, the inputs of the gates at a level are also indexed by a number from 0 to M. Therefore, bits are needed to encode an index (IP1_ID and IP2_ID in Figure 3) in binary. The inputs to a gate at level i can be the output from any gate at level . Finally, the length of chromosome is given by M * (GATE_ID + (N − 1) * (IP1_ID + IP2_ID + GATE_ID)).
We used GA to design four different combinational circuits. These circuits differ in the number of base points they support. A circuit can support points enclosed in rectangle A in Figure 2 as a base point for scalar multiplication. In other words, a circuit can perform correct multiplication of any six-bit secret key with any point in rectangle A in Figure 2. Similarly, , , and circuits can perform correct scalar multiplication of any six-bit secret key with any point enclosed in rectangle B, C, and D in Figure 2, respectively.
Multi-objective Fitness Function: A primary operation involved in GA is the evaluation of adherence of evolved solutions to the imposed constraints. GA uses a fitness function to evaluate the competence of evolved solutions. We use a multi-objective fitness function for our GA which is based on aggregation by variable objective weighting [38]. In aggregations by the variable objective weighting scheme, the fitness function is represented as the weighted sum of the objectives. Each objective is assigned a weight such that , and the scalar fitness value is calculated by summing up the weighted objective values . In our case, there are three governing constraints (or objectives), viz., correctness in input/output behavior, minimization of propagation delay, and minimization of the size of the evolved circuit. for correctness in input/output behavior is set to and for circuit size and propagation delay are set to and , respectively.
In order to quantify the correctness in input/output behavior, we incorporate the notion of expected output and observed output. A reward function is defined, which counts the number of observed outputs that are equal to the expected outputs. The count is considered as reward value. , where represents the simulation inputs (refer Figure 2) which are the points on the elliptic curve. We used these simulation points to check the correctness in input/output behavior of the evolved combinational circuit. represents the expected output of the circuit with as an input and represents the observed output of the evolved combinational circuit. The expected output is computed by implementing the double-and-add scalar multiplication algorithm.
Our other design objective is the minimization of the size of the evolved circuit. We estimate the necessary area for an evolved circuit using the concept of gate equivalence [39], which is a basic unit of measure for digital circuit complexity. This measure is more accurate than the simple number of the gates concept. We formulate a function, , to represent the gate-equivalent value of an evolved circuit. Our final objective is minimization of the propagation delay of evolved circuit. The finite time that a circuit takes to reflect the change in input on its output values is known as propagation delay. Propagation delay is different for different gates. We measured the propagation delay using the path having the highest delay, called the worst-case delay path (or critical path). The represents the delay function in our fitness function. We employ the representation of a combinational circuit as a directed acyclic graph to compute the critical path (as shown in Figure 1). The gate-equivalent values and propagation delay values for the gates in our evolved circuit are shown in Table 2. The following equation shows the fitness function we used for our GA.
Genetic Algorithm: For the genetic algorithm, we have employed a CHC-adaptive search algorithm [40] with the parameter settings listed in Table 3. The CHC algorithm is based on the elitist selection method that uses a high probability of crossover () and no mutation. In the following, we elaborate the working of our version of CHC GA. For initialization, we randomly select a group of individuals (combinational circuits), which are then set as the starting point of the algorithm. These individuals are represented by a data structure having a chromosome and a fitness value of chromosomes as components. These initial sets of individuals constitute a parent population, which we denote as .

Table 3.
Parameters for our CHC GA.
The GA solution advances by spawning a child population () from the parent population by using a reproduction operator called crossover operator. During the crossover, the GA selects two random individuals (i.e., parents) from . Before performing the crossover operations, one needs to check whether the hamming distance (HD) of the parents is greater than or equal to a certain threshold (denoted as ) or not. If the requirement is satisfied by the two individuals (parents), the crossover operation can be carried out. This mechanism is known as incest prevention in CHC GA. For crossover operation, a half of the bits from the random chromosome locations that are different in the two parents are exchanged. This type of crossover is referred to as half-uniform crossover. In case the requirement for is not satisfied, is decremented by one, and another parent (i.e., two individuals) is selected randomly for crossover. This process continues until the GA finds parents eligible for crossover/mating. However, in case of convergence in local maxima, will keep decreasing and hit zero value without finding any eligible parents for mating. At this point, the CHC GA is restarted with the initial population of elite individuals (i.e., individuals with the best fitness value) from the current parent population. The remaining population () (i.e., individuals) are generated by randomly flipping bits of the elite individuals.
The crossover operations in the CHC GA generate the child population. To produce the next generation of individuals, both the the child and parent population are merged into a single pool, and the individuals are sorted in the descending order of the fitness value. A total of individuals having the best fitness values are selected as parents for producing the next generation of child populations.
5. Converting Combinational Circuit into Asynchronous Circuit
The focus of digital design has primarily been on synchronous, clocked architectures over the last three decades. However, as clock rates have significantly increased while feature size has decreased, clock skew has become a major problem. To achieve acceptable skew, high-performance chips must dedicate increasingly larger portions of their area for clock drivers. This causes these chips to dissipate increasingly higher power. As these trends continue, the clock is becoming more and more difficult to manage, while clocked circuits’ inherent power inefficiencies are emerging as the dominant factor hindering increased performance. Furthermore, increased power consumption makes these circuits susceptible to power analysis SCAs. These issues have caused renewed interest in asynchronous digital design. Asynchronous, clockless circuits require less power, generate less noise, and produce less electromagnetic interference (EMI), compared to their synchronous counterparts. Furthermore, delay-insensitive asynchronous paradigms provide additional advantages, including substantially reduced crosstalk between analog and digital circuits, ease of integrating multi-rate circuits, and facilitation of component reuse. Currently, companies such as ARM, Phillips, Intel, and others are incorporating asynchronous logic into some of their products using their own proprietary tools.
In this section, we convert the non-conventional combinational circuit for scalar multiplication generated by our GA into a -based design that is capable of mitigating both power- and timing-based SCAs [34].
5.1. Multi-Threshold Dual-Spacer Dual-Rail Delay-Insensitive Logic ()
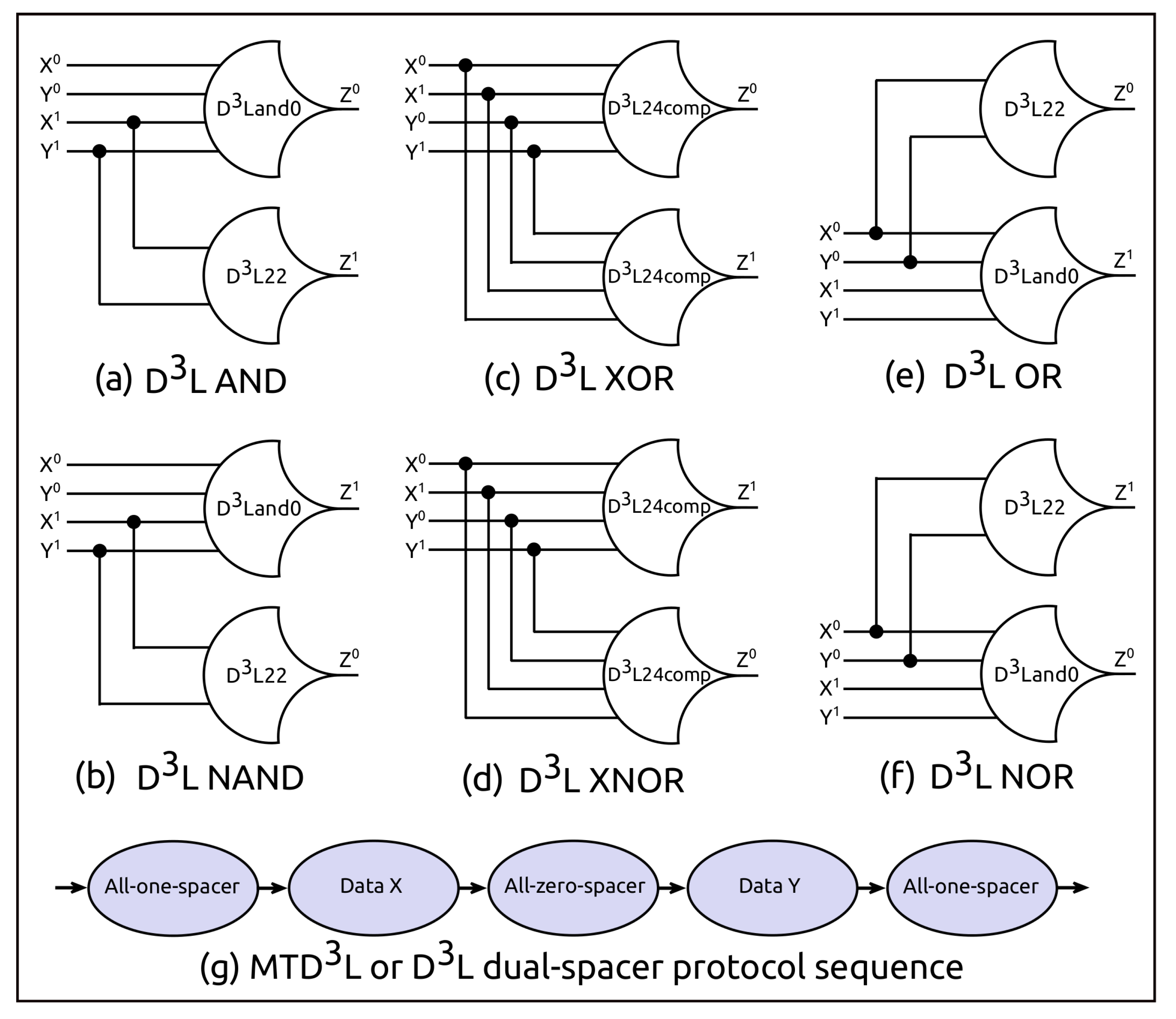
[14] is a delay-insensitive asynchronous logic family. It is developed by combining the dual-spacer dual-rail delay-insensitive logic () [13] with the multi-threshold NULL convention logic (MTNCL) [16] paradigm. The logic gates and registers of are the same as those of . However, the input-incompleteness [41] of is rectified by incorporating the sleep signal concept of MTNCL.
represents a signal with three states: DATA0, DATA1, and NULL (or spacer) state as shown in Table 4. These states are coded using two rails (or wires). Asserting a TRUE value on Rail0 represents DATA0 and asserting a TRUE value on Rail1 represents DATA1. There are two NULL (or spacer) states in representation: all-zero-spacer, and all-one-spacer. The dual-spacer protocol sequence is shown in Figure 4g. As shown in the protocol, a circuit must return to the spacer after one data cycle before starting a new data cycle. In other words, the data and spacer must alternate in a circuit. This ensures that the number of times each dual-rail signal switches is independent from the input data. The only information that the switching reveals is the number of data values processed which makes power variation significantly smaller than synchronous designs. In addition, in circuit, altering from an all-zero-spacer to all-one-spacer after every data set (as shown in Figure 4g) allows both rails to have identical switching activity regardless of the data being processed. Therefore, the difference in switching activities between these two rails does not cause much difference in power consumption. Hence, it is hard for an attacker to decode which rail is switching based on the power consumption variation between two rails.

Table 4.
and dual-rail encoding truth table [13].
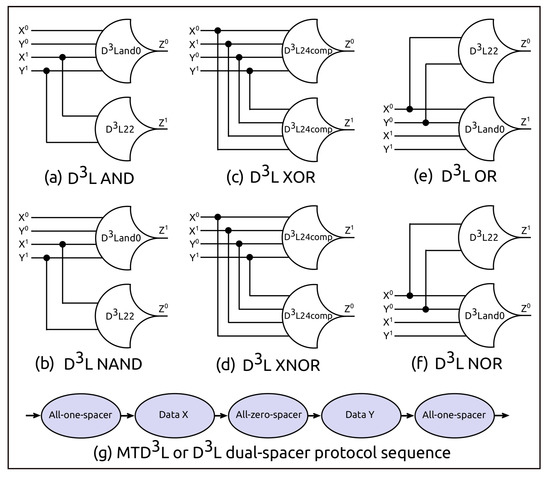
Figure 4.
gates used in designing a scalar multiplication circuit.
5.2. Gates, Registers, and Early Completion-Checking
Gates: The basic gates used in logic family are the gates of logic family. Here, we briefly describe the basic gates of logic family. logic family consists of 27 basic gates called threshold gates [42]. These 27 gates constitute the set of all functions consisting of four or fewer variables. Each gate has n inputs and a threshold value m, and the gate is denoted as . For example, a gate has A, B, and C as its inputs, and will only assert its output when two or more of its inputs have been asserted. All basic gates of standard Boolean logic can be converted into threshold gates. Figure 4a–f shows the threshold gate version of the basic Boolean logic gates.
Registers: In , each combinational block should be bracketed by input and output register stages to alternate a DATA wavefront and NULL (or spacer) wavefront to achieve delay-insensitivity. Therefore, does not require a reference clocking signal because consecutive DATA wavefronts are separated by NULL wavefronts. Each register has a single bit request and acknowledge signal, and , respectively, through which two adjacent register stages interact. The acknowledge signals from registers are combined in completion detection circuitry to produce the request signal(s) to the previous register stage. and alternate between logic 0 and logic 1. The logic 0 is interpreted as a request for NULL (i.e., rfn), and logic 1 is interpreted as request for DATA (i.e., rfd). Timing is locally handled by this delay-insensitive handshaking protocol. There are three types of registers in , viz., basic register, spacer generator register, and filter register. A basic register is used to store dual-rail data. The spacer generator register generates all-one-spacers and all-zero-spacers alternatively to embed the spacer in the input data. A filter register is essential in certain situations in which a basic register cannot handle dual-spacer protocol (e.g., the ring registers used to store data).
Early completion-checking: An asynchronous circuit is delay-insensitive if it is input-complete. Input-completeness requires that all outputs of a combinational circuit may not transition from NULL to DATA until all inputs have transitioned from NULL to DATA, and vice-versa. uses the notion of early completion-checking to provide input-completeness. Early completion utilizes the inputs of register at Stage J, along with the request to register at Stage J to generate the request signal to register (refer to Figure 5). It ensures input-completeness through the sleep mechanism such that input-incomplete logic functions can be used to design the circuit, which decreases area and power and increases speed. The combinational circuit is put to sleep only after all inputs are NULL. During sleep mode, all gates are simultaneously forced to logic 0. The circuit wakes up and performs computations when all of its input values become DATA (either DATA0 or DATA1).
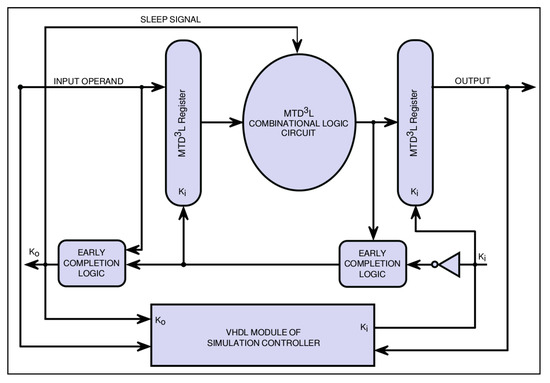
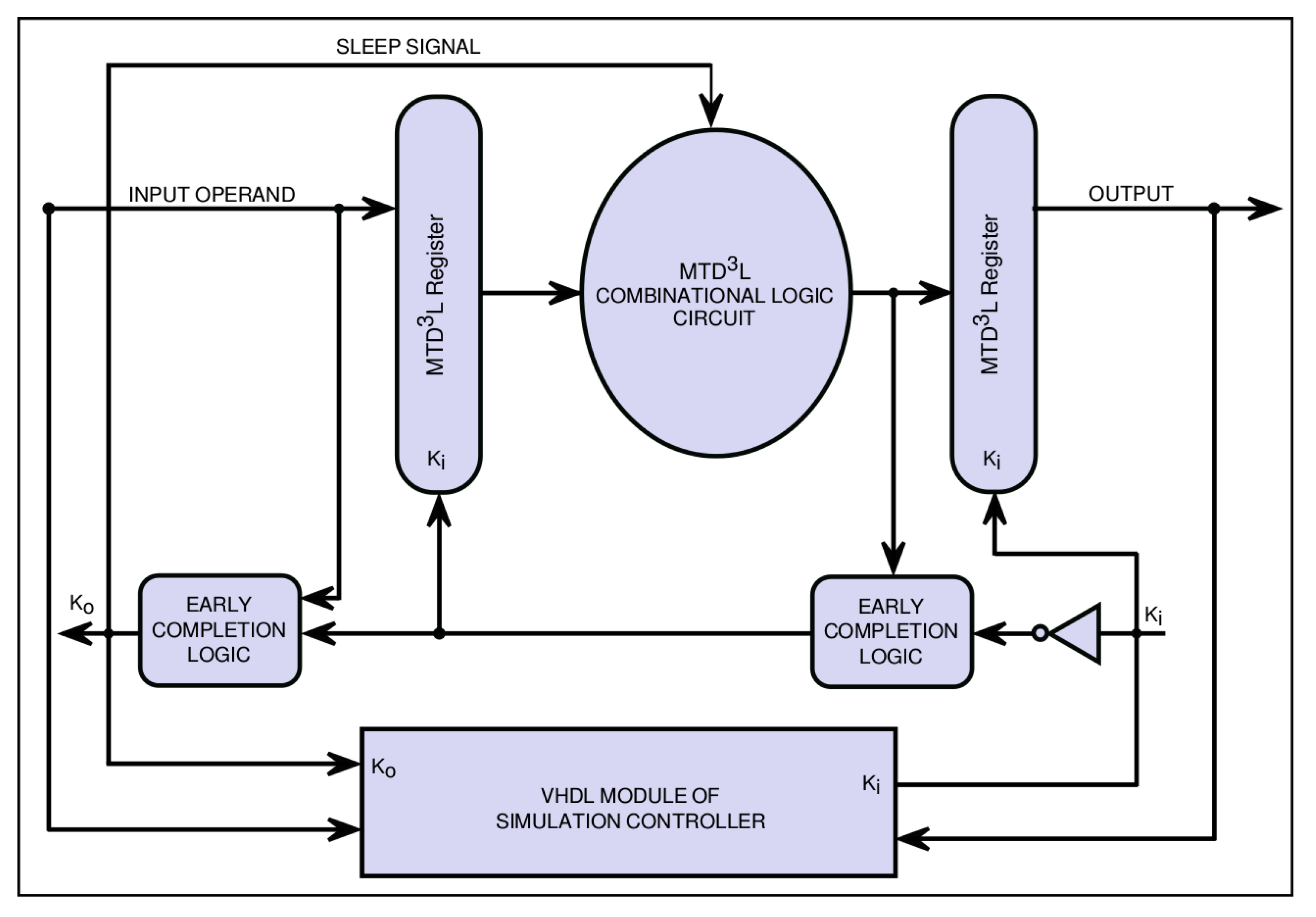
Figure 5.
High-level circuit diagram for elliptic curve scalar multiplication.
Designing delay-insensitive asynchronous circuit for scalar multiplication: To design -based delay-insensitive asynchronous circuits from the combinational circuit generated by our GA (Section 4), we employ the following steps. First, the single-rail signals are converted into dual-rail signals. Second, the Boolean logic gates are substituted by threshold gates, shown in Figure 4, to generate the combinational circuit. Third, to achieve clock-free operation, delay-insensitive registers are added on each side of a combinational circuit with local handshaking signals and early completion-checking logic. Figure 5 shows the high-level architecture of our final -based asynchronous circuit for elliptic curve scalar multiplication. The high-level architecture shows the basic signal connection setup for functional verification.
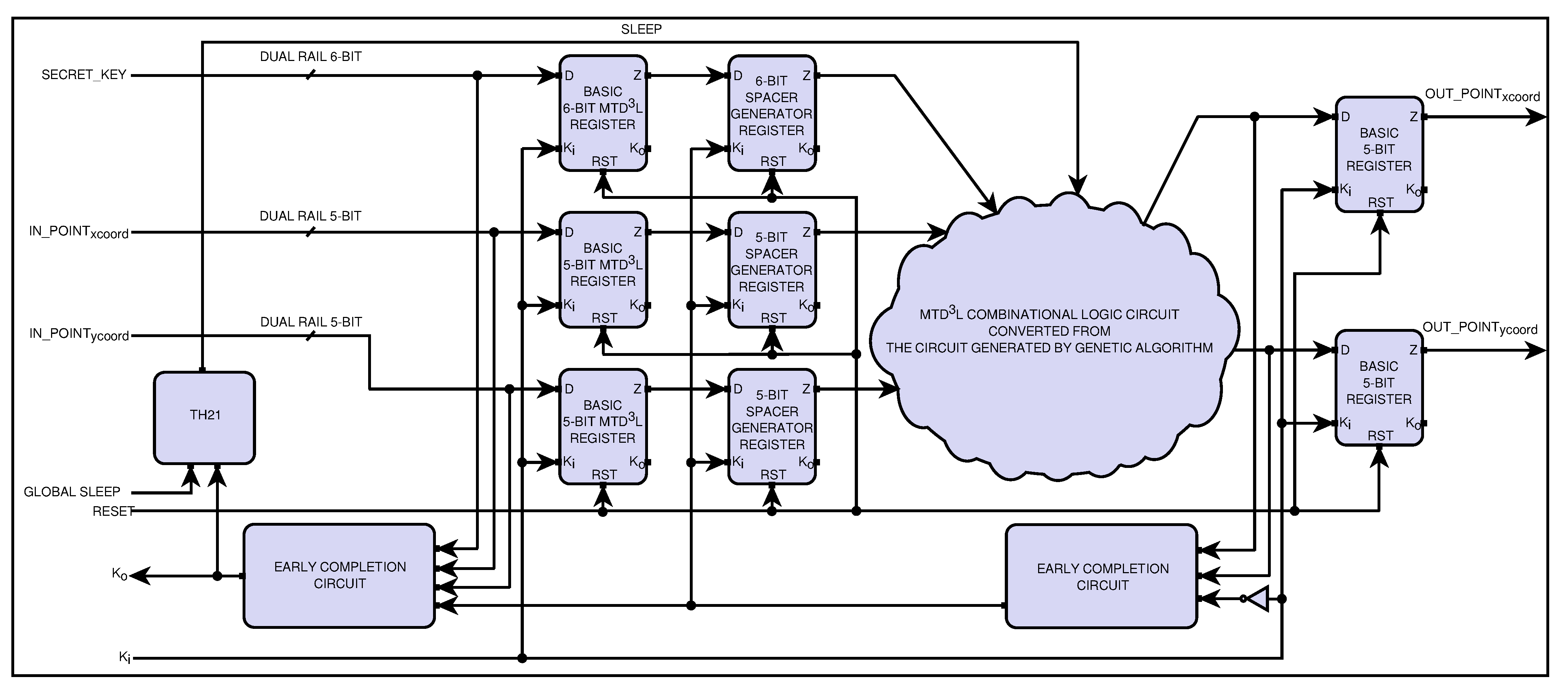
The detailed internal architecture of the -based asynchronous circuit for elliptic curve scalar multiplication is shown in Figure 6. The scalar multiplication circuit takes a secret key and a base point in the elliptic curve as input. The secret key is of 6-bit length, while the x- and y-value of the base point are of 5-bit lengths. The basic registers take the inputs from the input interface. The spacer generator registers, then, embeds the spacer (all-one-spacer and all-zero-spacer, alternatively) into the input data. Next, the output of the spacer generator register is fed to the combinational circuit. Finally, the output of the combinational circuit is latched to the basic register.
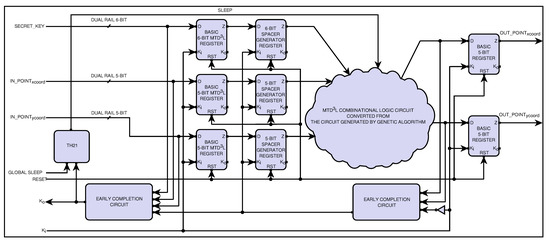
Figure 6.
The delay-insensitive asynchronous circuit of elliptic curve scalar multiplication.
6. Design of Secure and Dependable ECC Core
In this section, we propose a novel ECC processor architecture that simultaneously integrates security and dependability in the design. We first provide an overview of the proposed ECC processor. We then explain the dependability and security features assimilated in our proposed ECC processor.
6.1. Architecture Overview
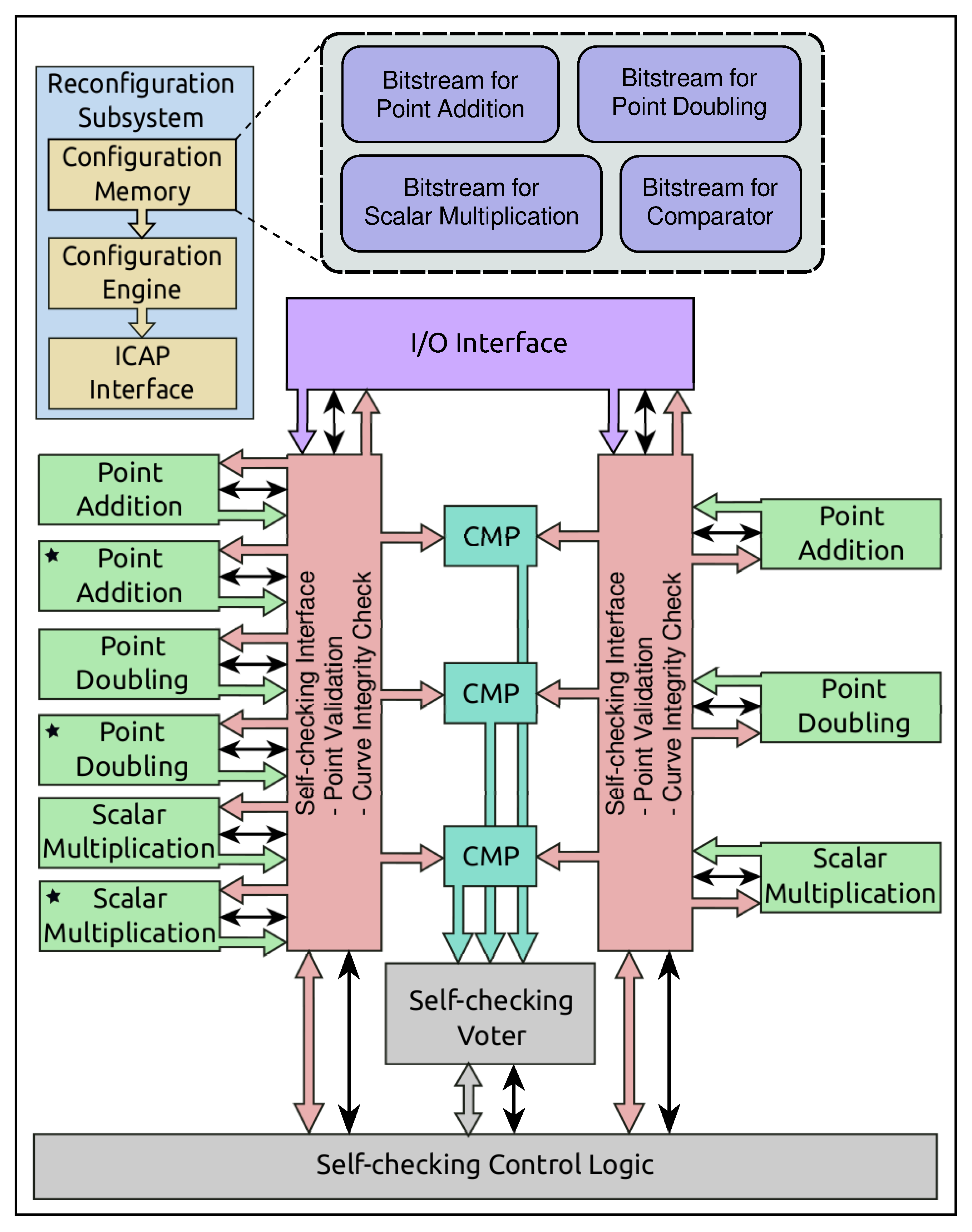
Figure 7 shows the internal architecture of our proposed secure and dependable ECC processor. It is a clock-free delay-insensitive asynchronous circuit. The basic components of the ECC processor are scalar multiplication, point-addition, and point-doubling modules. These modules are first generated by our GA, and then are transformed into delay-insensitive circuits (refer Section 4 and Section 5). A Berger code based totally on a self-checking circuit design paradigm [43] is leveraged to design a self-checking voter, self-checking control logic, and self-checking interface because these circuits are capable of detecting any unidirectional error within themselves. The rest of the other components operate in N-modular redundancy to provide fault tolerance to the ECC processor.
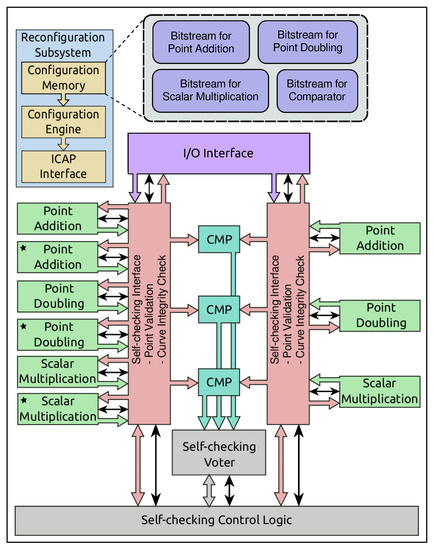
Figure 7.
Internal architecture of a secure and dependable ECC processor.
The ECC processor takes input from the I/O interface. Inputs could be point(s) in an elliptic curve, elliptic curve parameters, and/or a scalar value. A self-checking interface fetches the input and performs point-validation and curve integrity-checking to scrutinize any faulty input. Then, it supplies the input to point addition, point-doubling, and/or scalar multiplication module. There are three copies of each of point addition, point-doubling, and scalar multiplication modules inside ECC processor. Two copies of a module operate in dual modular redundancy (DMR) to detect operational error while the third copy is a spare module (indicated by * in Figure 7) and it remains idle (in sleep state) during error-free operation of the modules in DMR. The spare module is activated by the self-checking control unit only when an operational error is detected. The outputs of DMR modules are compared by comparators (CMP). These comparators operate in triple-modular redundancy to provide fault tolerance. The self-checking voter takes the outputs of comparators and generates the voting result. The voting result signifies whether there is any fault in CMP and/or current operating modules in DMR.
When modules in DMR detect operational error(s), then both of these modules perform recomputations to rectify the soft-errors due to transient faults. The number of recomputations depends on the real-time deadline and propagation delay of the circuit. If the soft-error persist even after a few recomputations, then the self-checking control unit localizes the faulty module(s). To do so, the self-checking control unit activates the spare module. The spare module performs computations on the input data for which there was an error. The self-checking control unit, then, compares the output of the spare module with the previously generated outputs of the modules in DMR to localize the faulty module(s). After the detection of the faulty module(s), self-checking control unit signals reconfiguration subsystem to dynamically reconfigure the faulty module with a new bitstream. During the reconfiguration process, the spare module handles the job of the faulty module. We refer to this fault-tolerant mechanism as fault tolerance using self-reconfiguration in the DMR system (FT-SR-DMR) [44].
6.2. Dependability
The first fault-tolerant (FT) feature of our proposed system is DMR [23]. DMR is an FT technique that executes critical computations on two modules (one of the module is redundant) and detects an error at the end of computation if there is a mismatch between the two modules’ output. DMR can be generalized to N modular redundancy when the computation is executed on N modules. However, to reduce the cost and area overhead of the design, often DMR is used, and thus we leverage DMR in our ECC processor design. This reduced cost and area overhead come at the cost of inability of the DMR-based FT systems to identify or localize the faulty module among the two operating modules in case of an error. To resolve this identification or localization issue, our proposed ECC processor leverages spare modules (one for point addition, one for point-doubling, and one for scalar multiplication), which are marked by * in Figure 7. These spare modules provide dynamic redundancy and are in unpowered or standby mode, that is, they are activated only once a fault is detected to localize the faulty module(s). This standby dynamic redundancy saves power and provides energy efficiency to the ECC processor as the modules are not powered during the normal operation.
The second FT feature of our ECC processor is the inclusion of totally self-checking (TSC) circuits [44,45]. In TSC circuits, the occurrence of faults can be detected by noticing the circuit output. The output words of a TSC circuit belong to a specific code (Berger code in our case). A TSC circuit also includes a checker to observe the output of the functional circuit to detect any fault(s) in the circuit. The reliability of TSC circuits depends on their ability to function correctly even in the occurrence of internal fault(s).
The final FT feature integrated by our proposed ECC processor is partial reconfiguration (PR) of programmable logic fabric (PLF) of an FPGA. Our proposed ECC processor is able to heal the faulty module(s) by using the PR technology, which modifies a subset of programmable logic by loading a partial bitstream [44]. We note that this PR capability is available in modern programmable hardware devices. For instance, Xilinx FPGAs have a dedicated internal configuration access port (ICAP) that provides a direct interface to the configuration memory. We have utilized LogiCORE IP (Intellectual Property) XPS (Xilinx Platform Studio) HWICAP (Hardware ICAP) [46] to perform dynamic PR.
6.3. Security
The main components of the ECC processor are point addition, point-doubling, and scalar multiplication. The security of these crypto-components of the proposed ECC processor is based on the following design innovations.
The first security-relevant design feature of the proposed ECC processor is the use of combinational logic circuits as opposed to sequential logic circuits. The outputs of combinational logic circuits depend only on the present input and do not require any memory to perform internal operations. This removes one attack surface, that is, memory (e.g., registers), which can be exploited by an attacker to analyze the circuit under operation to mount attacks on sequential circuits. Additionally, contrary to sequential circuits, combinational circuits do not use clocks, and thus do not have disparate stages of operation. Hence, all of the components of the combinational circuit are functioning for all possible inputs, and thus contribute equally to the propagation delay and power consumption of the whole circuit. This makes simple timing and power analysis attacks typically ineffective against combinational circuits.
The second security-relevant design feature is the use of a genetic algorithm with multi-objective fitness function to produce standard Boolean logic-based combinational circuits for point addition, point-doubling, and scalar multiplication. The use of GA to design combinational logic circuits provides four main benefits. First, the combinational logic circuits designed using GA are typically highly non-conventional, which enhances the security of the resulting cryptosystem. Second, it will be extremely difficult for an attacker to design the exact same circuit that was evolved using a GA, which makes power template attacks difficult to carry out [15]. Third, a GA engenders multiple circuits which are functionally the same. These functionally equivalent circuits can be dynamically switched to bolster the security of the cryptosystem. Fourth, large combinational logic circutis, which are infeasible to design manually, can be designed using a GA.
The third security-related design feature of the proposed ECC processor is the usage of circuits. The combinational circuit modules of the cryptosystem (i.e., point addition, point-doubling, and scalar multiplication for the ECC processor) are first generated by a GA and, then these circuits are transformed into delay-insensitive circuits (refer Section 4 and Section 5). eliminates the need for clock signals and is able to perform operations asynchronously by implementing a delay-insensitive hand-shake protocol. This helps enable masking of start times and end times of operations of different sub-blocks or instruction processing, and thus provide nearly constant power traces and energy consumption, which makes it difficult for an attacker to launch timing and power attacks. Finally, circuits show robust circuit operation under process, voltage, and temperature (PVT) variations, and have low noise/electromagnetic emissions, which enhance the robustness of circuits against SCAs [13,14,16].
7. Security Analysis of the Proposed Elliptic Curve Cryptosystem
In this section, we analyze the security of the proposed elliptic curve cryptosystem against various types of attacks mentioned in our threat model (Section 2).
Power, Timing, and Electromagnetics Attacks: Delay-insensitive circuits have no clock tree, so their noise and electromagnetic interference spectrum are significantly flatter across the entire frequency domain. Moreover, dual-spacer protocol of not only decouples data from switching activity at the signal-level, but also balances the switching activity between the rails of each dual-rail signal, making it much more difficult for an attacker to correlate data with power consumption. Additionally, mitigates timing attacks by inserting delay elements to break the timing-data correlation that exists in delay-insensitive asynchronous designs. The side-channel resistance of dual-rail circuit design paradigms like is discussed in detail in [13,14,16,47].
Fault-Injection Attacks: The architecture of our ECC processor shown in Figure 7 is capable of detecting and correcting multiple transient faults and one permanent fault (see Section 6). Therefore, if an attacker tries to inject or induce soft-errors, the device can detect and correct the error thus preventing the device from behaving abnormally. In addition, the ECC processor designed using logic has robust circuit operation under process, voltage, and temperature variations. These delay-insensitive circuits are highly tolerant to power supply variations. Thus, the supply voltages can be dramatically reduced to meet desired performance while decreasing power consumption. Another significant advantage of is the tolerance of vast temperature differences, making these circuits well-suited for operation in harsh environments, like outer space. Hence, our proposed asynchronous delay-insensitive ECC processor shows robustness against simple fault attacks based on power supply variation and temperature manipulation [14].
Hardware Trojans: Our ECC processor architecture implemented with the approach also enables easier detection of the hardware Trojan. Since the approach tries to flatten the delay and power regardless of the circuit switching activities, if the adversary put Trojan circuit elements into the ECC processor, the circuit paths with Trojan circuit elements have a high possibility of being outliers. It means that the hardware Trojan will be easily identified by using a simple statistical delay or power analysis.
8. Results and Analysis
Experimental Setup: We have implemented our ECC hardware prototype in Xilinx KC705 [48]. The sub-component hardware modules (e.g., evolved combinational circuits, controllers) have been implemented in VHDL, and functionally, verification is done using Xilinx ISE ISIM Simulator [49]. The execution time and power consumption of the evolved circuits and the ECC processor are obtained using Xilinx ISE 14.7.
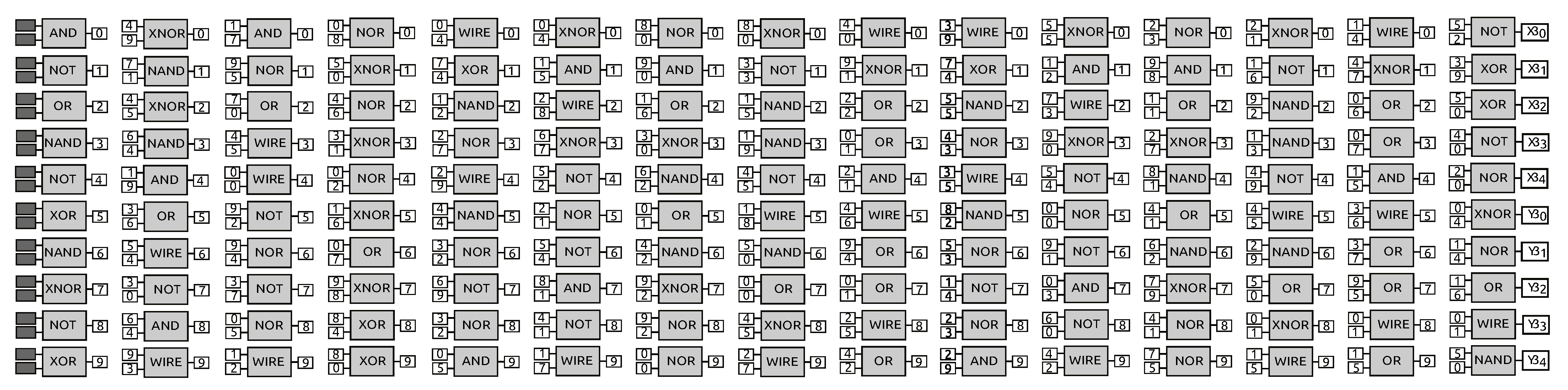
Functional Verification of Evolved Circuit Generated by GA:Figure 8 shows the combinational circuit evolved using our GA. This circuit performs elliptic curve scalar multiplication of a 6-bit scalar value with any base points enclosed in rectangle A in Figure 2. As shown in Figure 8, the output of each gate is designated by a number from 0 to 9. These outputs are connected to the inputs of any gates in immediate next level. The input ports of the gates on the leftmost side act as input interface and are connected to external inputs. The inputs are two 5-bit (x,y) coordinates of a base point in an elliptic curve and a 6-bit secret key. The output of the circuit is taken from the rightmost level. The output is a 5-bit (x,y) coordinate of a point in the elliptic curve, which is the product of the secret key and the base point.

Figure 8.
Evolved combinational circuit for elliptic curve scalar multiplication.
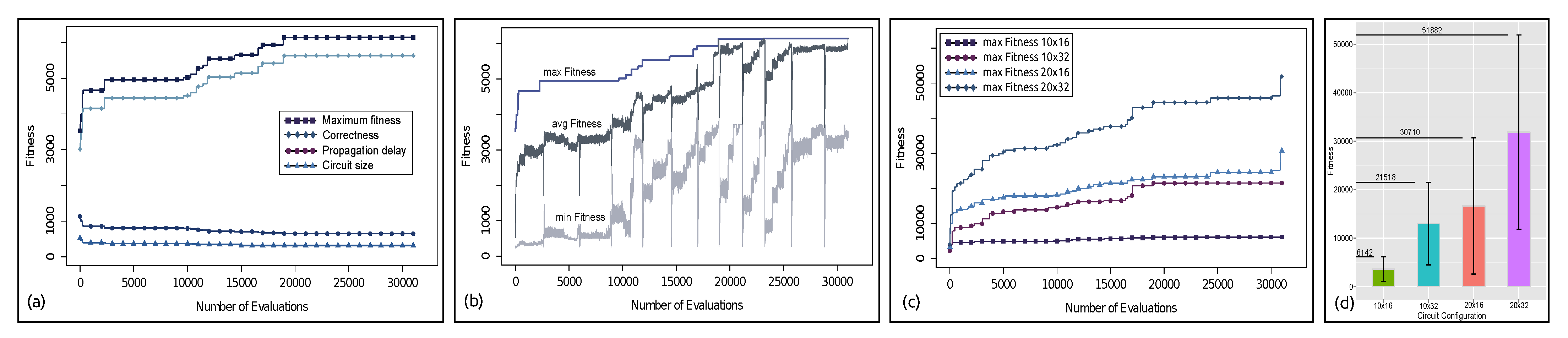
Figure 9 depicts the result of our genetic algorithm execution. As explained in Section 4, the multi-objective fitness function of our GA has three main goals: (i) maximizing the correctness in input/output behavior, (ii) minimizing the circuit delay (i.e., propagation delay), and (III) minimizing the circuit size. As shown in Figure 9a, the fitness value continuously increases as the number of evaluations (i.e., generations) increases. Figure 9a also shows that the correctness value (also fitness value) increases with the number of evaluations, reaching the maximum value at 23,119-th iteration of the evaluations. The propagation delay and circuit size values in the fitness function decrease with the number of evaluations. Figure 9b depicts the maximum (max), average (avg), and minimum (min) fitness values as the number of evaluations increases. Results indicate that the maximum fitness value increases steadily with the number of evaluations; however, the average and minimum fitness value curves can be divided into a number of segments separated by abrupt high-to-low-to-high transitions. These transitions are due to the multiple GA restarts, a property of the CHC GA [40].
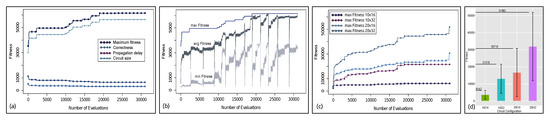
Figure 9.
(a) Correctness, propagation delay, circuit size, and maximum fitness value of evolved combinational circuit for elliptic curve scalar multiplication. (b) The maximum, average, and minimum fitness value achieved by our genetic algorithm for circuit configuration. (c) The maximum fitness achieved by our GA for four circuit configurations. (d) The fitness values attained by our GA for four circuit configurations.
We used our GA to generate four different combinational circuits which differ in the number of base points they support. circuit can support points enclosed in rectangle A in Figure 2 as base point for scalar multiplication. Similarly, , , and circuits can perform correct scalar multiplication of any 6-bit secret key with any base point enclosed in rectangle B, C, and D in Figure 2, respectively. Figure 9c shows the curve for maximum fitness with respect to the number of evaluations for four different circuit configurations. The converging nature of the maximum fitness curves confirms that a larger combinational circuit which can perform scalar multiplication of a larger secret key over a large prime field can be generated by our GA. Finally, Figure 9d depicts the maximum, average, and minimum fitness values obtained by our GA for four circuit configurations. The bar graphs represent the average fitness value of the GA and the lower and upper ends of the error bars represent the minimum and maximum fitness values. The fitness values are averaged over 30 runs.
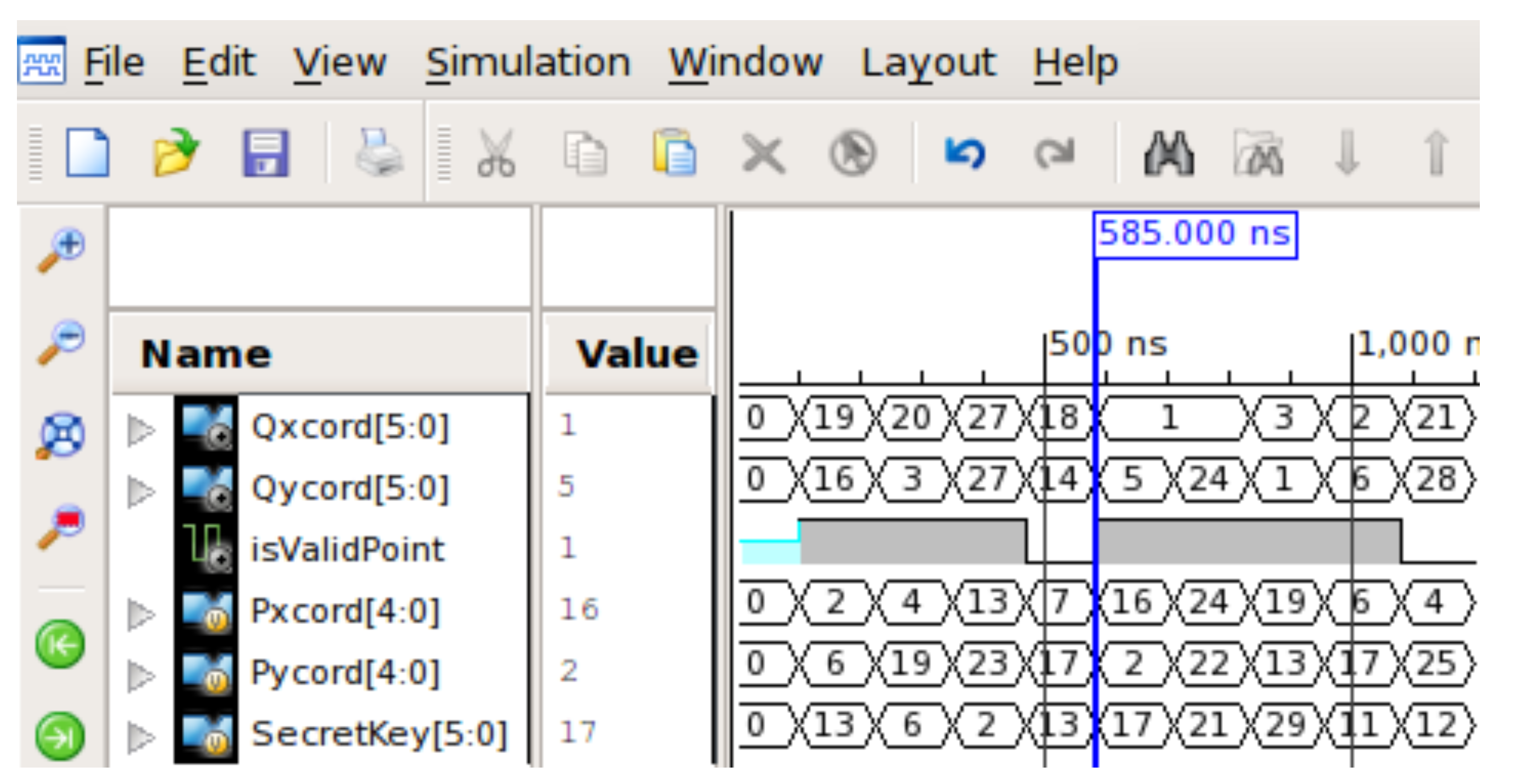
The evolved combinational circuit for elliptic curve scalar multiplication shown in Figure 8 is implemented in VHDL hardware description language and simulated with ISIM simulator by Xilinx. Figure 10 shows the simulation waveform for 9 random sample inputs among which two of the samples are illegal. The evolved circuit can correctly perform the elliptic curve scalar multiplication between a 6-bit secret key and a valid base point in the elliptic curve. If the base point is invalid, then a wrapper combinational circuit built around the evolved combinational circuit flags the output as invalid. This is marked by vertical line at simulation time ns in Figure 10.
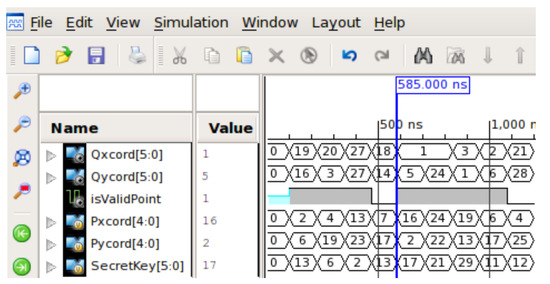
Figure 10.
ISIM simulator waveform for functional verification of evolved combinational circuit for elliptic curve scalar multiplication.
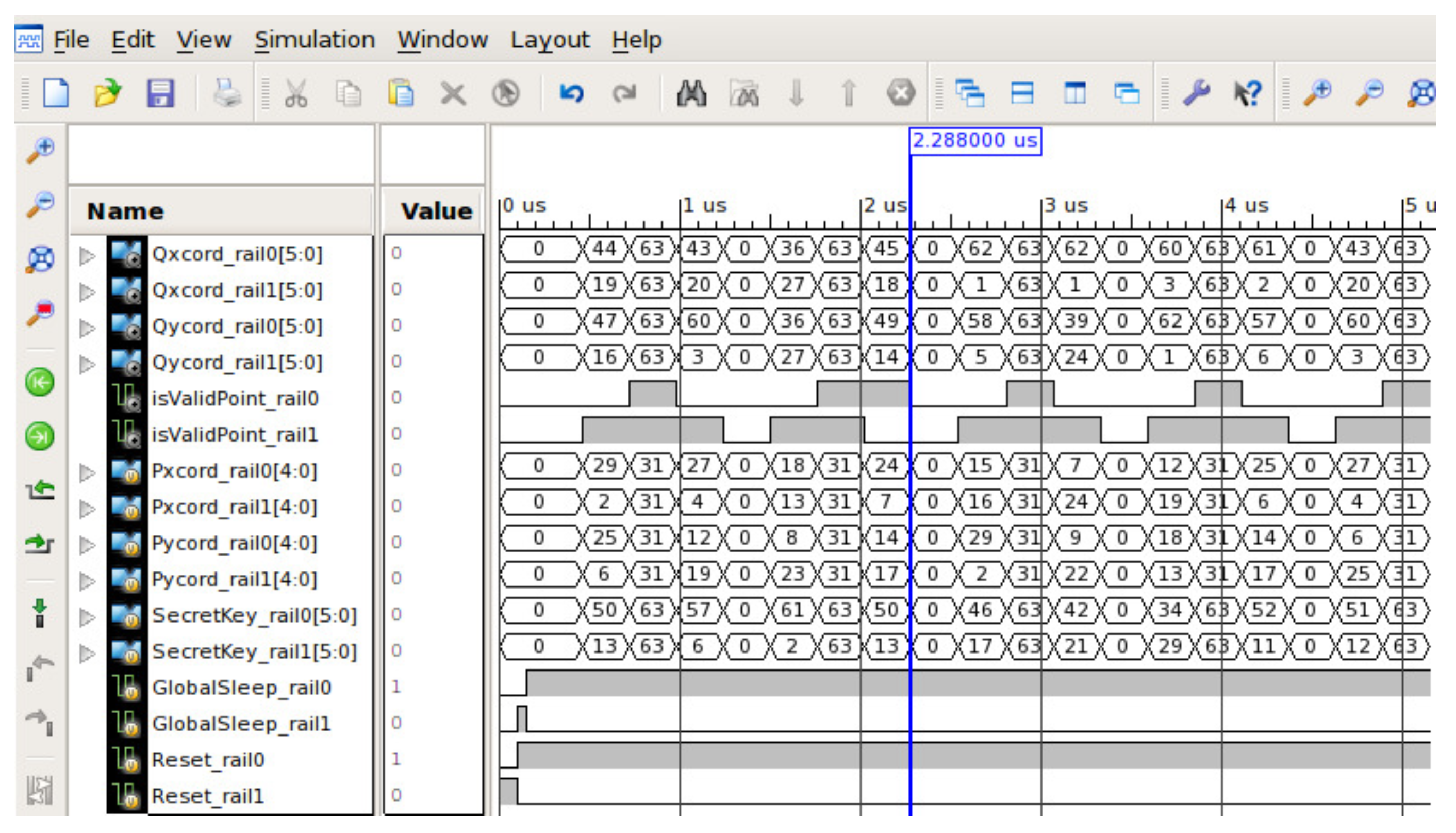
Functional Verification of Asynchronous Circuit:Figure 5 shows the high-level circuit diagram of circuit for elliptic curve scalar multiplication. The detailed internal architecture of elliptic curve scalar multiplication circuit is shown in Figure 6. This circuit is implemented in VHDL and simulated with ISIM simulator. VHDL package is used to define the threshold gates and dual-rail signals. The simulation controller shown in Figure 5 generates the random binary input samples for testing the scalar multiplication circuit. The simulation controller has a single-rail to dual-rail converter module that converts random binary samples into dual-rail signals. The output acknowledgement signal, , from the scalar multiplication circuit controls the internal modules of the simulation controller.
Figure 11 shows the waveform of circuit performing scalar multiplication. In dual-rail logic, the 6-bit secret-key is represented by 12-bit dual-rail signals, and the 5-bit base point value is represented by 10-bit dual-rail signals. In addition, two samples are separated by an all-one-spacer or all-zero-spacer. The alteration between various input/output DATA and two spacers are clearly shown in simulation (refer Figure 11). To represent a single-rail signal (say Pxcord[4:0]) in Figure 10) in dual-rail format, we created two signals (Pxcord_rail0[4:0] and Pxcord_rail1[4:0] in Figure 11). The rail1 signal holds the exact value of a single-rail signal, and the rail0 signal holds the one’s complement of the single-rail signal. If Pxcord[4:0] is 2 (or ), then Pxcord_rail1 is 2 (or ) and Pxcord_rail0 is 29 (or ). Therefore, if we monitor the value of rail1 signals in Figure 11, then we can compare them with the corresponding values in Figure 10 to verify the functional correctness of our circuit. The comparison of single-rail and dual-rail outputs using the same input values verifies that is functionally correct. If we compare Figure 10 and Figure 11 using the same input values, then it is apparent that is functionally correct.
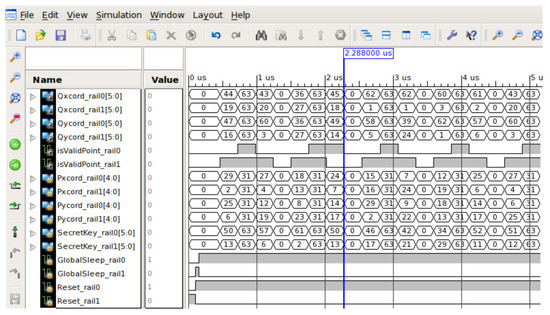
Figure 11.
ISIM simulator waveform for functional verification of asynchronous circuit for elliptic curve scalar multiplication.
Propagation Delay, Circuit Size, and Energy Consumption Profile: Although circuits provide enhanced resilience against SCAs (Section 7), they incur propagation delay, circuit size, and energy overheads as compared to the baseline circuits (i.e., same combinational circuits without using ). Consequently, we quantify propagation delay, circuit size, and energy consumption of the baseline circuits (here evolved combinational circuits for point addition, point-doubling, and scalar multiplication) and circuits. Table 5 shows the values of propagation delay, circuit size, and energy consumption profile of the evolved combinational circuits for elliptic curve point addition (ECPA), point-doubling (ECPD), and scalar multiplication (ECSM). The size and propagation delay of the evolved circuit are computed using the concept of gate equivalent [39], which is a basic unit of measure for digital circuit complexity. The circuit size value in Table 5 shows the factor by which the circuit is bigger than a NOT gate. For example, ECPA has circuit size of 237, which means it requires more circuit area than a typical NOT gate. Results in Table 5 reveal that we can employ a genetic algorithm to generate combinational circuits for an elliptic curve arithmetic. The interesting observation is that all the three circuits (for ECPA, ECPD, and ECSM) have circuit configuration, which means each of the three circuits is made up of 160-logic gates. These three circuits have comparable propagation delay and energy consumption. This is essential to thwart simple power and timing analysis attack which is based on the timing differences in different point operation executions.

Table 5.
The propagation delay, circuit size, and energy consumption profile of the evolved circuit.
Table 6 shows the delay, size, and energy data for the delay-insensitive clock-free circuits which are created by transforming the combinational circuits generated by our genetic algorithm. circuit requires input and output registrations, early completion detection circuitry, interaction of handshaking signals between adjacent register stages, and dual-rail representation of a single bit of data for correct functional operation. This introduces significant overhead in terms of propagation delay, circuit size, and energy consumption. Obviously, circuits have delay, size, and energy overheads as compared to the baseline circuits.

Table 6.
The propagation delay, circuit size, and energy consumption profile of circuit using design approach.
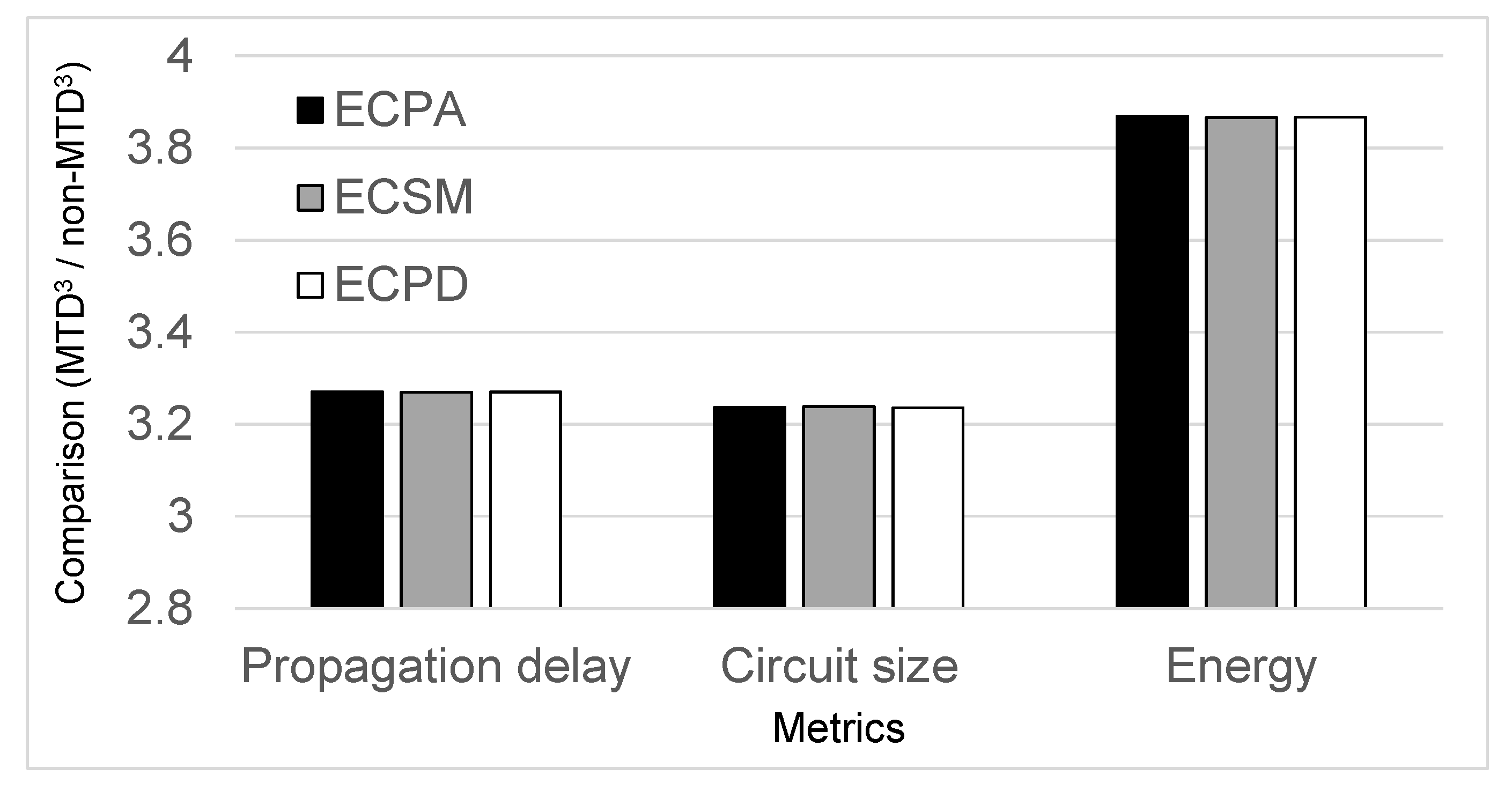
Figure 12 summarizes overheads of the circuit implementation using design approach over the same evolved circuit without circuits. Results indicate that design leads to 3.27×, 3.24×, and 3.87× higher propagation delay, circuit size, and energy, respectively, as compare to the non- design. Thus, it is evident that -based circuits have more overhead with respect to pure combinational circuits that do not use . However, these costs come with the advantages of nearly constant power consumption during operation, low noise and electromagnetic emanations, which provide enhanced resilience against SCAs. Nevertheless, the overhead of our secure design is much lesser than some prior secure designs [50], that is, 3× for our secure design versus 6× for some prior secure designs [50]. We note that designing circuits that incur minimum propagation delay, circuit size, and energy overheads as compared to the baseline circuits is a challenging endeavor. As process technology advances, we believe the overheads of will be reduced due to the improved transistor device performance and energy efficiency. An efficient trade-off between the security and overhead (e.g., in terms of delay, area, and power) is an important research topic, though we leave thorough investigations on this trade-off as our future work.
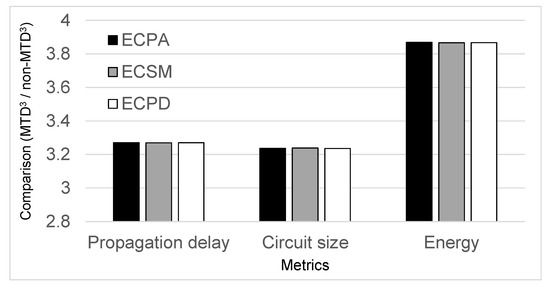
Figure 12.
overhead comparison in terms of propagation delay, circuit size, and energy.
9. Conclusions
In this article, we propose the design of a secure and dependable elliptic curve cryptosystem processor. We utilize genetic algorithm to evolve non-conventional combinational circuits for point operations in elliptic curves. We transform the evolved non-conventional combinational circuits to multi-threshold dual-spacer dual-rail delay-insensitive logic () in order to mitigate timing-, power-, and fault-based SCAs. We validate our design methodology by designing and functionally verifying a combinational circuit that can perform scalar multiplication of 6-bit secret-key with 5-bit base point. The GA reliably designs combinational circuits for scalar multiplication over the elliptic curve prime field. Our methodology can be effectively scaled towards designing full sized 160-bit scalar multiplication circuits. Finally, we proposed the fault-tolerant architecture of ECC processor which can tolerate multiple transient faults and one permanent fault. Results reveal that our design methodology is resilient to power- and timing-based SCAs, and incurs around overhead in terms of area and propagation delay as compared to standard evolved combinational circuits.
As our future work, we plan to further devise techniques to reduce the propagation delay, circuit size, and energy overhead from implementations of the ECC processor. Furthermore, we plan to implement our ECC processor as ASIC with standard library cells.
Author Contributions
Conceptualization, B.P. and A.M.; methodology, B.P.; software, B.P.; validation, B.P.; formal analysis, B.P.; investigation, A.M.; resources, A.M.; data curation, B.P.; writing—original draft preparation, B.P. and A.M.; writing—review and editing, B.P., A.M., J.K. and M.A.K.; visualization, B.P.; supervision, A.M.; project administration, A.M.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request due to proprietary restrictions. The data presented in this study can be made available on request from the corresponding author. The data are not publicly available due to proprietary restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lauter, K. The Advantages of Elliptic Curve Cryptography for Wireless Security. IEEE Wirel. Commun. 2004, 11, 62–67. [Google Scholar] [CrossRef]
- Maletsky, K. RSA vs. ECC Comparison for Embedded Systems; Technical Report; Security ICs, Atmel: San Jose, CA, USA, 2015. [Google Scholar]
- Skorobogatov, S. Side-Channel Attacks: New Directions and Horizons. 2011. Available online: https://www.cl.cam.ac.uk/~sps32/ECRYPT2011_2.pdf (accessed on 5 September 2021).
- Liao, K.; Cui, X.; Liao, N.; Wang, T.; Yu, D.; Cui, X. High-Performance Noninvasive Side-Channel Attack Resistant ECC Coprocessor for GF(2m). IEEE Trans. Ind. Electron. 2016, 64, 727–738. [Google Scholar] [CrossRef]
- Lee, J.W.; Chung, S.C.; Chang, H.C.; Lee, C.Y. Efficient Power-Analysis-Resistant Dual-Field Elliptic Curve Cryptographic Processor Using Heterogeneous Dual-Processing-Element Architecture. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2014, 22, 49–61. [Google Scholar] [CrossRef]
- Zheng, G.; Dawu, G.; Kan, Y.; Junrong, L.; Yuming, H. A Novel Method for Power Analysis Based on Combinational Logic in Block Cipher Circuit. Chin. J. Electron. 2014, 23, 151–156. [Google Scholar]
- Yang, B.; Wu, K.; Karri, R. Scan based side channel attack on dedicated hardware implementations of Data Encryption Standard. In Proceedings of the 2004 International Conferce on Test, Charlotte, NC, USA, 26–28 October 2004; pp. 339–344. [Google Scholar]
- Alasad, Q.; Yuan, J.; Lin, J. Resilient AES Against Side-Channel Attack Using All-Spin Logic. In Proceedings of the 2018 on Great Lakes Symposium on VLSI, Chicago, IL, USA, 23–25 May 2018; pp. 57–62. [Google Scholar] [CrossRef]
- Alasad, Q.; Lin, J.; Yuan, J.S.; Fan, D.; Awad, A. Resilient and Secure Hardware Devices Using ASL. ACM J. Emerg. Technol. Comput. Syst. 2021, 17, 1–26. [Google Scholar] [CrossRef]
- Khadem, B.; Rajavzadeh, S. Construction of Side Channel Attack Resistant S-Boxes Using Genetic Algorithms Based on Coordinate Functions. arXiv 2021, arXiv:2102.09799. [Google Scholar]
- Picek, S.; Ege, B.; Batina, L.; Jakobovic, D.; Chmielewski, L.; Golub, M. On Using Genetic Algorithms for Intrinsic Side-Channel Resistance: The Case of AES S-Box. In Proceedings of the First Workshop on Cryptography and Security in Computing Systems, Vienna, Austria, 20 January 2014; pp. 13–18. [Google Scholar]
- Liu, H. The Switching Glitch Power Leakage Model. J. Softw. 2011, 6, 1787–1794. [Google Scholar] [CrossRef][Green Version]
- Cilio, W.; Linder, M.; Porter, C.; Di, J.; Thompson, D.R.; Smith, S.C. Mitigating Power- and Timing-based Side-Channel Attacks Using Dual-Spacer Dual-Rail Delay-Insensitive Asynchronous Logic. Microelectron. J. 2013, 44, 258–269. [Google Scholar] [CrossRef]
- Linder, M.; Di, J.; Smith, S.C. Multi-Threshold Dual-Spacer Dual-Rail Delay-Insensitive Logic (MTD3L): A Low Overhead Secure IC Design Methodology. J. Low Power Electron. Appl. 2013, 3, 300–336. [Google Scholar] [CrossRef]
- Poudel, B.; Louis, S.J.; Munir, A. Evolving Side-Channel Resistant Reconfigurable Hardware for Elliptic Curve Cryptography. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017. [Google Scholar]
- Zhou, L.; Parameswaran, R.; Parsan, F.A.; Smith, S.C.; Di, J. Multi-Threshold NULL Convention Logic (MTNCL): An Ultra-Low Power Asynchronous Circuit Design Methodology. J. Low Power Electron. Appl. 2015, 5, 81–100. [Google Scholar] [CrossRef]
- Joye, M.; Tunstall, M. (Eds.) Fault Analysis in Cryptography; Springer: Berlin, Germany, 2012. [Google Scholar]
- Paar, C.; Pelzl, J. Understanding Cryptography; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ouladj, M.; Guilley, S. Side-Channel Analysis of Embedded Systems: An Efficient Algorithmic Approach; Springer: Berlin, Germany, 2021. [Google Scholar]
- Goubin, L. A Refined Power-Analysis Attack on Elliptic Curve Cryptosystems. In Public Key Cryptography—PKC 2003; Springer: Berlin/Heidelberg, Germany, 2002; pp. 199–211. [Google Scholar]
- Akishita, T.; Takagi, T. Zero-Value Point Attacks on Elliptic Curve Cryptosystem. In Information Security: 6th International Conference, ISC 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 218–233. [Google Scholar]
- Batina, L.; Djukanovic, M.; Heuser, A.; Picek, S. It Started with Templates: The Future of Profiling in Side-Channel Analysis. In Security of Ubiquitous Computing Systems; Avoine, G., Hernandez-Castro, J., Eds.; Springer: Cham, Switzerland, 2021; pp. 133–145. [Google Scholar]
- Koren, I.; Krishna, C.M. Fault-Tolerant Systems; Morgan Kaufmann Publishers: San Mateo, CA, USA, 2007. [Google Scholar]
- Fan, J.; Guo, X.; Mulder, E.D.; Schaumont, P.; Preneel, B.; Verbauwhede, I. State-of-the-art of secure ECC implementations: A survey on known side-channel attacks and countermeasures. In Proceedings of the 2010 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Anaheim, CA, USA, 13–14 June 2010; pp. 78–87. [Google Scholar]
- Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Nannipieri, P.; Fanucci, L.; Saponara, S. Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications. Energies 2021, 14, 4676. [Google Scholar] [CrossRef]
- Joye, M.; Yen, S.M. The Montgomery Powering Ladder. In Cryptographic Hardware and Embedded Systems—CHES 2002; Kaliski, B.S., Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 291–302. [Google Scholar]
- Barbosa, M.; Page, D. On the Automatic Construction of Indistinguishable Operations. In Cryptography and Coding; Smart, N.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 233–247. [Google Scholar]
- Liardet, P.Y.; Smart, N.P. Preventing SPA/DPA in ECC Systems Using the Jacobi Form. In Cryptographic Hardware and Embedded Systems—CHES 2001; Koç, Ç.K., Naccache, D., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 391–401. [Google Scholar]
- Akhter, F. A Novel Elliptic Curve Cryptography Scheme Using Random Sequence. In Proceedings of the IEEE International Conference on Computer and Information Engineering (ICCIE), Rajshahi, Bangladesh, 26–27 November 2015; pp. 46–49. [Google Scholar]
- Dupuy, W.; Kunz-Jacques, S. Resistance of Randomized Projective Coordinates against Power Analysis. In Proceedings of the CHES’05 7th International Conference on Cryptographic Hardware and Embedded Systems, Edinburgh, UK, 29 August–1 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–14. [Google Scholar]
- Joye, M.; Tymen, C. Protections Against Differential Analysis for Elliptic Curve Cryptography. In Proceedings of the Third International Workshop on Cryptographic Hardware and Embedded Systems CHES 2001, Paris, France, 14–16 May 2001; pp. 377–390. [Google Scholar]
- Dominguez-Oviedo, A.; Hasan, M.A. Algorithm-Level Error Detection for Montgomery Ladder-Based ECSM. J. Cryptogr. Eng. 2011, 57–69. [Google Scholar] [CrossRef]
- Liu, R.; Zeng, S.Y.; Ding, L.; Kang, L.; Li, H.; Chen, Y.; Liu, Y.; Han, Y. An Efficient Multi-Objective Evolutionary Algorithm for Combinational Circuit Design. In Proceedings of the First NASA/ESA Conference on Adaptive Hardware and Systems (AHS’06), Istanbul, Turkey, 15–18 June 2006; pp. 215–221. [Google Scholar]
- Soliman, A.T.; Abbas, H.M. Combinational circuit design using evolutionary algorithms. In Proceedings of the CCECE 2003—Canadian Conference on Electrical and Computer Engineering. Toward a Caring and Humane Technology, Montreal, QC, Canada, 4–7 May 2003; pp. 251–254. [Google Scholar]
- Miller, J.F.; Job, D.; Vassilev, V.K. Principles in the Evolutionary Design of Digital Circuits—Part I. Genet. Program. Evolvable Mach. 2000, 1, 7–35. [Google Scholar] [CrossRef]
- Louis, S.J. Genetic Learning for Combinational Logic Design. Soft Comput. 2005, 9, 38–43. [Google Scholar] [CrossRef]
- Bos, J.W.; Halderman, J.A.; Heninger, N.; Moore, J.; Naehrig, M.; Wustrow, E. Elliptic Curve Cryptography in Practice. In Financial Cryptography and Data Security: 18th International Conference; Springer: Berlin/Heidelberg, Germany, 2014; pp. 157–175. [Google Scholar]
- Tan, K.; Khor, E.; Lee, T. Multiobjective Evolutionary Algorithms and Applications. In Multiobjective Evolutionary Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Ercegovac, M.D.; Lang, T.; Moreno, J. Introduction to Digital Systems. In Introduction to Digital Systems; John Wiley: New York, NY, USA, 1999. [Google Scholar]
- Eshelman, L.J. The CHC Adaptive Search Algorithm: How to Have Safe Search When Engaging in Nontraditional Genetic Recombination. In Foundations of Genetic Algorithms; Elsevier: Amsterdam, The Netherlands, 1991; pp. 265–283. [Google Scholar]
- Fant, K.M.; Brandit, S.A. Considerations of Completeness in the Expression of Combinational Processes. Available online: http://www.theseusresearch.com/complete01.htm (accessed on 5 September 2021).
- Fant, K.M.; Brandt, S.A. NULL Convention Logic: A complete and consistent logic for asynchronous digital circuit synthesis. In Proceedings of the International Conference on Application Specific Systems, Architectures and Processors, Chicago, IL, USA, 19–21 August 1996; pp. 261–273. [Google Scholar]
- Kavousianos, X.; Nikolos, D.; Foukarakis, G.; Gnardellis, T. New Efficient Totally Self-Checking Berger Code Checkers. Integr. VLSI J. 1999, 28, 101–118. [Google Scholar] [CrossRef]
- Poudel, B.; Munir, A. Design and Evaluation of a Reconfigurable ECU Architecture for Secure and Dependable Automotive CPS. IEEE Trans. Dependable Secur. Comput. (TDSC) 2021, 18, 235–252. [Google Scholar] [CrossRef]
- Lala, P.K. Self-Checking and Fault-Tolerant Digital Design; Morgan Kaufmann Publishers: San Mateo, CA, USA, 2000. [Google Scholar]
- Xilinx. LogiCORE IP XPS HWICAP v5.01a Product Specification. Available online: https://www.xilinx.com/support/documentation/ip_documentation/xps_hwicap/v5_01_a/xps_hwicap.pdf (accessed on 1 November 2021).
- Wu, J.; Kim, Y.B.; Choi, M. Low-power Side-channel Attack-resistant Asynchronous S-box Design for AES Cryptosystems. In Proceedings of the 20th Symposium on Great Lakes Symposium on VLSI, Providence, RI, USA, 16–18 May 2010; pp. 459–464. [Google Scholar]
- Xilinx. Xilinx Kintex-7 FPGA KC705 Evaluation Kit. 2021. Available online: https://www.xilinx.com/products/boards-and-kits/ek-k7-kc705-g.html/ (accessed on 10 May 2021).
- Xilinx. ISE Design Suite. Available online: https://www.xilinx.com/products/design-tools/ise-design-suite.html (accessed on 5 September 2021).
- Tiri, K.; Verbauwhede, I. A VLSI Design Flow for Secure Side-Channel Attack Resistant ICs. In Proceedings of the Conference on Design, Automation and Test in Europe, Munich, Germany, 7–11 March 2005; pp. 58–63. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).