Evaluation of In Vivo Spike Detection Algorithms for Implantable MTA Brain—Silicon Interfaces
Abstract
1. Introduction
- An implanted chip receives power from a battery or from harvesting systems that are intrinsically capable of providing limited power;
- The wireless data transmission between the sensor and the external interface cannot manage a flow of raw data coming from the entire sensor (at least 10 kS/sec/pixel);
- Being in contact with living tissue, the temperature of the device must remain within the heat dissipation capacity of the tissue to avoid damage.
- The standard deviation-based threshold crossing [9], a golden standard for most of the real-time systems due to its extremely low resource footprint combined with a performance sufficient to work as a spike sorting preprocessing step;
2. Materials and Methods
2.1. Figure of Merit for Implanted Spike Detection Algorithms
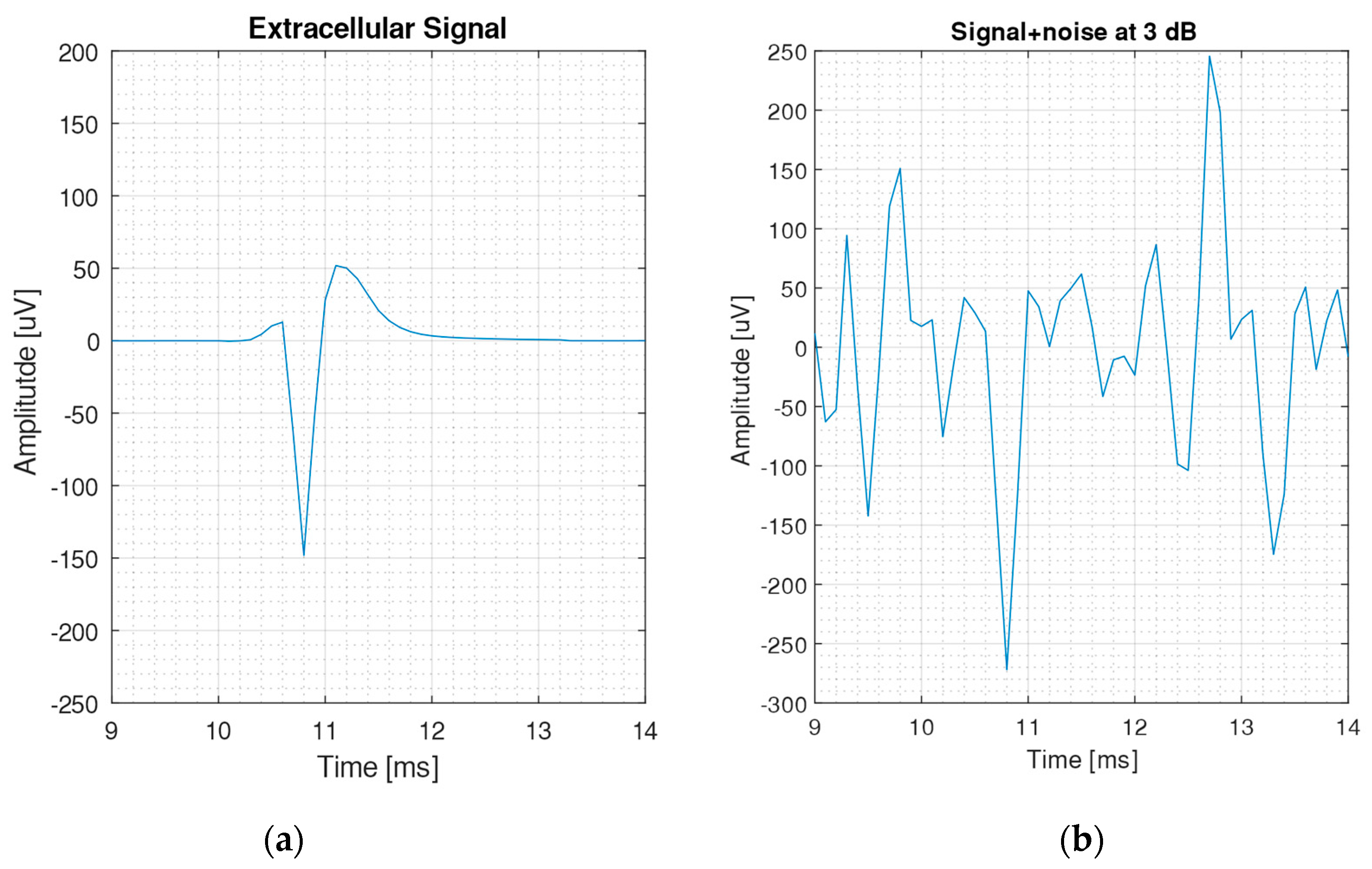
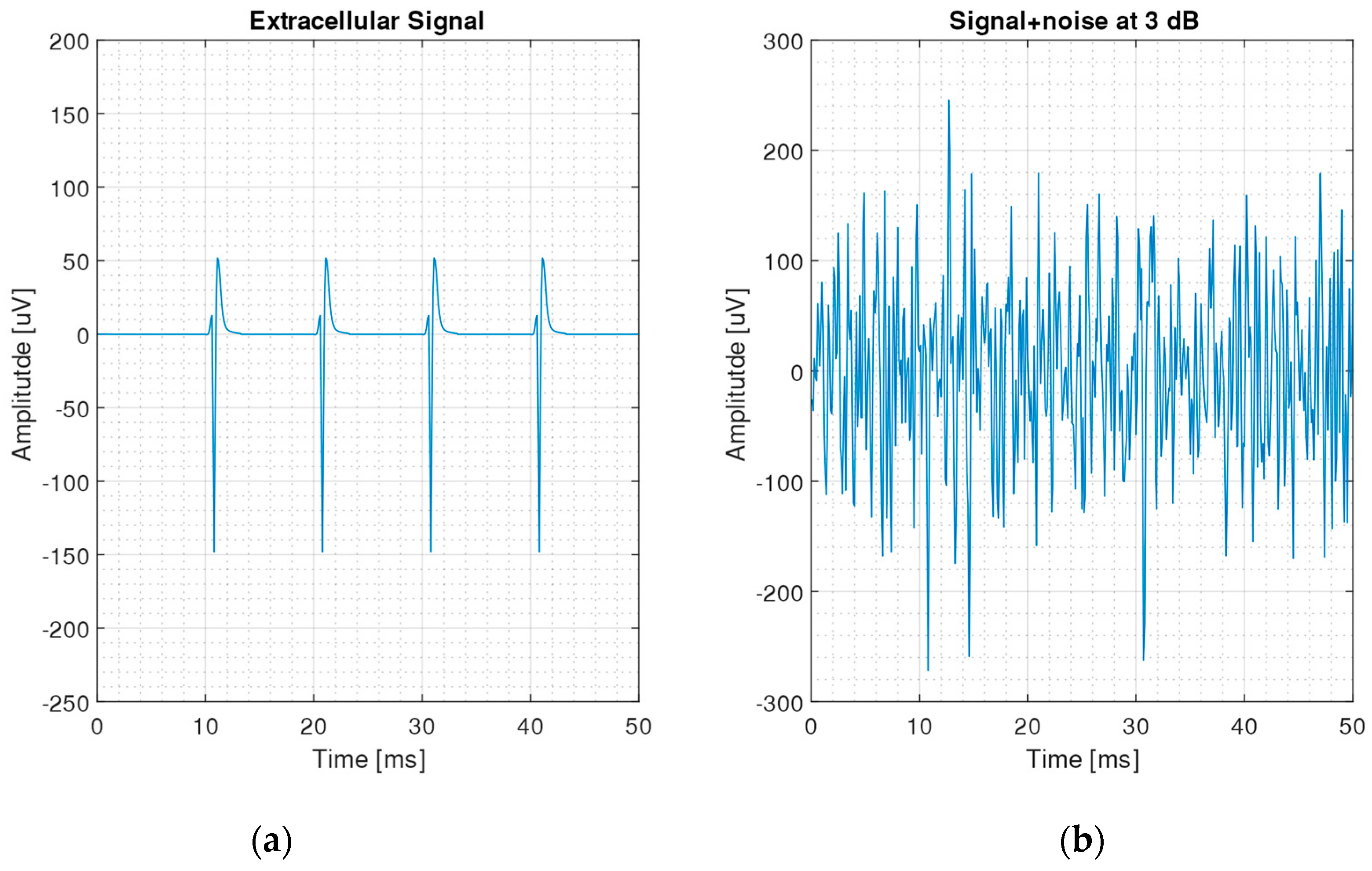
2.2. Generation of Neural Signals
2.3. Spike Detection Algorithms
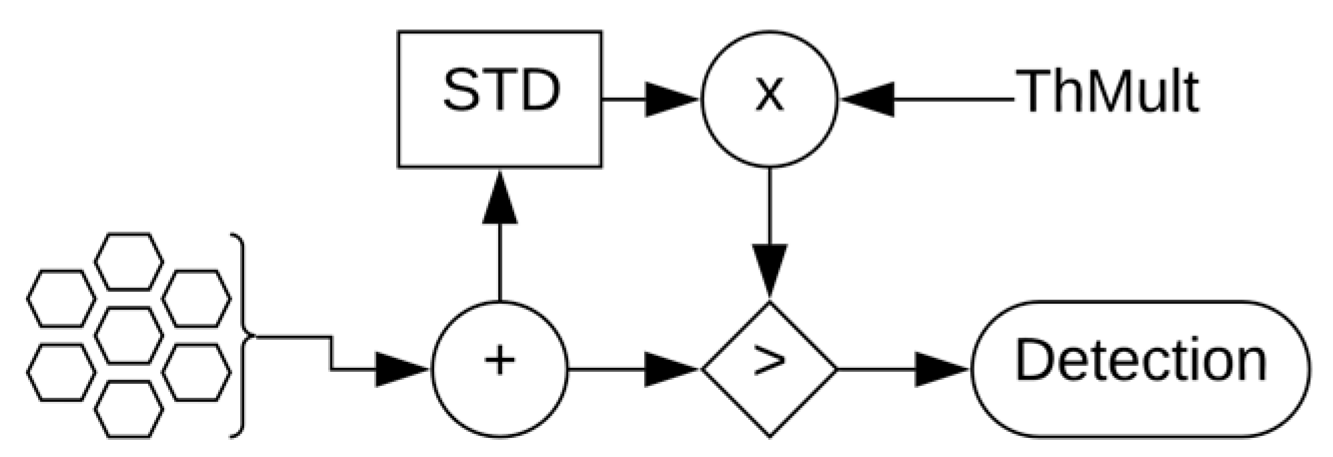
2.3.1. Threshold Crossing
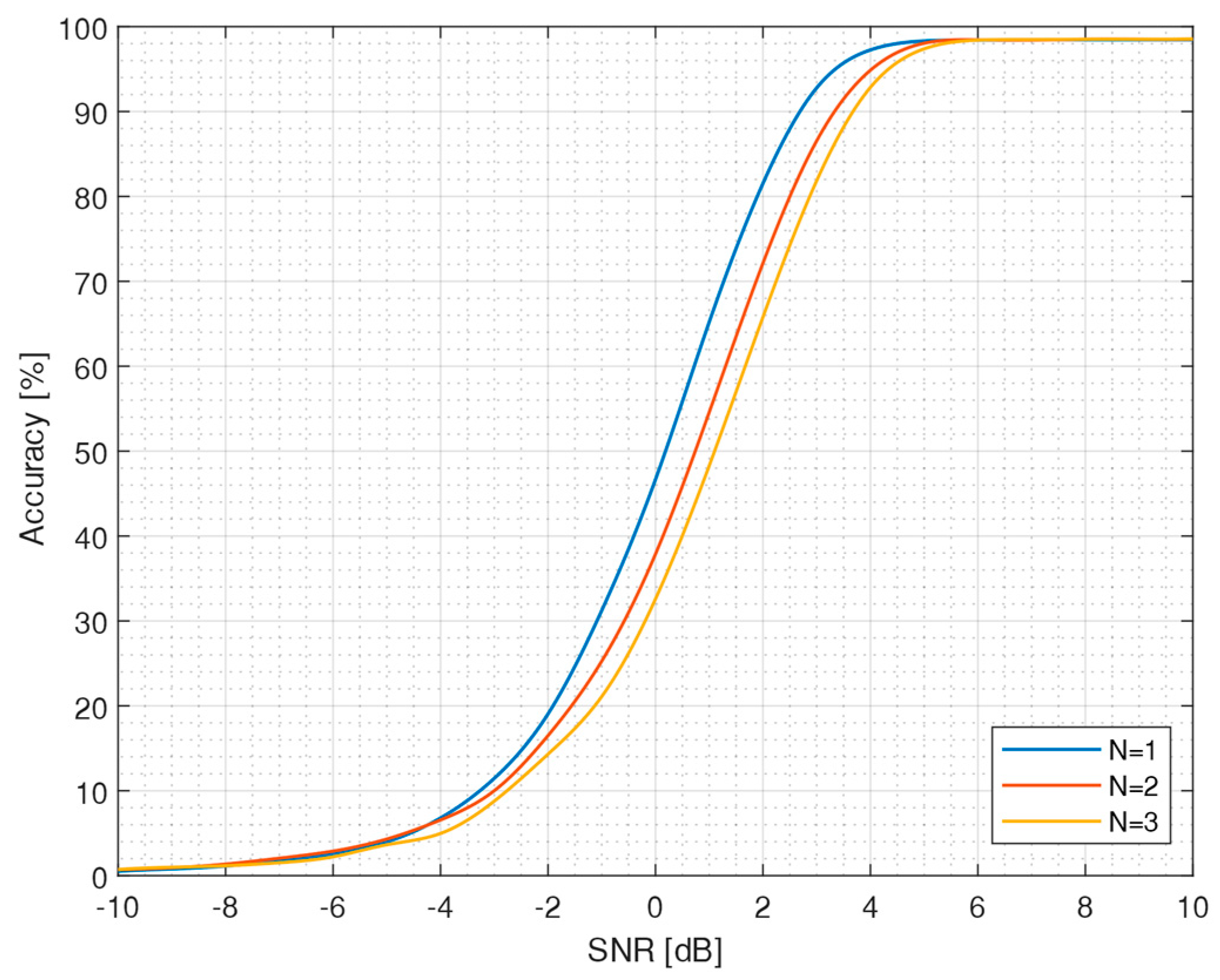
2.3.2. Correlation Algorithm
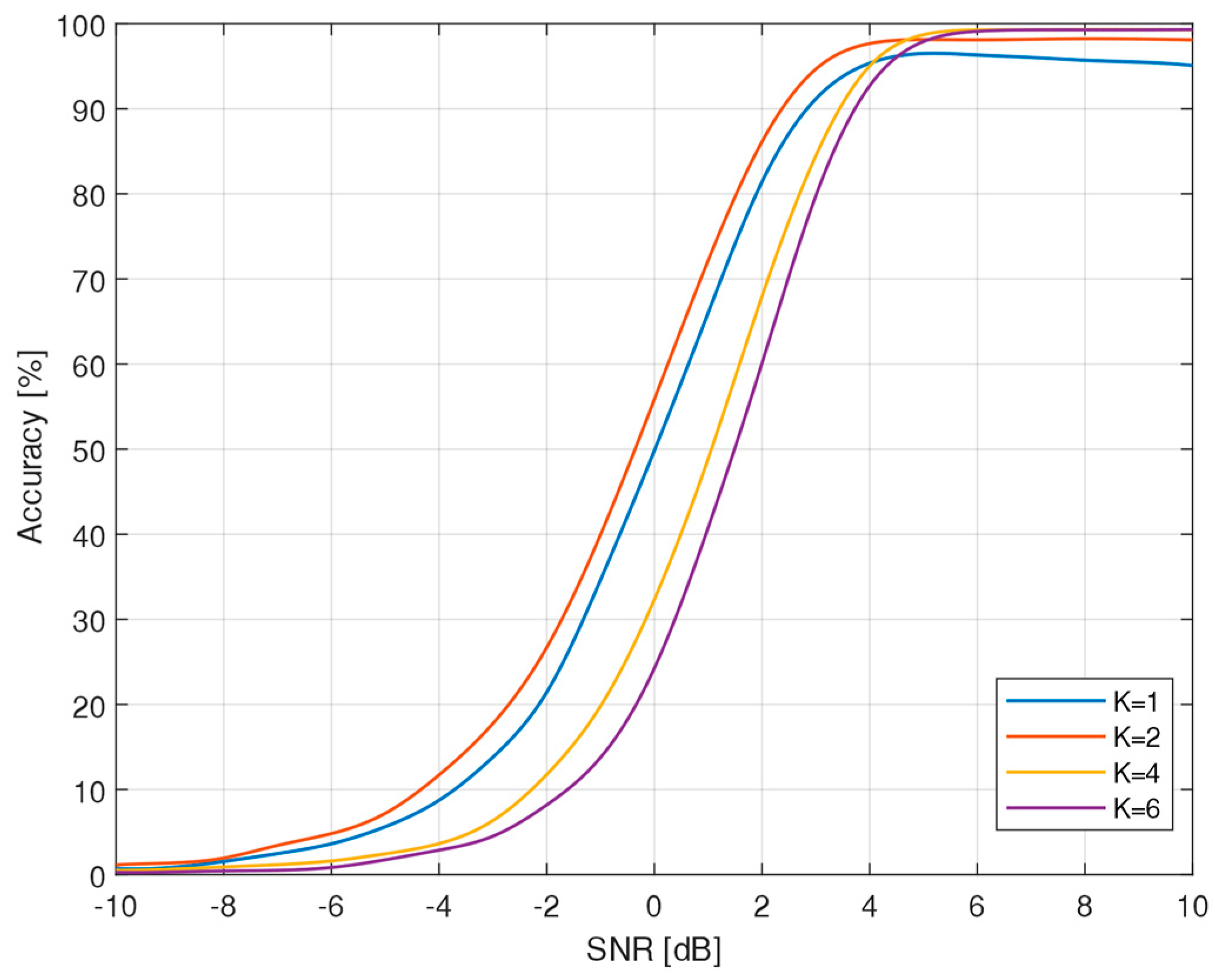
2.3.3. SNEO
3. Results
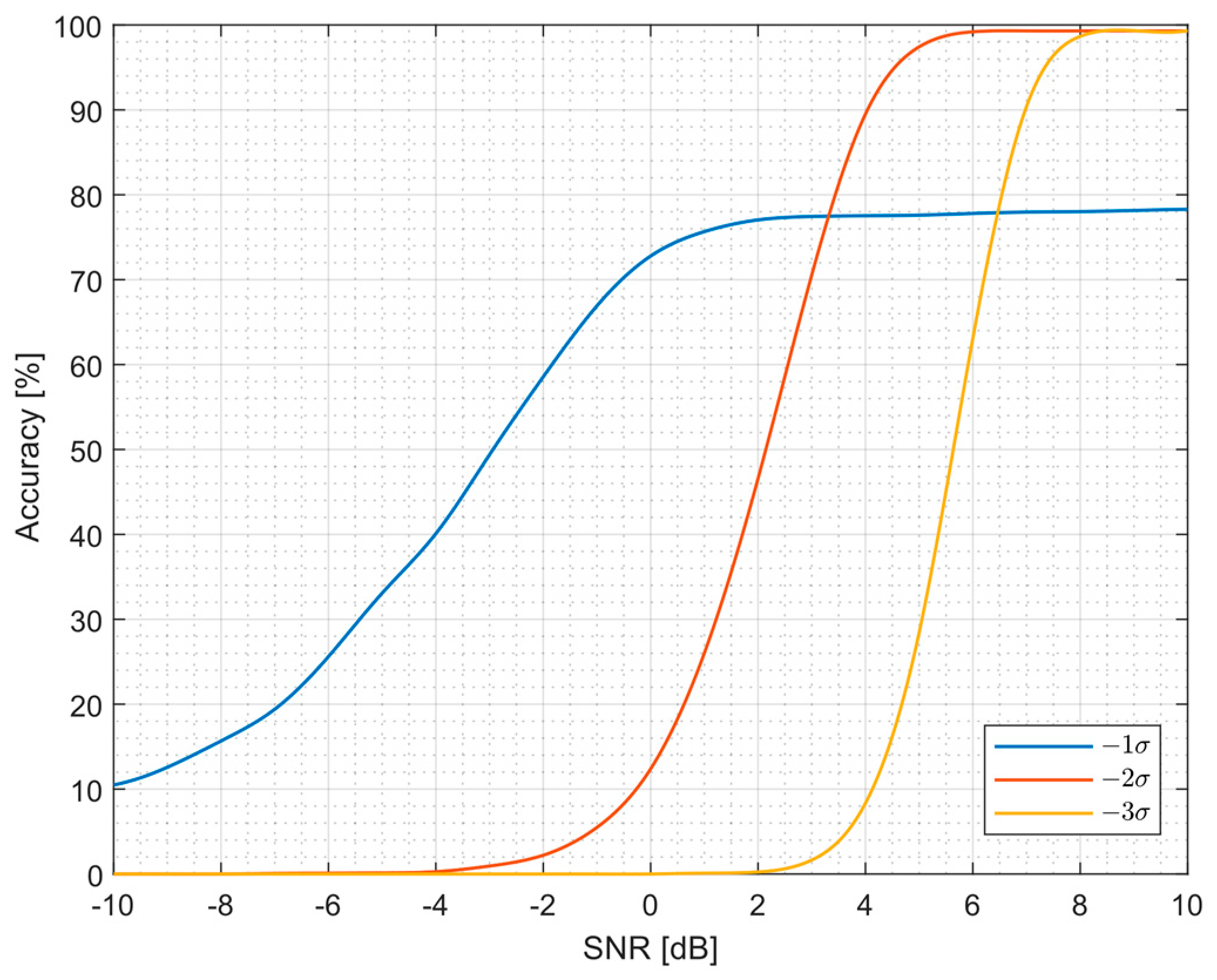
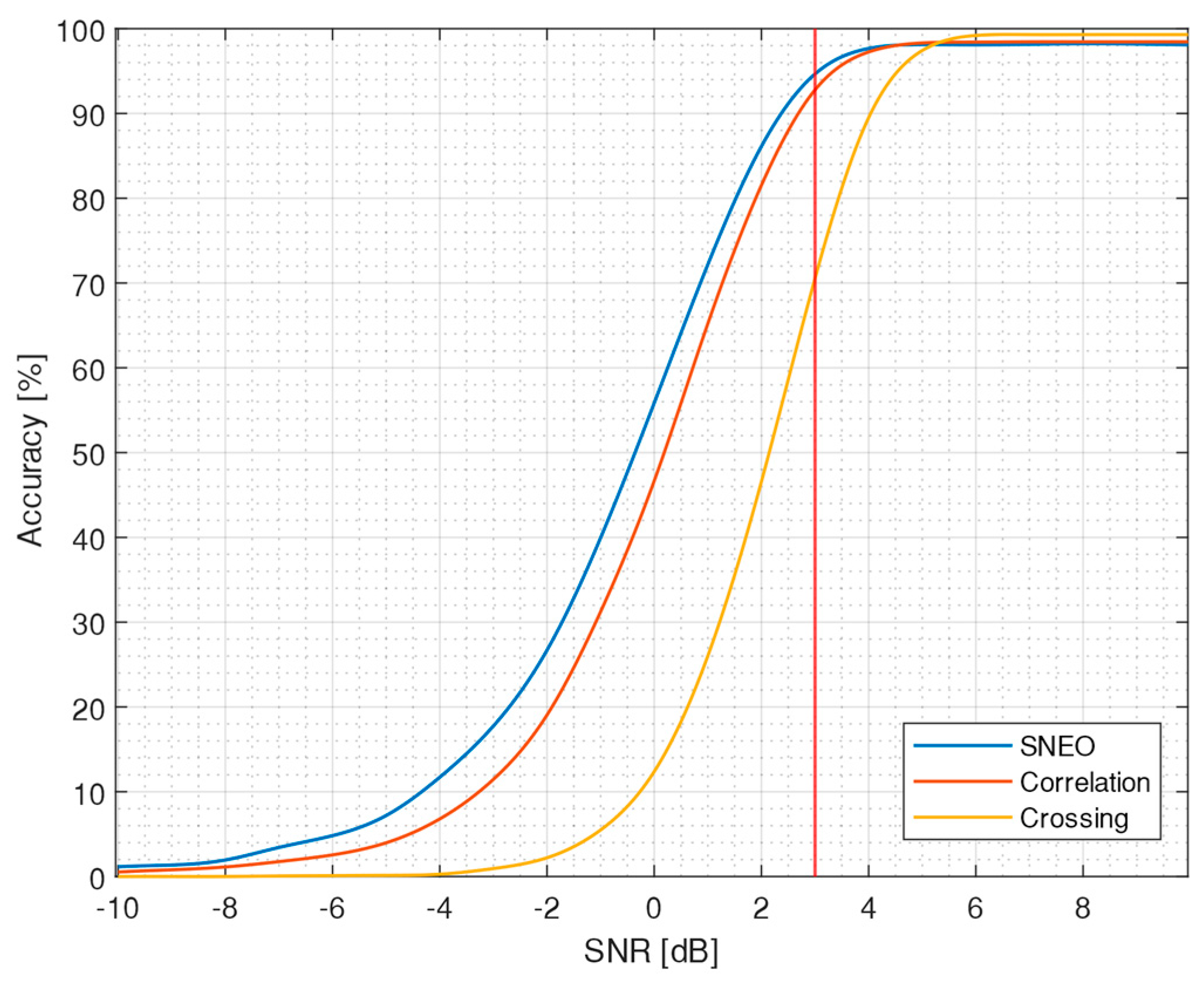
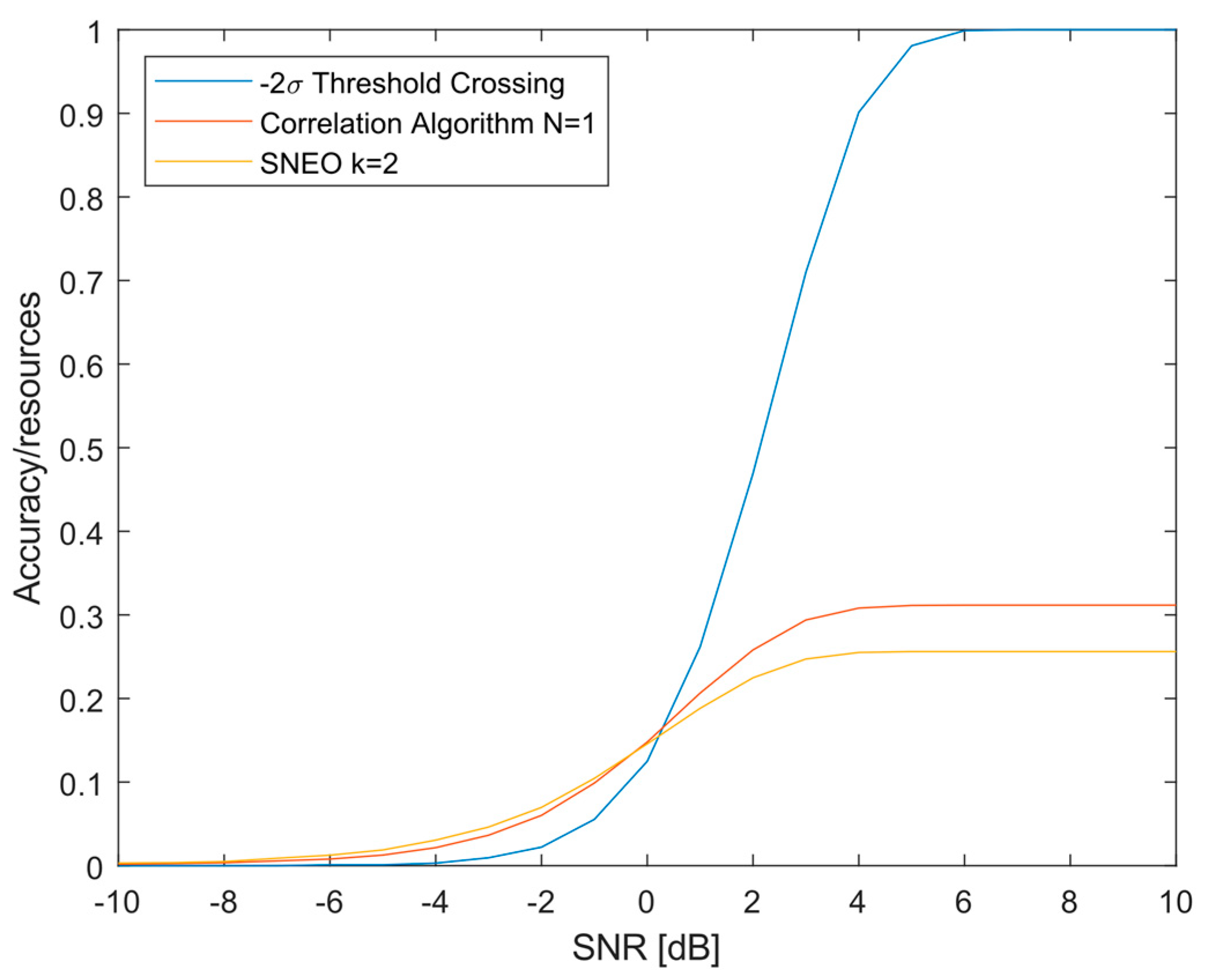
3.1. Algorithm Accuracy
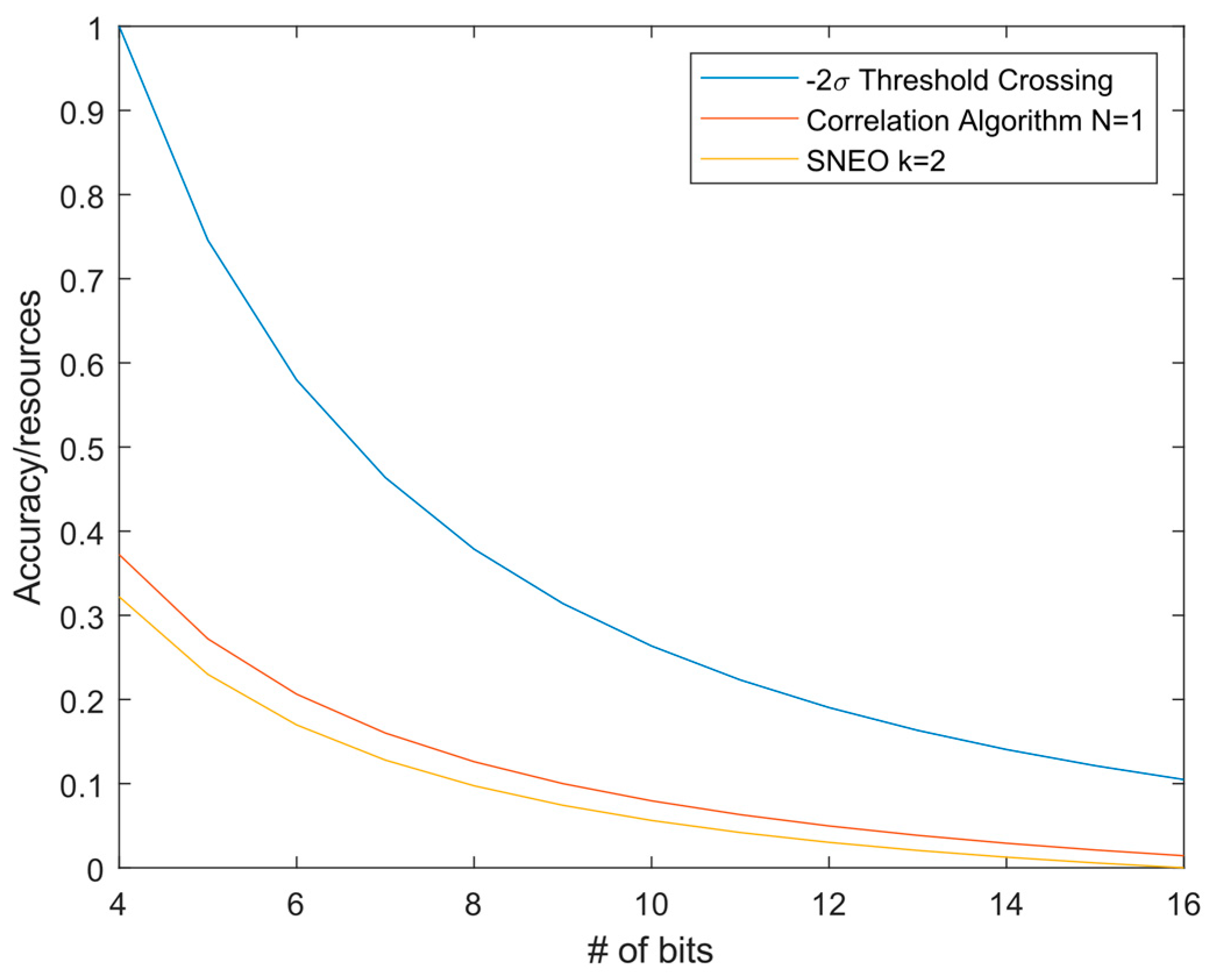
3.2. Resource Consumption
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thewes, R.; Bertotti, G.; Dodel, N.; Keil, S.; Schroder, S.; Boven, K.-H.; Zeck, G.; Mahmud, M.; Vassanelli, S. Neural tissue and brain interfacing CMOS devices—An introduction to state-of-the-art, current and future challenges. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 1826–1829. [Google Scholar] [CrossRef]
- Hutzler, M.; Fromherz, P. Silicon chip with capacitors and transistors for interfacing organotypic brain slice of rat hippocampus. Eur. J. Neurosci. 2004, 19, 2231–2238. [Google Scholar] [CrossRef] [PubMed]
- Schröder, S.; Cecchetto, C.; Keil, S.; Mahmud, M.; Brose, E.; Dogan, O.; Bertotti, G.; Wolanski, D.; Tillack, B.; Schneidewind, J.; et al. CMOS-compatible purely capacitive interfaces for high-density in-vivo recording from neural tissue. In Proceedings of the 2015 IEEE Biomedical Circuits and Systems Conference (BioCAS), Atlanta, GA, USA, 22–24 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Jang, H.-J.; Cho, W.-J. High performance silicon-on-insulator based ion-sensitive field-effect transistor using high-k stacked oxide sensing membrane. Appl. Phys. Lett. 2011, 99, 043703. [Google Scholar] [CrossRef]
- Vassanelli, S.; Mahmud, M.; Girardi, S.; Maschietto, M. On the Way to Large-Scale and High-Resolution Brain-Chip Interfacing. Cogn. Comput. 2012, 4, 71–81. [Google Scholar] [CrossRef]
- Eversmann, B.; Jenkner, M.; Hofmann, F.; Paulus, C.; Brederlow, R.; Holzapfl, B.; Fromherz, P.; Merz, M.; Brenner, M.; Schreiter, M.; et al. A 128 × 128 cmos biosensor array for extracellular recording of neural activity. IEEE J. Solid-State Circuits 2003, 38, 2306–2317. [Google Scholar] [CrossRef]
- Voelker, M.; Fromherz, P. Signal Transmission from Individual Mammalian Nerve Cell to Field-Effect Transistor. Small 2005, 1, 206–210. [Google Scholar] [CrossRef]
- Girardi, S.; Maschietto, M.; Zeitler, R.; Mahmud, M.; Vassanelli, S. High resolution cortical imaging using electrolyte-(metal)-oxide-semiconductor field effect transistors. In Proceedings of the 2011 5th International IEEE/EMBS Conference on Neural Engineering, Cancun, Mexico, 27 April–1 May 2011; pp. 269–272. [Google Scholar] [CrossRef]
- Lewicki, M. A review of methods for spike sorting: The detection and classification of neural action potentials. Netw. Comput. Neural Syst. 1998, 9, R53–R78. [Google Scholar] [CrossRef]
- Lambacher, A.; Vitzthum, V.; Zeitler, R.; Eickenscheidt, M.; Eversmann, B.; Thewes, R.; Fromherz, P. Identifying firing mammalian neurons in networks with high-resolution multi-transistor array (MTA). Appl. Phys. A 2011, 102, 1–11. [Google Scholar] [CrossRef]
- Vallicelli, E.A.; Reato, M.; Maschietto, M.; Vassanelli, S.; Guarrera, D.; Rocchi, F.; Collazuol, G.; Zeitler, R.; Baschirotto, A.; De Matteis, M. Neural Spike Digital Detector on FPGA. Electronics 2018, 7, 392. [Google Scholar] [CrossRef]
- Tambaro, M.; Vallicelli, E.A.; Tomasella, D.; Baschirotto, A.; Vassanelli, S.; Maschietto, M.; De Matteis, M. A 10 MSample/Sec Digital Neural Spike Detection for a 1024 Pixels Multi Transistor Array Sensor. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 711–714. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Ray, G.C. A new interpretation of nonlinear energy operator and its efficacy in spike detection. IEEE Trans. Biomed. Eng. 1998, 45, 180–187. [Google Scholar] [CrossRef] [PubMed]
- Ng, A.K.; Ang, K.K.; Guan, C.; Guan, C. Automatic selection of neuronal spike detection threshold via smoothed Teager energy histogram. In Proceedings of the 2013 6th International IEEE/EMBS Conference on Neural Engineering (NER), San Diego, CA, USA, 6–8 November 2013; pp. 1437–1440. [Google Scholar] [CrossRef]
- Choi, J.H.; Jung, H.K.; Kim, T.; Taejeong, K. A New Action Potential Detector Using the MTEO and Its Effects on Spike Sorting Systems at Low Signal-to-Noise Ratios. IEEE Trans. Biomed. Eng. 2006, 53, 738–746. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Kung, J.; Chai, S.; Yalamanchili, S.; Mukhopadhyay, S. Neurocube: A Programmable Digital Neuromorphic Architecture with High-Density 3D Memory. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016; pp. 380–392. [Google Scholar] [CrossRef]
- Hirai, Y.; Matsuoka, T.; Tani, S.; Isami, S.; Tatsumi, K.; Ueda, M.; Kamata, T. A Biomedical Sensor System with Stochastic A/D Conversion and Error Correction by Machine Learning. IEEE Access 2019, 7, 21990–22001. [Google Scholar] [CrossRef]


| Filter | Standard Deviation | Threshold Crossing | Correlation Algorithm | SNEO | |
|---|---|---|---|---|---|
| Adder | 4 | 1 + 1 1 | 6 | 20 1 | 1 + 6 1 + (4 k) 2 |
| Multiplicator | 5 | 1 | 2 * | 3 + 2 * | 2 + (4 k + 1) 1 + 2 * |
| Comparator | 0 | 1 | 1 | 1 2 | 1 2 |
| Divisor | 0 | 0 | 0 | 7 | 0 |
| Register | 4 1 | 1 1 | 0 | 21 1 | 2 k + (4 k + 1) 1 |
| STD | 0 | - | 1 | 7 | 1 |
| Weighted Total | 254 N + 30 N 2 | 121 N + 6 N 2 | 235 N + 6 N 2 + STD | 995 N+42 N 2 + 7 * STD | 557 N + 602 kN + 36 N 2 + 48 kN 2 + STD 1 |
| 5-bit, k = 2 | 2020 | 755 | 2080 | 11,310 | 13,615 |
| 8-bit, k = 4 | 3952 | 1352 | 3616 | 20,112 | 25,240 |
| Threshold Crossing | Correlation Algorithm | SNEO | |
|---|---|---|---|
| True Positive (%) | 73 | 93 | 96 |
| False Positive (%) | 4 | 1 | 2 |
| Accuracy (%) | 70 | 93 | 95 |
| Resources (8 bit) | 3616 | 20,320 | 41,016 |
| FoM (3 dB) | 0.40 | 0.12 | 0.10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tambaro, M.; Vallicelli, E.A.; Saggese, G.; Strollo, A.; Baschirotto, A.; Vassanelli, S. Evaluation of In Vivo Spike Detection Algorithms for Implantable MTA Brain—Silicon Interfaces. J. Low Power Electron. Appl. 2020, 10, 26. https://doi.org/10.3390/jlpea10030026
Tambaro M, Vallicelli EA, Saggese G, Strollo A, Baschirotto A, Vassanelli S. Evaluation of In Vivo Spike Detection Algorithms for Implantable MTA Brain—Silicon Interfaces. Journal of Low Power Electronics and Applications. 2020; 10(3):26. https://doi.org/10.3390/jlpea10030026
Chicago/Turabian StyleTambaro, Mattia, Elia Arturo Vallicelli, Gerardo Saggese, Antonio Strollo, Andrea Baschirotto, and Stefano Vassanelli. 2020. "Evaluation of In Vivo Spike Detection Algorithms for Implantable MTA Brain—Silicon Interfaces" Journal of Low Power Electronics and Applications 10, no. 3: 26. https://doi.org/10.3390/jlpea10030026
APA StyleTambaro, M., Vallicelli, E. A., Saggese, G., Strollo, A., Baschirotto, A., & Vassanelli, S. (2020). Evaluation of In Vivo Spike Detection Algorithms for Implantable MTA Brain—Silicon Interfaces. Journal of Low Power Electronics and Applications, 10(3), 26. https://doi.org/10.3390/jlpea10030026






