Abstract
The warehouse picking process is one of the most critical components of logistics operations. Human–robot collaboration (HRC) is seen as an important trend in warehouse picking, as it combines the strengths of both humans and robots in the picking process. However, in current human–robot collaboration frameworks, there is a lack of effective communication between humans and robots, which results in inefficient task execution during the picking process. To address this, this paper considers trust as a communication bridge between humans and robots and proposes the Stackelberg trust-based human–robot collaboration framework for warehouse picking, aiming to achieve efficient and effective human–robot collaborative picking. In this framework, HRC with trust for warehouse picking is defined as the Partially Observable Stochastic Game (POSG) model. We model human fatigue with the logistic function and incorporate its impact on the efficiency reward function of the POSG. Based on the POSG model, belief space is used to assess human trust, and human strategies are formed. An iterative Stackelberg trust strategy generation (ISTSG) algorithm is designed to achieve the optimal long-term collaboration benefits between humans and robots, which is solved by the Bellman equation. The generated human–robot decision profile is formalized as a Partially Observable Markov Decision Process (POMDP), and the properties of human–robot collaboration are specified as PCTL (probabilistic computation tree logic) with rewards, such as efficiency, accuracy, trust, and human fatigue. The probabilistic model checker PRISM is exploited to verify and analyze the corresponding properties of the POMDP. We take the popular human–robot collaboration robot TORU as a case study. The experimental results show that our framework improves the efficiency of human–robot collaboration for warehouse picking and reduces worker fatigue while ensuring the required accuracy of human–robot collaboration.
1. Introduction
1.1. Motivation
With the rapid advancement of the internet economy and information technology, e-commerce has experienced explosive growth in recent years, which has also driven the expansion of the logistics industry [1]. The logistics system has also become a key factor restricting the development of e-commerce and related industries [2], in which timeliness and cost are major limiting factors [3]. There are two primary activities in the entire logistics process: warehouse picking and logistics distribution. Recently, distribution efficiency has improved significantly and has reached a saturation point. Warehouse picking efficiency plays an important role in the entire logistics process [4].
Traditional warehouse picking systems rely on manual labor. Manual picking offers greater flexibility for handling the diversity of goods and requires lower initial investment costs. It is inefficient and unsuitable for large-scale, long-duration operations [5]. Automated warehouse picking systems, such as the pioneering Amazon Kiva system, have clearly improved the efficiency of warehouse picking [6]. However, the growth of e-commerce has introduced diversification, large-scale operations, and the customization of goods, which adds complexity to logistics [7]. Amazon has also indicated that automated technology cannot completely replace human involvement in the picking process. This is due to current technological limitations and humans’ superior cognitive abilities in handling complex tasks [8]. Emerging human–robot collaboration systems for warehouse picking combine the low cost, high efficiency, and flexibility of manual and automated picking, which achieves greater accuracy and efficiency [9], increases flexibility, and reduces downtime [10].
However, there are some communication barriers that undermine the effectiveness of current HRC frameworks. First, asymmetric information persists, as robots follow rigid protocols without adapting to human operators’ cognitive states [11]. Second, the trust-calibration dilemma stems from missing mutual trust models. This creates polarized behaviors: workers either distrust robots and manually verify outputs or over-trust automation and skip interventions. Systems exacerbate this by failing to quantify trust through measurable signals like intervention frequency [12].
Effective human–robot collaboration requires the modeling of human cognitive processes and complex social attitudes (e.g., trust, guilt, shame). If robots can detect human biases or excessive trust and accurately predict human behavior, collaboration can be significantly improved [13]. To establish more effective collaboration between workers and picking robots, it is essential for robots to understand the level of workers’ trust in them and make decisions accordingly. How does trust influence the operational process in human–robot collaborative picking? Low trust in robots leads workers to excessively intervene in their tasks (e.g., checking product labels), which disrupts the workflow and drastically reduces efficiency. This will also cause workers to accumulate fatigue. Conversely, excessive trust can result, in which workers are unwilling or unable to intervene even if it is necessary. This may also cause workers to overestimate the capabilities of automation and neglect the monitoring of robot performance. For instance, if a robot misidentifies an item and the worker does not double-check it, an incorrect product may be delivered to the customer. Therefore, it is crucial to establish a reasonable trust model between humans and robots to model and evaluate human trust levels. This enables robots to appropriately decide when to execute or relinquish tasks during collaboration.
Our proposed framework uses the Stackelberg strategy from game theory. This strategy establishes hierarchical decision-making between two agents. The robot acts as the leader, first optimizing its strategy by predicting how the human worker (follower) will respond optimally. We provide complete technical details about these game-theoretic methods in Section 3 (Theoretical Foundations).
1.2. Our Contributions
This work aims to improve decision-making in human–robot collaboration for warehouse picking by evaluating human trust in robots. To achieve this, an online trust model for human–robot collaboration is established, which involves the interaction between the worker and the picking robot, human trust dynamics, and the robot’s evaluation of human trust. Based on this trust evaluation, the robot infers human intentions and adopts the optimal strategy. The existing works on the former do not adequately address such a complex operational process. This paper proposes a Stackelberg trust-based human–robot collaboration framework for warehouse picking, with the following specific contributions:
- Human trust modeling and evaluation: We define HRC with trust for warehouse picking as the Partially Observable Stochastic Game (POSG) and exploit a Bayesian posterior belief space to assess human trust in real time. Additionally, we use the logistic function to model human fatigue, which is specified as the collaboration efficiency reward function in the POSG.
- Human–robot decision-making based on multi-round trust: We combine the Stackelberg strategy with the Bellman equation to design iterative Stackelberg trust strategy generation. It is solved by a model-based exhaustive strategy search and can achieve the optimal strategy for the robot’s long-term benefits while considering human trust. Furthermore, human strategies are generated using the sigmoid function based on human trust.
- Decision analysis by probabilistic model checking: We formalize the generated human–robot decisions into a Partially Observable Markov Decision Process (POMDP). We specify the properties of the human–robot collaboration framework for warehouse picking as PCTL formulae, such as efficiency, accuracy, trust, and human fatigue. These are verified using the probabilistic model-checking tool PRISM. We establish a no-trust model and a single-round trust-based HRC for comparison with our framework.
1.3. Structure of This Paper
The remainder of this paper is organized as follows: Section 2 introduces the related works. Section 3 provides an overview of relevant foundational knowledge. Section 4 proposes the Stackelberg trust-based human–robot collaboration framework for warehouse picking. Section 5 demonstrates the reliability of the proposed framework through experiments. Section 6 concludes the paper and outlines potential directions for future research.
2. Related Works
This section reviews related works on two main topics: (1) trust in automation and (2) warehouse picking. For each topic, we identify gaps in the current works and discuss their relevance to this study.
2.1. Trust in Automation
Quantitative models of trust can generally be categorized by different dimensions: probabilistic models, deterministic models, cognitive models, and neural models. Additionally, they can be classified into offline models and online models based on the type of input data used to generate predictions.
- (1)
- Offline Trust Models
Traditional trust models are mostly offline and use a set of predefined parameters as the input to generate predictions. These models often rely on feedback loops to determine the next state of a human–automation system at a given time, including trust levels, reliance on automation, and task performance. Lee et al. used time series analysis to model the dynamic impact of system failures on operator trust, predicting trust levels through a trust transfer function based on failure occurrences, automation, and human performance [14]. Gao et al. extended decision field theory to model the relationship between trust in automation and reliance behavior [15]. Akash et al., building on the psychological literature, established a third-order linear automation trust model linking trust directly to experience [16]. Hu et al. refined Gao’s model by introducing additional parameters to construct a second-order linear automation trust model, achieving more accurate predictions of trust dynamics [17].
Offline trust models are suitable for evaluating the performance trends and overall efficacy of human–automation systems under different initial conditions. They provide researchers with insights into how various factors interact and influence human behavior. Additionally, since these models rely solely on initial parameters, they are well-suited for predicting system behavior during the design phase of automation systems.
- (2)
- Online Trust Models
For the real-time evaluation of trust states in human–robot collaboration, online trust models are necessary. These models incorporate parameters from the initial settings and use observed data during system operation to generate situational evidence-based predictions. Xu et al. proposed an Online Probabilistic Trust Inference Model (OPTIMo) using a dynamic Bayesian network (DBN) to infer moment-to-moment trust states based on the observed interaction history [18]. Petković et al. developed a hidden Markov model (HMM)-based algorithm for human intent estimation in flexible robotic warehouses, employing a Theory of Mind (ToM)-based approach [19]. Sheng constructed a POMDP-based trust evaluation model in autonomous driving, exploring the relationship between route planning and trust, where trust is treated as a partially observable state variable representing human psychological states [20]. Huang et al. investigated cognitive reasoning between humans and robots in stochastic multi-agent (SMG) environments, proposing an Autonomous Stochastic Multi-Agent System (ASMAS) with a new probabilistic rational temporal logic, PRTL*, to capture traditional beliefs and intentions [21].
While these models focus on trust evaluation, the critical aspect of human–robot collaboration is not trust itself but leveraging trust to make better decisions, enabling stable and efficient collaboration. Additionally, these models are not directly applicable to human–robot collaborative picking scenarios, where humans cannot compute optimal strategies in real time and instead make decisions influenced by their trust in robots. Robots’ predictions of human behavior should also be based on trust, which serves as a “bridge” in collaborative picking. Therefore, a new method is needed to evaluate trust and use it to facilitate better human–robot decision-making.
2.2. Warehouse Picking
Research on industrial picking operations has progressed through three main stages: manual picking, automated picking, and human–robot collaborative picking.
- (1)
- Manual Picking
Traditional picking operations rely on manual labor, where tasks are performed by workers manually moving goods or using simple equipment like forklifts and trailers. De Koster et al. demonstrated that the efficiency of manual picking is heavily influenced by warehouse layout and operations, conducting studies on warehouse design, storage allocation, order processing, and zoning [22]. Caron et al. proposed a simulation method for designing efficient picking areas to improve productivity in manual picking systems [23]. Kim et al. introduced a negotiation mechanism for real-time task allocation and developed new algorithms to optimize the picking process [24]. While these studies improved the efficiency and scalability of manual picking, the increasing picking volume driven by e-commerce, diverse delivery routes, and varying customer demands rendered manual picking costly and inefficient for modern logistics needs.
- (2)
- Automated Picking
In fully automated picking systems, all picking tasks are executed according to system-generated instructions. Hausman et al. conducted pioneering research on automated picking systems [25]. Pazour developed efficient algorithms to study the impact of product location allocation on expected throughput [26]. Li et al. examined storage allocation and order batching problems in Kiva mobile delivery systems [27]. Despite advancements, fully automated picking remains unachievable due to limitations in equipment size and capacity. Oversized and overweight items cannot be handled solely by robots, and manual work continues to play a vital role.
- (3)
- Human–Robot Collaborative Picking
To address the limitations of manual and automated picking, current research focuses on collaborative robots that work with humans to complete tasks in warehouse picking operations. Verbeet et al. proposed a process model for collaborative picking environments that allows robots and humans to work together while enabling robots to improve their performance through human feedback [28]. Rey et al. developed a human–robot collaborative system for industrial tasks aimed at optimizing picking operations [29]. Baechler et al. introduced a prototype of a novel manual picking assistance system and evaluated its effectiveness using three different approaches [30]. Compared to traditional manual and automated picking systems, human–robot collaboration combines their strengths. Manual picking has high labor costs, low efficiency, and slow response times, which are inadequate for the demands of e-commerce. Fully automated systems, on the other hand, are unsuitable for handling diverse, small-batch, and multi-order scenarios. Collaborative picking effectively addresses these challenges by integrating the advantages of both approaches.
While human–robot collaborative picking has improved efficiency and performance, achieving higher levels of collaboration requires robots to predict human behavior. Since robots cannot directly capture human psychological states, it is necessary to construct an appropriate model to predict human behavior. This study adopts the concept of trust to achieve this goal.
3. Theoretical Foundations
3.1. Game Theory
Game theory is a mathematical framework for studying interactions between decision-makers, focusing on formulating strategies to achieve optimal outcomes. In game theory, decision-makers are referred to as players, who choose their actions based on the behavior of their opponents, leading to specific outcomes or payoffs. The primary goal of game theory is to analyze and predict players’ behaviors under various scenarios and identify optimal decision strategies.
Stochastic games, a model within game theory, are often represented as a tuple to describe interactions among multiple participants where the outcomes of actions involve randomness. In these games, each participant faces multiple possible actions at every step, with results influenced by probability distributions. The randomness can arise from uncertain environments, random events, or the actions of other participants. Unlike deterministic games, stochastic games are closer to real-world scenarios, as they allow the modeling of uncertainty and risk [31]. Analyzing stochastic games often involves probabilistic and statistical methods to determine optimal strategies and potential outcomes for participants.
Two important subtypes of games in game theory are incomplete information games and imperfect information games. In incomplete information games, players lack full knowledge about certain elements of the game, such as participant types, preferences, payoff functions, or strategy spaces. In imperfect information games, players do not have full visibility of all the previous actions or decisions made by others, meaning some historical information is unavailable.
A Partially Observable Stochastic Game (POSG) is an advanced model in game theory combining features of incomplete and imperfect information games with elements of stochastic dynamic systems. It describes interactions among multiple agents in dynamic, uncertain environments [32]. In POSGs, players have partial observations of the environment or other participants, and the environment itself evolves dynamically with randomness. POSGs are widely applied in fields such as robotics, autonomous driving, and military decision-making, where complex decision-making is required in dynamic and uncertain settings. These characteristics make POSGs highly relevant for modeling intricate human–machine interactions and competition or cooperation among intelligent systems.
3.2. Stackelberg Strategy
The Stackelberg strategy originates from the Stackelberg game, which is a leader–follower model in economics, and game theory proposed by Heinrich von Stackelberg in 1934. It has applications in economics, management, engineering optimization, and network security [33].
The core concept of the Stackelberg game lies in the information asymmetry between roles in the game. The leader acts first, and their strategy is observed by the follower, who then adopts an optimal response strategy. The leader anticipates the follower’s reaction and incorporates this into their decision-making, forming a forward-looking optimization process. The Stackelberg strategy formulation is expressed as follows:
where and are the strategies of the leader and the follower, respectively, and and are their respective payoff functions. The Stackelberg equilibrium represents a stable outcome of the interaction between the leader and the follower, embodying the leader’s advantage in the game.
3.3. Probabilistic Model Checking
Model checking is an automated verification technique used to ensure finite-state systems satisfy specific properties or specifications. Probabilistic model checking is a branch of this technique focusing on systems with probabilistic or nondeterministic behaviors. Unlike traditional model checking, which primarily verifies Boolean logic properties, probabilistic model checking quantifies the likelihood of certain system behaviors meeting given specifications. Probabilistic attributes capture uncertainty and randomness in the environment, as well as nondeterministic decision-making in models [34].
Markov decision processes (MDPs) are commonly used for modeling and reasoning about agents’ strategic behavior in stochastic environments. System properties are specified using temporal logics such as CTL (computation tree logic) or its probabilistic extension, PCTL (probabilistic CTL). The Partially Observable Markov Decision Process (POMDP) extends MDPs by introducing partial observability of the environment. It allows for modeling and analysis under conditions where agents’ abilities to observe the environment are limited. PCTL is further extended to describe the behaviors of systems with probabilistic dynamics, incorporating reward structures and constraints [35].
Model checking is crucial for designing and analyzing communication networks, stochastic algorithms, embedded systems, and other systems involving probabilistic decision-making and uncertainty.
4. Stackelberg Trust-Based Human–Robot Collaboration Framework for Warehouse Picking
In this section, we propose the Stackelberg trust-based human–robot collaboration framework for warehouse picking. It contains three components: (1) a POSG is defined to model and evaluate the human–robot collaboration framework with trust and human fatigue (Section 4.2), (2) human–robot collaborative strategies are solved based on multi-round trust (Section 4.3), and (3) human–robot decision-making is verified by probabilistic model checking. We first overview the framework in Section 4.1.
4.1. HRC Framework Overview
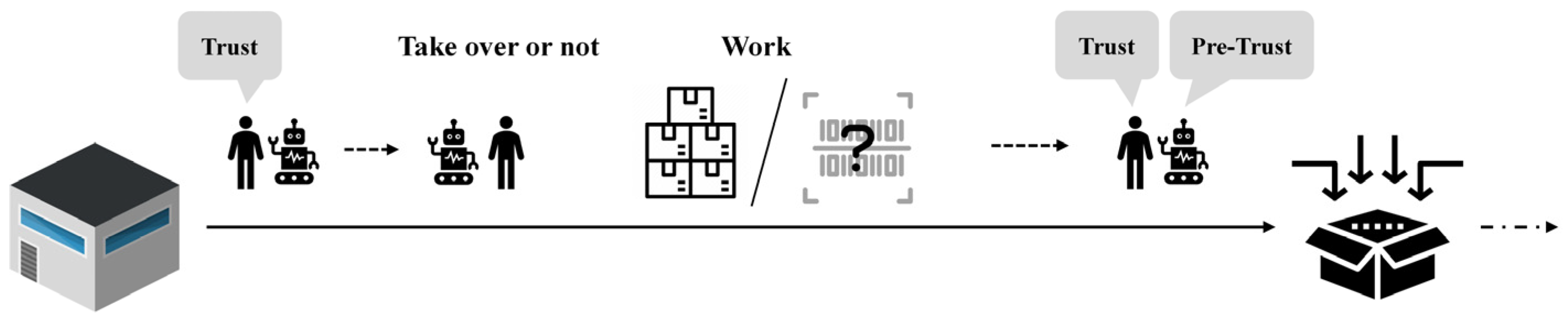
The HRC scenario for warehouse picking in this work is illustrated in Figure 1, which depicts human–robot collaboration to complete picking tasks. They first reach a designated task point and then decide whether to execute the task. The human decides to either take over the task or allow the robot to perform it, which is influenced by their trust in the robot’s capabilities. The outcome of the task affects the human’s trust level, which is updated accordingly. In certain tasks, scenarios such as blurred identification codes may occur, potentially compromising execution accuracy. However, during this process, the robot cannot directly observe the human’s trust level. Instead, the robot predicts the human’s trust based on historical states after the task is completed and uses this prediction to influence the robot’s intervention decision for the next task. In this scenario, we do not consider the impact of layout and planning issues.
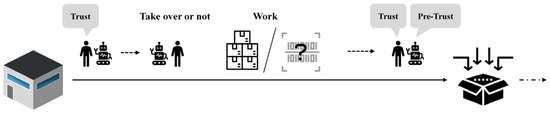
Figure 1.
Human–robot collaborative picking process.
4.1.1. Task Classification
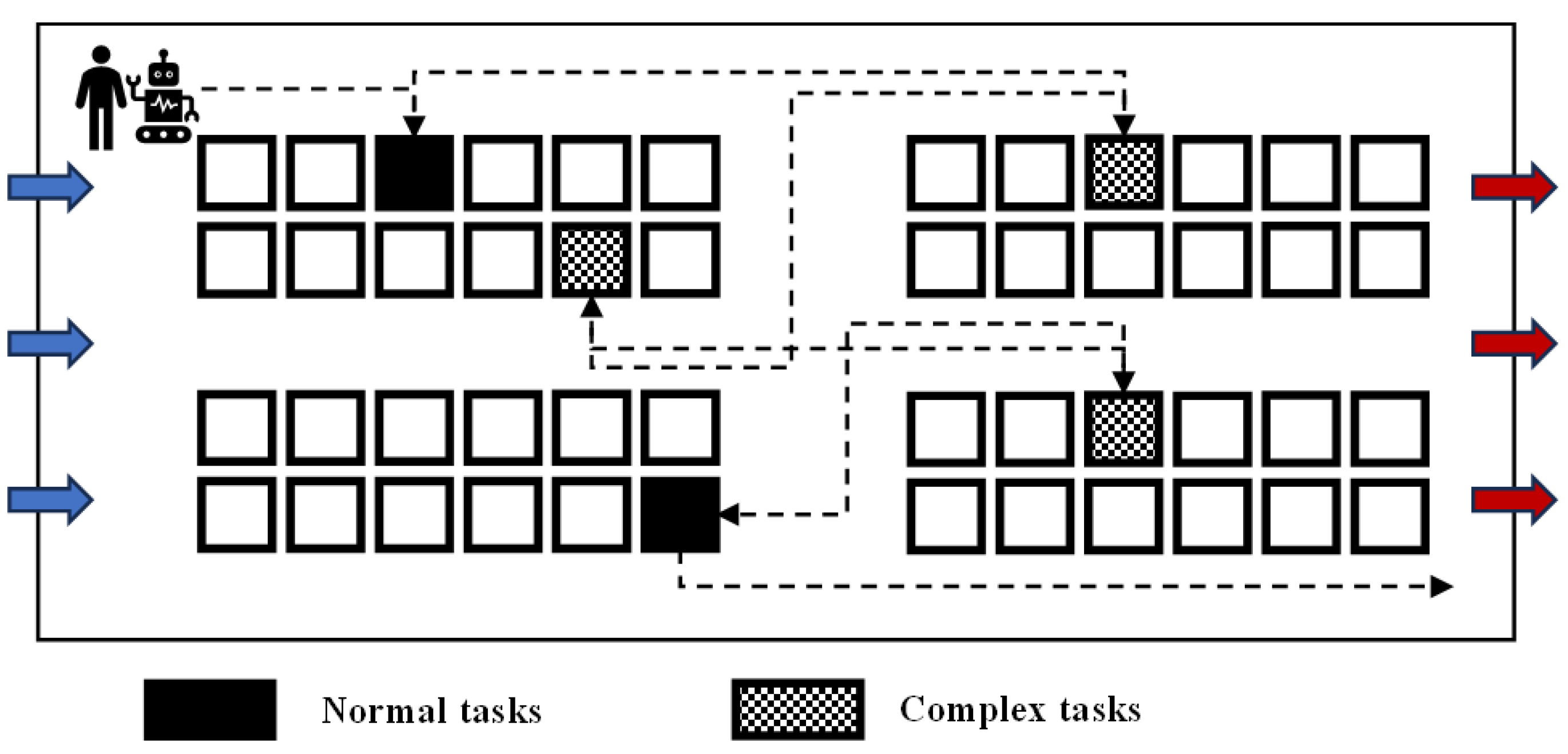
The real-world warehouse environment is not always ideal. Goods may have damaged or unclear identification codes or may be fragile—such goods are categorized as complex picking tasks. Other goods in normal condition are classified as normal picking tasks, as shown in Figure 2. Robots are less suited to handling complex tasks due to the likelihood of errors (e.g., misidentification, quantity mismatches). For such tasks, skilled workers can leverage their experience to achieve higher accuracy, although it takes them more time.
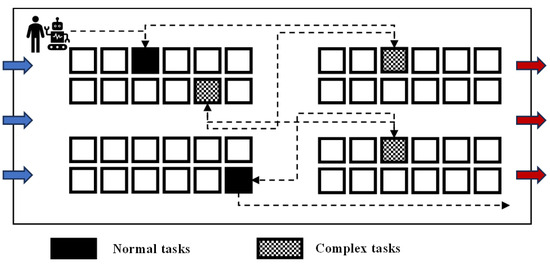
Figure 2.
Task classification.
4.1.2. Human–Robot Work States
In the described work environment, the human and robot collaboratively reach a task point where they identify the task type and decide whether to execute it. Human decisions are influenced by their trust level in the robot, while the robot evaluates and considers human trust levels when making its decisions. Key considerations include the following:
- If both the robot and the human decide to execute the task, the human checks the robot’s completed work. Frequent occurrences of this scenario disrupt the workflow and reduce efficiency;
- The state in which the robot chooses to execute the task while the human does not, which indicates that the human trusts the robot’s execution results. The frequent occurrence of this state may reduce the accuracy of collaboration;
- The state in which the robot frequently withdraws from tasks, leaving the human to take over. This leads to worker fatigue accumulation and a reduction in efficiency.
Thus, to reduce the occurrence of the above states, we optimize the robot’s decision-making based on the human’s trust state in the robot.
4.1.3. Stackelberg Trust-Based HRC Framework
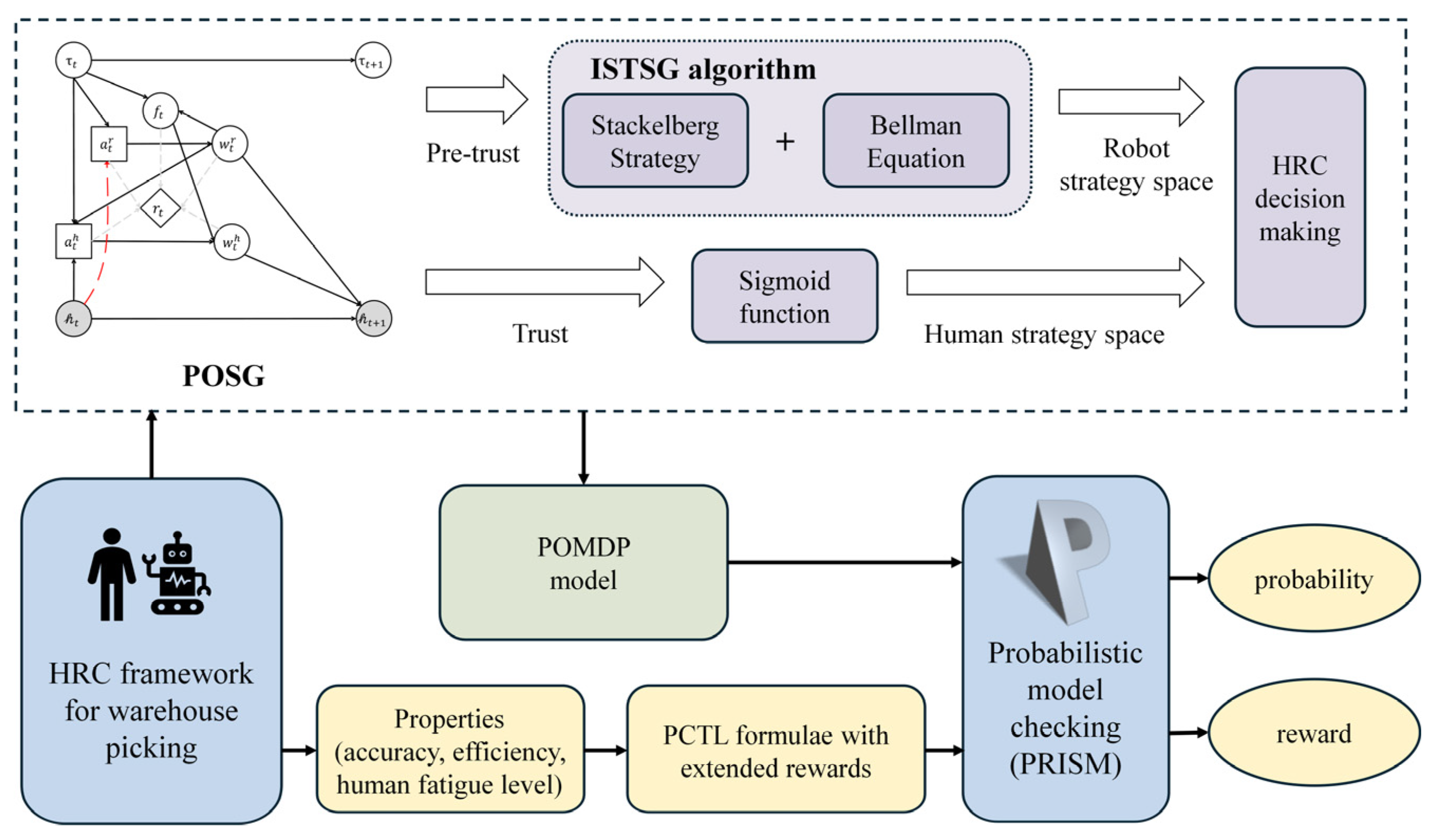
The Stackelberg trust-based human–robot framework for warehouse picking is illustrated in Figure 3. It contains three parts. First, the POSG is defined to model and evaluate human trust. Specifically, trust between the human and the robot is considered a hidden human state. This hidden state is modeled and calculated in a partially observable form. Since the model involves actions, states, and environmental states of both human and robot agents, game theory is used to establish interactions between them. Human trust dynamics are modeled using a linear Gaussian system, and Bayesian posterior belief space updates are employed for the robot to evaluate human trust. Then, based on human trust levels, a sigmoid function is applied to generate the human strategy space. An iterative Stackelberg trust strategy generation (ISTSG) algorithm is designed to solve the optimal robot strategy space, which is implemented by the Stackelberg strategy and the Bellman equation. This process forms the foundation for decision-making in human–robot collaboration. Finally, the obtained human–robot collaboration decision strategies are formalized as a Partially Observable Markov Decision Process (POMDP) model. The properties of human–robot collaborative picking are described as PCTL formulae with extended rewards. The POMDP model and PCTL formulae are verified and analyzed by the probabilistic model-checking tool PRISM. This enables our framework to be checked to establish whether it meets the probabilistic requirements and achieves efficiency optimization.
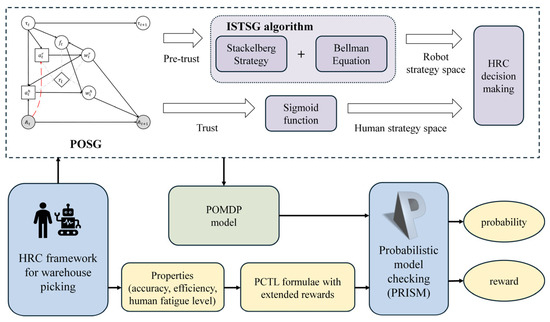
Figure 3.
Stackelberg trust-based HRC framework for warehouse picking.
4.2. Trust Prediction Based on the POSG
In human–robot collaborative warehouse picking, the robot cannot directly observe human trust. Therefore, human trust is treated as an imperfect information state, which is modeled using partially observable states, and the human–robot collaborative picking framework is established as a POSG.
4.2.1. The POSG Model
Definition 1.
An HRC with trust for warehouse picking is defined as a POSG , where
- : a set of players (human and robot);
- is a finite set of states;
- is a finite set of actions of player ;
- is a finite set of observations;
- is an observation function;
- is a transition function;
- is the reward function when actions have been jointly played in the joint state ;
- is the initial belief over states.
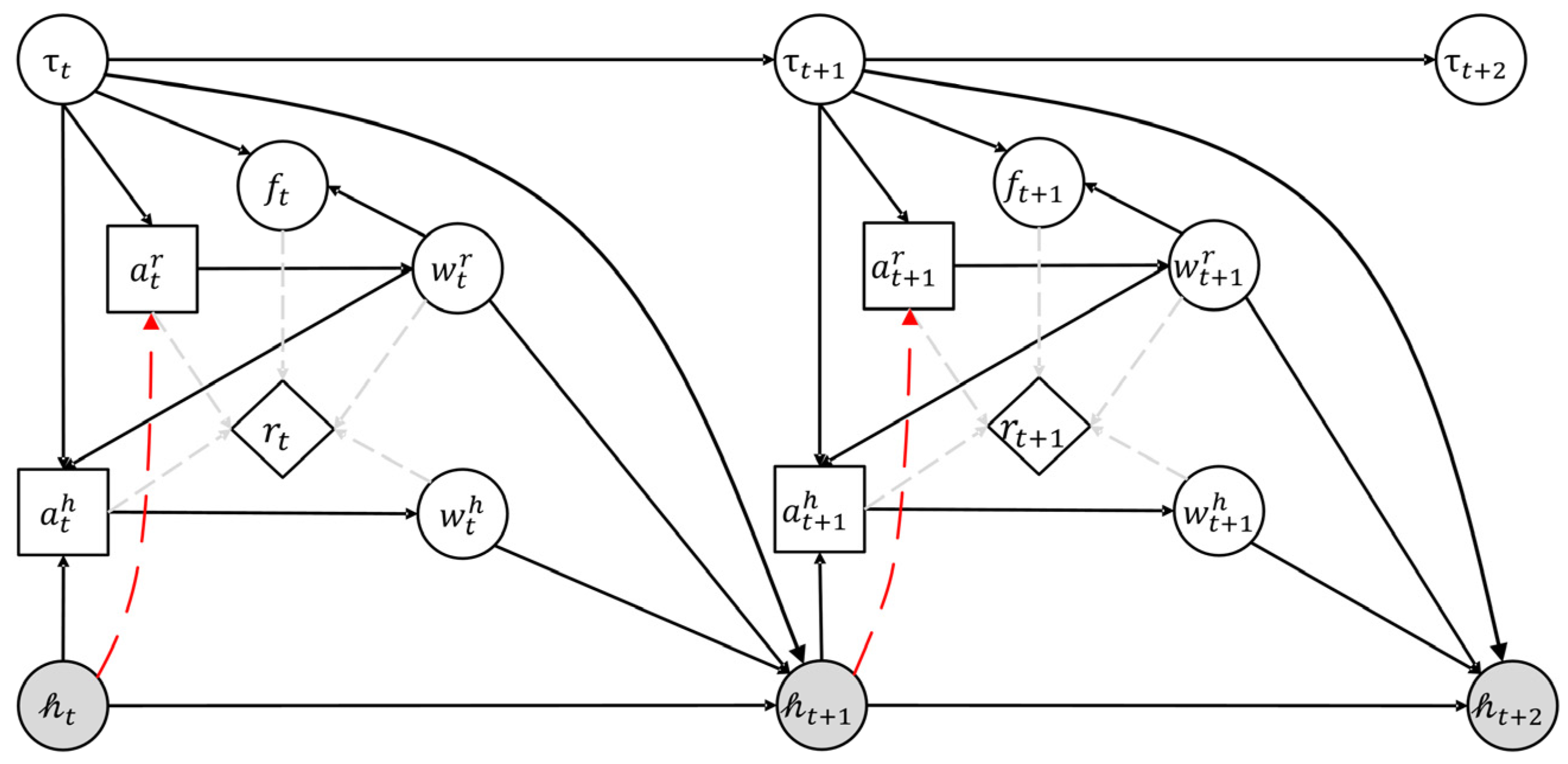
The game flow is shown in Figure 4, where humans and robots are participants. In this figure, circles represent states, squares represent actions, and diamonds represent reward functions. At time , the actions represent robot and human actions for task execution, which is observable for each player. The state at time is , which includes the following: means task type and is randomly distributed with probability , which influences the robot’s success rate, and both the human and robot can identify task types; means the work states of humans and robots , observable by each other, which depend only on their own actions and are determined by the transition function ; means the task outcome (success/failure), influenced by the task type and robot work state and is determined by ; means the human trust state, which is an internal trust level represented as a partially observable (gray circles in Figure 4) state accessible to the robot through the observation function (red dashed line in Figure 4). The solution for partially observable states involves establishing observations and updating them using the observation function . The HRC system’s real-time reward depends on the joint human–robot state and actions. The initial belief , representing the probability of distribution over states, is the shared knowledge between humans and robots. Some of the symbol interpretations in this framework are given in Appendix A.
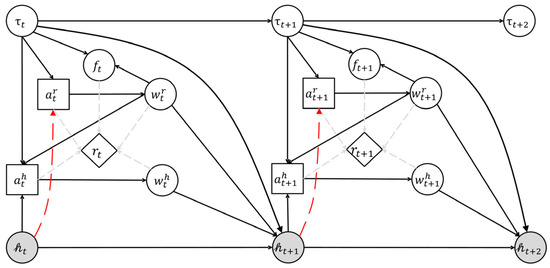
Figure 4.
POSG for HRC with trust.
Definition 2.
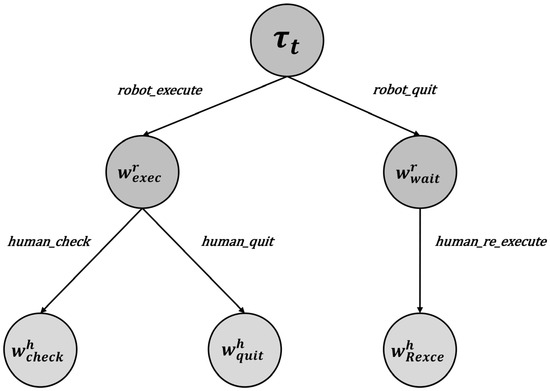
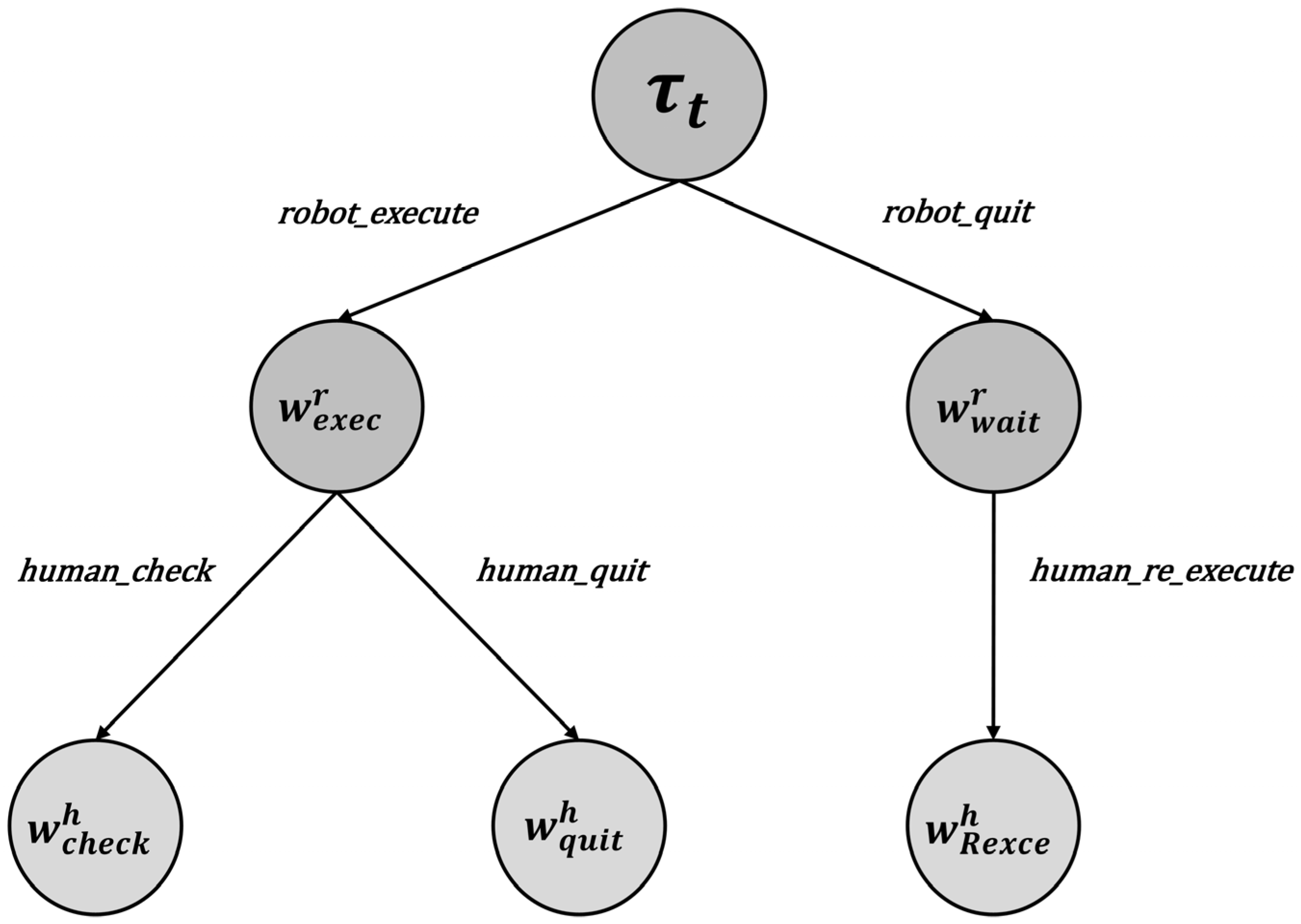
State Transitions As shown in Figure 5, the state transition diagram at time is depicted, and the explanation of states is given in Appendix B. Nodes with a dotted matrix background represent the “Task Start” state and indicate the task type. Nodes with a vertical line background represent the robot’s work state, while nodes with a grid background represent the human’s work state. At the beginning of a task, the robot first decides whether to execute the task. After observing the robot’s choice, the human makes a corresponding decision. Once the human executes their decision, they transition to the corresponding work state based on the observed outcome of the robot’s task execution.

Figure 5.
State transition diagram.
Definition 3.
Trust In this study, trust is defined as a hidden state of the human, which is not directly observable by the robot. The human’s trust level changes based on the robot’s actions for different tasks and the human’s corresponding responses. For example, if the robot opts not to execute a task, the human’s trust in the robot decreases. Trust is also task-dependent; for example, certain task types may exacerbate or mitigate trust changes. When the human decides to check the robot’s task execution, their trust level may change positively or negatively, depending on the observed outcomes.
The evolution of human trust is modeled as a linear Gaussian system, a method widely used in related studies [18,20,36]. The trust transition is linked to the work states of both the human and the robot:
where represents a Gaussian distribution with mean and standard deviation . The linear parameters and standard deviation are state-dependent. This study selects trust-related parameters using heuristic methods. Additionally, it optimizes these parameters based on human behavioral science principles, which includes loss aversion and framing effects.
The robot evaluates the human’s trust state based on observed outcomes.
Definition 4.
Observation Path The robot’s observation path is defined as follows:
where represents the observation update at time . This process combines the prior observation with the environmental state at time . It incorporates both human and robot actions along with their respective state data. The complete sequence initiates from the initial belief .
Using this observable path, the robot infers the human’s trust state through a belief state represented by a probability distribution.
Definition 5.
Belief The belief state in the POSG represents the robot’s conditional probability distribution of the human’s trust in each state:
where represents the observation probability. It indicates the likelihood of observing a specific outcome given the trust state and the task . Additionally, it considers the robot’s action and the robot’s work state . This explains the relationship between the new observation data and the trust state. is the total probability of transitioning from the previous trust state to the new trust state, which combines the transition function and prior belief. The normalization factor ensures that the updated belief is a valid probability distribution:
The belief update step provides the robot with an updated belief at each time step , which represents a new probability distribution over the human trust state . From this updated belief, the robot can further compute the predictive evaluation , which is treated as a specific measure derived from the belief distribution to predict the human trust state:
4.2.2. Reward Function
The reward function in the POSG represents the system’s immediate return in each state. We extend this reward function to the following two types: relates to collaborative efficiency and relates to collaborative accuracy. The symbol interpretations in reward function are given in Appendix C.
Efficiency Reward Function Related to Fatigue
When considering the reward function for human–robot collaborative efficiency, we incorporate human factors by treating human fatigue as a factor influencing the efficiency reward function. We model fatigue and recovery using the framework from Glock et al. [37]. This model has been adapted for our operating scenario. The implementation incorporates their original data and parameter settings.
For different task types, the robot does not show significant differences in execution time, while humans achieve higher execution accuracy on complex tasks but require more time. The regular time reward function for task execution is denoted as . Additionally, for humans, continuous operations lead to fatigue accumulation, which causes a decrease in execution efficiency. The fatigue accumulation reward function is denoted as . Considering the above factors, the efficiency reward function for human–robot picking is defined as follows:
A reasonable explanation is provided here for the efficiency of human–robot operations. The regular time reward function for different work states is shown in Table 1. Among them, the efficiency is highest when the robot executes tasks alone without human inspection. Efficiency decreases when the robot exits the task and the human executes it, as the subjectivity of the human results in slightly lower efficiency for complex tasks compared to normal tasks. The efficiency is lowest when the robot executes the task and the human inspects it. In this case, the value is set as the expected efficiency of correcting errors and performing inspection tasks when no errors are found. Therefore, when handling complex tasks with lower robot accuracy, the reward value in this state also decreases.

Table 1.
Reward function related to efficiency.
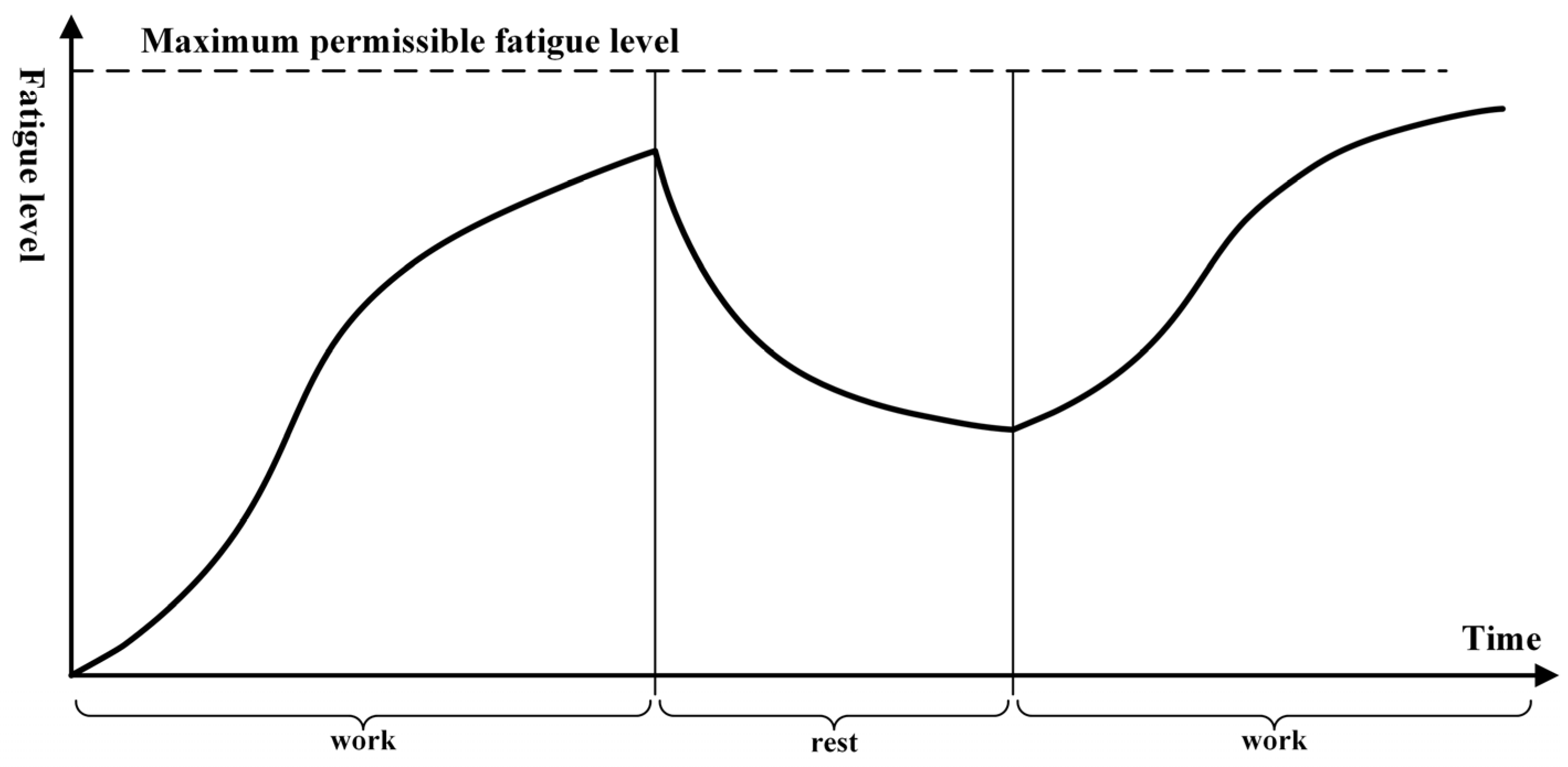
In a long-term working environment, workers’ accumulated fatigue leads to an increase in their working time. However, during non-working periods, their fatigue is alleviated, and they gradually recover. For the fatigue accumulation function of humans during continuous work
At the same time, when the human is not involved in tasks, their fatigue is alleviated. The fatigue recovery function at this point is
The fatigue function is triggered under different human states:
where is the sigmoid function, represents the fatigue level at time , and and represent the fatigue levels under different continuous work states. The continuous fatigue function is discretized into different fatigue levels. and are the coefficients of the fatigue growth rate and decay rate, respectively, representing the impact of work or rest states on fatigue levels; indicates the most recent time point at which a switch between work and rest states occurred; represents the time point when the fatigue levels reach half of the maximum; and is the maximum fatigue level. In a healthy state, a worker’s accumulated fatigue does not significantly affect their work time beyond a certain point. However, the higher the fatigue level is, the longer the time required to complete the same task. The fatigue function is shown in Figure 6. Therefore, the fatigue reward function is determined by the human’s fatigue level and the basic task execution time:
where is the coefficient representing the impact of fatigue on execution efficiency.
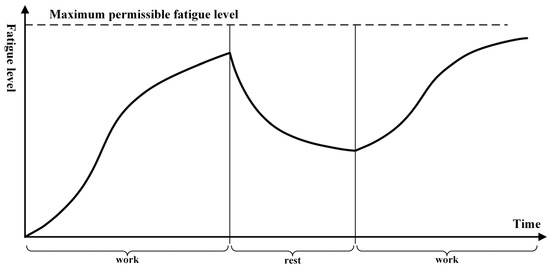
Figure 6.
Human fatigue function.
Accuracy Reward Function
We provide the reward function related to accuracy based on the states of the human and robot , as shown in Table 2.

Table 2.
Reward function related to accuracy.
4.3. Human–Robot Decision-Making Based on Multi-Round Trust
In this section, we first provide a rationale for human–robot strategies. We first derive the human strategy based on human trust. Then, we generate the optimal robot strategy through the robot’s multi-round trust evaluation of humans. The symbol interpretations in human–robot decision-making are given in Appendix D.
In traditional decision-making models, decisions are often made based on precise calculations of the value function. However, in human–robot collaborative picking environments, humans typically struggle to accurately evaluate various benefits due to limitations in energy and computational capacity. Instead, human decisions are more influenced by their level of trust in robots. Trust serves as a cognitive simplification mechanism, which enables humans to make quick decisions in complex environments. While these decisions may not always be optimal, they still reflect a certain level of reliance on the robot’s reliability.
- (1)
- Human Strategy
This study uses trust as a weighting factor in decision-making. Trust directly influences human confidence in the robot’s actions, which is reflected in the decision-making process. For instance, when humans have high trust in robots, they are more likely to rely on the robot’s actions and intervene in the picking tasks with a lower probability. In the decision-making process, a function is introduced to weigh the probability of human choices [20]:
where is the sigmoid function, and represents the benchmark for execution probability under different task types and robot work states. The function is expressed as a step function, which acts as a trust-weighted function. This function reflects how humans recognize different task types during the process and react accordingly. For instance, humans show a significantly strong willingness to intervene when robots handle more complex tasks compared to normal tasks. Of course, this correlates with their trust in the robot. Hence, task types are integrated into the trust-weighted function. The most crucial aspect of the trust-weighted function is the human’s current trust state in the robot, which has a profound impact on the probability of intervention. From the human action probability matrix, human strategy is derived.
- (2)
- Multi-Round Robot Strategy
The collaborative picking process between humans and robots can be considered a sequential game, where participants take turns making decisions in a specific order. Each participant’s decision can be influenced by prior events or the actions of other participants. A key feature of this type of game is that agents can observe previous actions, which influence their decisions and ultimately shape the outcome. The Stackelberg game is a typical sequential game that clearly defines a decision-making order, where the leader moves first and the follower moves subsequently. The leader makes decisions while fully anticipating the follower’s response, which enables more rational decisions. After observing the leader’s decisions, the follower adopts an optimal strategy based on their best interests.
We aim to consider the impact of the robot’s decision in the current round on subsequent rounds in a continuous working state; in other words, a multi-round chain reaction. We combine the Stackelberg strategy with the Bellman equation to solve the robot’s multi-round optimal strategy. This process is referred to as the ISTSG algorithm, which solves trust-based human–robot collaborative strategies.
First, based on the definitions and working mechanisms of the trust model proposed in this study for the human–robot collaborative picking mode, the robot is designated as the leader and the human as the follower. Trust evaluation serves as a bridge for the robot leader to anticipate the human follower’s responses. Through the robot’s trust evaluation of the human, predictions of the human’s strategy are derived:
Since humans find it difficult to calculate optimal benefits (including task accuracy and time efficiency) in real time during continuous work, they instead make decisions based on their trust in the robot. Therefore, we aim to achieve optimal benefits by adjusting the robot’s strategy. First, a baseline system accuracy is set to determine the range of robot strategies:
where represents the system’s requirement for the minimum accuracy of picking tasks, is the probability function of the robot strategy set that meets the system’s minimum requirements, is the discount factor, and represents the task execution accuracy at round . The function differs slightly from , where denotes the probability distribution of task types in the environment. The overall significance of this formula is to calculate the range of robot strategies. These strategies must meet the system’s required minimum collaborative picking accuracy. The discount factor determines the precision and scope of the calculation, thereby reducing computational complexity. The Stackelberg strategy combined with the Bellman equation is used to solve the optimal strategy, according to (14):
We use a model-based exhaustive strategy search to solve the optimal strategy space from the strategy set, combining a grid search with a forward multi-stage decision simulation. Specifically, by simulating the forward multi-stage decision space, we update the belief space and trust value for each round and use a discount factor to accumulate multi-stage rewards, reflecting time preference. The parameters for the forward stages are subjected to brute-force enumeration. Candidate strategies are compared to determine the optimal strategy that yields the best benefits. The algorithm is shown in Algorithm 1.
| Algorithm 1. Iterative Stackelberg Trust Strategy Generation | ||
| Input: | ||
| Output: | ||
| 1 | Initialization; | |
| 2 | ; | |
| 3 | Determine effective turn probability accuracy; | |
| 4 | ): | |
| 5 | Evaluating human strategies: | |
| 6 | ; | |
| 7 | Find a policy set that meets system requirements: | |
| 8 | perform | |
perform end End | ||
| 9 | , including the corresponding execution probability of the human | |
| 10 | Maximum value: | |
| 11 | : | |
| 13 | ||
4.4. Decision Analysis with Probabilistic Model Checking
In this section, we will use the probabilistic model-checking tool PRISM to verify and analyze the human–robot collaboration strategies. First, we formalize the human–robot collaboration strategies as a POMDP.
Definition 6.
The human–robot collaboration strategies are formalized as a POMDP , where
- is a finite set of states;
- is a finite set of actions;
- is a finite set of observations;
- is an observation function;
- is a transition function;
- is the reward function;
- is the initial belief over states.
If the human–robot strategies are determined, the state transition relationships between the human and robot can be established through module in PRISM.
Second, we specify the property of human–robot collaborative picking as a PCTL with rewards. The syntax of the PCTL formulae includes the following:
where is a state formula, is a path formula, is an atomic proposition, , , is a reward structure, , and . The probabilistic operator () is used to specify the trust probability distribution and the probability distribution of human fatigue. Additionally, we use reward operators () to specify and calculate the efficiency and accuracy of collaboration. The intuitive meanings of the and operators are as follows:
- : The probability that a path satisfying path formula satisfies the bound .
- : The expected value of reward formula or or , under reward structure , satisfies the bound .
We use reward properties to verify the HCR system’s efficiency and accuracy. The reward property is set as described in Section 4.2.2. The reward for accuracy is calculated by dividing the number of correct rounds by the total number of rounds. We also use probabilistic properties to verify the probability distributions of trust values and human fatigue levels and calculate their expected values. The variation in trust values helps demonstrate the effectiveness of our framework in influencing human trust.
5. Experiment
In this section, we conduct experiments to validate our framework. The experiments are completed on an AMD Ryzen 7 5800H CPU with 3.2 GHz and 40 GB memory. The ISTG algorithm is implemented by Python 3.10.9, and the PRISM version is PRISM 4.7 (GUI model). We take the human–robot collaborative picking process in [38,39] as the case. It uses robot TORU developed by Magazino GmbH in Zalando for human–robot collaborative picking. Unlike other picking robots that can only transport shelves (such as pallets or crates), the mobile TORU utilizes artificial intelligence and a 3D camera to identify, grab, and transport individual items. Furthermore, TORU robots have already been deployed in parallel with workers in the Zalando warehouse. With laser scanners and 3D sensors, TORU can ensure worker safety within the same workspace. It offers higher efficiency and a lower cost compared to traditional shelf-handling robots. However, it is still limited by technological constraints, particularly the robot’s ability to handle picking frames with inaccuracies, such as the need to neatly arrange goods. Workers sometimes need to intervene to check tasks, which reduces workflow efficiency. Our framework effectively enhances this human–robot collaboration with robot TORU. We obtained the TORU datasheet from Magazino and collected related simulation data. These datasets were used to configure the experimental parameters. The corresponding models and properties to be verified can be downloaded from https://github.com/Gyoun9/HRC_trust_prism (accessed on 17 February 2025).
First, a Partially Observable Stochastic Game (POSG) was developed using Python to simulate uncertainty and decision-making interactions in a human–robot collaborative environment. Within this model, human trust is represented as a linear Gaussian system, with parameters derived from prior works on human–robot trust [20]. To enable a real-time evaluation of human trust by the robot, a Bayesian posterior-based belief space representation was employed. The effectiveness of the proposed trust modeling and evaluation approach is experimentally validated in Section 5.1. Second, we generated human strategies using a sigmoid function based on dynamic trust evolution and constructed three different robot strategy models for comparative analysis. These models include the following: (1) a no-trust model that disregards human trust factors; (2) a single-round trust strategy model that considers human trust but optimizes robot decisions based solely on single-round rewards; and (3) a multi-round trust strategy model incorporating multi-round optimization. This part is completed in Section 5.2. Third, we formalized both human and robot strategies as a Partially Observable Markov Decision Process (POMDP) within the PRISM model checker. The extended reward-based PCTL formula was then used to specify and verify the key properties of human–robot collaborative picking. By comparing the three robot strategy models, we analyzed the advantages of our framework in terms of collaboration efficiency, decision-making rationality, and system stability. This part is completed in Section 5.3.
5.1. Human Trust and Evaluation
This subsection focuses on exploring and quantifying the dynamics of human trust in robots under different scenarios. To achieve this goal, the states in the POSG model were meticulously designed. Specifically, task types were categorized into normal tasks and complex tasks . The normal tasks are less challenging, and robots typically achieve high accuracy in completing them. In contrast, complex tasks are more difficult, and robots demonstrate lower accuracy when handling them. In addition to considering whether the robot executes the task, human behavior was also incorporated into the analysis. These three factors generated six distinct scenarios, which will be explained in detail later.
To evaluate the impact of these scenarios on human trust, the trust value was set within a range of 1–7, which is inspired by the 7-point Likert scale. This scale, commonly used in psychology, is a questionnaire-based metric that captures varying degrees of human psychological attitudes toward other entities. In this study, it represents the degree of human trust in robots. The dynamic changes in trust were modeled using the linear Gaussian system, where the mean is controlled by parameters and . Parameter represents the relationship between trust change and initial trust, with larger deviations from the standard indicating more significant trust changes at higher trust levels. Parameter adjusts trust change for smaller trust values, exerting greater influence at lower trust levels. The standard deviation controls the uncertainty of trust changes, with higher values indicating broader trust variations and increased uncertainty. The parameters of the linear Gaussian system are referenced from previous studies on human–robot trust, with the data sourced from surveys [20].
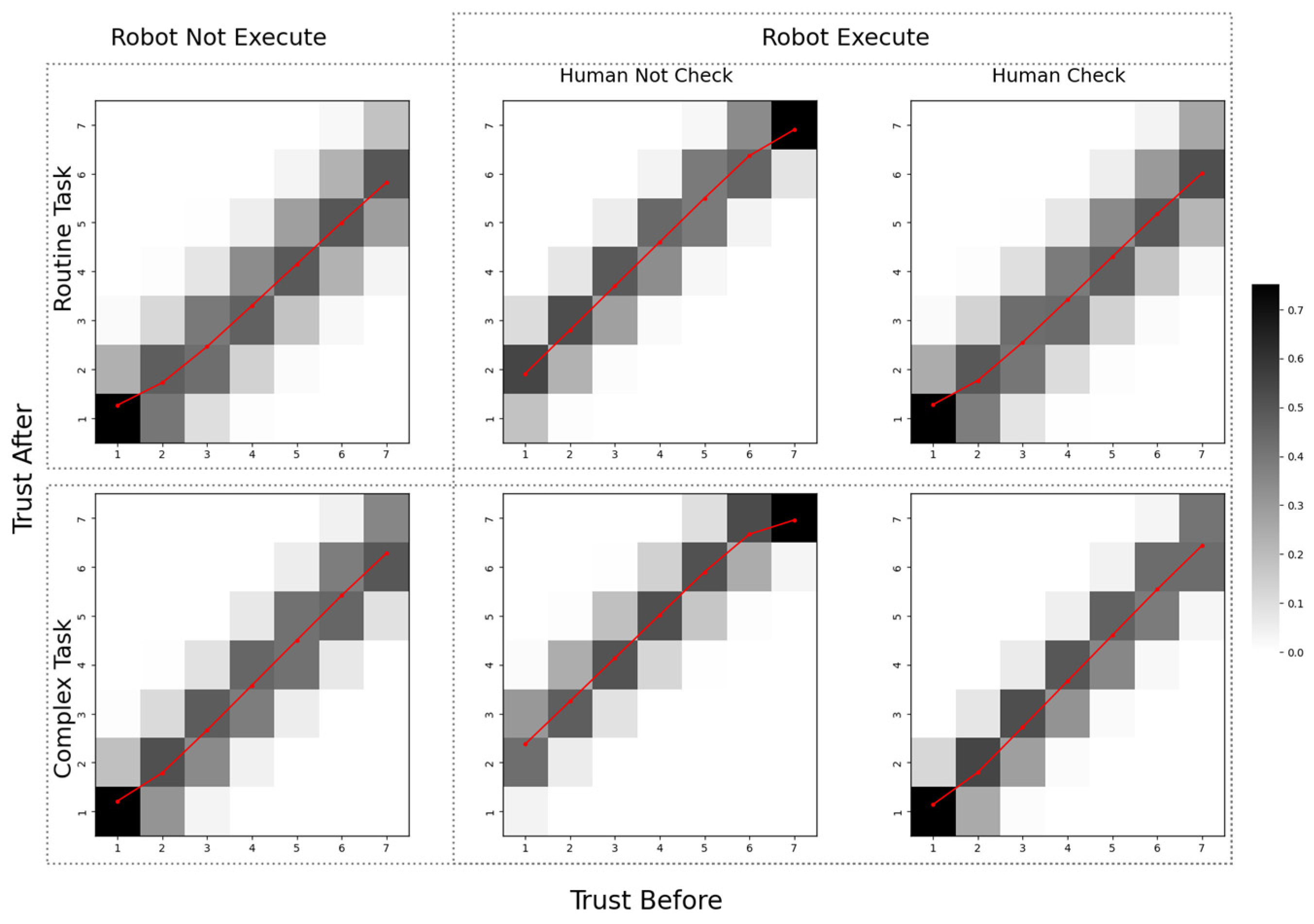
The changes in human trust are represented as a trust transition matrix, as shown in Figure 7. The horizontal axis represents the initial trust value, while the vertical axis represents the updated trust value. Each element of the matrix indicates the probability of trust transitioning from one state to another. The shade of color in different matrix cells indicates the corresponding transition probabilities, with darker colors representing higher probabilities. Additionally, red line segments are used to denote the expected values of trust transitions.
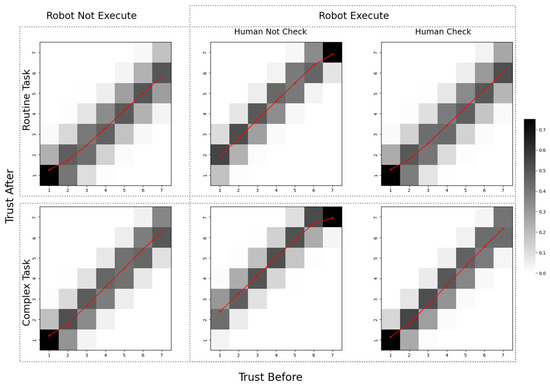
Figure 7.
Trust transition matrix.
Furthermore, we implemented the belief space approach described in Section 4.2 within the program. We constructed the belief space and defined the belief update function according to Equation (3). This update mechanism was integrated into the POSG state transition process to enable dynamic belief updates. Additionally, we established the robot’s trust evaluation of humans based on Equation (5), with its variations represented by the red line in Figure 7. The experimental results demonstrate that the proposed POSG model effectively models human trust. It also enables real-time robot trust assessment through the Bayesian posterior-based belief space.
5.2. Human Strategy and Robot Strategy
In this subsection, the strategies for both humans and robots are generated, with the primary focus on robot strategies based on human trust. To support the proposed framework, three types of robot strategy models are considered.
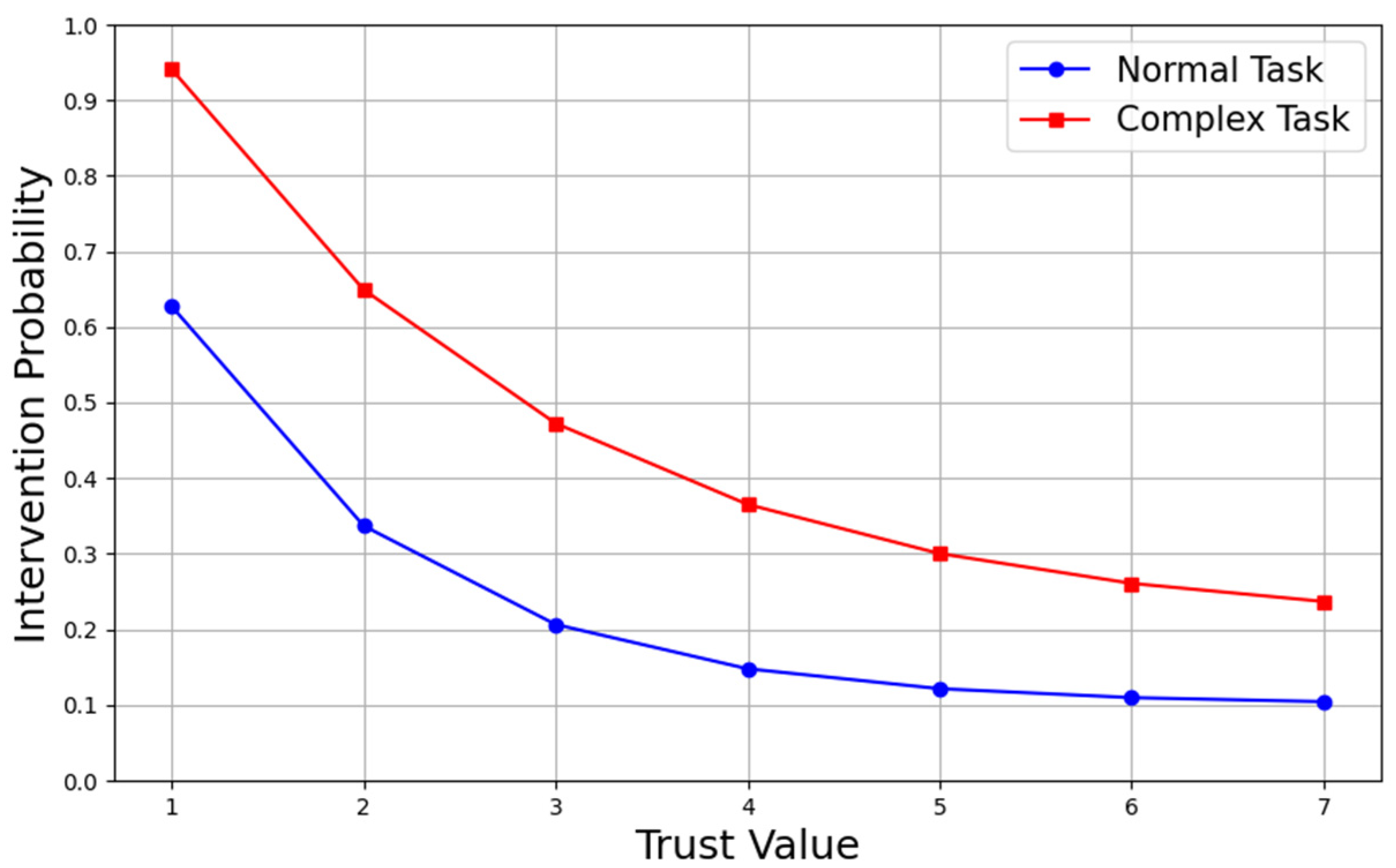
For human strategies, the strategy for tasks is given by Equation . As a follower in the collaborative system, humans first observe and consider the actions of the robot leader. If the robot chooses action (not executing the task), the human strategy becomes a pure strategy, . If the robot chooses action (executing the task), the human strategy is influenced by trust and depends on the task type. The human strategy is expressed as a set of probabilities for executing actions, as shown in Figure 8. The intervention probabilities under different trust states are provided for various task types. The blue line indicates the intervention probability for regular tasks, while the red line represents the probability for complex tasks.
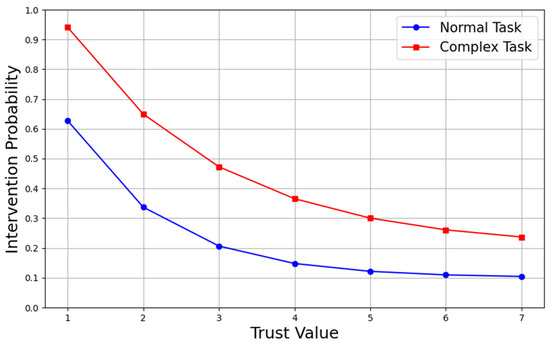
Figure 8.
Human intervention probability for tasks.
For the robot strategy model, the main contribution of this study is the proposed strategy algorithm, where robots consider long-term rewards based on human trust dynamics. To validate the effectiveness of our framework, three types of robot strategy models are considered:
- No-Trust Model: In this model, the robot ignores human trust during the collaborative process. While human strategies are influenced by their own trust levels, the robot does not consider these trust factors. The robot is fixed to execute regular tasks and opts out of complex tasks, with no adjustments based on the progression of events in the human–robot collaboration.
- Single-Round Trust Strategy Model: In this model, the robot evaluates human trust using the belief space and assesses human strategies based on the evaluated trust. For each task, the robot applies the single-round Stackelberg strategy to achieve optimal benefits within that round:
- Multi-Round Trust Strategy Model: We adopt the multi-round trust strategy into the human–robot collaboration. This model not only considers the impact of trust on the current task but also considers how the robot’s decisions influence future states. It achieves better long-term benefits and adjusts future human trust through the robot’s decision-making process.
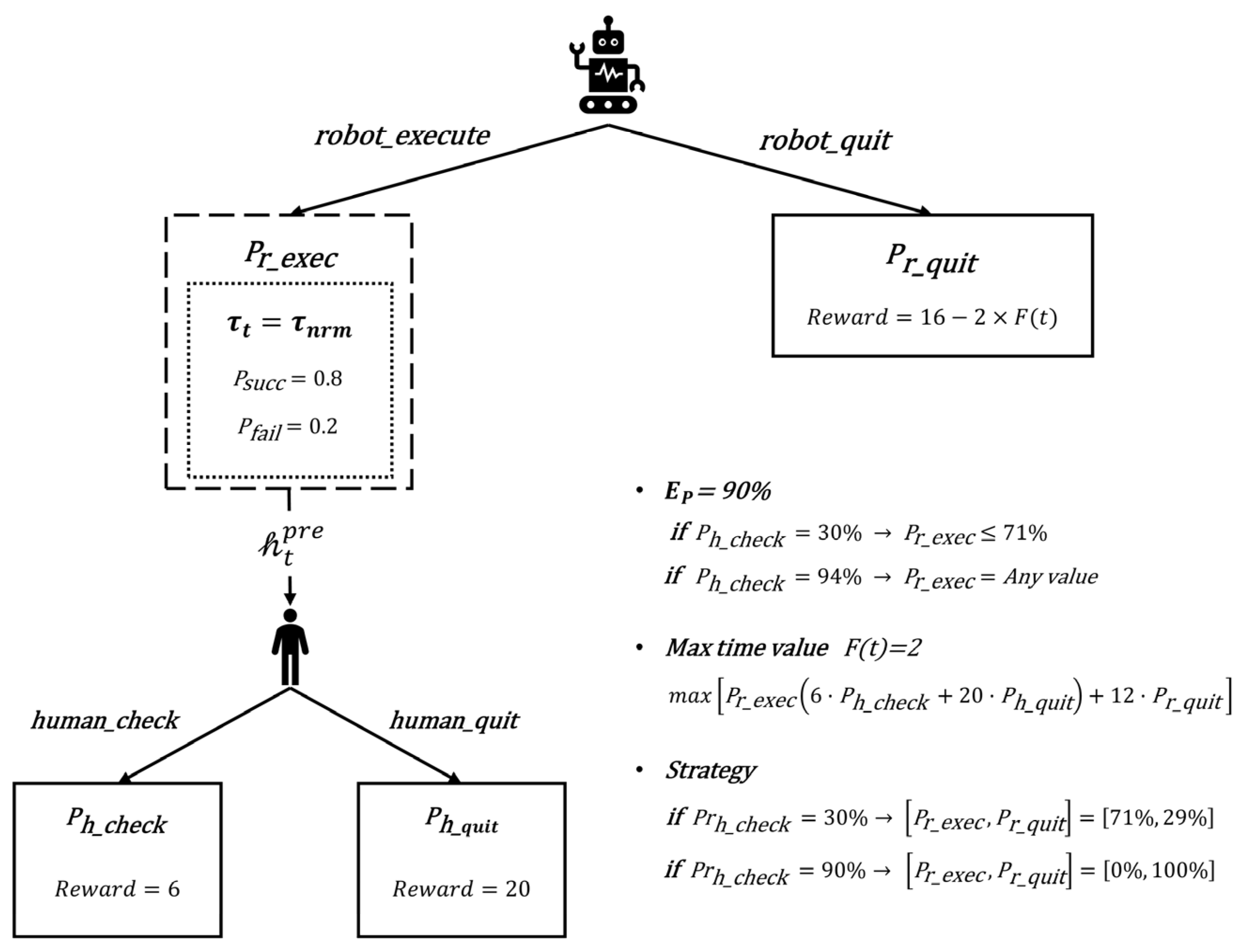
For the single-round trust-based strategy model, we use the example shown in Figure 9 for explanation. A collaborative human–robot configuration encounters a task node where the task type is a complex task . This task type determines the robot’s task execution success rate as . The system’s requirement for human–robot collaborative picking accuracy is set as . Under different trust states , the human intervention probability is derived using Equation . Based on Equation , the range of robot action probabilities that satisfy the system’s accuracy requirement is obtained. Within this range, the robot’s single-round optimal strategy is further calculated. The reward function depends on the human fatigue level, which is assumed to be in this example. When , the mixed strategy is obtained. When , the pure strategy is derived.
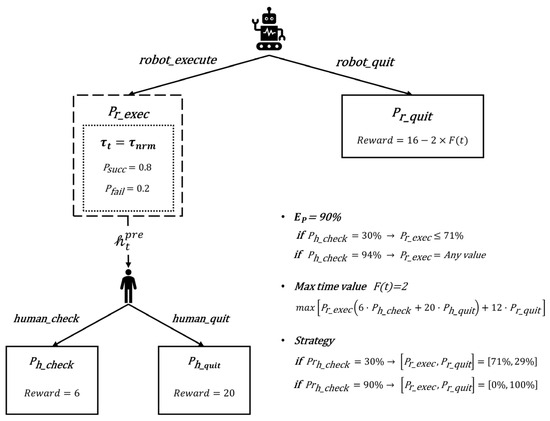
Figure 9.
Robot strategy for a specific task in the single-round trust-based strategy model.
For the strategy spaces generated by the three robot strategy models, we subsequently constructed corresponding formal models in PRISM to validate their effectiveness and applicability in human–robot collaborative picking tasks.
5.3. Formal Modeling and Verification
We used the method presented in Section 4.4 to formally model and verify three strategy models. We then compared our framework with the no-trust model and the single-round trust strategy model to demonstrate the advantages of our proposed approach.
5.3.1. POMDP Model
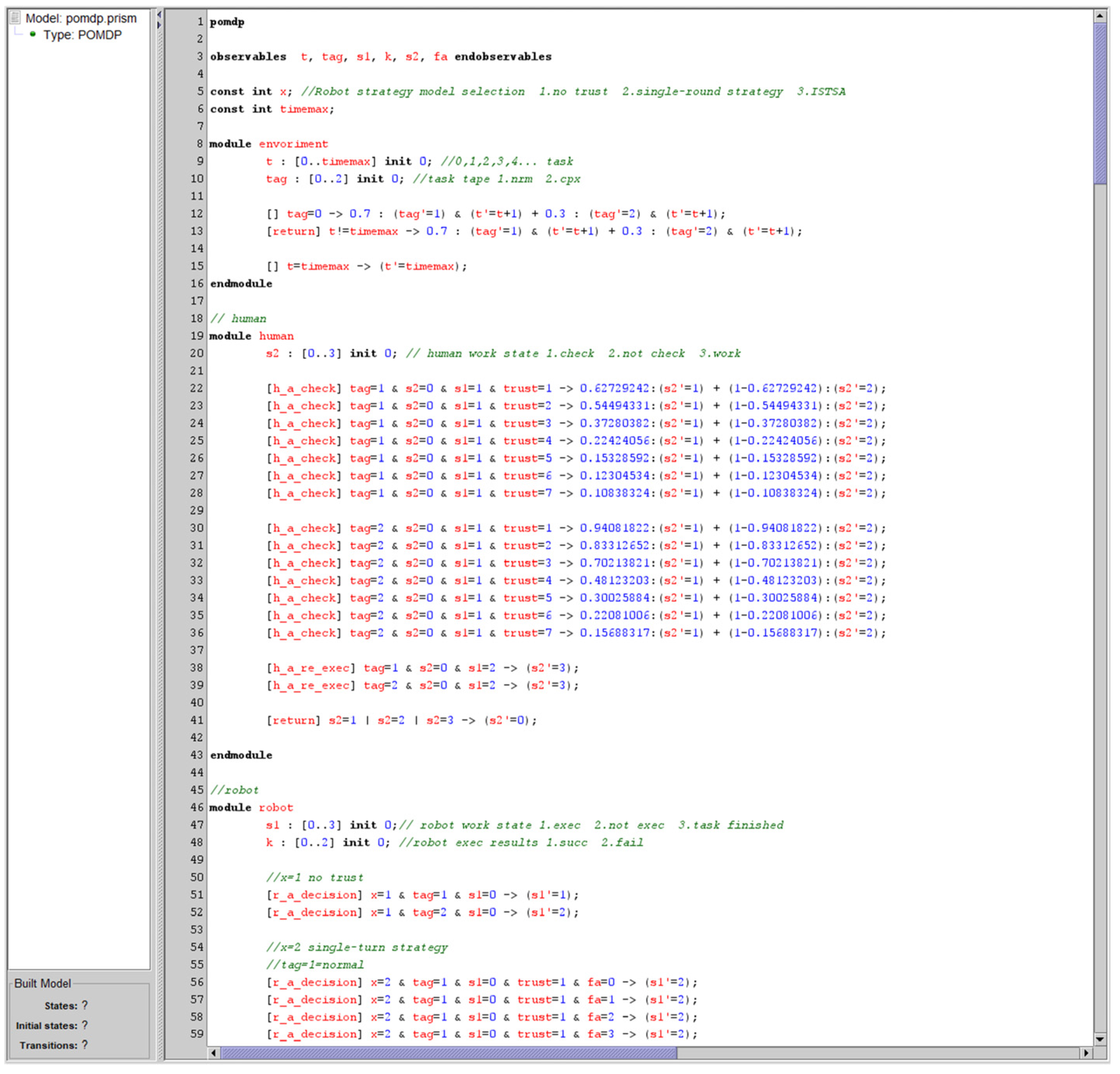
Figure 10 illustrates the constructed POMDP model. First, a constant const int x is defined as a control switch for selecting different robot strategy models. Corresponding modules are then created to implement state transitions for the environment, human, robot, and trust components within the model.
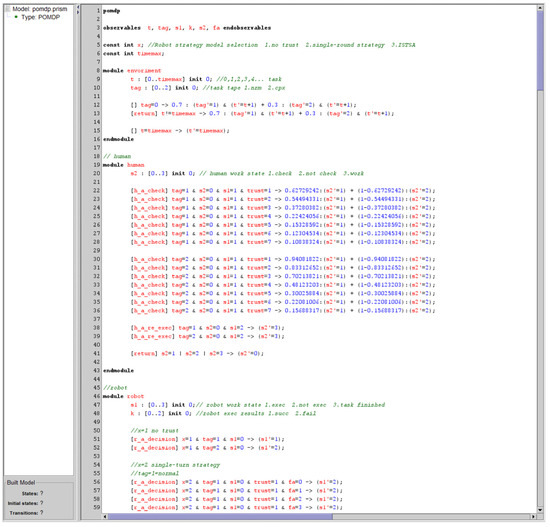
Figure 10.
PRISM model.
Explanation The environment module handles the probabilistic transitions of task types and implements the functionality for round timing. The human module manages the state transitions of humans, which reflect their strategies under different trust states. The robot module governs the state transitions of the robot and represents the robot strategies under the three trust strategy models: no-trust, single-round trust-based, and multi-round trust-based strategies. The fatigue module models the changes in human fatigue levels, which influence the reward function. The trust module models the transitions of human trust states, representing them as partially observable states. Two reward functions are defined in the model: one related to work efficiency and the other to task accuracy.
5.3.2. Model Verification
Our goal is to optimize the efficiency of human–robot collaborative picking while considering human factors to reduce human fatigue during work. We formalized the properties using the extended reward PCTL formula described in Equation (15) and validated our framework by changing the probability distribution of task types in the environment. To match the characteristics of continuous human–robot collaboration in industrial environments, the experiment simulates 100 consecutive rounds of collaboration. The PRISM model-checking tool is used for simulation, with a sample size of 10,000 to meet the verification requirements of the system.
- (1)
- Trust
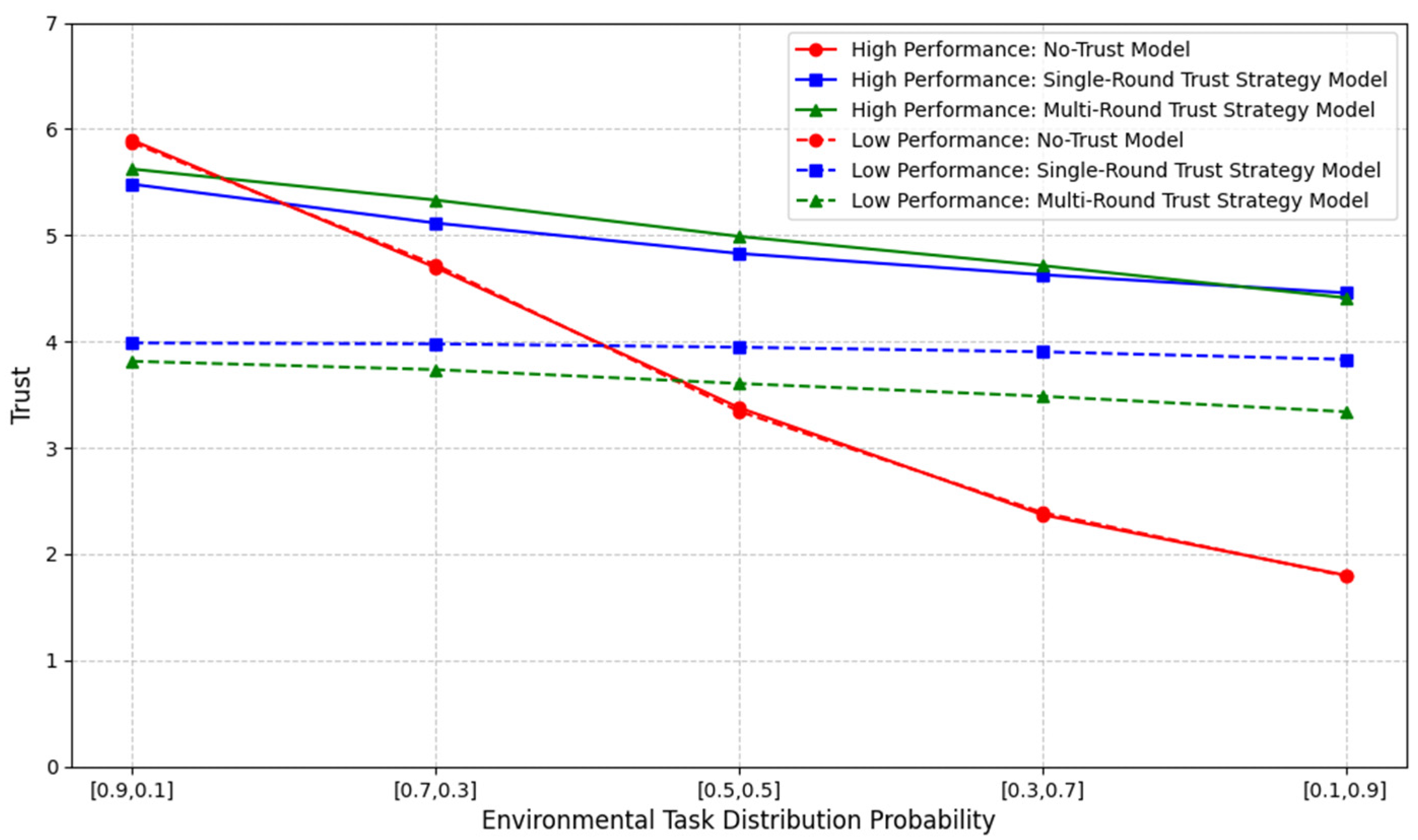
First, we used the probabilistic formula to verify the reasonableness of human trust dynamics and the effectiveness of the trust evaluation in the proposed model. The results are shown in Figure 11, where represents different trust states, and the corresponding reachable probability value is calculated based on the probabilistic formula. Finally, the expected trust value is computed as , yielding the resulting data. Two groups of robots with different performance levels were set up as a comparative experiment, and the task type distribution probability in the environment was varied. For example, a horizontal axis label of [0.7, 0.3] indicates that regular tasks occur with a probability of 0.7 and complex tasks with a probability of 0.3. In the figure, the solid line represents the average trust probability when humans collaborate with high-performance robots, while the dashed line represents low-performance robots. It is evident that in the trust-independent model, human trust varies with changes in the task-type distribution in the environment. In contrast, in the trust-based model, trust is proportional to the robot’s performance.
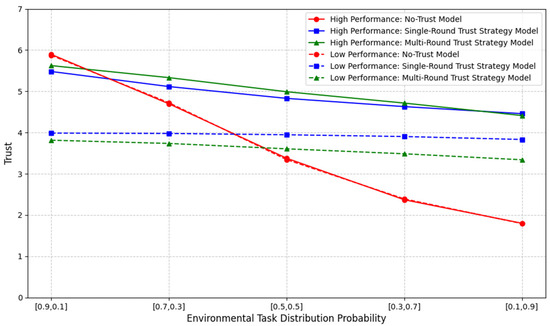
Figure 11.
Trust dynamics.
- (2)
- Efficiency
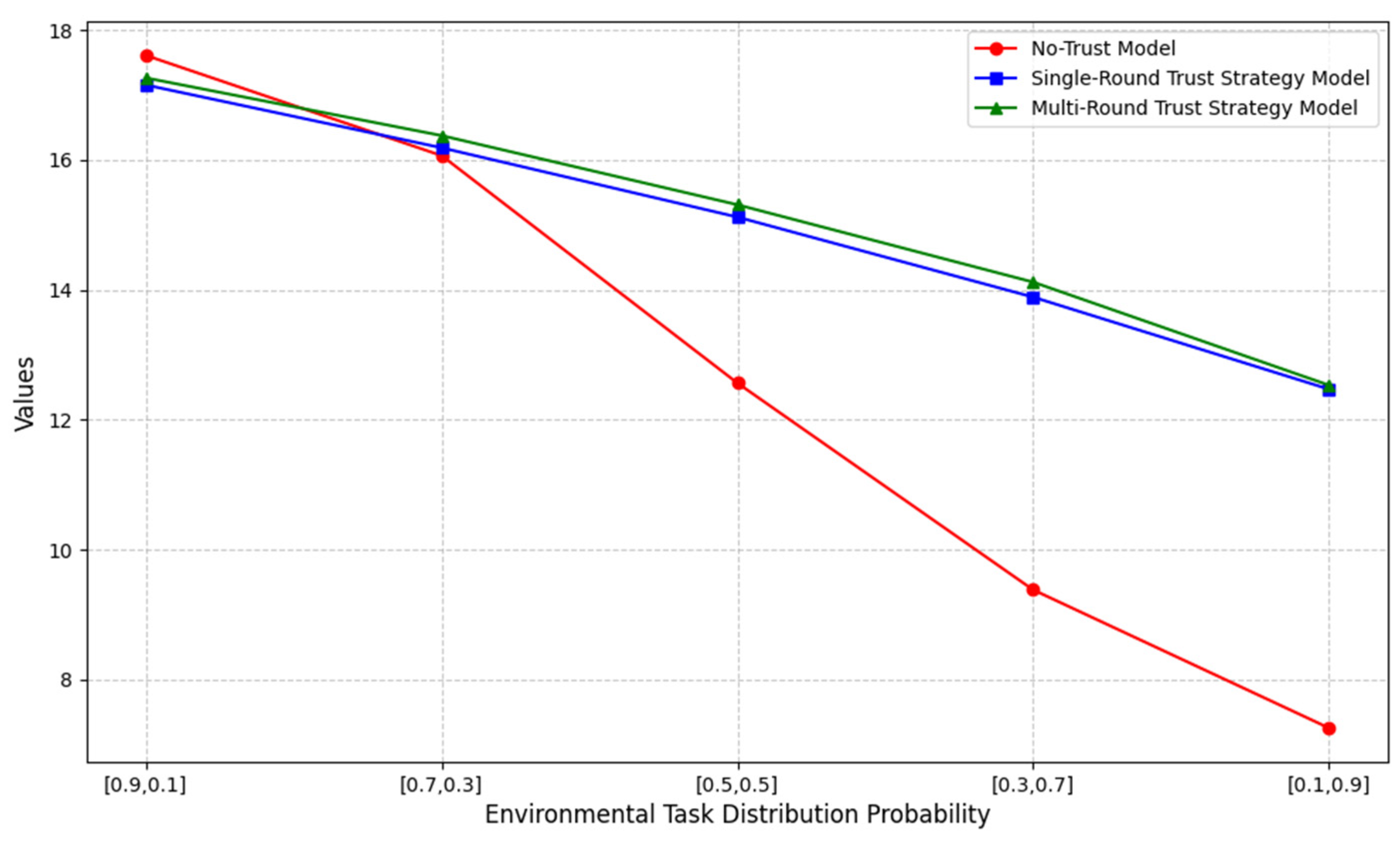
In subsequent experiments, we based our analysis on the high-performance robot. Using the reward formula , the system’s picking efficiency was verified and compared. The results are shown in Figure 12, which represents the reward function related to human–robot collaborative efficiency.
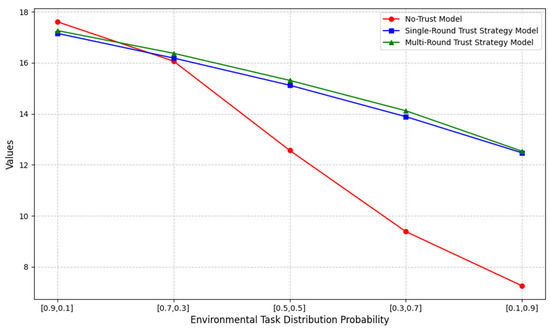
Figure 12.
Efficiency values.
To provide a more intuitive representation, we compared the multi-round trust strategy model data with the no-trust model and the single-round trust strategy model, as shown in Table 3. The table presents efficiency comparisons under different environmental settings. We compared the average values of the data for each environmental state. It is evident that our framework significantly outperforms the no-trust model, with an overall improvement of approximately 20.24% in work efficiency. Compared to the single-round trust strategy model, our framework achieves a smaller but notable improvement of around 1.05% in efficiency.

Table 3.
Model efficiency values comparison.
- (3)
- Fatigue
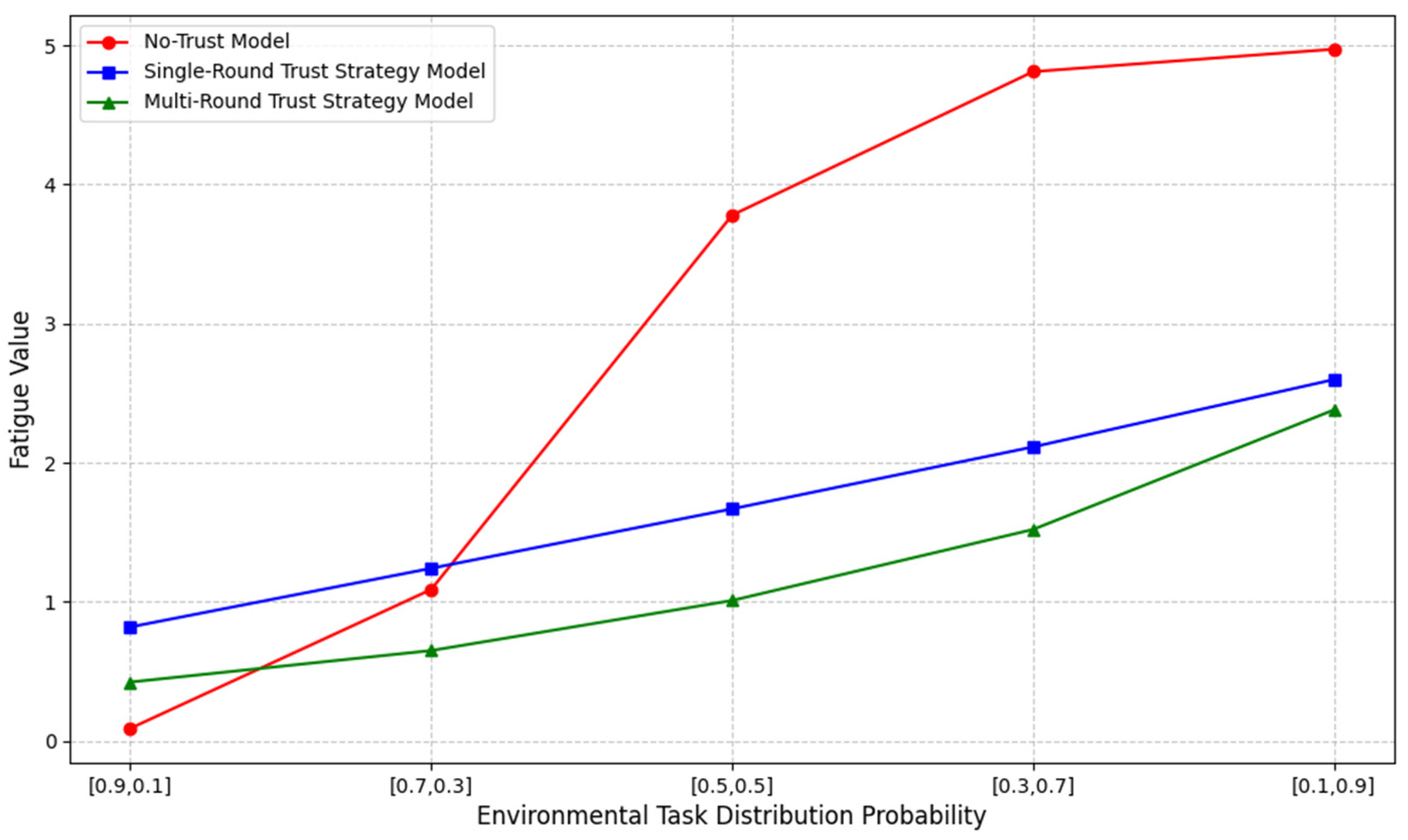
Next, we applied the probabilistic formula , and similarly, we calculated the final result by taking the expectation of the fatigue levels and their corresponding probabilities. The results are shown in Figure 13, which presents data on worker fatigue levels in human–robot collaboration. The environmental settings used for this validation follow those established in the efficiency experiments.
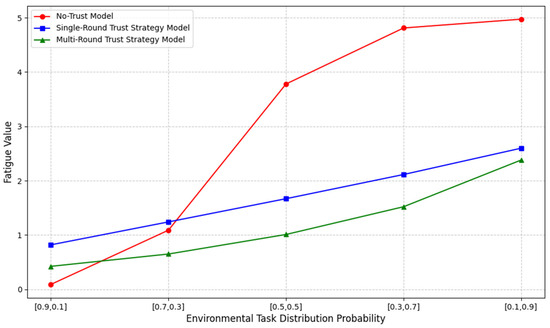
Figure 13.
Fatigue levels.
Similarly, to make the data more intuitive, a comparison of fatigue levels is presented in Table 4. Our framework significantly alleviates human fatigue during work compared to the other two models. From the average values shown in the table, the multi-round trust strategy model reduces worker fatigue by approximately 59.40% compared to the no-trust model. Additionally, it achieves a substantial reduction of 29.10% in worker fatigue compared to the single-round trust strategy model.

Table 4.
Model fatigue levels comparison.
- (4)
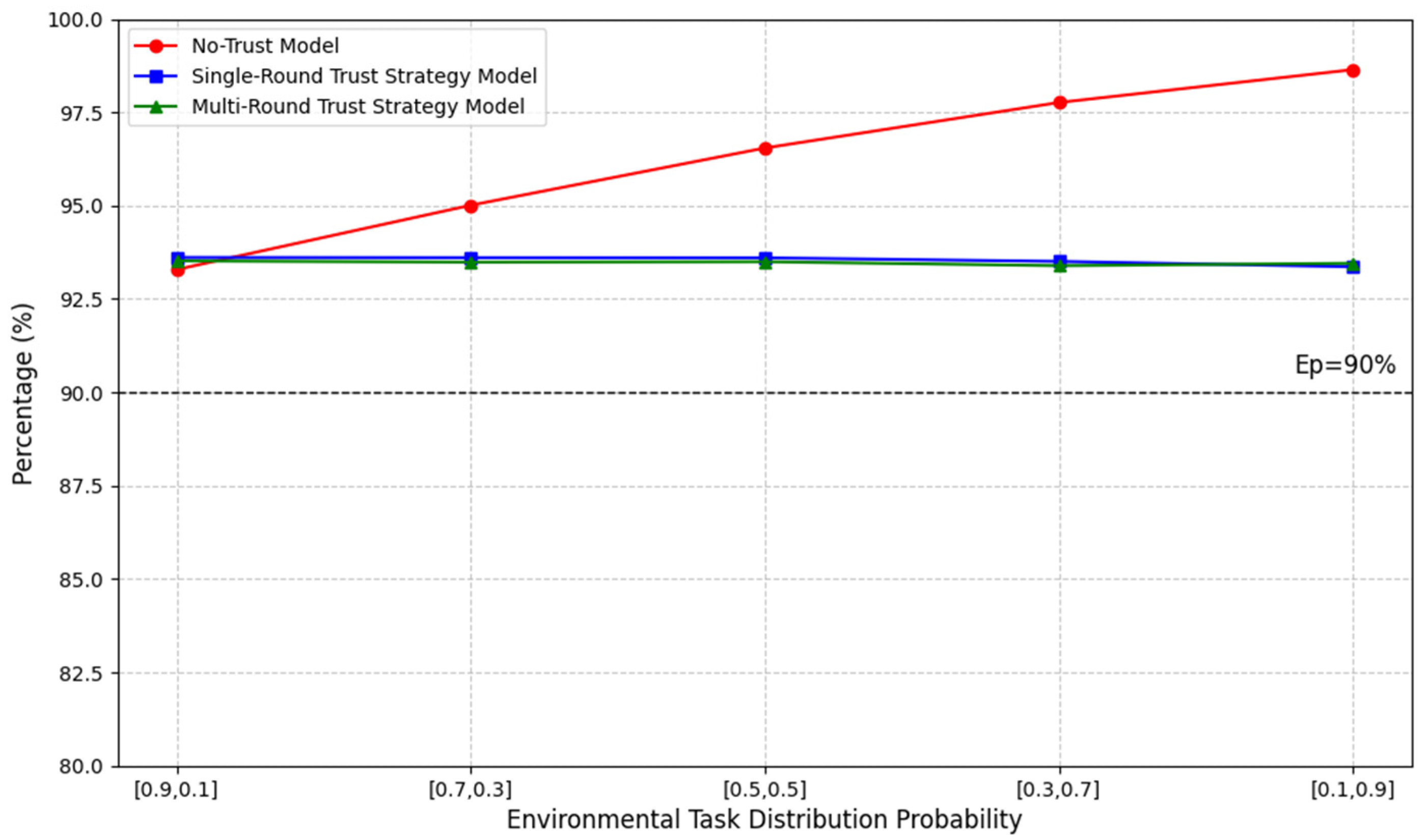
- Accuracy
Next, we applied the reward formula to validate and compare the picking accuracy of the system. The results are shown in Figure 14, which represents the reward function related to the accuracy of the human–robot collaborative work. The environmental settings follow those established in the efficiency experiments. In the figure, the black dashed line represents the system accuracy requirement set in the experiment, . As shown, when the environment contains a higher proportion of complex tasks, the no-trust model achieves relatively higher accuracy. This is because the no-trust model is configured to avoid robot execution of complex tasks, leaving these tasks primarily to human workers. While this setup improves accuracy in such cases, it negatively impacts work efficiency and poses potential health risks to workers due to increased workload and fatigue.
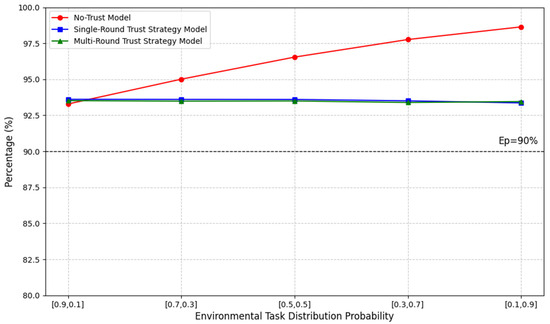
Figure 14.
Accuracy.
Similarly, to make the data more intuitive, a comparison of accuracy data is presented in Table 5, where the data is presented using percentage differences. While our framework incurs a certain degree of accuracy loss, it still meets the requirements of the collaborative picking system. Moreover, it achieves significantly higher improvement in human–robot collaborative picking efficiency and a substantial reduction in worker fatigue levels.

Table 5.
Model accuracy comparison.
The experimental results demonstrate that our framework is effective in stabilizing human trust levels. These trust states align with the robot’s operational performance range. This stabilization prevents collaboration disruptions from trust fluctuations. Furthermore, comparing the three trust models reveals that considering long-term trust dynamics improves both work efficiency and reduces worker fatigue.
6. Conclusions and Future Work
This paper proposes a Stackelberg trust strategy-based human–robot collaboration framework for warehouse picking. By constructing a POSG model, the collaborative operation scenario is modeled, and human trust is represented as a hidden state in a partially observable form. A Bayesian posterior-based state space is employed for the real-time evaluation of human trust by robots. This framework further considers the impact of human factors in the work environment on human–robot collaboration, specifically incorporating the human fatigue function into the collaboration efficiency reward function. Based on trust dynamics, human strategies are generated, and the Stackelberg strategy is utilized to solve the robot’s strategy. To account for the effects of continuous work in industrial environments, the Bellman equation is applied to achieve multi-round Stackelberg strategy solutions, referred to as the ISTSG algorithm. A POMDP model was constructed in PRISM to represent the derived strategies, with no-trust and single-round trust strategy models set up as baselines for comparison. Experiments were conducted to validate the proposed framework. The experimental results demonstrate that the proposed framework improves the efficiency of human–robot collaboration and significantly reduces human fatigue within collaborative tasks.
This work primarily focuses on the warehouse picking environment, but the proposed framework can be extended to various scenarios in the future. Moreover, this framework only considers one-to-one human–robot collaboration, while multi-robot scenarios are a future trend. Consequently, one-to-many human–robot collaborations will be a key focus for future research. Future work will explore two key extensions. First, we will analyze additional environmental factors like robot path selection impacts. Second, we plan to implement multiple reinforcement learning algorithms as comparative benchmarks.
Author Contributions
Conceptualization, Y.L. and F.G.; methodology, Y.L. and Y.M.; software, F.G.; validation, Y.L., F.G., and Y.M.; formal analysis, Y.L.; investigation, Y.L.; resources, F.G.; data curation, F.G.; writing—original draft preparation, Y.L. and F.G.; writing—review and editing, Y.L.; visualization, F.G.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Social Science Fund of China under Grant No. 24BGL111.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank all those who contributed to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Definition of Symbols in the Stackelberg Trust-Based HRC Framework
| Symbols | Definition | |
| A set of players (human and robot). | ||
| The task type at time . | ||
| The work states of each player at time . | ||
| The task outcome (success/failure) at time . | ||
| The human trust state at time . | ||
| The actions of each player at time . | ||
| The observation at time . | ||
| The belief state at time . | ||
| A Gaussian distribution with mean and standard deviation . | ||
| The observation path at time . | ||
| The trust dynamics of trust obeying a Gaussian distribution at time . | ||
| Assessment of trust through belief space. | ||
Appendix B. Definitions of States in
| States | Definition | |
| environment | The task type in the environment is a normal task. | |
| The task type in the environment is a complex task. | ||
| robot | The robot is executing tasks. | |
| The robot does not execute tasks and is waiting for the human to execute tasks. | ||
| human | The human is checking the robot’s execution results. | |
| The human does not check the robot’s execution results. | ||
| The human is re-executing the task. | ||
Appendix C. Definition of Symbols in the Reward Function
| Symbols | Definition |
| The reward functions on collaborative efficiency. | |
| The reward functions on collaborative efficiency. | |
| The regular time reward function. | |
| The time reward function is associated with human fatigue. | |
| The fatigue level at time . | |
| The fatigue levels under work states. | |
| The fatigue levels under rest states. | |
| The maximum fatigue level. | |
| The sigmoid function. | |
| The coefficients of fatigue growth rate. | |
| The coefficients of fatigue decay rate. | |
| The most recent time point at which a switch between work and rest states occurred. | |
| The time point when the fatigue levels reach half of the maximum. | |
| The impact of fatigue on execution efficiency. |
Appendix D. Definition of Symbols in Human–Robot Decision-Making
| Symbols | Definition |
| Probability of execution for an action of each player at time . | |
| The strategies of each player . | |
| Predictions for human strategies. | |
| The optimal strategies for the robot. | |
| The probability function of the robot strategy set that meets the system’s minimum requirements. | |
| The task execution accuracy at time . | |
| The system’s requirement for the minimum accuracy of picking tasks. | |
| The discount factor for probability. | |
| The discount factor for reward. |
References
- Hua, L.; Wu, Y. Strategic Analysis of Vertical Integration in Cross-Border e-Commerce Logistics Service Supply Chains. Transp. Res. Part E Logist. Transp. Rev. 2024, 188, 103626. [Google Scholar] [CrossRef]
- Akıl, S.; Ungan, M.C. E-Commerce Logistics Service Quality: Customer Satisfaction and Loyalty. J. Electron. Commer. Organ. (JECO) 2022, 20, 1–19. [Google Scholar] [CrossRef]
- Dong, Z. Construction of Mobile E-Commerce Platform and Analysis of Its Impact on E-Commerce Logistics Customer Satisfaction. Complexity 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Chen, X. The Development Trend and Practical Innovation of Smart Cities under the Integration of New Technologies. Front. Eng. Manag. 2019, 6, 485–502. [Google Scholar] [CrossRef]
- Tubis, A.A.; Rohman, J.; Smok, A.; Dopart, D. Analysis of Human Errors in the Traditional and Automated Order-Picking System. In International Conference on Intelligent Systems in Production Engineering and Maintenance; Springer: Berlin/Heidelberg, Germany, 2023; pp. 406–419. [Google Scholar]
- Bogue, R. Growth in E-Commerce Boosts Innovation in the Warehouse Robot Market. Ind. Robot Int. J. 2016, 43, 583–587. [Google Scholar] [CrossRef]
- Barreto, L.; Amaral, A.; Pereira, T. Industry 4.0 Implications in Logistics: An Overview. Procedia Manuf. 2017, 13, 1245–1252. [Google Scholar] [CrossRef]
- Bose, N. Amazon Dismisses Idea Automation Will Eliminate All Its Warehouse Jobs Soon-Reuters; Reuters. 2019. Available online: https://www.reuters.com/article/business/amazon-dismisses-idea-automation-will-eliminate-all-its-warehouse-jobs-soon-idUSKCN1S74B5/ (accessed on 2 May 2019).
- Zhu, S.; Wang, H.; Zhang, X.; He, X.; Tan, Z. A Decision Model on Human-Robot Collaborative Routing for Automatic Logistics. Adv. Eng. Inform. 2022, 53, 101681. [Google Scholar] [CrossRef]
- Boschetti, G.; Sinico, T.; Trevisani, A. Improving Robotic Bin-Picking Performances through Human–Robot Collaboration. Appl. Sci. 2023, 13, 5429. [Google Scholar] [CrossRef]
- Hopko, S.; Wang, J.; Mehta, R. Human Factors Considerations and Metrics in Shared Space Human-Robot Collaboration: A Systematic Review. Front. Robot. AI 2022, 9, 799522. [Google Scholar] [CrossRef]
- Loizaga, E.; Bastida, L.; Sillaurren, S.; Moya, A.; Toledo, N. Modelling and Measuring Trust in Human–Robot Collaboration. Appl. Sci. 2024, 14, 1919. [Google Scholar] [CrossRef]
- Kok, B.C.; Soh, H. Trust in Robots: Challenges and Opportunities. Curr. Robot. Rep. 2020, 1, 297–309. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Moray, N. Trust, Control Strategies and Allocation of Function in Human-Machine Systems. Ergonomics 1992, 35, 1243–1270. [Google Scholar] [CrossRef]
- Gao, J.; Lee, J.D. Extending the Decision Field Theory to Model Operators’ Reliance on Automation in Supervisory Control Situations. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2006, 36, 943–959. [Google Scholar] [CrossRef]
- Akash, K.; Hu, W.-L.; Reid, T.; Jain, N. Dynamic Modeling of Trust in Human-Machine Interactions. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1542–1548. [Google Scholar]
- Hu, W.-L.; Akash, K.; Reid, T.; Jain, N. Computational Modeling of the Dynamics of Human Trust during Human–Machine Interactions. IEEE Trans. Hum. Mach. Syst. 2018, 49, 485–497. [Google Scholar] [CrossRef]
- Xu, A.; Dudek, G. Optimo: Online Probabilistic Trust Inference Model for Asymmetric Human-Robot Collaborations. In Proceedings of the Tenth Annual ACM/IEEE International Conference on Human-Robot Interaction, Portland, OR, USA, 2–5 March 2015; pp. 221–228. [Google Scholar]
- Petković, T.; Puljiz, D.; Marković, I.; Hein, B. Human Intention Estimation Based on Hidden Markov Model Motion Validation for Safe Flexible Robotized Warehouses. Robot. Comput. Integr. Manuf. 2019, 57, 182–196. [Google Scholar] [CrossRef]
- Sheng, S.; Pakdamanian, E.; Han, K.; Wang, Z.; Lenneman, J.; Parker, D.; Feng, L. Planning for Automated Vehicles with Human Trust. ACM Trans. Cyber-Phys. Syst. 2022, 6, 1–21. [Google Scholar] [CrossRef]
- Huang, X.; Kwiatkowska, M.; Olejnik, M. Reasoning about Cognitive Trust in Stochastic Multiagent Systems. ACM Trans. Comput. Log. (TOCL) 2019, 20, 1–64. [Google Scholar] [CrossRef]
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and Control of Warehouse Order Picking: A Literature Review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Caron, F.; Marchet, G.; Perego, A. Layout Design in Manual Picking Systems: A Simulation Approach. Integr. Manuf. Syst. 2000, 11, 94–104. [Google Scholar] [CrossRef]
- Kim, B.; Graves, R.J.; Heragu, S.S.; Onge, A.S. Intelligent Agent Modeling of an Industrial Warehousing Problem. Iie Trans. 2002, 34, 601–612. [Google Scholar] [CrossRef]
- Hausman, W.H.; Schwarz, L.B.; Graves, S.C. Optimal Storage Assignment in Automatic Warehousing Systems. Manag. Sci. 1976, 22, 629–638. [Google Scholar] [CrossRef]
- Ramtin, F.; Pazour, J.A. Product Allocation Problem for an AS/RS with Multiple in-the-Aisle Pick Positions. IIE Trans. 2015, 47, 1379–1396. [Google Scholar] [CrossRef]
- Li, X.; Hua, G.; Huang, A.; Sheu, J.-B.; Cheng, T.C.E.; Huang, F. Storage Assignment Policy with Awareness of Energy Consumption in the Kiva Mobile Fulfilment System. Transp. Res. Part E Logist. Transp. Rev. 2020, 144, 102158. [Google Scholar] [CrossRef]
- Ghelichi, Z.; Kilaru, S. Analytical Models for Collaborative Autonomous Mobile Robot Solutions in Fulfillment Centers. Appl. Math. Model. 2021, 91, 438–457. [Google Scholar] [CrossRef]
- Rey, R.; Cobano, J.A.; Corzetto, M.; Merino, L.; Alvito, P.; Caballero, F. A Novel Robot Co-Worker System for Paint Factories without the Need of Existing Robotic Infrastructure. Robot. Comput. Integr. Manuf. 2021, 70, 102122. [Google Scholar] [CrossRef]
- Baechler, A.; Baechler, L.; Autenrieth, S.; Kurtz, P.; Hoerz, T.; Heidenreich, T.; Kruell, G. A Comparative Study of an Assistance System for Manual Order Picking—Called Pick-by-Projection—With the Guiding Systems Pick-by-Paper, Pick-by-Light and Pick-by-Display. In Proceedings of the 2016 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016; pp. 523–531. [Google Scholar]
- Owen, G. Game Theory; Emerald Group Publishing: Bingley, UK, 2013; ISBN 1-78190-508-8. [Google Scholar]
- Hansen, E.A.; Bernstein, D.S.; Zilberstein, S. Dynamic Programming for Partially Observable Stochastic Games. In Proceedings of the AAAI, San Jose, CA, USA, 25–29 July 2004; Volume 4, pp. 709–715. [Google Scholar]
- Leitmann, G. On Generalized Stackelberg Strategies. J. Optim. Theory Appl. 1978, 26, 637–643. [Google Scholar] [CrossRef]
- Kwiatkowska, M.; Norman, G.; Parker, D. PRISM 4.0: Verification of Probabilistic Real-Time Systems. In Proceedings of the Computer Aided Verification: 23rd International Conference, CAV 2011, Snowbird, UT, USA, 14–20 July 2011; Proceedings 23. Springer: Berlin/Heidelberg, Germany, 2011; pp. 585–591. [Google Scholar]
- Forejt, V.; Kwiatkowska, M.; Norman, G.; Parker, D. Automated Verification Techniques for Probabilistic Systems. In Formal Methods for Eternal Networked Software Systems; Bernardo, M., Issarny, V., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6659, pp. 53–113. ISBN 978-3-642-21454-7. [Google Scholar]
- Chen, M.; Nikolaidis, S.; Soh, H.; Hsu, D.; Srinivasa, S. Trust-Aware Decision Making for Human-Robot Collaboration: Model Learning and Planning. ACM Trans. Hum. Robot Interact. (THRI) 2020, 9, 1–23. [Google Scholar] [CrossRef]
- Glock, C.H.; Grosse, E.H.; Kim, T.; Neumann, W.P.; Sobhani, A. An Integrated Cost and Worker Fatigue Evaluation Model of a Packaging Process. Int. J. Prod. Econ. 2019, 207, 107–124. [Google Scholar] [CrossRef]
- Winkelhaus, S.; Zhang, M.; Grosse, E.H.; Glock, C.H. Hybrid Order Picking: A Simulation Model of a Joint Manual and Autonomous Order Picking System. Comput. Ind. Eng. 2022, 167, 107981. [Google Scholar] [CrossRef]
- Zhang, M.; Grosse, E.H.; Glock, C.H. Ergonomic and economic evaluation of a collaborative hybrid order picking system. Int. J. Prod. Econ. 2023, 258, 108774. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).