Comparative Study of Application of Production Sequencing and Scheduling Problems in Tire Mixing Operations with ADAM, Grey Wolf Optimizer, and Genetic Algorithm
Abstract
1. Introduction
2. Literature Review
- The ADAM Optimizer was adapted for discrete mixer assignment and sequencing to minimize makespan under capacity constraints.
- A finite difference gradient approximation was introduced to enable gradient-based optimization in the discrete assignment setting.
- A hybrid data-driven and rule-based scheduling framework was proposed to improve robustness against variable setup durations and machine availability.
- The ADAM Optimizer method was compared to the Grey Wolf Optimizer (GWO) and Genetic Algorithm (GA) on parallel machine instances with sequence-dependent setups, reporting solution quality and computational effort.
- Practical benefits were demonstrated on representative mixing scenarios, including reduced idle time, improved resource utilization, and shorter production cycles.
3. Problem Statement
4. Methodology
4.1. Model Assumptions
- Every compound is considered indivisible and allocated to only one machine;
- Every machine operates simultaneously, though with separate capabilities;
- The outputs of all machines should be temporally aligned so that they can be mixed simultaneously;
- Each machine’s setup time depends on the last sequence;
- The processing and setup times for compounds and machines are fixed;
- As soon as a compound starts processing, it cannot stop until it is complete;
- Nevertheless, each compound can only be assigned to machines that satisfy specific capacity and operational feasibility conditions.
4.2. Mathematical Models and Integrated Optimization Processes for Problem Optimization
4.2.1. Objective Function and Constraints
4.2.2. ADAM Optimizer
4.2.3. Grey Wolf Optimizer (GWO)
4.2.4. Genetic Algorithm (GA)
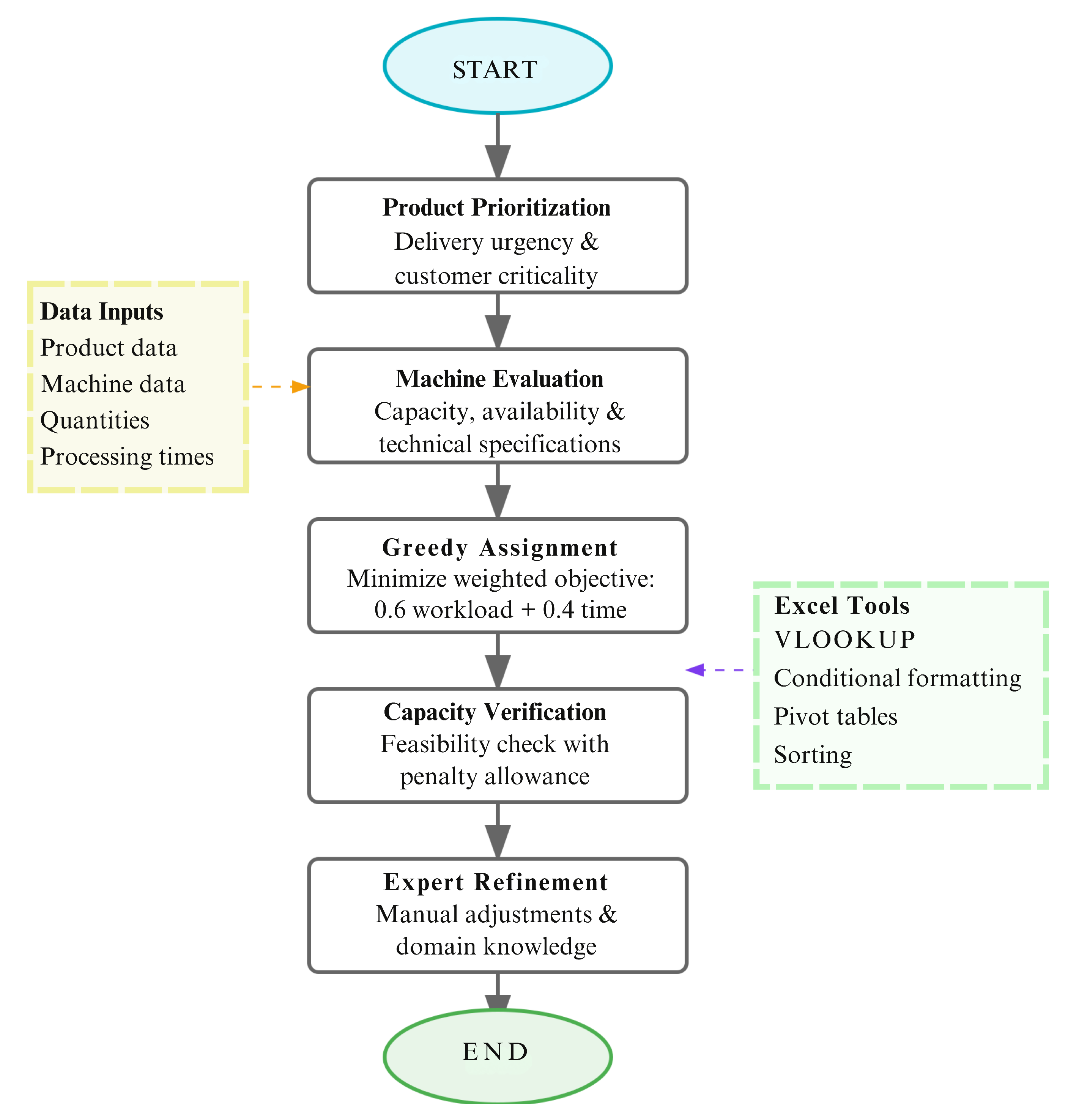
4.2.5. Company Method: Manual Allocation
4.2.6. Experimental Study
5. Results and Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rodgers, B.; Waddell, W.H. The science of rubber compounding. In The Science and Technology of Rubber; Academic Press: Cambridge, MA, USA, 2013; pp. 417–471. [Google Scholar] [CrossRef]
- Celtik, F.; Kilic, E.; Bora, M.O.; Altuncu, E. Effect of Liquid Rubbers on The Thermal and Adhesion Properties of the Tire Skim Compound. Acad. Perspect. Procedia 2021, 4, 101–110. [Google Scholar] [CrossRef]
- Temel, A.; Ayaz, M.; Aygül, V. Digital transformation for improved energy and product efficiency in tire production: A case study. Eng. Res. Express 2023, 5, 045048. [Google Scholar] [CrossRef]
- Çavdaroğlu, C.; Olgun, U.; Altuncu, E. Use of expanded perlite as green filler for the preparation of EPDM-perlite rubber composites with improved thermal stability and insulation properties. Polym. Compos. 2024, 45, 12754–12772. [Google Scholar] [CrossRef]
- Türkşen, I.B.; Zarandi, M.F. Production planning and scheduling: Fuzzy and crisp approaches. In Practical Applications of Fuzzy Technologies; Springer: Boston, MA, USA, 1999; pp. 479–529. [Google Scholar] [CrossRef]
- Akman, G.; Tapsahanoğlu, S. Determining the optimal product mix in multiple constraints manufacturing environment: An application in the textile industry. Ind. Textila 2022, 73, 564–573. [Google Scholar] [CrossRef]
- Boyacı, A.İ.; Akman, G. Applying Theory of Constraints-Thinking Processes in Logistics Industry: A Case Study. Atlas Int. Ref. J. Soc. Sci. 2018, 4, 513–528. [Google Scholar] [CrossRef]
- Terzi, M.; Arbaoui, T.; Yalaoui, F.; Benatchba, K. Solving the unrelated parallel machine scheduling problem with setups using late acceptance hill climbing. In Intelligent Information and Database Systems; Springer: Cham, Switzerland, 2020; pp. 249–258. [Google Scholar] [CrossRef]
- Muñoz, L.F.R.; Villalobos, J.R.; Fowler, J. Exact and heuristic algorithms for the parallel machine total completion time scheduling problem with dual resources, ready times, and sequence-dependent setup times. Comput. Oper. Res. 2022, 143, 105787. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.; Abd Elaziz, M. Enhanced salp swarm algorithm based on firefly algorithm for unrelated parallel machine scheduling with setup times. Appl. Math. Model. 2021, 94, 285–305. [Google Scholar] [CrossRef]
- Martins, M.S.E.; Sousa, J.M.C.; Vieira, S. A systematic review on reinforcement learning for industrial combinatorial optimization problems. Appl. Sci. 2025, 15, 1211. [Google Scholar] [CrossRef]
- Sun, T.; Wang, J.; Fan, G.; Liu, Z. Submodular batch scheduling on parallel machines. Nav. Res. Logist. (NRL) 2024, 72, 242–259. [Google Scholar] [CrossRef]
- Kiss, L.; Molnár, M.J.; Mészáros, L. Improving the mechanical properties of vulcanizates containing ground tire rubber: Recipe optimization with the Taguchi method. Polym. Adv. Technol. 2024, 35, e6389. [Google Scholar] [CrossRef]
- Uruk, Z.; Kiraz, A.; Karaağaç, B. Optimization of rubber mixture production using a validated technological sequence of methods. Polym. Eng. Sci. 2024, 64, 5435–5449. [Google Scholar] [CrossRef]
- Zhao, S.; Sheng, L.; He, W.; Zhu, N.; Li, Y.; Ji, D.; Guo, K. Design and optimization of a novel ellipsoidal baffle mixer with high mixing efficiency and low pressure drop. J. Chem. Technol. Biotechnol. 2022, 97, 3121–3131. [Google Scholar] [CrossRef]
- Demiryürek, R.; Çolak, N.G.; Hatipoğlu, G.; Er, M.; Malkoc, H.; Guleryuz, O.; Ateş, M.N. Roll-to-roll manufacturing method of aqueous-processed thick lini 0.5 mn 0.3 co 0.2 o 2 electrodes for lithium-ion batteries. Int. J. Energy Res. 2021, 45, 21182–21194. [Google Scholar] [CrossRef]
- Remy, B.; Glasser, B.J.; Khinast, J. The effect of mixer properties and fill level on granular flow in a bladed mixer. AIChE J. 2009, 56, 336–353. [Google Scholar] [CrossRef]
- Brinke, J.T.; Swaaij, P.V.; Reuvekamp, L.A.; Noordermeer, J.W.M. The influence of silane sulfur and carbon rank on processing of a silica reinforced tire tread compound. Rubber Chem. Technol. 2003, 76, 12–35. [Google Scholar] [CrossRef]
- Dhakal, P.; Das, S.R.; Poudyal, H.; Chandy, A.J. Numerical simulations of partially-filled rubber mixing in a 2-wing rotor-equipped chamber. J. Appl. Polym. Sci. 2016, 134, 44250. [Google Scholar] [CrossRef]
- Rajamani, D.; Adil, G.K. Scheduling and sequencing of rubber compounds on Banbury mixers in a tyre company. Int. J. Adv. Manuf. Technol. 1998, 14, 298–305. [Google Scholar] [CrossRef]
- Ghosh, A.; Banerjee, R.; Sushmitha, H.; Chanda, J.; Ghosh, P.; Mukhopadhyay, R. Preferential migration of carbon black in NR/EPDM blends investigated through microscopic approaches. Rubber Chem. Technol. 2025, 98, 109–123. [Google Scholar] [CrossRef]
- Arani, M.; Momenitabar, M.; Priyanka, T.J. Unrelated parallel machine scheduling problem considering job splitting, inventories, shortage, and resource: A meta-heuristic approach. Systems 2024, 12, 37. [Google Scholar] [CrossRef]
- Arık, O.A.; Schutten, J.; Topan, E. Weighted earliness/tardiness parallel machine scheduling problem with a common due date. Expert Syst. Appl. 2022, 187, 115916. [Google Scholar] [CrossRef]
- Çakar, T.; Köker, R.; Sarı, Y. Parallel robot scheduling to minimize mean tardiness with unequal release date and precedence constraints using a hybrid intelligent system. Int. J. Adv. Robot. Syst. 2012, 9, 54381. [Google Scholar] [CrossRef]
- Bilge, Ü.; Kıraç, F.; Kurtulan, M.; Pekgün, P. A tabu search algorithm for parallel machine total tardiness problem. Comput. Oper. Res. 2004, 31, 397–414. [Google Scholar] [CrossRef]
- Strusevich, V.A. Complexity and approximation of open shop scheduling to minimize the makespan: A review of models and approaches. Comput. Oper. Res. 2022, 144, 105732. [Google Scholar] [CrossRef]
- Soper, A.J.; Strusevich, V.A. Preemptive and non-preemptive scheduling on two unrelated parallel machines. J. Sched. 2022, 25, 659–674. [Google Scholar] [CrossRef]
- Kaya, S.; Karaçizmeli, İ.H.; Aydilek, İ.B.; Tenekeci, M.E.; Gümüşçü, A. The effects of initial populations in the solution of flow shop scheduling problems by hybrid firefly and particle swarm optimization algorithms. Pamukkale Univ. J. Eng. Sci. 2020, 26, 140–149. [Google Scholar] [CrossRef]
- Demir, H.İ.; Uygun, O.; Cil, I.; Ipek, M.; Sari, M. Process Planning and Scheduling with SLK Due-Date Assignment where Earliness, Tardiness and Due-Dates are Punished. J. Ind. Intell. Inf. 2015, 3, 173–180. [Google Scholar] [CrossRef]
- Erden, C.; Demir, H.İ.; Kökçam, A.H. Solving integrated process planning, dynamic scheduling, and due date assignment using metaheuristic algorithms. Math. Probl. Eng. 2019, 2019, 1572614. [Google Scholar] [CrossRef]
- Demir, H.İ.; Erden, C. Dynamic integrated process planning, scheduling, and due-date assignment using ant colony optimization. Comput. Ind. Eng. 2020, 149, 106799. [Google Scholar] [CrossRef]
- Demir, H.İ.; Erden, C.; Kökçam, A.H.; Göksu, A. A tabu search and hybrid evolutionary strategies algorithms for the integrated process planning and scheduling with due-date agreement. J. Intell. Syst. Theory Appl. 2021, 4, 24–36. [Google Scholar] [CrossRef]
- İnce, N.; Deliktaş, D.; Selvi, İ.H. A comprehensive literature review of the flow shop group scheduling problems: Systematic and bibliometric reviews. Int. J. Prod. Res. 2024, 62, 4565–4594. [Google Scholar] [CrossRef]
- Demir, H.İ.; Kökçam, A.H.; Erden, C. Integrated Process Planning, Scheduling, and Due-Date Assignment; CRC Press: Boca Raton, FL, USA, 2023; p. 55. [Google Scholar] [CrossRef]
- Özbayrak, M.; Cagil, G.; Kubat, C. How successfully does JIT handle machine breakdowns in an automated manufacturing system? J. Manuf. Technol. Manag. 2004, 15, 479–494. [Google Scholar] [CrossRef]
- Deliktaş, D.; Torkul, O.; Üstün, Ö. A flexible job shop cell scheduling with sequence-dependent family setup times and intercellular transportation times using conic scalarization method. Int. Trans. Oper. Res. 2017, 26, 2410–2431. [Google Scholar] [CrossRef]
- Kaplanoğlu, V. Multi-agent-based approach for single machine scheduling with sequence-dependent setup times and machine maintenance. Appl. Soft Comput. 2014, 23, 165–179. [Google Scholar] [CrossRef]
- Itu, A. Industrial Scheduling in the Digital Era: Challenges, State-of-the-Art Methods, and Deep Learning Perspectives. Appl. Sci. 2025, 15, 10823. [Google Scholar] [CrossRef]
- Pinedo, M. Planning and Scheduling in Manufacturing and Services; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Bakır, H. Performance Assessment of Natural Survivor Method-Based Metaheuristics in Global Optimization and Engineering Design Problems. Sak. Univ. J. Comput. Inf. Sci. 2024, 7, 227–243. [Google Scholar] [CrossRef]
- Bakır, H.; Duman, S.; Güvenç, U.; Kahraman, H.T. Improved adaptive gaining-sharing knowledge algorithm with FDB-based guiding mechanism for optimization of optimal reactive power flow problem. Electr. Eng. 2023, 105, 3121–3160. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Katı, M.; Aras, S.; Taşci, D.A. Development of the natural survivor method (NSM) for designing an updating mechanism in metaheuristic search algorithms. Eng. Appl. Artif. Intell. 2023, 122, 106121. [Google Scholar] [CrossRef]
- Emiroğlu, S. Parameter estimation of induction motors using hybrid GWO-cs algorithm. Sak. Univ. J. Sci. 2023, 27, 361–369. [Google Scholar] [CrossRef]
- Erdoğmuş, P. A new solution approach for non-linear equation systems with grey wolf. Sak. Univ. J. Comput. Inf. Sci. 2018, 1, 1–11. [Google Scholar] [CrossRef]
- Hajariwala, D.C.; Patil, S.S.; Patil, S.M. A Review of Metaheuristic Algorithms for Job Shop Scheduling. Eng. Access 2025, 11, 65–91. [Google Scholar]
- Zhang, M.; Lu, Y.; Hu, Y.; Amaitik, N.; Xu, Y. Dynamic Scheduling Method for Job-Shop Manufacturing Systems by Deep Reinforcement Learning with Proximal Policy Optimization. Sustainability 2022, 14, 5177. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Xia, Y.; Ji, Y. Application of a Novel Metaheuristic Algorithm Inspired by Adam Gradient Descent in Distributed Permutation Flow Shop Scheduling Problem and Continuous Engineering Problems. Sci. Rep. 2025, 15, 1678. [Google Scholar] [CrossRef]
- Butrat, A.; Supsomboon, S. Modified Resource-Constrained Project Scheduling to Minimize Idle Time for Banbury Mixing Process: A Case Study in the Tire Manufacturing Industry. Manuf. Syst. Prod. Eng. 2023, 31, 263–270. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X. Production Scheduling of Prefabricated Components Considering Delivery Methods. Sci. Rep. 2023, 13, 15094. [Google Scholar] [CrossRef]
- Ngwu, C.; Liu, Y.; Wu, R. Reinforcement Learning in Dynamic Job Shop Scheduling: A Comprehensive Review of AI-Driven Approaches in Modern Manufacturing. J. Intell. Manuf. 2025; early access. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014; Available online: https://www.elsevier.com/books/constrained-optimization-and-lagrange-multiplier-methods/bertsekas/978-1-4832-6047-1 (accessed on 1 October 2025).
- Jang, E.; Gu, S.; Poole, B. Categorical Reparameterization with Gumbel-Softmax. arXiv 2017, arXiv:1611.01144. [Google Scholar] [CrossRef]
- Nesterov, Y.; Spokoiny, V. Random gradient-free minimization of convex functions. Found. Comput. Math. 2017, 17, 527–566. [Google Scholar] [CrossRef]
- Spall, J.C. Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. Autom. Control 1992, 37, 332–341. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, Y. Explorative Binary Gray Wolf with Quadratic Interpolation for Feature Selection. Biomimetics 2024, 9, 648. [Google Scholar] [CrossRef]
- Ghafari, R.; Mansouri, N. Swarm intelligence techniques and their applications in fog/edge computing: An in-depth review. Artif. Intell. Rev. 2025, 58, 359. [Google Scholar] [CrossRef]
- Goli, P.; Gampa, S.R.; Alluri, A.; Gutta, B.; Jasthi, K.; Das, D. Optimum sizing of solar photovoltaic panels at optimum tilt and azimuth angles using grey wolf optimization algorithm for distribution systems. Inventions 2025, 10, 79. [Google Scholar] [CrossRef]
- Tumbaz, M.N.M.; İpek, M. Energy demand forecasting: Avoiding multi-collinearity. Arab. J. Sci. Eng. 2020, 46, 1663–1675. [Google Scholar] [CrossRef]
- Arık, O.A. Optimal policies for minimizing total job completion times and deviations from common due dates in unrelated parallel machine scheduling. Opsearch 2024, 61, 1654–1680. [Google Scholar] [CrossRef]
- Elyasi, M.; Selcuk, Y.S.; Özener, O.Ö.; Çoban, E. Imperialist competitive algorithm for unrelated parallel machine scheduling with sequence-and-machine-dependent setups and compatibility and workload constraints. Comput. Ind. Eng. 2024, 190, 110086. [Google Scholar] [CrossRef]
- Duan, J.; Liu, F.; Zhang, Q.; Qin, J.; Zhou, Y. Genetic programming hyper-heuristic-based solution for dynamic energy-efficient scheduling of hybrid flow shop scheduling with machine breakdowns and random job arrivals. Expert Syst. Appl. 2024, 254, 124375. [Google Scholar] [CrossRef]
- Uruk, Z.; Yalçıner, A.Y. Two-machine flow shop scheduling with fuzzy processing times and flexible operations. Eur. J. Ind. Eng. 2024, 18, 100–119. [Google Scholar] [CrossRef]
- Turgay, S.; Aydın, A. An effective heuristic algorithm for flexible flow shop scheduling problems with parallel batch processing. Manuf. Serv. Oper. Manag. 2023, 4, 109. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992; Available online: https://books.google.com.tr/books?id=5EgGaBkwvWcC (accessed on 21 October 2025).
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Denizhan, B.; Yıldırım, E.; Akkan, Ö. An order-picking problem in a medical facility using genetic algorithm. Processes 2025, 13, 22. [Google Scholar] [CrossRef]
- Yıldırım, E.; Denizhan, B. A two-echelon pharmaceutical supply chain optimization via genetic algorithm. In Recent Advances in Intelligent Manufacturing and Service Systems; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022; pp. 77–87. [Google Scholar] [CrossRef]
- Çelikbilek, C.; Tunacan, T.; Süer, G.A.; Dulkadır, Ö. Scheduling comparison between multi-objective mathematical models and genetic algorithms approach in the textile industry. Int. J. Serv. Oper. Manag. 2016, 25, 236. [Google Scholar] [CrossRef]
- Koca, M.; Avcı, İ. Optimization Planning Techniques with Meta-Heuristic Algorithms in IoT: Performance and QoS Evaluation. Sak. Univ. J. Comput. Inf. Sci. 2024, 7, 173–186. [Google Scholar] [CrossRef]
- Xu, R.; Tuo, Y.; Chen, H.; Xu, J. Scheduling parallel cranes for unit-load automated storage and retrieval systems with shared storage. Systems 2023, 12, 3. [Google Scholar] [CrossRef]
- Bamatraf, K.; Gharbi, A. Variable neighborhood search for minimizing the makespan in a uniform parallel machine scheduling. Systems 2024, 12, 221. [Google Scholar] [CrossRef]
- Cui, H.; Zhao, Q.; Wang, H.; Guo, Y.; Guo, J. Integrating Order Splitting and Acceptance with Batch Delivery in Parallel Machine Scheduling. Systems 2024, 12, 354. [Google Scholar] [CrossRef]
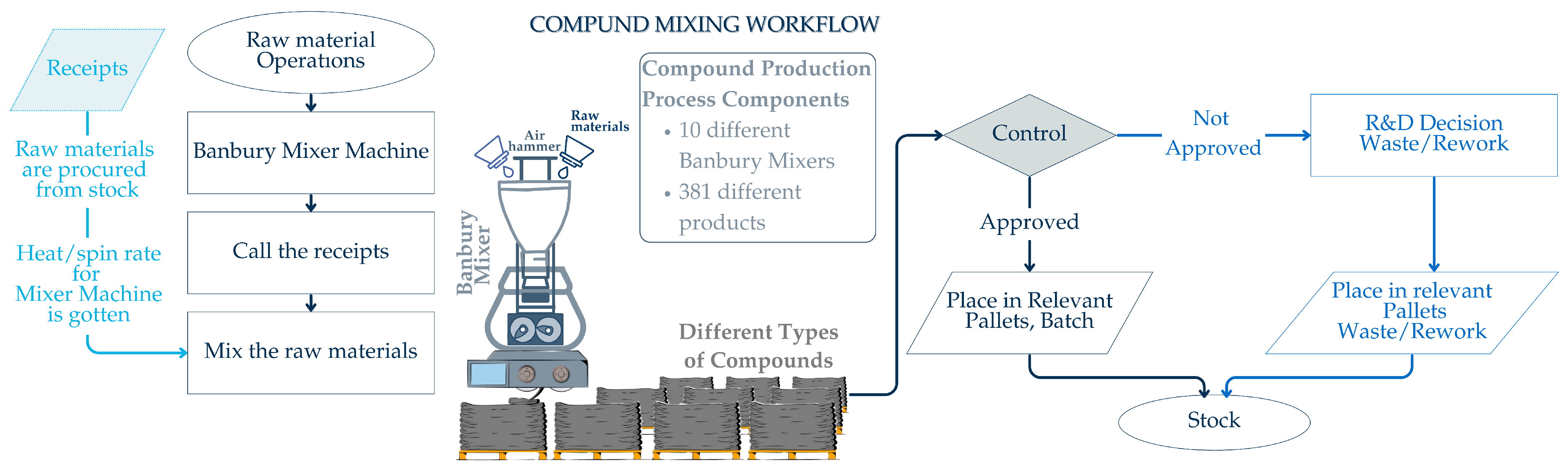
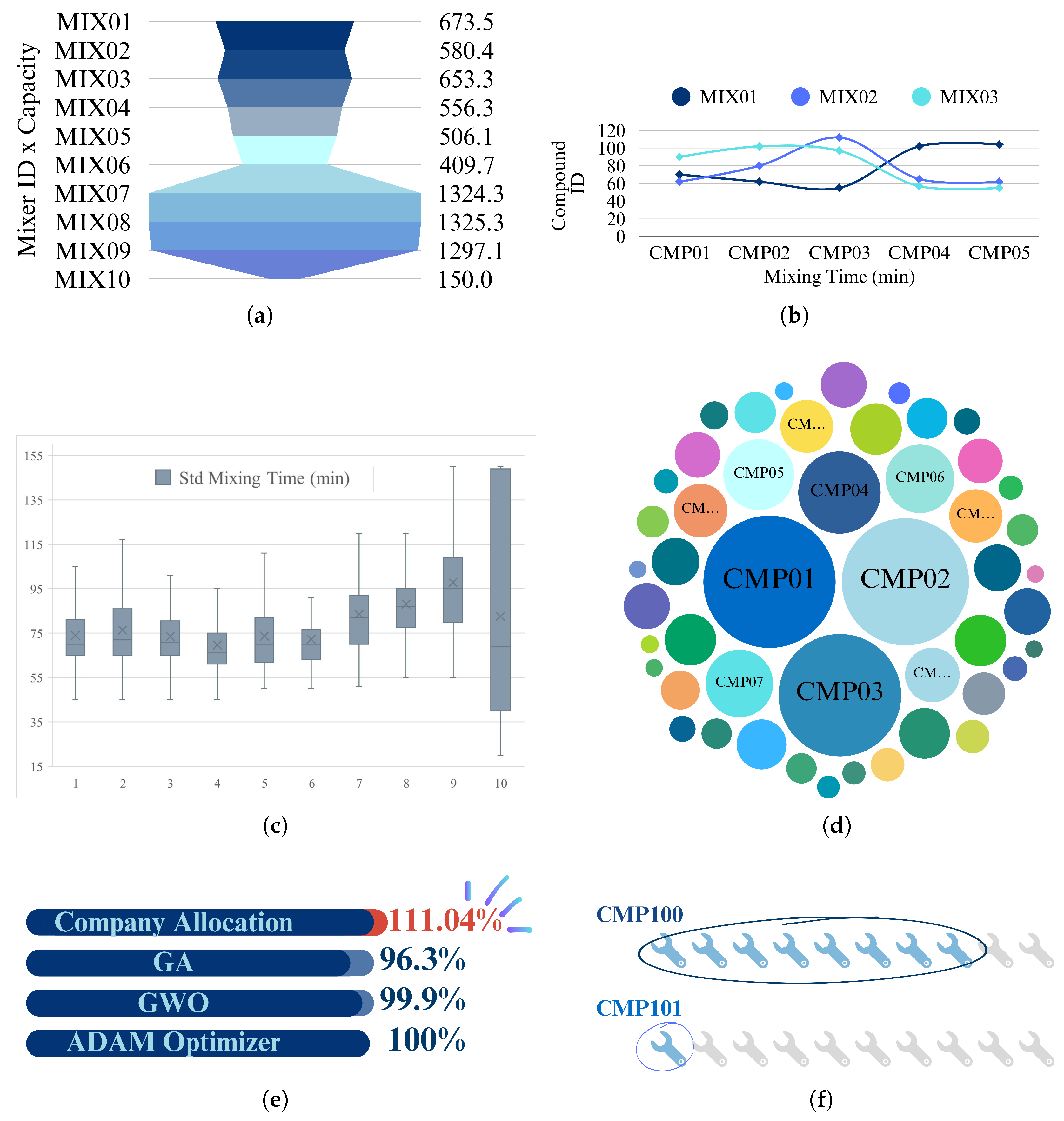


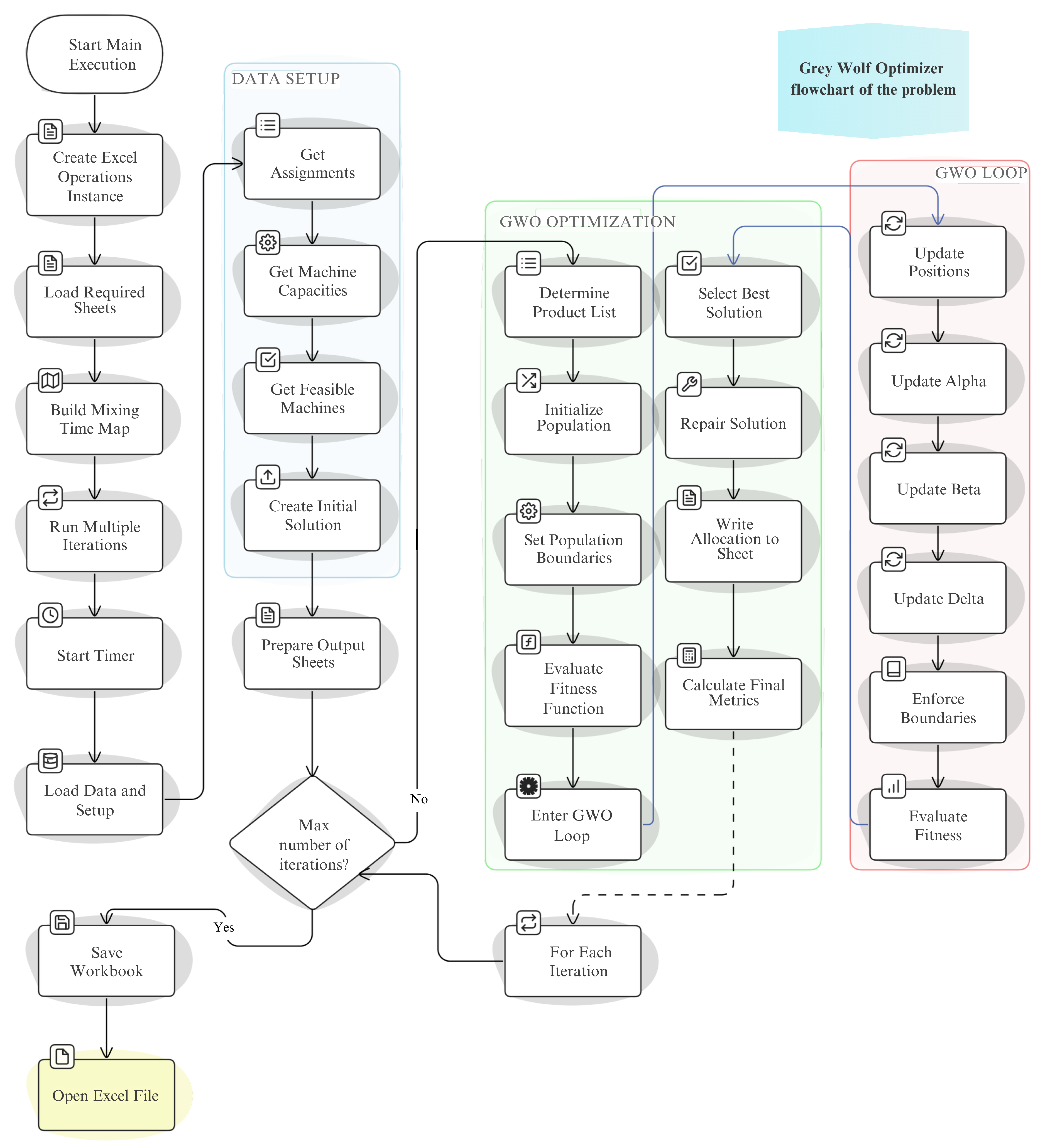
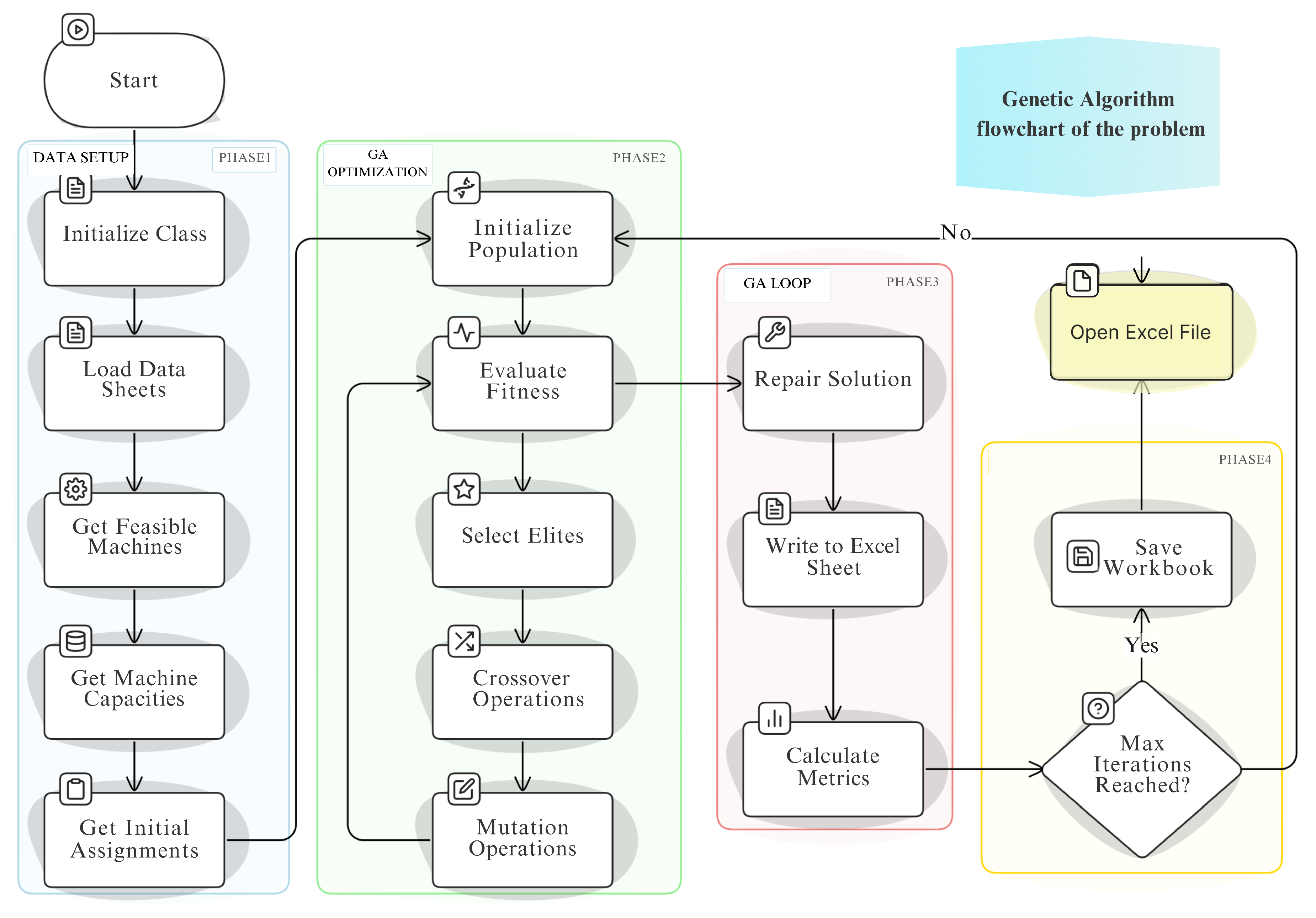

| Parameter | Value/Range |
|---|---|
| Set of products/compound types | 381 |
| Set of mixers/machines | 10 |
| Feasible mixers for the product | Given per product |
| Quantity of the product (L) | Given per product |
| Processing time in the mixer | Given per product–mixer pair |
| Capacity of the mixer (L) | Given per mixer |
| The total workload of the mixer | Computed |
| The total assigned quantity in the mixer (L) | Computed |
| Penalty coefficient for capacity violation |
| Parameter | Description | Value/Range |
|---|---|---|
| Continuous assignment vector | ||
| Learning rate | 0.01 | |
| First-moment decay rate | 0.9 | |
| Second-moment decay rate | 0.999 | |
| Small constant for stability | ||
| Finite difference step (adaptive; see text) | reference | |
| Gradient estimate at iteration t | Computed | |
| First-moment estimate | Computed | |
| Second-moment estimate | Computed | |
| Bias-corrected first moment | Computed | |
| Bias-corrected second moment | Computed |
| Parameter | Description | Value/Range |
|---|---|---|
| Wolf i’s position matrix | ||
| a | Exploration–exploitation parameter | |
| A | The coefficient for position update | |
| C | The coefficient for position update | |
| Random values for search dynamics | ||
| Best solutions (leaders) | Computed | |
| Distance from the prey | Computed | |
| Updated position |
| Parameter | Description | Value/Range |
|---|---|---|
| N | Population size | 500 |
| Crossover probability | 0.8 | |
| Mutation probability | 0.1 | |
| k | Tournament selection size | 0.3 |
| Crossover | Order crossover (OX) | 0.5 |
| Child[a:b] | Subsequence from Parent 1 | Selected randomly |
| Remaining Genes | Filled from Parent 2 | Keeping relative order |
| Mutation | Swap mutation | – |
| Random swap positions | ||
| Selection | Tournament selection | – |
| Repair | Feasibility correction | Adjusts infeasible solutions |
| Parameter | Description | Value/Range |
|---|---|---|
| Workload factor weight | 0.6 | |
| Processing time factor weight | 0.4 | |
| Capacity utilization threshold | 0.9 | |
| Capacity violation allowance | 0.1 | |
| Feasible machine set for product p | Qualification matrix | |
| Current machine workload | Real-time data | |
| Machine capacity (L) | Equipment specifications | |
| Processing time matrix | Historical records | |
| Product quantity requirement (L) | Customer orders |
| Method | Time Complexity | Space Complexity | Convergence Type | Parameters |
|---|---|---|---|---|
| ADAM | Gradient-based | |||
| GWO | Population-based | |||
| GA | Evolutionary | |||
| Manual | Deterministic | Excel-based |
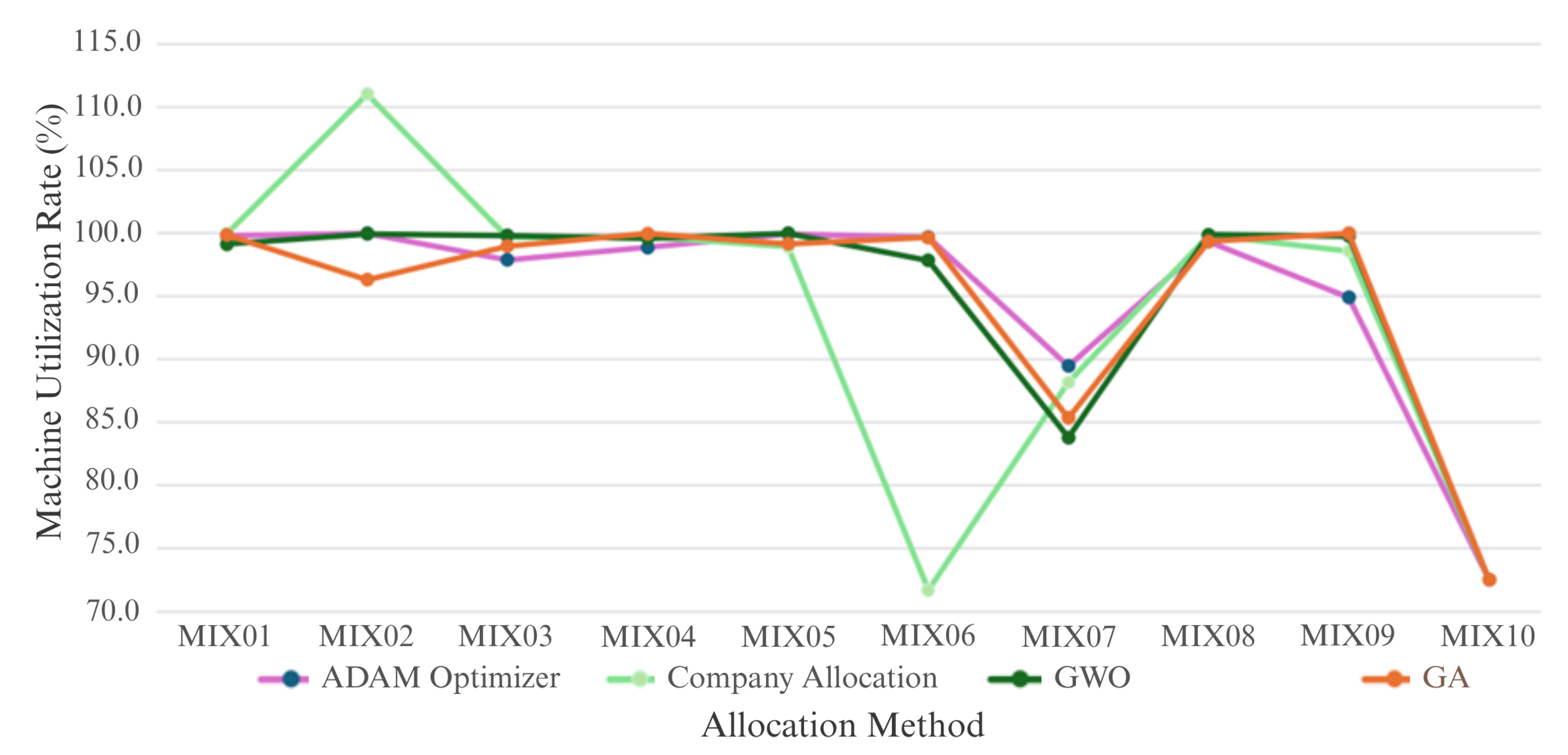
| Method | Mixer | Allocated Qty (L) | Capacity (L) | Utilization % | Makespan (min) | Total Exec. Time—10 Runs (h:mm:ss.ms) |
|---|---|---|---|---|---|---|
| ADAM | MIX01 | 672.07 | 673.50 | 99.79 | 0:01:15.26 | |
| MIX02 | 580.42 | 580.43 | 100.00 | |||
| MIX03 | 639.58 | 653.30 | 97.90 | |||
| MIX04 | 550.10 | 556.30 | 98.89 | |||
| MIX05 | 505.81 | 506.10 | 99.94 | |||
| MIX06 | 408.45 | 409.70 | 99.69 | |||
| MIX07 | 1184.89 | 1324.30 | 89.47 | 15,571.001 | ||
| MIX08 | 1316.46 | 1325.30 | 99.33 | |||
| MIX09 | 1231.10 | 1297.10 | 94.91 | |||
| MIX10 | 108.78 | 150.00 | 72.52 | |||
| GWO | MIX01 | 672.53 | 673.50 | 99.86 | 0:32:50.06 | |
| MIX02 | 559.06 | 580.43 | 96.32 | |||
| MIX03 | 646.71 | 653.30 | 98.99 | |||
| MIX04 | 556.15 | 556.30 | 99.97 | |||
| MIX05 | 501.88 | 506.10 | 99.17 | |||
| MIX06 | 408.31 | 409.70 | 99.66 | |||
| MIX07 | 1130.42 | 1324.30 | 85.36 | 17,349.793 | ||
| MIX08 | 1316.86 | 1325.30 | 99.36 | |||
| MIX09 | 1296.98 | 1297.10 | 99.99 | |||
| MIX10 | 108.77 | 150.00 | 72.51 | |||
| GA | MIX01 | 667.68 | 673.50 | 99.14 | 1:21:33.0 | |
| MIX02 | 580.20 | 580.43 | 99.96 | |||
| MIX03 | 652.14 | 653.30 | 99.82 | |||
| MIX04 | 554.08 | 556.30 | 99.60 | |||
| MIX05 | 506.05 | 506.10 | 99.99 | |||
| MIX06 | 400.89 | 409.70 | 97.85 | |||
| MIX07 | 1109.90 | 1324.30 | 83.81 | 17,727.685 | ||
| MIX08 | 1323.68 | 1325.30 | 99.88 | |||
| MIX09 | 1294.29 | 1297.10 | 99.78 | |||
| MIX10 | 108.77 | 150.00 | 72.51 | |||
| Company Allocation | MIX01 | 673.35 | 673.50 | 99.98 | 5:00:00.00 | |
| MIX02 | 644.49 | 580.43 | 111.04 | Bottleneck | ||
| MIX03 | 651.24 | 653.30 | 99.69 | |||
| MIX04 | 554.86 | 556.30 | 99.74 | |||
| MIX05 | 500.68 | 506.10 | 98.93 | |||
| MIX06 | 293.80 | 409.70 | 71.71 | |||
| MIX07 | 1167.89 | 1324.30 | 88.19 | 20,643.303 | ||
| MIX08 | 1323.61 | 1325.30 | 99.87 | |||
| MIX09 | 1278.99 | 1297.10 | 98.60 | |||
| MIX10 | 108.77 | 150.00 | 72.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yıldırım, E.; Denizhan, B. Comparative Study of Application of Production Sequencing and Scheduling Problems in Tire Mixing Operations with ADAM, Grey Wolf Optimizer, and Genetic Algorithm. Systems 2025, 13, 998. https://doi.org/10.3390/systems13110998
Yıldırım E, Denizhan B. Comparative Study of Application of Production Sequencing and Scheduling Problems in Tire Mixing Operations with ADAM, Grey Wolf Optimizer, and Genetic Algorithm. Systems. 2025; 13(11):998. https://doi.org/10.3390/systems13110998
Chicago/Turabian StyleYıldırım, Elif, and Berrin Denizhan. 2025. "Comparative Study of Application of Production Sequencing and Scheduling Problems in Tire Mixing Operations with ADAM, Grey Wolf Optimizer, and Genetic Algorithm" Systems 13, no. 11: 998. https://doi.org/10.3390/systems13110998
APA StyleYıldırım, E., & Denizhan, B. (2025). Comparative Study of Application of Production Sequencing and Scheduling Problems in Tire Mixing Operations with ADAM, Grey Wolf Optimizer, and Genetic Algorithm. Systems, 13(11), 998. https://doi.org/10.3390/systems13110998






