Unreported Cases for Age Dependent COVID-19 Outbreak in Japan
Abstract
1. Introduction
2. Data
3. Methods
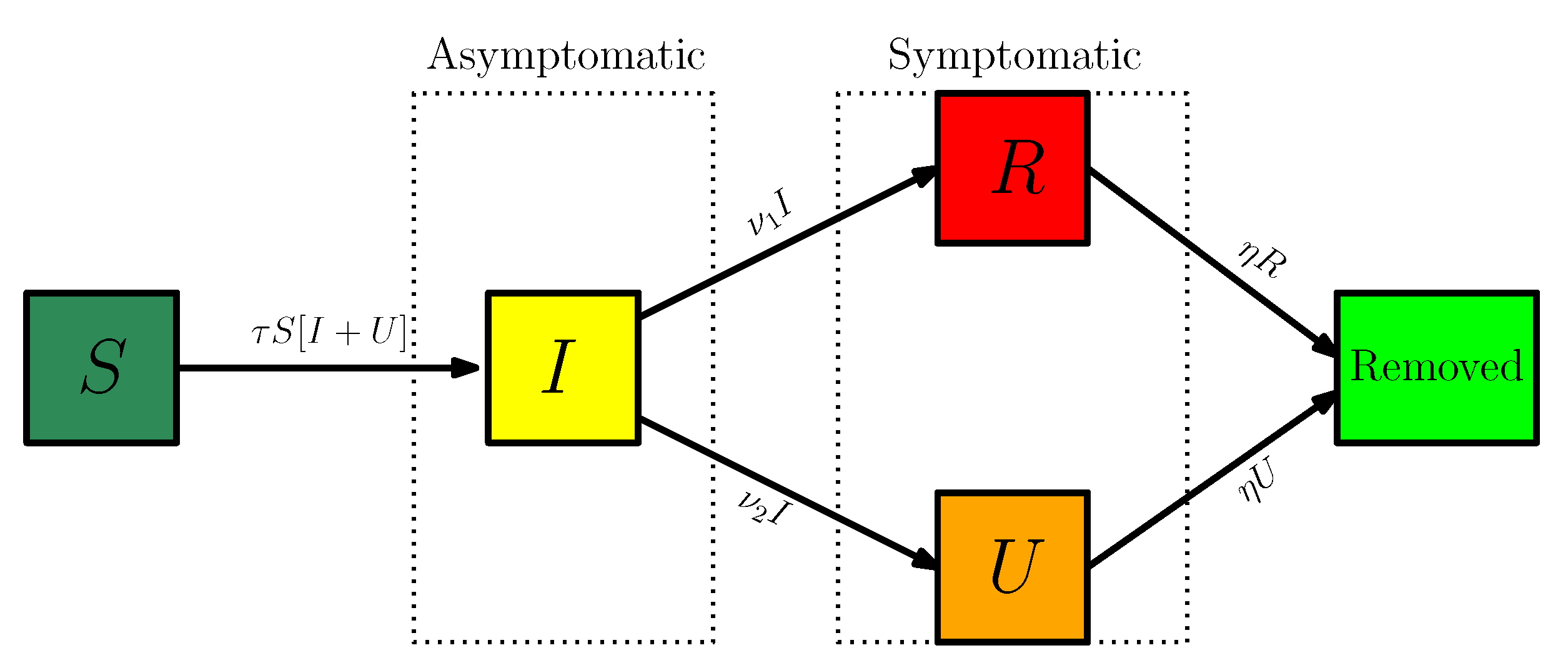
3.1. SIUR Model
3.2. Comparison of the Model (1) with the Data
3.3. Model SIUR with Age Structure
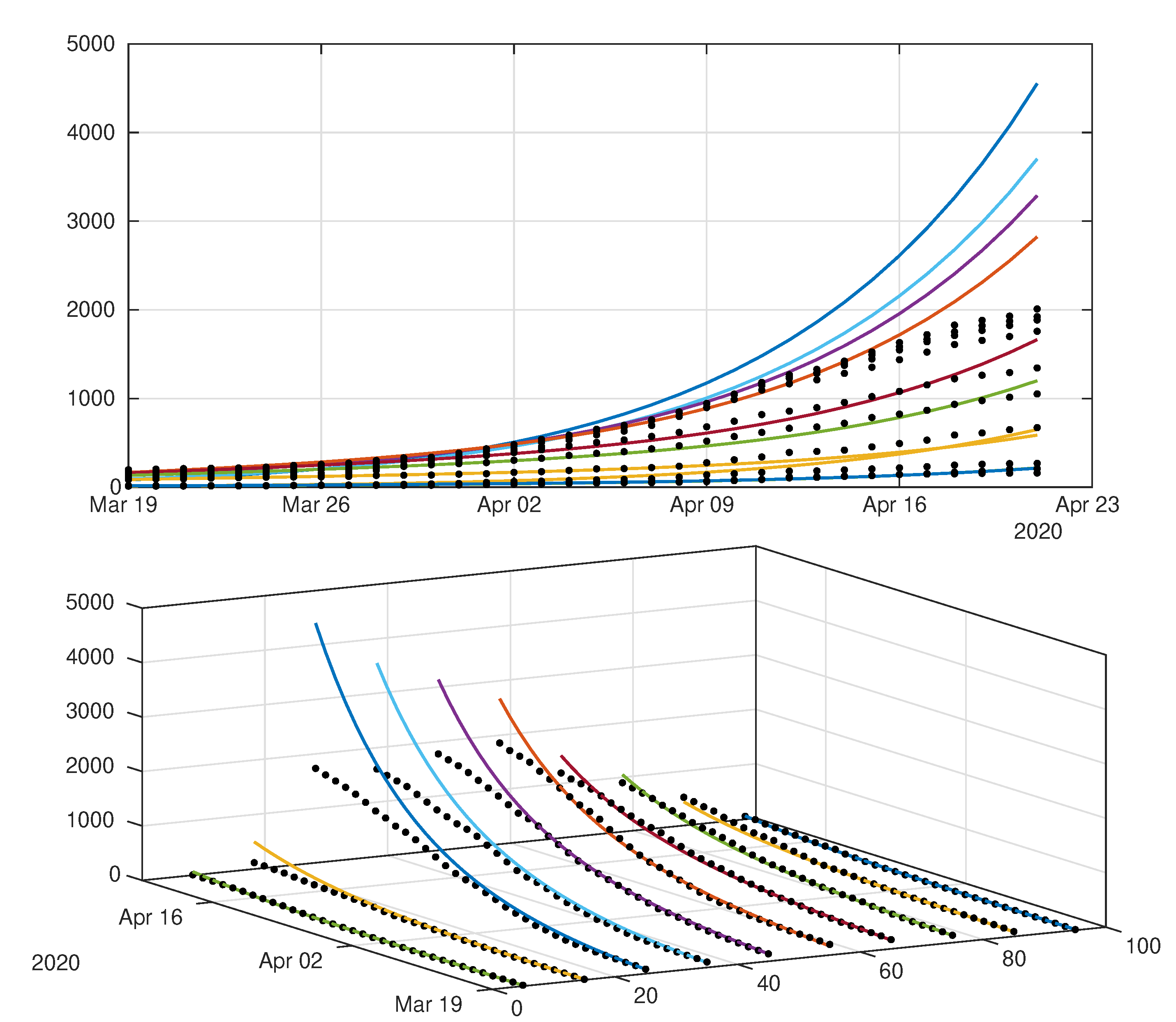
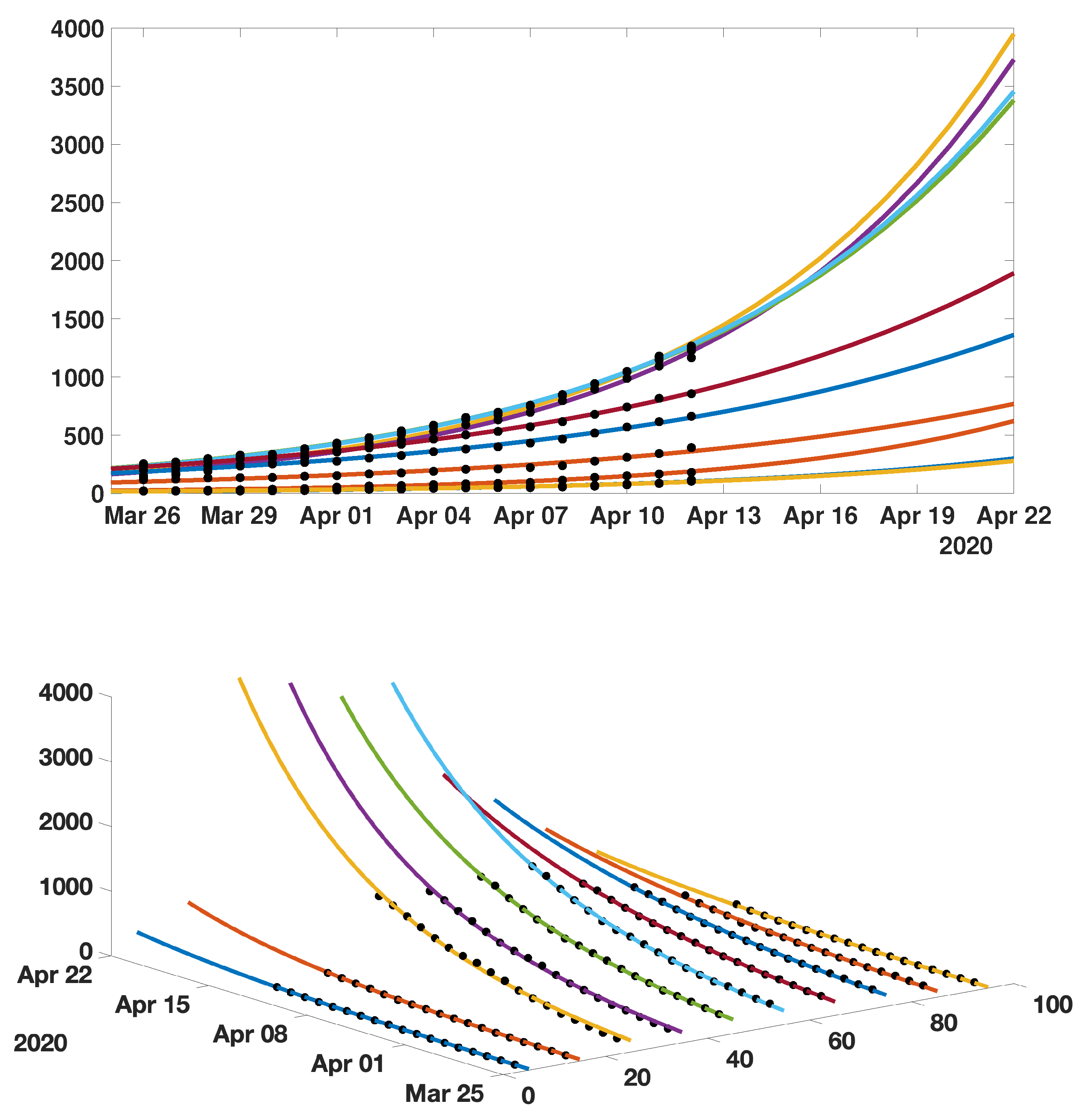
4. Results
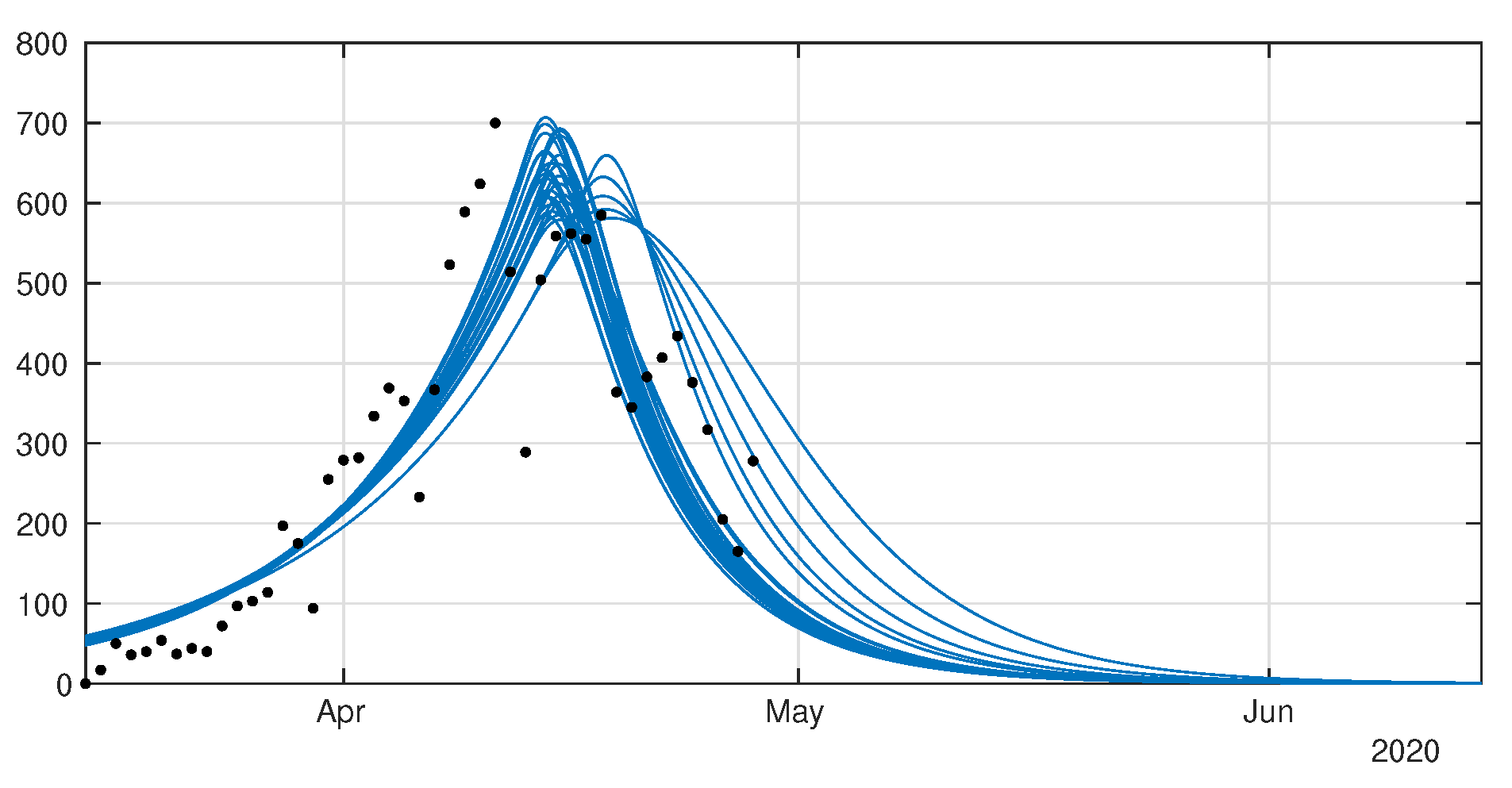
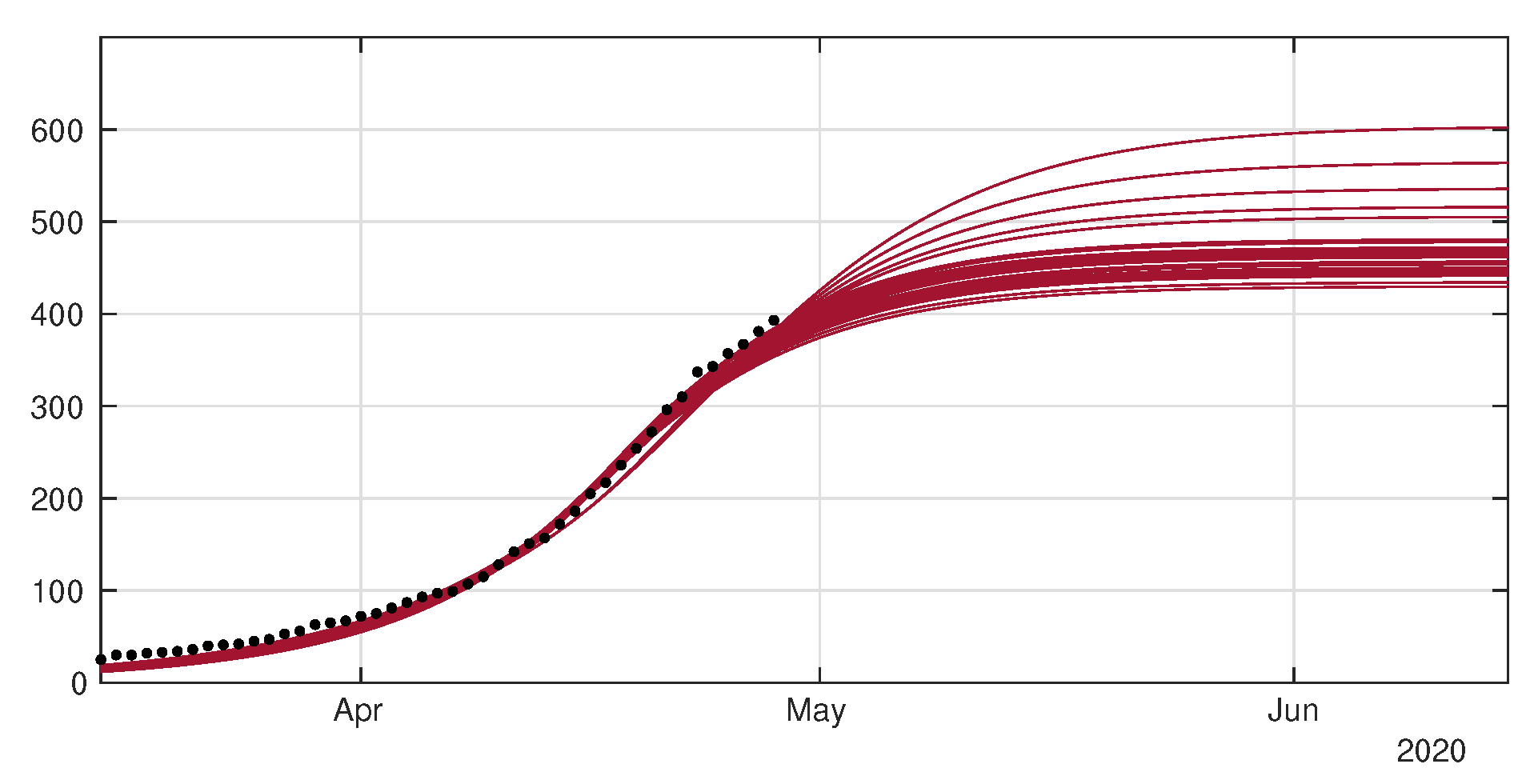
4.1. Model without Age Structure
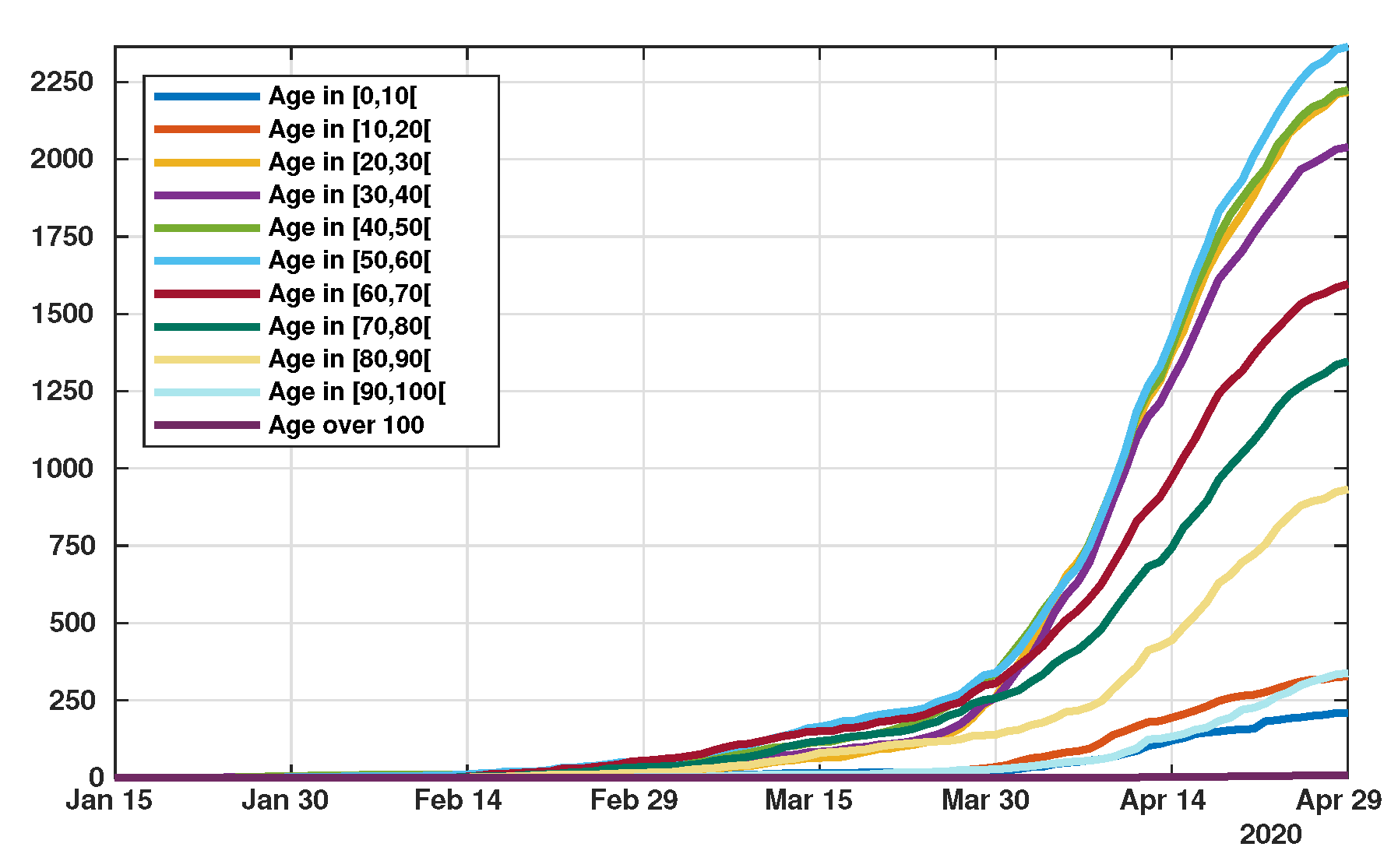
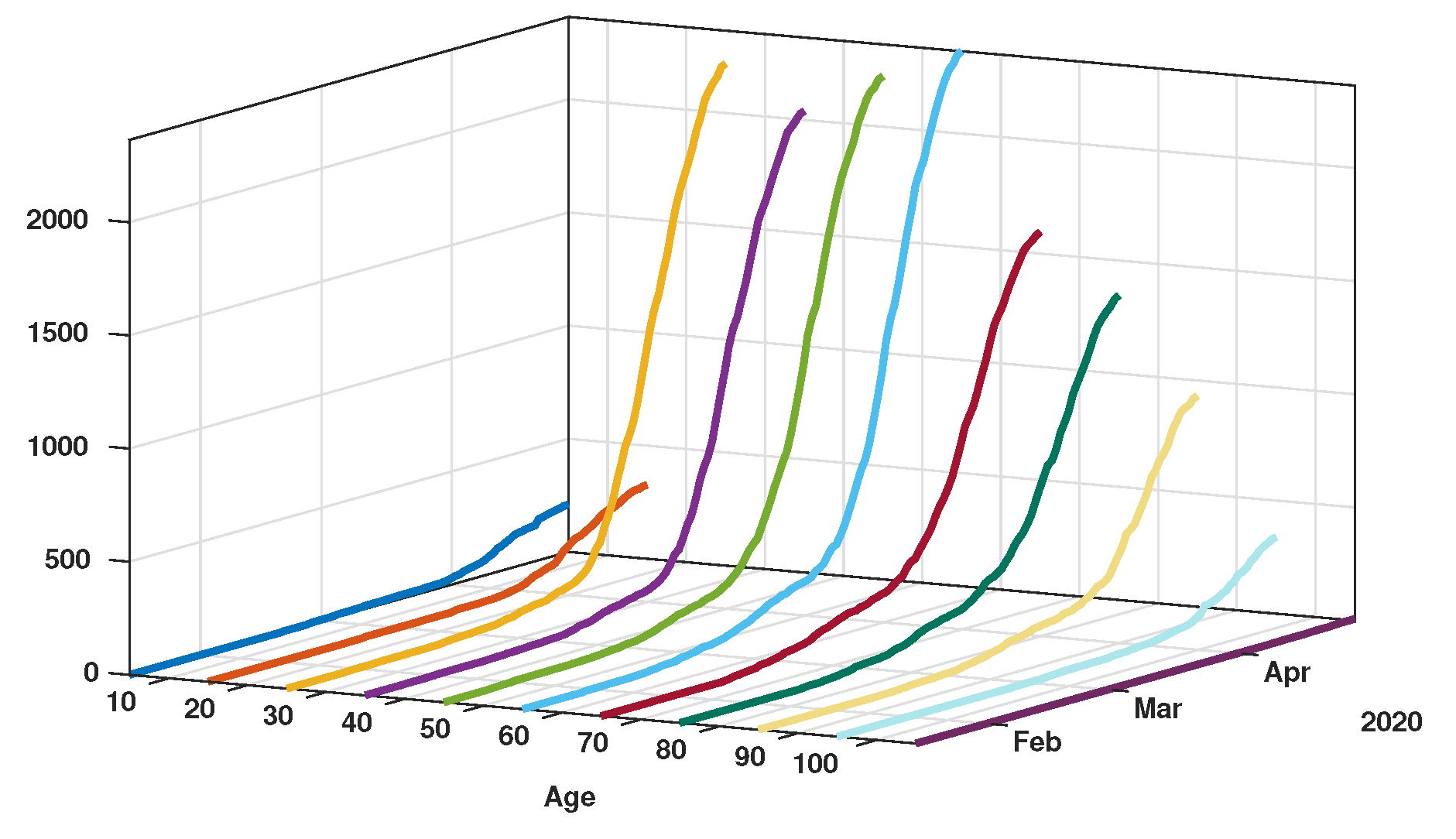
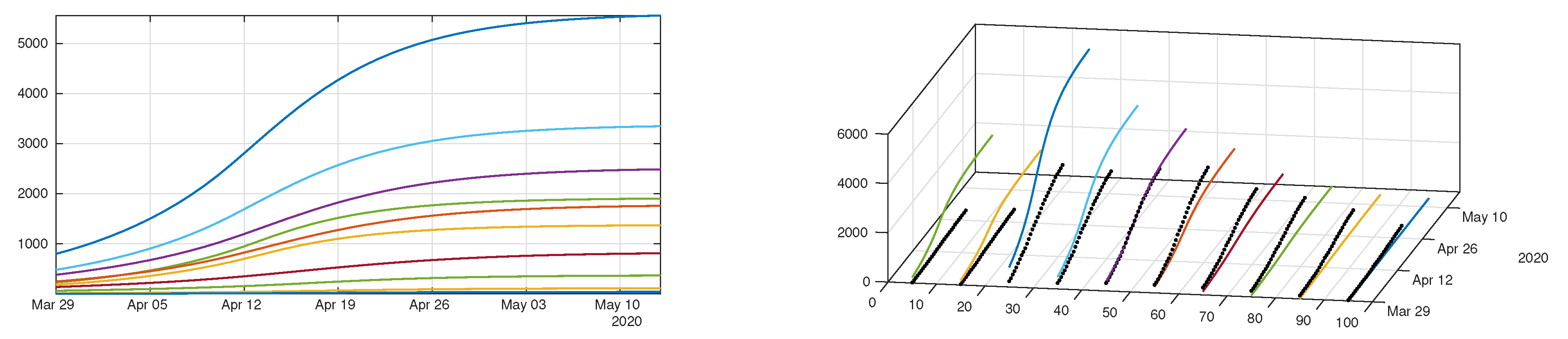
4.2. Model with Age Structure
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Method to Fit of the Age Structured Model to the Data
Appendix B. Construction of the Contact Matrix
References
- WHO Timeline—COVID-19. Available online: https://www.who.int/news-room/detail/27-04-2020-who-timeline---covid-19 (accessed on 21 May 2020).
- World Health Organization. Pneumonia of Unknown Cause—China. Disease Outbreak News. 5 January 2020. Available online: https://www.who.int/csr/don/05-january-2020-pneumonia-of-unkown-cause-china/en/ (accessed on 21 May 2020).
- Guan, W.J.; Ni, Z.Y.; Hu, Y.; Liang, W.H.; Ou, C.Q.; He, J.X.; Liu, L.; Shan, H.; Lei, C.L.; Hui, D.S.C.; et al. Clinical Characteristics of Coronavirus Disease 2019 in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.E.; Li, Z.; Chiew, C.J.; Yong, S.E.; Toh, M.P.; Lee, V.J. Presymptomatic Transmission of SARS-CoV-2—Singapore, January 23–March 16, 2020. Morb. Mortal. Wkly. Rep. 2020, 69, 411. [Google Scholar] [CrossRef] [PubMed]
- Rothe, C.; Schunk, M.; Sothmann, P.; Bretzel, G.; Froeschl, G.; Wallrauch, C.; Zimmer, T.; Thiel, V.; Janke, C.; Guggemos, W.; et al. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N. Engl. J. Med. 2020, 382, 970–971. [Google Scholar] [CrossRef]
- Zou, L.; Ruan, F.; Huang, M.; Liang, L.; Huang, H.; Hong, Z.; Yu, J.; Kang, M.; Song, Y.; Xia, J.; et al. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N. Engl. J. Med. 2020, 382, 1177–1179. [Google Scholar] [CrossRef]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- World Health Organization. Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19). 2020. Available online: https://www.who.int/publications-detail/report-of-the-who-china-joint-mission-on-coronavirus-disease-2019-(covid-19) (accessed on 6 May 2020).
- World Health Organization. Coronavirus Disease 2019 (COVID-19): Situation Report, 104. 2020. Available online: https://apps.who.int/iris/handle/10665/332058 (accessed on 21 May 2020).
- Cao, Q.; Chen, Y.C.; Chen, C.L.; Chiu, C.H. SARS-CoV-2 infection in children: Transmission dynamics and clinical characteristics. J. Formos. Med. Assoc. 2020, 119, 670–673. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, L.; Du, H.; Zhang, J.; Li, Y.Y.; Qu, J.; Zhang, W.; Wang, Y.; Bao, S.; Li, Y.; et al. SARS-CoV-2 Infection in Children. N. Engl. J. Med. 2020, 382, 1663–1665. [Google Scholar] [CrossRef]
- Prem, K.; Liu, Y.; Russell, T.W.; Kucharski, A.J.; Eggo, R.M.; Davies, N.; Flasche, S.; Clifford, S.; Pearson, C.A.B.; Munday, J.D.; et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 2020, 5. [Google Scholar] [CrossRef]
- Singh, R.; Adhikari, R. Age-structured impact of social distancing on the COVID-19 epidemic in India. arXiv 2020, arXiv:2003.12055. [Google Scholar]
- To, K.K.W.; Tsang, O.T.Y.; Leung, W.S.; Tam, A.R.; Wu, T.C.; Lung, D.C.; Yip, C.C.-Y.; Cai, J.-P.; Chan, J.M.-C.; Chik, T.S.-H.; et al. Temporal profiles of viral load in posterior oropharyngeal saliva samples and serum antibody responses during infection by SARS-CoV-2: An observational cohort study. Lancet Infect. Dis. 2020, 20, 565–574. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Bushman, M.; Kishore, N.; Niehus, R.; de Salazar, P.M.; Cowling, B.J.; Lipsitch, M.; Leung, G.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat. Med. 2020, 26, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.G.; Klepac, P.; Liu, Y.; Prem, K.; Jit, M.; Eggo, R.M.; CMMID COVID-19 Working Group. Age-dependent effects in the transmission and control of COVID-19 epidemics. MedRxiv 2020. [Google Scholar] [CrossRef]
- Jones, T.C.; Mühlemann, B.; Veith, T.; Biele, G.; Zuchowski, M.; Hoffmann, J.; Stein, A.; Edelmann, A.; Corman, V.M.; Drosten, C. An analysis of SARS-CoV-2 viral load by patient age. medRxiv 2020. [Google Scholar] [CrossRef]
- Ayoub, H.H.; Chemaitelly, H.; Seedat, S.; Mumtaz, G.R.; Makhoul, M.; Abu-Raddad, L.J. Age could be driving variable SARS-CoV-2 epidemic trajectories worldwide. medRxiv 2020. [Google Scholar] [CrossRef]
- Chikina, M.; Pegden, W. Modeling strict age-targeted mitigation strategies for COVID-19. arXiv 2020, arXiv:2004.04144. [Google Scholar]
- Prem, K.; Cook, A.R.; Jit, M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput. Biol. 2017, 13, e1005697. [Google Scholar] [CrossRef]
- Ayoub, H.H.; Chemaitelly, H.; Mumtaz, G.R.; Seedat, S.; Awad, S.F.; Makhoul, M.; Abu-Raddad, L.J. Characterizing key attributes of the epidemiology of COVID-19 in China: Model-based estimations. medRxiv 2020. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding unreported cases in the 2019-nCov epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef]
- Portal Site of Official Statistics of Japan Website. Reference Table for the Year 2019: Computation of Population by Age (Single Years) and Sex—Total Population, Japanese Population. 2020. Available online: http://www.stat.go.jp/english/data/jinsui/index.htm (accessed on 6 May 2020).
- Griette, Q.; Liu, Z.; Magal, P. Estimating the last day for COVID-19 outbreak in mainland China. medRxiv 2020. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. Math. Biosci. Eng. 2020, 17, 3040–3051. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infect. Dis. Model. 2020. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A model to predict COVID-19 epidemics with applications to South Korea, Italy, and Spain. SIAM News 2020, 53, 4. [Google Scholar]
- Liu, Z.; Magal, P.; Webb, G. Predicting the number of reported and unreported cases for the COVID-19 epidemic in China, South Korea, Italy, France, Germany and United Kingdom. medRxiv 2020. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- van den Driessche, P.; Watmough, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Munasinghe, L.; Asai, Y.; Nishiura, H. Quantifying heterogeneous contact patterns in Japan: A social contact survey. Theor. Biol. Med. Model. 2019, 16, 6. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds,, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday,, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008, 5, e74. [Google Scholar] [CrossRef]
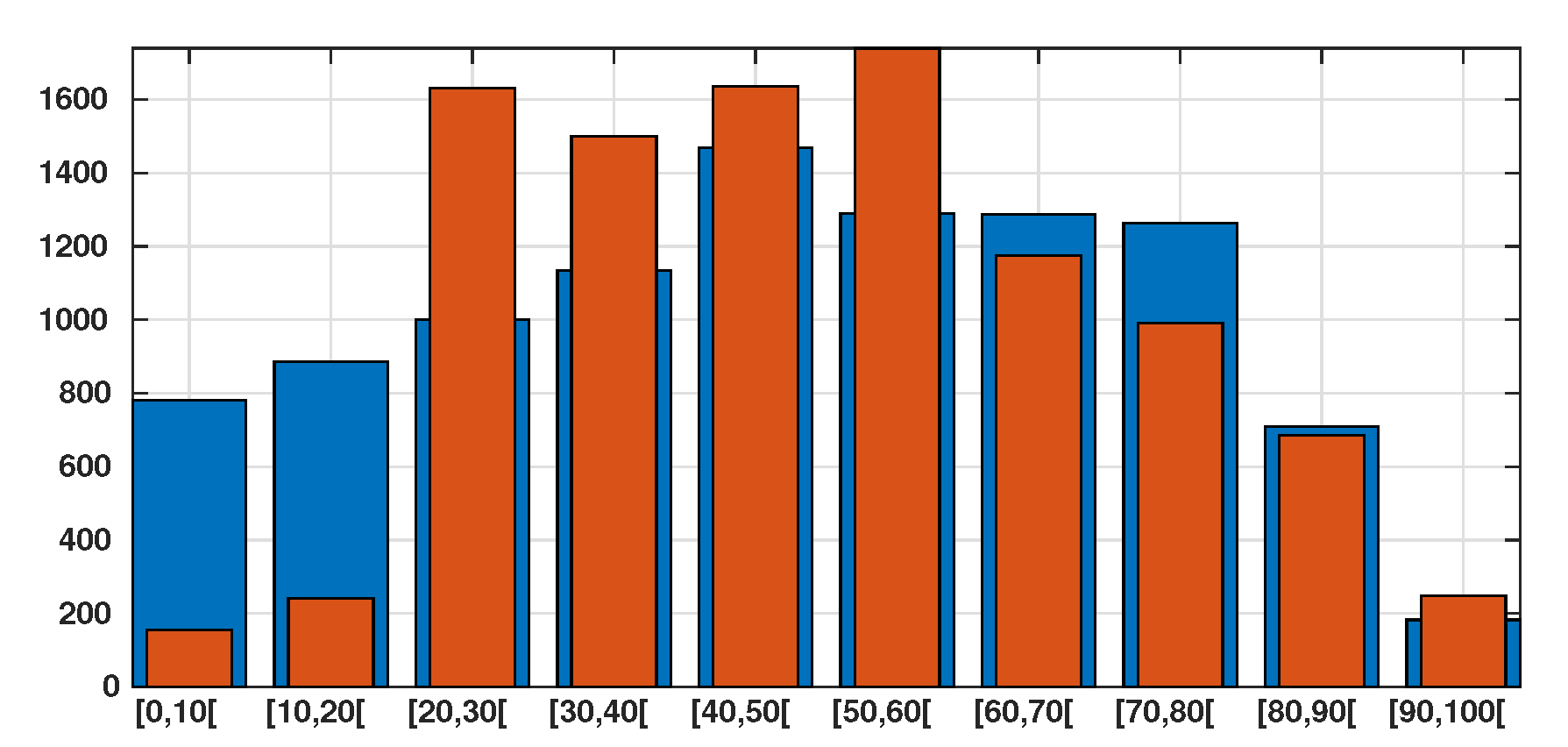
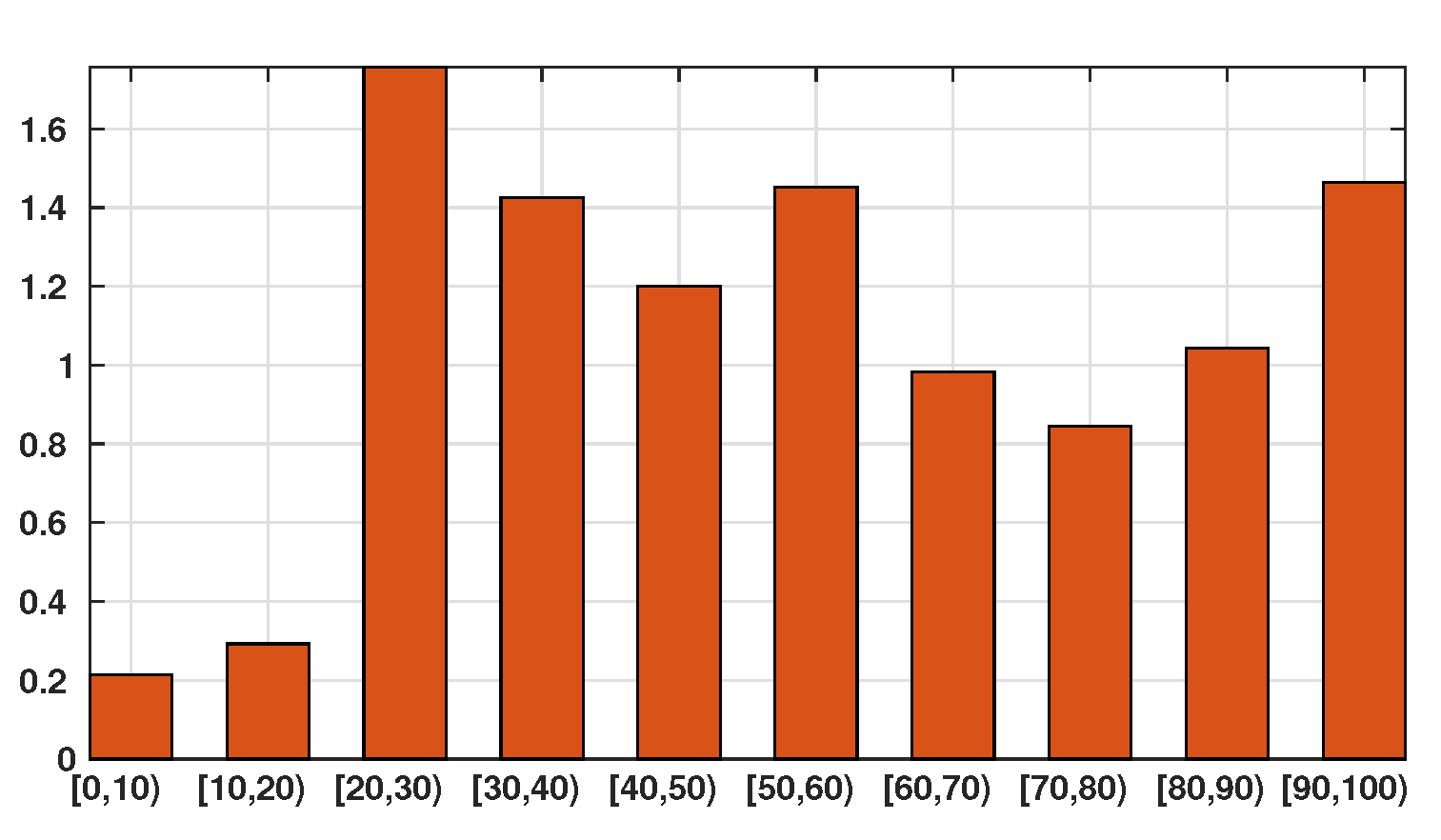




| Age group | ||||||||||
| Age class for 2019 | 9,859,515 | 11,171,044 | 12,627,964 | 14,303,042 | 18,519,755 | 16,277,853 | 16,231,582 | 15,926,926 | 8,939,954 | 2,309,313 |
| Age class per 10,000 people | 781 | 885 | 1000 | 1133 | 1467 | 1290 | 1286 | 1262 | 709 | 183 |
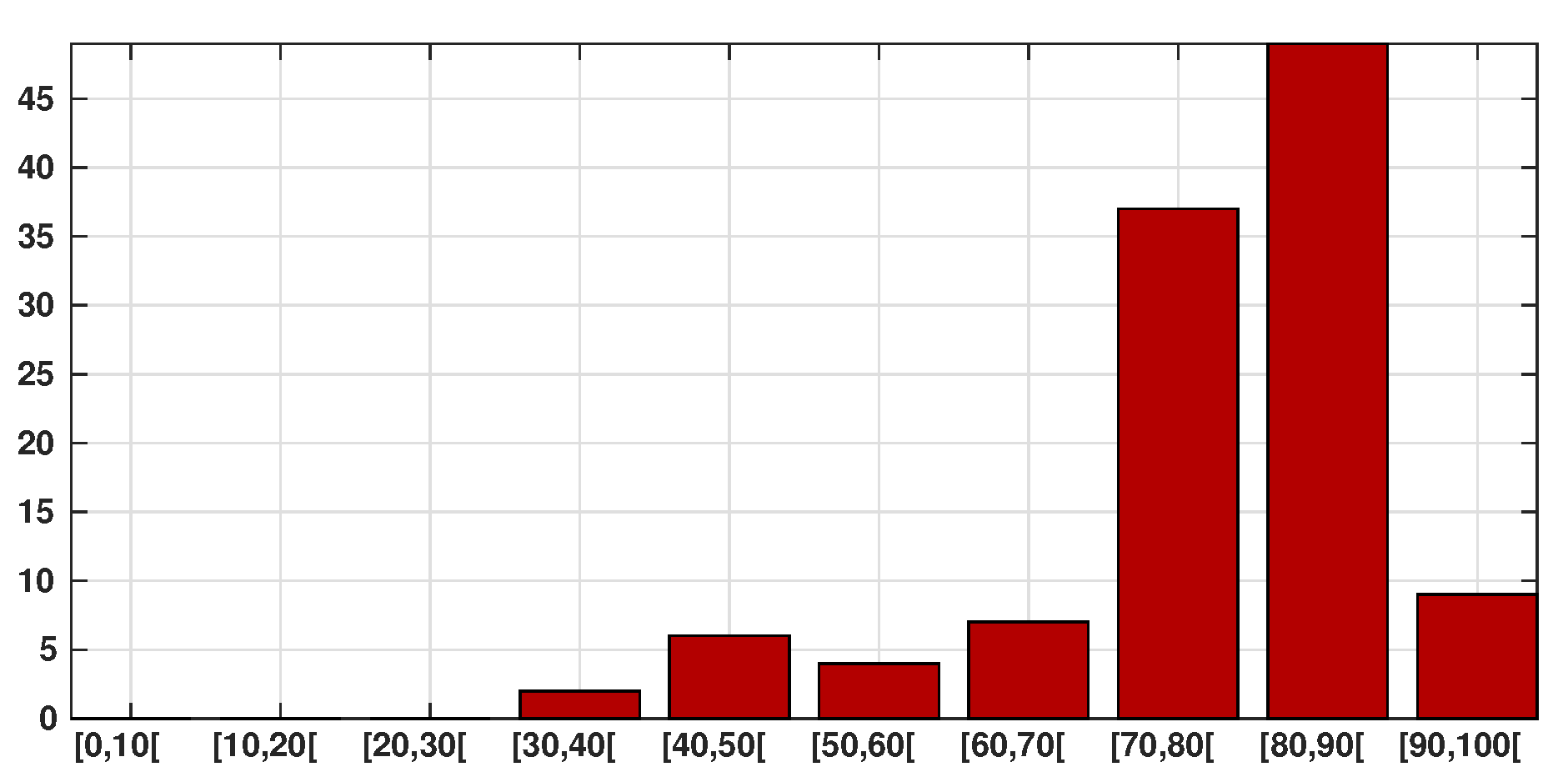
| Confirmed Cases | 211 | 327 | 2216 | 2034 | 2220 | 2355 | 1566 | 1289 | 857 | 304 |
| Death | 0 | 0 | 0 | 2 | 6 | 4 | 7 | 37 | 49 | 9 |
| Dataset | Japanese Population | Infected | Deceased |
|---|---|---|---|
| First Quartile | 28 | 28 | 68 |
| Median | 48 | 44 | 75 |
| Third Quartile | 67 | 59 | 81 |
| Symbol | Interpretation | Method | |
|---|---|---|---|
| Time at which the epidemic started | fitted | ||
| Number of susceptible at time | fixed | ||
| Number of asymptomatic infectious at time | fitted | ||
| Number of unreported symptomatic infectious at time | fitted | ||
| Transmission rate at time t | fitted | ||
| D | First day of public intervention | fitted | |
| Intensity of the public intervention | fitted | ||
| Average time during which asymptomatic infectious are asymptomatic | fixed | ||
| f | Fraction of asymptomatic infectious that become reported symptomatic infectious | fixed | |
| Rate at which asymptomatic infectious become reported symptomatic | fixed | ||
| Rate at which asymptomatic infectious become unreported symptomatic | fixed | ||
| Average time symptomatic infectious have symptoms | fixed |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Griette, Q.; Magal, P.; Seydi, O. Unreported Cases for Age Dependent COVID-19 Outbreak in Japan. Biology 2020, 9, 132. https://doi.org/10.3390/biology9060132
Griette Q, Magal P, Seydi O. Unreported Cases for Age Dependent COVID-19 Outbreak in Japan. Biology. 2020; 9(6):132. https://doi.org/10.3390/biology9060132
Chicago/Turabian StyleGriette, Quentin, Pierre Magal, and Ousmane Seydi. 2020. "Unreported Cases for Age Dependent COVID-19 Outbreak in Japan" Biology 9, no. 6: 132. https://doi.org/10.3390/biology9060132
APA StyleGriette, Q., Magal, P., & Seydi, O. (2020). Unreported Cases for Age Dependent COVID-19 Outbreak in Japan. Biology, 9(6), 132. https://doi.org/10.3390/biology9060132