Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions
Abstract
1. Introduction
2. Results
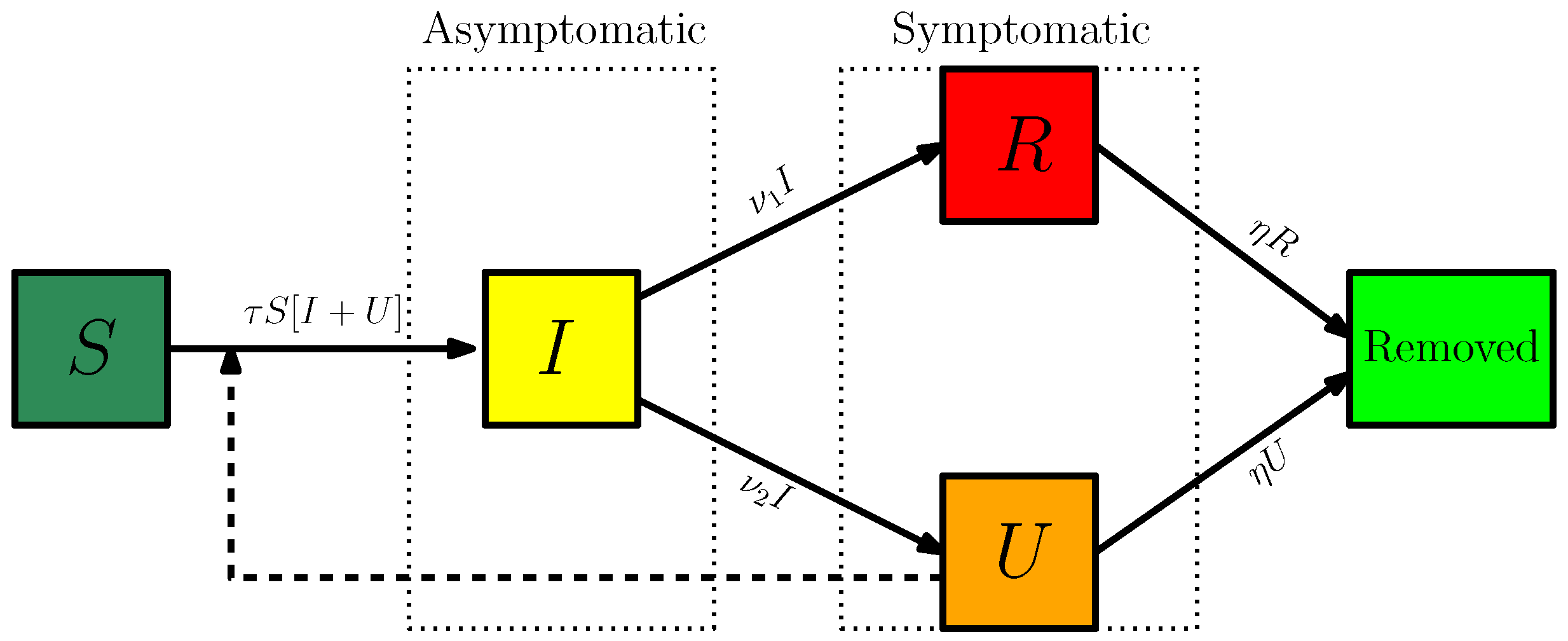
2.1. The Model and Data
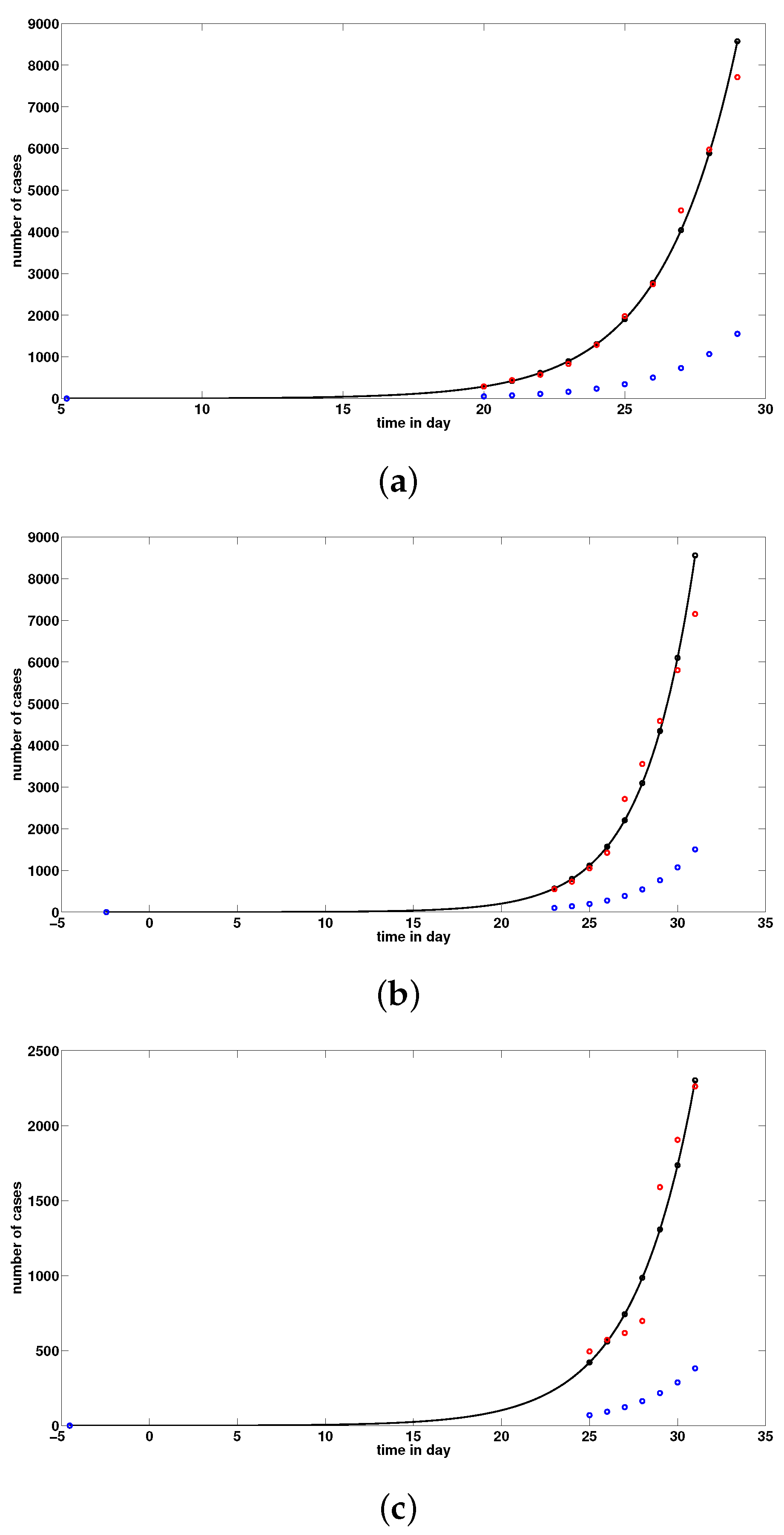
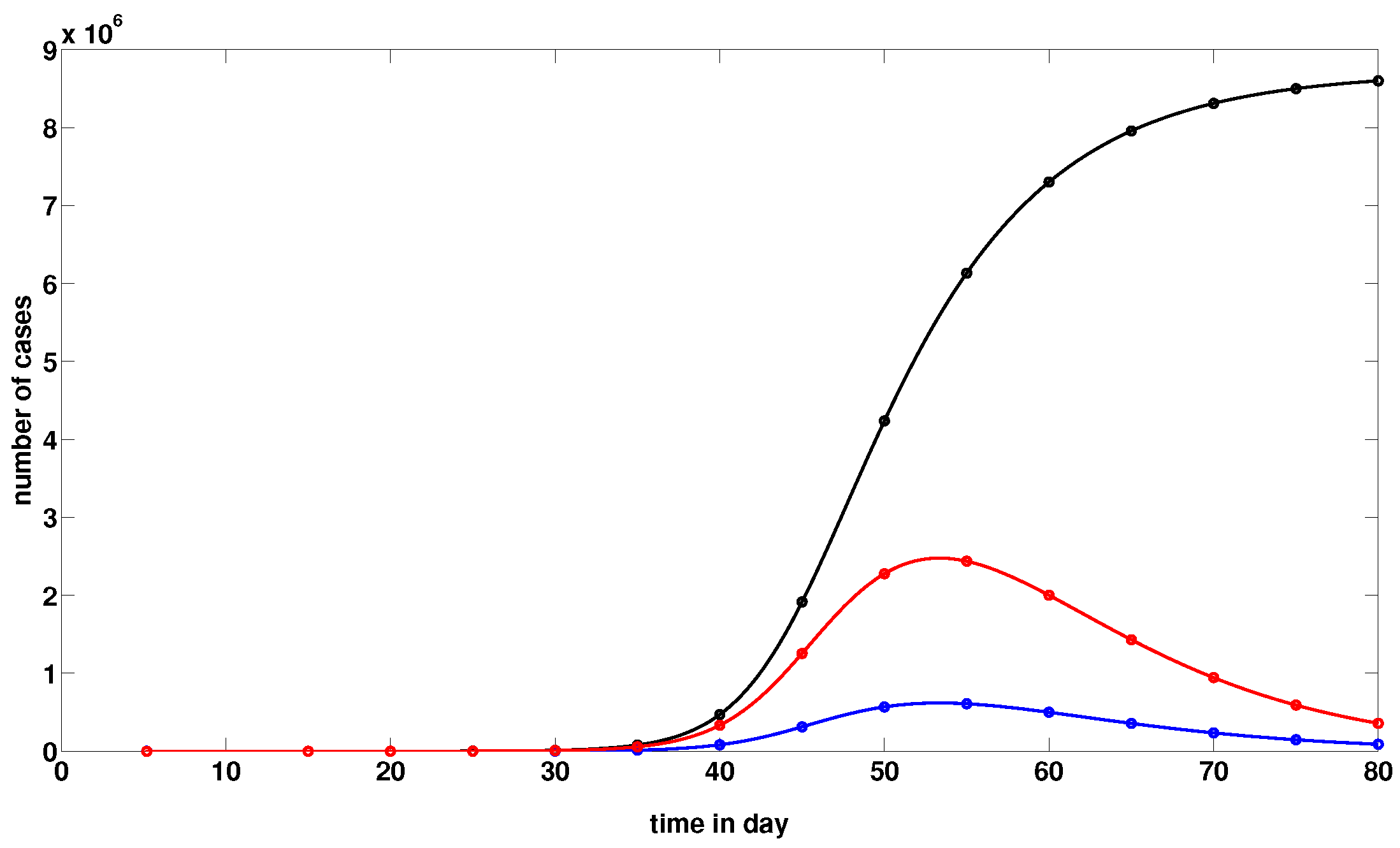
2.2. Comparison of Model (1) with the Data
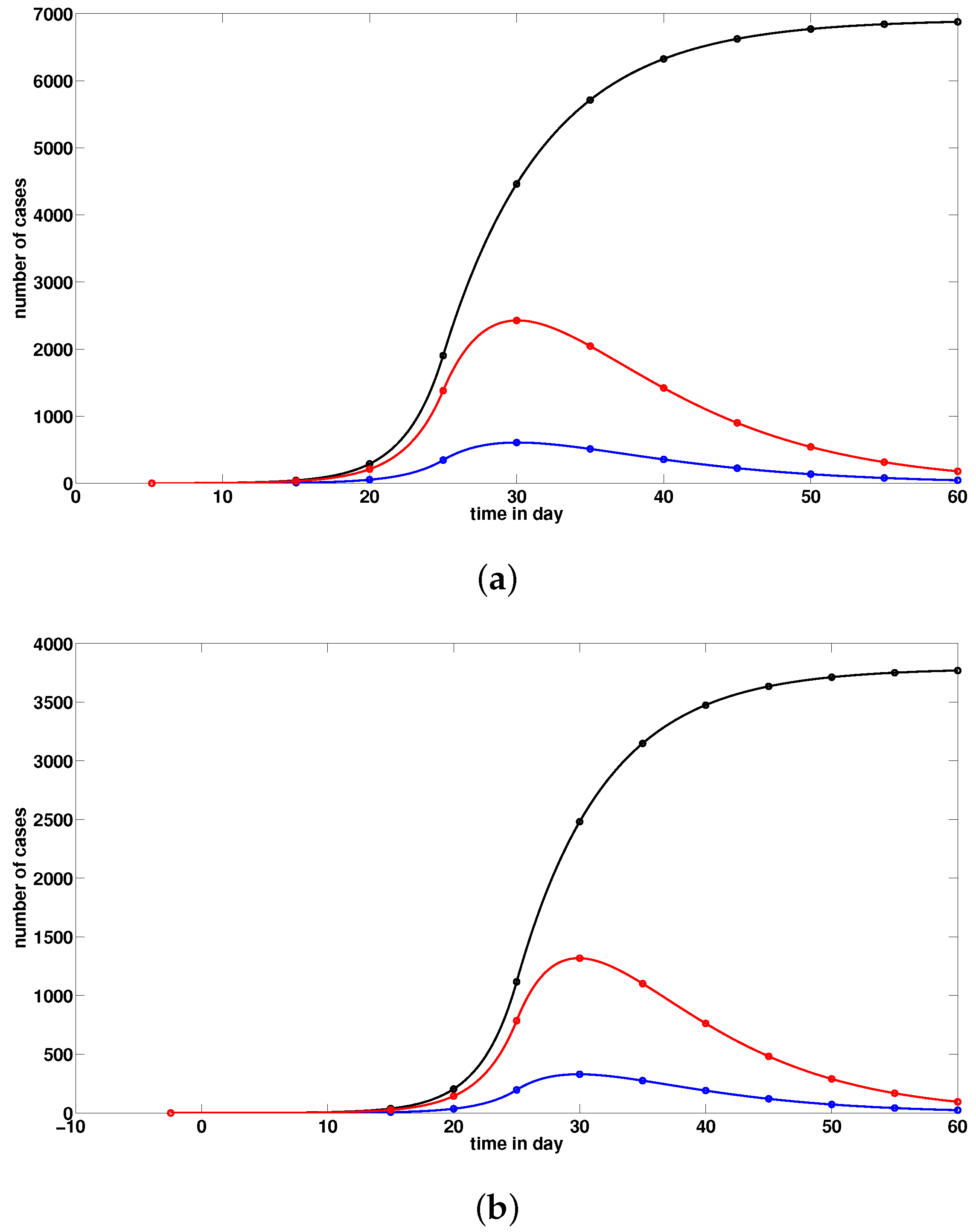
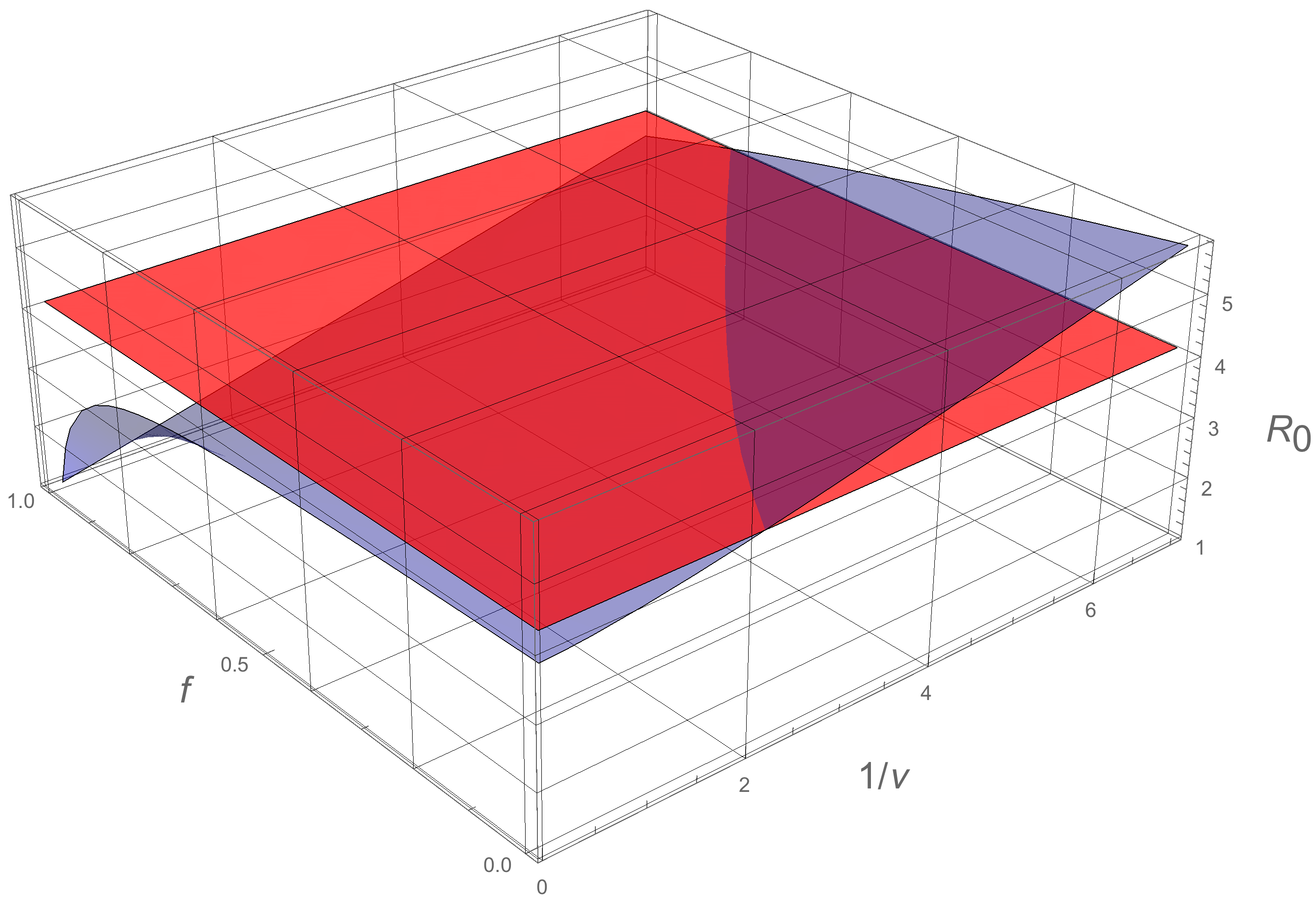
2.3. Numerical Simulations
3. Discussion
4. Materials and Methods
4.1. Method to Estimate the Parameters of (1) from the Number of Reported Cases
4.2. Computation of the Basic Reproductive Number
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chinese Center for Disease Control and Prevention. Available online: http://www.chinacdc.cn/jkzt/crb/zl/szkb_11803/jszl_l11809/ (accessed on 30 January 2020).
- New England Journal of Medicine, Letter to the Editor. Available online: https://www.nejm.org/doi/full/10.1056/NEJMc2001468 (accessed on 30 January 2020).
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of 2019-nCov and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3525558 (accessed on 30 January 2020). [CrossRef] [PubMed]
- Magal, P.; Webb, G. The parameter identification problem for SIR epidemic models: Identifying Unreported Cases. J. Math. Biol. 2018, 77, 1629–1648. [Google Scholar] [CrossRef] [PubMed]
- Ducrot, A.; Magal, P.; Nguyen, T.; Webb, G. Identifying the Number of Unreported Cases in SIR Epidemic Models. Math. Med. Biol. J. IMA 2019. [Google Scholar] [CrossRef] [PubMed]
- Wuhan Municipal Health Commission. Available online: http://wjw.wuhan.gov.cn/front/web/list3rd/yes/802 (accessed on 30 January 2020).
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
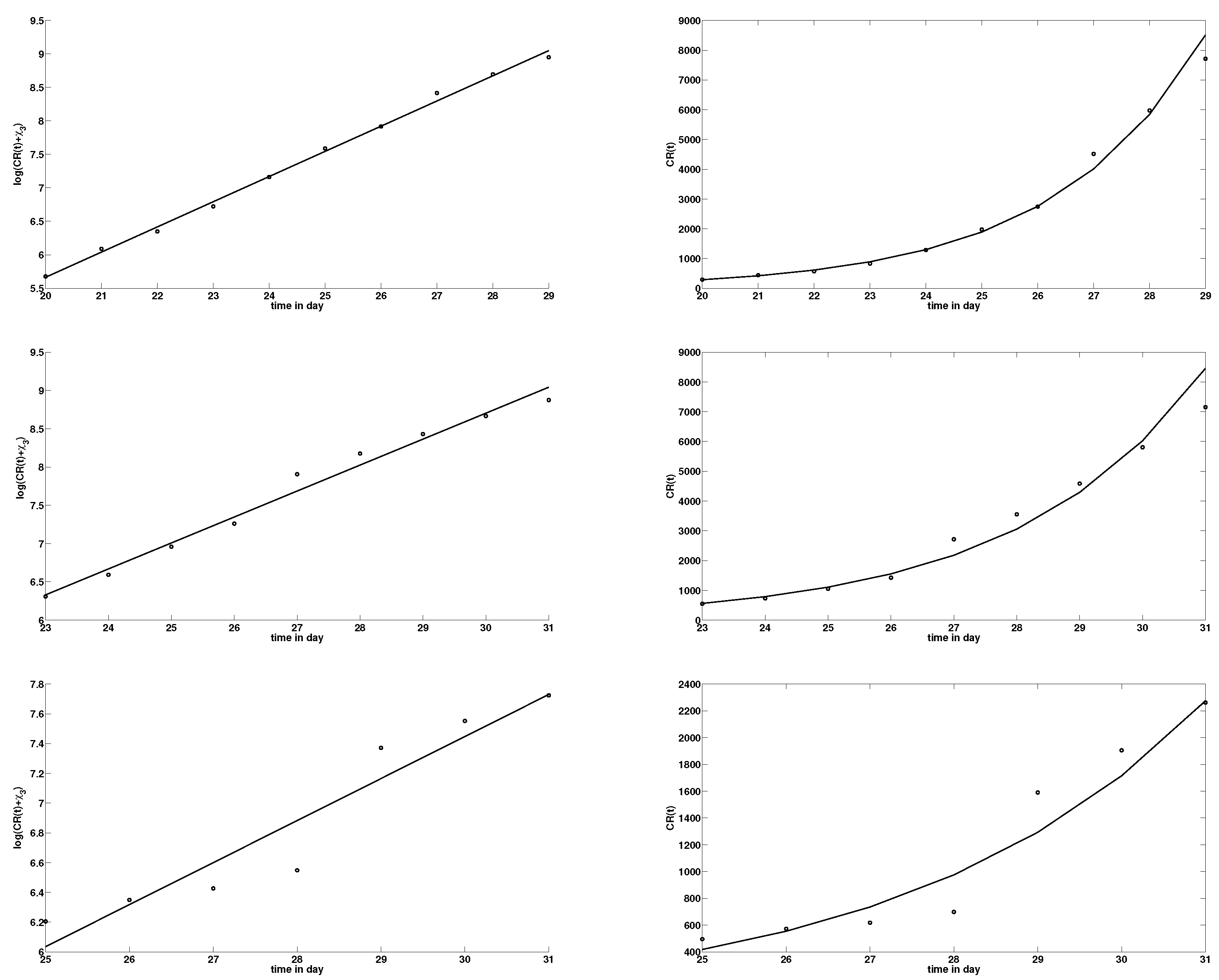

| Symbol | Interpretation | Method | |
|---|---|---|---|
| Time at which the epidemic started | fitted | ||
| Number of susceptible at time | fixed | ||
| Number of asymptomatic infectious at time | fitted | ||
| Number of unreported symptomatic infectious at time | fitted | ||
| Transmission rate | fitted | ||
| Average time during which asymptomatic infectious are asymptomatic | fixed | ||
| f | Fraction of asymptomatic infectious that become reported symptomatic infectious | fixed | |
| Rate at which asymptomatic infectious become reported symptomatic | fitted | ||
| Rate at which asymptomatic infectious become unreported symptomatic | fitted | ||
| Average time symptomatic infectious have symptoms | fixed |
| Date January | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
|---|---|---|---|---|---|---|---|---|---|---|
| Confirmed cases (cumulated) for mainland China | 291 | 440 | 571 | 830 | 1287 | 1975 | 2744 | 4515 | 5974 | 7711 |
| Mortality cases (cumulated) for mainland China | 9 | 17 | 25 | 41 | 56 | 80 | 106 | 132 | 170 |
| Date January | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
|---|---|---|---|---|---|---|---|---|---|
| Confirmed cases (cumulated) for Hubei | 549 | 729 | 1052 | 1423 | 2714 | 3554 | 4586 | 5806 | 7153 |
| Mortality cases (cumulated) for Hubei | 24 | 39 | 52 | 76 | 100 | 125 | 162 | 204 | 249 |
| Date January | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
|---|---|---|---|---|---|---|---|---|---|
| Confirmed cases (cumulated) for Wuhan | 495 | 572 | 618 | 698 | 1590 | 1905 | 2261 | 2639 | 3215 |
| Mortality cases (cumulated) for Wuhan | 23 | 38 | 45 | 63 | 85 | 104 | 129 | 159 | 192 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions. Biology 2020, 9, 50. https://doi.org/10.3390/biology9030050
Liu Z, Magal P, Seydi O, Webb G. Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions. Biology. 2020; 9(3):50. https://doi.org/10.3390/biology9030050
Chicago/Turabian StyleLiu, Zhihua, Pierre Magal, Ousmane Seydi, and Glenn Webb. 2020. "Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions" Biology 9, no. 3: 50. https://doi.org/10.3390/biology9030050
APA StyleLiu, Z., Magal, P., Seydi, O., & Webb, G. (2020). Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions. Biology, 9(3), 50. https://doi.org/10.3390/biology9030050






