Limitations of the Farquhar–von Caemmerer–Berry Model in Estimating the Maximum Electron Transport Rate: Evidence from Four C3 Species
Simple Summary
Abstract
1. Introduction
2. Material and Methods
2.1. Plant Material
2.2. Gas Exchange and Chl Fluorescence Measurement
2.3. JA-max Estimated by the FvCB Model
2.4. An Empirical Model for the CO2 Response of Electron Transport Rate (Model 1)
2.5. Statistical Analyses
3. Results
3.1. An–Ci Curve Analysis
3.2. Comparison of Jmax Estimates
4. Discussion
4.1. Why Can Current Technology Validate the Estimation of JA-max by the FvCB Model?
4.2. What Explains the Discrepancies Between Estimated JA-max and Observed Jf-max?
4.3. Can a More Comprehensive Framework Improve JA-max or Jf-max Estimation?
4.4. Should We Rethink the Estimation of JA-max?
4.5. How Does Overestimating JA-max Affect Agricultural and Environmental Research?
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Onoda, Y.; Hikosaka, K.; Hirose, T. Seasonal change in the balance between capacities of RuBP carboxylation and RuBP regeneration affects CO2 response of photosynthesis in Polygonum cuspidatum. J. Exp. Bot. 2005, 56, 755–763. [Google Scholar] [CrossRef] [PubMed]
- Sharkey, T.D.; Bernacchi, C.J.; Fa Rquhar, G.D.; Singsaas, E.L. Fitting photosynthetic carbon dioxide response curves for C3 leaves. Plant Cell Environ. 2007, 30, 1035–1040. [Google Scholar] [CrossRef] [PubMed]
- von Caemmerer, S. Steady-state models of photosynthesis. Plant Cell Environ. 2013, 36, 1617–1630. [Google Scholar] [CrossRef]
- Sharkey, T.D. What gas exchange data can tell us about photosynthesis. Plant Cell Environ. 2016, 39, 1161–1163. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Busch, F.A.; Struik, P.C.; Sharkey, T.D. Evolution of a biochemical model of steady-state photosynthesis. Plant Cell Environ. 2021, 44, 2811–2837. [Google Scholar] [CrossRef]
- Yin, X.; Amthor, J.S. Estimating leaf day respiration from conventional gas exchange measurements. New Phytol. 2024, 241, 52–58. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef]
- von Caemmerer, S.; Farquhar, G.D. Some relationships between the biochemistry of photosynthesis and the gas exchange of leaves. Planta 1981, 153, 376–387. [Google Scholar] [CrossRef]
- Harley, P.C.; Sharkey, T.D. An improved model of C3 photosynthesis at high CO2: Reversed O2 sensitivity explained by lack of glycerate reentry into the chloroplast. Photosynth. Res. 1991, 27, 169–178. [Google Scholar] [CrossRef]
- von Caemmerer, S. Biochemical Models of Leaf Photosynthesis; CSIRO Publishing: Victoria, Australia, 2000. [Google Scholar]
- Silva-Pérez, V.; Furbank, R.T.; Condon, A.G.; Evans, J.R. Biochemical model of C3 photosynthesis applied to wheat at different temperatures. Plant Cell Environ. 2017, 40, 1552–1564. [Google Scholar] [CrossRef]
- Ye, Z.P.; Robakowski, P.; Suggett, D.J. A mechanistic model for the light response of photosynthetic electron transport rate based on light harvesting properties of photosynthetic pigment molecules. Planta 2013, 237, 837–847. [Google Scholar] [CrossRef]
- Ye, Z.P.; Suggett, J.D.; Robakowski, P.; Kang, H.J. A mechanistic model for the photosynthesis-light response based on the photosynthetic electron transport of photosystem II in C3 and C4 species. New Phytol. 2013, 199, 110–120. [Google Scholar] [CrossRef] [PubMed]
- Miao, Z.; Xu, M.; Lathrop, R.G., Jr.; Wang, Y. Comparison of the A–Cc curve fitting methods in determining maximum ribulose 1,5-bisphosphate carboxylase/oxygenase carboxylation rate, potential light saturated electron transport rate and leaf dark respiration. Plant Cell Environ. 2009, 32, 109–122. [Google Scholar] [CrossRef]
- Patrick, L.D.; Ogle, K.; Tissue, D.T. A hierarchical Bayesian approach for estimation of photosynthetic parameters of C3 plants. Plant Cell Environ. 2009, 32, 1695–1709. [Google Scholar] [CrossRef]
- Bellasio, C.; Beerling, D.J.; Griffiths, H. An Excel tool for deriving key photosynthetic parameters from combined gas exchange and chlorophyll fluorescence: Theory and practice. Plant Cell Environ. 2016, 39, 1180–1197. [Google Scholar] [CrossRef] [PubMed]
- Busch, F.A.; Sage, R.F. The sensitivity of photosynthesis to O2 and CO2 concentration identifies strong Rubisco control above the thermal optimum. New Phytol. 2017, 213, 1036–1051. [Google Scholar] [CrossRef] [PubMed]
- Walker, A.P.; Quaife, T.; Bodegom, P.V.; Kauwe, M.D.; Keenan, T.F.; Joiner, J.; Lomas, M.R.; Macbean, N.; Xu, C.; Yang, X. The impact of alternative trait-scaling hypotheses for the maximum photosynthetic carboxylation rate (Vcmax) on global gross primary production. New Phytol. 2017, 215, 1370–1386. [Google Scholar] [CrossRef]
- Anderegg, W.R.; Wolf, A.; Arango-Velez, A.; Choat, B.; Chmura, D.J.; Jansen, S.; Kolb, T.; Li, S.; Meinzer, F.C.; Pita, P. Woody plants optimise stomatal behaviour relative to hydraulic risk. Ecol. Lett. 2018, 21, 968–977. [Google Scholar] [CrossRef]
- Dusenge, M.E.; Duarte, A.G.; Way, D.A. Plant carbon metabolism and climate change: Elevated CO2 and temperature impacts on photosynthesis, photorespiration and respiration. New Phytol. 2019, 221, 32–49. [Google Scholar] [CrossRef] [PubMed]
- Fabre, D.; Yin, X.; Michael, D.; Anne, C.V.; Sandrine, R.; Lauriane, R.; Armelle, S.; Delphine, L. Is triose phosphate utilization involved in the feedback inhibition of photosynthesis in rice under conditions of sink limitation? J. Exp. Bot. 2019, 70, 5773–5785. [Google Scholar] [CrossRef]
- Han, T.; Zhu, G.; Ma, J.; Wang, S.; Zhang, K. Sensitivity analysis and estimation using a hierarchical Bayesian method for the parameters of the FvCB biochemical photosynthetic model. Photosynth. Res. 2020, 143, 45–66. [Google Scholar] [CrossRef] [PubMed]
- Long, S.P.; Bernacchi, C.J. Gas exchange measurements, what can they tell us about the underlying limitations to photosynthesis? Procedures and sources of error. J. Exp. Bot. 2003, 54, 2393–2401. [Google Scholar] [CrossRef] [PubMed]
- Verheijen, L.M.; Aerts, R.; Brovkin, V.; Cavender-Bares, J.; Cornelissen, J.H.; Kattge, J.; Van Bodegom, P.M. Inclusion of ecologically based trait variation in plant functional types reduces the projected land carbon sink in an earth system model. Glob. Change Biol. 2015, 21, 3074–3086. [Google Scholar] [CrossRef]
- Norby, R.J.; Gu, L.; Haworth, I.C.; Jensen, A.M.; Turner, B.L.; Walker, A.P.; Warren, J.M.; Weston, D.J.; Xu, C.; Winter, K. Informing models through empirical relationships between foliar phosphorus, nitrogen and photosynthesis across diverse woody species in tropical forests of Panama. New Phytol. 2017, 215, 1425–1437. [Google Scholar] [CrossRef]
- Rogers, A.; Serbin, S.P.; Ely, K.S.; Sloan, V.L.; Wullschleger, S.D. Terrestrial biosphere models underestimate photosynthetic capacity and CO2 assimilation in the Arctic. New Phytol. 2017, 216, 1090–1103. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.Y.; Oijen, M.V.; Schapendonk, A. Extension of a biochemical model for the generalized stoichiometry of electron transport limited C3 photosynthesis. Plant Cell Environ. 2004, 27, 1211–1222. [Google Scholar] [CrossRef]
- Dubois, J.J.B.; Fiscus, E.L.; Booker, F.L.; Flowers, M.; Reid, C.D. Optimizing the statistical estimation of the parameters of the Farquhar–von Caemmerer–Berry model of photosynthesis. New Phytol. 2007, 176, 402–414. [Google Scholar] [CrossRef] [PubMed]
- Ellsworth, D.S.; Crous, K.Y.; Lambers, H.; Cooke, J. Phosphorus recycling in photorespiration maintains high photosynthetic capacity in woody species. Plant Cell Environ. 2015, 38, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- Bernacchi, C.J.; Bagley, J.E.; Serbin, S.P.; Ruiz-Vera, U.M.; Rosenthal, D.M.; Vanloocke, A. Modelling C3 photosynthesis from the chloroplast to the ecosystem. Plant Cell Environ. 2013, 36, 1641–1657. [Google Scholar] [CrossRef]
- Yin, X.; Struik, P.C.; Romero, P.; Harbinson, J.; Vos, J. Using combined measurements of gas exchange and chlorophyll fluorescence to estimate parameters of a biochemical C3 photosynthesis model: A critical appraisal and a new integrated approach applied to leaves in a wheat (Triticum aestivum) canopy. Plant Cell Environ. 2009, 32, 448–464. [Google Scholar] [CrossRef]
- Gu, L.H.; Pallardy, S.G.; Law, B.E.; Wullschleger, S.D. Reliable estimation of biochemical parameters from C3 leaf photosynthesis-intercellular carbon dioxide response curves. Plant Cell Environ. 2010, 33, 1852–1874. [Google Scholar] [CrossRef] [PubMed]
- Farquhar, G.D.; Busch, F.A. Changes in the chloroplastic CO2 concentration explain much of the observed Kok effect: A model. New Phytol. 2017, 214, 570. [Google Scholar] [CrossRef] [PubMed]
- Moualeu-Ngangue, D.P.; Chen, T.W.; Stützel, H. A new method to estimate photosynthetic parameters through net assimilation rateintercellular space CO2 concentration (A-Ci) curve and chlorophyll fluorescence measurements. New Phytol. 2017, 213, 1543–1554. [Google Scholar] [CrossRef]
- Lenz, K.E.; Host, G.E.; Roskoski, K.; Noormets, A.; Sôber, A.; Karnosky, D.F. Analysis of a Farquhar-von Caemmerer-Berry leaf-level photosynthetic rate model for Populus tremuloides in the context of modeling and measurement limitations. Environ. Pollut. 2010, 158, 1015–1022. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.P.; Duan, S.H.; An, T.; Kang, H.J. Construction of CO2-response model of electron transport rate in C4 crop and its application. Chin. J. Plant Ecol. 2018, 42, 1000. [Google Scholar] [CrossRef]
- Zelitch, I. Selection and characterization of tobacco plants with novel O2-resistant photosynthesis. Plant Physiol. 1989, 90, 1457–1464. [Google Scholar] [CrossRef]
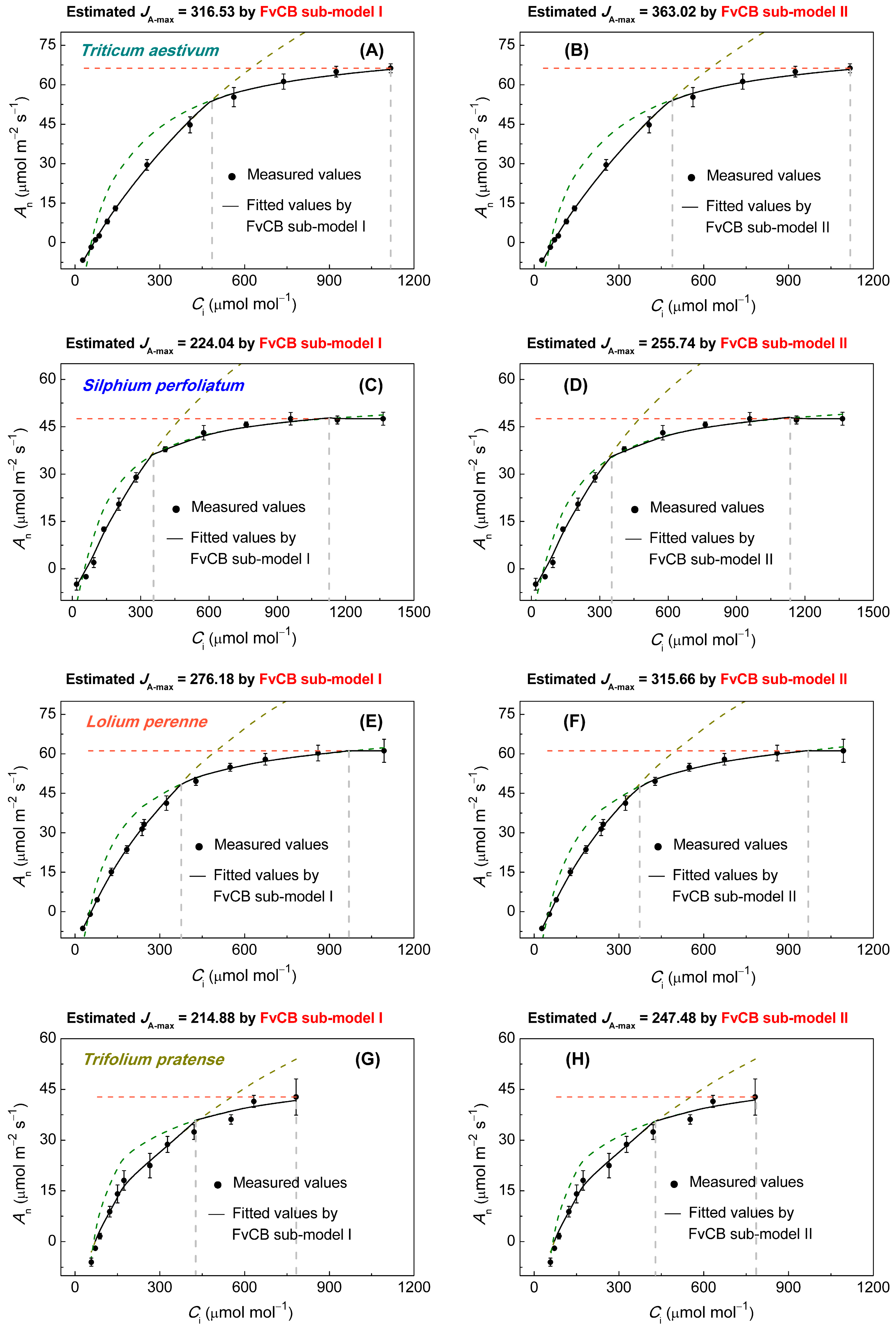
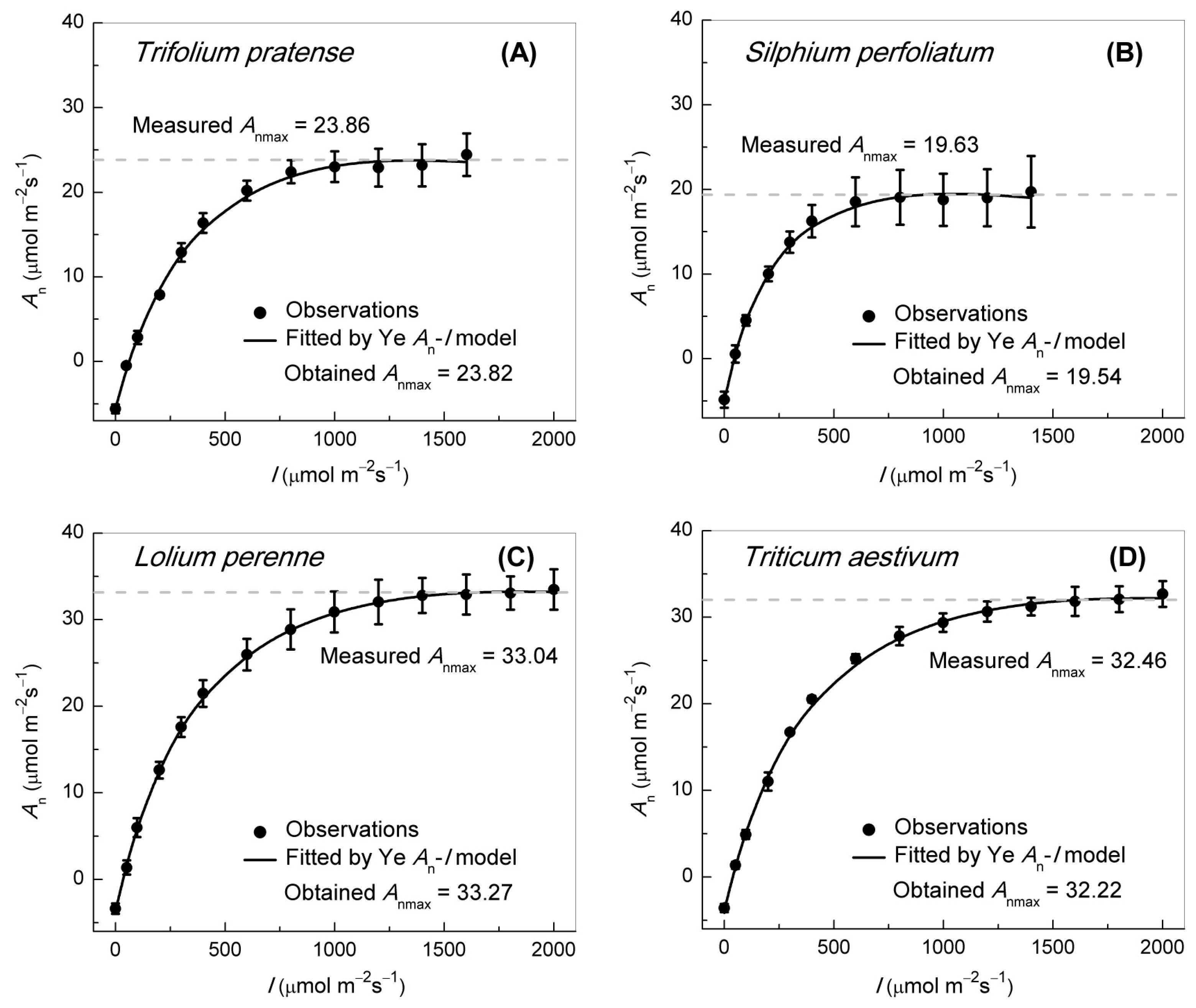
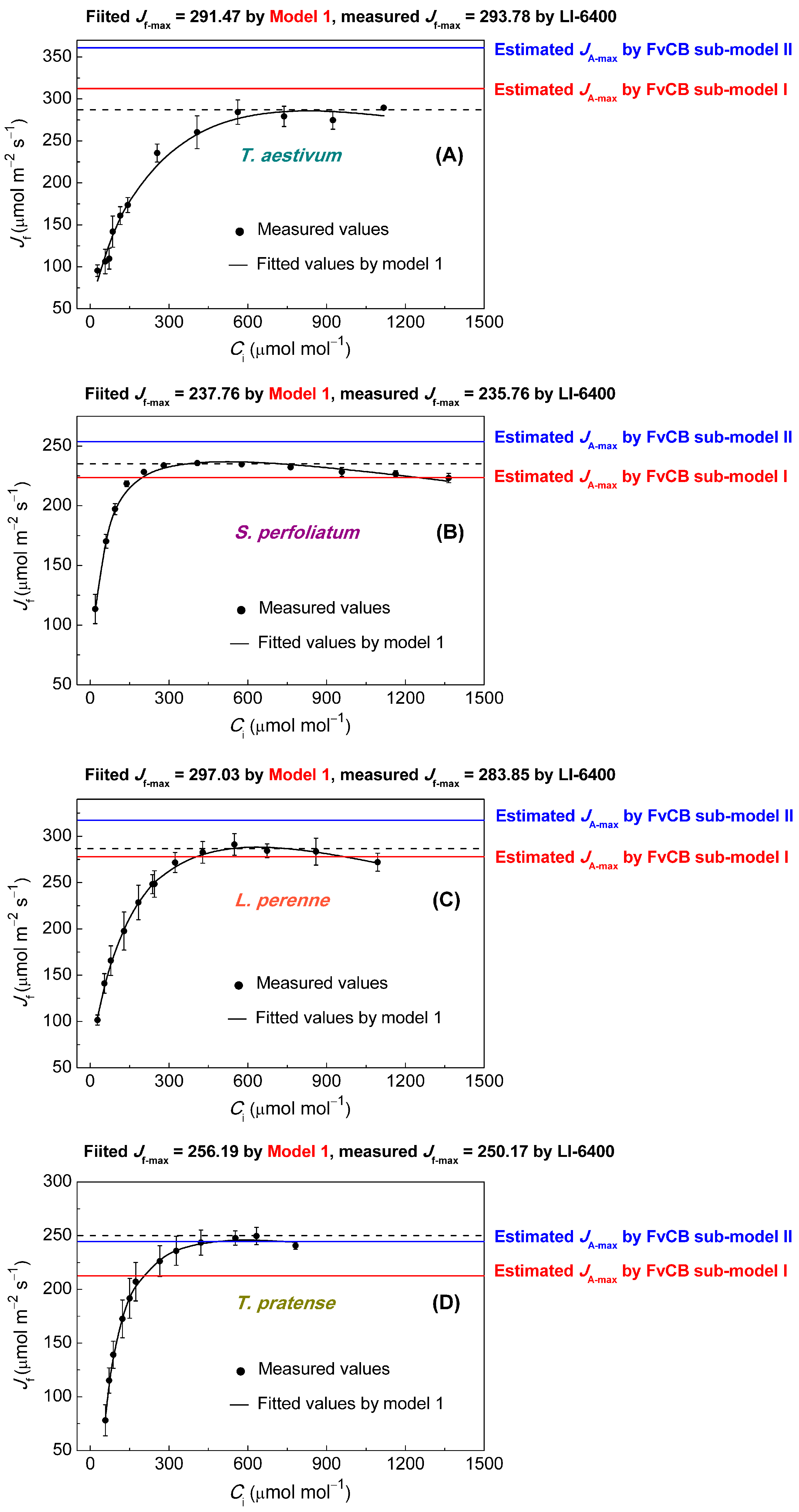
| Species | Fitted JA-max Values by FvCB Sub-Model I | Fitted JA-max Values by FvCB Sub-Model II | Fitted Jf-max Values by Empirical Model | Observed Jf-max Values by Li-6400 |
|---|---|---|---|---|
| Triticum aestivum | 316.53 ± 5.42 b | 363.02 ± 6.07 a | 291.47 ± 0.65 c | 293.78 ± 3.13 c |
| Silphium perfoliatum | 224.04 ± 2.47 c | 255.74 ± 2.73 a | 237.76 ± 1.36 b | 235.76 ± 0.98 b |
| Lolium perenne | 276.18 ± 7.20 b | 315.66 ± 8.57 a | 297.03 ± 10.23 b | 283.85 ± 3.36 b |
| Trifolium pratense | 214.88 ± 3.31 b | 247.48 ± 3.60 a | 256.19 ± 6.17 a | 250.17 ± 4.33 a |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Hu, W.; Zhou, S.; Robakowski, P.; Kang, H.; An, T.; Wang, F.; Xiao, Y.; Yang, X. Limitations of the Farquhar–von Caemmerer–Berry Model in Estimating the Maximum Electron Transport Rate: Evidence from Four C3 Species. Biology 2025, 14, 630. https://doi.org/10.3390/biology14060630
Ye Z, Hu W, Zhou S, Robakowski P, Kang H, An T, Wang F, Xiao Y, Yang X. Limitations of the Farquhar–von Caemmerer–Berry Model in Estimating the Maximum Electron Transport Rate: Evidence from Four C3 Species. Biology. 2025; 14(6):630. https://doi.org/10.3390/biology14060630
Chicago/Turabian StyleYe, Zipiao, Wenhai Hu, Shuangxi Zhou, Piotr Robakowski, Huajing Kang, Ting An, Fubiao Wang, Yi’an Xiao, and Xiaolong Yang. 2025. "Limitations of the Farquhar–von Caemmerer–Berry Model in Estimating the Maximum Electron Transport Rate: Evidence from Four C3 Species" Biology 14, no. 6: 630. https://doi.org/10.3390/biology14060630
APA StyleYe, Z., Hu, W., Zhou, S., Robakowski, P., Kang, H., An, T., Wang, F., Xiao, Y., & Yang, X. (2025). Limitations of the Farquhar–von Caemmerer–Berry Model in Estimating the Maximum Electron Transport Rate: Evidence from Four C3 Species. Biology, 14(6), 630. https://doi.org/10.3390/biology14060630






