The Multistage 20-m Shuttle Run Test for Predicting VO2Peak in 6–9-Year-Old Children: A Comparison with VO2Peak Predictive Equations
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Procedures
2.3. Anthropometric Assessment
2.4. mSRT Test Protocol
2.5. Prediction of Peak Oxygen Consumption
2.6. Statistical Analysis
3. Results
4. Discussion
4.1. Constraints Associated with Using a Portable Gas Analyzer
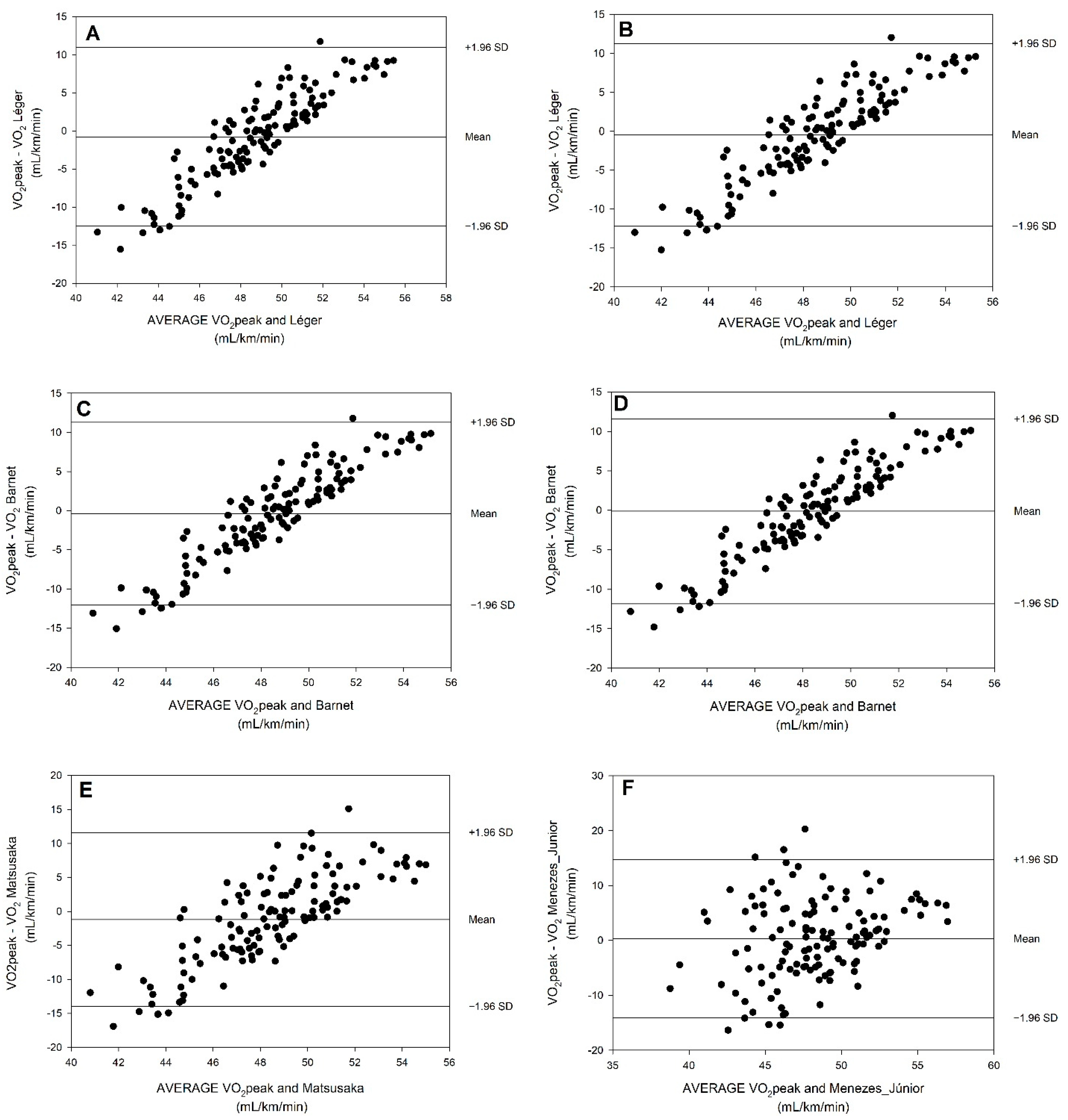
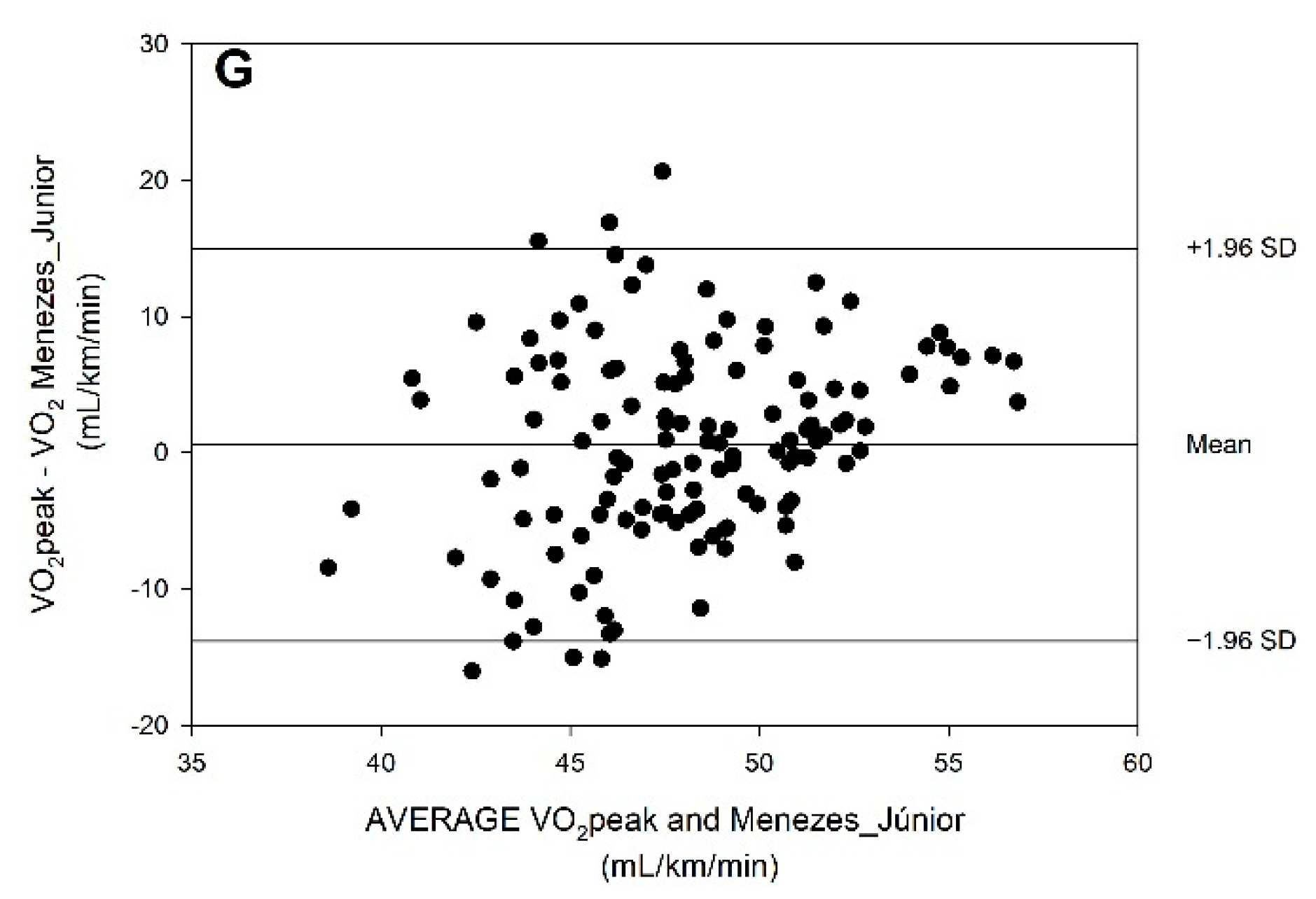
4.2. Agreement of VO2peak Based on Predictive Equations as Compared with VO2peak Measured by Direct Oximetry
4.3. Fat Mass Influence on the Results of Predictive Equations for Predicting VO2peak
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- de Menezes-Junior, F.J.; de Jesus, Í.C.; Mota, J.; Lopes, M.d.F.A.; Corazza, P.R.P.; Tadiotto, M.C.; Tozo, T.A.A.; Purim, K.S.M.; Ronque, E.R.V.; Leite, N. Validation of Equations to Estimate the Peak Oxygen Uptake in Adolescents from 20 Metres Shuttle Run Test. J. Sports Sci. 2020, 38, 2588–2596. [Google Scholar] [CrossRef] [PubMed]
- Welsman, J.; Armstrong, N. The 20 m Shuttle Run Is Not a Valid Test of Cardiorespiratory Fitness in Boys Aged 11-14 Years. BMJ Open Sport Exerc. Med. 2019, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Pozuelo-Carrascosa, D.P.; García-Hermoso, A.; Álvarez-Bueno, C.; Sánchez-López, M.; Martinez-Vizcaino, V. Effectiveness of School-Based Physical Activity Programmes on Cardiorespiratory Fitness in Children: A Meta-Analysis of Randomised Controlled Trials. Br. J. Sports Med. 2018, 52, 1234–1240. [Google Scholar] [CrossRef] [PubMed]
- Ross, R.M. ATS/ACCP Statement on Cardiopulmonary Exercise Testing. Am. J. Respir. Crit. Care Med. 2003, 167, 211–277. [Google Scholar] [CrossRef]
- Tomkinson, G.R.; Lang, J.J.; Tremblay, M.S.; Dale, M.; Leblanc, A.G.; Belanger, K.; Ortega, F.B.; Léger, L. International Normative 20 m Shuttle Run Values from 1 142 026 Children and Youth Representing 50 Countries. Br. J. Sports Med. 2017, 51, 1545–1554. [Google Scholar] [CrossRef]
- Armstrong, N.; Tomkinson, G.; Ekelund, U. Aerobic Fitness and Its Relationship to Sport, Exercise Training and Habitual Physical Activity during Youth. Br. J. Sports Med. 2011, 45, 849–858. [Google Scholar] [CrossRef]
- Tambalis, K.D.; Panagiotakos, D.B.; Psarra, G.; Sidossis, L.S. Association of Cardiorespiratory Fitness Levels with Dietary Habits and Lifestyle Factors in Schoolchildren. Appl. Physiol. Nutr. Metab. 2019, 44, 539–545. [Google Scholar] [CrossRef]
- Dencker, M.; Wollmer, P.; Karlsson, M.K.; Lindén, C.; Andersen, L.B.; Thorsson, O. Body Fat, Abdominal Fat and Body Fat Distribution Related to VO2PEAK in Young Children. Int. J. Pediatr. Obes. 2011, 6. [Google Scholar] [CrossRef]
- Ramírez-Vélez, R.; Correa-Bautista, J.E.; Mota, J.; Garcia-Hermoso, A. Comparison of Different Maximal Oxygen Uptake Equations to Discriminate the Cardiometabolic Risk in Children and Adolescents. J. Pediatr. 2018, 194, 152–157.e1. [Google Scholar] [CrossRef]
- Ruggero, C.J.; Petrie, T.; Sheinbein, S.; Greenleaf, C.; Martin, S. Cardiorespiratory Fitness May Help in Protecting Against Depression among Middle School Adolescents. J. Adolesc. Heal. Off. Publ. Soc. Adolesc. Med. 2015, 57, 60–65. [Google Scholar] [CrossRef]
- Carnethon, M.R.; Gulati, M.; Greenland, P. Prevalence and Cardiovascular Disease Correlates of Low Cardiorespiratory Fitness in Adolescents and Adults. J. Am. Med. Assoc. 2005, 294, 2981–2988. [Google Scholar] [CrossRef] [PubMed]
- Ortega, F.B.; Ruiz, J.R.; Castillo, M.J.; Sjöström, M. Physical Fitness in Childhood and Adolescence: A Powerful Marker of Health. Int. J. Obes. 2008, 32, 1–11. [Google Scholar] [CrossRef]
- Lang, J.J.; Belanger, K.; Poitras, V.; Janssen, I.; Tomkinson, G.R.; Tremblay, M.S. Systematic Review of the Relationship between 20 m Shuttle Run Performance and Health Indicators among Children and Youth. J. Sci. Med. Sport 2018, 21, 383–397. [Google Scholar] [CrossRef] [PubMed]
- Mora-Gonzalez, J.C.; Sanchez, C.; Martinez, B.; Sanchez, G.; Jonatan, D.; Léger, L.; Ortega, F.B. Estimating-VO 2 Max in Children Aged 5 – 6 Years through the Preschool-Adapted 20-m Shuttle-Run Test ( PREFIT ). Eur. J. Appl. Physiol. 2017, 117, 2295–2307. [Google Scholar] [CrossRef] [PubMed]
- Léger, L.A.; Mercier, D.; Gadoury, C.; Lambert, J. Aerobic Capacity of 6 to 17-Year-Old Quebecois - 20 Meter Shuttle Run Test with 1 Minute Stages. Can. J. Appl. Physiol. 1984, 9, 64–69. [Google Scholar]
- Saint-Maurice, P.F.; Welk, G.J.; Finn, K.J.; Kaj, M.; Saint-maurice, P.F.; Finn, K.J. Research Quarterly for Exercise and Sport Cross-Validation of a PACER Prediction Equation for Assessing Aerobic Capacity in Hungarian Youth Cross-Validation of a PACER Prediction Equation for Assessing Aerobic Capacity in Hungarian Youth. Res. Q. Exerc. Sport 2015, 86, S66–S73. [Google Scholar] [CrossRef]
- Hamlin, M.J.; Fraser, M.; Lizamore, C.A.; Draper, N.; Shearman, J.P.; Kimber, N.E. Measurement of Cardiorespiratory Fitness in Children from Two Commonly Used Field Tests After Accounting for Body Fatness and Maturity By. J. Hum. Kinet. 2014, 40, 83–92. [Google Scholar] [CrossRef][Green Version]
- Matsuzaka, A.; Takahashi, Y.; Yamazoe, M.; Kumakura, N.; Ikeda, A.; Wilk, B.; Bar-Or, O. Validity of the Multistage 20-m Shuttle-Run Test for Japanese Children, Adolescents, and Adults. Pediatr. Exerc. Sci. 2004, 16, 113–125. [Google Scholar] [CrossRef]
- Ruiz, J.R.; Ramirez-Lechuga, J.; Ortega, F.B.; Castro-Piñero, J.; Benitez, J.M.; Arauzo-Azofra, A.; Sanchez, C.; Sjöström, M.; Castillo, M.J.; Gutierrez, A.; et al. Artificial Neural Network-Based Equation for Estimating VO2max from the 20 m Shuttle Run Test in Adolescents. Artif. Intell. Med. 2008, 44, 233–245. [Google Scholar] [CrossRef]
- Barnett, A.; Chan, L.Y.; Bruce, L.C. A Preliminary Study of the 20-m Multistage Shuttle Run as a Predictor of Peak VO2 in Hong Kong Chinese Students. Pediatr. Exerc. Sci. 1993, 5, 42–50. [Google Scholar] [CrossRef]
- Ayala-Guzmán, C.I.; Ortiz-Hernández, L. Validity of Equations for Estimating Aerobic Fitness in Mexican Youth. J. Sports Sci. 2019, 37, 1884–1891. [Google Scholar] [CrossRef] [PubMed]
- Batista, M.B.; Romanzini, C.L.P.; Castro-Piñero, J.; Ronque, E.R.V. Validade De Testes De Campo Para Estimativa Da Aptidão Cardiorrespiratória Em Crianças E Adolescentes: Uma Revisão Sistemática. Rev. Paul. Pediatr. 2017, 35, 222–233. [Google Scholar] [CrossRef] [PubMed]
- Ernesto, C.; Da Silva, F.M.; Pereira, L.A.; De Melo, G.F. Cross Validation of Different Equations to Predict Aerobic Fitness by the Shuttle Run 20 Meters Test in Brazilian Students. J. Exerc. Physiol. Online 2015, 18, 46–55. [Google Scholar]
- Melo, X.; Santa-Clara, H.; Almeida, J.P.; Carnero, E.A.; Sardinha, L.B.; Bruno, P.M.; Fernhall, B. Comparing Several Equations That Predict Peak VO2 Using the 20-m Multistage-Shuttle Run-Test in 8-10-Year-Old Children. Eur. J. Appl. Physiol. 2011, 111, 839–849. [Google Scholar] [CrossRef] [PubMed]
- McVeigh, S.K.; Payne, A.C.; Scott, S. The Reliability and Validity of the 20-Meter Shuttle Test as a Predictor of Peak Oxygen Uptake in Edinburgh School Children, Age 13 to 14 Years. Pediatr. Exerc. Sci. 1995, 7, 69–79. [Google Scholar] [CrossRef]
- Mahar, M.T.; Guerieri, A.M.; Hanna, M.S.; Kemble, C.D. Estimation of Aerobic Fitness from 20-m Multistage Shuttle Run Test Performance. Am. J. Prev. Med. 2011, 41, S117–S123. [Google Scholar] [CrossRef]
- Armstrong, N.; Welsman, J. Scientific Rigour in the Assessment and Interpretation of Youth Cardiopulmo-Nary Fitness: A Response to the Paper ‘normative Reference Values and International Comparisons for the 20-Metre Shuttle Run Test: Analysis of 69,960 Test Results among Chinese Ch. J. Sport. Sci. Med. 2020, 19, 627–629. [Google Scholar]
- Ruiz, J.R.; Silva, G.; Oliveira, N.; Ribeiro, J.C.; Oliveira, J.F.; Mota, J. Criterion-Related Validity of the 20-m Shuttle Run Test in Youths Aged 13-19 Years. J. Sports Sci. 2009, 27, 899–906. [Google Scholar] [CrossRef]
- Mayorga-Vega, D.; Aguilar-Soto, P.; Viciana, J. Criterion-Related Validity of the 20-m Shuttle Run Test for Estimating Cardiorespiratory Fitness: A Meta-Analysis. J. Sport. Sci. Med. 2015, 14, 536–547. [Google Scholar]
- Selvadurai, H.; Cooper, P.; Meyers, N.; Blimkie, C.; Smith, L.; Mellis, C.; Van Asperen, P. Validation of Shuttle Tests in Children with Cystic Fibrosis. Pediatr. Pulmonol. 2003, 35, 133–138. [Google Scholar] [CrossRef]
- Dourado, V.Z.; Guerra, R.; Godoy, I. Reference Values for the Incremental Shuttle Walk Test in Healthy Subjects: From the Walk Distance to Physiological Responses. J. Bras. Pneumol. 2013, 39, 190–197. [Google Scholar] [CrossRef]
- Tufanin, A.; Souza, G.F.; Tisi, G.R.; Tufik, S.; Tu, M.; Nascimento, O.A. Cardiac, Ventilatory, and Metabolic Adjustments in Chronic Obstructive Pulmonary Disease Patients during the Performance of Glittre Activities of Daily Living Test. Chron. Respir. Dis. 2014, 11, 247–255. [Google Scholar] [CrossRef] [PubMed]
- Sperandio, E.F.; Vidotto, M.; Yi, L.C.; Gotfryd, A. Functional Exercise Capacity, Lung Function and Chest Wall Deformity in Functional Exercise Capacity, Lung Function and Chest Wall Deformity in Patients with Adolescent Idiopathic Scoliosis. Fisioter. Mov. Curitiba 2015, 28, 563–572. [Google Scholar] [CrossRef]
- Scalco, J.C.; Minsky, R.C.; Mayer, A.F.; Caputo, F.; Schivinski, C.I.S. Comparison of the Physiological Responses Induced by Different Pediatric Exercise Field Tests in Children. Pediatr. Pulmonol. 2019, 54, 1431–1438. [Google Scholar] [CrossRef] [PubMed]
- Itaborahy, B.D.H.; Wamosy, R.M.G.; Scalco, J.C.; Schivinski, C.I.S. Use of Portable Gas Analyzers during Pediatric Field Testing. Pediatr. Pulmonol. 2020, 55, 1264–1272. [Google Scholar] [CrossRef]
- Gault, M.L.; Clements, R.E.; Willems, M.E. Effect of Wearing the Cosmed K4b2 Metabolic System on 1 Mile Walking Performance in Older Adults. J. Hum. Kinet. 2009, 21, 41–48. [Google Scholar] [CrossRef]
- Bar-Or, O. The Child and the Adolescent Athlete; Balckwell Science Ltd.: Oxford, UK, 1996. [Google Scholar]
- Ross, W.D.; Carr, R.V.; Carter, J.E.L. Anthropometry Illustrated [CD Rom]; Turnpike Electronic Publications Inc.: Vancouver, BC, USA, 2000. [Google Scholar]
- Marfell-Jones, M.; Nevill, A.M.; Stewart, A.D. Anthropometric Surrogates for Fatness and Health. In Body Composition in Sport, Exercise and Health; Stewart, A.D., Sutton, L., Eds.; Routledge: London, UK, 2012; pp. 126–146. [Google Scholar]
- Lohman, T.G.; Roche, A.F.; Martorell, R. Anthropometric Standardization Reference Manual, 1st ed.; Books, H.K., Ed.; Human Kinetics Books: Champaign, IL, USA, 1988. [Google Scholar]
- Slaughter, M.H.; Lohman, T.G.; Boileau, R.A.; Horswill, C.A.; Stillman, R.J.; Van Loan, M.D.; Bemben, D.A. Skinfold Equations for Estimations of Body Fatness in Children and Youth. Hum. Biol. 1988, 60, 709–723. [Google Scholar]
- Léger, L.A.; Mercier, D.; Gadoury, C.; Lambert, J. The Multistage 20 Metre Shuttle Run Test for Aerobic Fitness. J. Sports Sci. 1988, 6, 93–101. [Google Scholar] [CrossRef]
- Plowman, S.A. Muscular Strength, Endurance, and Flexibility Assessments. In Fitnessgram/Activitygram Reference Guide; Plowman, S.A., Meredith, M.D., Eds.; The Cooper In: Dallas, TX, USA, 2013. [Google Scholar]
- Mclaughlin, J.E.; King, G.A.; Howley, E.T.; Bassett, D.R.; Ainsworth, B.E. Validation of the COSMED K4 b 2 Portable Metabolic System. Int. J. Sport. Med. 2001, 22, 280–284. [Google Scholar] [CrossRef]
- Fernhall, B.; Pitetti, K.H.; Vukovich, M.D.; Stubbs, N.; Hensen, T.; Winnick, J.P.; Short, F.X. Validation of Cardiovascular Fitness Field Tests in Children with Mental Retardation. Am. J. Ment. Retard. 1998, 102, 602–612. [Google Scholar] [CrossRef]
- Mahar, M.T.; Welk, G.J.; Rowe, D.A.; Crotts, D.J.; McIver, K.L.; Less, V. Development and Validation of a Regression Model to Estimate VO2peak from PACER 20-m Shuttle Run Performance. J. Phys. Act. Health 2006, 3, S34–S46. [Google Scholar] [CrossRef]
- Silva, G.; Oliveira, N.L.; Aires, L.; Mota, J.; Oliveira, J.; Ribeiro, J.C. Calculation and Validation of Models for Estimating VO 2max from the 20-m Shuttle Run Test in Children and Adolescents. Arch. Exerc. Health Dis. 2012, 3, 145–152. [Google Scholar] [CrossRef]
- Quinart, S.; Mougin, F.; Simon-Rigaud, M.L.; Nicolet-Guénat, M.; Nègre, V.; Regnard, J. Evaluation of Cardiorespiratory Fitness Using Three Field Tests in Obese Adolescents: Validity, Sensitivity and Prediction of Peak O2. J. Sci. Med. Sport 2014, 17, 521–525. [Google Scholar] [CrossRef] [PubMed]
- Burns, R.D.; Hannon, J.C.; Brusseau, T.A.; Eisenman, P.A.; Saint-Maurice, P.F.; Welk, G.J.; Mahar, M.T. Cross-Validation of Aerobic Capacity Prediction Models in Adolescents. Pediatr. Exerc. Sci. 2015, 27, 404–411. [Google Scholar] [CrossRef]
- Mahar, M.T.; Welk, G.J.; Rowe, D.A. Estimation of Aerobic Fitness from PACER Performance with and without Body Mass Index. Meas. Phys. Educ. Exerc. Sci. 2018, 22, 239–249. [Google Scholar] [CrossRef]
- Scott, S.N.; Springer, C.M.; Oody, J.F.; McClanahan, M.S.; Wiseman, B.D.; Kybartas, T.J.; Coe, D.P. Development and Validation of a Pacer Prediction Equation for VO2peak in 10- To 15-Year-Old Youth. Pediatr. Exerc. Sci. 2019, 31, 223–228. [Google Scholar] [CrossRef]
- Flouris, A.D.; Metsios, G.S.; Koutedakis, Y. Enhancing the Efficacy of the 20 m Multistage Shuttle Run Test. Br. J. Sports Med. 2005, 39, 166–170. [Google Scholar] [CrossRef][Green Version]
- Cosmed Cosmed K4 B2 User Manual, 9th ed.; COSMED Srl: Rome, Italy, 2003.
- Astorino, T.A.; Willey, J.; Kinnahan, J.; Larsson, S.M.; Welch, H.; Dalleck, L.C. Elucidating Determinants of the Plateau in Oxygen Consumption at VO2max. Br. J. Sports Med. 2005, 39, 655–660. [Google Scholar] [CrossRef]
- Astorino, T.A.; Robergs, R.A.; Ghiasvand, F.; Marks, D.; Burns, S. Incidence of the Oxygen Plateau at VO2max during Exercise Testing to Volitional Fatigue. J. Exerc. Physiol. Online 2000, 3, 1–12. [Google Scholar]
- Falk, B.; Dotan, R. Measurement and Interpretation of Maximal Aerobic Power in Children. Pediatr. Exerc. Sci. 2019, 31, 144–151. [Google Scholar] [CrossRef]
- Barker, A.R.; Williams, C.A.; Jones, A.M.; Armstrong, N. Establishing Maximal Oxygen Uptake in Young People during a Ramp Cycle Test to Exhaustion. Br. J. Sports Med. 2011, 45, 498–503. [Google Scholar] [CrossRef] [PubMed]
- Lemura, L.M.; Cohen, S.L.; Root, J.; Chelland, S.A. Treadmill and Cycle Ergometry Testing in 5- to 6-Year-Old Children. Eur. J. Appl. Physiol. 2001, 85, 472–478. [Google Scholar] [CrossRef] [PubMed]
- Takken, T.; Bongers, B.C.; Van Brussel, M.; Haapala, E.A.; Hulzebos, E.H.J. Cardiopulmonary Exercise Testing in Pediatrics. Ann. Am. Thorac. Soc. 2017, 14, S123–S128. [Google Scholar] [CrossRef]
- Armstrong, N.; Welsman, J.R. Assessment and Interpretation of Aerobic Fitness in Children and Adolescents. Exerc. Sport Sci. Rev. 1994, 22, 435–476. [Google Scholar] [CrossRef] [PubMed]
- Cicone, Z.S.; Holmes, C.J.; Fedewa, M.V.; MacDonald, H.V.; Esco, M.R. Age-Based Prediction of Maximal Heart Rate in Children and Adolescents: A Systematic Review and Meta-Analysis. Res. Q. Exerc. Sport 2019, 90, 417–428. [Google Scholar] [CrossRef]
- Machado, F.A.; Denadai, B.S. Validity of Maximum Heart Rate Prediction Equations for Children and Adolescents. Arq. Bras. Cardiol. 2011, 97, 136–140. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3–13. [Google Scholar] [CrossRef]
- Menezes-Júnior, F.J.d.; Jesus, Í.C.d.; Leite, N. Predictive Equations of Maximum Oxygen Consumption by Shuttle Run Test in Children and Adolescents: A Systematic Review. Rev. Paul. Pediatr. 2019, 37, 241–251. [Google Scholar] [CrossRef]
- Ré, A.H.N. Crescimento, Maturação e Desenvolvimento Na Infância e Adolescência: Implicações Para o Esporte./Growth, Maturation and Development during Childhood and Adolescence: Implications for Sports Practice. Motricidade 2011, 7, 55–67. [Google Scholar] [CrossRef]
- Rowland, T. Oxygen Uptake and Endurance Ftness in Children, Revisited. Pediatr. Exerc. Sci. 2013, 25, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Scott, S.N.; Thompson, D.L.; Coe, D.P. The Ability of the PACER to Elicit Peak Exercise Response in the Youth. Med. Sci. Sports Exerc. 2013, 45, 1139–1143. [Google Scholar] [CrossRef] [PubMed]
- Batista, M.B.; Cyrino, E.S.; Arruda, M.; Dourado, A.C.; Coelho-E-Silva, M.J.; Ohara, D.; Romanzini, M.; Ronque, E.R. Validity of Equations for Estimating V[Combining Dot above]O2peak from the 20-m Shuttle Run Test in Adolescents Aged 11–13. J. Strength Cond. Res. 2013, 27, 2774–2781. [Google Scholar] [CrossRef] [PubMed]
| NR | Equations | References |
|---|---|---|
| #1 | VO2peak = 31.025 + (3.238 × SPEED) − (3.248 × AGE) + (0.1536 × AGE × SPEED), SPEED, maximal speed (km/h); AGE, years | Leger et al. [42] |
| #2 | VO2peak = 28.3 − (2.1 × GENDER) − (0.7 × TRI_SK) + (2.6 × MS), GENDER, M = 0/F = 1; TRI_SK, tricipital skinfold (cm); MS, maximal speed (km/h) | Barnett et al. [20] |
| #3 | VO2peak = 25.8 − (6.6 × GENDER) − (0.2 × BM) + (3.2 × MS), GENDER, M = 0/F = 1; BM, body mass (kg); MS, maximal speed (km/h) | |
| #4 | VO2peak = 24.2 − (5.0 × GENDER) − (0.8 × AGE) + (3.4 × MS), GENDER, M = 0/F = 1; AGE, years; MS, maximal speed (km/h) | |
| #5 | VO2peak = (0.35 × TL) − (0.59 × BMI) − (4.61 × GENDER) + 50.6, TL, total laps (no); BMI, body mass index (kg/m2); GENDER, M = 1/F = 2 | Fernhall et al. [45] |
| #6 | VO2peak = 25.9 − (2.21 × GENDER) − (0.0449 × AGE) − (0.831 × BMI) + (4.12 × MS), GENDER, M = 1/F = 0; AGE, years; BMI, body mass index (kg/m2); MS, maximal speed (km/h) | Matsuzaka et al. [18] |
| #7 | VO2peak = 61.1 − (2.20 × GENDER) − (0.462 × AGE) − (0.862 × BMI) + (0.192 × TL), GENDER, M = 0/F = 1; BMI, body mass index (kg/m2); TL, Total laps (no) | |
| #8 | VO2peak = 47.438 + (PACER × 0.142) + (GENDER × 5.134) − (BM × 0.197), PACER, maximal speed (km/h); GENDER, M = 1/F = 0; BM, body mass (kg) | Mahar et al. [46] |
| #9 | VO2peak = 50.945 + (PACER × 0.126) + (GENDER × 4.946) − (BM × 0.655), PACER, maximal speed (km/h); GENDER, M = 1/F = 0; BM, body mass (kg) | |
| #10 | 10 VO2peak = (1/(1 + exp( − (1/(1 + exp(−((A1 ×0.8 + (−0.7)) × (−1.03329) + (B1 × 0.114285714286 + (−1.38571428571)) × 0.54719 + (C1 × 0.012213740458 + (−0.406870229008)) × 0.61542 + (D1 × 0.0195598978221 + (−2.76356892177)) × −0.51381 + (E1 × 0.0842105263158 + (−0.0684210526316)) × (−0.92239) + (−0.34242)))) × (−0.95905) + 1/(1 + exp(−((A1 × 0.8 + (−0.7)) × (−1.19367) + (B1 × 0.114285714286 + (−1.38571428571)) × (−1.54924) + (C1 × 0.012213740458 + (−0.406870229008)) × (−3.18931) + (D1 × 0.0195598978221 + (−2.76356892177)) × 0.77773 + (E1 × 0.0842105263158 + (−0.0684210526316)) × 3.31887 + (−0.55696)))) × 2.19501 + 1/(1 + exp(−((A1 × 0.8 + (−0.7)) × 1.38191 + (B1 × 0.114285714286 + (−1.38571428571)) × (−2.14449) + (C1 × 0.012213740458 + (−0.406870229008)) × 0.0485 + (D1 × 0.0195598978221 + (−2.76356892177)) × 0.10879 + (E1 × 0.0842105263158 + (−0.0684210526316)) × (−4.90052) + 0.53905))) × (−2.567) + (−0.05105)))) − (−0.478945173945))/0.0204587840012, A1, boys = 1/girls = 2; B1, age (years); C1, weight (kg); D1, height (cm); E1, total time (min) | Ruiz et al. [19] |
| #11 | VO2peak = 41.76799 + (0.49261 × PACER) − (0.00290 × PACER ^ 2) − (0.61613 × BMI) + (0.34787 × GENDER × AGE), PACER, maximal speed (km/h); BMI, body mass index (kg/m2); GENDER, boy = 1/girl = 0 | Mahar et al. [26] |
| #12 | 12 VO2peak = 43.313 + 4.567 × GENDER − 0.560 × BMI + 2.785 × STAGE, GENDER, boys = 1/girls = 0; BMI, body mass index (kg/m2); STAGE, Total time (min) | Silva et al. [47] |
| #13 | VO2peak = (1/(1 + EXP(−((1/(1 + EXP(−(+((STAGE)/11) × −5.309 + (GENDER) × −1.968 + ((AGE − 10)/8) × 4.394 + ((HEIGHT −141)/46) × 1.881 + ((WEIGHT − 37)/59) × 3.078 + ((BMI − 16.23)/13.68) × 4.429 − 4.302)))) × −1.782 + (1/(1 + EXP(−(+((STAGE)/11) × 1.790 + (GENDER) × 2.253 + ((GENDER − 10)/8) × 1.770 + ((HEIGHT − 141)/46) × -1.060 + ((WEIGHT − 37)/59) × 4.978 + ((BMI − 16.23)/13.68) × − 3.610 − 2.705)))) × 9.988 + (1/(1 + EXP(−(+((STAGE)/11) × 5.528 + (GENDER) × −6.357 + ((AGE − 10)/8) × − 1.068 + ((HEIGHT − 141)/46) × 0.663 + ((WEIGHT − 37)/59) × 1.333 + ((BMI − 16.23)/13.68) × 0.825 − 1.608)))) × 6.384 + (1/(1 + EXP(−(+((STAGE)/11) × 8.144 + (GENDER) × −0.724 + ((AGE − 10)/8) × −0.329 + ((HEIGHT − 141)/46) × 6.170 + ((WEIGHT − 37)/59) × − 0.573 + ((BMI − 16.23)/13.68) × 0.373 − 4.679)))) × −4.278 − 3.886)))) × 39.83 + 29.17, STAGE, total laps; GENDER, boys = 1/girls = 0; AGE, years; HEIGHT, cm; WEIGHT, kg; BMI, body mass index (kg/m2) | |
| #14 | VO2peak = 19.66 + (2.21 × MS) + (0.05 × AGE) + (2.08 × GENDER) − (0.38 × BMI), MS, maximal speed (km/h); AGE, years; GENDER, F = 0/M = 1; BMI, body mass index (kg/m2) | Quinart et al. [48] |
| #15 | VO2peak = 45.619 + (0.353 × PACER) − (1.121 × AGE), PACER, total laps (no); AGE, years | Burns et al. [49] |
| #16 | VO2peak = 44.862 + (0.347 × PACER) − (1.050 × AGE), PACER, total laps (no); AGE, years | Mahar et al. [50] |
| #17 | VO2peak = 49.367 + (PACER × 0.331) − (AGE × 0.777) − (BMI × 0.369), PACER, total laps (no); AGE, years; BMI, body mass index (kg/m2) | |
| #18 | VO2peak = 52.934 + 0.256 × (LAPS) − 0.924 × (BMI) + 0.468 × (GENDER × AGE), LAPS, total laps (no); BMI, body mass index (kg/m2); Gender, F = 0/M = 1; AGE, years | Scott et al. [51] |
| #19 | VO2peak = 44.942 + (0.646 × AGE) − (6.586 × GENDER) + (0.318 × PACER) − (0.243 × WAIST_CIRC), AGE, years; GENDER, F = 1/M = 0; PACER, total laps (no); WAIST_CIRC, waist circumference (cm) | Ayala-Guzman and Ortiz-Hernandez [21] |
| #20 | VO2peak = 37.009 + (0.408 × AGE) − (4.759 × GENDER) + (0.284 × PACER) − (0.312 × BF), AGE, years; GENDER, F = 1/M = 0; PACER, total laps (no); BF, body fat (%) | |
| #21 | VO2peak = 46.802 + (0.381 × LAPS) + (−3.682 × BMI-Z) + (−0.0568 × HEIGHT × AGE) + (3.078 × GENDER), LAPS, total laps (no); BMI-Z, body mass index (Z_score); HEIGHT, m; AGE, months; GENDER, F = 0/M = 1 | Menezes-Junior et al. [1] |
| #22 | VO2peak = 54.051 + (0.324 × LAPS) + (−2.626 × BMI-Z) + (−0.276 × %FM) + (−0.0493 × HEIGHT × AGE) + (2.016 × GENDER), LAPS, total laps (no); BMI-Z, body mass index (Z_score); %FM, fat mass (%); HEIGHT, m; AGE, months; GENDER, F = 0/M = 1 |
| Girls (n = 63) | Boys (n = 67) | Total (n = 130) | |
|---|---|---|---|
| Age (years) | 7.59 ± 0.12 | 7.76 ± 0.12 | 7.68 ± 0.94 |
| Anthropometric variables | |||
| Height (cm) | 128.70 ± 7.52 | 130.14 ± 9.23 | 129.44 ± 8.45 |
| Body mass (kg) | 29.22 ± 6.14 | 31.02 ± 8.87 | 30.15 ± 7.70 |
| Fat mass (%) | 16.92 ± 5.10 | 15.59 ± 6.64 | 16.23 + 5.96 |
| Body mass index (kg/m2) | 17.50 ± 2.51 | 17.97 ± 2.78 | 17.74 ± 2.65 |
| Body mass index z-score (kg/m2) | 0.53 ± 0.93 | 0.73 ± 0.88 | 0.63 ± 0.91 |
| Waist circumference (cm) | 56.72 ± 6.19 | 58.95 ± 8.98 | 57.87 ± 7.80 |
| Tricipital skinfold (cm) | 11.70 ± 3.96 * | 10.11 ± 4.33 | 10.88 ± 4.22 |
| Subscapular skinfold (cm) | 6.76± 2.82 | 6.39 ± 3.33 | 6.57 ± 3.13 |
| Metabolic and cardiovascular variables | |||
| Heart rate peak (bpm) | 193.42 ± 9.0 | 194.09 ± 8.19 | 193.77 ± 8.56 |
| VO2peak (ml/kg/min) | 46.97 ± 5.07 * | 49.69 ± 6.19 | 48.37 ± 5.81 |
| Performance variables from the multistage 20-m shuttle run test | |||
| Maximal speed with PGA (km/h) | 9.55 ± 0.42 ** | 9.92 ± 0.77 | 9.74 ± 0.65 |
| Maximal speed without PGA (km/h) | 9.44 ± 0.54 ** | 9.88 ± 0.81 | 9.67 ± 0.73 |
| Total laps with PGA (nr) | 19.92 ± 7.03 ** | 26.22 ± 12.66 | 23.17 ± 10.76 |
| Total laps without PGA (nr) | 18.46 ± 8.19 ** | 25.99 ± 12.99 | 22.34 ± 11.52 |
| Total time with PGA (s) | 159.86 ± 52.21 ** | 206.12 ± 87.45 | 183.70 ± 75.90 |
| Total time without PGA (s) | 149.96 ± 62.00 ** | 207.76 ± 92.64 | 179.75 ± 84.14 |
| Girls (n = 63) | Boys (n = 67) | Total (n = 130) | ||||
|---|---|---|---|---|---|---|
| Diff (CI 95%) | PGA vs. nPGA | Diff (CI 95%) | PGA vs. nPGA | Diff (CI 95%) | PGA vs. nPGA | |
| MS-PGA (km/h) − MS-nPGA (km/h) | 0.11 (0.03–0.20) | p = 0.010; d = 0.23 | 0.04 (−0.03–0.11) | p = 0.301; d = 0.05 | 0.07 (0.02–0.13) | p = 0.009; d = 0.10 |
| TL-PGA (nr) − TL-nPGA (nr) | 1.46 (0.54–2.38) | p = 0.002; d = 0.19 | 0.24 (−0.61–1.09) | p = 0.557; d = 0.02 | 0.83 (0.20–1.46) | p = 0.010; d = 0.07 |
| TT-PGA (s) − TT-nPGA (s) | 9.90 (2.10–17.69) | p = 0.014; d = 0.17 | −1.64 (−8.47–5.20) | p = 0.634; d = −0.02 | 3.95 (−1.24–9.14) | p = 0.135; d = 0.05 |
| Girls (n = 63) | Boys (n = 67) | Total (n = 130) | |||||
|---|---|---|---|---|---|---|---|
| Mean ± SD | PGA vs. nPGA | Mean ± SD | PGA vs. nPGA | Girls vs. Boys | Mean ± SD | PGA vs. nPGA | |
| VO2peak measured | 46.97 ± 5.07 | 49.69 ± 6.19 | p = 0.007; g = 0.48 | 48.37 ± 5.81 | |||
| Leger et al. [42] | 1 48.46 ± 1.09 a |
p
= 0.012 d = 0.27 | 1 49.81 ± 2.98 a* |
p
= 0.306 d = 0.05 | p = 0.002; g = 0.59 | 1 49.15 ± 2.60 a |
p
= 0.010 d = 0.12 |
| 1 47.97 ± 2.25 b | 1 49.65 ± 3.17 b* | p = 0.001; g = 0.61 | 1 48.83 ± 2.88 b | ||||
| Barnett et al. [20] | 2 42.84 ± 3.30 a |
p
= 0.010 d = 0.09 | 2 47.01 ± 4.11 a |
p
= 0.301 d = 0.02 | p < 0.001; g = 1.12 | 2 44.99 ± 4.27 a |
p
= 0.009 d = 0.05 |
| 2 42.54 ± 3.41 b | 2 46.91 ± 4.11 b | p < 0.001; g = 1.15 | 2 44.79 ± 4.37 b | ||||
| 3 43.92 ± 1.96 a |
p
= 0.010 d = 0.18 | 3 51.33 ± 3.23 a |
p
= 0.301 d = 2.75 | p < 0.001; g = 2.75 | 3 47.74 ± 4.59 a |
p
= 0.009 d = 0.05 | |
| 3 43.55 ± 2.12 b | 3 51.74 ± 3.29 b | p < 0.01; g = 2.94 | 3 47.50 ± 4.74 b | ||||
| 4 45.60 ± 1.31 a |
p
= 0.010 d = 0.26 | 4 51.71 ± 2.33 a |
p
= 0.301 d = 0.05 | p < 0.001; g = 3.21 | 4 48.75 ± 3.61 a |
p
= 0.009 d = 0.07 | |
| 4 45.21 ± 1.66 b | 4 51.59 ± 2.47 b | p < 0.001; g = 3.01 | 4 48.50 ± 3.83 b | ||||
| Fernhall et al. [45] | 5 39.89 ± 4.08 a |
p
= 0.004 d = 0.08 | 5 42.82 ± 6.07 a |
p
= 0.201 d = 0.04 | p = 0.002; g = 0.56 | 5 41.40 ± 5.39 a |
p
= 0.010 d = 0.05 |
| 5 39.54 ± 4.30 b | 5 42.58 ± 6.41 b | p = 0.002; g = 0.55 | 5 41.11 ± 6.68 b | ||||
| Matsuzaka et al. [18] | 6 48.15 ± 3.14 a |
p
= 0.010 d = 0.14 | 6 51.48 ± 4.38 a |
p
= 0.301 d = 0.03 | p < 0.001; g = 0.87 | 6 49.87 ± 4.16 a |
p
= 0.09 d = 0.07 |
| 6 47.68 ± 3.39 b | 6 51.33 ± 4.48 b | p < 0.001; g = 0.91 | 6 49.56 ± 4.37 b | ||||
| 7 45.48 ± 3.04 a |
p
= 0.004 d = 0.06 | 7 45.79 ± 4.14 a |
p
= 0.201 d = 0.03 | p = 0.632; g = 0.08 | 7 45.64 ± 3.64 a |
p
= 0.010 d = 0.04 | |
| 7 45.29 ± 3.14 b | 7 45.66 ± 4.30 b | p = 0.583; g = 0.10 | 7 45.48 ± 3.77 b | ||||
| Mahar et al. [46] | 8 43.04 ± 1.22 a |
p
= 0.010 d = 0.02 | 8 47.87 ± 1.77 a |
p
= 0.301 d = 0.01 | p < 0.001; g = 3.16 | 8 45.53 ± 2.86 a |
p
= 0.09 d = 0.00 |
| 8 43.02 ± 1.21 b | 8 47.86 ± 1.76 b | p < 0.001; g = 3.19 | 8 45.52 ± 2.86 b | ||||
| 9 33.01 ± 4.03 a |
p
= 0.010 d = 0.00 | 9 36.82 ± 5.83 a |
p
= 0.301 d = 0.00 | p < 0.001; g = 0.76 | 9 35.00 ± 5.37 a |
p
= 0.09 d = 0.01 | |
| 9 33.00 ± 4.02 b | 9 36.82 ± 5.82 b | p < 0.001; g = 0.76 | 9 34.97 ± 5.37 b | ||||
| Ruiz et al. [19] | 10 32.07 ± 1.95 a |
p
= 0.126 d = 0.09 | 10 42.07 ± 6.68 a |
p
= 0.391 d = 0.03 | p < 0.001; g = 2.01 | 10 37.22 ± 7.06 a |
p
= 0.950 d = 0.00 |
| 10 31.87 ± 2.27 b | 10 42.28 ± 6.96 b | p < 0.001; g = 1.99 | 10 37.23 ± 7.38 b | ||||
| Mahar et al. [26] | 11 35.42 ± 1.62 a |
p
= 0.010 d = 0.03 | 11 35.29 ± 1.83 a |
p
= 0.295 d = 0.01 | p = 0.671; g = 0.08 | 11 35.36 ± 1.73 a |
p
= 0.08 d = 0.02 |
| 11 35.37 ± 1.62 b | 11 35.28 ± 1.83 b | p = 0.752; g = 0.05 | 11 35.32 ± 1.72 b | ||||
| Silva et al. [47] | 12 42.68 ± 3.89 a |
p
= 0.124 d = 0.05 | 12 45.74 ± 5.62 a |
p
= 0.461 d = 0.03 | p < 0.001; g = 0.63 | 12 44.26 ± 5.08 a |
p
= 0.135 d = 0.04 |
| 12 42.46 ± 4.32 b | 12 45.59 ± 6.06 b | p = 0.001; g = 0.59 | 12 44.07 ± 5.50 b | ||||
| 13 34.69 ± 4.84 a |
p
= 0.019 d = 0.06 | 13 35.10 ± 6.04 a |
p
=0.177 d = 0.06 | p = 0.664; g = 0.07 | 13 34.90 ± 5.47 a |
p
= 0.023 d = 0.07 | |
| 13 34.40 ± 4.61 b | 13 34.73 ± 5.77 b | p = 0.669; g = 0.06 | 13 34.54 ± 5.22 b | ||||
| Quinart et al. [48] | 14 34.49 ± 1.56 a |
p
= 0.010 d = 0.15 | 14 37.22 ± 2.24 a |
p
= 0.301 d = 0.04 | p < 0.001; g = 1.41 | 14 35.90 ± 2.37 a |
p
= 0.009 d = 0.07 |
| 14 34.24 ± 1.71 b | 14 37.14 ± 2.24 b | p < 0.001; g = 1.45 | 14 35.73 ± 2.49 b | ||||
| Burns et al. [49] | 15 44.15 ± 2.19 a |
p
=0.02 d = 0.21 | 15 46.18 ± 4.05 a |
p
= 0.577 d = 0.02 | p = 0.001; g = 0.62 | 15 45.19 ± 3.43 a |
p
= 0.010 d = 0.08 |
| 15 43.63 ± 2.67 b | 15 46.09 ± 4.17 b | p < 0.001; g = 0.70 | 15 44.90 ± 3.72 b | ||||
| Mahar et al. [50] | 16 43.81 ± 2.16 a |
p
= 0.02 d = 0.21 | 16 45.81 ± 3.40 a |
p
= 0.577 d = 0.02 | p = 0.001; g = 0.70 | 16 44.84 ± 3.38 a |
p
= 0.010 d = 0.08 |
| 16 43.30 ± 2.62 b | 16 45.73 ± 4.11 b | p < 0.001; g = 0.70 | 16 44.55 ± 3.67 b | ||||
| 17 43.61 ± 2.56 a |
p
= 0.02 d = 0.18 | 17 45.39 ± 4.31 a |
p
= 0.577 d = 0.00 | p = 0.005; g = 0.50 | 17 44.52 ± 3.67 a |
p
= 0.010 d = 0.07 | |
| 17 43.12 ± 2.96 b | 17 45.31 ± 4.42 b | p = 0.001; g = 0.58 | 17 44.25 ± 3.92 b | ||||
| Scott et al. [51] | 18 41.86 ± 3.30 a |
p
= 0.02 d = 0.11 | 18 46.67 ± 4.75 a |
p
= 0.577 d = 0.01 | p < 0.001; g = 1.17 | 18 44.34 ± 4.75 a |
p
= 0.010 d = 0.04 |
| 18 41.49 ± 3.53 b | 18 46.61 ± 4.81 b | p < 0.001; g = 1.21 | 18 44.13 ± 4.95 b | ||||
| Ayala-Guzman & Ortiz-Hernandez [21] | 19 35.81 ± 3.07 a |
p
= 0.02 d = 0.14 | 19 43.97 ± 5.30 a |
p
= 0.577 d = 0.15 | p < 0.001; g = 1.87 | 19 40.02 ± 5.97 a |
p
= 0.010 d = 0.04 |
| 19 35.35 ± 3.37 b | 19 43.89 ± 5.40 b | p < 0.001; g = 1.88 | 19 39.75 ± 6.23 b | ||||
| 20 35.73 ± 2.93 a |
p
= 0.02 d = 0.14 | 20 42.76 ± 4.80 a |
p
= 0.577 d = 0.01 | p < 0.001; g = 1.76 | 20 39.35 ± 5.33 a |
p
= 0.010 d = 0.04 | |
| 20 35.31 ± 3.24 b | 20 42.69 ± 4.81 b | p < 0.001; g = 1.79 | 20 39.11 ± 5.53 b | ||||
| Menezes-Junior et al. [1] | 21 45.76 ± 4.80 a |
p
= 0.02 d = 0.11 | 21 50.26 ± 6.41 a |
p
= 0.577 d = 0.01 | p < 0.001; g = 0.79 | 21 48.08 ± 6.10 a |
p
= 0.010 d = 0.05 |
| 21 45.21 ± 5.10 b | 21 50.17 ± 6.50 b | p < 0.001; g = 0.85 | 21 47.77 ± 6.35 b | ||||
| 22 48.65 ± 4.81 a |
p
= 0.02 d = 0.10 | 22 52.34 ± 6.53 a |
p
= 0.577 d = 0.01 | p < 0.001; g = 0.64 | 22 50.55 ± 6.03 a |
p
= 0.010 d = 0.04 | |
| 22 48.18 ± 5.07 b | 22 52.26 ± 6.55 b | p < 0.001; g = 0.69 | 22 50.28 ± 6.20 b | ||||
| References | Equation Number * | Girls (n = 63) | Boys (n = 67) | Total (n = 130) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Diff (CI 95%) | p | d | Diff (CI 95%) | p | d | Diff (CI 95%) | p | d | ||
| Leger et al. [42] | 1 | −1.00 (−2.20–0.20) | 0.101 | 0.25 | 0.041 (−0.99–1.07) | 0.936 | 0.01 | −0.46 (1.24–0.32) | 0.243 | 0.10 |
| Barnett et al. [20] | 2 | 4.43 (3.44–5.42) | <0.001 | 1.03 | 2.78 (1.78–3.77) | <0.001 | 0.53 | 3.58 (2.87–4.28) | <0.001 | 0.70 |
| 3 | 3.41 (2.38–4.45) | <0.001 | 0.88 | −1.53 (−2.48–−0.57) | 0.002 | 0.41 | 0.87 (0.05–1.68) | 0.037 | 0.16 | |
| 4 | 1.75 (0.60–2.91) | 0.004 | 0.47 | −1.90 (−2.96–−0.83) | 0.001 | 0.40 | −0.13 (−0.96–0.71) | 0.763 | 0.03 | |
| Fernhall et al. [45] | 5 | 7.43 (5.81–9.04) | <0.001 | 1.58 | 7.11 (5.19–9.04) | <0.001 | 1.13 | 7.26 (6.02–8.51) | <0.001 | 1.16 |
| Matsuzaka et al. [18] | 6 | −0.72 (−1.71–0.27) | 0.153 | 0.16 | −1.64 (−2.49–−0.78) | <0.001 | 0.30 | −1.19 (−1.84–−0.54) | <0.001 | 0.23 |
| 7 | 1.67 (0.21–3.14) | 0.026 | 0.40 | 4.03 (2.34–5.73) | <0.001 | 0.76 | 2.89 (1.76–4.02) | <0.001 | 0.59 | |
| Mahar et al. [46] | 8 | 3.95 (2.76–5.13) | <0.001 | 1.07 | 1.82 (.42–3.23) | 0.012 | 0.40 | 2.85 (1.92–3.78) | <0.001 | 0.62 |
| 9 | 13.97 (12.69–15.25) | <0.001 | 3.05 | 12.87 (11.19–14.55) | <0.001 | 2.14 | 13.40 (12.35–14.46) | <0.001 | 2.40 | |
| Ruiz et al. [19] | 10 | 15.10 (14.03–16.17) | <0.001 | 3.84 | 7.41 (6.42–8.41) | <0.001 | 1.13 | 11.14 (10.16–12.12) | <0.001 | 1.68 |
| Mahar et al. [26] | 11 | 11.59 (10.50–12.69) | <0.001 | 3.08 | 14.41 (13.09–15.73) | <0.001 | 3.16 | 13.05 (12.16–13.93) | <0.001 | 3.05 |
| Silva et al. [47] | 12 | 4.51 (2.88–6.13) | <0.001 | 0.96 | 4.10 (2.21–5.99) | <0.001 | 0.67 | 4.30 (3.06–5.53) | <0.001 | 0.76 |
| 13 | 12.63 (10.82–14.43) | <0.001 | 2.59 | 14.96 (12.82–17.10) | <0.001 | 2.50 | 13.83 (12.43–15.23) | <0.001 | 2.50 | |
| Quinart et al. [48] | 14 | 12.72 (11.67–13.78) | <0.001 | 3.36 | 12.55 (11.47–13.63) | <0.001 | 2.70 | 12.64 (11.89–13.38) | <0.001 | 2.83 |
| Burns et al. [49] | 15 | 3.34 (2.21–4.46) | <0.001 | 0.82 | 3.60 (2.71–4.48) | <0.001 | 0.68 | 3.47 (2.77–4.17) | <0.001 | 0.71 |
| Mahar et al. [50] | 16 | 3.67 (2.55–4.79) | <0.001 | 0.91 | 3.96 (3.07–4.85) | <0.001 | 0.75 | 3.82 (3.12–4.52) | <0.001 | 0.79 |
| 17 | 3.84 (2.81–4.88) | <0.001 | 0.93 | 4.38 (3.55–5.22) | <0.001 | 0.81 | 4.12 (3.47–4.77) | <0.001 | 0.83 | |
| Scott et al. [51] | 18 | 5.48 (4.50–6.46) | <0.001 | 1.25 | 3.08 (2.21–3.94) | <0.001 | 0.56 | 4.24 (3.56–4.92) | <0.001 | 0.79 |
| Ayala-Guzman and Ortiz-Hernandez [21] | 19 | 11.62 (10.62–12.62) | <0.001 | 2.70 | 5.79 (4.98–6.61) | <0.001 | 1.00 | 8.62 (7.81–9.43) | <0.001 | 1.43 |
| 20 | 11.66 (10.70–12.61) | <0.001 | 2.71 | 7.00 (6.20–7.80) | <0.001 | 1.26 | 9.26 (8.52–9.99) | <0.001 | 1.63 | |
| Menezes-Junior et al. [1] | 21 | 1.76 (0.64–2.88) | 0.003 | 0.25 | −0.48 (−1.42–0.45) | 0.305 | 0.08 | 0.60 (−0.14–1.35) | 0.111 | 0.10 |
| 22 | −1.21 (−2.30–−0.12) | 0.031 | 0.24 | −2.57 (−3.59–−1.56) | <0.001 | 0.40 | −1.91 (−2.66–−1.17) | <0.001 | 0.32 | |
| Equations and References | LoA | Slope | R | R2 | SEE | |
|---|---|---|---|---|---|---|
| #1, a, b Leger et al. [42] | −12.53 | 10.96 a | 1.837 ** | 0.907 ** | 0.822 | 2.53 |
| −12.20 | 11.28 b | 1.838 ** | 0.908 ** | 0.823 | 2.52 | |
| #4, a, b Barnett et al. [20] | −12.06 | 11.30 a | 1.873 ** | 0.927 ** | 0.859 | 2.25 |
| −11.79 | 11.53 b | 1.875 ** | 0.927 ** | 0.860 | 2.24 | |
| #6, b Matsuzaka et al. [18] | −14.01 | 11.62 b | 1.265 ** | 0.618 ** | 0.383 | 5.16 |
| #21, a, b Menezes-Junior et al. [1] | −14.12 | 14.69 a | 0.588 * | 0.286 * | 0.082 | 7.07 |
| −13.82 | 15.03 b | 0.582 * | 0.283 * | 0.080 | 7.09 | |
| Girls | ||||||
|---|---|---|---|---|---|---|
| Equations and references | LoA | Slope | R | R2 | SEE | |
| #1, a, b Leger et al. [42] | −12.88 | 9.58 a | 2.043 ** | 0.924 ** | 0.851 | 2.21 |
| −12.55 | 9.90 b | 2.044 ** | 0.924 ** | 0.854 | 2.72 | |
| #4, a, b Barnett et al. [20] | −12.39 | 9.86 a | 2.056 ** | 0.940 ** | 0.884 | 1.95 |
| −12.13 | 10.11 b | 2.056 ** | 0.914 ** | 0.885 | 1.94 | |
| #6, a Matsuzaka et al. [18] | −14.44 | 10.68 b | 1.633 ** | 0.673 ** | 0.454 | 4.77 |
| #21, a, b Menezes-Junior et al. [1] | −14.42 | 13.97 a | 0.922 * | 0.362 * | 0.131 | 6.80 |
| −14.12 | 14.30 b | 0.915 * | 0.359 * | 0.003 | 4.61 | |
| Boys | ||||||
| #1, a, b Leger et al. [42] | −12.04 | 12.10 a | 1.730 ** | 0.896 ** | 0.804 | 2.75 |
| −11.72 | 12.42 b | 1.731 ** | 0.897 ** | 0.805 | 2.74 | |
| #4, a, b Barnett et al. [20] | −11.57 | 12.47 a | 1.778 ** | 0.918 ** | 0.843 | 2.45 |
| −11.32 | 12.73 b | 1.780 ** | 0.919 ** | 0.844 | 4.22 | |
| #6, a Matsuzaka et al. [18] | −13.55 | 12.47 b | 1.088 ** | 0.581 ** | 0.338 | 3.17 |
| #21, a, b Menezes-Junior et al. [1] | −13.88 | 15.42 a | 0.427 | 0.231 | 0.039 | 7.33 |
| −13.58 | 15.75 b | 0.421 | 0.228 * | 0.037 | 3.86 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brito, J.P.; Domingos, C.; Pereira, A.F.; Moutão, J.; Oliveira, R. The Multistage 20-m Shuttle Run Test for Predicting VO2Peak in 6–9-Year-Old Children: A Comparison with VO2Peak Predictive Equations. Biology 2022, 11, 1356. https://doi.org/10.3390/biology11091356
Brito JP, Domingos C, Pereira AF, Moutão J, Oliveira R. The Multistage 20-m Shuttle Run Test for Predicting VO2Peak in 6–9-Year-Old Children: A Comparison with VO2Peak Predictive Equations. Biology. 2022; 11(9):1356. https://doi.org/10.3390/biology11091356
Chicago/Turabian StyleBrito, João Paulo, Christophe Domingos, Ana Fátima Pereira, João Moutão, and Rafael Oliveira. 2022. "The Multistage 20-m Shuttle Run Test for Predicting VO2Peak in 6–9-Year-Old Children: A Comparison with VO2Peak Predictive Equations" Biology 11, no. 9: 1356. https://doi.org/10.3390/biology11091356
APA StyleBrito, J. P., Domingos, C., Pereira, A. F., Moutão, J., & Oliveira, R. (2022). The Multistage 20-m Shuttle Run Test for Predicting VO2Peak in 6–9-Year-Old Children: A Comparison with VO2Peak Predictive Equations. Biology, 11(9), 1356. https://doi.org/10.3390/biology11091356









