Keeping 21st Century Paleontology Grounded: Quantitative Genetic Analyses and Ancestral State Reconstruction Re-Emphasize the Essentiality of Fossils
Abstract
:Simple Summary
Abstract
1. Introduction
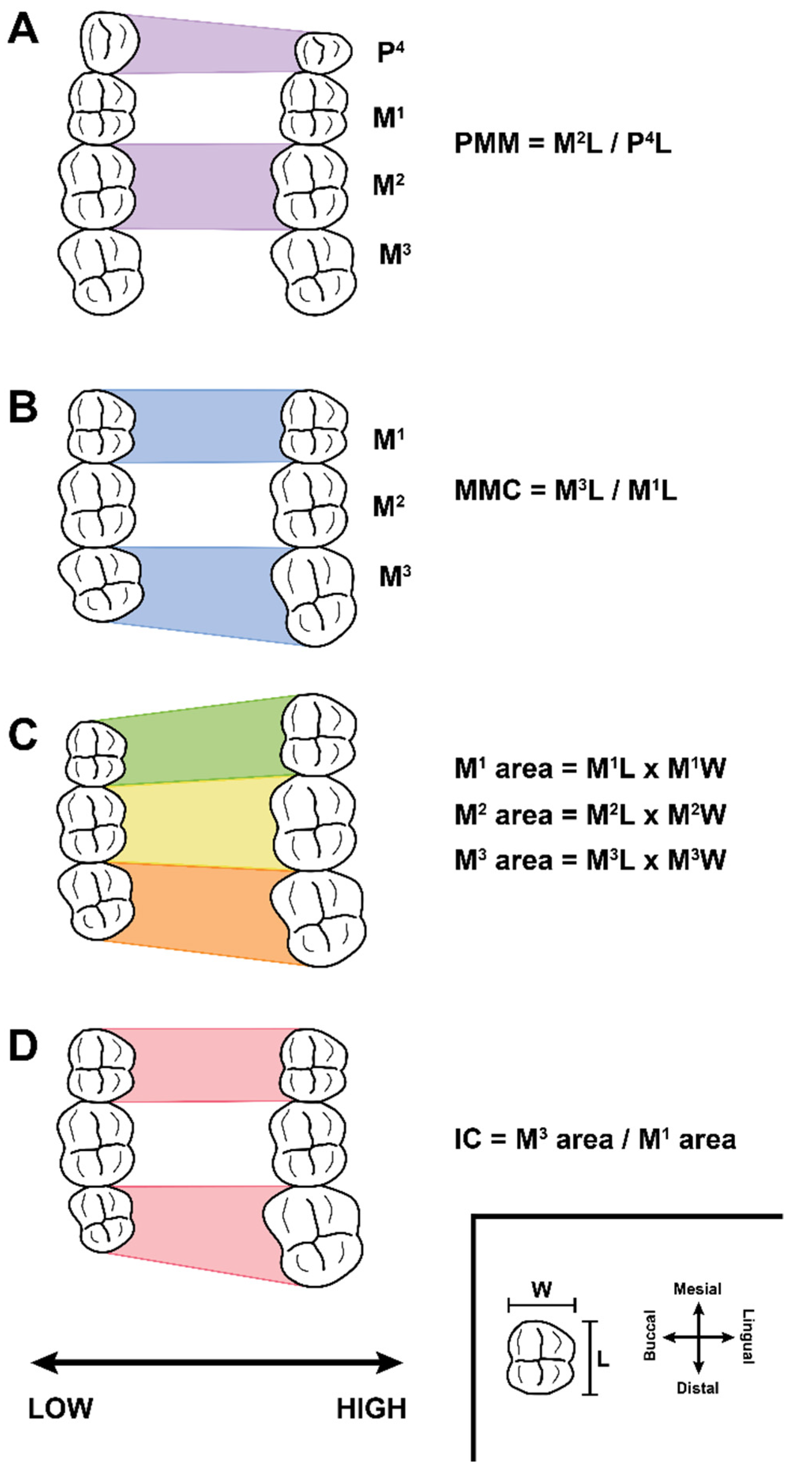
2. Background: Traditional and G:P-Mapped Dental Traits
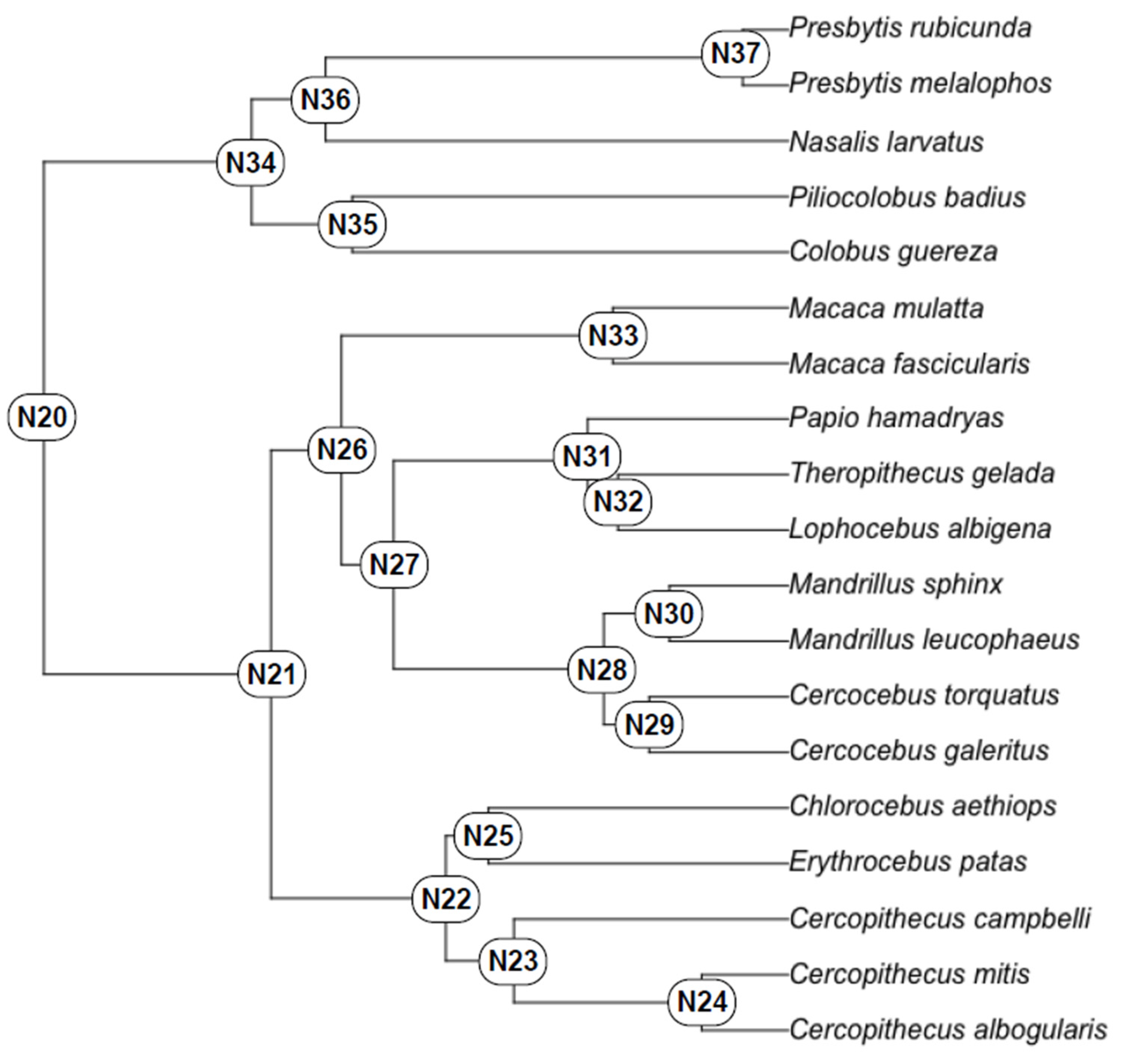
3. Materials and Methods
4. Results
4.1. Test of Hypothesis 1: G:P-Mapped Dental Traits Can Provide Evidence of Phylogeny and Selection
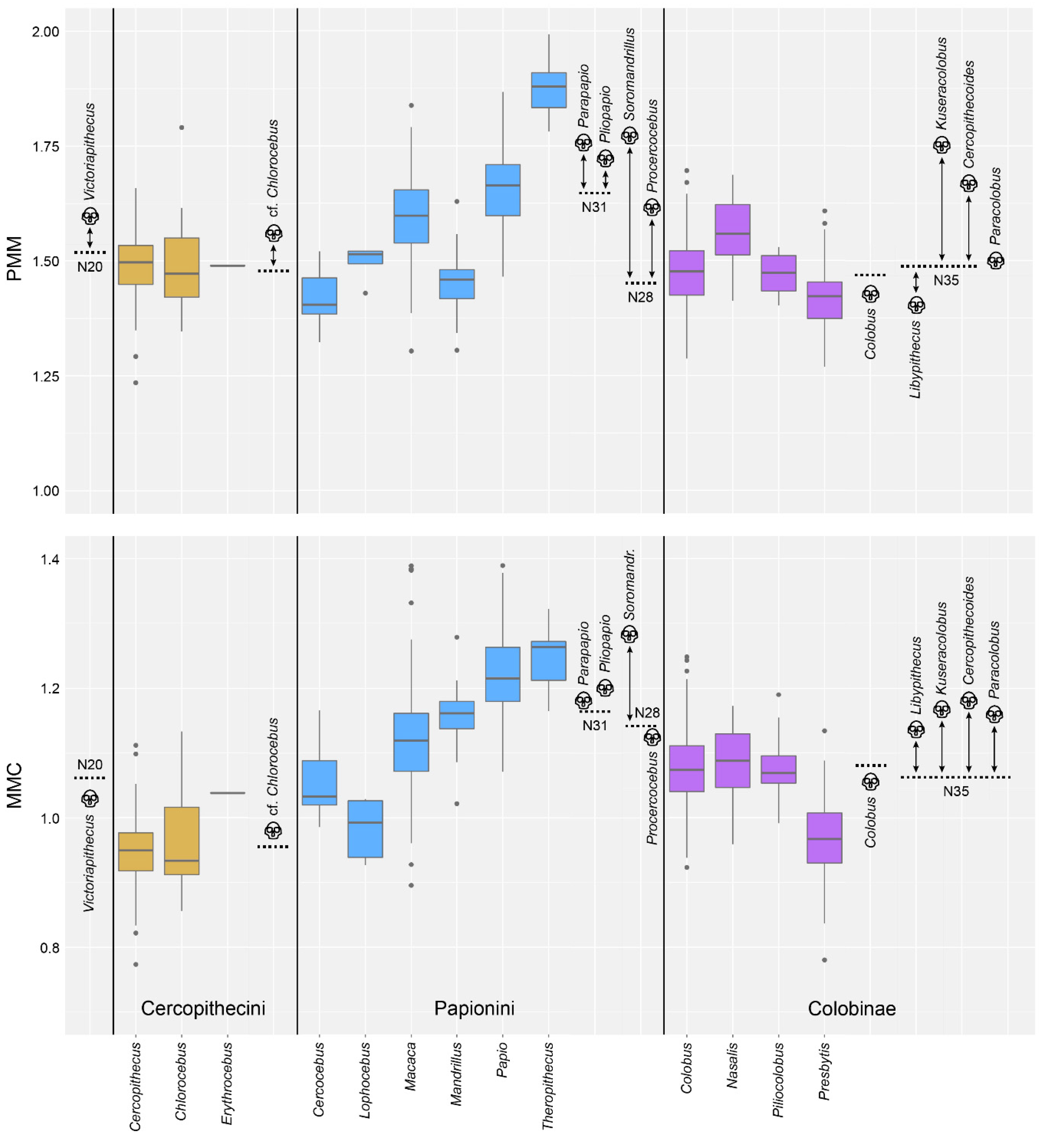
4.2. Test of Hypothesis 2: G:P-Mapped Traits Reveal a Range of Morphological Variation That Cannot Be Predicted Solely through Extant Variation
5. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stucky, R.K.; Krishtalka, L. The application of geologic remote sensing to vertebrate biostratigraphy: General results from the Wind River basin, Wyoming. Mt. Geol. 1991, 28, 75–82. [Google Scholar]
- Anemone, R.; Emerson, C.; Conroy, G. Finding fossils in new ways: An artificial neural network approach to predicting the location of productive fossil localities. Evol. Anthropol. Issues News Rev. 2011, 20, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Anemone, R.L.; Conroy, G.C. (Eds.) New Geospatial Approaches to the Anthropological Sciences; University of New Mexico Press: Albuquerque, NM, USA, 2018. [Google Scholar]
- Hlusko, L.J. Geospatial approaches to hominid paleontology in Africa: What is old, what is new, and what doesn’t change. In New Geospatial Approaches in Anthropology; Anemone, R., Conroy, G., Eds.; SAR Press: Santa Fe, NM, USA, 2018; pp. 39–58. [Google Scholar]
- Reed, D.; Barr, W.A.; Mcpherron, S.P.; Bobe, R.; Geraads, D.; Wynn, J.G.; Alemseged, Z. Digital data collection in paleoanthropology. Evol. Anthropol. Issues News Rev. 2015, 24, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Cunningham, J.A.; Rahman, I.A.; Lautenschlager, S.; Rayfield, E.J.; Donoghue, P.C. A virtual world of paleontology. Trends Ecol. Evol. 2014, 29, 347–357. [Google Scholar] [CrossRef] [PubMed]
- Otero, A.; Moreno, A.P.; Falkingham, P.L.; Cassini, G.; Ruella, A.; Militello, M.; Toledo, N. Three-dimensional image surface acquisition in vertebrate paleontology: A review of principal techniques. Publ. Electrón. Asoc. Paleontol. Argent. 2020, 20, 1–14. [Google Scholar] [CrossRef]
- Rohlf, F.J.; Marcus, L.F. A revolution morphometrics. Trends Ecol. Evol. 1993, 8, 129–132. [Google Scholar] [CrossRef]
- Mitteroecker, P.; Schaefer, K. Thirty years of geometric morphometrics: Achievements, challenges, and the ongoing quest for biological meaningfulness. Yearb. Biol Anthr. 2022, 178, 181–210. [Google Scholar] [CrossRef]
- Cirilli, O.; Melchionna, M.; Serio, C.; Bernor, R.L.; Bukhsianidze, M.; Lordkipanidze, D.; Rook, L.; Profico, A.; Raia, P. Target deformation of the Equus stenonis holotype skull: A virtual reconstruction. Front. Earth Sci. 2020, 8, 247. [Google Scholar] [CrossRef]
- Morimoto, N.; Kunimatsu, Y.; Nakatsukasa, M.; Ponce de Leon, M.S.; Zollikofer, C.P.; Ishida, H.; Sasaki, T.; Suwa, G. Variation of bony labyrinthine morphology in Mio− Plio− Pleistocene and modern anthropoids. Am. J. Phys. Anthropol. 2020, 173, 276–292. [Google Scholar] [CrossRef]
- Monson, T.A.; Fecker, D.; Scherrer, M. Neutral evolution of human enamel–dentine junction morphology. Proc. Natl. Acad. Sci. USA 2020, 117, 26183–26189. [Google Scholar] [CrossRef]
- Lautenschlager, S. Digital reconstruction of soft-tissue structures in fossils. Paleontol. Soc. Pap. 2016, 22, 101–117. [Google Scholar] [CrossRef]
- Kochiyama, T.; Ogihara, N.; Tanabe, H.C.; Kondo, O.; Amano, H.; Hasegawa, K.; Suzuki, H.; Ponce de León, M.S.; Zollikofer, C.P.; Bastir, M.; et al. Reconstructing the Neanderthal brain using computational anatomy. Sci. Rep. 2018, 8, 6296. [Google Scholar] [CrossRef] [PubMed]
- Haile-Selassie, Y.; Melillo, S.M.; Vazzana, A.; Benazzi, S.; Ryan, T.M. A 3.8-million-year-old hominin cranium from Woranso-Mille, Ethiopia. Nature 2019, 573, 214–219. [Google Scholar] [CrossRef] [PubMed]
- Tafforeau, P.; Boistel, R.; Boller, E.; Bravin, A.; Brunet, M.; Chaimanee, Y.; Cloetens, P.; Feist, M.; Hoszowska, J.; Jaeger, J.J.; et al. Applications of X-ray synchrotron microtomography for non-destructive 3D studies of paleontological specimens. Appl. Phys. A 2006, 83, 195–202. [Google Scholar] [CrossRef]
- Smith, T.M.; Tafforeau, P. New visions of dental tissue research: Tooth development, chemistry, and structure. Evol. Anthropol. Issues News Rev. 2008, 17, 213–226. [Google Scholar] [CrossRef]
- Kimura, Y.; Jacobs, L.L.; Cerling, T.E.; Uno, K.T.; Ferguson, K.M.; Flynn, L.J.; Patnaik, R. Fossil mice and rats show isotopic evidence of niche partitioning and change in dental ecomorphology related to dietary shift in Late Miocene of Pakistan. PLoS ONE 2013, 8, e69308. [Google Scholar] [CrossRef]
- Levin, N.E.; Haile-Selassie, Y.; Frost, S.R.; Saylor, B.Z. Dietary change among hominins and cercopithecids in Ethiopia during the early Pliocene. Proc. Natl. Acad. Sci. USA 2015, 112, 12304–12309. [Google Scholar] [CrossRef]
- Ma, J.; Wang, Y.; Jin, C.; Yan, Y.; Qu, Y.; Hu, Y. Isotopic evidence of foraging ecology of Asian elephant (Elephas maximus) in South China during the Late Pleistocene. Quat. Int. 2017, 443, 160–167. [Google Scholar] [CrossRef]
- Souron, A. Morphology, diet, and stable carbon isotopes: On the diet of Theropithecus and some limits of uniformitarianism in paleoecology. Am. J. Phys. Anthropol. 2018, 166, 261–267. [Google Scholar] [CrossRef]
- Smith, T.M.; Austin, C.; Green, D.R.; Joannes-Boyau, R.; Bailey, S.; Dumitriu, D.; Fallon, S.; Grün, R.; James, H.F.; Moncel, M.H.; et al. Wintertime stress, nursing, and lead exposure in Neanderthal children. Sci. Adv. 2018, 4, eaau9483. [Google Scholar] [CrossRef]
- Reynard, B.; Balter, V. Trace elements and their isotopes in bones and teeth: Diet, environments, diagenesis, and dating of archeological and paleontological samples. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2014, 416, 4–16. [Google Scholar] [CrossRef]
- Courtenay, L.A.; Huguet, R.; González-Aguilera, D.; Yravedra, J. A hybrid geometric morphometric deep learning approach for cut and trampling mark classification. Appl. Sci. 2019, 10, 150. [Google Scholar] [CrossRef]
- Domínguez-Rodrigo, M.; Cifuentes-Alcobendas, G.; Jiménez-García, B.; Abellán, N.; Pizarro-Monzo, M.; Organista, E.; Baquedano, E. Artificial intelligence provides greater accuracy in the classification of modern and ancient bone surface modifications. Sci. Rep. 2020, 10, 18862. [Google Scholar] [CrossRef]
- Martín-Perea, D.M.; Courtenay, L.A.; Domingo, M.S.; Morales, J. Application of artificially intelligent systems for the identification of discrete fossiliferous levels. PeerJ 2020, 8, e8767. [Google Scholar] [CrossRef] [PubMed]
- Gorur, K.; Kaya Ozer, C.; Ozer, I.; Can Karaca, A.; Cetin, O.; Kocak, I. Species-level microfossil prediction for Globotruncana genus using machine learning models. Arab. J. Sci. Eng. 2022, 1–18. [Google Scholar] [CrossRef]
- Monson, T.A.; Armitage, D.W.; Hlusko, L.J. Using machine learning to classify extant apes and interpret the dental morphology of the chimpanzee-human last common ancestor. PaleoBios 2018, 35, 1–20. [Google Scholar] [CrossRef]
- Püschel, T.A.; Marcé-Nogué, J.; Gladman, J.T.; Bobe, R.; Sellers, W.I. Inferring locomotor behaviours in Miocene New World monkeys using finite element analysis, geometric morphometrics and machine-learning classification techniques applied to talar morphology. J. R. Soc. Interface 2018, 15, 20180520. [Google Scholar] [CrossRef]
- Millar, M. Predicting Theropod Hunting Tactics using Machine Learning. Open Sci. J. 2019, 4. [Google Scholar] [CrossRef]
- Wiens, J.J. Paleontology, genomics, and combined-data phylogenetics: Can molecular data improve phylogeny estimation for fossil taxa? Syst. Biol. 2009, 58, 87–99. [Google Scholar] [CrossRef]
- Geisler, J.H.; McGowen, M.R.; Yang, G.; Gatesy, J. A supermatrix analysis of genomic, morphological, and paleontological data from crown Cetacea. BMC Evol. Biol. 2011, 11, 112. [Google Scholar] [CrossRef]
- O’Leary, M.A.; Bloch, J.I.; Flynn, J.J.; Gaudin, T.J.; Giallombardo, A.; Giannini, N.P.; Goldberg, S.L.; Kraatz, B.P.; Luo, Z.X.; Meng, J.; et al. The placental mammal ancestor and the post–K-Pg radiation of placentals. Science 2013, 339, 662–667. [Google Scholar] [CrossRef] [PubMed]
- Weidenreich, F. The Dentition of Sinanthoropus Pekinensis: A Comparative Odontography of the Hominids; Palaeontologia Sinica: New Series D, No. 1; Geological Survey of China: Beijing, China, 1937; Volume 101, pp. 1–180. [Google Scholar]
- Gould, S.J. On the scaling of tooth size in mammals. Am. Zool. 1975, 15, 353–362. [Google Scholar] [CrossRef]
- Fleagle, J.G.; McGraw, W.S. Skeletal and dental morphology supports diphyletic origin of baboons and mandrills. Proc. Natl. Acad. Sci. USA 1999, 96, 1157–1161. [Google Scholar] [CrossRef]
- Gingerich, P.D. Environment and evolution through the Paleocene–Eocene thermal maximum. Trends Ecol. Evol. 2006, 21, 246–253. [Google Scholar] [CrossRef]
- Hlusko, L.J.; Schmitt, C.A.; Monson, T.A.; Brasil, M.F.; Mahaney, M.C. The Integration of quantitative genetics, paleontology, and neontology reveals genetic underpinnings of primate dental evolution. Proc. Natl. Acad. Sci. USA 2016, 113, 9262–9267. [Google Scholar] [CrossRef]
- Hlusko, L.J. Recent insights into the evolution of quantitative traits in non-human primates. Curr. Opin. Genet. Dev. 2018, 53, 15–20. [Google Scholar] [CrossRef]
- Rizk, O.T.; Amugongo, S.; Mahaney, M.C.; Hlusko, L.J. The quantitative genetic analysis of primate dental variation: History of the approach and prospects for the future. In Technique and Application in Dental Anthropology; Irish, J.D., Nelson, G.C., Eds.; Cambridge University Press: Cambridge, CA, USA, 2008; ISBN 13: 9780521870610. [Google Scholar]
- Hlusko, L.J.; Mahaney, M.C. Genetic contributions to expression of the baboon cingular remnant. Arch. Oral Biol. 2003, 48, 663–672. [Google Scholar] [CrossRef]
- Hlusko, L.J.; Sage, R.D.; Mahaney, M.C. Evolution of modularity in the mammalian dentition: Mice and monkeys share a common dental genetic architecture. J. Exp. Zool. Part B Mol. Dev. Evol. 2011, 316, 21–49. [Google Scholar] [CrossRef]
- Hardin, A.M. Genetic correlations in the rhesus macaque dentition. J. Hum. Evol. 2020, 148, 102873. [Google Scholar] [CrossRef]
- Cunha, A.S.; Dos Santos, L.V.; Marañón-Vásquez, G.A.; Kirschneck, C.; Gerber, J.T.; Stuani, M.B.; Matsumoto, M.A.N.; Vieira, A.R.; Scariot, R.; Küchler, E.C. Genetic variants in tooth agenesis–related genes might be also involved in tooth size variations. Clin. Oral Investig. 2021, 25, 1307–1318. [Google Scholar] [CrossRef] [PubMed]
- Stojanowski, C.M.; Paul, K.S.; Seidel, A.C.; Duncan, W.N.; Guatelli-Steinberg, D. Heritability and genetic integration of tooth size in the South Carolina Gullah. Am. J. Phys. Anthropol. 2017, 164, 505–521. [Google Scholar] [CrossRef] [PubMed]
- Hardin, A.M. Genetic contributions to dental dimensions in brown-mantled tamarins (Saguinus fuscicollis) and rhesus macaques (Macaca mulatta). Am. J. Phys. Anthropol. 2019, 168, 292–302. [Google Scholar] [CrossRef] [PubMed]
- Hardin, A.M. Genetic correlations in the dental dimensions of Saguinus fuscicollis. Am. J. Phys. Anthropol. 2019, 169, 557–566. [Google Scholar] [CrossRef]
- Hardin, A.M.; Knigge, R.P.; Duren, D.L.; Williams-Blangero, S.; Subedi, J.; Mahaney, M.C.; Sherwood, R.J. Genetic influences on dentognathic morphology in the Jirel population of Nepal. Anat. Rec. 2022; Early View. [Google Scholar] [CrossRef]
- Hlusko, L.J.; Lease, L.R.; Mahaney, M.C. The evolution of genetically correlated traits: Tooth size and body size in baboons. Am. J. Phys. Anthropol. 2006, 131, 420–427. [Google Scholar] [CrossRef] [PubMed]
- Hlusko, L.J.; Mahaney, M.C. Of mice and monkeys: Quantitative genetic analyses of size variation along the dental arcade. In Dental Perspectives on Human Evolution: State of the Art Research in Dental Paleoanthropology; Bailey, S., Hublin, J.-J., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 237–245. [Google Scholar]
- Hlusko, L.J.; Mahaney, M.C. The baboon model for dental development. In The Baboon in Biomedical Research; Springer: New York, NY, USA, 2009; pp. 207–223. [Google Scholar]
- Brasil, M.F.; Monson, T.A.; Schmitt, C.A.; Hlusko, L.J. A genotype:phenotype approach to testing taxonomic hypotheses in hominids. Sci. Nat. 2020, 107, 40. [Google Scholar] [CrossRef] [PubMed]
- Monson, T.A.; Boisserie, J.-R.; Brasil, M.F.; Clay, S.; Dvoretzky, R.; Ravindramurthy, S.R.; Schmitt, C.A.; Souron, A.; Takenaka, R.; Ungar, P.; et al. Evidence of strong stabilizing effects on the evolution of boreoeutherian (Mammalia) dental proportions. Ecol. Evol. 2019, 9, 7597–7612. [Google Scholar] [CrossRef] [PubMed]
- Zuercher, M.E.; Monson, T.A.; Dvoretzky, R.R.; Ravindramurthy, S.; Hlusko, L.J. Dental variation in megabats (Chiroptera: Pteropodidae): Tooth metrics correlate with body size and tooth proportions reflect phylogeny. J. Mamm. Evol. 2021, 28, 543–558. [Google Scholar] [CrossRef]
- Kavanagh, K.D.; Evans, A.R.; Jernvall, J. Predicting evolutionary patterns of mammalian teeth from development. Nature 2007, 449, 427–432. [Google Scholar] [CrossRef]
- Halliday, T.J.; Goswami, A. Testing the inhibitory cascade model in Mesozoic and Cenozoic mammaliaforms. BMC Evol. Biol. 2013, 13, 79. [Google Scholar] [CrossRef] [PubMed]
- Couzens, A.M.; Evans, A.R.; Skinner, M.M.; Prideaux, G.J. The role of inhibitory dynamics in the loss and reemergence of macropodoid tooth traits. Evolution 2016, 70, 568–585. [Google Scholar] [CrossRef] [PubMed]
- Wilson, L.; Madden, R.; Kay, R.; Sánchez-Villagra, M. Testing a developmental model in the fossil record: Molar proportions in South American ungulates. Paleobiology 2012, 38, 308–321. [Google Scholar] [CrossRef]
- Labonne, G.; Laffont, R.; Renvoise, E.; Jebrane, A.; Labruère, C.; Chateau-Smith, C.; Navarro, N.; Montuire, S. When less means more: Evolutionary and developmental hypotheses in rodent molars. J. Evol. Biol. 2012, 25, 2102–2111. [Google Scholar] [CrossRef]
- Carter, K.E.; Worthington, S. The evolution of anthropoid molar proportions. BMC Evol. Biol. 2016, 16, 110. [Google Scholar] [CrossRef]
- Roseman, C.C.; Delezene, L.K. The inhibitory cascade model is not a good predictor of molar size covariation. Evol. Biol. 2019, 46, 229–238. [Google Scholar] [CrossRef]
- Bermúdez de Castro, J.M.; Modesto-Mata, M.; García-Campos, C.; Sarmiento, S.; Martín-Francés, L.; Martínez de Pinillos, M.; Martinón-Torres, M. Testing the inhibitory cascade model in a recent human sample. J. Anat. 2021, 239, 1170–1181. [Google Scholar] [CrossRef]
- Bermúdez de Castro, J.M.; Modesto-Mata, M.; Martín-Francés, L.; García-Campos, C.; Martínez de Pinillos, M.; Martinón-Torres, M. Testing the inhibitory cascade model in the Middle Pleistocene Sima de los Huesos (Sierra de Atapuerca, Spain) hominin sample. J. Anat. 2021, 238, 173–184. [Google Scholar] [CrossRef]
- Grieco, T.M.; Rizk, O.T.; Hlusko, L.J. A modular framework characterizes micro- and macroevolution of Old World monkey dentitions. Evolution 2013, 67, 241–259. [Google Scholar] [CrossRef]
- Grieco, T.M.; Rizk, O.T.; Hlusko, L.J. Data from: A Modular Framework Characterizes Micro- and Macroevolution of Old World Monkey Dentitions. Dryad, Dataset. 2012. Available online: https://datadryad.org/stash/dataset/doi:10.5061/dryad.693j8 (accessed on 1 January 2022). [CrossRef]
- Frost, S.R. Fossil Cercopithecidae from the Afar Depression, Ethiopia: Species Systematics and Comparison to the Turkana Basin. Doctoral Dissertation, City University of New York, New York, NY, USA, 2001. [Google Scholar]
- Frost, S.R.; Alemseged, Z. Middle Pleistocene fossil Cercopithecidae from Asbole, Afar Region, Ethiopia. J. Hum. Evol. 2007, 53, 227–259. [Google Scholar] [CrossRef] [PubMed]
- Freedman, L. The fossil Cercopithecoidea of South Africa. Ann. Transvaal Mus. 1957, 23, 121–262. [Google Scholar]
- Frost, S.R.; Haile-Selassie, Y.; Hlusko, L.J. Chapter 6 Cercopithecidae. In Ardipithecus kadabba: Late Miocene Evidence from Middle Awash, Ethiopia; Haile-Selassie, Y., WoldeGabriel, G., Eds.; University of California Press: Berkeley, CA, USA, 2009. [Google Scholar]
- Frost, S.R.; Jablonski, N.G.; Haile-Selassie, Y. Early Pliocene Cercopithecidae from Woranso-Mille (Central Afar, Ethiopia) and the origins of the Theropithecus oswaldi lineage. J. Hum. Evol. 2014, 76, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Frost, S.R. Fossil Cercopithecidae from the Middle Pleistocene Dawaitoli Formation, Middle Awash Valley, Afar Region, Ethiopia. Am. J. Phys. Anthropol. 2007, 134, 460–471. [Google Scholar] [CrossRef]
- Frost, S.R.; Marcus, L.F.; Bookstein, F.L.; Reddy, D.P.; Delson, E. Cranial allometry, phylogeography, and systematics of large-bodied papionins (Primates: Cercopithecinae) inferred from geometric morphometric analysis of landmark data. Anat. Rec. 2003, 275A, 1048–1072. [Google Scholar] [CrossRef]
- Hlusko, L.J. A new large Pliocene colobine species (Mammalia: Primates) from Asa Issie, Ethiopia. Geobios 2006, 39, 57–69. [Google Scholar] [CrossRef]
- Hlusko, L.J. A new late Miocene species of Paracolobus and other Cercopithecoidea (Mammalia: Primates) fossils from Lemudong’o, Kenya. Kirtlandia 2007, 56, 72–85. [Google Scholar]
- Benefit, B.K. The permanent dentition and phylogenetic position of Victoriapithecus from Maboko Island, Kenya. J. Hum. Evol. 1993, 25, 83–172. [Google Scholar] [CrossRef]
- Hlusko, L.J.; Weiss, K.M.; Mahaney, M.C. Statistical genetic comparison of two techniques for assessing molar crown size in pedigreed baboons. Am. J. Phys. Anthropol. 2002, 117, 182–189. [Google Scholar] [CrossRef]
- Almasy, L.; Blangero, J. Multipoint quantitative-trait linkage analysis in general pedigrees. Am. J. Hum. Genet. 1998, 62, 1198–1211. [Google Scholar] [CrossRef]
- Edwards, A.W.F. Likelihood; Johns Hopkins University Press: Baltimore, MD, USA, 1992. [Google Scholar]
- Hopper, J.L.; Mathews, J.D. Extensions to multivariate normal models for pedigree analysis. Ann. Hum. Genet. 1982, 46, 373–383. [Google Scholar] [CrossRef] [PubMed]
- Boehnke, M.; Moll, P.P.; Kottke, B.A.; Weidman, W.H. Partitioning the variability of fasting plasma glucose levels in pedigrees. Genetic and environmental factors. Am. J. Epidemiol. 1987, 125, 679–689. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 1 January 2022).
- Komsta, L.; Novomestky, F. Moments: Moments, Cumulants, Skewness, Kurtosis and Related Tests. R. R Package Version 0.14.1. Available online: https://cran.r-project.org/web/packages/moments/index.html (accessed on 1 January 2022).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009. [Google Scholar]
- Harmon, L.; Weir, J.; Brock, C.; Glor, R.; Challenger, W.; Hunt, G.; FitzJohn, R.; Pennell, M.; Slater, G.; Brown, J.; et al. Package ‘Geiger’. Analysis of Evolutionary Diversification. Available online: https://cran.r-project.org/web/packages/geiger/geiger.pdf (accessed on 1 January 2022).
- Arnold, C.; Matthews, L.J.; Nunn, C.L. The 10kTrees Website: A New Online Resource for Primate Phylogeny. Evol. Anthr. 2010, 19, 114–118. [Google Scholar] [CrossRef]
- Meyer, D.; Rinaldi, I.D.; Ramlee, H.; Perwitasari-Farajallah, D.; Hodges, J.K.; Roos, C. Mitochondrial phylogeny of leaf monkeys (genus Presbytis, Eschscholtz, 1821) with implications for taxonomy and conservation. Mol. Phylogenet. Evol. 2011, 59, 311–319. [Google Scholar] [CrossRef]
- Kembel, S.W.; Cowan, P.D.; Helmus, M.R.; Cornwell, W.K.; Morlon, H.; Ackerly, D.D.; Webb, C.O. Picante: R tools for integrating phylogenies and ecology. Bioinformatics 2010, 26, 1463–1464. [Google Scholar] [CrossRef]
- Blomberg, S.P.; Garland, T., Jr.; Ives, A.R. Testing for phylogenetic signal in comparative data: Behavioral traits are more labile. Evolution 2003, 57, 717–745. [Google Scholar] [CrossRef]
- Revell, L.J.; Harmon, L.J.; Collar, D.C. Phylogenetic signal, evolutionary process, and rate. Syst. Biol. 2008, 57, 591–601. [Google Scholar] [CrossRef]
- Revell, L.J. Phytools: An R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 2012, 3, 217–223. [Google Scholar] [CrossRef]
- Garamszegi, L.Z.; Møller, A.P. Effects of sample size and intraspecific variation in phylogenetic comparative studies: A meta-analytic review. Biol. Rev. 2010, 85, 797–805. [Google Scholar] [CrossRef]
- Raaum, R.L.; Sterner, K.N.; Noviello, C.M.; Stewart, C.B.; Disotell, T.R. Catarrhine primate divergence dates estimated from complete mitochondrial genomes: Concordance with fossil and nuclear DNA evidence. J. Hum. Evol. 2005, 48, 237–257. [Google Scholar] [CrossRef]
- Liedigk, R.; Roos, C.; Brameier, M.; Zinner, D. Mitogenomics of the Old World monkey tribe Papionini. BMC Evol. Biol. 2014, 14, 176. [Google Scholar] [CrossRef] [PubMed]
- Ting, N. Mitochondrial relationships and divergence dates of the African colobines: Evidence of Miocene origins for the living colobus monkeys. J. Hum. Evol. 2008, 55, 312–325. [Google Scholar] [CrossRef] [PubMed]
- Jablonski, N.G. Fossil Old World monkeys: The late Neogene radiation. In The Primate Fossil Record; Cambridge University Press: Cambridge, UK, 2002; pp. 255–299. [Google Scholar]
- Gilbert, C.C. Craniomandibular morphology supporting the diphyletic origin of mangabeys and a new genus of the Cercocebus/Mandrillus clade, Procercocebus. J. Hum. Evol. 2007, 53, 69–102. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, C.C. Cladistic analysis of extant and fossil African papionins using craniodental data. J. Hum. Evol. 2013, 64, 399–433. [Google Scholar] [CrossRef]
- Frost, S.R.; Gilbert, C.C.; Nakatsukasa, M. The Colobine Fossil Record. Colobines Nat. Hist. Behav. Ecol. Divers. 2022, 3, 13. [Google Scholar]
- Jablonski, N.G.; Frost, S.R. Cercopithecoidea. In Cenozoic Mammals of Africa; Werdelin, L., Sanders, W.J., Eds.; University of California Press: Berkeley, CA, USA, 2010; pp. 393–428. [Google Scholar]
- Koh, C.; Bates, E.; Broughton, E.; Do, N.T.; Fletcher, Z.; Mahaney, M.C.; Hlusko, L.J. Genetic integration of molar cusp size variation in baboons. Am. J. Phys. Anthropol. 2010, 142, 246–260. [Google Scholar] [CrossRef]
- Darwin, C. The Origin of Species by Natural Selection: Or, the Preservation of Favored Races in the Struggle for Life; John Murray: London, UK, 1859. [Google Scholar]
- Lande, R. Quantitative genetic analysis of multivariate evolution, applied to brain: Body size allometry. Evolution 1979, 33, 402–416. [Google Scholar] [CrossRef]
- Lande, R.; Arnold, S.J. The measurement of selection on correlated characters. Evolution 1983, 37, 1210–1226. [Google Scholar] [CrossRef]
- Cheverud, J.M. Quantitative genetics and developmental constraints on evolution by selection. J. Theor. Biol. 1984, 110, 155–171. [Google Scholar] [CrossRef]
- Roff, D.A. Evolutionary Quantitative Genetics; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Hlusko, L.J.; Suwa, G.; Kono, R.; Mahaney, M.C. Genetics and the evolution of primate enamel thickness: A baboon model. Am. J. Phys. Anthropol. 2004, 124, 223–233. [Google Scholar] [CrossRef]
- Marroig, G.; Cheverud, J.M. Size as a line of least evolutionary resistance: Diet and adaptive morphological radiation in New World monkeys. Evolution 2005, 59, 1128–1142. [Google Scholar] [CrossRef] [PubMed]
- Stojanowski, C.M.; Paul, K.S.; Seidel, A.C.; Duncan, W.N.; Guatelli-Steinberg, D. Quantitative genetic analyses of postcanine morphological crown variation. Am. J. Phys. Anthropol. 2019, 168, 606–631. [Google Scholar] [CrossRef] [PubMed]
- Paul, K.S.; Stojanowski, C.M.; Hughes, T.E.; Brook, A.H.; Townsend, G.C. Patterns of heritability across the human diphyodont dental complex: Crown morphology of Australian twins and families. Am. J. Phys. Anthropol. 2020, 172, 447–461. [Google Scholar] [CrossRef] [PubMed]
- Paul, K.S.; Stojanowski, C.M.; Hughes, T.; Brook, A.H.; Townsend, G.C. Genetic correlation, pleiotropy, and molar morphology in a longitudinal sample of Australian twins and families. Genes 2020, 13, 996. [Google Scholar] [CrossRef]
- Willis, M.S.; Swindler, D.R. Molar size and shape variations among Asian colobines. Am. J. Phys. Anthropol. Off. Publ. Am. Assoc. Phys. Anthropol. 2004, 125, 51–60. [Google Scholar] [CrossRef]
- Monson, T.A.; Hlusko, L.J. Breaking the rules: Phylogeny, not life history, explains dental eruption sequence in primates. Am. J. Phys. Anthropol. 2018, 167, 217–233. [Google Scholar] [CrossRef]
- Frazier, B.C. The Cranial Morphology of Dwarf Primate Species. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 15 December 2010. [Google Scholar]
- Huxley, J.S. Problems of Relative Growth; Methuen: London, UK, 1932. [Google Scholar]
- Collard, M.; O’Higgins, P. Ontogeny and homoplasy in the papionine monkey face. Evol. Dev. 2001, 3, 322–331. [Google Scholar] [CrossRef]
- Monson, T.A.; Brasil, M.F.; Stratford, D.J.; Hlusko, J. Patterns of craniofacial variation and taxonomic diversity in the South African Cercopithecidae fossil record. Palaeontol. Electron. 2017, 20, 1–20. [Google Scholar] [CrossRef]
- Monson, T.A. Patterns and magnitudes of craniofacial covariation in extant cercopithecids. Anat. Rec. 2020, 303, 3068–3084. [Google Scholar] [CrossRef]
- Perelman, P.; Johnson, W.E.; Roos, C.; Seuánez, H.N.; Horvath, J.E.; Moreira, M.A.M.; Rumpler, Y. A molecular phylogeny of living primates. PLoS Genet. 2011, 7, e1001342. [Google Scholar] [CrossRef]
- Lumsden, A. Pattern formation in the molar dentition of the mouse. J. Biol. Buccale 1979, 7, 77–103. [Google Scholar]
- Lumsden, A.; Osborn, J. Development of mouse dentition in culture. J. Dent. Res. 1976, 55, 136. [Google Scholar]
- Sofaer, J.A. Co-ordinated growth of successively initiated tooth germs in the mouse. Arch. Oral Biol. 1977, 22, 71–72. [Google Scholar] [CrossRef]
- Lucas, P.W.; Corlett, R.T.; Luke, D.A. Postcanine tooth size and diet in anthropoid primates. Z. Morphol. Anthropol. 1986, 76, 253–276. [Google Scholar] [CrossRef]
- Evans, A.R.; Daly, E.S.; Catlett, K.K.; Paul, K.S.; King, S.J.; Skinner, M.M.; Nesse, H.P.; Hublin, J.J.; Townsend, G.C.; Schwartz, G.T.; et al. A simple rule governs the evolution and development of hominin tooth size. Nature 2016, 530, 477–480. [Google Scholar] [CrossRef]
- Vitek, N.S.; Roseman, C.C.; Bloch, J.I. Mammal molar size ratios and the inhibitory cascade at the intraspecific scale. Integr. Org. Biol. 2020, 2, obaa020. [Google Scholar] [CrossRef]
- Sofaer, J.A.; Bailit, H.L.; Maclean, J. A developmental basis for differential tooth reduction during hominoid evolution. Evolution 1971, 25, 509–517. [Google Scholar] [CrossRef]
- Marshall, L.G.; Corrucini, R.S. Variability, evolutionary rates, and allometry in dwarfing lineages. Paleobiology 1978, 4, 101–119. [Google Scholar] [CrossRef]
- Townsend, G.; Bockmann, M.; Hughes, T.; Brook, A. Genetic, environmental and epigenetic influences on variation in human tooth number, size and shape. Odontology 2012, 100, 1–9. [Google Scholar] [CrossRef]
- Polly, P.D. Development with a bite. Nature 2007, 449, 413–414. [Google Scholar] [CrossRef]
- Polly, P.D. Quantitative genetics provides predictive power for paleontological studies of morphological evolution. Proc. Natl. Acad. Sci. USA 2016, 113, 9142–9144. [Google Scholar] [CrossRef] [PubMed]
- Finarelli, J.A.; Flynn, J.J. Ancestral state reconstruction of body size in the Caniformia (Carnivora, Mammalia): The effects of incorporating data from the fossil record. Syst. Biol. 2006, 55, 301–313. [Google Scholar] [CrossRef] [PubMed]
- Monson, T.A.; Coleman, J.; Hlusko, L.J. Craniodental allometry, prenatal growth rates, and the evolutionary loss of the third molars in New World monkeys. Anat. Record 2019, 302, 1419–1433. [Google Scholar] [CrossRef] [PubMed]

| Subfamily | Tribe | Genus | Species | Number of Individuals |
|---|---|---|---|---|
| Cercopithecinae | Cercopithecini | Cercopithecus | albogularis | 1 |
| Cercopithecus | campbelli | 9 | ||
| Cercopithecus | mitis | 95 | ||
| Chlorocebus | aethiops | 28 | ||
| Erythrocebus | patas | 2 | ||
| Papionini | Cercocebus | atys | 4 | |
| Cercocebus | galeritus | 1 | ||
| Cercocebus | torquatus | 20 | ||
| Lophocebus | albigena | 3 | ||
| Macaca | fascicularis | 98 | ||
| Macaca | mulatta | 76 | ||
| Mandrillus | leucophaeus | 1 | ||
| Mandrillus | sphinx | 17 | ||
| Papio | hamadryas | 127 | ||
| Theropithecus | gelada | 10 | ||
| Colobinae | Colobini | Colobus | guereza | 125 |
| Nasalis | larvatus | 30 | ||
| Piliocolobus | badius | 15 | ||
| Presbytini | Presbytis | melalophos | 83 | |
| Presbytis | rubicunda | 80 | ||
| TOTAL | 825 | |||
| Subfamily | Tribe | Genus | Species | Number of Individuals | Source |
|---|---|---|---|---|---|
| Cercopithecinae | Cercopithecini | Cercopithecus | sp. (Andalee) | 30 | 1 |
| Cercopithecus | sp. (Upper Andalee) | 5 | 1 | ||
| cf. Chlorocebus | Asbole | 13 | 2 | ||
| cf. Chlorocebus | sp. (Chai Baro) | 105 | 3 | ||
| cf. Chlorocebus | sp. (Faro Daba) | 223 | 3 | ||
| Papionini | Papio | hamadryas angusticeps | 12 | 4, 5 | |
| Papio | hamadryas robinsoni | 29 | 4, 6 | ||
| Papio | hamadryas ssp. (Asbole) | 10 | 2 | ||
| Papio | hamadryas ssp. (Chai Baro) | 143 | 3 | ||
| Papio | hamadryas ursinus | 1 | 4 | ||
| Papio | izodi | 7 | 4, 6, 7 | ||
| Parapapio | broomi | 34 | 4, 6, 7 | ||
| Parapapio | jonesi | 12 | 4, 7 | ||
| Parapapio | whitei | 16 | 4, 6, 7 | ||
| Pliopapio | alemui | 5 | 8 | ||
| Procercocebus | antiquus | 8 | 6, 7 | ||
| Soromandrillus | quadratirostris | 11 | 9 | ||
| Theropithecus | oswaldi cf. darti | 124 | 10 | ||
| Theropithecus | oswaldi darti | 4 | 7 | ||
| Theropithecus | oswaldi leakeyi | 12 | 2, 11 | ||
| Theropithecus | oswaldi oswaldi | 8 | 4 | ||
| Colobinae | Colobini | Cercopithecoides | kimeui | 12 | 9, 12 |
| Cercopithecoides | meaveae | 2 | 9 | ||
| Cercopithecoides | williamsi | 91 | 9 | ||
| Colobus | cf. guereza (Faro Daba) | 360 | 3 | ||
| Colobus | sp. (Andalee) | 31 | 1 | ||
| Colobus | sp. (Asbole) | 47 | 2 | ||
| Colobus | sp. (Upper Andalee) | 4 | 1 | ||
| Kuseracolobus | aramisi | 5 | 8 | ||
| Kuseracolobus | hafu | 14 | 13 | ||
| Libypithecus | markgrafi | 3 | 9 | ||
| Microcolobus | tugenensis | 1 | 9 | ||
| Paracolobus | chemeroni | 1 | 9 | ||
| Paracolobus | enkorikae | 8 | 14 | ||
| Paracolobus | mutiwa | 22 | 9 | ||
| Rhinocolobus | turkanaensis | 23 | 9 | ||
| Victoriapithecinae | Victoriapithecus | macinnesi | 40 | 15 | |
| TOTAL | 1436 | ||||
| Trait | h2 | h2 se | p-Value | Number of Individuals | Proportion of Variance Due to Covariates |
|---|---|---|---|---|---|
| LM1 2D area | 0.611 | 0.110 | <0.001 | 461 | 0.353 ** |
| LM2 2D area | 0.728 | 0.091 | <0.001 | 537 | 0.413 ** |
| LM3 2D area | 0.261 | 0.190 | 0.260 | 221 | 0.490 * |
| RM1 2D area | 0.703 | 0.132 | <0.001 | 440 | 0.281 * |
| RM2 2D area | 0.681 | 0.103 | <0.001 | 531 | 0.366 * |
| RM3 2D area | 0.726 | 0.275 | 0.004 | 171 | 0.508 * |
| L IC | 0.181 | 0.156 | 0.100 | 170 | 0.103 * |
| R IC | 0.604 | 0.333 | 0.006 | 127 | 0.094 * |
| L MMC | 0.001 | 0.141 | 0.496 | 191 | 0.082 ** |
| L PMM | 0.491 | 0.093 | <0.001 | 402 | 0.022 * |
| R MMC | 0.238 | 0.228 | 0.096 | 140 | 0.044 * |
| R PMM | 0.527 | 0.114 | <0.001 | 380 | 0.030 * |
| M1 Area | M2 Area | M3 Area | ||||
|---|---|---|---|---|---|---|
| Mean (n) | StDv | Mean (n) | StDv | Mean (n) | StDv | |
| Extant Genera | ||||||
| Cercocebus | 59.17 (15) | 4.79 | 70.55 (15) | 6.91 | 65.30 (15) | 8.64 |
| Cercopithecus | 32.75 (91) | 5.75 | 40.44 (96) | 5.16 | 31.59 (88) | 4.90 |
| Chlorocebus | 34.56 (27) | 9.13 | 42.58 (27) | 10.88 | 35.08 (25) | 12.47 |
| Colobus | 45.31 (110) | 5.11 | 55.19 (119) | 5.97 | 51.88 (105) | 6.26 |
| Erythrocebus | 39.29 (1) | - | 48.16 (1) | - | 47.06 (1) | - |
| Lophocebus | 47.32 (6) | 2.21 | 58.06 (6) | 3.86 | 49.32 (5) | 4.45 |
| Macaca | 44.26 (174) | 8.30 | 58.91 (174) | 12.73 | 55.94 (148) | 12.40 |
| Mandrillus | 95.96 (18) | 10.64 | 130.4 (18) | 12.86 | 132.03 (18) | 12.29 |
| Nasalis | 49.24 (30) | 5.49 | 59.35 (30) | 4.58 | 54.79 (30) | 5.36 |
| Papio | 161.85 (84) | 23.28 | 230.63 (106) | 34.04 | 242.68 (104) | 40.53 |
| Piliocolobus | 39.36 (15) | 2.42 | 44.78 (15) | 2.56 | 45.32 (15) | 3.23 |
| Presbytis | 32.11 (151) | 2.39 | 34.24 (153) | 2.70 | 30.86 (145) | 3.05 |
| Theropithecus | 96.15 (9) | 11.11 | 140.87 (9) | 11.61 | 145.15 (9) | 11.66 |
| Fossil Genera | ||||||
| Cercopithecoides | 78.92 (22) | 16.74 | 104.41 (25) | 22.32 | 98.85 (22) | 19.59 |
| Cercopithecus | 34.59 (7) | 3.41 | 45.77(7) | 3.58 | 36.00 (3) | 10.11 |
| cf. Chlorocebus | 30.61 (48) | 2.43 | 38.59 (45) | 4.01 | 30.83 (37) | 3.77 |
| Colobus | 43.59 (85) | 5.23 | 51.64 (73) | 7.44 | 48.50 (59) | 6.38 |
| Kuseracolobus | 95.88 (1) | - | 103.4 (1) | - | 76.54 (1) | - |
| Libypithecus | 48.90 (2) | 2.97 | 58.93 (2) | 3.78 | 65.95 (2) | 0.49 |
| Papio | 95.81 (37) | 13.39 | 139.68 (42) | 22.23 | 137.82 (33) | 29.59 |
| Paracolobus | 84.95 (4) | 27.92 | 127.95 (9) | 31.10 | 129.37 (8) | 39.24 |
| Parapapio | 97.06 (20) | 16.92 | 135.16 (20) | 24.73 | 127.91 (28) | 23.93 |
| Pliopapio | 54.02 (1) | - | 73.1 (1) | - | 66.75 (1) | - |
| Procercocebus | 97.83 (4) | 7.80 | 134.44 (5) | 10.40 | 120.29 (5) | 11.99 |
| Rhinocolobus | 85.70 (4) | 8.13 | 104.31 (3) | 2.92 | 114.32 (4) | 13.56 |
| Soromandrillus | 121.41 (4) | 12.21 | 198.79 (6) | 28.07 | 205.49 (6) | 30.60 |
| Theropithecus | 1.34 (6) | 0.03 | 1.34 (6) | 0.03 | 1.34 (6) | 0.03 |
| Victoriapithecus | 42.19 (8) | 1.30 | 57.45 (9) | 4.58 | 44.55 (5) | 4.15 |
| MMC | PMM | IC | ||||
|---|---|---|---|---|---|---|
| Mean (n) | StDv | Mean (n) | StDv | Mean (n) | StDv | |
| Extant Genera | ||||||
| Cercocebus | 1.05 (15) | 0.05 | 1.42 (15) | 0.06 | 1.10 (15) | 0.10 |
| Cercopithecus | 0.95 (92) | 0.06 | 1.49 (103 | 0.08 | 0.97 (76) | 0.09 |
| Chlorocebus | 0.96 (24) | 0.07 | 1.48 (26) | 0.10 | 1.02 (24) | 0.13 |
| Colobus | 1.08 (118) | 0.06 | 1.47 (120) | 0.07 | 1.15 (93) | 0.10 |
| Erythrocebus | 1.04 (1) | - | 1.48 (1) | - | 1.20 (1) | - |
| Lophocebus | 0.98 (5) | 0.05 | 1.49 (6) | 0.03 | 1.04 (5) | 0.11 |
| Macaca | 1.12 (149) | 0.08 | 1.59 (174) | 0.09 | 1.26 (148) | 0.14 |
| Mandrillus | 1.16 (18) | 0.05 | 1.45 (18) | 0.08 | 1.38 (18) | 0.12 |
| Nasalis | 1.09 (30) | 0.05 | 1.57 (29) | 0.08 | 1.12 (30) | 0.10 |
| Papio | 1.22 (86) | 0.07 | 1.65 (99) | 0.09 | 1.46 (71) | 0.13 |
| Piliocolobus | 1.08 (15) | 0.05 | 1.47 (15) | 0.04 | 1.15 (15) | 0.09 |
| Presbytis | 0.97 (151) | 0.05 | 1.41 (160) | 0.07 | 0.96 (138) | 0.08 |
| Theropithecus | 1.25 (8) | 0.05 | 1.88 (10) | 0.06 | 1.53 (8) | 0.06 |
| Fossil Genera | ||||||
| Cercopithecoides | 1.18 (13) | 0.15 | 1.64 (18) | 0.15 | 1.27 (7) | 0.25 |
| Cercopithecus | 0.92 (2) | 0.03 | 1.51 (4) | 0.15 | 0.85 (2) | 0.04 |
| cf. Chlorocebus | 0.98(26) | 0.07 | 1.55 (40) | 0.11 | 1.01 (22) | 0.09 |
| Colobus | 1.07 (55) | 0.09 | 1.44 (66) | 0.08 | 1.12 (46) | 0.10 |
| Kuseracolobus | 1.17 (1) | - | 1.65 (2) | 0.14 | - | - |
| Libypithecus | 1.14 (2) | 0.06 | 1.41 (2) | 0.10 | 1.35 (2) | 0.09 |
| Papio | 1.20 (32) | 0.10 | 1.72 (36) | 0.14 | 1.42 (21) | 0.24 |
| Paracolobus | 1.16 (3) | 0.20 | 1.54 (4) | 0.10 | 1.26 (3) | 0.23 |
| Parapapio | 1.18 (23) | 0.13 | 1.74 (22) | 0.11 | 1.34 (19) | 0.21 |
| Pliopapio | 1.20 (1) | - | 1.72 (1) | - | 1.24 (1) | - |
| Procercocebus | 1.13 (4) | 0.03 | 1.61 (5) | 0.03 | 1.42 (2) | 0.19 |
| Rhinocolobus | 1.19 (3) | 0.07 | 1.43 (3) | 0.07 | 1.26 (2) | 0.16 |
| Soromandrillus | 1.28 (6) | 0.05 | 1.78 (6) | 0.13 | 1.55 (4) | 0.10 |
| Theropithecus | 1.34 (6) | 0.03 | 1.34 (6) | 0.03 | 1.62 (5) | 0.06 |
| Victoriapithecus | 1.01 (4) | 0.05 | 1.59 (2) | 0.08 | 1.05 (3) | 0.12 |
| Traits | |||||||
|---|---|---|---|---|---|---|---|
| M1 2D Area | M2 2D Area | M3 2D Area | IC | MMC | PMM | ||
| Summary p-Value | 0.0004 | <0.0001 | <0.0001 | 0.003 | 0.004 | 0.009 | |
| Genera: | |||||||
| Colobines | Presbytis | 0.027 * | 0.004 ** | 0.003 ** | 0.078 | 0.100 | 0.765 |
| Nasalis | 0.560 | 0.381 | 0.436 | 0.967 | 0.385 | 0.029 * | |
| Piliocolobus | 0.153 | 0.041 * | 0.091 | 0.663 | 0.503 | 0.270 | |
| Colobus | 0.346 | 0.206 | 0.277 | 0.659 | 0.510 | 0.252 | |
| Papionins | Macaca | 0.233 | 0.310 | 0.474 | 0.075 | 0.088 | 0.006 ** |
| Papio | <0.0001 *** | <0.0001 *** | <0.0001 *** | 0.007 ** | 0.009 ** | 0.005 ** | |
| Theropithecus | 0.006 ** | 0.0002 *** | <0.0001 *** | 0.003 ** | 0.005 ** | 0.0002 *** | |
| Lophocebus | 0.380 | 0.227 | 0.123 | 0.361 | 0.251 | 0.112 | |
| Mandrillus | 0.008 ** | 0.0003 *** | <0.0001 *** | 0.002 ** | 0.004 ** | 0.288 | |
| Cercopith-ecins | Chlorocebus | 0.077 | 0.029 * | 0.017 * | 0.308 | 0.111 | 0.238 |
| Erythrocebus | 0.151 | 0.068 | 0.123 | 0.371 | 0.899 | 0.174 | |
| Cercopithecus | 0.019 * | 0.004 ** | 0.002 ** | 0.039 * | 0.026 * | 0.091 | |
| Trait | K-Value | K p-Value |
|---|---|---|
| M1A | 0.6595 | 0.070 |
| M2A | 0.6727 | 0.058 |
| M3A | 0.6606 | 0.055 |
| IC | 0.6251 | 0.045 |
| MMC | 0.6324 | 0.035 |
| PMM | 0.6379 | 0.059 |
| ASR Node | ASR MMC | ASR PMM | Molecular Divergence | Possible Fossil Representative | MMC Value | PMM Value | Geological Age |
|---|---|---|---|---|---|---|---|
| 20 | 1.07 | 1.52 | 16 Ma | Victoriapithecus | 1.03 | 1.59 | 19–12.5 Ma |
| 28 | 1.14 | 1.45 | 5 Ma | Procercocebus | 1.13 | 1.62 | 2.5 Ma |
| 28 | 1.14 | 1.45 | 5 Ma | Soromandrillus | 1.28 | 1.78 | 2–3 Ma |
| 29 | 1.10 | 1.43 | 2 Ma | Procercocebus | 1.13 | 1.62 | 2.5 Ma |
| 30 | 1.18 | 1.45 | 2.5 Ma | Soromandrillus | 1.28 | 1.78 | 2–3 Ma |
| 31 | 1.17 | 1.66 | 2 Ma | Parapapio | 1.18 | 1.76 | 2–5 Ma |
| 31 | 1.17 | 1.66 | 2 Ma | Pliopapio | 1.20 | 1.72 | 4.4 Ma |
| 35 | 1.07 | 1.49 | <7.5 Ma | Paracolobus | 1.16 | 1.50 | 2–6 Ma |
| 35 | 1.07 | 1.49 | <7.5 Ma | Cercopithecoides | 1.18 | 1.67 | 2–5 Ma |
| 35 | 1.07 | 1.49 | <7.5 Ma | Kuseracolobus | 1.17 | 1.75 | 4–4.4 Ma |
| 35 | 1.07 | 1.49 | <7.5 Ma | Libypithecus | 1.14 | 1.41 | 5 Ma |
| ASR Tip | MMC | PMM | Molecular Divergence | Possible Fossil Representative | MMC Value | PMM Value | Geological Age |
| Chlorocebus aethiops | 0.96 | 1.48 | 1 Ma | cf. Chlorocebus (Ethiopia) | 0.98 | 1.56 | 100–600 ka |
| Colobus guereza | 1.08 | 1.47 | <1.6 Ma | Colobus sp. (Ethiopia) | 1.06 | 1.44 | 100–600 ka |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monson, T.A.; Brasil, M.F.; Mahaney, M.C.; Schmitt, C.A.; Taylor, C.E.; Hlusko, L.J. Keeping 21st Century Paleontology Grounded: Quantitative Genetic Analyses and Ancestral State Reconstruction Re-Emphasize the Essentiality of Fossils. Biology 2022, 11, 1218. https://doi.org/10.3390/biology11081218
Monson TA, Brasil MF, Mahaney MC, Schmitt CA, Taylor CE, Hlusko LJ. Keeping 21st Century Paleontology Grounded: Quantitative Genetic Analyses and Ancestral State Reconstruction Re-Emphasize the Essentiality of Fossils. Biology. 2022; 11(8):1218. https://doi.org/10.3390/biology11081218
Chicago/Turabian StyleMonson, Tesla A., Marianne F. Brasil, Michael C. Mahaney, Christopher A. Schmitt, Catherine E. Taylor, and Leslea J. Hlusko. 2022. "Keeping 21st Century Paleontology Grounded: Quantitative Genetic Analyses and Ancestral State Reconstruction Re-Emphasize the Essentiality of Fossils" Biology 11, no. 8: 1218. https://doi.org/10.3390/biology11081218
APA StyleMonson, T. A., Brasil, M. F., Mahaney, M. C., Schmitt, C. A., Taylor, C. E., & Hlusko, L. J. (2022). Keeping 21st Century Paleontology Grounded: Quantitative Genetic Analyses and Ancestral State Reconstruction Re-Emphasize the Essentiality of Fossils. Biology, 11(8), 1218. https://doi.org/10.3390/biology11081218






