Estimation of Age-at-Death Using Cortical Bone Histomorphometry of the Rib and Femur: A Validation Study on a British Population
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample
2.2. Sample Preparation and Data Acquisition
2.3. Statistical Analysis
3. Results
3.1. Intra-Observer Error
3.2. Rib Analysis
3.2.1. Histomorphometric Analysis
3.2.2. Age Estimation Methods
3.3. Femur Analysis
3.3.1. Histomorphometric Analysis
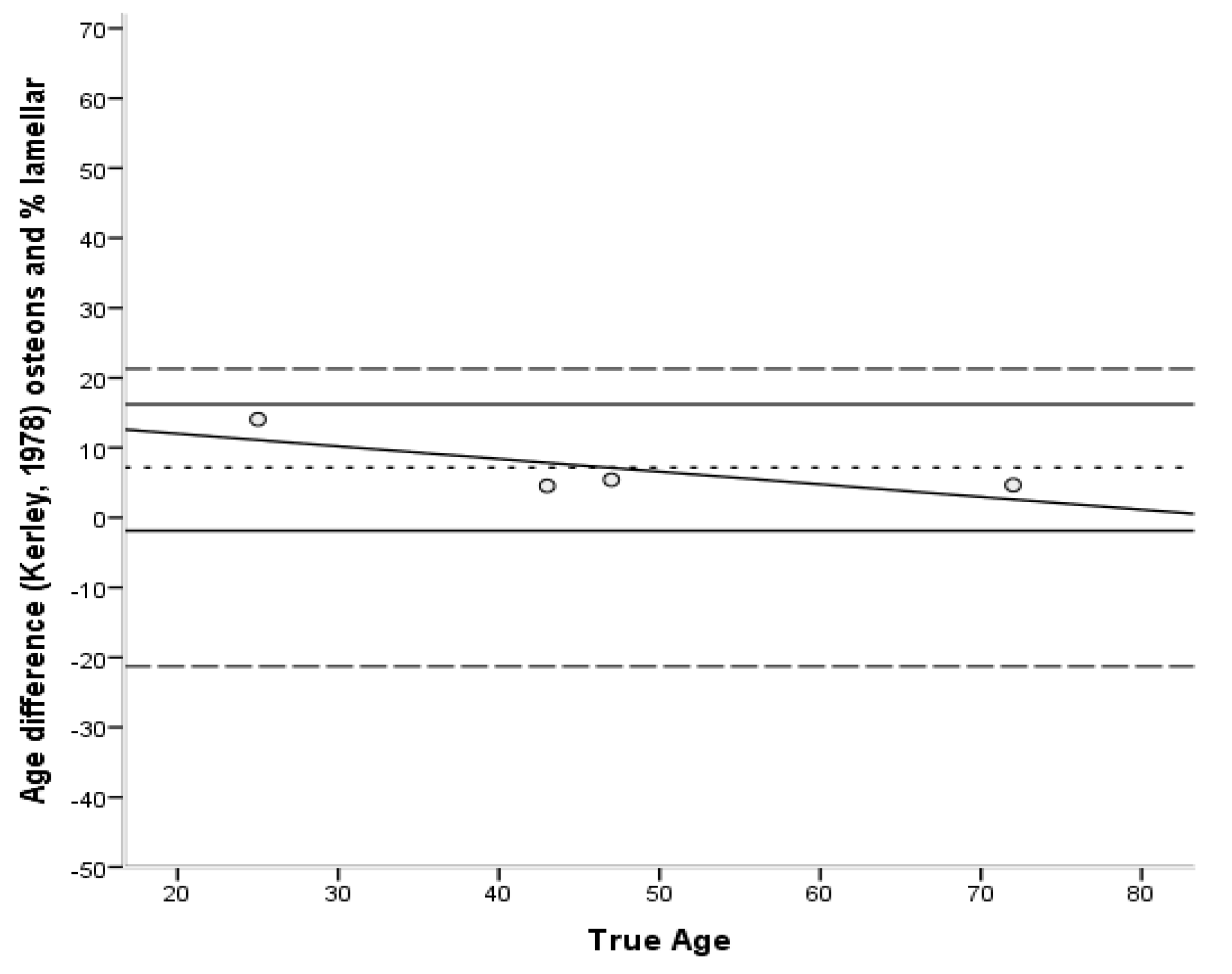
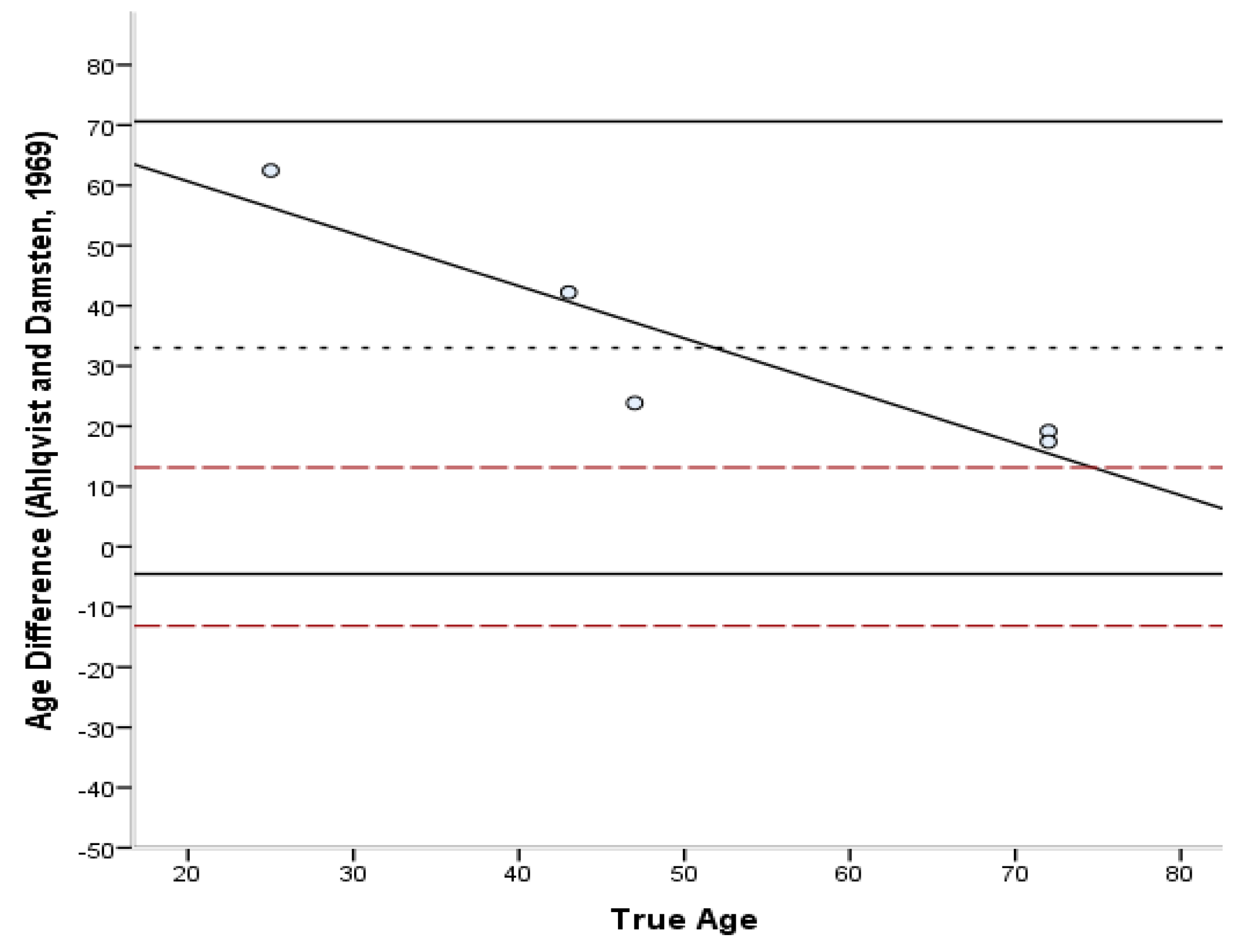
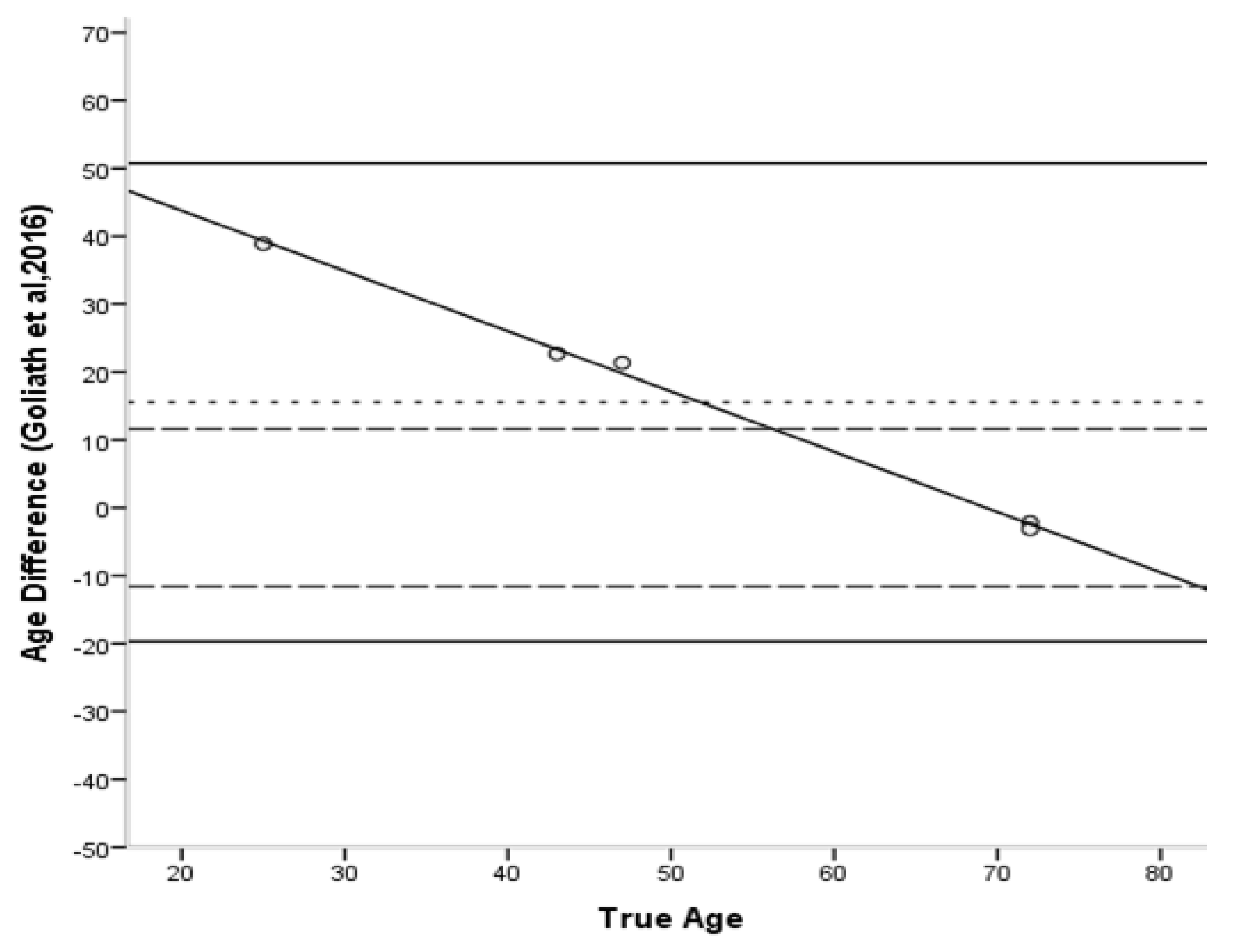
3.3.2. Age Estimation Methods
3.4. Differences in Femur and Rib Histomorphometrics
4. Discussion
4.1. Histomorphomeric Analysis
4.2. Histological Methods
4.2.1. Rib Methods
4.2.2. Femur Methods
4.3. Ribs or Femora?
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Results of the Age-Estimation Methods for the Rib and Femur Sample
| Rib Code | Real Age | Stout and Paine [28] Estimated Age | Stout et al. [26] Estimated Age | Cho et al. [7] Estimated Age | Goliath et al. [16] Estimated Age |
|---|---|---|---|---|---|
| 4 | 1.5 | 16.2 | 20.3 | 11.1 | 59.4 |
| 39 | 2.8 | 19.9 | 27.0 | 46.3 | 50.3 |
| 16 | 27.0 | 27.3 | 44.1 | 43.4 | 62.5 |
| 18 | 28.0 | 23.9 | 35.8 | 38.5 | 59.3 |
| 20 | 29.0 | 22.5 | 32.5 | 36.5 | 53.8 |
| 6 | 38.0 | 23.7 | 35.4 | 24.2 | 75.3 |
| 7 | 38.0 | 30.3 | 51.4 | 47.4 | 65.5 |
| 11 | 42.0 | 26.2 | 41.2 | 42.2 | 81.6 |
| 8 | 43.0 | 25.0 | 38.3 | 32.1 | 81.7 |
| 2 | 69.0 | 41.5 | 79.9 | 55.6 | 77.8 |
| 5 | 69.0 | 42.7 | 82.7 | 54.9 | 78.3 |
| Femur Code | Real Age | Kerley Osteon eq. [33] Estimated Age | Kerley %lamellar eq. [33] Estimated Age | Kerley Average Value [33] Estimated Age | Ahlqvist and Damsten [34] Estimated Age | Goliath et al. [16] Estimated Age |
|---|---|---|---|---|---|---|
| 29 | 25.0 | 39.8 | 68.0 | 53.9 | 87.5 | 63.9 |
| 24 | 43.0 | 53.7 | 62.7 | 58.2 | 85.2 | 65.7 |
| 34 | 47.0 | 53.7 | 64.5 | 59.1 | 70.9 | 68.4 |
| 26 | 72.0 | 60.2 | 69.6 | 64.9 | 91.2 | 69.8 |
| 33 | 72.0 | 30.6 | 70.4 | 50.5 | 89.4 | 68.9 |
References
- Lovejoy, C.O.; Meindl, R.S.; Pryzbeck, T.R.; Mensforth, R.P. Chronological Metamorphosis of the Auricular Surface of the Ilium: A New Method for the Determination of Adult Skeletal Age at Death. Am. J. Phys. Anthropol. 1985, 68, 15–28. [Google Scholar] [CrossRef] [PubMed]
- Meindl, R.S.; Lovejoy, C.O. Ectocranial Suture Closure: A Revised Method for the Determination of Skeletal Age at Death Based on the Lateral-Anterior Sutures. Am. J. Phys. Anthropol. 1985, 68, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Brooks, S.; Suchey, J. Skeletal Age Determination Based on the Os Pubis: A Comparison of the Acsadi-Nemeskeri and Suchey-Brooks Methods. J. Hum. Evol. 1990, 5, 227–238. [Google Scholar] [CrossRef]
- İşcan, M.Y.; Loth, S.R.; Wright, R.K. Metamorphosis at the Sternal Rib End: A New Method to Estimate Age at Death in White Males. Am. J. Phys. Anthropol. 1984, 65, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Singh, I.J.; Gunberg, D.L. Estimation of Age at Death in Human Males from Quantitative Histology of Bone Fragments. Am. J. Phys. Anthropol. 1970, 33, 373–381. [Google Scholar] [CrossRef]
- Márquez-Grant, N. An Overview of Age Estimation in Forensic Anthropology: Perspectives and Practical Considerations. Ann. Hum. Biol. 2015, 42, 308–322. [Google Scholar] [CrossRef]
- Cho, H.; Stout, S.D.; Madsen, R.W.; Streeter, M.A. Population-Specific Histological Age-Estimating Method: A Model for Known African-American and European-American Skeletal Remains. J. Forensic Sci. 2002, 47, 12–18. [Google Scholar] [CrossRef]
- García-Donas, J.G.; Paine, R.R.; Bonicelli, A.; Kranioti, E.F. Age Estimation for Two Mediterranean Populations: Rib Histomorphometry Applied to Forensic Identification and Bone Remodelling Research. Int. J. Legal Med. 2022, 136, 1469–1481. [Google Scholar] [CrossRef]
- Clarke, B. Normal Bone Anatomy and Physiology. Clin. J. Am. Soc. Nephrol. 2008, 3, S131–S139. [Google Scholar] [CrossRef] [Green Version]
- Kular, J.; Tickner, J.; Chim, S.M.; Xu, J. An Overview of the Regulation of Bone Remodelling at the Cellular Level. Clin. Biochem. 2012, 45, 863–873. [Google Scholar] [CrossRef]
- Robling, A.G.; Stout, S.D. Histomorphometry of Human Cortical Bone: Applications to Age Estimation. In Biological Anthropology of the Human Skeleton; Katzenberg, M.A., Saunders, S.R., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; pp. 149–182. ISBN 978-0-470-24584-2. [Google Scholar]
- Kerley, E.R. The Microscopic Determination of Age in Human Bone. Am. J. Phys. Anthropol. 1965, 23, 149–163. [Google Scholar] [CrossRef] [PubMed]
- Ortner, D.J. Aging Effects on Osteon Remodeling. Calcif. Tissue Res. 1975, 18, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Crowder, C.; Heinrich, J.; Stout, S.D. Rib Histomorphometry for Adult Age Estimation. In Forensic Microscopy for Skeletal Tissues; Bell, L.S., Ed.; Humana Press: Totowa, NJ, USA, 2012; Volume 915, pp. 109–127. ISBN 978-1-61779-976-1. [Google Scholar]
- Currey, J.D. Some Effects of Ageing in Human Haversian Systems. J. Anat. 1964, 98, 69–75. [Google Scholar] [PubMed]
- Goliath, J.R.; Stewart, M.C.; Stout, S.D. Variation in Osteon Histomorphometrics and Their Impact on Age-at-Death Estimation in Older Individuals. Forensic Sci. Int. 2016, 262, 282.e1–282.e6. [Google Scholar] [CrossRef]
- Cummaudo, M.; Cappella, A.; Biraghi, M.; Raffone, C.; Màrquez-Grant, N.; Cattaneo, C. Histomorphological Analysis of the Variability of the Human Skeleton: Forensic Implications. Int. J. Legal Med. 2018, 132, 1493–1503. [Google Scholar] [CrossRef] [Green Version]
- Chan, A.H.W.; Crowder, C.M.; Rogers, T.L. Variation in Cortical Bone Histology within the Human Femur and Its Impact on Estimating Age at Death. Am. J. Phys. Anthropol. 2007, 132, 80–88. [Google Scholar] [CrossRef] [PubMed]
- Cummaudo, M.; Raffone, C.; Cappella, A.; Márquez-Grant, N.; Cattaneo, C. Histomorphometric Analysis of the Variability of the Human Skeleton: Forensic Implications. Leg. Med. 2020, 45, 101711. [Google Scholar] [CrossRef]
- Hillier, M.L.; Bell, L.S. Differentiating Human Bone from Animal Bone: A Review of Histological Methods. J. Forensic Sci. 2007, 52, 249–263. [Google Scholar] [CrossRef]
- Frost, H.M. A 2003 Update of Bone Physiology and Wolff’s Law for Clinicians. Angle Orthod. 2004, 74, 3–15. [Google Scholar]
- Skedros, J.G.; Su, S.C.; Bloebaum, R.D. Biomechanical Implications of Mineral Content and Microstructural Variations in Cortical Bone of Horse, Elk, and Sheep Calcanei. Anat. Rec. 1997, 249, 297–316. [Google Scholar] [CrossRef]
- Pollitzer, W.S.; Anderson, J.J. Ethnic and Genetic Differences in Bone Mass: A Review with a Hereditary vs Environmental Perspective. Am. J. Clin. Nutr. 1989, 50, 1244–1259. [Google Scholar] [CrossRef] [PubMed]
- Heaney, R.P.; Recker, R.R.; Saville, P.D. Menopausal Changes in Bone Remodeling. J. Lab. Clin. Med. 1978, 92, 964–970. [Google Scholar] [CrossRef]
- Parfitt, A.M. Quantum Concept of Bone Remodeling and Turnover: Implications for the Pathogenesis of Osteoporosis. Calcif. Tissue Int. 1979, 28, 1–5. [Google Scholar] [CrossRef]
- Stout, S.D.; Dietze, W.H.; Işcan, M.Y.; Loth, S.R. Estimation of Age at Death Using Cortical Histomorphometry of the Sternal End of the Fourth Rib. J. Forensic Sci. 1994, 39, 778–784. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-S.; Kim, D.-I.; Park, D.-K.; Lee, J.-H.; Chung, N.-E.; Lee, W.-T.; Han, S.-H. Assessment of Histomorphological Features of the Sternal End of the Fourth Rib for Age Estimation in Koreans. J. Forensic Sci. 2007, 52, 1237–1242. [Google Scholar] [CrossRef] [PubMed]
- Stout, S.D.; Paine, R.R. Histological Age Estimation Using Rib and Clavicle. Am. J. Phys. Anthropol. 1992, 87, 111–115. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, V.M.; Agnew, A.M. Examination of Factors Potentially Influencing Osteon Size in the Human Rib. Anat. Rec. 2016, 299, 313–324. [Google Scholar] [CrossRef] [PubMed]
- Klepinger, L.L. Fundamentals of Forensic Anthropology; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-471-21006-1. [Google Scholar]
- Lazenby, R.A. Inherent Deficiencies in Cortical Bone Microstructural Age Estimation Techniques. Ossa 1984, 9–11, 95–103. [Google Scholar]
- Crowder, C.M. Evaluating the Use of Quantitative Bone Histology to Estimate Adult Age at Death. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2005. [Google Scholar]
- Kerley, E.R.; Ubelaker, D.H. Revisions in the Microscopic Method of Estimating Age at Death in Human Cortical Bone. Am. J. Phys. Anthropol. 1978, 49, 545–546. [Google Scholar] [CrossRef]
- Ahlqvist, J.; Damsten, O. A Modification of Kerley’s Method for the Microscopic Determination of Age in Human Bone. J. Forensic Sci. 1969, 14, 205–212. [Google Scholar]
- García-Donas, J.G.; Dalton, A.; Chaplin, I.; Kranioti, E.F. A Revised Method for the Preparation of Dry Bone Samples Used in Histological Examination: Five Simple Steps. HOMO 2017, 68, 283–288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crowder, C.; Rosella, L. Assessment of Intra- and Intercostal Variation in Rib Histomorphometry: Its Impact on Evidentiary Examination. J. Forensic Sci. 2007, 52, 271–276. [Google Scholar] [CrossRef] [PubMed]
- García-Donas, J.G.; Dyke, J.; Paine, R.R.; Nathena, D.; Kranioti, E.F. Accuracy and Sampling Error of Two Age Estimation Techniques Using Rib Histomorphometry on a Modern Sample. J. Forensic Leg. Med. 2016, 38, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Guitar, B. Stuttering: An Integrated Approach to Its Nature and Treatment; Lippincott Williams & Wilkins: Baltimore, MD, USA, 2006; ISBN 978-0-7817-3920-7. [Google Scholar]
- Ulijaszek, S.J.; Kerr, D.A. Anthropometric Measurement Error and the Assessment of Nutritional Status. Br. J. Nutr. 1999, 82, 165–177. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S.M.; Scott, N.M.; Neiswanger, K.; Marazita, M.L. Intraobserver Error Associated with Measurements of the Hand. Am. J. Hum. Biol. 2005, 17, 368–371. [Google Scholar] [CrossRef]
- Ward, R.E.; Jamison, P.L. Measurement Precision and Reliability in Craniofacial Anthropometry: Implications and Suggestions for Clinical Applications. J. Craniofac. Genet. Dev. Biol. 1991, 11, 156–164. [Google Scholar]
- Student The Probable Error of a Mean. Biometrika 1908, 6, 1–25. [CrossRef]
- Glass, G.V.; Peckham, P.D.; Sanders, J.R. Consequences of Failure to Meet Assumptions Underlying the Fixed Effects Analyses of Variance and Covariance. Rev. Educ. Res. 1972, 42, 237–288. [Google Scholar] [CrossRef]
- Lovejoy, C.O.; Meindl, R.S.; Mensforth, R.P.; Barton, T.J. Multifactorial Determination of Skeletal Age at Death: A Method and Blind Tests of Its Accuracy. Am. J. Phys. Anthropol. 1985, 68, 1–14. [Google Scholar] [CrossRef]
- Altman, D.G.; Bland, J.M. Measurement in Medicine: The Analysis of Method Comparison Studies. Statistician 1983, 32, 307–317. [Google Scholar] [CrossRef]
- Aiello, L.C.; Molleson, T. Are Microscopic Ageing Techniques More Accurate than Macroscopic Ageing Techniques? J. Archaeol. Sci. 1993, 20, 689–704. [Google Scholar] [CrossRef]
- Crowder, C.M.; Pfeiffer, S. The Application of Cortical Bone Histomorphometry to Estimate Age at Death. In Age Estimation of the Human Skeleton; Latham, K.E., Finnegan, M., Eds.; Charles C Thomas Pub Ltd.: Springfield, IL, USA, 2010; ISBN 978-0-398-07950-5. [Google Scholar]
- Gocha, T.P.; Agnew, A.M. Spatial Variation in Osteon Population Density at the Human Femoral Midshaft: Histomorphometric Adaptations to Habitual Load Environment. J. Anat. 2016, 228, 733–745. [Google Scholar] [CrossRef] [PubMed]
- Miszkiewicz, J.J.; Mahoney, P. Histomorphometry and Cortical Robusticity of the Adult Human Femur. J. Bone Miner. Metab. 2018, 37, 90–104. [Google Scholar] [CrossRef] [PubMed]
- Miszkiewicz, J.J.; Mahoney, P. Ancient Human Bone Microstructure in Medieval England: Comparisons between Two Socio-Economic Groups: Ancient Human Bone Microstructure and Social Status. Anat. Rec. 2016, 299, 42–59. [Google Scholar] [CrossRef]
- Marotti, G. Map of Bone Formation Rate Values Recorded throughout the Skeleton of the Dog. In Bone Morphometry; Jaworski, Z.F.G., Ed.; University of Ottawa Press: Ottawa, ON, Canada, 1976; pp. 202–207. [Google Scholar]
- Mulhern, D.M. Rib Remodeling Dynamics in a Skeletal Population from Kulubnarti, Nubia. Am. J. Phys. Anthropol. 2000, 111, 519–530. [Google Scholar] [CrossRef]
- Cho, H.; Stout, S.D. Age-Associated Bone Loss and Intraskeletal Variability in the Imperial Romans. J. Anthropol. Sci. 2011, 89, 109–125. [Google Scholar] [CrossRef]
- Pfeiffer, S. Variability in Osteon Size in Recent Human Populations. Am. J. Phys. Anthropol. 1998, 106, 219–227. [Google Scholar] [CrossRef]
- Pfeiffer, S. Palaeohistology: Health and Disease. In The Biological Anthropology of the Human Skeleton; Katzenberg, M.A., Saunders, S.R., Eds.; Wiley-Blackwell: New York, NY, USA, 2000; pp. 287–302. ISBN 978-0-471-31616-9. [Google Scholar]
- Eleazer, C.D.; Jankauskas, R. Mechanical and Metabolic Interactions in Cortical Bone Development. Am. J. Phys. Anthropol. 2016, 160, 317–333. [Google Scholar] [CrossRef]
- Britz, H.M.; Thomas, C.D.L.; Clement, J.G.; Cooper, D.M.L. The Relation of Femoral Osteon Geometry to Age, Sex, Height and Weight. Bone 2009, 45, 77–83. [Google Scholar] [CrossRef]
- Goliath, J. Variation in Osteon Circularity and Its Impact on Estimating Age at Death. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2010. [Google Scholar]
- Goldman, H.M.; Hampson, N.A.; Guth, J.J.; Lin, D.; Jepsen, K.J. Intracortical Remodeling Parameters Are Associated With Measures of Bone Robustness: Intracortical Remodeling and Bone Robustness. Anat. Rec. 2014, 297, 1817–1828. [Google Scholar] [CrossRef] [Green Version]
- Pitfield, R.; Deter, C.; Mahoney, P. Bone Histomorphometric Measures of Physical Activity in Children from Medieval England. Am. J. Phys. Anthropol. 2019, 169, 730–746. [Google Scholar] [CrossRef] [PubMed]
- Streeter, M. The Determination of Age in Subadult from the Rib Cortical Microstructure. In Forensic Microscopy for Skeletal Tissues; Bell, L.S., Ed.; Humana Press: Totowa, NJ, USA, 2012; Volume 915, pp. 101–108. ISBN 978-1-61779-976-1. [Google Scholar]
- García-Donas, J.G.; Bonicelli, A.; Scholl, A.R.; Lill, C.; Paine, R.R.; Kranioti, E.F. Rib Histomorphometry: A Reliability and Validation Study with a Critical Review of Histological Techniques for Forensic Age Estimation. Leg. Med. 2021, 49, 101827. [Google Scholar] [CrossRef] [PubMed]
- Dudar, J.C.; Pfeiffer, S.; Saunders, S.R. Evaluation of Morphological and Histological Adult Skeletal Age-at-Death Estimation Techniques Using Ribs. J. Forensic Sci. 1993, 38, 677–685. [Google Scholar] [CrossRef]
- Smith, R.J. Logarithmic Transformation Bias in Allometry. Am. J. Phys. Anthropol. 1993, 90, 215–228. [Google Scholar] [CrossRef]
- Zaki, R.; Bulgiba, A.; Ismail, R.; Ismail, N.A. Statistical Methods Used to Test for Agreement of Medical Instruments Measuring Continuous Variables in Method Comparison Studies: A Systematic Review. PLoS ONE 2012, 7, e37908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfeiffer, S.; Lazenby, R.; Chiang, J. Brief Communication: Cortical Remodeling Data Are Affected by Sampling Location. Am. J. Phys. Anthropol. 1995, 96, 89–92. [Google Scholar] [CrossRef]
- Lazenby, R. Continuing periosteal apposition I: Documentation, hypotheses, and interpretation. Am. J. Phys. Anthropol. 1990, 82, 451–472. [Google Scholar] [CrossRef]







| Sample No | Sex | Age |
|---|---|---|
| Rib_4 | - | 1.5 y |
| Rib_39 | F | 2.8 y |
| Rib_16 | F | 27 y |
| Rib_18 | F | 28 y |
| Rib_20 | M | 29 y |
| Rib_6 | M | 38 y |
| Rib_7 | M | 38 y |
| Rib_11 | M | 42 y |
| Rib_8 1 | M | 43 y |
| Rib_2 | F | 69 y |
| Rib_5 | F | 69 y |
| Femur_29 | M | 25 y |
| Femur_24 1 | M | 43 y |
| Femur_34 | M | 47 y |
| Femur_26 | M | 72 y |
| Femur_33 | M | 72 y |
| Histomorphometric Variable | Definition for Rib Methods | Definition for Femur Methods |
|---|---|---|
| Cortical area | the total area of the cortex in mm2 | the total area of the cortex in mm2 |
| Intact osteon number (N.On) | - | the total number of osteons that have an intact Haversian canal and can be recognized over 80% of their area, counted in all four fields [12,33] |
| Fragmented osteon number (N.On.Fg) | - | the number of remodelled osteons counted in all four fields [12,33] |
| Non-Haversian Canals | - | the number of primary vascular canals counted in all four fields [12,33] |
| The percentage of circumferential lamellar bone (% lamellar bone) | - | the amount of un-remodelled lamellar bone divided by the total field area, averaged for all four fields [12,33] |
| Intact osteon density (OPDI): | the number of osteons whose canals’ perimeter shows less than 10% of bone resorption per mm2 of cortical area [7,16,26,28] | intact osteon number (N.On) [12,33] per mm2 of cortical area [16] |
| Fragmentary osteon density (OPDF) | the number of remodelled osteons whose canals’ perimeter shows more than 10% of bone resorption, per mm2 of cortical area. Fragments without visible canal were also counted [7,16,26,28] | fragmented osteon number (N.On.F) [12,33] per mm2 of cortical area [16] |
| Osteon population density (OPD): | the sum of OPDI and OPDF [7,16,26,28] | the sum of OPDI and OPDF [16] |
| Osteon Area (On.Ar) | the area in mm2 occupied by a structurally complete osteon, including the Haversian canal [7,16] | the area in mm2 occupied by a structurally complete osteon, including the Haversian canal [16] |
| Relative Cortical Area (Ct.Ar/Tt.Ar) | the cortical area divided by the total area of the cross-section [7] | - |
| Osteon Circularity (On.Cr) | the degree of similarity of the osteon shape to a true circle defined by the index: (4 π(area/perimeter2)) [16] | the degree of similarity of the osteon shape to a true circle defined by the index: (4 π(area/perimeter2)) [16] |
| The percentage of osteonal bone (% osteonal bone) | - | the area occupied by osteons and osteon fragments in relation to the total evaluated area [34] |
| Variable | TEM | %TEM | R |
|---|---|---|---|
| On.N | 5.59 | 2.64 | 0.89 |
| On.N.Fg | 8.02 | 2.28 | 0.97 |
| Tt.Ar | 0.21 | 0.28 | 1.00 |
| Es.Ar | 0.14 | 0.28 | 1.00 |
| Ct.Ar | 0.18 | 0.70 | 0.99 |
| OPDI | 0.19 | 2.31 | 0.96 |
| OPDF | 0.30 | 2.14 | 0.99 |
| OPD | 0.21 | 0.95 | 0.99 |
| On.Ar | 0.002 | 4.08 | 0.99 |
| On.Cr | 0.01 | 0.60 | 0.97 |
| Ct.Ar/Tt.Ar | 0.002 | 0.54 | 0.99 |
| Variable | Stout and Paine [28] | Stout et al. [26] | Cho et al. [7] | Goliath et al. [16] | Current Sample | |
|---|---|---|---|---|---|---|
| Age | Mean | 28.600 | 39.200 | 37.824 | 62.960 | 35.200 |
| SD | 12.900 | 19.090 | 2.413 | 10.215 | 21.800 | |
| Min | 13.000 | 11.000 | 17.000 | 39.000 | 1.500 | |
| Max | 62.000 | 88.000 | 82.000 | 82.000 | 69.000 | |
| OPD | Mean | 18.030 | 16.010 | 20.071 | 23.590 | 18.110 |
| SD | 7.180 | SEM: 0.750 | 0.975 | 5.930 | 5.640 | |
| Min | - | - | - | 13.440 | 8.660 | |
| Max | - | - | - | 42.330 | 27.720 | |
| On.Ar. | Mean | - | - | 0.039 | 0.024 | 0.035 |
| SD | - | - | 0.001 | 0.009 | 0.220 | |
| Min | - | - | - | 0.012 | 0.005 | |
| Max | - | - | - | 0.043 | 0.155 | |
| Ct.Ar/Tt.Ar | Mean | - | - | 0.343 | - | 0.430 |
| SD | - | - | 0.023 | - | 0.139 | |
| Min | - | - | - | - | 0.215 | |
| Max | - | - | - | - | 0.750 | |
| On.Cr | Mean | - | - | - | 0.905 | 0.915 |
| SD | - | - | - | 0.014 | 0.463 | |
| Min | - | - | - | 0.864 | 0.636 | |
| Max | - | - | - | 0.924 | 0.981 |
| Males | Females | Pooled Data | ||||
|---|---|---|---|---|---|---|
| Variable | Mean | SD | Mean | SD | Mean | SD |
| OPD | 17.516 | 2.228 | 20.598 | 6.640 | 18.112 | 5.640 |
| On.Ar | 0.036 | 0.008 | 0.029 | 0.006 | 0.035 | 0.220 |
| On.Cr | 0.920 | 0.020 | 0.910 | 0.020 | 0.915 | 0.463 |
| Ct.Ar/Tt.Ar | 0.409 | 0.065 | 0.388 | 0.123 | 0.430 | 0.139 |
| Stout and Paine [28] | Stout et al. [26] | Cho et al. [7] | Goliath et al. [16] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group | Bias | Inac | Rang | Bias | Inac | Rang | Bias | Inac | Rang | Bias | Inac | Rang |
| Juvenile | 15.9 | 15.9 | 14.7–17.2 | 21.5 | 21.5 | 18.8–24.3 | 26.6 | 26.6 | 9.6–43.5 | 52.7 | 52.7 | 47.5–57.9 |
| <40 | −6.5 | 6.6 | 0.3–4.3 | 7.8 | 8.9 | 2.6–17.1 | 6.0 | 11.5 | 7.5–16.4 | 31.3 | 31.3 | 24.8–37.3 |
| >40 | −21.9 | 21.9 | 15.8–27.5 | 4.8 | 7.5 | 0.8–13.7 | −9.6 | 9.7 | 0.2–14.1 | 24.1 | 24.1 | 8.8–39.6 |
| Total | −8.0 | 13.9 | 0.3–27.5 | 9.2 | 10.7 | 0.8–4.3 | 4.1 | 13.6 | 0.2–43.5 | 32.6 | 32.6 | 8.8–57.9 |
| Stout and Paine [28] | Stout et al. [26] | Cho et al. [7] | Goliath et al. [16] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group | Bias | Inac | Rang | Bias | Inac | Rang | Bias | Inac | Rang | Bias | Inac | Rang |
| Males | −12.5 | 12.5 | 6.5–18 | 1.8 | 4.0 | 0.8–13.4 | −1.5 | 8.4 | 0.8–13.4 | 33.6 | 33.6 | 24.8–39.6 |
| Females | −8.1 | 15.1 | 0.3–27.5 | 14.7 | 14.7 | 7.8–24.3 | 8.6 | 19.6 | 10.5–43.5 | 26.5 | 26.5 | 8.8–47.5 |
| Total | −8.0 | 13.9 | 0.3–27.5 | 9.2 | 10.7 | 0.8–4.3 | 4.1 | 13.6 | 0.2–43.5 | 32.6 | 32.6 | 8.8–57.9 |
| Variable | Kerley [12,33] | Ahlqvist and Damsten [34] | Goliath et al. [16] | Current Sample | |
|---|---|---|---|---|---|
| Age | Mean | 41.600 | 55.000 | 62.960 | 51.800 |
| SD | - | - | 10.210 | 20.000 | |
| Min | 0.000 | - | 39.000 | 25.000 | |
| Max | 95.000 | - | 82.000 | 72.000 | |
| OPD | Mean | - | 24.320 | 23.880 | |
| SD | - | - | 5.550 | 2.150 | |
| Min | - | - | 15.660 | 21.480 | |
| Max | - | - | 41.100 | 25.970 | |
| On.Ar. | Mean | - | - | 0.034 | 0.047 |
| SD | - | - | 0.013 | 0.027 | |
| Min | - | - | 0.014 | 0.006 | |
| Max | - | - | 0.065 | 0.140 | |
| On.Cr | Mean | - | - | 0.906 | 0.933 |
| SD | - | - | 0.022 | 0.029 | |
| Min | - | - | 0.844 | 0.815 | |
| Max | - | - | 0.927 | 0.978 |
| Femur Code | Age | On.N.Fg | Age Estimation |
|---|---|---|---|
| 29 | 25 | 83 | 78.8 |
| 24 | 43 | 64 | 68.1 |
| 34 | 47 | 97 | 77.7 |
| 26 | 72 | 78 | 77.2 |
| 33 | 72 | 136 | 11.6 |
| Method | Bias | Inaccur. | Range |
|---|---|---|---|
| Kerley Osteons [33] | 5.1 | 11.0 | 6.7–14.8 |
| Kerley % lamellar [33] | 15.2 | 16.9 | 1.6–42.9 |
| Kerley Osteons + % lamellar [33] | 7.2 | 7.2 | 4.5–14.1 |
| Ahlqvist and Damsten [34] | 33.0 | 33.0 | 17.4–62.5 |
| Goliath et al. [16] | 15.5 | 17.6 | 2.2–38.9 |
| Bone | N | Mean | SD | Std. Error Mean | |
|---|---|---|---|---|---|
| OPD | femur | 5 | 23.884 | 2.156 | 0.964 |
| rib | 11 | 18.112 | 5.640 | 1.700 | |
| On.Ar | femur | 5 | 0.047 | 0.007 | 0.003 |
| rib | 11 | 0.035 | 0.009 | 0.0028 | |
| On.Cr | femur | 5 | 0.933 | 0.006 | 0.0029 |
| rib | 11 | 0.913 | 0.0195 | 0.0059 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karydi, C.; García-Donas, J.G.; Tsiminikaki, K.; Bonicelli, A.; Moraitis, K.; Kranioti, E.F. Estimation of Age-at-Death Using Cortical Bone Histomorphometry of the Rib and Femur: A Validation Study on a British Population. Biology 2022, 11, 1615. https://doi.org/10.3390/biology11111615
Karydi C, García-Donas JG, Tsiminikaki K, Bonicelli A, Moraitis K, Kranioti EF. Estimation of Age-at-Death Using Cortical Bone Histomorphometry of the Rib and Femur: A Validation Study on a British Population. Biology. 2022; 11(11):1615. https://doi.org/10.3390/biology11111615
Chicago/Turabian StyleKarydi, Christina, Julieta Gómez García-Donas, Konstantina Tsiminikaki, Andrea Bonicelli, Konstantinos Moraitis, and Elena F. Kranioti. 2022. "Estimation of Age-at-Death Using Cortical Bone Histomorphometry of the Rib and Femur: A Validation Study on a British Population" Biology 11, no. 11: 1615. https://doi.org/10.3390/biology11111615
APA StyleKarydi, C., García-Donas, J. G., Tsiminikaki, K., Bonicelli, A., Moraitis, K., & Kranioti, E. F. (2022). Estimation of Age-at-Death Using Cortical Bone Histomorphometry of the Rib and Femur: A Validation Study on a British Population. Biology, 11(11), 1615. https://doi.org/10.3390/biology11111615






