Quantitative Load Dependency Analysis of Local Trabecular Bone Microstructure to Understand the Spatial Characteristics in the Synthetic Proximal Femur
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
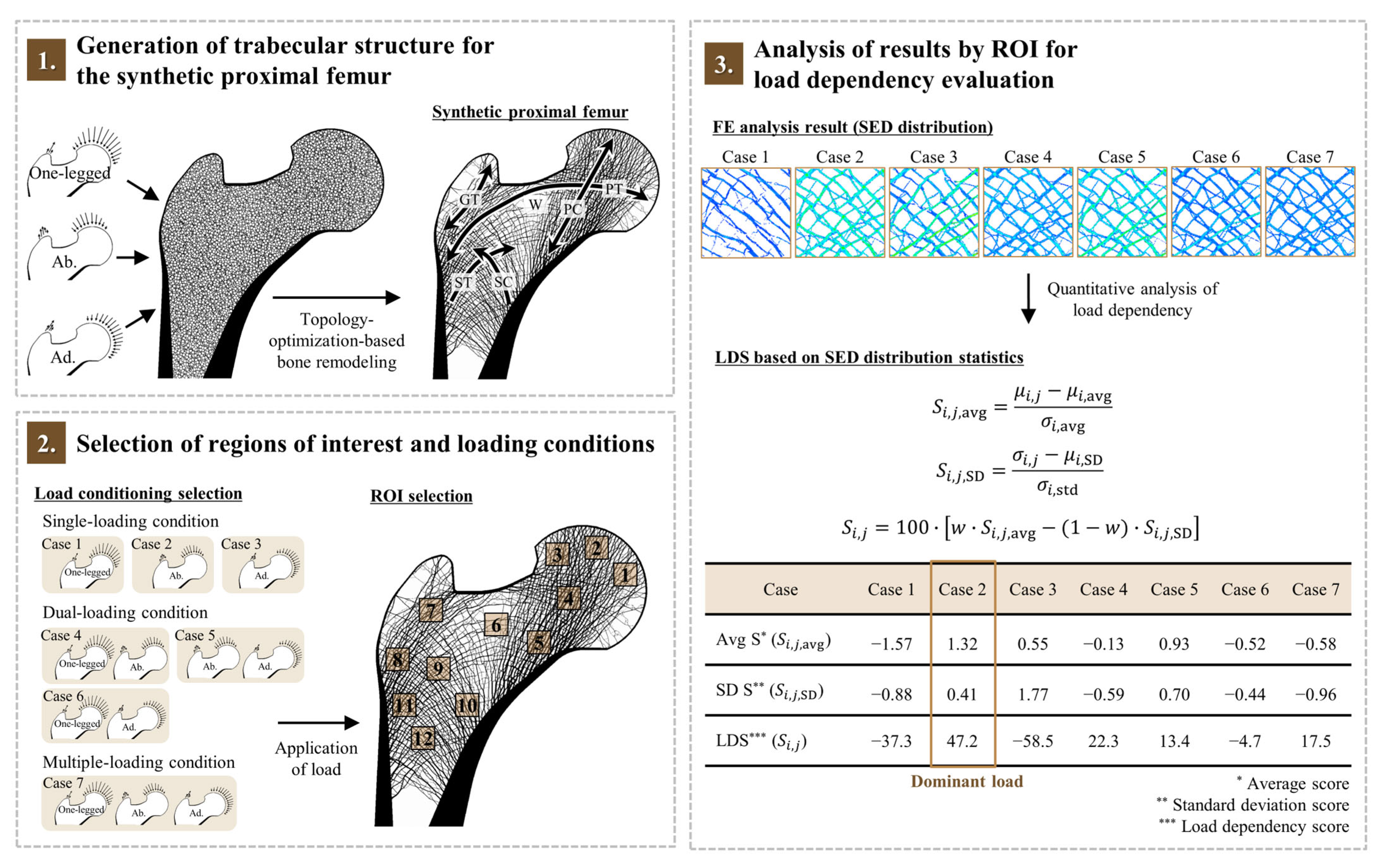
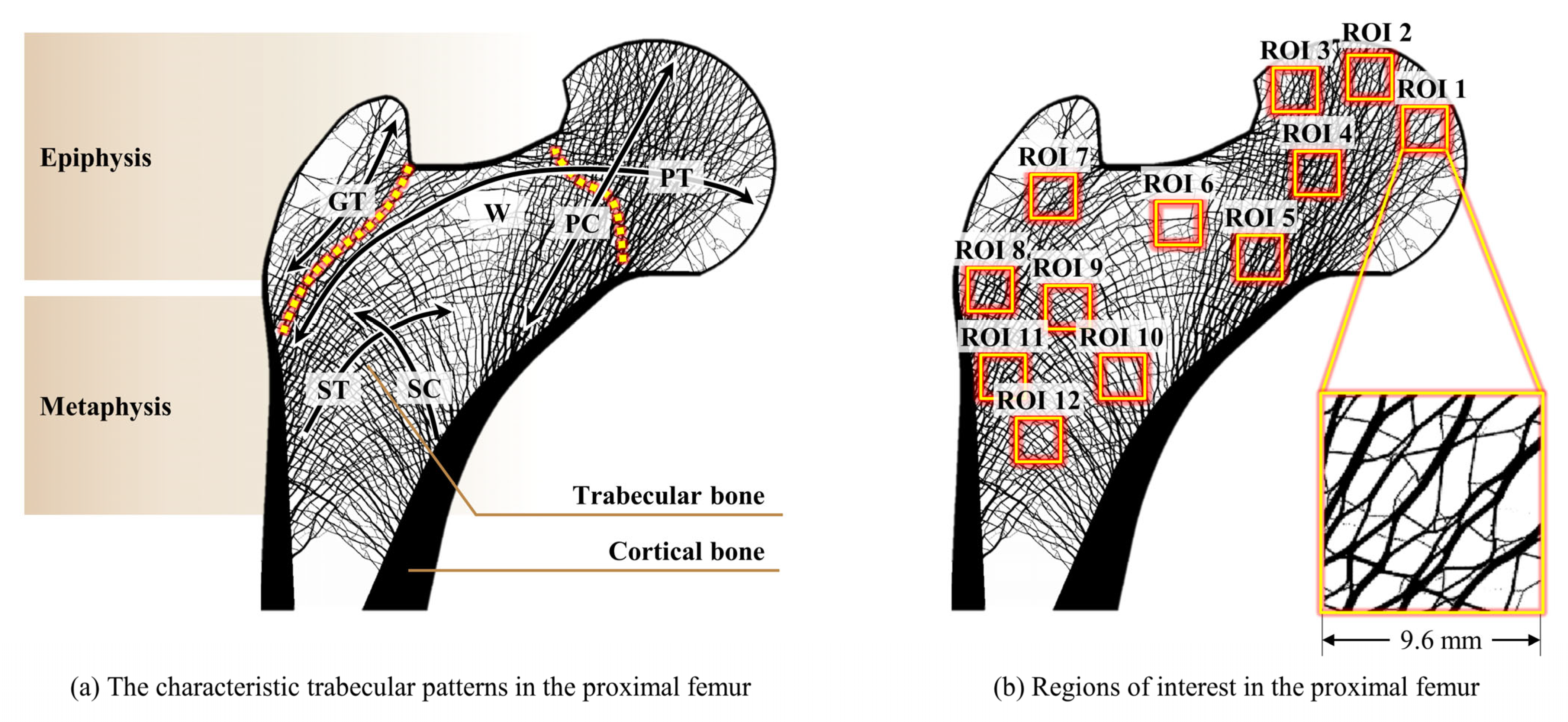
2.1. Generation of Trabecular Structure for the Synthetic Proximal Femur
2.2. Selection of Regions of Interest and Loading Conditions
2.3. Analysis of Results by ROI for Load Dependency Evaluation
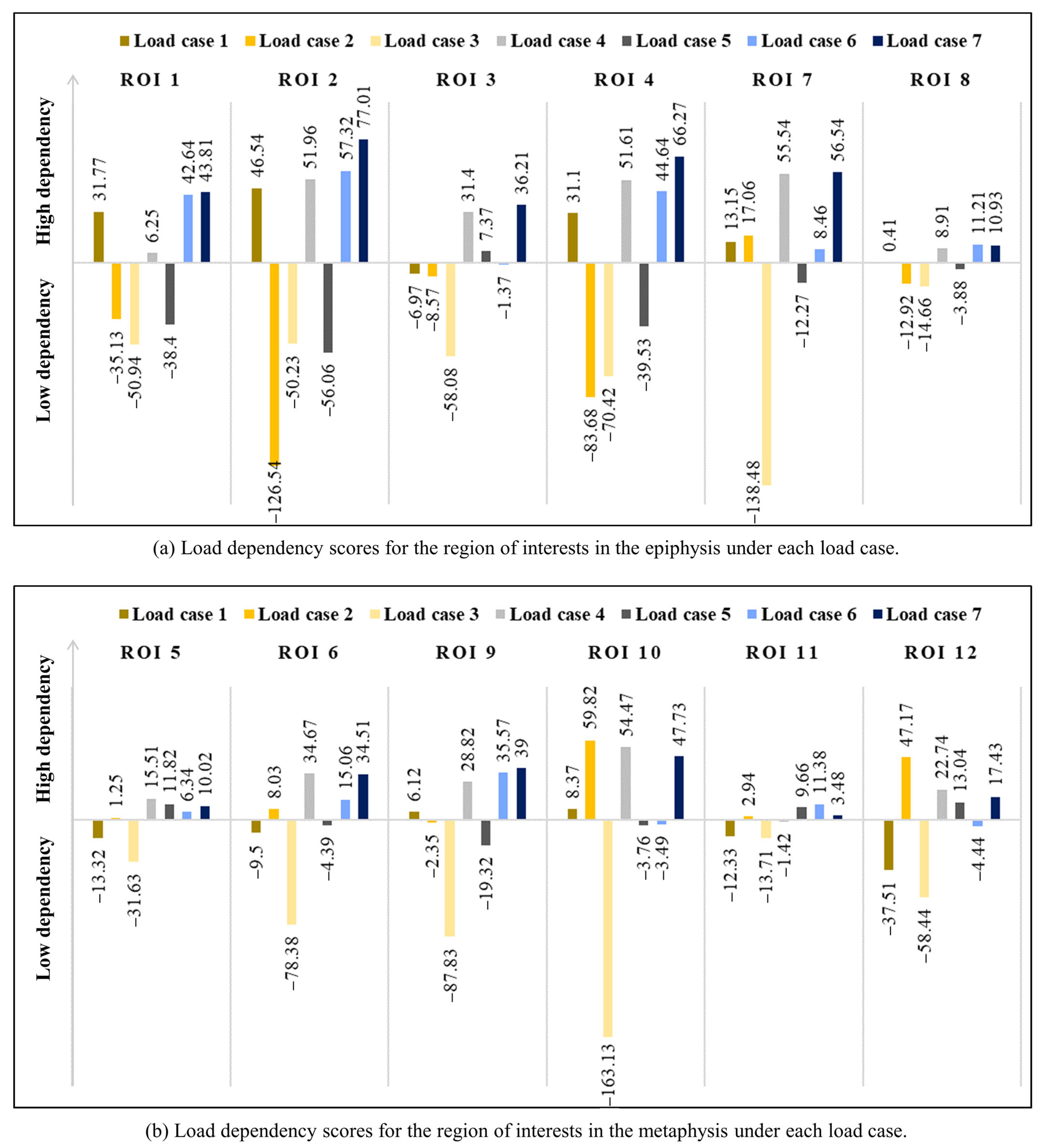
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Avg | Average |
| FE | Finite element |
| LDS | Load dependency score |
| ROI | Region of interest |
| S | Score |
| SD | Standard deviation |
| SED | Strain energy density |
References
- Raisz, L.G. Pathogenesis of Osteoporosis: Concepts, Conflicts, and Prospects. J. Clin. Investig. 2005, 115, 3318–3325. [Google Scholar] [CrossRef] [PubMed]
- Ward, F.O. Outlines of Human Osteology; Henry Renshaw: London, UK, 1876. [Google Scholar]
- Meyer, G.H. Von Archief Fur Den Anatomische Und Physiologischen Wissenschaften Im Medizin. Die Archit. Der Spongiosa 1867, 34, 615–628. [Google Scholar]
- Karl. , C. Die Graphische Statik; Meyer and Zeller: Zürich, Switzerland, 1866. [Google Scholar]
- Wolff, J. The Classic: On the Significance of the Architecture of the Spongy Substance for the Question of Bone Growth: A Preliminary Publication. Clin. Orthop. Relat. Res. 2011, 469, 3077–3078. [Google Scholar] [CrossRef]
- Cowin, S.C. (Ed.) Bone Mechanics Handbook; CRC Press: Boca Raton, FL, USA, 2001; Volume 240, ISBN 9780429125447. [Google Scholar]
- Pearson, O.M.; Lieberman, D.E. The Aging of Wolff’s “Law”: Ontogeny and Responses to Mechanical Loading in Cortical Bone. Am. J. Phys. Anthropol. 2004, 125, 63–99. [Google Scholar] [CrossRef]
- Frost, H.M. Bone “Mass” and the “Mechanostat”: A Proposal. Anat. Rec. 1987, 219, 1–9. [Google Scholar] [CrossRef]
- Garijo, N.; Martínez, J.; García-Aznar, J.M.; Pérez, M.A. Computational Evaluation of Different Numerical Tools for the Prediction of Proximal Femur Loads from Bone Morphology. Comput. Methods Appl. Mech. Eng. 2014, 268, 437–450. [Google Scholar] [CrossRef]
- Maïmoun, L.; Sultan, C. Effects of Physical Activity on Bone Remodeling. Metabolism 2011, 60, 373–388. [Google Scholar] [CrossRef] [PubMed]
- Borer, K.T. Physical Activity in the Prevention and Amelioration of Osteoporosis in Women. Sport. Med. 2005, 35, 779–830. [Google Scholar] [CrossRef]
- Zerwekh, J.E.; Ruml, L.A.; Gottschalk, F.; Pak, C.Y.C. The Effects of Twelve Weeks of Bed Rest on Bone Histology, Biochemical Markers of Bone Turnover, and Calcium Homeostasis in Eleven Normal Subjects. J. Bone Miner. Res. 2009, 13, 1594–1601. [Google Scholar] [CrossRef]
- Vico, L.; Chappard, D.; Palle, S.; Bakulin, A.V.; Novikov, V.E.; Alexandre, C. Trabecular Bone Remodeling after Seven Days of Weightlessness Exposure (BIOCOSMOS 1667). Am. J. Physiol. Integr. Comp. Physiol. 1988, 255, R243–R247. [Google Scholar] [CrossRef]
- Campoli, G.; Weinans, H.; Zadpoor, A.A. Computational Load Estimation of the Femur. J. Mech. Behav. Biomed. Mater. 2012, 10, 108–119. [Google Scholar] [CrossRef] [PubMed]
- Huiskes, R.; Weinans, H.; Grootenboer, H.J.; Dalstra, M.; Fudala, B.; Slooff, T.J. Adaptive Bone-Remodeling Theory Applied to Prosthetic-Design Analysis. J. Biomech. 1987, 20, 1135–1150. [Google Scholar] [CrossRef] [PubMed]
- Weinans, H.; Huiskes, R.; Grootenboer, H.J. The Behavior of Adaptive Bone-Remodeling Simulation Models. J. Biomech. 1992, 25, 1425–1441. [Google Scholar] [CrossRef] [PubMed]
- Mullender, M.G.; Huiskes, R.; Weinans, H. A Physiological Approach to the Simulation of Bone Remodeling as a Self-Organizational Control Process. J. Biomech. 1994, 27, 1389–1394. [Google Scholar] [CrossRef] [PubMed]
- Kameo, Y.; Miya, Y.; Hayashi, M.; Nakashima, T.; Adachi, T. In Silico Experiments of Bone Remodeling Explore Metabolic Diseases and Their Drug Treatment. Sci. Adv. 2020, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Adachi, T.; Tomita, Y.; Sakaue, H.; Tanaka, M. Simulation of Trabecular Surface Remodeling Based on Local Stress Nonuniformity. JSME Int. J. Ser. C 1997, 40, 782–792. [Google Scholar] [CrossRef]
- Adachi, T.; Tsubota, K.; Tomita, Y.; Hollister, S.J. Trabecular Surface Remodeling Simulation for Cancellous Bone Using Microstructural Voxel Finite Element Models. J. Biomech. Eng. 2001, 123, 403–409. [Google Scholar] [CrossRef]
- Tsubota, K.; Adachi, T.; Tomita, Y. Functional Adaptation of Cancellous Bone in Human Proximal Femur Predicted by Trabecular Surface Remodeling Simulation toward Uniform Stress State. J. Biomech. 2002, 35, 1541–1551. [Google Scholar] [CrossRef]
- Tsubota, K.; Suzuki, Y.; Yamada, T.; Hojo, M.; Makinouchi, A.; Adachi, T. Computer Simulation of Trabecular Remodeling in Human Proximal Femur Using Large-Scale Voxel FE Models: Approach to Understanding Wolff’s Law. J. Biomech. 2009, 42, 1088–1094. [Google Scholar] [CrossRef]
- Huiskes, R.; Ruimerman, R.; van Lenthe, G.H.; Janssen, J.D. Effects of Mechanical Forces on Maintenance and Adaptation of Form in Trabecular Bone. Nature 2000, 405, 704–706. [Google Scholar] [CrossRef]
- Ruimerman, R.; Hilbers, P.; van Rietbergen, B.; Huiskes, R. A Theoretical Framework for Strain-Related Trabecular Bone Maintenance and Adaptation. J. Biomech. 2005, 38, 931–941. [Google Scholar] [CrossRef] [PubMed]
- McNamara, L.M.; Prendergast, P.J. Bone Remodelling Algorithms Incorporating Both Strain and Microdamage Stimuli. J. Biomech. 2007, 40, 1381–1391. [Google Scholar] [CrossRef] [PubMed]
- Hollister, S.J.; Brennan, J.M.; Kikuchi, N. A Homogenization Sampling Procedure for Calculating Trabecular Bone Effective Stiffness and Tissue Level Stress. J. Biomech. 1994, 27, 433–444. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, P.R.; Rodrigues, H.C.; Jacobs, C.R.; Pellegrini, V.D. A Material Optimisation Model For Bone Remodelling Around Cementless Hip Stems. In Proceedings of the 9th European Conference on Computational Mechanics, Munich, Germany, 30 August–3 September 1999. [Google Scholar]
- Bagge, M. A Model of Bone Adaptation as an Optimization Process. J. Biomech. 2000, 33, 1349–1357. [Google Scholar] [CrossRef]
- Jang, I.G.; Kim, I.Y. Computational Study of Wolff’s Law with Trabecular Architecture in the Human Proximal Femur Using Topology Optimization. J. Biomech. 2008, 41, 2353–2361. [Google Scholar] [CrossRef]
- Jang, I.G.; Kim, I.Y. Computational Simulation of Trabecular Adaptation Progress in Human Proximal Femur during Growth. J. Biomech. 2009, 42, 573–580. [Google Scholar] [CrossRef]
- Jang, I.G.; Kim, I.Y. Computational Study on the Effect of Loading Alteration Caused by Disc Degeneration on the Trabecular Architecture in Human Lumbar Spine. J. Biomech. 2010, 43, 492–499. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, Y.; Kim, J.J.; Jang, I.G. Homeostasis-Based Aging Model for Trabecular Changes and Its Correlation with Age-Matched Bone Mineral Densities and Radiographs. Eur. J. Radiol. 2015, 84, 2261–2268. [Google Scholar] [CrossRef]
- Goda, I.; Ganghoffer, J.-F.; Czarnecki, S.; Czubacki, R.; Wawruch, P. Topology Optimization of Bone Using Cubic Material Design and Evolutionary Methods Based on Internal Remodeling. Mech. Res. Commun. 2019, 95, 52–60. [Google Scholar] [CrossRef]
- Huo, M.; He, S.; Zhang, Y.; Feng, Y.; Lu, J. Simulation on Bone Remodeling with Stochastic Nature of Adult and Elderly Using Topology Optimization Algorithm. J. Biomech. 2022, 136, 111078. [Google Scholar] [CrossRef]
- Wolff, J. Das Gesetz Der Transformation Der Knochen. DMW—Dtsch. Med. Wochenschr. 1893, 19, 1222–1224. [Google Scholar] [CrossRef]
- Frost, H.M. Bone’s Mechanostat: A 2003 Update. Anat. Rec. 2003, 275, 1081–1101. [Google Scholar] [CrossRef] [PubMed]
- Phillips, A.T.M.; Villette, C.C.; Modenese, L. Femoral Bone Mesoscale Structural Architecture Prediction Using Musculoskeletal and Finite Element Modelling. Int. Biomech. 2015, 2, 43–61. [Google Scholar] [CrossRef]
- Warner, S.E.; Shea, J.E.; Miller, S.C.; Shaw, J.M. Adaptations in Cortical and Trabecular Bone in Response to Mechanical Loading with and without Weight Bearing. Calcif. Tissue Int. 2006, 79, 395–403. [Google Scholar] [CrossRef]
- Fischer, K.J.; Jacobs, C.R.; Carter, D.R. Computational Method for Determination of Bone and Joint Loads Using Bone Density Distributions. J. Biomech. 1995, 28, 1127–1135. [Google Scholar] [CrossRef]
- Fischer, K.J.; Jacobs, C.R.; Levenston, M.E.; Cody, D.D.; Carter, D.R. Bone Load Estimation for the Proximal Femur Using Single Energy Quantitative CT Data. Comput. Methods Biomech. Biomed. Engin. 1998, 1, 233–245. [Google Scholar] [CrossRef]
- Fischer, K.J.; Jacobs, C.R.; Levenston, M.E.; Cody, D.D.; Carters, D.R. Proximal Femoral Density Patterns Are Consistent with Bicentric Joint Loads. Comput. Methods Biomech. Biomed. Engin. 1999, 2, 271–283. [Google Scholar] [CrossRef]
- Fischer, K.J.; Eckstein, F.; Becker, C. Density-Based Load Estimation Predicts Altered Femoral Load Directions For Coxa Vara And Coxa Valga. J. Musculoskelet. Res. 1999, 3, 83–92. [Google Scholar] [CrossRef]
- Bona, M.A.; Martin, L.D.; Fischer, K.J. A Contact Algorithm for Density-Based Load Estimation. J. Biomech. 2006, 39, 636–644. [Google Scholar] [CrossRef]
- Christen, P.; van Rietbergen, B.; Lambers, F.M.; Müller, R.; Ito, K. Bone Morphology Allows Estimation of Loading History in a Murine Model of Bone Adaptation. Biomech. Model. Mechanobiol. 2012, 11, 483–492. [Google Scholar] [CrossRef]
- Christen, P.; Ito, K.; Santos, A.A.; Müller, R.; van Rietbergen, B. Validation of a Bone Loading Estimation Algorithm for Patient-Specific Bone Remodelling Simulations. J. Biomech. 2013, 46, 941–948. [Google Scholar] [CrossRef] [PubMed]
- Christen, P.; Ito, K.; Knippels, I.; Müller, R.; van Lenthe, G.H.; van Rietbergen, B. Subject-Specific Bone Loading Estimation in the Human Distal Radius. J. Biomech. 2013, 46, 759–766. [Google Scholar] [CrossRef] [PubMed]
- Warden, S.J.; Carballido-Gamio, J.; Weatherholt, A.M.; Keyak, J.H.; Yan, C.; Kersh, M.E.; Lang, T.F.; Fuchs, R.K. Heterogeneous Spatial and Strength Adaptation of the Proximal Femur to Physical Activity: A Within-Subject Controlled Cross-Sectional Study. J. Bone Miner. Res. 2020, 35, 681–690. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Nagrath, A.R.; Maini, P.S. Changes in Trabecular Pattern of the Upper End of the Femur as an Index of Osteoporosis. J. Bone Jt. Surg. 1970, 52, 457–467. [Google Scholar] [CrossRef]
- Boyle, C.; Kim, I.Y. Three-Dimensional Micro-Level Computational Study of Wolff’s Law via Trabecular Bone Remodeling in the Human Proximal Femur Using Design Space Topology Optimization. J. Biomech. 2011, 44, 935–942. [Google Scholar] [CrossRef]
- Phillips, A.T.M. Structural Optimisation: Biomechanics of the Femur. Proc. Inst. Civ. Eng.-Eng. Comput. Mech. 2012, 165, 147–154. [Google Scholar] [CrossRef]
- San Antonio, T.; Ciaccia, M.; Müller-Karger, C.; Casanova, E. Orientation of Orthotropic Material Properties in a Femur FE Model: A Method Based on the Principal Stresses Directions. Med. Eng. Phys. 2012, 34, 914–919. [Google Scholar] [CrossRef]
- Mathai, B.; Dhara, S.; Gupta, S. Orthotropic Bone Remodelling around Uncemented Femoral Implant: A Comparison with Isotropic Formulation. Biomech. Model. Mechanobiol. 2021, 20, 1115–1134. [Google Scholar] [CrossRef]
- Cui, W.-Q.; Won, Y.-Y.; Baek, M.-H.; Lee, D.-H.; Chung, Y.-S.; Hur, J.-H.; Ma, Y.-Z. Age-and Region-Dependent Changes in Three-Dimensional Microstructural Properties of Proximal Femoral Trabeculae. Osteoporos. Int. 2008, 19, 1579–1587. [Google Scholar] [CrossRef]
- Chen, H. Bone Three-Dimensional Microstructural Features of the Common Osteoporotic Fracture Sites. World J. Orthop. 2014, 5, 486. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, Y. Femoral Bone Mineral Density Distribution Is Dominantly Regulated by Strain Energy Density in Remodeling. Biomed. Mater. Eng. 2000, 31, 179–190. [Google Scholar] [CrossRef] [PubMed]
- Chun, B.J.; Jang, I.G. Determination of the Representative Static Loads for Cyclically Repeated Dynamic Loads: A Case Study of Bone Remodeling Simulation with Gait Loads. Comput. Methods Programs Biomed. 2021, 200, 105924. [Google Scholar] [CrossRef] [PubMed]
- Van Rietbergen, B.; Müller, R.; Ulrich, D.; Rüegsegger, P.; Huiskes, R. Tissue Stresses and Strain in Trabeculae of a Canine Proximal Femur Can Be Quantified from Computer Reconstructions. J. Biomech. 1999, 32, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Beaupré, G.S.; Orr, T.E.; Carter, D.R. An Approach for Time-Dependent Bone Modeling and Remodeling-Theoretical Development. J. Orthop. Res. 1990, 8, 651–661. [Google Scholar] [CrossRef]
- Beaupré, G.S.; Orr, T.E.; Carter, D.R. An Approach for Time-Dependent Bone Modeling and Remodeling-Application: A Preliminary Remodeling Simulation. J. Orthop. Res. 1990, 8, 662–670. [Google Scholar] [CrossRef] [PubMed]
- Jang, I.G.; Kim, I.Y. Application of Design Space Optimization to Bone Remodeling Simulation of Trabecular Architecture in Human Proximal Femur for Higher Computational Efficiency. Finite Elem. Anal. Des. 2010, 46, 311–319. [Google Scholar] [CrossRef]
- Kim, J.J.; Jang, I.G. Image Resolution Enhancement for Healthy Weight-Bearing Bones Based on Topology Optimization. J. Biomech. 2016, 49, 3035–3040. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.; Schiffer, A.; Kim, J.J.; Jang, I.G.; Lee, S.; Kim, T.-Y. Numerical Predictions of the Interaction between Highly Nonlinear Solitary Waves and the Microstructure of Trabecular Bone in the Femoral Head. J. Mech. Behav. Biomed. Mater. 2020, 109, 103805. [Google Scholar] [CrossRef]
- Choi, J.W.; Kim, J.J. Structural Behavior Analysis According to Porous Structures of the Bone Scaffold in the Femoral Head. J. Korean Soc. Precis. Eng. 2022, 39, 627–633. [Google Scholar] [CrossRef]
- Bouxsein, M.L.; Boyd, S.K.; Christiansen, B.A.; Guldberg, R.E.; Jepsen, K.J.; Müller, R. Guidelines for Assessment of Bone Microstructure in Rodents Using Micro-Computed Tomography. J. Bone Miner. Res. 2010, 25, 1468–1486. [Google Scholar] [CrossRef]
- Chen, Y.; Pani, M.; Taddei, F.; Mazzà, C.; Li, X.; Viceconti, M. Large-Scale Finite Element Analysis of Human Cancellous Bone Tissue Micro Computer Tomography Data: A Convergence Study. J. Biomech. Eng. 2014, 136, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Verhulp, E.; van Rietbergen, B.; Huiskes, R. Comparison of Micro-Level and Continuum-Level Voxel Models of the Proximal Femur. J. Biomech. 2006, 39, 2951–2957. [Google Scholar] [CrossRef] [PubMed]
- Bendsøe, M.P. Optimal Shape Design as a Material Distribution Problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Simonen, F.A.; Weis, E.B. On the Mathematical Analysis of Stress in the Human Femur. J. Biomech. 1972, 5, 203–215. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409. [Google Scholar] [CrossRef]
- Svanberg, K. The Method of Moving Asymptotes—A New Method for Structural Optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Van Rietbergen, B.; Weinans, H.; Huiskes, R.; Odgaard, A. A New Method to Determine Trabecular Bone Elastic Properties and Loading Using Micromechanical Finite-Element Models. J. Biomech. 1995, 28, 69–81. [Google Scholar] [CrossRef] [PubMed]
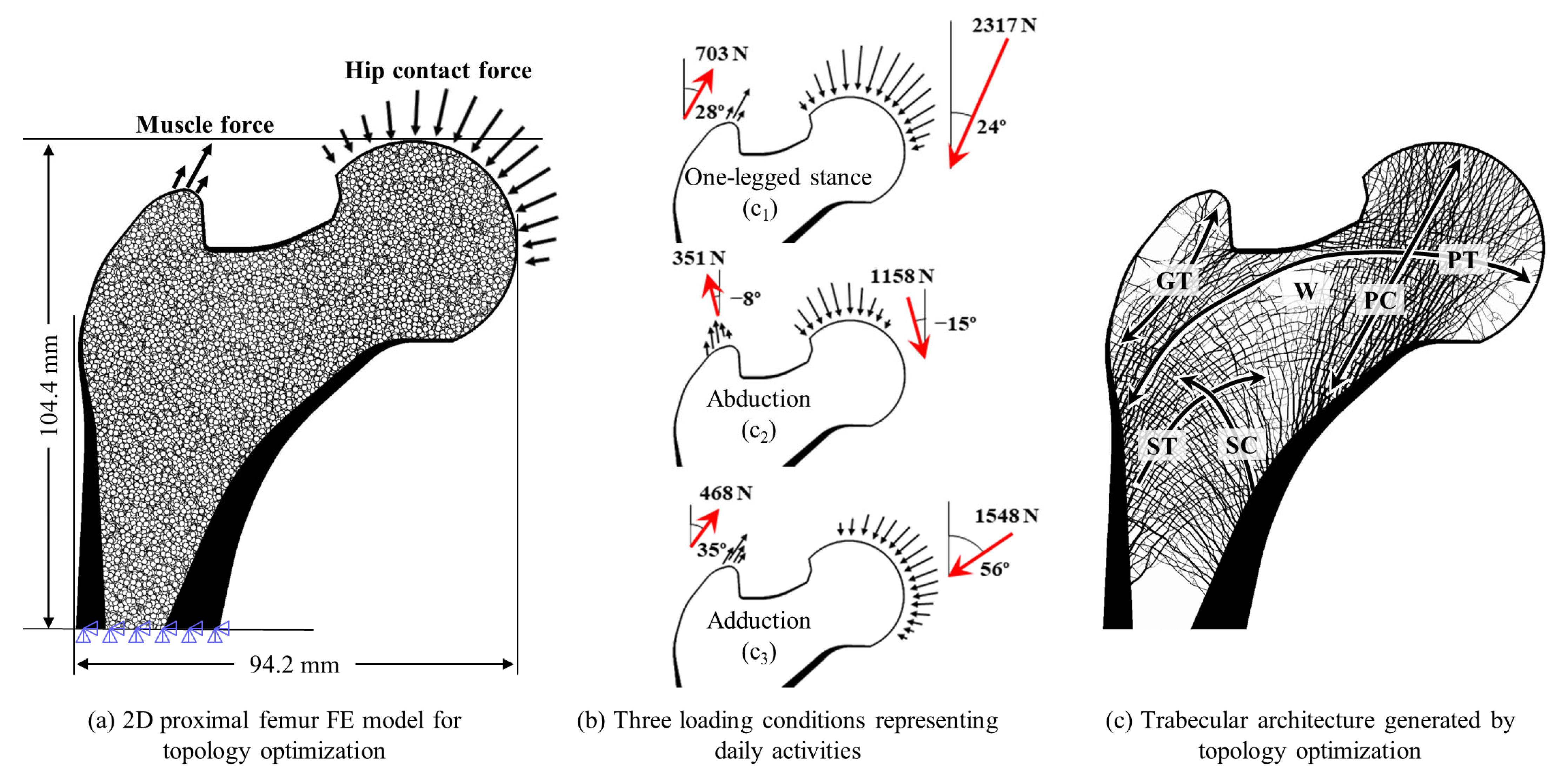
| Type of Load Case | Load Case | Loading Condition | Normalized Weight |
|---|---|---|---|
| Single-loading condition | 1 | One-legged stance | c1 = 1.0 |
| 2 | Abduction | c2 = 1.0 | |
| 3 | Adduction | c3 = 1.0 | |
| Dual-loading condition | 4 | One-legged stance | c1 = 0.5 |
| Abduction | c2 = 0.5 | ||
| 5 | Abduction | c2 = 0.5 | |
| Adduction | c3 = 0.5 | ||
| 6 | One-legged stance | c1 = 0.5 | |
| Adduction | c3 = 0.5 | ||
| Multiple-loading condition | 7 | One-legged stance | c1 = 0.6 |
| Abduction | c2 = 0.2 | ||
| Adduction | c3 = 0.2 |
| Location | Category | Metric | Load Case | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| Global | SED | Avg. [J/mm2] | 1.37 × 10−1 | 1.47 × 10−1 | 7.20 × 10−2 | 1.42 × 10−1 | 1.09 × 10−1 | 1.05 × 10−1 | 1.26 × 10−1 |
| SD [J/mm2] | 7.69 × 10−2 | 1.10 × 10−1 | 9.19 × 10−2 | 6.11 × 10−2 | 7.85 × 10−2 | 4.75 × 10−2 | 4.60 × 10−2 | ||
| Score | Avg. S * | 0.65 | 1.03 | −1.81 | 0.84 | −0.41 | −0.56 | 0.24 | |
| SD. S ** | 0.16 | 1.57 | 0.80 | −0.51 | 0.23 | −1.09 | −1.16 | ||
| LDS *** | 25.48 | −24.45 | −131.38 | 68.18 | −31.92 | 25.20 | 68.88 | ||
| Location | Category | Metric | Load Case | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| ROI 1 | SED | Avg. [J/mm2] | 1.46 × 10−1 | 7.82 × 10−3 | 1.48 × 10−1 | 7.71 × 10−2 | 7.81 × 10−2 | 1.47 × 10−1 | 1.19 × 10−1 |
| SD [J/mm2] | 7.40 × 10−2 | 1.23 × 10−2 | 1.51 × 10−1 | 3.61 × 10−2 | 7.76 × 10−2 | 6.50 × 10−2 | 3.91 × 10−2 | ||
| Score | Avg. S * | 0.82 | −1.83 | 0.85 | −0.50 | −0.48 | 0.84 | 0.30 | |
| SD. S ** | 0.20 | −1.18 | 1.93 | −0.65 | 0.28 | 0.00 | −0.58 | ||
| LDS *** | 31.77 | −35.13 | −50.94 | 6.25 | −38.40 | 42.64 | 43.81 | ||
| ROI 2 | SED | Avg. [J/mm2] | 1.63 × 10−1 | 6.30 × 10−2 | 4.57 × 10−2 | 1.13 × 10−1 | 5.43 × 10−2 | 1.04 × 10−1 | 1.20 × 10−1 |
| SD [J/mm2] | 7.42 × 10−2 | 9.86 × 10−2 | 5.36 × 10−2 | 4.38 × 10−2 | 6.11 × 10−2 | 3.63 × 10−2 | 3.61 × 10−2 | ||
| Score | Avg. S * | 1.61 | −0.75 | −1.16 | 0.43 | −0.95 | 0.22 | 0.60 | |
| SD. S ** | 0.73 | 1.80 | −0.18 | −0.61 | 0.15 | −0.94 | −0.95 | ||
| LDS *** | 46.54 | −126.54 | −50.23 | 51.96 | −56.06 | 57.32 | 77.01 | ||
| ROI 3 | SED | Avg. [J/mm2] | 9.77 × 10−2 | 1.88 × 10−1 | 7.59 × 10−2 | 1.43 × 10−1 | 1.32 × 10−1 | 8.68 × 10−2 | 1.11 × 10−1 |
| SD [J/mm2] | 5.68 × 10−2 | 1.59 × 10−1 | 7.56 × 10−2 | 7.50× 10−2 | 8.30 × 10−2 | 3.99 × 10−2 | 3.52 × 10−2 | ||
| Score | Avg. S * | −0.56 | 1.78 | −1.12 | 0.62 | 0.33 | −0.84 | −0.21 | |
| SD. S ** | −0.44 | 2.03 | 0.02 | 0.01 | 0.20 | −0.85 | −0.96 | ||
| LDS *** | −6.97 | −8.57 | −58.08 | 31.40 | 7.37 | −1.37 | 36.21 | ||
| ROI 4 | SED | Avg. [J/mm2] | 1.69 × 10−1 | 1.14 × 10−1 | 3.38 × 10−2 | 1.41 × 10−1 | 7.37 × 10−2 | 1.01 × 10−1 | 1.31 × 10−1 |
| SD [J/mm2] | 6.36 × 10−2 | 8.21 × 10−2 | 4.52 × 10−2 | 4.51 × 10−2 | 5.03 × 10−2 | 3.15 × 10−2 | 3.59 × 10−2 | ||
| Score | Avg. S * | 1.33 | 0.11 | −1.68 | 0.71 | −0.79 | −0.18 | 0.49 | |
| SD. S ** | 0.75 | 1.82 | −0.31 | −0.31 | −0.01 | −1.10 | −0.84 | ||
| LDS *** | 31.10 | −83.68 | −70.42 | 51.61 | −39.53 | 44.64 | 66.27 | ||
| ROI 7 | SED | Avg. [J/mm2] | 1.20 × 10−1 | 1.83 × 10−1 | 6.61 × 10−2 | 1.51 × 10−1 | 1.24 × 10−1 | 9.33 × 10−2 | 1.22 × 10−1 |
| SD [J/mm2] | 5.49 × 10−2 | 9.37 × 10−2 | 9.24 × 10−2 | 5.47 × 10−2 | 6.96 × 10−2 | 3.99 × 10−2 | 3.55 × 10−2 | ||
| Score | Avg. S * | −0.07 | 1.60 | −1.50 | 0.75 | 0.03 | −0.78 | −0.02 | |
| SD. S ** | −0.34 | 1.32 | 1.26 | −0.35 | 0.28 | −0.99 | −1.18 | ||
| LDS *** | 13.15 | 17.06 | −138.48 | 55.54 | −12.27 | 8.46 | 56.54 | ||
| ROI 8 | SED | Avg. [J/mm2] | 1.60 × 10−1 | 1.81 × 10−1 | 1.12 × 10−2 | 1.70 × 10−1 | 9.61 × 10−2 | 8.57 × 10−2 | 1.34 × 10−1 |
| SD [J/mm2] | 5.94 × 10−2 | 7.23 × 10−2 | 1.33 × 10−2 | 5.94 × 10−2 | 3.87 × 10−2 | 2.88 × 10−2 | 4.59 × 10−2 | ||
| Score | Avg. S * | 0.67 | 1.02 | −1.81 | 0.84 | −0.39 | −0.57 | 0.24 | |
| SD. S ** | 0.69 | 1.33 | −1.58 | 0.69 | −0.33 | −0.82 | 0.02 | ||
| LDS *** | 0.41 | −12.92 | −14.66 | 8.91 | −3.88 | 11.21 | 10.93 | ||
| Location | Category | Metric | Load Case | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| ROI 5 | SED | Avg. [J/mm2] | 2.16 × 10−1 | 9.41 × 10−2 | 2.75 × 10−2 | 1.55 × 10−1 | 6.08 × 10−2 | 1.22 × 10−1 | 1.54 × 10−1 |
| SD [J/mm2] | 8.55 × 10−2 | 4.00 × 10−2 | 3.17 × 10−2 | 5.40 × 10−2 | 2.49 × 10−2 | 4.70 × 10−2 | 5.59 × 10−2 | ||
| Score | Avg. S * | 1.53 | −0.38 | −1.43 | 0.57 | −0.91 | 0.06 | 0.56 | |
| SD. S ** | 1.87 | −0.42 | −0.84 | 0.28 | −1.18 | −0.07 | 0.38 | ||
| LDS *** | −13.32 | 1.25 | −31.63 | 15.51 | 11.82 | 6.34 | 10.02 | ||
| ROI 6 | SED | Avg. [J/mm2] | 1.06 × 10−1 | 1.81 × 10−1 | 9.45 × 10−2 | 1.44 × 10−1 | 1.38 × 10−1 | 1.00 × 10−1 | 1.19 × 10−1 |
| SD [J/mm2] | 5.72× 10−2 | 1.02 × 10−1 | 7.79 × 10−2 | 6.52 × 10−2 | 7.73 × 10−2 | 4.28 × 10−2 | 4.79 × 10−2 | ||
| Score | Avg. S * | −0.66 | 1.80 | −1.03 | 0.59 | 0.39 | −0.85 | −0.23 | |
| SD. S ** | −0.49 | 1.71 | 0.52 | −0.10 | 0.50 | −1.19 | −0.94 | ||
| LDS *** | −9.50 | 8.03 | −78.38 | 34.67 | −4.39 | 15.06 | 34.51 | ||
| ROI 9 | SED | Avg. [J/mm2] | 1.15 × 10−1 | 1.79 × 10−1 | 5.25 × 10−2 | 1.47 × 10−1 | 1.16 × 10−1 | 8.40 × 10−2 | 1.16 × 10−1 |
| SD [J/mm2] | 4.05 × 10−2 | 5.84 × 10−2 | 4.37 × 10−2 | 4.40 × 10−2 | 4.59 × 10−2 | 2.67 × 10−2 | 3.41 × 10−2 | ||
| Score | Avg. S * | −0.02 | 1.55 | −1.55 | 0.77 | 0.01 | −0.78 | 0.01 | |
| SD. S ** | −0.14 | 1.66 | 0.18 | 0.21 | 0.40 | −1.53 | −0.79 | ||
| LDS *** | 6.12 | −2.35 | −87.83 | 28.82 | −19.32 | 35.57 | 39.00 | ||
| ROI 10 | SED | Avg. [J/mm2] | 1.21 × 10−1 | 1.79 × 10−1 | 8.79 × 10−2 | 1.50 × 10−1 | 1.33 × 10−1 | 1.05 × 10−1 | 1.26 × 10−1 |
| SD [J/mm2] | 5.31 × 10−2 | 7.53 × 10−2 | 1.06 × 10−1 | 5.48 × 10−2 | 6.82 × 10−2 | 4.59 × 10−2 | 3.89 × 10−2 | ||
| Score | Avg. S * | −0.26 | 1.69 | −1.38 | 0.71 | 0.14 | −0.80 | −0.10 | |
| SD. S ** | −0.45 | 0.53 | 1.89 | −0.37 | 0.22 | −0.76 | −1.07 | ||
| LDS *** | 8.37 | 59.82 | −163.13 | 54.47 | −3.76 | −3.49 | 47.73 | ||
| ROI 11 | SED | Avg. [J/mm2] | 1.17 × 10−1 | 2.16 × 10−1 | 5.46 × 10−2 | 1.66 × 10−1 | 1.35 × 10−1 | 8.57 × 10−2 | 1.24 × 10−1 |
| SD [J/mm2] | 4.76 × 10−2 | 7.45 × 10−2 | 2.79 × 10−2 | 5.98 × 10−2 | 4.61 × 10−2 | 2.96 × 10−2 | 4.46 × 10−2 | ||
| Score | Avg. S * | −0.22 | 1.67 | −1.40 | 0.72 | 0.13 | −0.81 | −0.08 | |
| SD. S ** | 0.03 | 1.68 | −1.18 | 0.78 | −0.06 | −1.08 | −0.16 | ||
| LDS *** | −12.33 | 2.94 | −13.71 | −1.42 | 9.66 | 11.38 | 3.48 | ||
| ROI 12 | SED | Avg. [J/mm2] | 5.54 × 10−2 | 2.10 × 10−1 | 1.69 × 10−1 | 1.33 × 10−1 | 1.89 × 10−1 | 1.12 × 10−1 | 1.09 × 10−1 |
| SD [J/mm2] | 3.66 × 10−2 | 7.38 × 10−2 | 1.13 × 10−1 | 4.48 × 10−2 | 8.21 × 10−2 | 4.90 × 10−2 | 3.44 × 10−2 | ||
| Score | Avg. S * | −1.58 | 1.32 | 0.55 | −0.12 | 0.93 | −0.52 | −0.57 | |
| SD. S ** | −0.88 | 0.41 | 1.77 | −0.59 | 0.70 | −0.45 | −0.95 | ||
| LDS *** | −37.51 | 47.17 | −58.44 | 22.74 | 13.04 | −4.44 | 17.43 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Chun, B.J.; Kim, J.J. Quantitative Load Dependency Analysis of Local Trabecular Bone Microstructure to Understand the Spatial Characteristics in the Synthetic Proximal Femur. Biology 2023, 12, 170. https://doi.org/10.3390/biology12020170
Kim J, Chun BJ, Kim JJ. Quantitative Load Dependency Analysis of Local Trabecular Bone Microstructure to Understand the Spatial Characteristics in the Synthetic Proximal Femur. Biology. 2023; 12(2):170. https://doi.org/10.3390/biology12020170
Chicago/Turabian StyleKim, Jisun, Bong Ju Chun, and Jung Jin Kim. 2023. "Quantitative Load Dependency Analysis of Local Trabecular Bone Microstructure to Understand the Spatial Characteristics in the Synthetic Proximal Femur" Biology 12, no. 2: 170. https://doi.org/10.3390/biology12020170
APA StyleKim, J., Chun, B. J., & Kim, J. J. (2023). Quantitative Load Dependency Analysis of Local Trabecular Bone Microstructure to Understand the Spatial Characteristics in the Synthetic Proximal Femur. Biology, 12(2), 170. https://doi.org/10.3390/biology12020170





