EEGs Disclose Significant Brain Activity Correlated with Synaptic Fickleness
Abstract
:Simple Summary
Abstract
1. Introduction
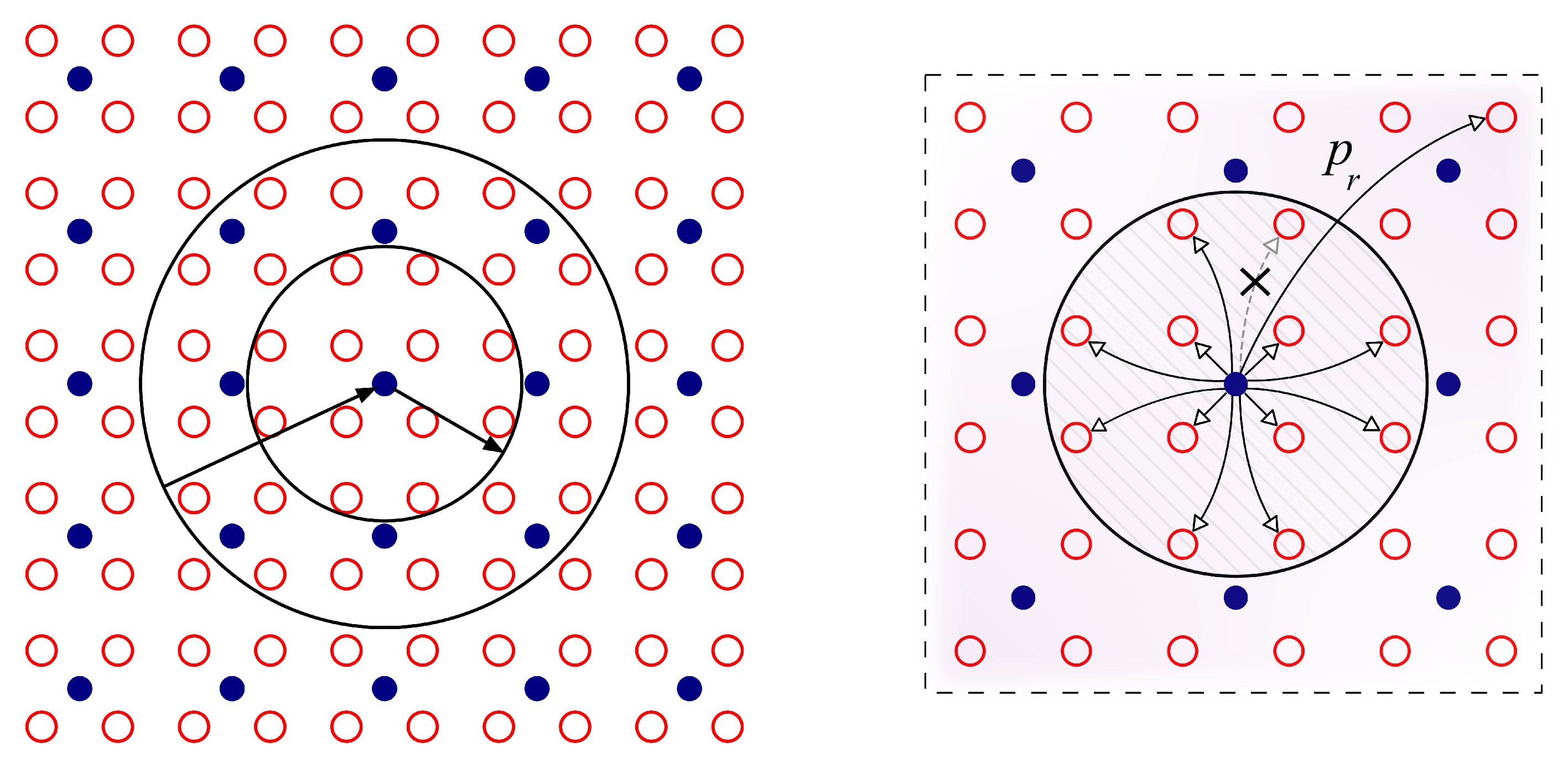
2. Materials and Methods
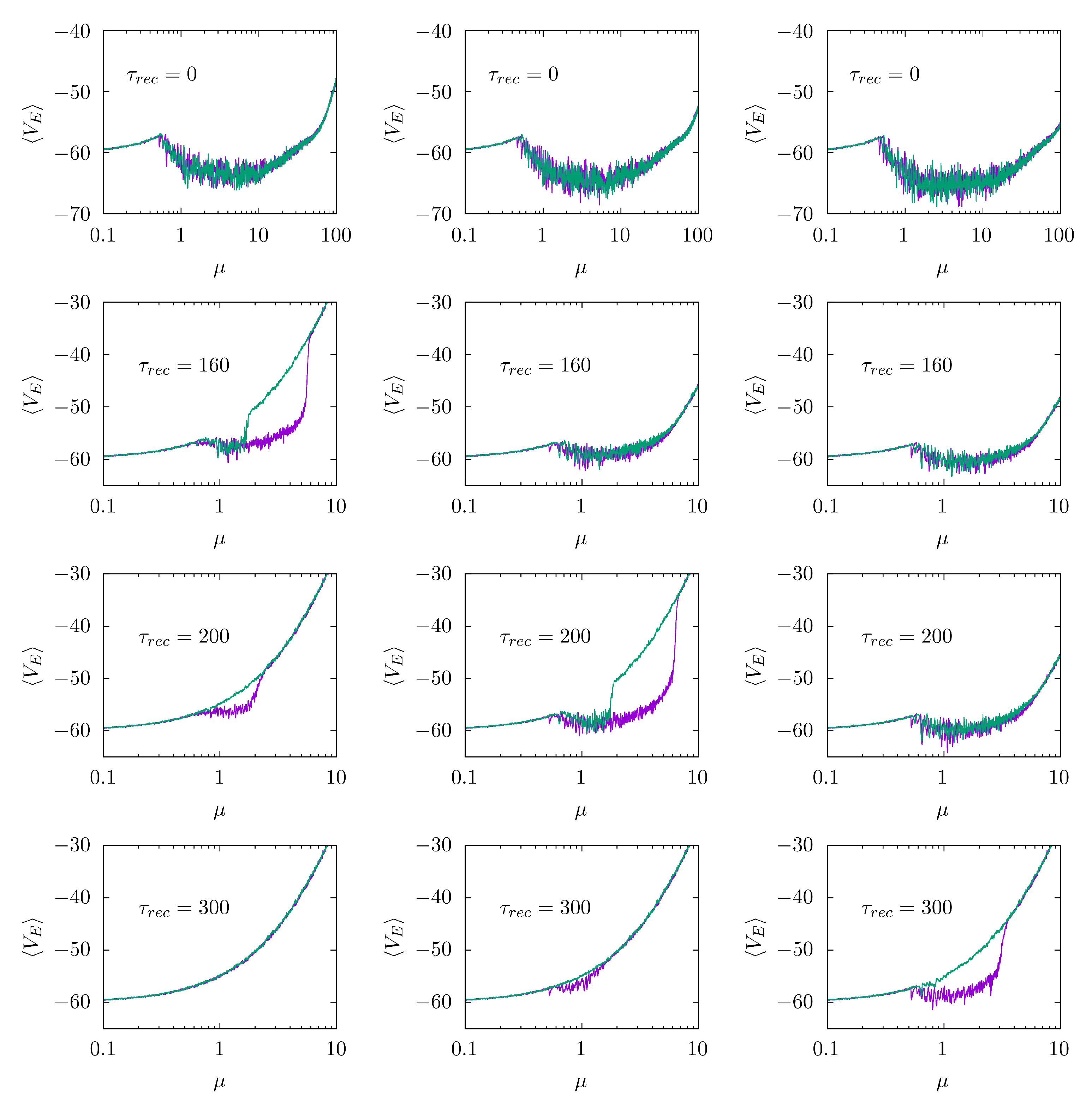
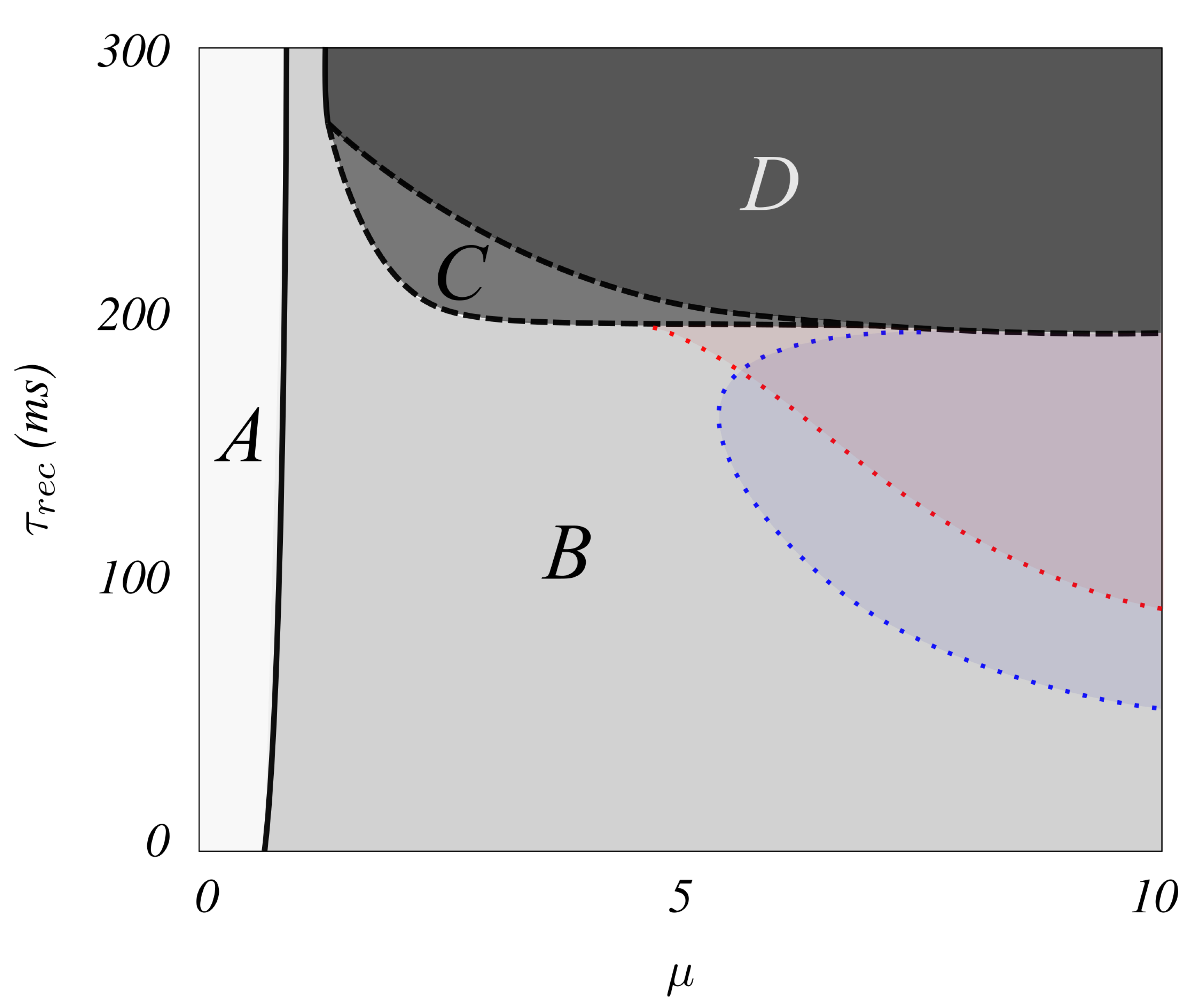
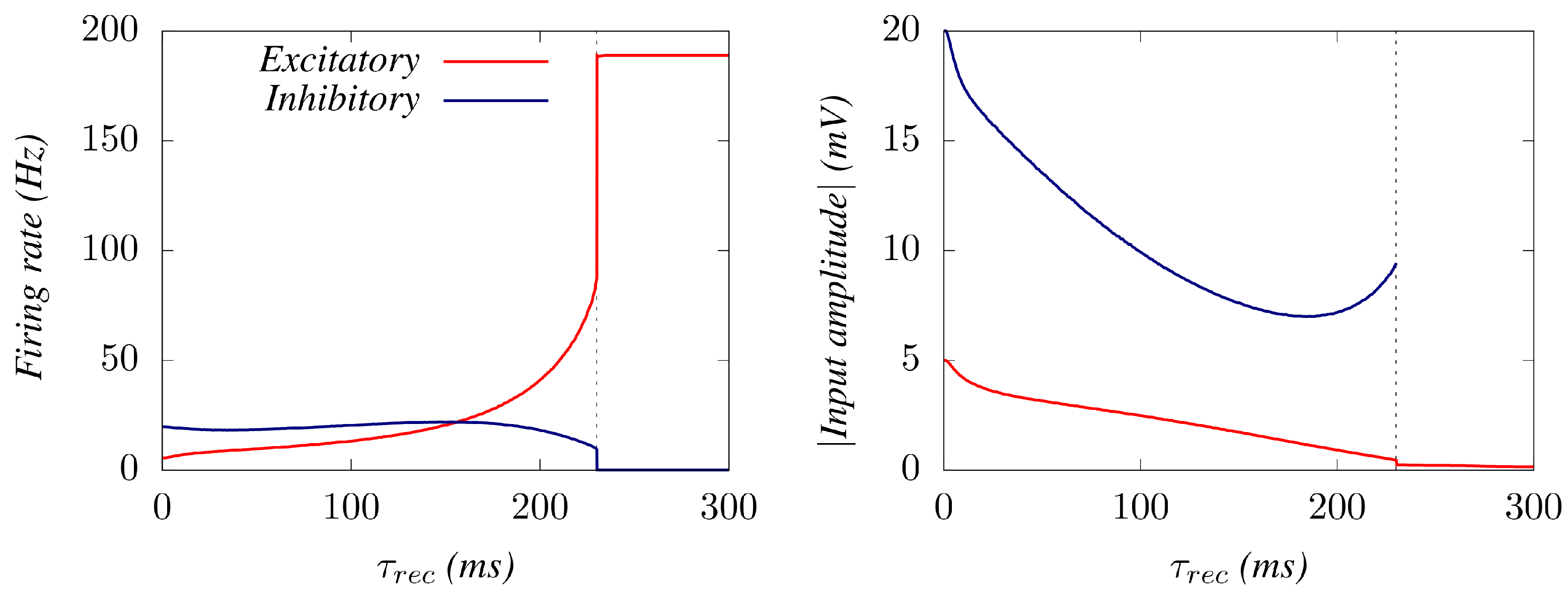
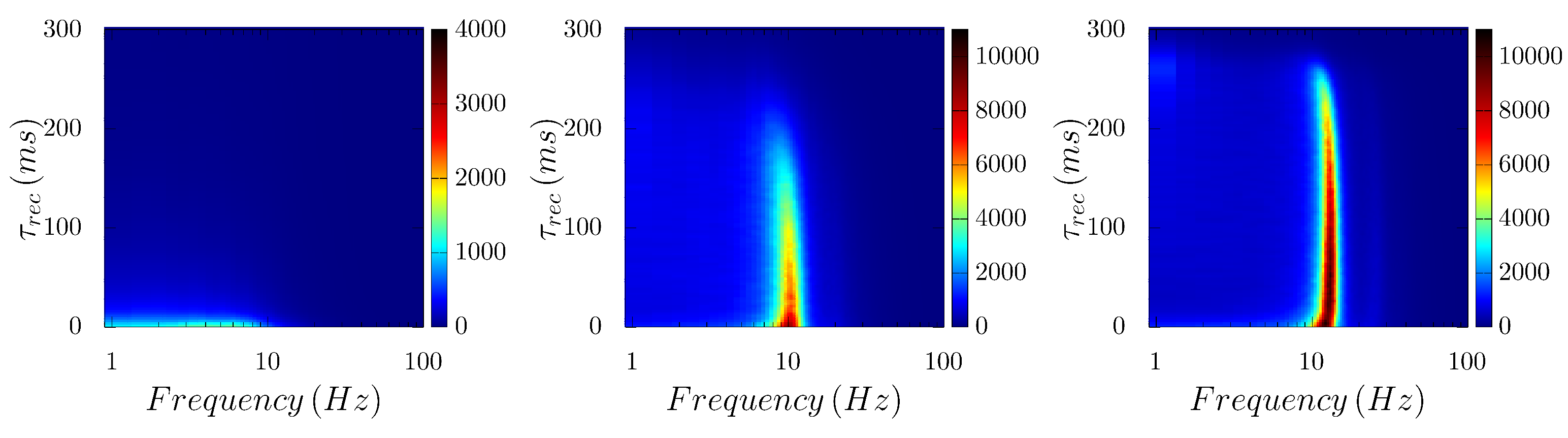
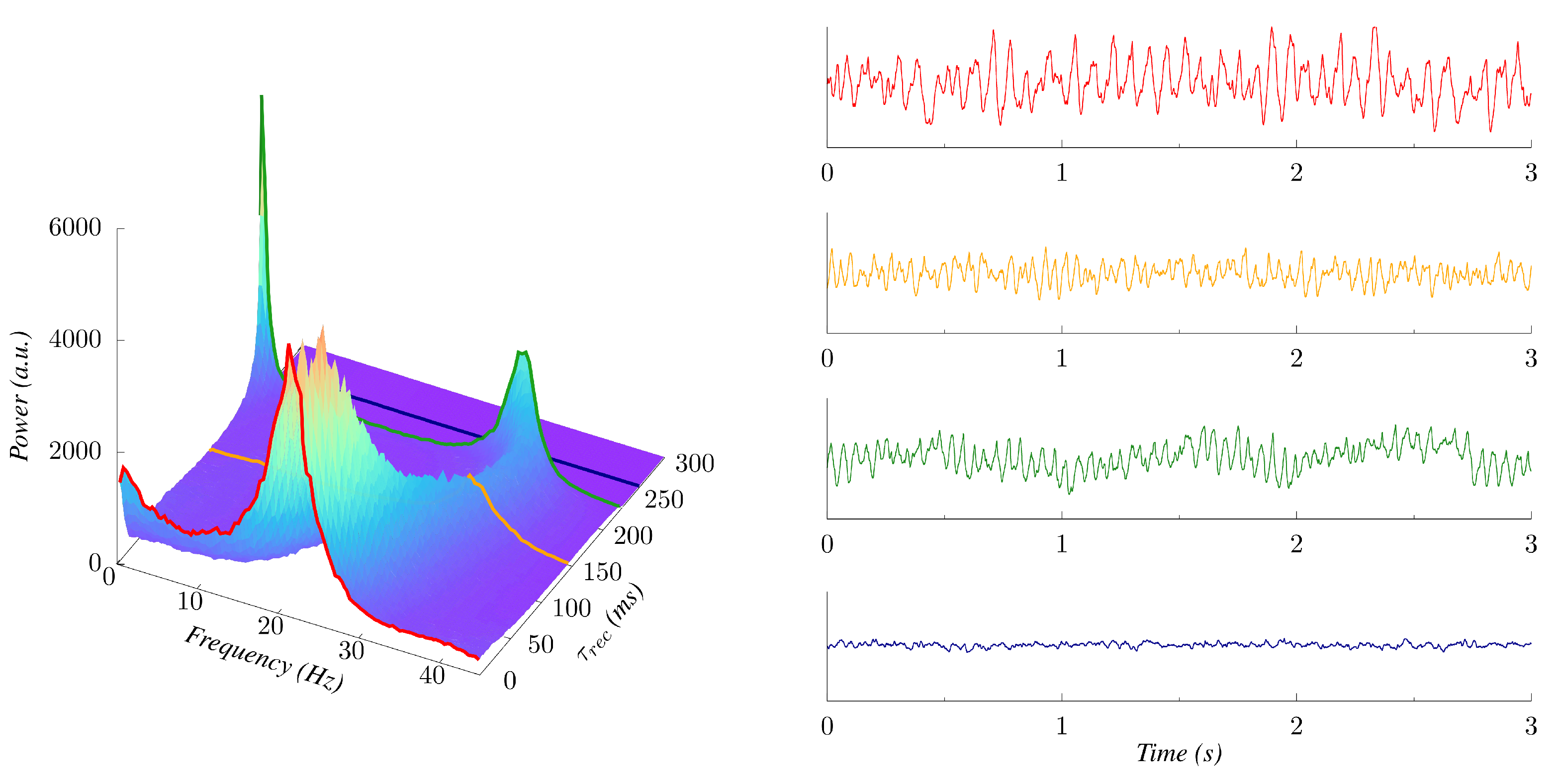
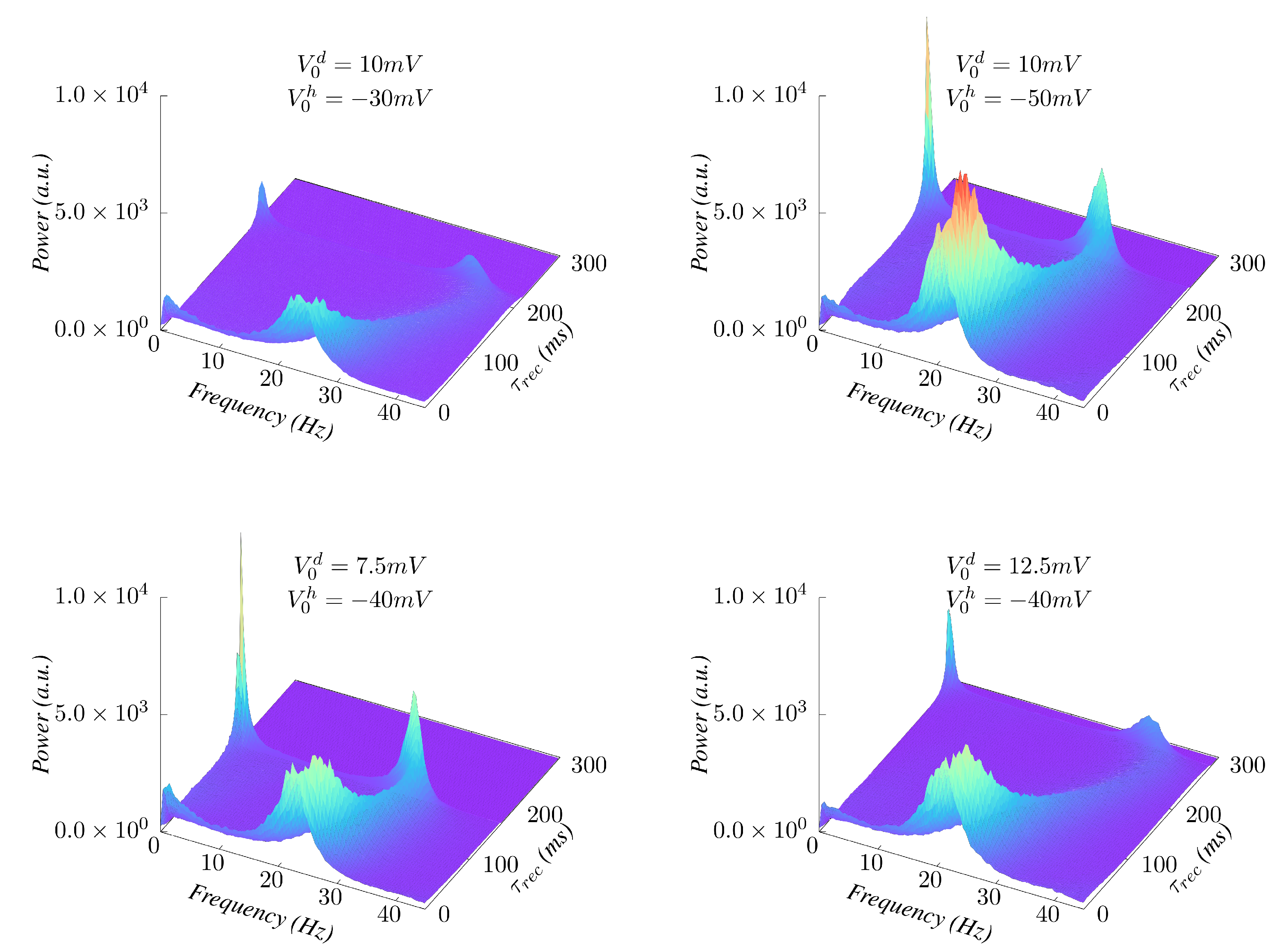
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marro, J.; Torres, J.J. Phase Transitions in Grey Matter: Brain Architecture and Mind Dynamics; AIP Publishing: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Wright, J.J. Simulation of EEG: Dynamic changes in synaptic efficacy, cerebral rhythms, and dissipative and generative activity in cortex. Biol. Cybern. 1999, 81, 131–147. [Google Scholar] [CrossRef] [PubMed]
- Barras, C.D.; Asadi, H.; Baldeweg, T.; Mancini, L.; Yousry, T.A.; Bisdas, S. Functional magnetic resonance imaging in clinical practice. Aust. Fam. (Neurol.) 2016, 45, 798–803. [Google Scholar]
- Ruijter, B.J.; Hofmeijer, J.; Meijer, H.G.E.; van Putten, M.J.A.M. Synaptic damage underlies EEG abnormalities in post anoxic encephalopathy: A computational study. Clin. Neurophysiol. 2017, 128, 1682–1695. [Google Scholar] [CrossRef]
- López-Madrona, V.J.; Pérez-Montoyo, E.; Álvarez-Salvado, E.; Moratal, D.; Herreras, O.; Pereda, E.; Mirasso, C.R.; Canals, S. Different theta frameworks coexist in the rat hippocampus and are coordinated during memory-guided and novelty tasks. eLife 2020, 9, e57313. [Google Scholar] [CrossRef]
- Cannon, J.; McCarthy, M.M.; Lee, S.; Lee, J.; Börgers, C.; Whittington, M.A.; Kopell, N. Neurosystems: Brain rhythms and cognitive processing. Eur. J. Neurosci. 2014, 39, 705–719. [Google Scholar] [CrossRef]
- Smith, S.J.M. EEG in the diagnosis, classification, and management of patients with epilepsy. J. Neurol. Psychiatry 2005, 76, ii2–ii7. [Google Scholar] [CrossRef] [Green Version]
- Palva, S.; Palva, J.M. New vistas for alpha-frequency band oscillations. Trends Neurosci. 2007, 30, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Faigle, R.; Sutter, R.; Kaplan, P.W. Electroencephalography of encephalopathy in patients with endocrine and metabolic disorders. J. Clin. Neurophysiol. 2013, 30, 505–516. [Google Scholar] [CrossRef] [Green Version]
- Houmani, N.; Vialatte, F.; Gallego-Jutglà, E.; Dreyfus, G.; Nguyen-Michel, V.H.; Mariani, J.; Kinugawa, K. Diagnosis of Alzheimer’s disease with electroencephalography in a differential framework. PLoS ONE 2018, 13, e0193607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gemein, L.A.W.; Schirrmeister, R.T.; Chrabąszcz, P.; Wilson, D.; Boedecker, J.; Schulze-Bonhage, A.; Hutter, F.; Ball, T. Machine-learning-based diagnostics of EEG pathology. NeuroImage 2020, 220, 117021. [Google Scholar] [CrossRef] [PubMed]
- Lopes da Silva, F.H.; Hoeks, A.; Smits, H.; Zetterberg, L.H. Model of brain rhythmic activity; the alpha-rhythm of the thalamus. Kybernetik 1974, 15, 27–37. [Google Scholar] [CrossRef]
- Dafilis, M.P.; Liley, D.T.; Cadusch, P.J. Robust chaos in a model of the electroencephalogram: Implications for brain dynamics. Chaos 2001, 11, 474–478. [Google Scholar] [CrossRef]
- Dafilis, M.P.; Liley, D.T.; Cadusch, P.J. Electrorhythmogenesis and anesthesia in a physiological mean field theory. Neurocomputing 2004, 58–60, 1197–1202. [Google Scholar]
- Liley, D.T.; Cadusch, P.J.; Dafilis, M.P. A spatially continuous mean field theory of electrocortical activity. Netw. Comput. Neural Syst. 2009, 13, 67. [Google Scholar] [CrossRef]
- Galadí, J.A.; Torres, J.J.; Marro, J. Emergence and interpretation of oscillatory behavior similar to brain waves and rhythms. Commun. Nonlinear Sci. Numer. 2020, 83, 105093. [Google Scholar] [CrossRef]
- Torres, J.J.; Elices, I.; Marro, J. Stochastic multi-resonances in complex nets of spiking neurons. Int. J. Complex Syst. Sci. 2013, 3, 21–25. [Google Scholar]
- Tsodyks, M.V.; Markram, H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc. Natl. Acad. Sci. USA 1997, 94, 719–723. [Google Scholar] [CrossRef] [Green Version]
- Zucker, R.S.; Regehr, W.G. Short-term synaptic plasticity. Annu. Rev. Physiol. 2002, 64, 355–405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uziel, A.; Markram, H. Synchrony generation in recurrent networks with frequency-dependent synapses. J. Neurosci. 2000, 20, RC50. [Google Scholar]
- Goldman, M.S.; Maldonado, P.; Abbott, L.F. Redundancy reduction and sustained firing with stochastic depressing synapses. J. Neurosci. 2002, 22, 584–591. [Google Scholar] [CrossRef]
- Tsodyks, M.; Pawelzik, K.; Markram, H. Neural Networks with Dynamic Synapses. Neural Comput. 1998, 10, 821–835. [Google Scholar] [CrossRef]
- Mejias, J.; Torres, J.J. The role of synaptic facilitation in coincidence spike detection. J. Comput. Neurosci. 2008, 24, 222–234. [Google Scholar] [CrossRef]
- Mongillo, G.; Barak, O.; Tsodyks, M. Synaptic theory of working memory. Science 2008, 319, 1543–1546. [Google Scholar] [CrossRef] [Green Version]
- Torres, J.J.; Kappen, H.J. Emerging phenomena in neural networks with dynamic synapses and their computational implications. Front. Comput. Neurosci. 2013, 7, 30. [Google Scholar] [CrossRef] [Green Version]
- Holcman, D.; Tsodyks, M. The emergence of up and down states in cortical networks. PLoS Comput. Biol. 2006, 2, e23. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Moon, J.Y.; Mashour, G.A.; Lee, U. Mechanisms of hysteresis in human brain networks during transitions of consciousness and unconsciousness: Theoretical principles and empirical evidence. PLoS Comput. Biol. 2018, 14, e1006424. [Google Scholar] [CrossRef] [PubMed]
- Lisman, J.E.; Jensen, O. The theta-gamma neural code. Neuron 2013, 77, 1002–1016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Headley, D.B.; Paré, D. Common oscillatory mechanisms across multiple memory systems. Npj Sci. Learn. 2017, 2, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gągol, A.; Magnuski, M.; Kroczek, B.; Kałamała, P.; Ociepka, M.; Santarnecchi, E.; Chuderski, A. Delta-gamma coupling as a potential neurophysiological mechanism of fluid intelligence. Intelligence 2018, 66, 54–63. [Google Scholar] [CrossRef]
- Lee, E.; Lee, J.; Kim, E. Excitation/inhibition imbalance in animal models of autism spectrum disorders. Biol. Psychiatry 2017, 81, 838–847. [Google Scholar] [CrossRef] [Green Version]
- Sohal, V.S.; Rubenstein, J.L. Excitation-inhibition balance as a framework for investigating mechanisms in neuropsychiatric disorders. Mol. Psychiatry 2019, 24, 1248–1257. [Google Scholar] [CrossRef]
- Meinecke, D.L.; Peters, A. Gaba immunoreactive neurons in rat visual cortex. J. Comput. Neurosci. 1987, 261, 388–404. [Google Scholar] [CrossRef]
- Heiss, J.E.; Katz, Y.; Ganmor, E.; Lampl, I. Shift in the balance between excitation and inhibition during sensory adaptation of s1 neurons. J. Neurosci. 2008, 28, 13320–13330. [Google Scholar] [CrossRef]
- Burkitt, A. A review of the integrate-and-fire neuron model: I. homogeneous synaptic input. Biol. Cybern. 2006, 95, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Shadlen, M.N.; Newsome, W.T. The Variable Discharge of Cortical Neurons: Implications for Connectivity, Computation, and Information Coding. J. Neurosci. 1998, 18, 3870–3896. [Google Scholar] [CrossRef] [PubMed]
- Hennig, M.H. Theoretical models of synaptic short term plasticity. Front. Comput. Neurosci. 2013, 7. [Google Scholar] [CrossRef]
- Bertram, R.; Sherman, A.; Stanley, E.F. Single-domain/bound calcium hypothesis of transmitter release and facilitation. J. Neurophysiol. 1996, 75, 1919–1931. [Google Scholar] [CrossRef] [PubMed]
- Jackman, S.L.; Regehr, W.G. The Mechanisms and Functions of Synaptic Facilitation. Neuron 2017, 94, 447–464. [Google Scholar] [CrossRef] [Green Version]
- Marro, J.; Dickman, R. Nonequilibrium Phase Transitions in Lattice Models; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pretel, J.; Torres, J.J.; Marro, J. EEGs Disclose Significant Brain Activity Correlated with Synaptic Fickleness. Biology 2021, 10, 647. https://doi.org/10.3390/biology10070647
Pretel J, Torres JJ, Marro J. EEGs Disclose Significant Brain Activity Correlated with Synaptic Fickleness. Biology. 2021; 10(7):647. https://doi.org/10.3390/biology10070647
Chicago/Turabian StylePretel, Jorge, Joaquín J. Torres, and Joaquín Marro. 2021. "EEGs Disclose Significant Brain Activity Correlated with Synaptic Fickleness" Biology 10, no. 7: 647. https://doi.org/10.3390/biology10070647
APA StylePretel, J., Torres, J. J., & Marro, J. (2021). EEGs Disclose Significant Brain Activity Correlated with Synaptic Fickleness. Biology, 10(7), 647. https://doi.org/10.3390/biology10070647





