Computer-Aided Design for Identifying Anticancer Targets in Genome-Scale Metabolic Models of Colon Cancer
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
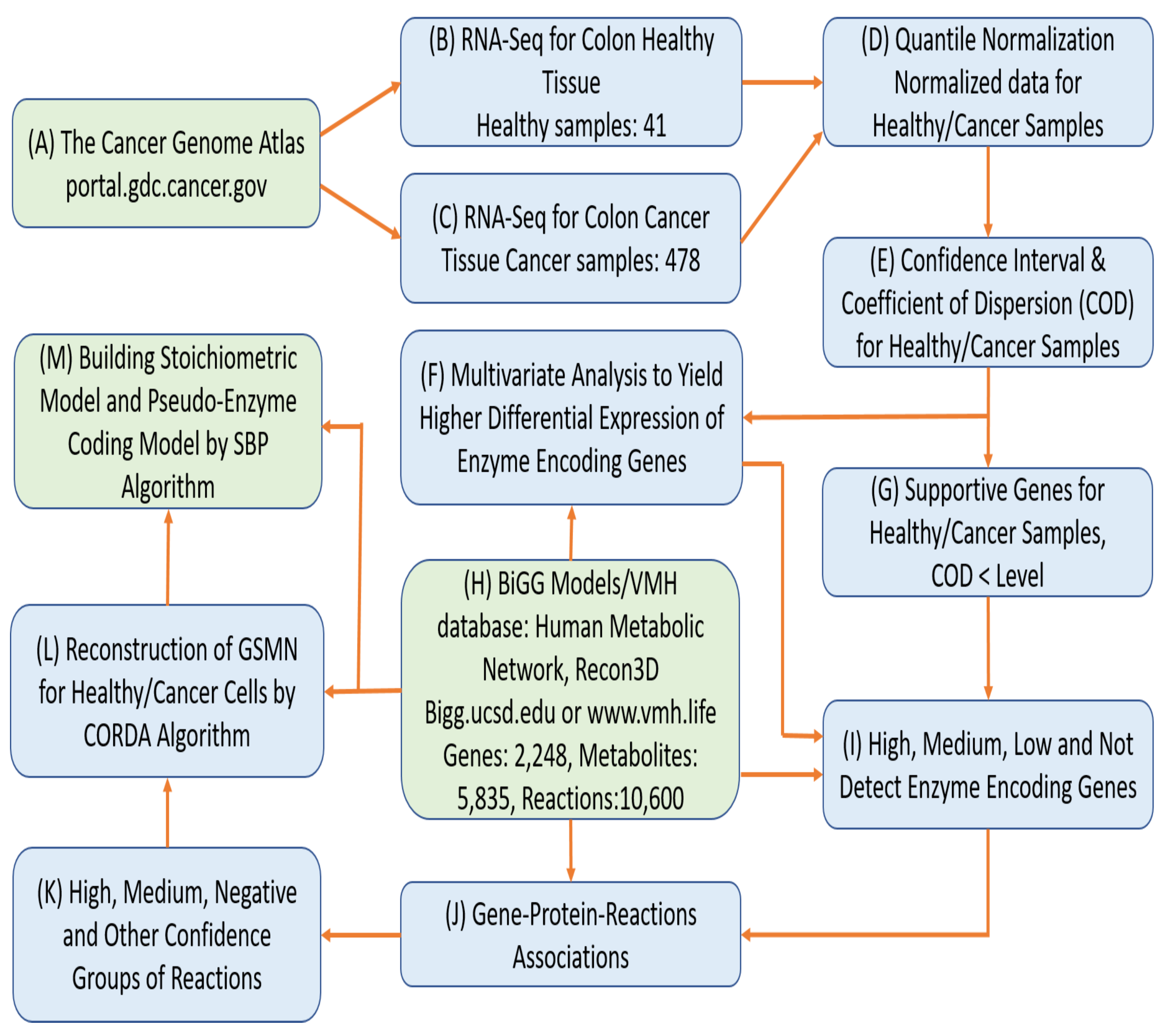
2.1. Reconstruction of Tissue-Specific GSMNs
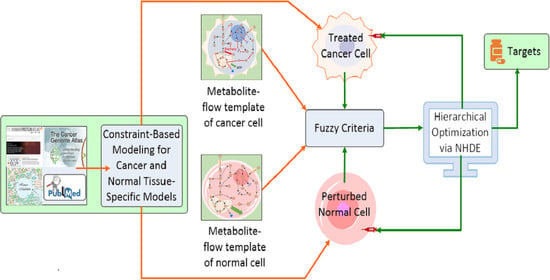
2.2. Optimization Framework for Target Identification
2.3. Hierarchical Fitness in Outer Optimization
2.4. Factor Analysis
3. Results and Discussion
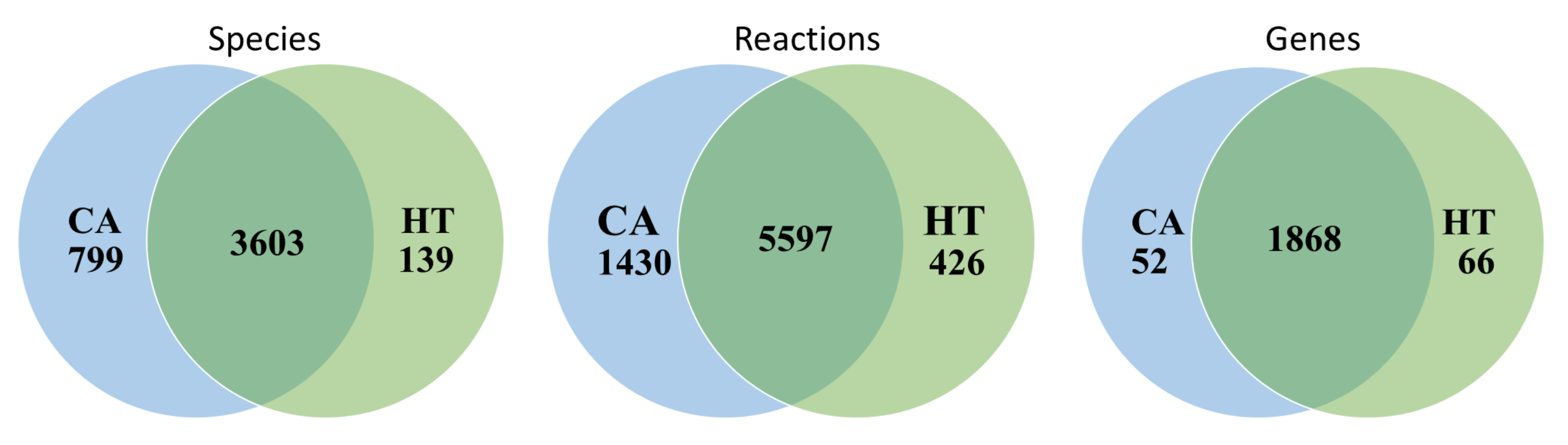
3.1. Reconstruction of Healthy and Cancerous Models
3.2. Gene-Centric Approach
3.3. Metabolite-Centric Approach
3.4. Factor Loading of Identified Targets
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Enzyme |
| ADSL | Adenylosuccinate lyase |
| ADSS2 | Adenylosuccinate synthetase isozyme 2 |
| BPGM | Bisphosphoglycerate mutase |
| CAD | CAD protein |
| CRLS1 | Cardiolipin synthase (CMP-forming) |
| DHODH | Dihydroorotate dehydrogenase (quinone) |
| EBP | 3--hydroxysteroid-(8),(7)-isomerase |
| ENO1 | -enolase |
| FDFT1 | Squalene synthase |
| G6PD | Glucose-6-phosphate 1-dehydrogenase |
| GAPDH | Glyceraldehyde-3-phosphate dehydrogenase |
| H6PD | GDH/6PGL endoplasmic bifunctional protein |
| HMGCR | 3-hydroxy-3-methylglutaryl-coenzyme A reductase |
| KDSR | 3-ketodihydrosphingosine reductase |
| LSS | Lanosterol synthase |
| MVD | Diphosphomevalonate decarboxylase |
| MVK | Mevalonate kinase |
| NSDHL | Sterol-4-alpha-carboxylate 3-dehydrogenase |
| PCK1 | Phosphoenolpyruvate carboxykinase |
| PGK1 | Phosphoglycerate kinase 1 |
| PGS1 | CDP-diacylglycerol-glycerol-3-phosphate 3-phosphatidyltransferase |
| PMVK | Phosphomevalonate kinase |
| PTDSS1 | Phosphatidylserine synthase 1 |
| RPIA | Ribose-5-phosphate isomerase |
| SPTLC1/2/3 | A complex of serine palmitoyltransferase |
| SQLE | Squalene monooxygenase |
| UMPS | Uridine 5-monophosphate synthase |
| Symbol | Metabolite |
| 13dpg | 3-Phospho-D-Glyceroyl Phosphate |
| 2pg | 2-Phospho-D-Glycerate |
| 3dsphgn | (2S)-1-Hydroxy-3-Oxooctadecan-2-Aminium |
| 3pg | 3-Phospho-D-Glycerate |
| 5dpmev | (R)-5-Diphosphomevalonate |
| 5mthf | 5-Methyltetrahydrofolate |
| 5pmev | (R)-5-Phosphonatomevalonate |
| 6pgc | 6-Phospho-D-Gluconate |
| 6pgl | 6-Phospho-D-Glucono-1,5-Lactone |
| accoa | Acetyl Coenzyme A |
| ach | Acetylcholine |
| akg | 2-Oxoglutarate |
| amet | S-Adenosyl-L-Methionine |
| amp | Adenosine Monophosphate |
| betald | Betaine Aldehyde |
| cdpdag-hs | Cytidine-5-Diphosphate-Diacylglycerol |
| chol | Choline |
| cit | Citrate |
| clpn-hs | Cardiolipin |
| crm-hs | N-Acylsphingosine |
| ctp | Cytidine-5-Triphosphate |
| dhap | Dihydroxyacetone Phosphate |
| dhcrm-hs | Dihydroceramide |
| dhf | 7,8-Dihydrofolate |
| dhor-S | (S)-Dihydroorotate |
| dmgly | N,N-Dimethylglycine |
| dtdp | Deoxythymidine-5-Diphosphate |
| dtmp | Deoxythymidine-5-Phosphate |
| dttp | Deoxythymidine-5-Triphosphate |
| dudp | Deoxyuridine-5-Diphosphate |
| dump | Deoxyuridine-5-Monophosphate |
| dutp | Deoxyuridine-5-Triphosphate |
| f6p | D-Fructose 6-Phosphate |
| fdp | D-Fructose 1,6-Bisphosphate |
| fol | Folate |
| g1p | D-Glucose 1-Phosphate |
| g3p | Glyceraldehyde 3-Phosphate |
| g3pc | Glycerophosphocholine |
| g6p | D-Glucose 6-Phosphate |
| glc-D | D-glucose |
| gln-L | L-Glutamine |
| glu-L | L-Glutamate |
| gly | Glycine |
| gmp | Guanosine-5-Monophosphate |
| hmgcoa | Hydroxymethylglutaryl Coenzyme A |
| icit | Isocitric Acid |
| imp | Inosine-5-Monophosphate |
| ipdp | Isopentenyl Diphosphate |
| maloca | Malonyl Coenzyme A |
| met-L | L-Methionine |
| mev-R | (R)-Mevalonate |
| mlthf | 5,10-Methylenetetrahydrofolate |
| oaa | Oxaloacetate |
| orot | Orotate |
| pa-hs | Phosphatidate |
| pail-hs | 1-Phosphatidyl-1D-Myo-Inositol |
| pchol-hs | Phosphatidylcholine |
| pe-hs | Phosphatidylethanolamine |
| pep | Phosphoenolpyruvate |
| pglyc-hs | Phosphatidylglycerol |
| pgp-hs | Phosphatidyl Glycerol Phosphate |
| pmtcoa | Palmitoyl Coenzyme A |
| prpp | 5-Phospho-Alpha-D-Ribose 1-Diphosphate |
| ps-hs | Phosphatidylserine |
| pyr | Pyruvate |
| r5p | Alpha-D-Ribose 5-Phosphate |
| ser-L | L-Serine |
| sphmyln-hs | Sphingomyelin |
| succoa | Succinyl Coenzyme A |
| thf | 5,6,7,8-Tetrahydrofolate |
| udp | Uridine Diphosphate |
| ump | Uridine-5-Monophosphate |
References
- Morozova, O.; Marra, M.A. Applications of next-generation sequencing technologies in functional genomics. Genomics 2008, 92, 255–264. [Google Scholar] [CrossRef] [Green Version]
- Barrett, T.; Wilhite, S.E.; Ledoux, P.; Evangelista, C.; Kim, I.F.; Tomashevsky, M.; Marshall, K.A.; Phillippy, K.H.; Sherman, P.M.; Holko, M.; et al. NCBI GEO: Archive for functional genomics data sets–update. Nucleic Acids Res. 2013, 41, D991–D995. [Google Scholar] [CrossRef] [Green Version]
- Uhlen, M.; Oksvold, P.; Fagerberg, L.; Lundberg, E.; Jonasson, K.; Forsberg, M.; Zwahlen, M.; Kampf, C.; Wester, K.; Hober, S.; et al. Towards a knowledge-based human protein atlas. Nat. Biotechnol. 2010, 28, 1248–50. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S.; Feunang, Y.D.; Marcu, A.; Guo, A.C.; Liang, K.; Vázquez-Fresno, R.; Sajed, T.; Johnson, D.; Li, C.; Karu, N.; et al. HMDB 4.0: The human metabolome database for 2018. Nucleic Acids Res. 2018, 46, D608–D617. [Google Scholar] [CrossRef]
- Winter, G.; Krömer, J.O. Fluxomics-connecting ’omics analysis and phenotypes. Environ. Microbiol. 2013, 15, 1901–16. [Google Scholar] [CrossRef] [PubMed]
- Paananen, J.; Fortino, V. An omics perspective on drug target discovery platforms. Briefings Bioinform. 2020, 21, 1937–1953. [Google Scholar] [CrossRef] [Green Version]
- Agren, R.; Mardinoglu, A.; Asplund, A.; Kampf, C.; Uhlen, M.; Nielsen, J. Identification of anticancer drugs for hepatocellular carcinoma through personalized genome-scale metabolic modeling. Mol. Syst. Biol. 2014, 10, 721. [Google Scholar] [CrossRef]
- Brul, S.; Angione, C. Human systems biology and metabolic modelling: A review–from disease metabolism to precision medicine. Biomed Res. Int. 2019, 2019, 8304260. [Google Scholar]
- Kell, D.B.; Goodacre, R. Metabolomics and systems pharmacology: Why and how to model the human metabolic network for drug discovery. Drug Discov Today 2014, 19, 171–182. [Google Scholar] [CrossRef]
- Yizhak, K.; Chaneton, B.; Gottlieb, E.; Ruppin, E. Modeling cancer metabolism on a genome scale. Mol. Syst. Biol. 2015, 11, 817. [Google Scholar] [CrossRef]
- Zielinski, D.C.; Jamshidi, N.; Corbett, A.J.; Bordbar, A.; Thomas, A.; Palsson, B.O. Systems biology analysis of drivers underlying hallmarks of cancer cell metabolism. Sci. Rep. 2017, 7, 41241–41241. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Sahoo, S.; Zielinski, D.C.; Altunkaya, A.; Dräger, A.; Mih, N.; Gatto, F.; Nilsson, A.; Preciat Gonzalez, G.A.; Aurich, M.K.; et al. Recon3D enables a three-dimensional view of gene variation in human metabolism. Nat. Biotechnol. 2018, 36, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Heirendt, L.; Arreckx, S.; Pfau, T.; Mendoza, S.N.; Richelle, A.; Heinken, A.; Haraldsdóttir, H.S.; Wachowiak, J.; Keating, S.M.; Vlasov, V.; et al. Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v.3.0. Nat. Protoc. 2019, 14, 639–702. [Google Scholar] [CrossRef] [Green Version]
- Hanahan, D.; Weinberg, R. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–74. [Google Scholar] [CrossRef] [Green Version]
- Pavlova, N.N.; Thompson, C.B. The emerging hallmarks of cancer metabolism. Cell Metab. 2016, 23, 27–47. [Google Scholar] [CrossRef] [Green Version]
- Folger, O.; Jerby, L.; Frezza, C.; Gottlieb, E.; Ruppin, E.; Shlomi, T. Predicting selective drug targets in cancer through metabolic networks. Mol. Syst. Biol. 2011, 7, 501. [Google Scholar] [CrossRef] [PubMed]
- Ghaffari, P.; Mardinoglu, A.; Nielsen, J. Cancer metabolism: A modeling perspective. Front. Physiol. 2015, 6, 382–382. [Google Scholar] [CrossRef] [Green Version]
- Jerby, L.; Ruppin, E. Predicting drug targets and biomarkers of cancer via genome-scale metabolic modeling. Clin. Cancer Res. 2012, 18, 5572. [Google Scholar] [CrossRef] [Green Version]
- Lewis, N.E.; Abdel-Haleem, A.M. The evolution of genome-scale models of cancer metabolism. Front. Physiol. 2013, 4, 237–237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nilsson, A.; Nielsen, J. Genome scale metabolic modeling of cancer. Metab. Eng. 2017, 43, 103–112. [Google Scholar] [CrossRef]
- Robinson, J.L.; Nielsen, J. Anticancer drug discovery through genome-scale metabolic modeling. Curr. Opin. Syst. Biol. 2017, 4, 1–8. [Google Scholar] [CrossRef]
- Agren, R.; Bordel, S.; Mardinoglu, A.; Pornputtapong, N.; Nookaew, I.; Nielsen, J. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT. PLoS Comput. Biol. 2012, 8, e1002518. [Google Scholar] [CrossRef] [PubMed]
- Bintener, T.; Pacheco, M.P.; Sauter, T. Towards the routine use of in silico screenings for drug discovery using metabolic modelling. Biochem. Soc. Trans. 2020, 48, 955–969. [Google Scholar] [CrossRef]
- Frezza, C.; Zheng, L.; Folger, O.; Rajagopalan, K.N.; MacKenzie, E.D.; Jerby, L.; Micaroni, M.; Chaneton, B.; Adam, J.; Hedley, A.; et al. Haem oxygenase is synthetically lethal with the tumour suppressor fumarate hydratase. Nature 2011, 477, 225–228. [Google Scholar] [CrossRef]
- Li, L.; Zhou, X.; Ching, W.K.; Wang, P. Predicting enzyme targets for cancer drugs by profiling human metabolic reactions in NCI-60 cell lines. BMC Bioinf. 2010, 11, 501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pacheco, M.P.; Bintener, T.; Ternes, D.; Kulms, D.; Haan, S.; Letellier, E.; Sauter, T. Identifying and targeting cancer-specific metabolism with network-based drug target prediction. EBioMedicine 2019, 43, 98–106. [Google Scholar] [CrossRef] [Green Version]
- Resendis-Antonio, O.; Checa, A.; Encarnación, S. Modeling core metabolism in cancer cells: Surveying the topology underlying the warburg effect. PLoS ONE 2010, 5, e12383. [Google Scholar] [CrossRef] [Green Version]
- Turanli, B.; Zhang, C.; Kim, W.; Benfeitas, R.; Uhlen, M.; Arga, K.Y.; Mardinoglu, A. Discovery of therapeutic agents for prostate cancer using genome-scale metabolic modeling and drug repositioning. EBioMedicine 2019, 42, 386–396. [Google Scholar] [CrossRef] [Green Version]
- Yizhak, K.; Gaude, E.; Le Dévédec, S.; Waldman, Y.Y.; Stein, G.Y.; van de Water, B.; Frezza, C.; Ruppin, E. Phenotype-based cell-specific metabolic modeling reveals metabolic liabilities of cancer. eLife 2014, 3, e03641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jalili, M.; Scharm, M.; Wolkenhauer, O.; Damaghi, M.; Salehzadeh-Yazdi, A. Exploring the metabolic heterogeneity of cancers: A benchmark study of context-specific models. J. Pers. Med. 2021, 11, 496. [Google Scholar] [CrossRef]
- Jerby, L.; Shlomi, T.; Ruppin, E. Computational reconstruction of tissue-specific metabolic models: Application to human liver metabolism. Mol. Syst. Biol. 2010, 6, 401. [Google Scholar] [CrossRef]
- Machado, D.; Herrgård, M. Systematic evaluation of methods for integration of transcriptomic data into constraint-based models of metabolism. PLoS Comput. Biol. 2014, 10, e1003580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Opdam, S.; Richelle, A.; Kellman, B.; Li, S.; Zielinski, D.C.; Lewis, N.E. A systematic evaluation of methods for tailoring genome-scale metabolic models. Cell Syst. 2017, 4, 318–329.e6. [Google Scholar] [CrossRef] [Green Version]
- Schultz, A.; Qutub, A.A. Reconstruction of tissue-specific metabolic networks using CORDA. PLoS Comput. Biol. 2016, 12, e1004808. [Google Scholar] [CrossRef]
- Vlassis, N.; Pacheco, M.P.; Sauter, T. Fast reconstruction of compact context-specific metabolic network models. PLoS Comput. Biol. 2014, 10, e1003424–e1003424. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Eddy, J.A.; Price, N.D. Reconstruction of genome-scale metabolic models for 126 human tissues using mCADRE. BMC Syst. Biol. 2012, 6, 153. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Chan, C. Human metabolic network: Reconstruction, simulation, and applications in systems biology. Metabolites 2012, 2, 242–53. [Google Scholar] [CrossRef] [Green Version]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2019. CA A Cancer J. Clin. 2019, 69, 7–34. [Google Scholar] [CrossRef] [Green Version]
- Taiwan Health Promotion Administration. Taiwan Cancer Registry, Cancer Statistics: Incidence and Mortality Rates for the Top 10 Cancer in Taiwan, 2008–2014. 2018. Available online: http://tcr.cph.ntu.edu.tw/ (accessed on 24 November 2018).
- Swainston, N.; Smallbone, K.; Hefzi, H.; Dobson, P.D.; Brewer, J.; Hanscho, M.; Zielinski, D.C.; Ang, K.S.; Gardiner, N.J.; Gutierrez, J.M.; et al. Recon 2.2: From reconstruction to model of human metabolism. Metabolomics 2016, 12, 109. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.S.; Wu, W.H.; Hsiu, W.S.; Liu, Y.J.; Chuang, K.W. Genome-scale metabolic modeling with protein expressions of normal and cancerous colorectal tissues for oncogene inference. Metabolites 2019, 10, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, W.H.; Li, F.Y.; Shu, Y.C.; Lai, J.M.; Chang, P.M.H.; Huang, C.Y.F.; Wang, F.S. Oncogene inference optimization using constraint-based modelling incorporated with protein expression in normal and tumour tissues. R. Soc. Open Sci. 2020, 7, 191241. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.T.; Lin, M.R.; Chen, W.C.; Wu, W.H.; Wang, F.S. Optimization of a modeling platform to predict oncogenes from genome-scale metabolic networks of non-small-cell lung cancers. FEBS Open Bio 2021, 11, 2078–2094. [Google Scholar] [CrossRef] [PubMed]
- National Cancer Institute of U.S. The Cancer Genome Atlas Program. Department of Health and Human Services. 2020. Available online: https://www.cancer.gov/about-nci/organization/ccg/research/structural-genomics/tcga (accessed on 1 July 2020).
- Gatto, F.; Miess, H.; Schulze, A.; Nielsen, J. Flux balance analysis predicts essential genes in clear cell renal cell carcinoma metabolism. Sci. Rep. 2015, 5, 10738. [Google Scholar] [CrossRef]
- Megchelenbrink, W.; Katzir, R.; Lu, X.; Ruppin, E.; Notebaart, R.A. Synthetic dosage lethality in the human metabolic network is highly predictive of tumor growth and cancer patient survival. Proc. Natl. Acad. Sci. USA 2015, 112, 12217–12222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pratapa, A.; Balachandran, S.; Raman, K. Fast-SL: An efficient algorithm to identify synthetic lethal sets in metabolic networks. Bioinformatics 2015, 31, 3299–3305. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.F.; Wang, F.S. Crisp and fuzzy optimization of a fed-batch fermentation for ethanol production. Ind. Eng. Chem. Res. 2003, 42, 6843–6850. [Google Scholar] [CrossRef]
- Huang, H.J.; Wang, F.S. Fuzzy decision-making design of chemical plant using mixed-integer hybrid differential evolution. Comput. Chem. Eng. 2002, 26, 1649–1660. [Google Scholar] [CrossRef]
- Hsu, K.C.; Wang, F.S. Fuzzy optimization for detecting enzyme targets of human uric acid metabolism. Bioinformatics 2013, 29, 3191–3198. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.S.; Jing, C.H.; Tsao, G.T. Fuzzy-decision-making problems of fuel ethanol production using a genetically engineered yeast. Ind. Eng. Chem. Res. 1998, 37, 3434–3443. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy set theory. WIREs Comp. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; et al. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2018, 46, D1074–D1082. [Google Scholar] [CrossRef]
- Satoh, K.; Yachida, S.; Sugimoto, M.; Oshima, M.; Nakagawa, T.; Akamoto, S.; Tabata, S.; Saitoh, K.; Kato, K.; Sato, S.; et al. Global metabolic reprogramming of colorectal cancer occurs at adenoma stage and is induced by MYC. Proc. Natl. Acad. Sci. USA 2017, 114, E7697–E7706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamaguchi, N.; Weinberg, E.M.; Nguyen, A.; Liberti, M.V.; Goodarzi, H.; Janjigian, Y.Y.; Paty, P.B.; Saltz, L.B.; Kingham, T.P.; Loo, J.M.; et al. PCK1 and DHODH drive colorectal cancer liver metastatic colonization and hypoxic growth by promoting nucleotide synthesis. eLife 2019, 8, e52135. [Google Scholar] [CrossRef]
- Li, L.; Ng, S.R.; Colón, C.I.; Drapkin, B.J.; Hsu, P.P.; Li, Z.; Nabel, C.S.; Lewis, C.A.; Romero, R.; Mercer, K.L.; et al. Identification of DHODH as a therapeutic target in small cell lung cancer. Sci. Transl. Med. 2019, 11. [Google Scholar] [CrossRef]
- Sykes, D.B. The emergence of dihydroorotate dehydrogenase (DHODH) as a therapeutic target in acute myeloid leukemia. Expert Opin. Ther. Targets 2018, 22, 893–898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdel-Magid, A.F. Use of dihydroorotate dehydrogenase inhibitors for treatment of autoimmune diseases and cancer. ACS Med. Chem. Lett. 2020, 11, 2072–2074. [Google Scholar] [CrossRef]
- Clendening, J.W.; Penn, L.Z. Targeting tumor cell metabolism with statins. Oncogene 2012, 31, 4967–78. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gray, R.T.; Loughrey, M.B.; Bankhead, P.; Cardwell, C.R.; McQuaid, S.; O’Neill, R.F.; Arthur, K.; Bingham, V.; McGready, C.; Gavin, A.T.; et al. Statin use, candidate mevalonate pathway biomarkers, and colon cancer survival in a population-based cohort study. Br. J. Cancer 2017, 116, 1652–1659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lipkin, S.M.; Chao, E.C.; Moreno, V.; Rozek, L.S.; Rennert, H.; Pinchev, M.; Dizon, D.; Rennert, G.; Kopelovich, L.; Gruber, S.B. Genetic variation in 3-hydroxy-3-methylglutaryl CoA reductase modifies the chemopreventive activity of statins for colorectal cancer. Cancer Prev. Res. 2010, 3, 597–603. [Google Scholar] [CrossRef] [Green Version]
- Tian, S.; Siu, F.M.; Lok, C.N.; Fung, Y.M.E.; Che, C.M. Anticancer auranofin engages 3-hydroxy-3-methylglutaryl-coenzyme A reductase (HMGCR) as a target. Met. Integr. Biometal Sci. 2019, 11, 1925–1936. [Google Scholar] [CrossRef]
- Longley, D.B.; Harkin, D.P.; Johnston, P.G. 5-fluorouracil: Mechanisms of action and clinical strategies. Nat. Rev. Cancer 2003, 3, 330–338. [Google Scholar] [CrossRef] [PubMed]
- Ishiguro, L.; Yang, M.; Sohn, K.J.; Streutker, C.J.; Grin, A.; Croxford, R.; Kim, Y.I. Folic acid supplementation adversely affects chemosensitivity of colon cancer cells to 5-fluorouracil. Nutr. Cancer 2016, 68, 780–90. [Google Scholar] [CrossRef] [PubMed]
- Handali, S.; Moghimipour, E.; Rezaei, M.; Ramezani, Z.; Kouchak, M.; Amini, M.; Angali, K.A.; Saremy, S.; Dorkoosh, F.A. A novel 5-Fluorouracil targeted delivery to colon cancer using folic acid conjugated liposomes. Biomed. Pharmacother. 2018, 108, 1259–1273. [Google Scholar] [CrossRef]
- Matherly, L.H.; Czajkowski, C.A.; Muench, S.P.; Psiakis, J.T. Role for cytosolic folate-binding proteins in the compartmentation of endogenous tetrahydrofolates and the 5-formyl tetrahydrofolate-mediated enhancement of 5-fluoro-2′-deoxyuridine antitumor activity in vitro. Cancer Res. 1990, 50, 3262–3269. [Google Scholar]
- Focaccetti, C.; Bruno, A.; Magnani, E.; Bartolini, D.; Principi, E.; Dallaglio, K.; Bucci, E.O.; Finzi, G.; Sessa, F.; Noonan, D.M.; et al. Effects of 5-Fluorouracil on Morphology, cell cycle, proliferation, apoptosis, autophagy and ROS production in endothelial cells and cardiomyocytes. PLoS ONE 2015, 10, e0115686. [Google Scholar] [CrossRef]
- Hou, Z.y.; Tong, X.p.; Peng, Y.b.; Zhang, B.k.; Yan, M. Broad targeting of triptolide to resistance and sensitization for cancer therapy. Biomed. Pharmacother. 2018, 104, 771–780. [Google Scholar] [CrossRef]
- Zeng, H.; Zhu, X.; Tian, Q.; Yan, Y.; Zhang, L.; Yan, M.; Li, R.; Li, X.; Wang, G.; Ma, J.; et al. In vivo antitumor effects of carboxymethyl chitosan-conjugated triptolide after oral administration. Drug Deliv. 2020, 27, 848–854. [Google Scholar] [CrossRef] [PubMed]
- Köhne, C.H.; Wils, J.; Lorenz, M.; Schöffski, P.; Voigtmann, R.; Bokemeyer, C.; Lutz, M.; Kleeberg, C.; Ridwelski, K.; Souchon, R.; et al. Randomized phase III study of high-dose fluorouracil given as a weekly 24-hour infusion with or without leucovorin versus bolus fluorouracil plus leucovorin in advanced colorectal cancer: European organization of Research and Treatment of Cancer Gastrointestinal Group Study 40952. J. Clin. Oncol. 2003, 21, 3721–3728. [Google Scholar]
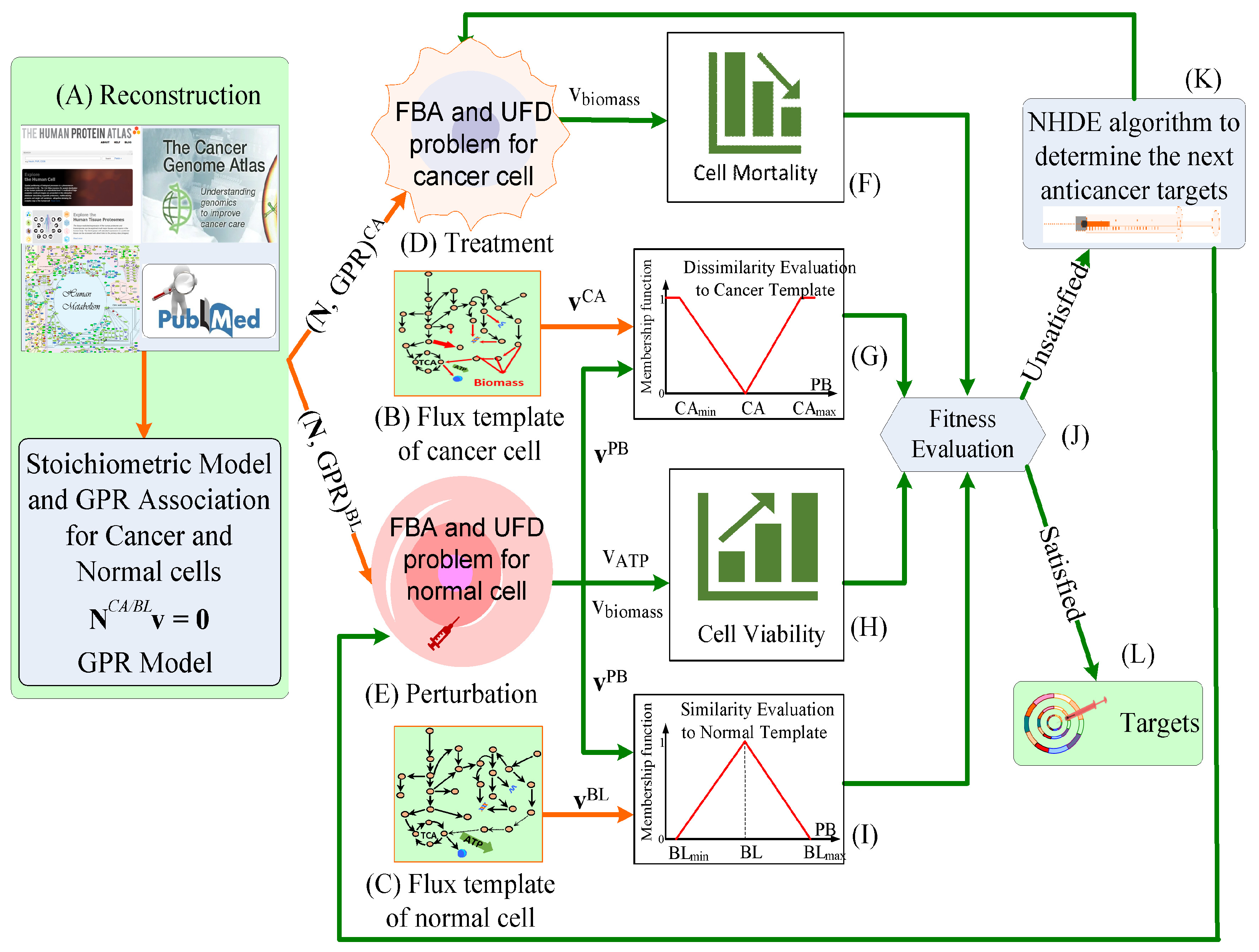

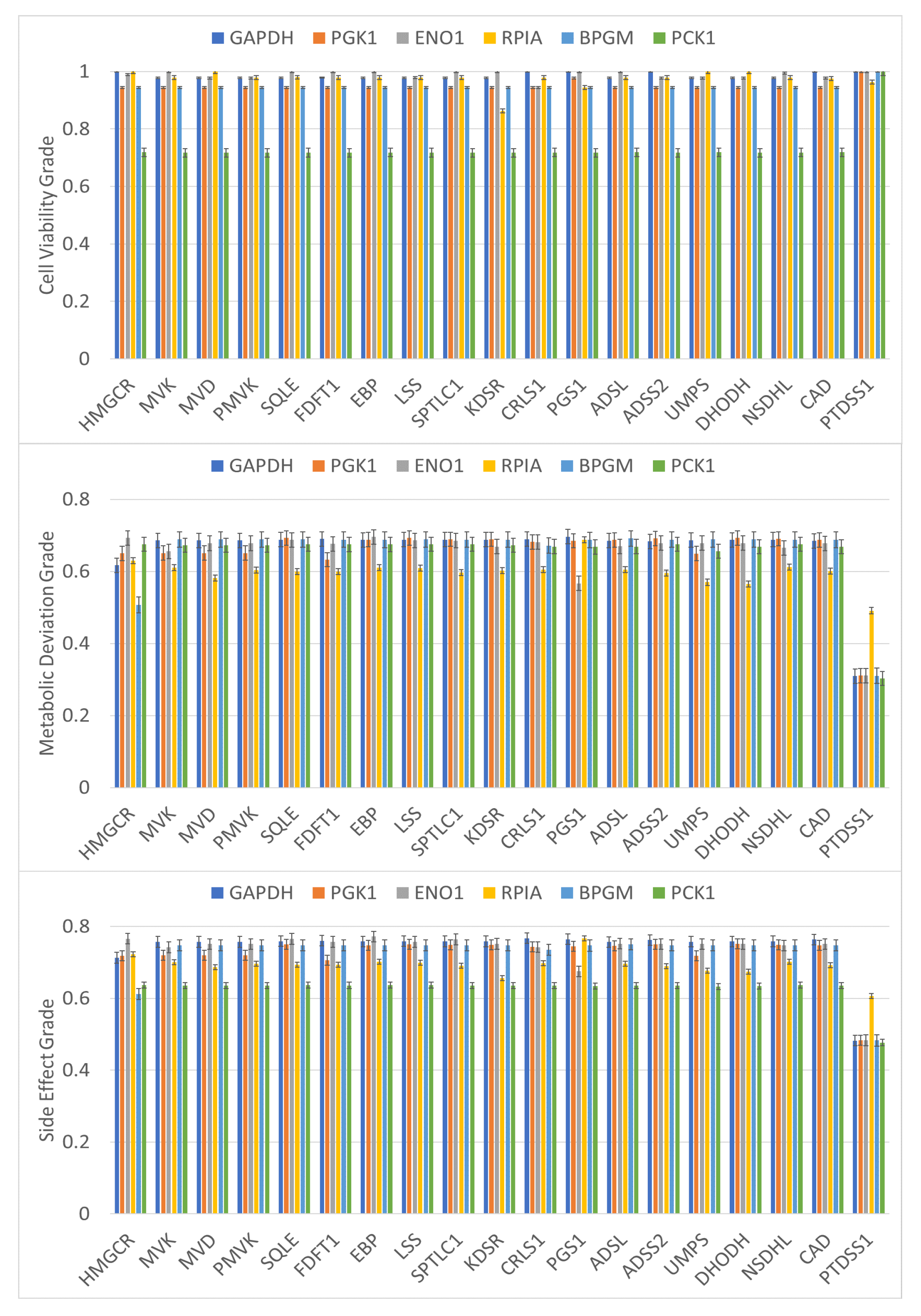
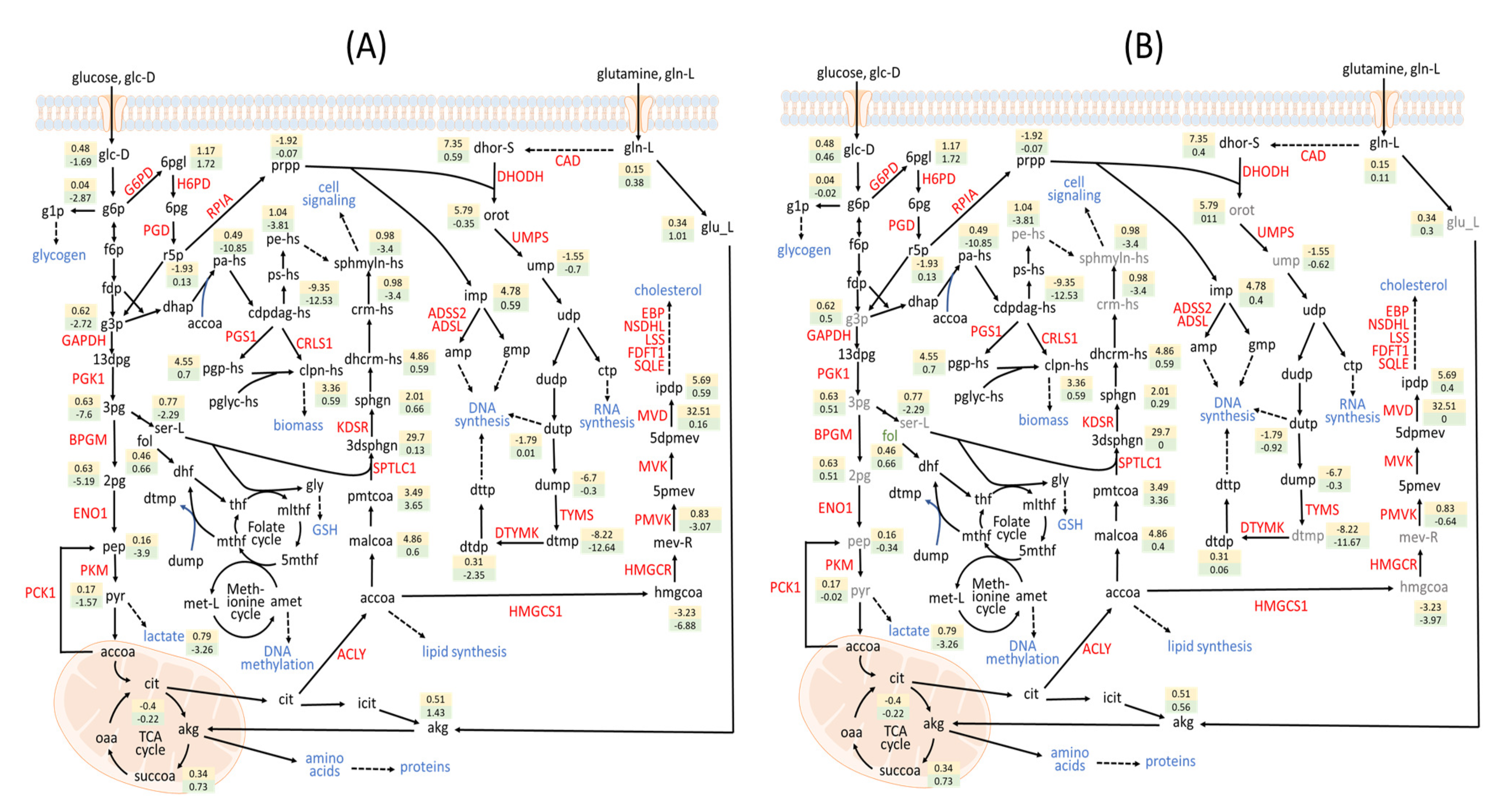

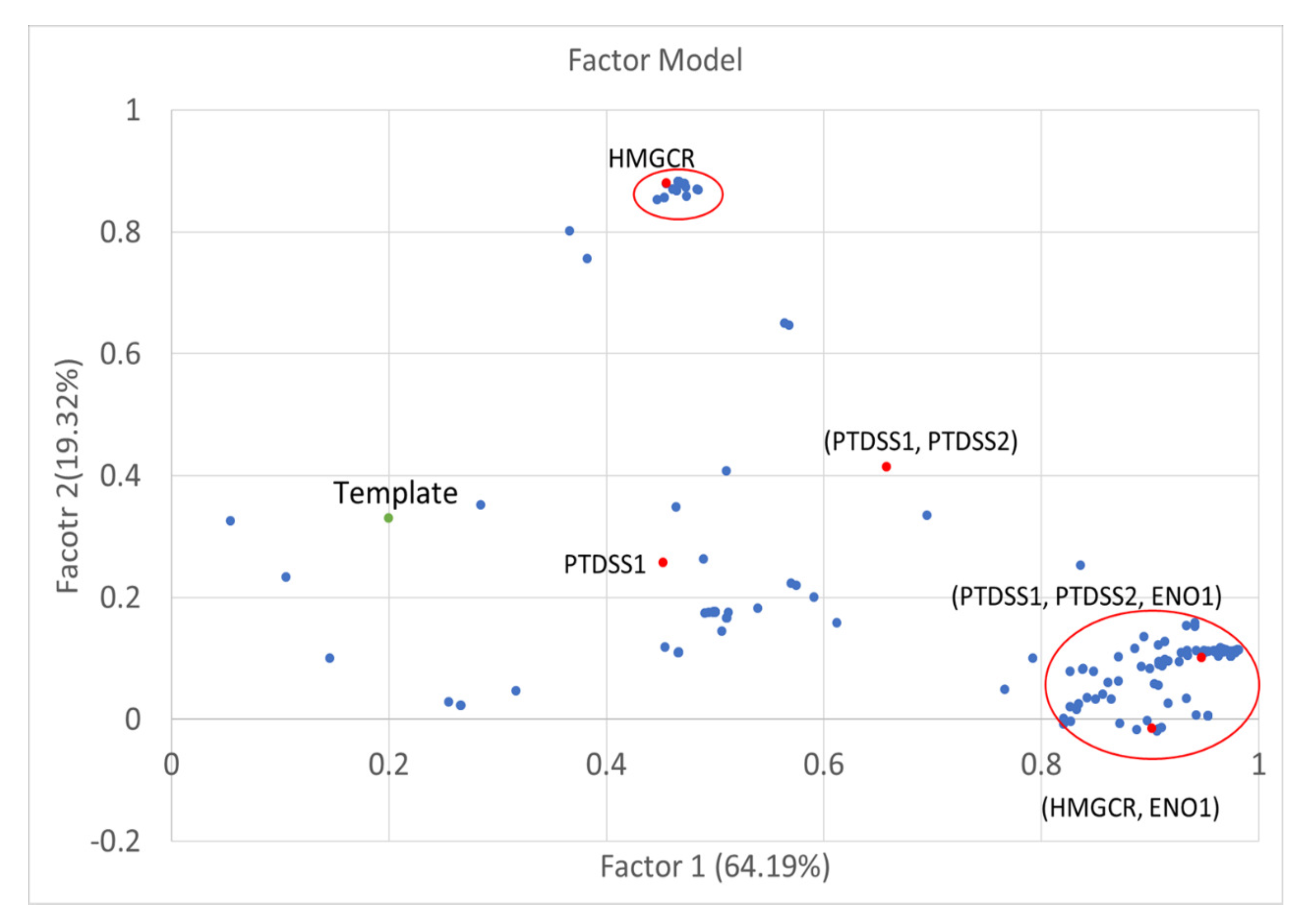
| Objectives in the outer optimization problem |
| 1. The first objective is to measure the mortality of treated cancer cells. |
| 2. The second objective is to obtain superior cell viability of normal cells in cancer treatment. |
| 3. The third objective is to keep the metabolic deviation of perturbed cells as dissimilar as possible to the cancer template. |
| 4. The fourth objective is to keep the metabolic deviation of perturbed cells as similar as possible to the normal template. |
| subject to the constraint-based models in the inner optimization problems |
| 1. FBA and UFD problems for treated cancer cells. |
| 2. FBA and UFD problems for perturbation of normal cells due to cancer treatment. |
| Gene | N/D | nDrugs | Ave. AE | Pathway | |||
|---|---|---|---|---|---|---|---|
| HMGCR | 0.719 | 0.675 | 0.637 | 50/51 | 20 | 8.77 | Cholesterol Biosynthesis, Statin Pathway, Mevalonate Pathway |
| MVK | 0.719 | 0.669 | 0.636 | 50/51 | 1 | – | Mevalonate Pathway, Regulation of Cholesterol Biosynthesis By SREBP |
| MVD | 0.719 | 0.669 | 0.636 | 48/51 | – | – | Mevalonate Pathway, Regulation of Cholesterol Biosynthesis By SREBP |
| PMVK | 0.719 | 0.669 | 0.636 | 23/51 | – | – | Mevalonate Pathway, Regulation of Cholesterol Biosynthesis By SREBP |
| SQLE | 0.719 | 0.672 | 0.637 | 3/51 | 4 | 6.73 | Cholesterol Biosynthesis III, Statin Pathway |
| FDFT1 | 0.719 | 0.674 | 0.637 | 8/51 | 1 | – | Cholesterol Biosynthesis III, Statin Pathway |
| EBP | 0.719 | 0.674 | 0.637 | 0/51 | 1 | 8.94 | Cholesterol Biosynthesis III |
| LSS | 0.719 | 0.672 | 0.637 | 0/51 | 2 | – | Cholesterol Biosynthesis III |
| NSDHL | 0.719 | 0.674 | 0.637 | 0/51 | 1 | – | Cholesterol Biosynthesis III |
| SPTLC1/2/3 | 0.719 | 0.670 | 0.636 | 37/51 | 2 | – | Sphingolipid Metabolism |
| KDSR | 0.719 | 0.670 | 0.636 | 6/51 | – | – | Sphingolipid Metabolism |
| CRLS1 | 0.719 | 0.669 | 0.636 | 38/51 | – | – | Glycerophospholipid Biosynthesis |
| PGS1 | 0.719 | 0.448 | 0.492 | 50/51 | – | – | Glycerophospholipid Biosynthesis |
| PTDSS1 | 1.0 | 0.303 | 0.477 | 8/51 | 1 | – | Glycerophospholipid Biosynthesis |
| ADSL | 0.719 | 0.669 | 0.636 | 49/51 | – | – | Metabolism of Nucleotides, Purine Metabolism |
| ADSS2 | 0.719 | 0.669 | 0.636 | 37/51 | 3 | – | Metabolism of Nucleotides, Purine Metabolism |
| UMPS | 0.719 | 0.655 | 0.632 | 29/51 | 2 | 9.82 | Metabolism of Nucleotides, Pyrimidine Biosynthesis |
| DHODH | 0.719 | 0.448 | 0.492 | 19/51 | 26 | 10.04 | Metabolism of Nucleotides, Pyrimidine Biosynthesis |
| CAD | 0.719 | 0.669 | 0.636 | 27/51 | 3 | 8.9 | Metabolism of Nucleotides, Pyrimidine Biosynthesis |
| RPIA | 0.719 | 0.675 | 0.637 | 6/51 | 1 | – | Pentose Phosphate Pathway |
| Metabolite | Symbol | Subclass | |||
|---|---|---|---|---|---|
| Hydroxymethylglutaryl Coenzyme A | hmgcoa | 0.712 | 0.668 | 0.636 | Fatty acyl thioesters |
| Mevalonate | mev-R | 0.719 | 0.674 | 0.637 | Fatty acids and conjugates |
| Orotate | orotsumpplementation | 0.718 | 0.673 | 0.637 | Pyrimidines and pyrimidine derivatives |
| Deoxythymidine-5-Phosphate | dtmp | 0.719 | 0.665 | 0.635 | Pyrimidine deoxyribonucleotides |
| Uridine-5-Monophosphate | ump | 0.701 | 0.67 | 0.626 | Pyrimidine ribonucleoside monophosphates |
| Phosphatidylethanolamine | pe-hs | 0.795 | 0.691 | 0.7 | Glycerophospholipids |
| L-Glutamate | glu-L | 0.783 | 0.663 | 0.675 | Amino acid |
| L-Serine | ser-L | 0.789 | 0.656 | 0.672 | Amino acid |
| N-Acylsphingosine | crm-hs | 0.75 | 0.664 | 0.665 | The parent compounds of the ceramide family |
| Sphingomyelin | sphmyln-hs | 0.75 | 0.655 | 0.658 | Phosphosphingolipids, fatty acyl group |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.-T.; Wang, T.-Y.; Chen, P.-R.; Wu, W.-H.; Lai, J.-M.; Chang, P.M.-H.; Hong, Y.-R.; Huang, C.-Y.F.; Wang, F.-S. Computer-Aided Design for Identifying Anticancer Targets in Genome-Scale Metabolic Models of Colon Cancer. Biology 2021, 10, 1115. https://doi.org/10.3390/biology10111115
Cheng C-T, Wang T-Y, Chen P-R, Wu W-H, Lai J-M, Chang PM-H, Hong Y-R, Huang C-YF, Wang F-S. Computer-Aided Design for Identifying Anticancer Targets in Genome-Scale Metabolic Models of Colon Cancer. Biology. 2021; 10(11):1115. https://doi.org/10.3390/biology10111115
Chicago/Turabian StyleCheng, Chao-Ting, Tsun-Yu Wang, Pei-Rong Chen, Wu-Hsiung Wu, Jin-Mei Lai, Peter Mu-Hsin Chang, Yi-Ren Hong, Chi-Ying F. Huang, and Feng-Sheng Wang. 2021. "Computer-Aided Design for Identifying Anticancer Targets in Genome-Scale Metabolic Models of Colon Cancer" Biology 10, no. 11: 1115. https://doi.org/10.3390/biology10111115
APA StyleCheng, C.-T., Wang, T.-Y., Chen, P.-R., Wu, W.-H., Lai, J.-M., Chang, P. M.-H., Hong, Y.-R., Huang, C.-Y. F., & Wang, F.-S. (2021). Computer-Aided Design for Identifying Anticancer Targets in Genome-Scale Metabolic Models of Colon Cancer. Biology, 10(11), 1115. https://doi.org/10.3390/biology10111115