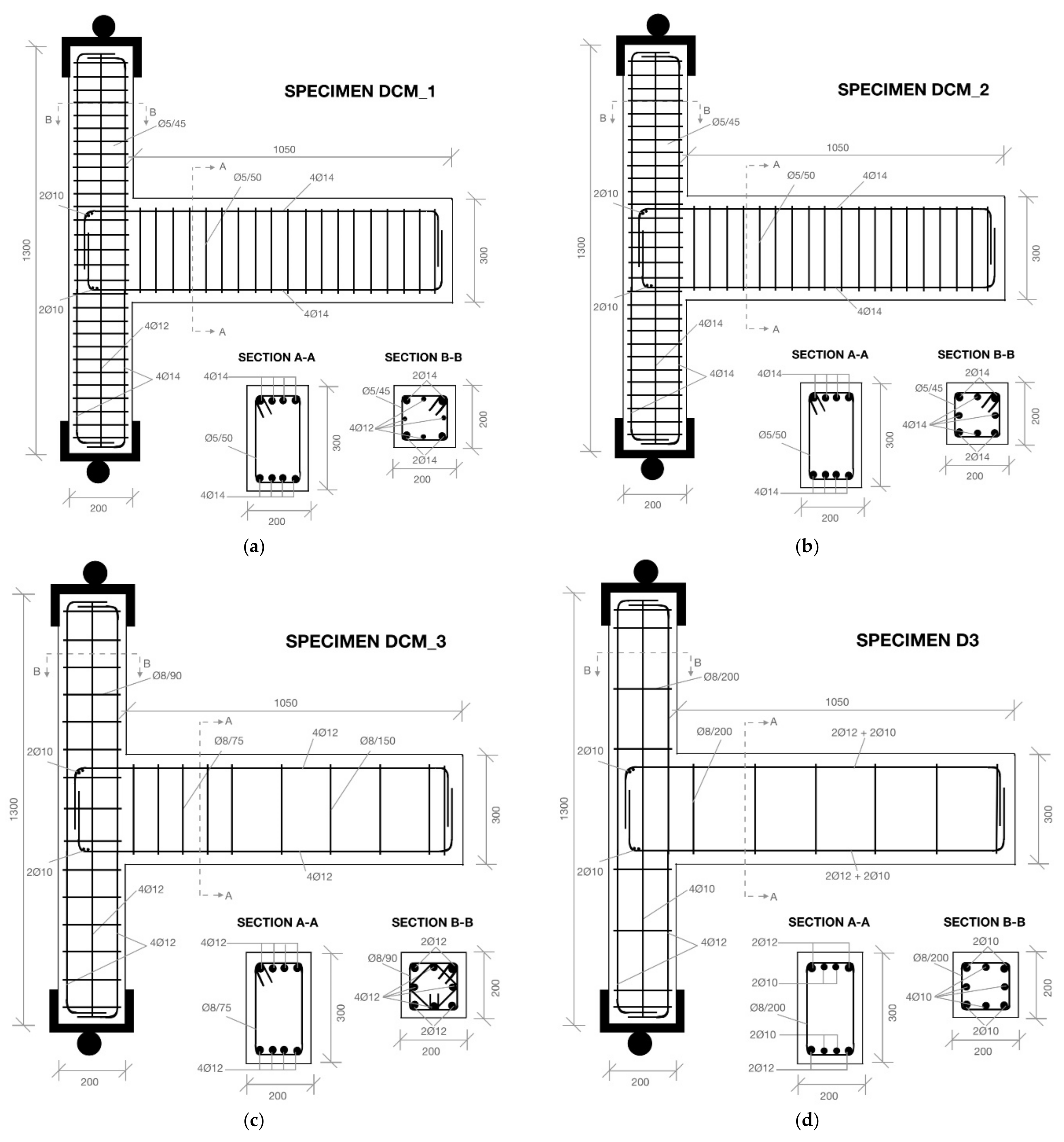
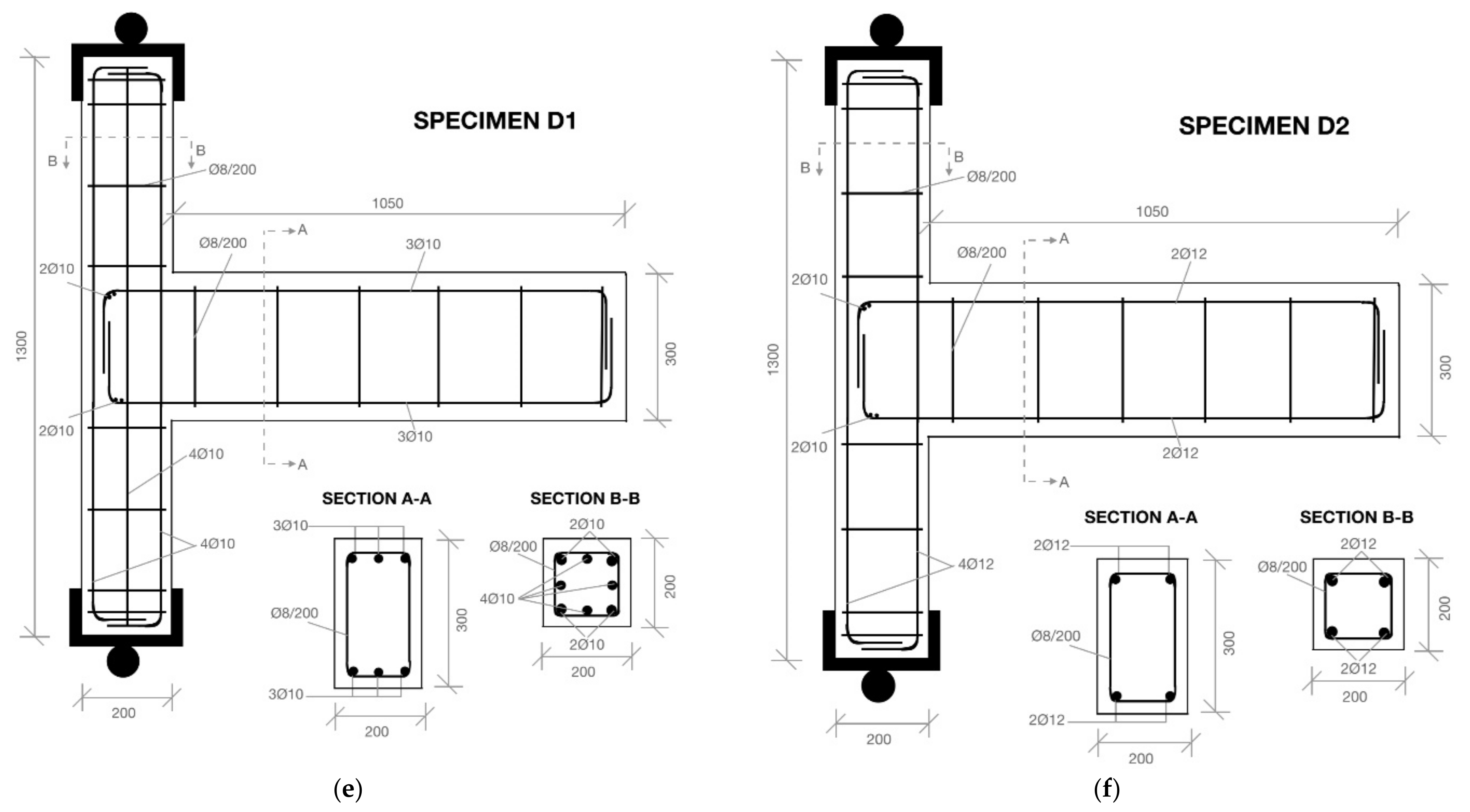
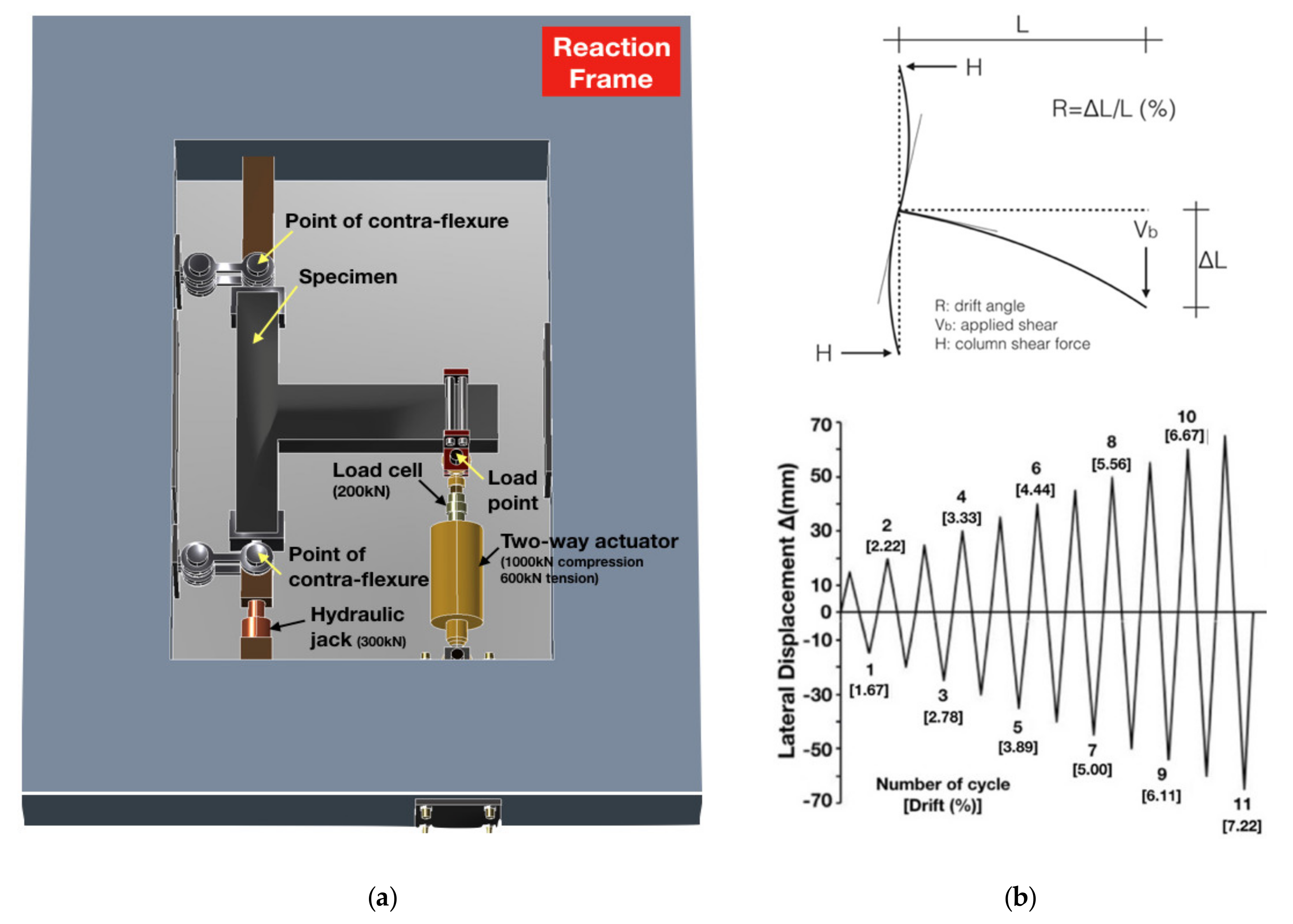
3.1. Interpretation of the Hysteresis Behavior of the Subassemblages
The cyclic lateral response of the exterior RC beam-to-column joint subassemblages, i.e., , , , , , and , is subsequently evaluated using data acquired from the experimental equipment during testing. Thus, the reliability of both the modern and the older code provisions for the design of beam–column connections was investigated by evaluating the perceived lateral strength, peak-to-peak stiffness, and hysteretic energy dissipation capacity.
Specimens
,
, and
were designed according to the current Eurocode provisions with the capacity design ratio
(i.e., 1.31, 1.60, and 1.49 for
,
, and
, respectively). Therefore, the seismic performance of these subassemblages would have to be consistent with the behavior documented in the seismic design philosophy of the modern codes, that is, the concentration of damage and the formation of the plastic hinges are to be found in the beam, while the beam–column joint region remains intact throughout testing. However, contrary to expectations, the specimens exhibited undesirable brittle shear failure of the joint region, while no cracking of the beam of the subassemblages was observed. In particular, hairline shear cracks appeared in both diagonal directions of the joint region during the first cycle of the earthquake-type loading of
,
, and
. This was attributed to the significantly increased value of the joint shear force, which was almost six times higher than the beam shear force. During the incremental amplitudes of the cyclic lateral displacement sequence, the joint shear cracks progressively dilated, causing disintegration of the core concrete. Meanwhile, for the drift angle, R, which was 3.33%, the bond stress value in the circumference of the beam reinforcing bars that were anchored in the joint region exceeded the doubled tensile strength of the concrete (
). As a result, splitting cracks were formed in the concrete perpendicular to the bars. The propagation of these cracks resulted in the gradual partial loss of the concrete cover in the rear face of the joint. It is worth noting that while the beam longitudinal bars were well anchored in the joint region, they were also welded to 2∅10 mm bar segments in the transverse direction (see
Figure 1a–c) to preclude slipping during tests. Furthermore, the closely spaced hoops of the columns did not open.
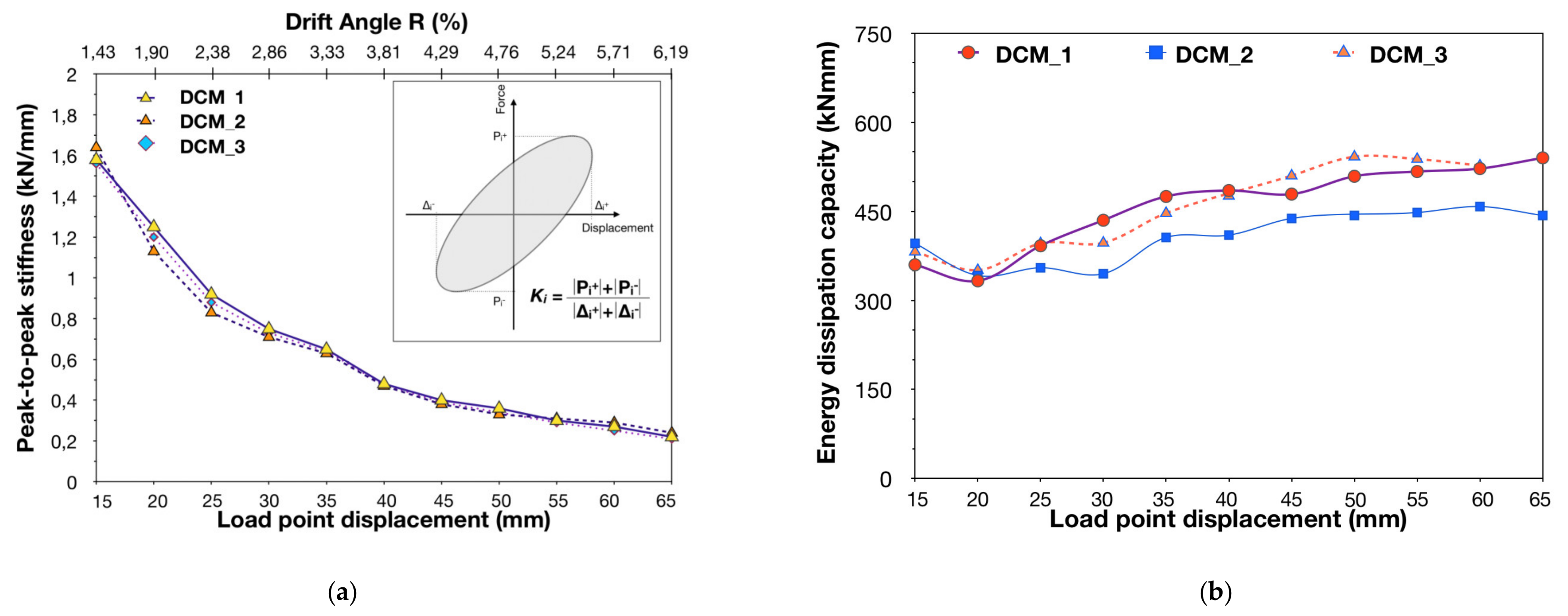
Subassemblages,
and
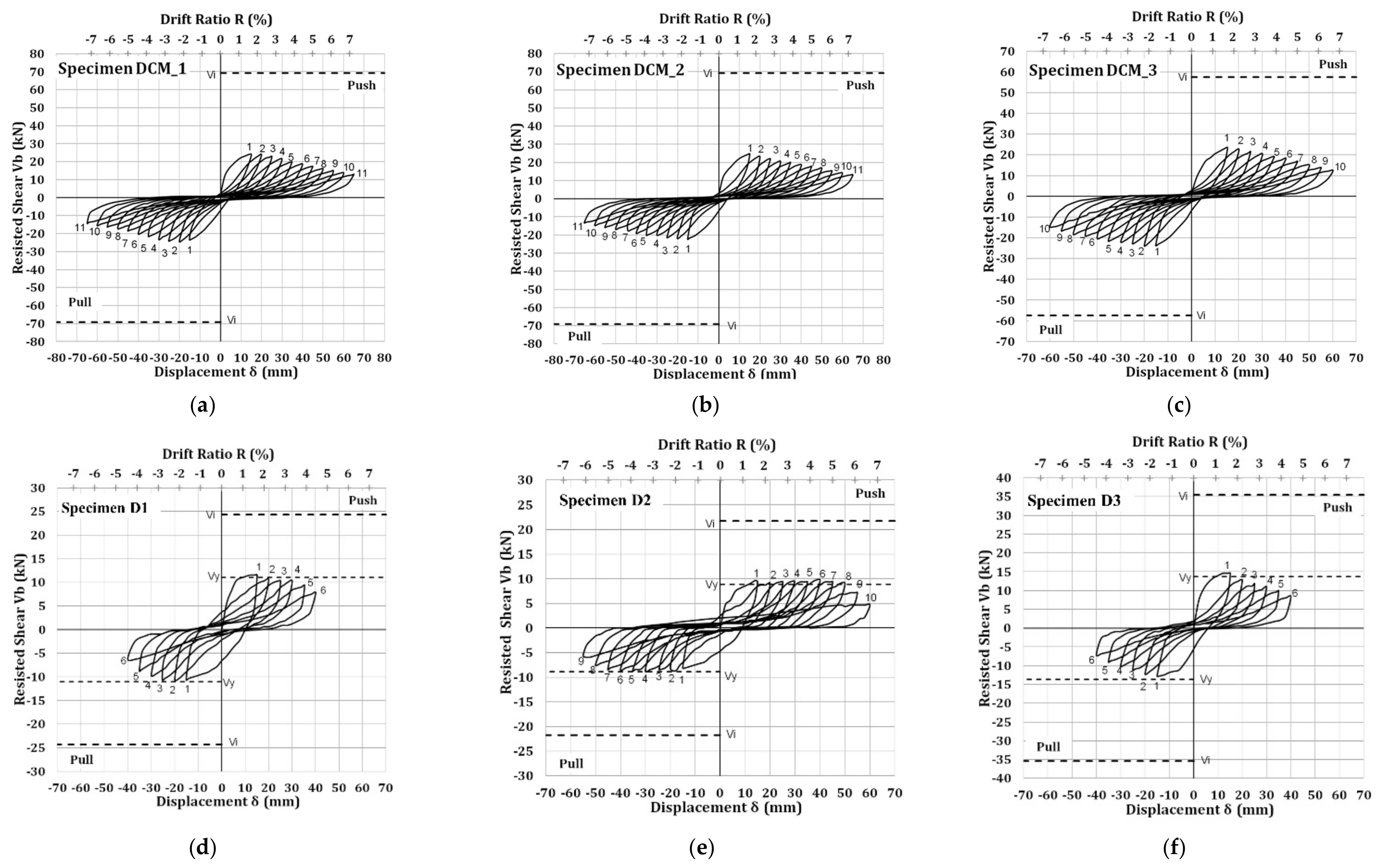
, showed a progressive slow-rate reduction of lateral strength and of peak-to-peak stiffness in both cases of the push half-cycles and the pull half-cycles of the earthquake-type loading (see
Figure 3a,b). In the case of specimen
, the reduction of lateral strength and peak-to-peak stiffness was more intensive than that in specimens
and
. This can be observed in the hysteresis loops of the subassemblages (see
Figure 3a–c). None of the three beam–column joint specimens developed its nominal flexural moment capacity, while the resisted shear forces, which were 22.83 kN for
, 24.63 kN for
, and 23.69 kN for
, were only a mere portion (33%, 35.6%, and 41.3%, respectively) of the shear capacity of the joints (69.17 kN and 57.41 kN). The peak-to-peak stiffness values of
and
were similar throughout testing. For instance,
retained 17.80% of its initial peak-to-peak stiffness at the end of testing. The corresponding values in the case of subassemblages
and
were 19.42 and 12.82%, respectively (see
Figure 4a). Moreover, specimens
,
, and
. showed poor energy dissipation capacity, characterized by a slight increase of energy dissipation values during the consecutive cycles of the earthquake-type loading. In particular, for drift angle R, which was 6.67%, the energy dissipated in the case of subassemblage
was 49.91% higher than that dissipated during the first cycle of loading. The corresponding values in the case of subassemblages
and
were 20% and 35.25%, respectively (see
Figure 4b). Ultimately, despite being designed according to current EC8 provisions for DCM, the beam–column joint subassemblages
,
, and
showed poor overall hysteresis behaviour, while exhibiting undesirable brittle shear failure of the joint region.
Thus, it was clearly demonstrated experimentally that designing the RC beam-to-column joint regions according to the current Eurocode provisions for DCM with flexural strength ratio is not always enough, neither to secure the formation of the plastic hinges solely in the beams nor to effectively preclude the brittle shear failure of the joints. Therefore, modern RC structures designed for DCM in earthquake-prone areas are still susceptible to possess controversial seismic performance and to develop undesirable failure mechanisms responsible for possible collapse. Furthermore, the efficiency and reliability of retrofitting measures, which were designed according to current Eurocode provisions for improving the cyclic response of beam–column joints of existing pre-1960s–1970s RC structures, are also questionable.
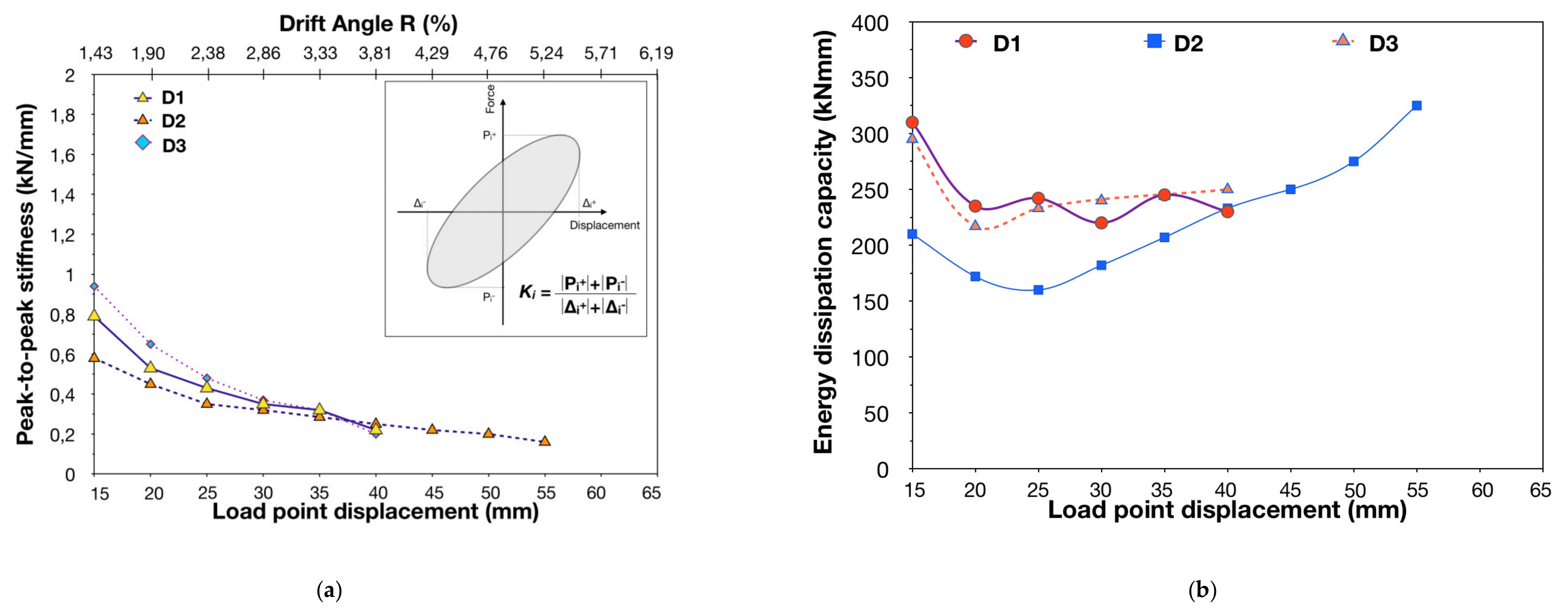
The beam–column joint subassemblages
,
, and
showed poor overall hysteresis behavior, dominated by the shear failure of the joint area. The latter is clearly reflected in the hysteresis loops of the specimens (see
Figure 3d–f). The initial damage of
,
, and
during the first cycle of the earthquake-type loading included hairline shear cracking of the joint region in both diagonal directions and the formation of the principal flexural crack in the beam in juncture with the joint. Thereupon, the damage evolved and was concentrated solely in the joint region of the specimens, while no further cracking—except for the principal flexural crack which gradually dilated during testing—was observed in the beams. None of the three subassemblages developed its nominal moment flexural capacity. In fact, the maximum shear force resisted by specimens
,
, and
corresponded to 63%, 52.6%, and 40.8% of its shear capacity, respectively. Subassemblage
exhibited a more stable hysteresis behaviour with respect to
and
. Nevertheless, the lateral strength values of
were slightly increased compared to the corresponding values of
. The beam–column joint specimens
and
failed prematurely in brittle shear for the drift angle value of R = 4.44%, while
failed for drift angle value of R = 6.67%. Moreover, the specimens showed particularly low energy dissipation capacity. In the case of specimen
, a continuous reduction of the energy dissipation capacity values was observed during the consecutive cycles of loading, owing to the severe shear damage of the joint region. For instance, at the end of the testing of
(for the lateral drift angle value of R = 4.44%), the energy dissipation capacity was 75.47% of the initial value during the first cycle of loading. The corresponding value in the case of specimen
was 85.32% (see
Figure 5a,b). In comparison, for the drift angle value R = 6.67%, specimen
showed a 53.37% increase in energy dissipation capacity with respect to the initial value (see
Figure 5b).
It is noteworthy that the subassemblages
,
, and
were designed with a capacity design ratio value of
(see
Table 1 and
Table 3). Nevertheless, they all developed excessive premature shear damaging of the joint. This was mainly attributed to the sparsely spaced stirrups in the columns and the joint region, which were unable to provide adequate confinement to the core concrete to withstand the significantly increased shear forces inserted to the joint of the specimens from the well-anchored beam longitudinal reinforcement. As a result,
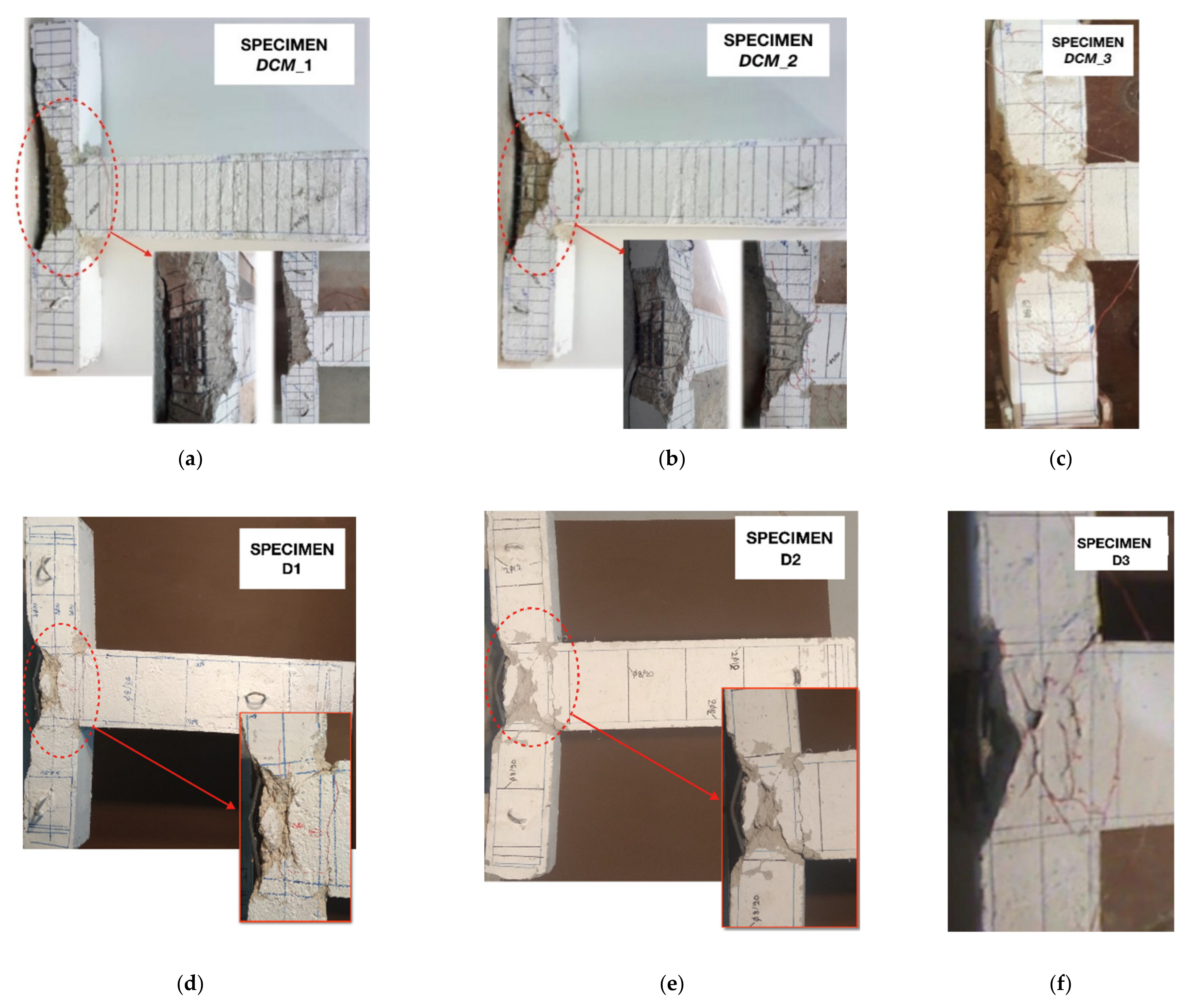
,
, and
literally collapsed, due to the loss of axial load carrying capacity, while buckling of the column longitudinal reinforcement occurred. This is clearly illustrated in the failure mode of the specimens (see
Figure 6d–f).
From the comprehensive interpretation of the hysteresis behavior of subassemblages , , , , , and , it is evident that the undesirable brittle shear failure of RC beam–column connections cannot always be effectively inhibited, considering only the design assumption of flexural ratio value of . On the other hand, the inner mechanisms of the joint region should necessarily be sufficiently described, while the shear capacity of the joint should also be accurately calculated.
3.2. Monitoring of the Steel Bar Micro-Strain
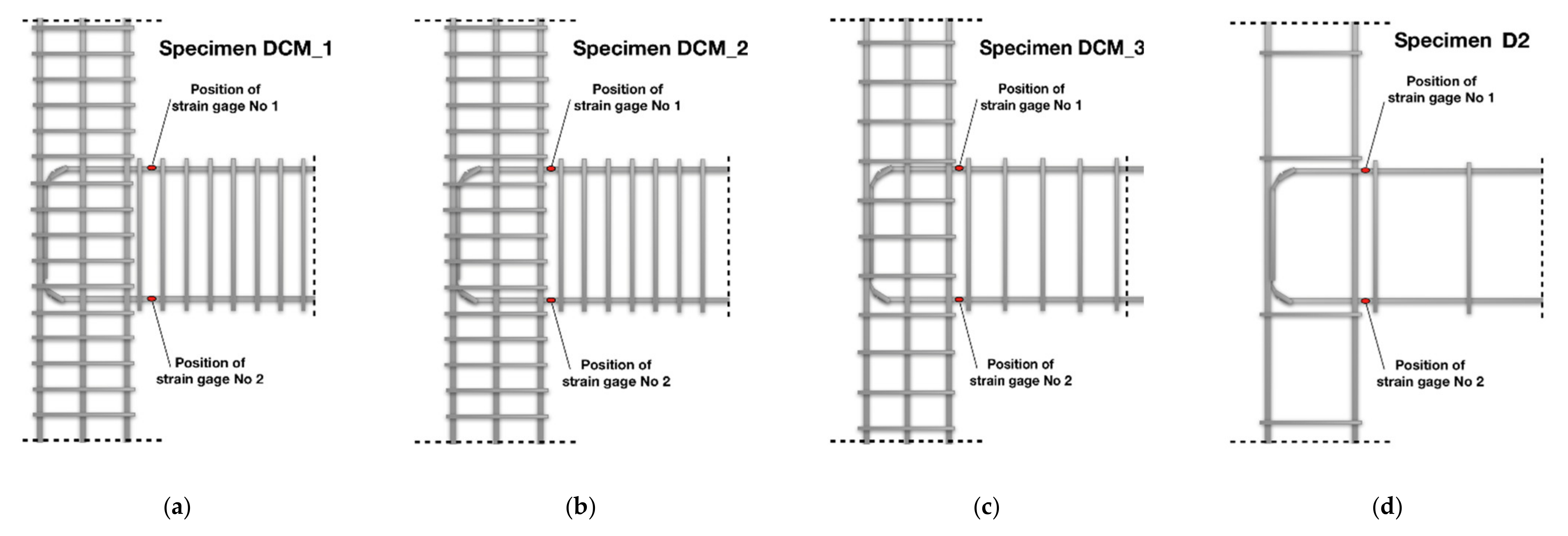
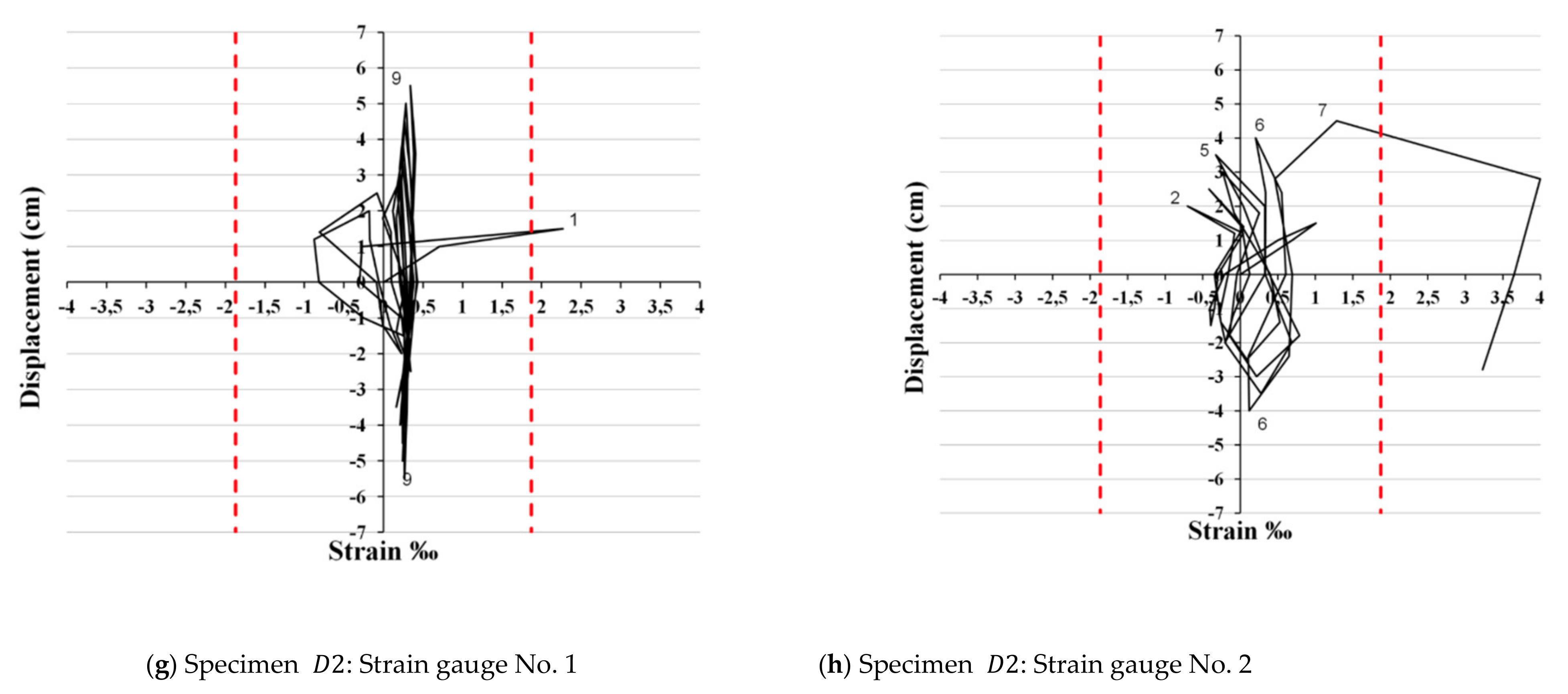
Monitoring of the steel strain value variations during the earthquake-type loading of the beam–column joint subassemblages was achieved using electrical resistant strain gauges, which were attached to the bars. The exact location of each strain gauge is presented in
Figure 7, while in
Figure 8 the plots of the load point displacement versus strain of reinforcement are illustrated. The latter provided critical and valuable information about the specimens’ response when they were subjected to inelastic cyclic lateral deformations [
33]. Similar work can be found in literature [
34,
35], where the transverse reinforcement and fiber hoop strains were monitored experimentally. In particular, the strain values that exceeded the yield strain were recorded during testing for both cases of the plain S220 bars of subassemblage
and the B500C beam reinforcement of specimens
,
, and
(see
Figure 8a–f).
A comprehensive interpretation of the data acquired using the strain gauges requires careful observation and analysis of the damage evolution. It is also worth noting that the most crucial factor for the seismic performance of the beam–column joint region is the combination of the capacity design ratio value (
ΣMRc/ΣMRb) and the value of coefficient
γ of the developed shear stresses in the joint (
). The latter can be found using the proposed analytical formulation of Tsonos, which also allows for the precise prediction of the ultimate shear capacity of the joint (
γult). It was proven experimentally [
14] that for values of the coefficient
γ < 0.5
γult, the developed shear stresses are low, and they allow for the concentration of damage solely in the beam, while the joint region remains intact. For high values of the coefficient
γ (
γ >
γult), shear damage of the joint occurs prior to the development of the beam flexural moment capacity. For intermediate values of the coefficient
γ (0.5
γult <
γ <
γult), it is possible that a mixed-type failure (including damage in the beam and the joint region) can occur. Under these lines, the damage evolution of the beam–column joint subassemblages is subsequently examined.
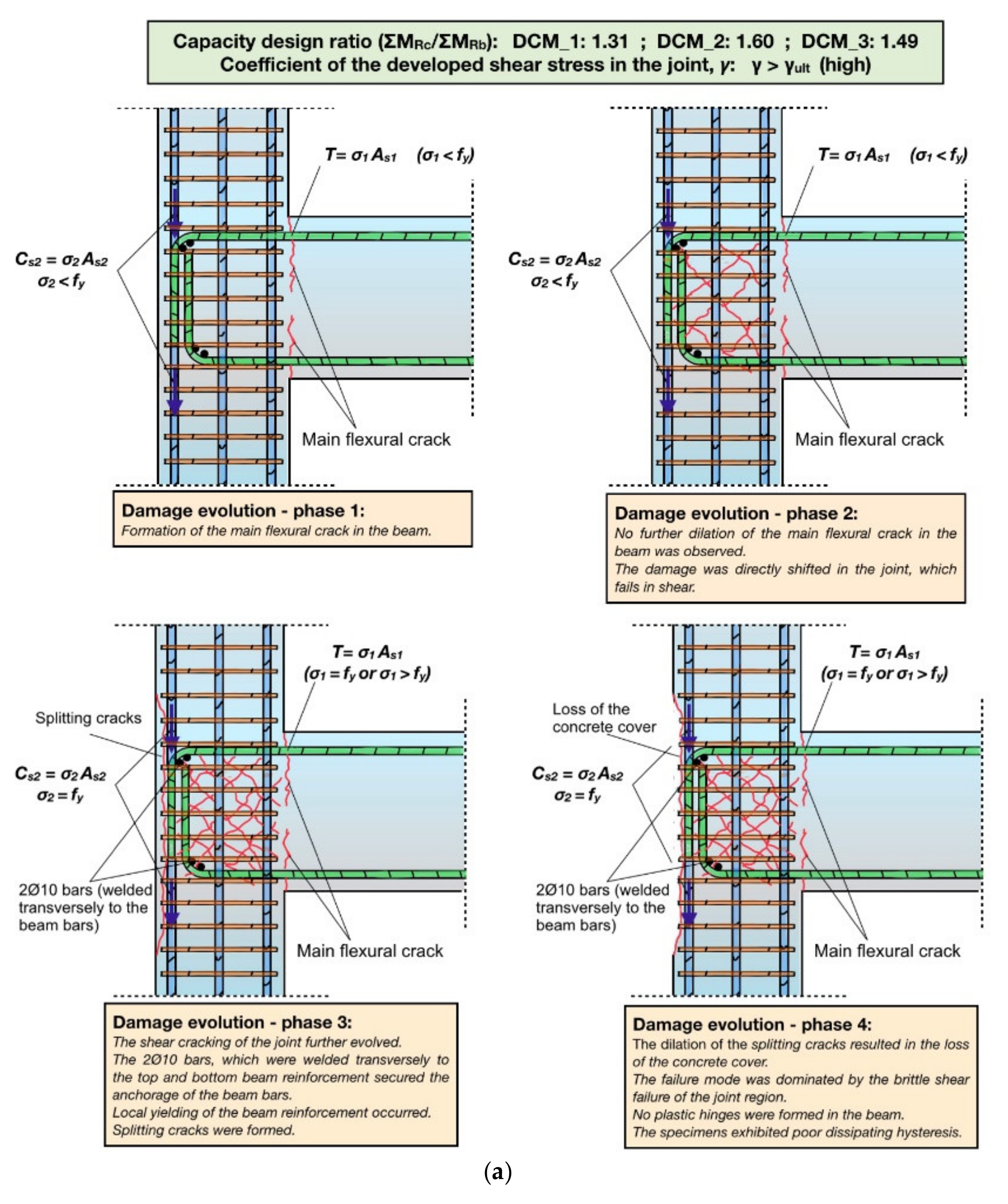
Specimens
,
, and
were designed with capacity design ratios of 1.31, 1.60, and 1.49, respectively, satisfying the requirement of EC8 for
ΣMRc/ΣMRb > 1.30. However, the developed shear stresses in the joint region of the subassemblages were significantly high and exceeded the ultimate shear capacities, as shown in
Table 4. As a result, early failure of the joint region of
,
, and
occurred. In particular, after the formation of the main flexural crack in the beam during the first cycle of the earthquake-type loading (see
Figure 9a, Phase 1), the damage was directly shifted in the joint region of the specimens, where shear cracking gradually evolved (see
Figure 9a, Phase 2). This is attributed to the particularly high value of the shear force introduced in the joint, which is six times the value of the shear force of the beam. After the fourth cycle, splitting cracks were formed along the longitudinal column bars in the back side of the joint specimens when the normal stress acting between the bars and the surrounding concrete exceeded the value 2
fct, where
fct is the tensile stress of the concrete (see
Figure 9a, Phase 3). The rapid dilation of these cracks resulted in the loss of the concrete cover (see
Figure 9a, Phase 4). Meanwhile, the use of 2Ø10 bars, which were welded perpendicular to the beam longitudinal reinforcement (see
Figure 1 and
Figure 9a), as well as the increased number of the ties in the joint region, secured the anchorage of the beam rebars and allowed for steel yielding. For instance, a continuous increase in maximum steel strain to post-yield values during consecutive cycles of loading was observed in the cases of
,
, and
(see
Figure 8a,c–f); the latter indicates the absence of bar slipping [
33]. The opposite is true for stable or decreasing strain values, which reflect hysteresis deterioration due to the slippage of the bars, as long as buckling has not taken place (see
Figure 8b,g). It is noteworthy that despite the yielding of the beam longitudinal reinforcement being eventually achieved, this occurred only locally in the position of the main flexural crack, where the strain gauges were attached to the rebars. This is also apparent from the absence of plastic hinges in the beam of the specimens, and this explains the low energy dissipation capacity of the subassemblages (see
Figure 6a–c and
Figure 9a). Thus, the overall seismic response of
,
, and
was dominated by the premature brittle shear failure of the joints, which prevented the development of the nominal moment flexural capacities of the specimens. Of course, this type of failure is not acceptable for modern structures, and this clearly demonstrates the importance of the combination of
ΣMRc/ΣMRb and
γ values as a key factor that controls the seismic performance of the beam–column joint region.
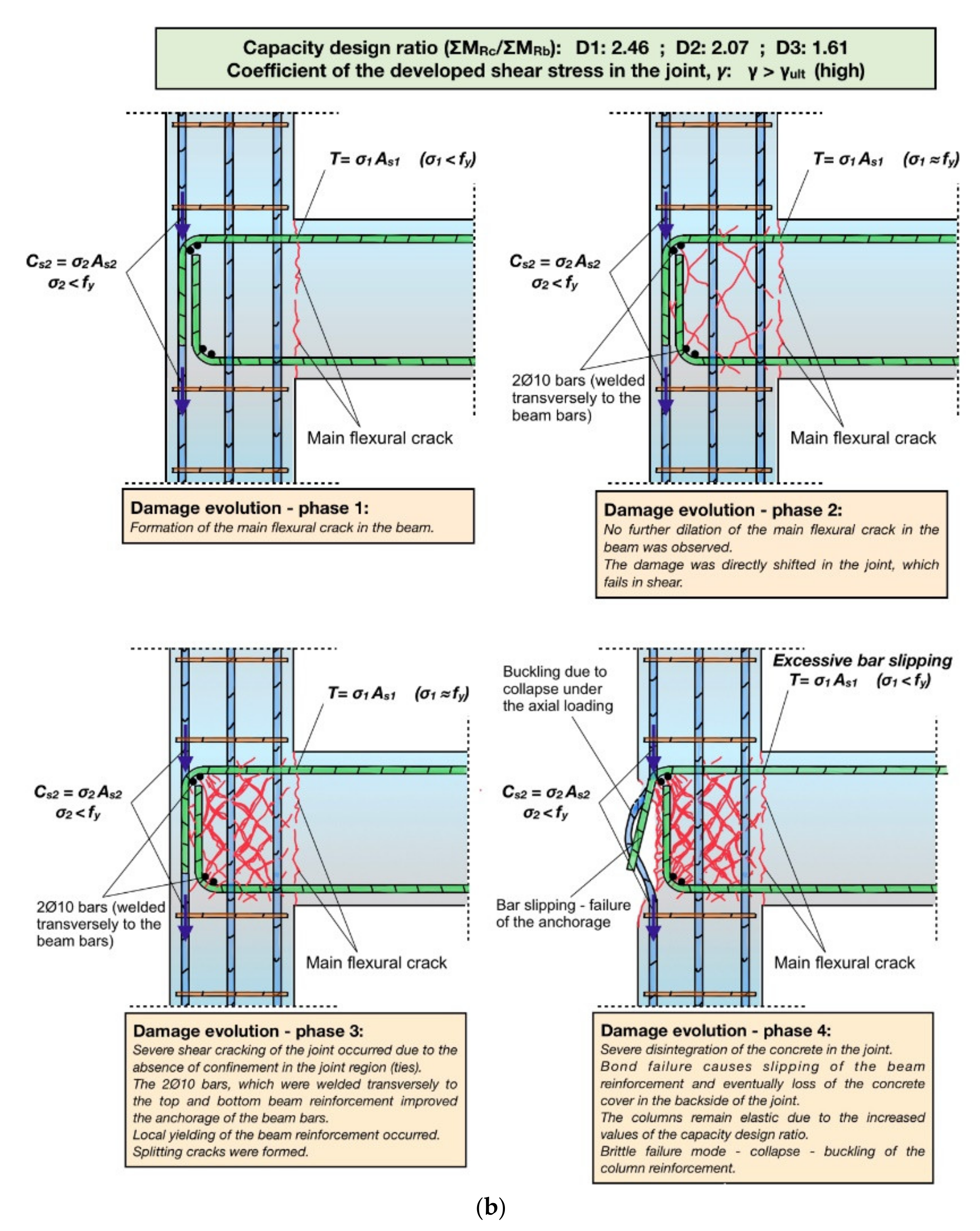
The capacity design ratios of subassemblages
,
, and
were 2.46, 2.07, and 1.61, respectively. These values were significantly increased with respect to the required value by EC8, i.e.,
ΣMRc/ΣMRb > 1.30, especially in the case of specimens
and
. Moreover, the developed shear stresses in the joint region were particularly high, exceeding the ultimate shear capacities of the joints (
γ > γult) (see
Table 4). Hence, after the formation of the main flexural crack in the beam in the vicinity of the joint (see
Figure 9b, Phase 1), the damage was shifted and concentrated solely in the joint region, which failed in shear (see
Figure 9b, Phase 2). However, contrary to subassemblages
,
, and
, which were confined with a significant number of horizontal ties in the joint region, the joints of
,
, and
were totally unconfined. As a result, the joint shear damage evolved rapidly and excessive disintegration of the core concrete occurred (see
Figure 9b, Phase 3). The latter also caused severe deterioration of the bond conditions between the longitudinal bars of the beam and the surrounding concrete, which eventually resulted in bond–slip failure and excessive slipping of the bars. This is clearly reflected by the descending strain values during the consecutive cycles of the earthquake-type loading (see
Figure 8g). It is noteworthy that due to the increased values of the capacity design ratio, the columns over and under the joint of specimens
,
, and
still remained elastic, while no splitting cracks were formed along the column longitudinal rebars in the joint region. Thus, the loss of the concrete cover in the back side of the beam–column joint specimens (see
Figure 9b, Phase 4) was caused by the slipping of the beam’s longitudinal reinforcement, which was adversely affected by the absence of horizontal ties in the joint region. Eventually, the significant reduction of the cross-section area of the joints resulted in the collapse of the subassemblages due to the loss of the axial load carrying capacity. The latter caused buckling of the longitudinal column reinforcement (see
Figure 6d–f and
Figure 9b). Consequently, although local yielding of some of the longitudinal beam bars may not be precluded (see
Figure 8h), the seismic performance of specimens
,
, and
was indisputably dominated by the explosive brittle shear failure of the joint region, which resulted in catastrophic collapse. This extremely dangerous failure mode caused many collapses of existing pre-1960s–1970s RC buildings during moderate-to-strong earthquake events worldwide.
3.3. Theoretical Considerations
Strong seismic excitations of the last sixty years revealed numerous serious structural deficiencies of RC structures built in the 1960s and 1970s (or previously) worldwide, owed mainly to lack of capacity design approach and/or poor detailing of reinforcement. For instance, the beam–column joint regions of these buildings were often found to be totally unconfined, in turn possessing minimal lateral strength, poor deformability and, hence, low ductility. As a result, damage of the joint regions incurred by earthquakes triggered brittle shear failure mechanisms while causing loss of structural integrity and catastrophic partial or general collapse [
1,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47]. Undesirable brittle earthquake damaging of beam–column connections has also been developed in many cases of modern RC frame structures, incorporating full seismic detail according to current building codes [
13,
14]. This clearly indicates that during future earthquakes, not only are the pre-1960s–1970s RC structures extremely susceptible to collapse because of beam–column joints’ failure, but the hysteresis behavior and safety of modern RC structures may be jeopardized as well due to premature joint shear damaging.
An analytical formulation for effectively preventing the collapse of RC buildings subjected to a large number of reversed inelastic lateral displacements was proposed by Tsonos [
14,
48]. The model ensures not only the formation of plastic hinges in the beams but also the final concentration of damage in these elements, while the columns and the joints remain intact during an earthquake. In particular, the ultimate shear capacity of the beam–column joint region is initially computed and is subsequently compared to the value of the connection’s shear stress developed when yielding of the beam longitudinal reinforcement is achieved. Therefore, the model accurately predicts whether the joint fails earlier than the beam or not. Moreover, during a strong seismic excitation, the shear forces acting in the beam–column joints are significantly higher than those acting in the adjacent columns [
49]. As a result, the joints fail earlier than the adjacent columns. It is noteworthy that the prediction of the actual values of connections’ shear stresses during an earthquake also involves predicting the actual values of the structures’ flexural strength ratio, M
R, with the same accuracy. Consequently, a model that precisely predicts the value of the joint’s shear stress could also generally predict the actual values of shear forces and moments resisted by the structures in the beams and columns, in the vicinity of the joint region during strong earthquakes.
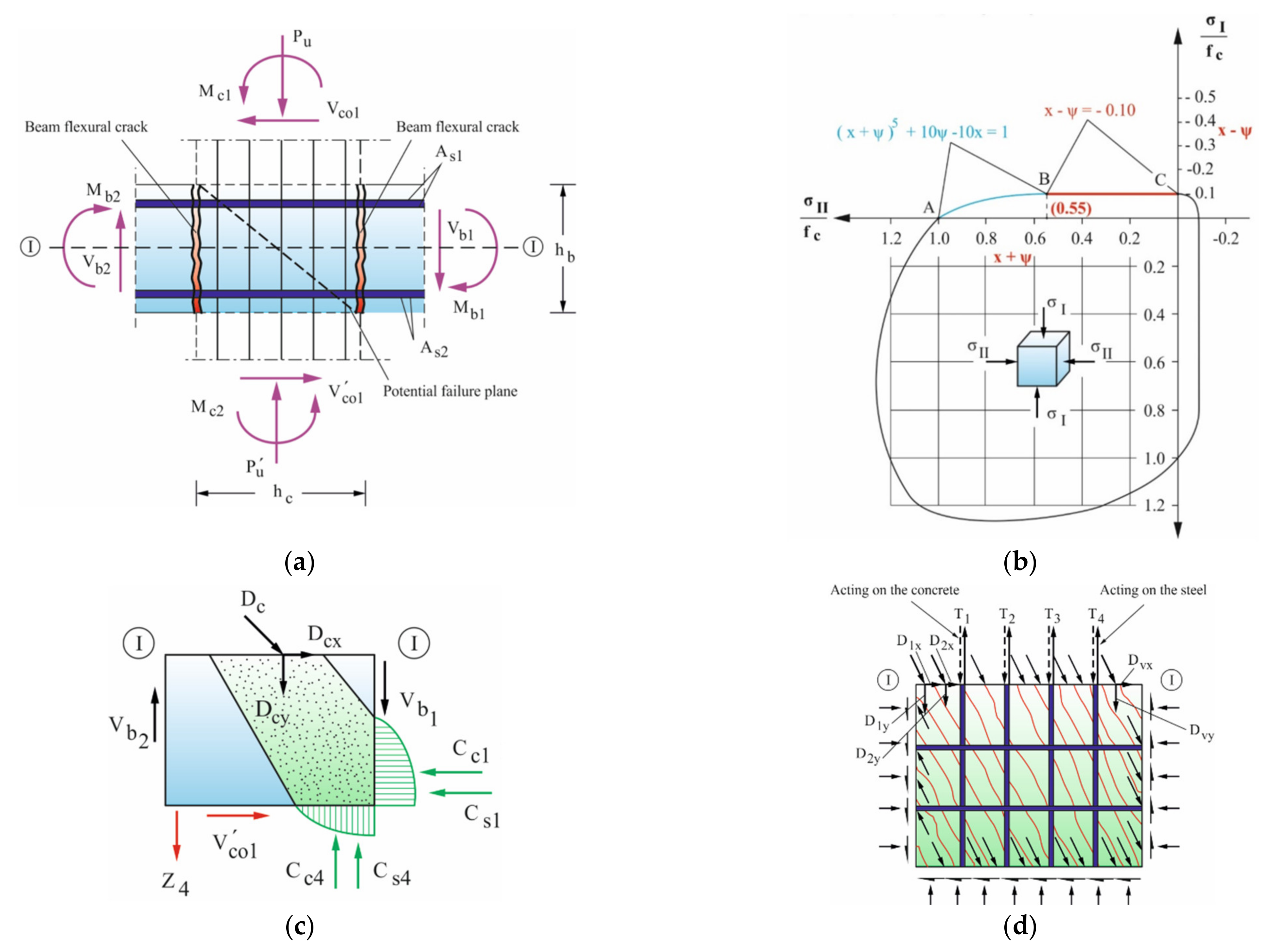
According to the analytical model, which was thoroughly explained by Tsonos [
48], the shear forces acting in the core of a beam–column joint of a moment resisting RC frame during a seismic event are resisted in two ways, i.e., (i) partly by a diagonal compression strut acting between diagonally opposite corners of the joint core and (ii) partly by a truss mechanism formed by horizontal and vertical reinforcement and concrete compression struts. Therefore, the ultimate concrete strength of the joint core under tension/compression controls the ultimate strength of the connection, while after concrete failure the strength is limited by the gradual crushing along the cross-diagonal cracks, especially along the potential failure planes (see
Figure 10a). In a previous work of Tsonos [
48], the main equation for calculating the ultimate joint shear strength, a fifth degree parabola (Equation (4)), was simplified and satisfactorily substituted with a linear equation (Equation (7)), with negligible effect on the results. The joint ultimate strength,
, depends both on the increased joint concrete compressive strength,
fc, (Equations (8) and(9)) due to the confining described in [
31] and also on the aspect ratio
α. Thus, the solution of the system of Equations (4)–(7) for a given value of the joint aspect ratio gives the ultimate shear strength,
, using standard mathematical analysis. The acting calculated joint shear stress is expressed as
(in MPa). It is calculated from the horizontal joint shear force, assuming that the top beam reinforcement yields. In Equations (4)–(7),
fc’ is the concrete compression strength;
fc is the increased joint concrete compressive strength due to confinement [
31];
fyh is the yield strength of the horizontal hoops; and ρ
s is the volume ratio of transverse reinforcement.
In
Table 4, the experimental and predicted values of concrete shear stress in the potential failure plane of subassemblages
DCM_1,
DCM_2,
DCM_3,
D1, D2, and
D3 are summarized. When the calculated joint shear stress
is greater or equal to the ultimate strength,
, then the predicted actual value of connection’s shear stress,
, is expected to be near
because the connection fails earlier than the adjacnt beam(s)” should be used. Otherwise, when the calculated joint shear stress
is lower than the connection’s ultimate strength,
, then the predicted actual value of connection’s shear stress,
, should be near
, while the connection permits yielding of reinforcement of the adjacent beam. The implementation of the analytical formulation allowed for the successful prediction of the failure mode of the specimens, which in all cases included undesirable premature brittle shear failure of the joint region (see
Table 4).
3.4. Use of Steel Fiber Reinforced Concrete for Reducing Conventional Reinforcement
From the performed experimental and analytical investigation, it was clearly demonstrated that the seismic behavior of RC beam–column connections depends on both the capacity design ratio value and on the value of coefficient γ of the joint shear stress. In fact, if the developed shear stress in the joint region is higher than half the value of the ultimate shear capacity, τult, the shear cracking of the joint cannot be precluded even for significantly higher capacity design ratio values than the required one by the EC8, regardless of the number of ties used to confine the joint. This results from the inherent low tensile strength of the concrete. Therefore, an attempt was made herein to prevent brittle failure modes and to secure the ductile seismic performance of the beam–column joints while also reducing the transverse steel reinforcement significantly. The latter was achieved by using steel fiber reinforced concrete instead of the conventional reinforced concrete, which is an innovative material with improved tensile strength.
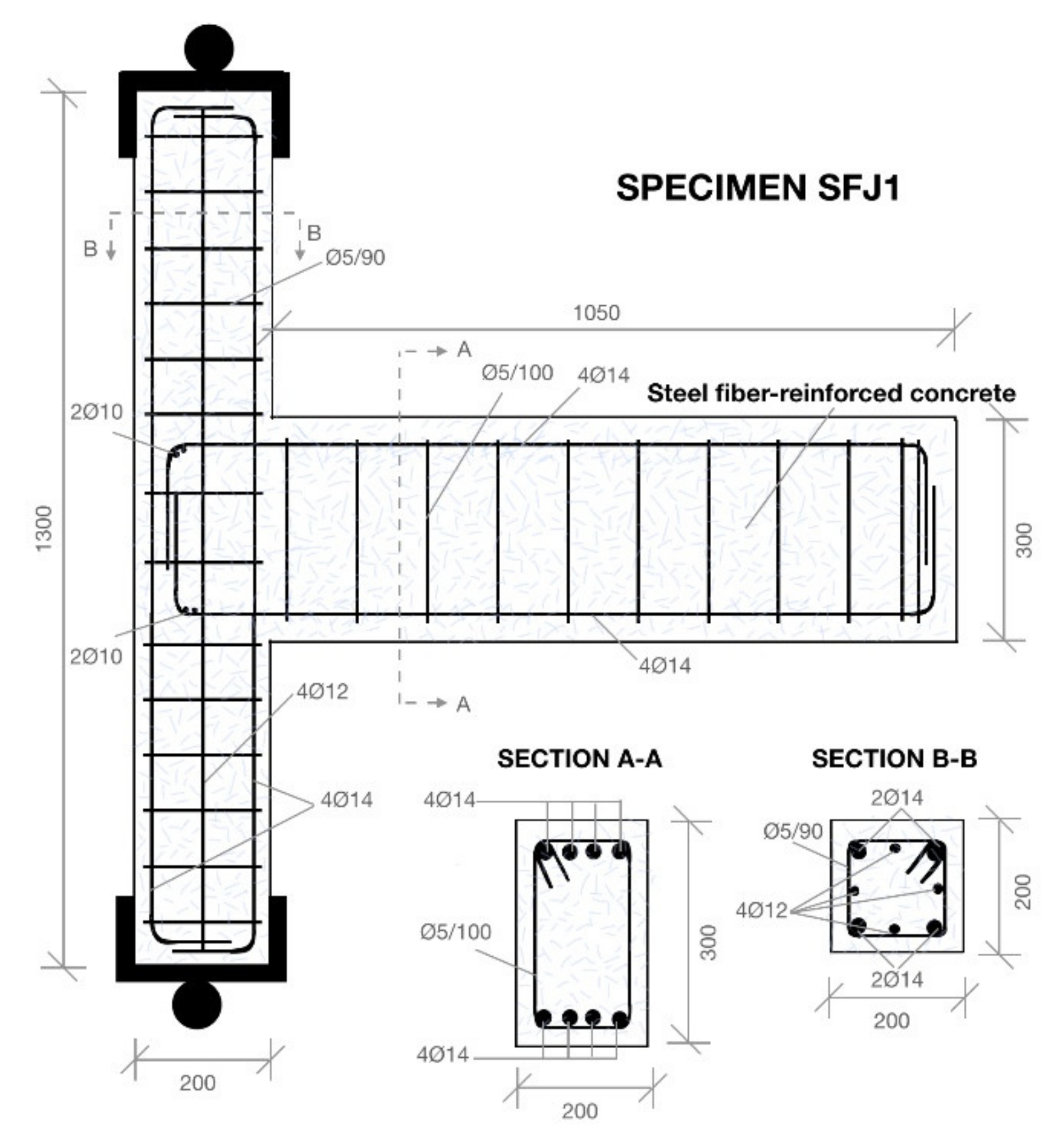
In particular, a beam–column joint subassemblage with similar cross-sectional dimensions as specimen
but with significantly reduced transverse steel reinforcement was constructed with steel fiber reinforced concrete of 20 MPa compressive strength (see
Figure 11). The specimen was designated SFJ1 and had the same longitudinal reinforcement in the columns and the beam as specimen
. However, the transverse reinforcement in the joint region of SFJ1 consisted of only 2Ø5 B500C ties, while it was half the corresponding transverse reinforcement of
in the columns and the beam. The steel fiber volume fraction ratio used for subassemblage SFJ1 was 1.5%. The steel fibers had a tensile strength (
Rm,nom) of 1270 N/mm, a Young’s modulus of ±210,000 N/mm
2, a length (l) of 30 mm, diameter (d) of 0.62 mm, and aspect ratio (l/d) of 45. Specimen SFJ1 was subjected to the same history of reversed lateral displacements as specimen
, depicted in
Figure 2b.
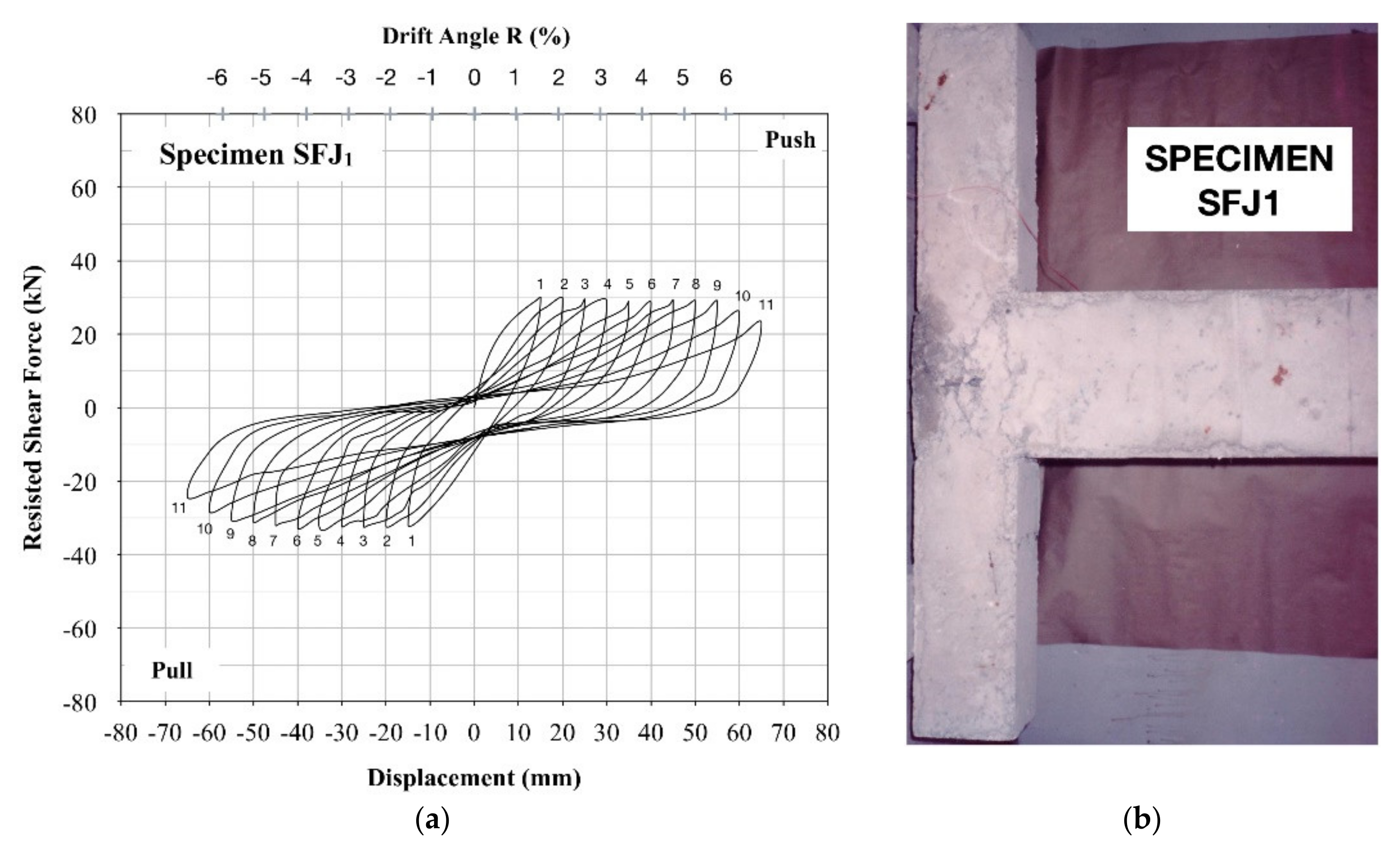
From the plots of resisted shear force versus displacement of subassemblages SFJ1 and
(shown in
Figure 3a and
Figure 12a, respectively), it was clearly demonstrated that specimen SFJ1 achieved an indisputable superiority in the hysteresis behavior with respect to
. In particular, SFJ1 exhibited a dissipating hysteresis response with continuously increasing values of dissipated seismic energy during the consecutive cycles of loading (see
Figure 12a and
Figure 13b), while preserving its lateral bearing capacity. Moreover, SFJ1 showed increased lateral resistance with respect to
. For instance, the values of the resisted shear force of SFJ1 were 27.66% and 43.18%, which show an increase compared to the corresponding values of specimen
during the first push half-cycle and pull half-cycle of loading, respectively. The corresponding values at the end of the 11th push half-cycle and the 11th pull half-cycle of loading were 88.8% and 70.4%, respectively. At the end of testing, SFJ1 retained 76.67% (11th push half-cycle) and 75% (11th pull half-cycle) of its initial lateral bearing strength during the first cycle. The corresponding values for subassemblage
were 54.47% and 59.06%, respectively (see
Figure 12a and
Figure 14a).
A significant increase in the peak-to-peak stiffness values of specimen SFJ1 was also achieved with respect to the values of
(see
Figure 13a). For instance, the peak-to-peak stiffness ratio value SFJ1/
during the first cycle of the earthquake-type loading was 1.26 while at the end of testing the corresponding ratio value was 1.45.
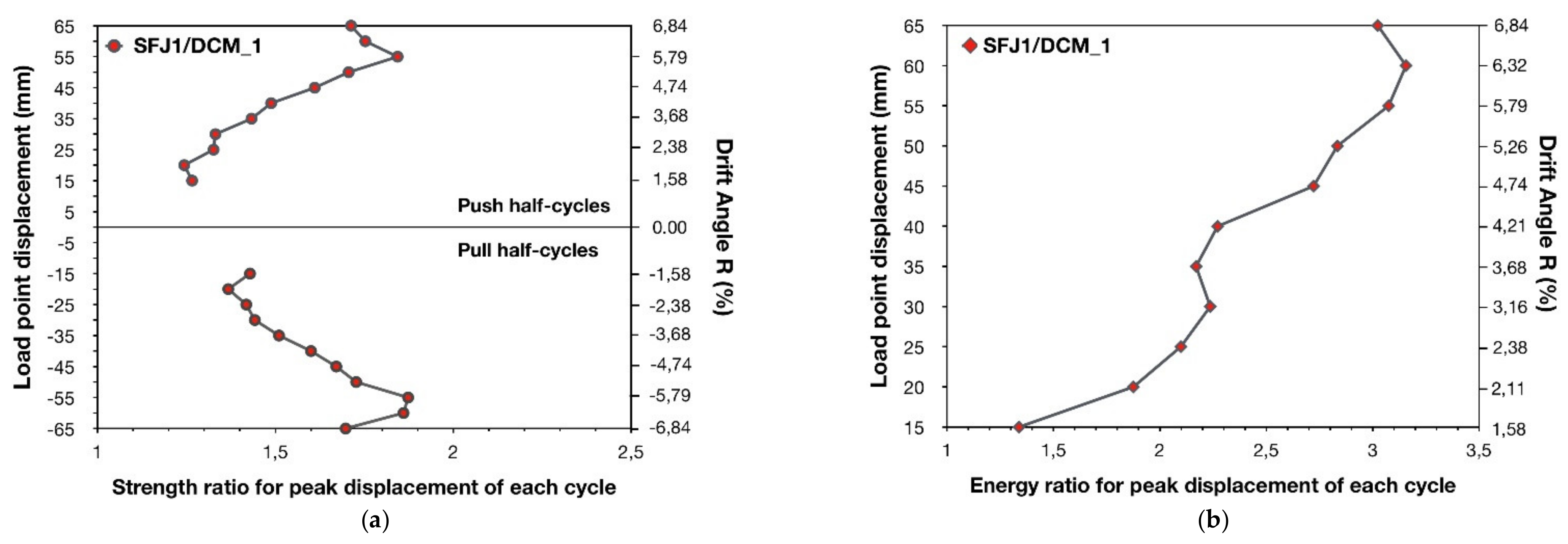
In
Figure 14b the energy dissipation capacity ratio SFJ1/
for peak displacement of each cycle versus load point displacement is illustrated. As can be observed, the energy dissipation capacity of subassemblage SFJ1 was substantially improved with respect to that of
(see
Figure 13b and
Figure 14b). For instance, during the earthquake-type loading, the energy dissipation ratio SFJ1/
ranged from 1.34 to 3.16, while for the lateral drift angle, R, equal to 6.84%, specimn SFJ1 dissipated, dissipated 302.34% more energy than
. Despite the significantly lower number of ties found in the joint of specimen SFJ1 with respect to the ties of
, the use of steel fiber reinforced concrete allowed for the dissipation of continuously incremental values of seismic energy during cycling. Indeed, a 220.41% increase in the amount of dissipated energy of SFJ1 was achieved after eleven cycles of loading with respect to the first cycle. Contrarily, the energy dissipation capacity of subassemblage
was poor and stable during cycling due to the excessive damage of the joint, which failed in brittle shear (see
Figure 15b).
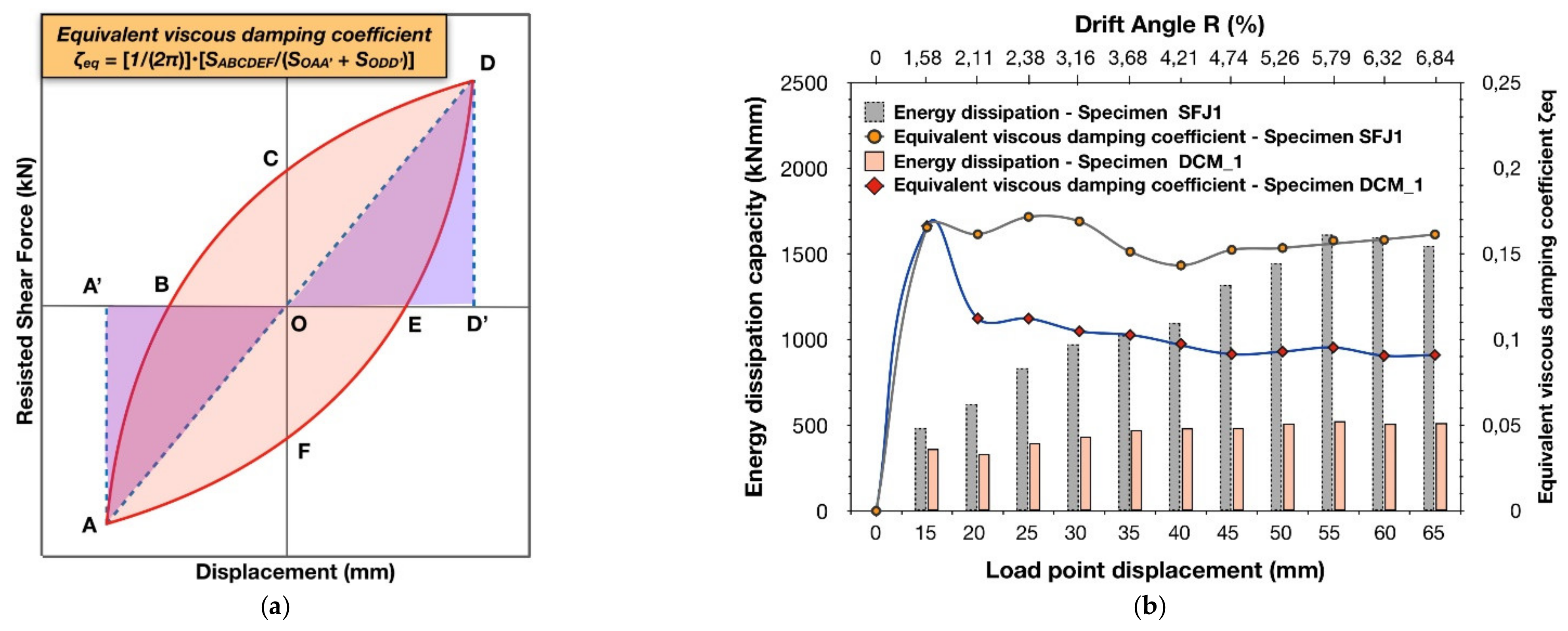
A crucial parameter for the seismic performance of RC structures is its ability to possess adequate displacement ductility, which allows for the dissipation of the kinetic energy induced by earthquakes through damping. The latter requires a ductile seismic response with the formation of the plastic hinges in the beam while the beam–column joints remain elastic. Therefore, it is useful to examine the equivalent viscous damping coefficient,
ζeq (see
Figure 15a), which is related to deformability and to the inelastic characteristics of the structural member, while consisting of both the hysteretic and the elastic damping. It is noteworthy that the equivalent viscous damping ratio values are higher for structural members that possess dissipating hysteresis behavior. Contrarily, poor energy dissipation capacity may result in the collapse of the structural member due to the cumulative seismic energy under small deformations. Coefficient
ζeq is expressed as the ratio of the energy dissipated within a given cycle of the lateral loading to the elastic strain energy corresponding to this cycle (see
Figure 15a). In
Figure 15b the energy dissipation capacity and the value of coefficient
ζeq per cycle of loading are shown, while
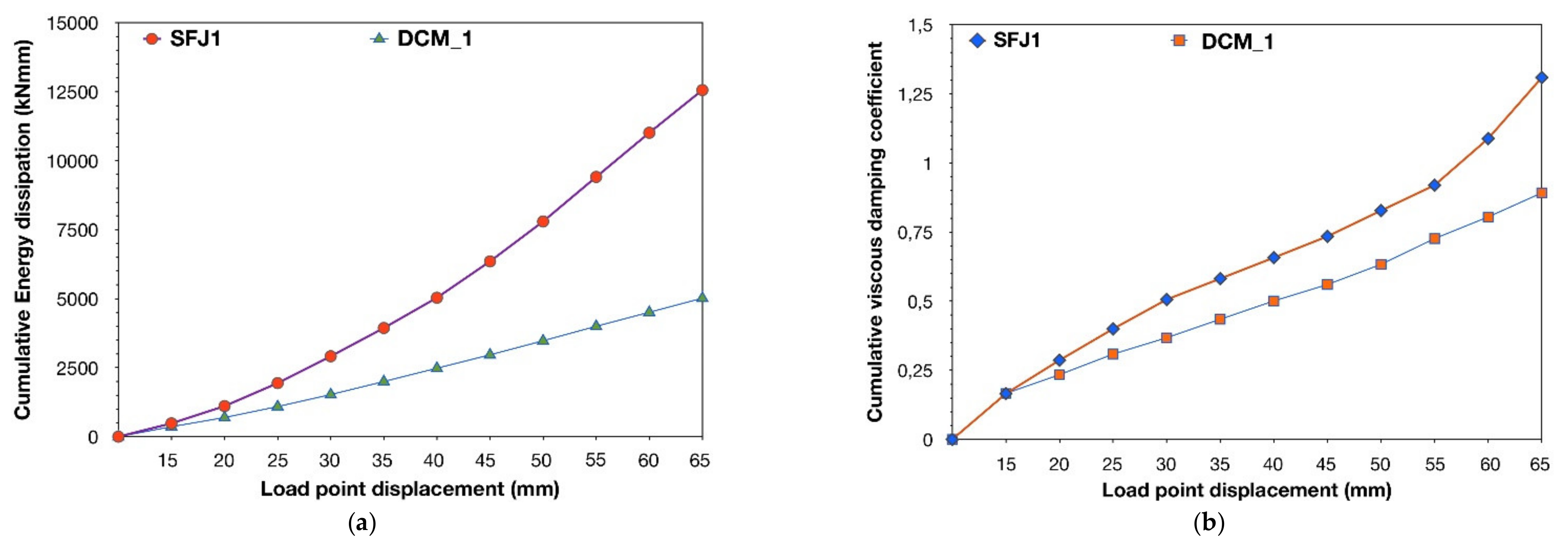
Figure 16a,b illustrates the cumulative dissipated energy and the cumulative equivalent viscous damping coefficient. As can be observed, the substantially increased energy dissipation capacity of subassemblage SFJ1 with respect to that of
resulted in higher values of the equivalent viscous damping coefficient,
ζeq, since the differences in the elastic strain energy were small.
Ultimately, the use of steel fiber reinforced concrete with a steel fiber volume fraction ratio of 1.5% allowed for the satisfactory concentration of damage in the beam of SFJ1, while the beam–column joint region remained almost intact, i.e., only hairline shear cracks were formed in the joint region (see
Figure 12b). Thus, the proposed design scheme was proven to be particularly satisfactory in securing the ductile seismic performance of the beam–column connection while being an effective alternative design solution to the one of the EC8.