Cracking Diagnosis in Fiber-Reinforced Concrete with Synthetic Fibers Using Piezoelectric Transducers
Abstract
:1. Introduction
- -
- Shape memory alloys have elastic behavior, are corrosion resistant, and have high fatigue failure life, damping capacities, and strength. However, they are expensive, temperature sensitive, and have high cycle fatigue, along with complicated design and heavy weight.
- -
- Magnetostrictive materials present higher energy density and intrinsic robustness, but they increase the complexity of the structural system, present low accuracy of experimental reproduction, are only suitable for ferromagnetic materials, and their induced energy depends on the proximity of the probe to the monitoring area.
- -
- Self-monitoring fiber-reinforced composites can be used simultaneously as reinforcing structural materials and as sensing materials that can monitor their own strain, damage, and temperature by their change in electrical resistance utilizing a simple technology. However, their sensitivity to strain is very low in the strain range, from zero to the point just before fiber fracture; their sensing repeatability requires improvement; and, to date, field applications in SHM of civil engineering structures have not been developed.
- -
- Optical fibers are flexible, corrosion resistant, take up less space, and have immunity to electromagnetic interference and tapping along with high bandwidth support and carrying capacity. Furthermore, fiber-optical sensors can be used in various in-situ and real-time surveillance applications in civil engineering structures, such as monitoring of strain, displacement, vibration, cracks, corrosion, and chloride-ion concentration. They have high sensing capability, the ability to operate in harsh environments, and a large sensing scope. Nevertheless, optical fibers have costly installation, cannot carry electrical power to operate terminal devices, are not suitable at higher optical powers and are fragile in some configurations, and the damage is difficult to repair when embedded. Furthermore, their ability to detect defects and damages along with their long-term sensing capabilities require further investigation.
2. Materials and Methods
2.1. Materials and Specimens
2.2. Compression Tests and Steps of the Repeated Loading
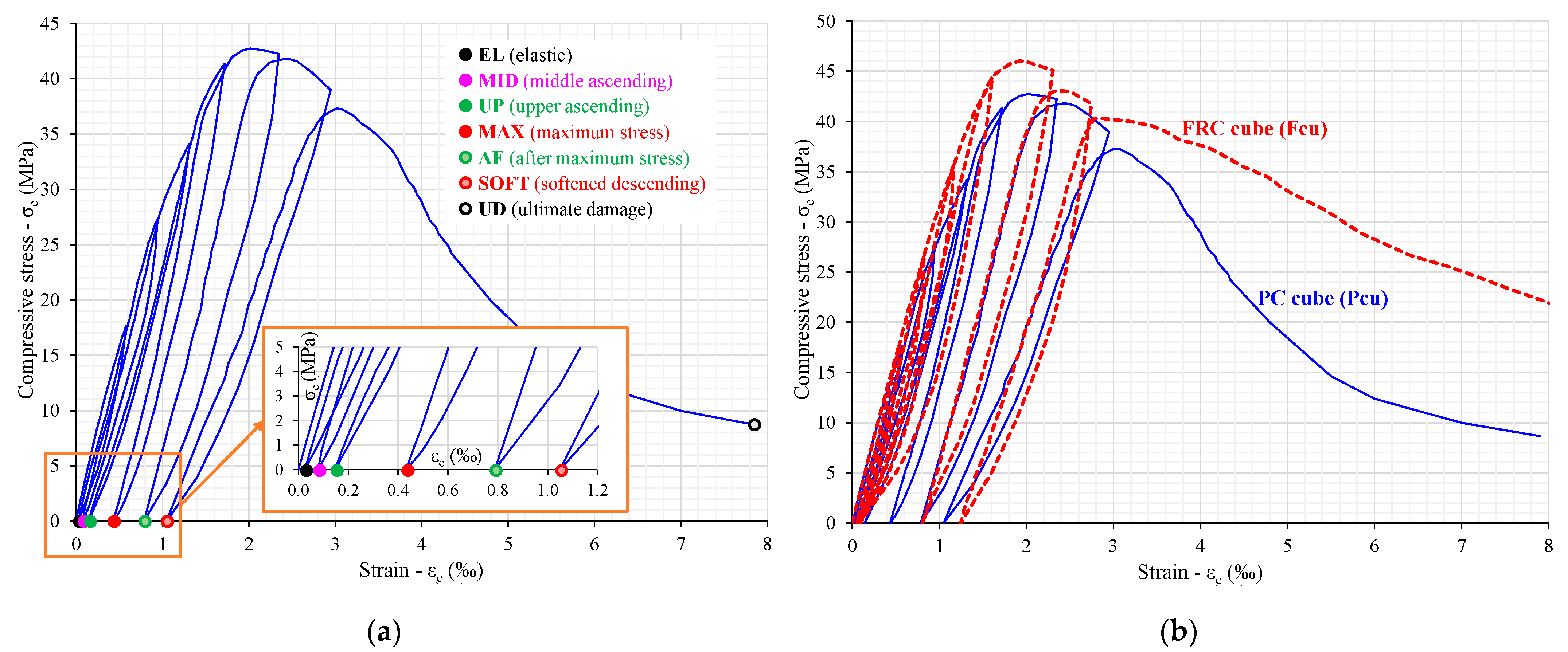
- The “EL” level equals 40% of the σmax, and up to this point the material has elastic properties;
- The “MID” level is a middle loading level of the ascending stress–strain part approximately equal to 60% of the σmax;
- The “UP” level is at the upper ascending stress–strain part approximately equal to the 85% of the σmax;
- The “MAX” level represents the maximum compressive strength σmax;
- The “AF” level is at the beginning of the descending stress–strain part and right after σmax;
- The “SOFT” level is located at the softened descending stress–strain part;
- “UD” represents the ultimate damage state point.
2.3. Damage Identification System and Measurements
3. Results and Observations
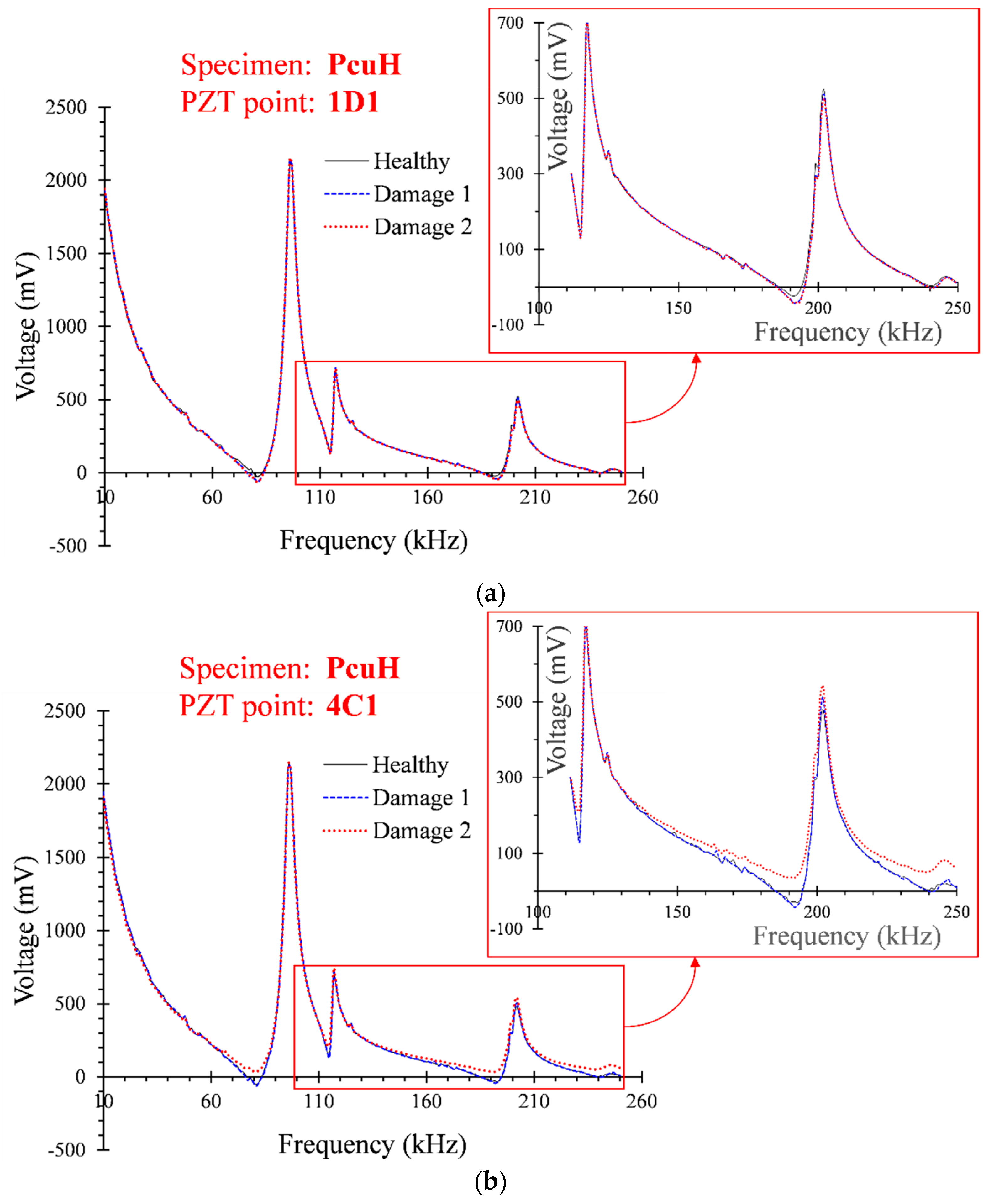
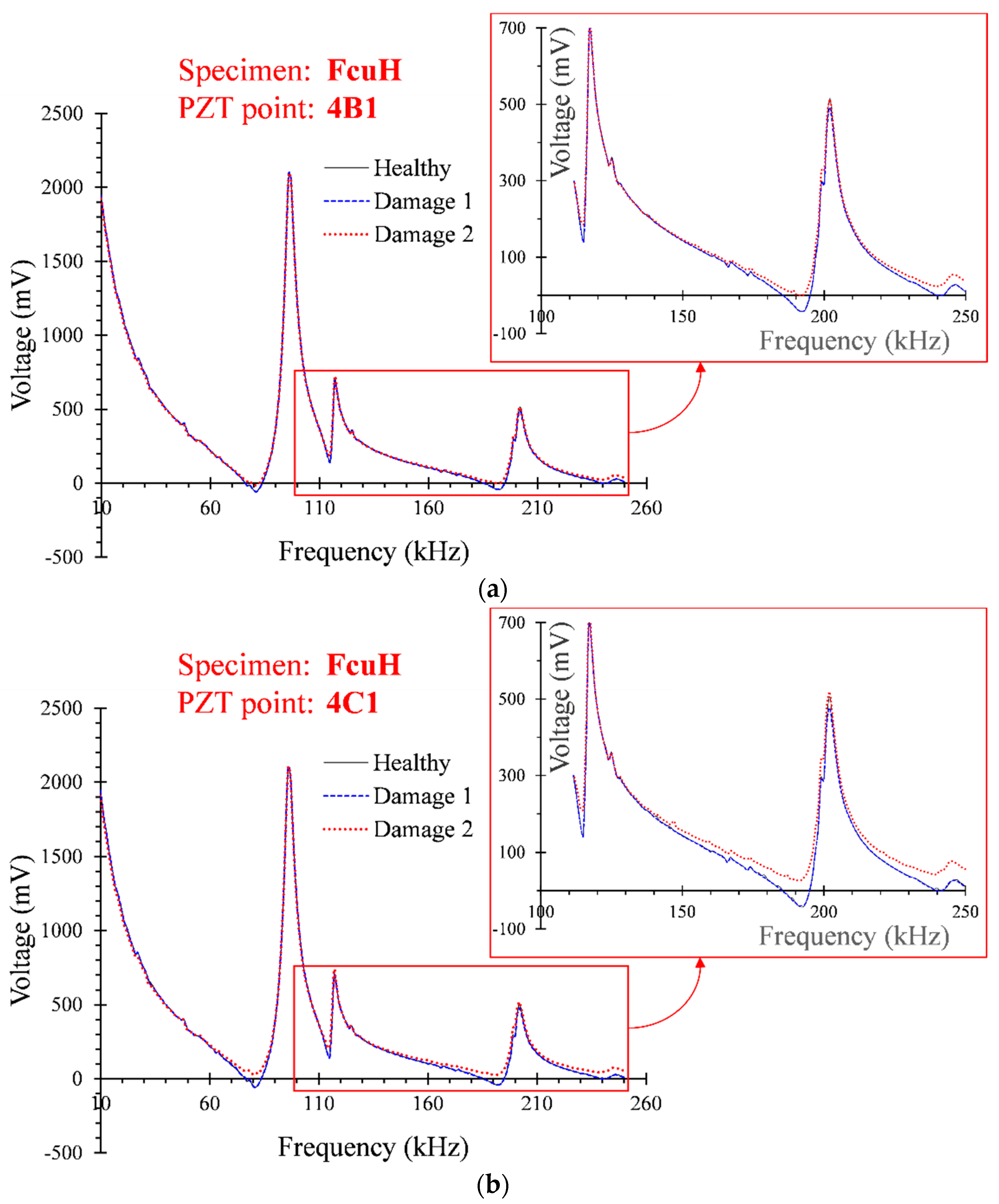
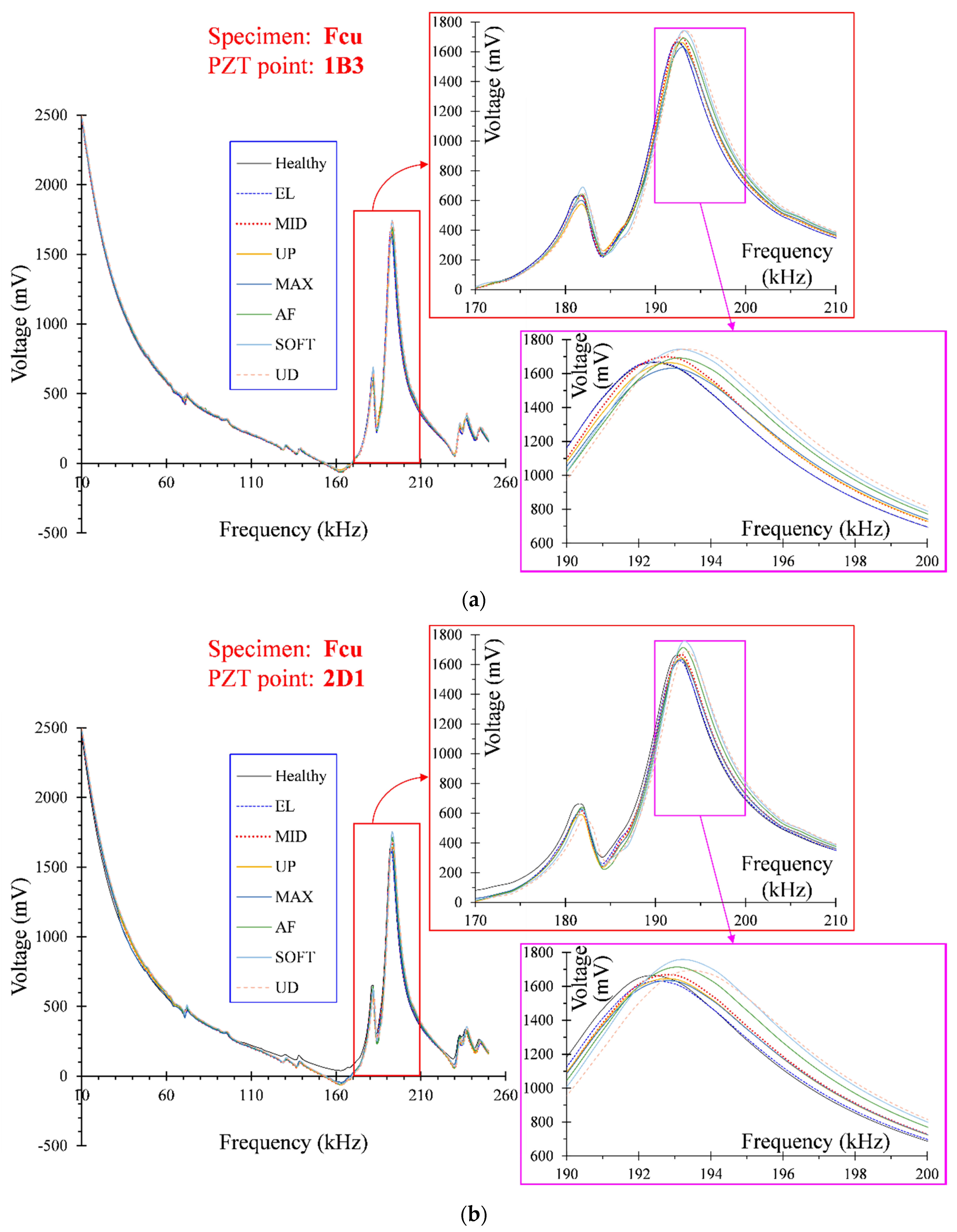
3.1. Verification of WiAMS by Measurements of Artificial Damage
3.2. Compression Stress versus Strain Behavior
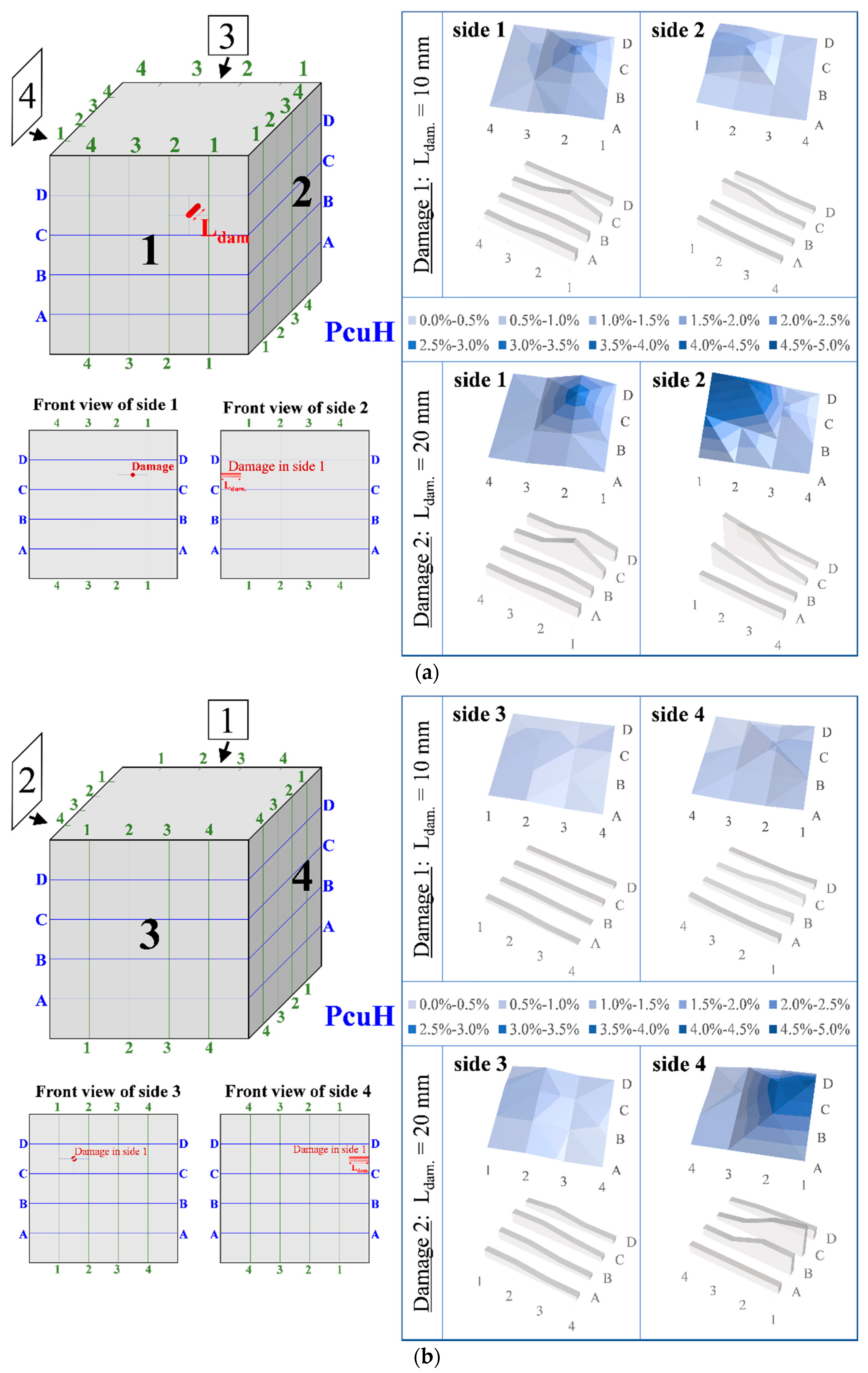
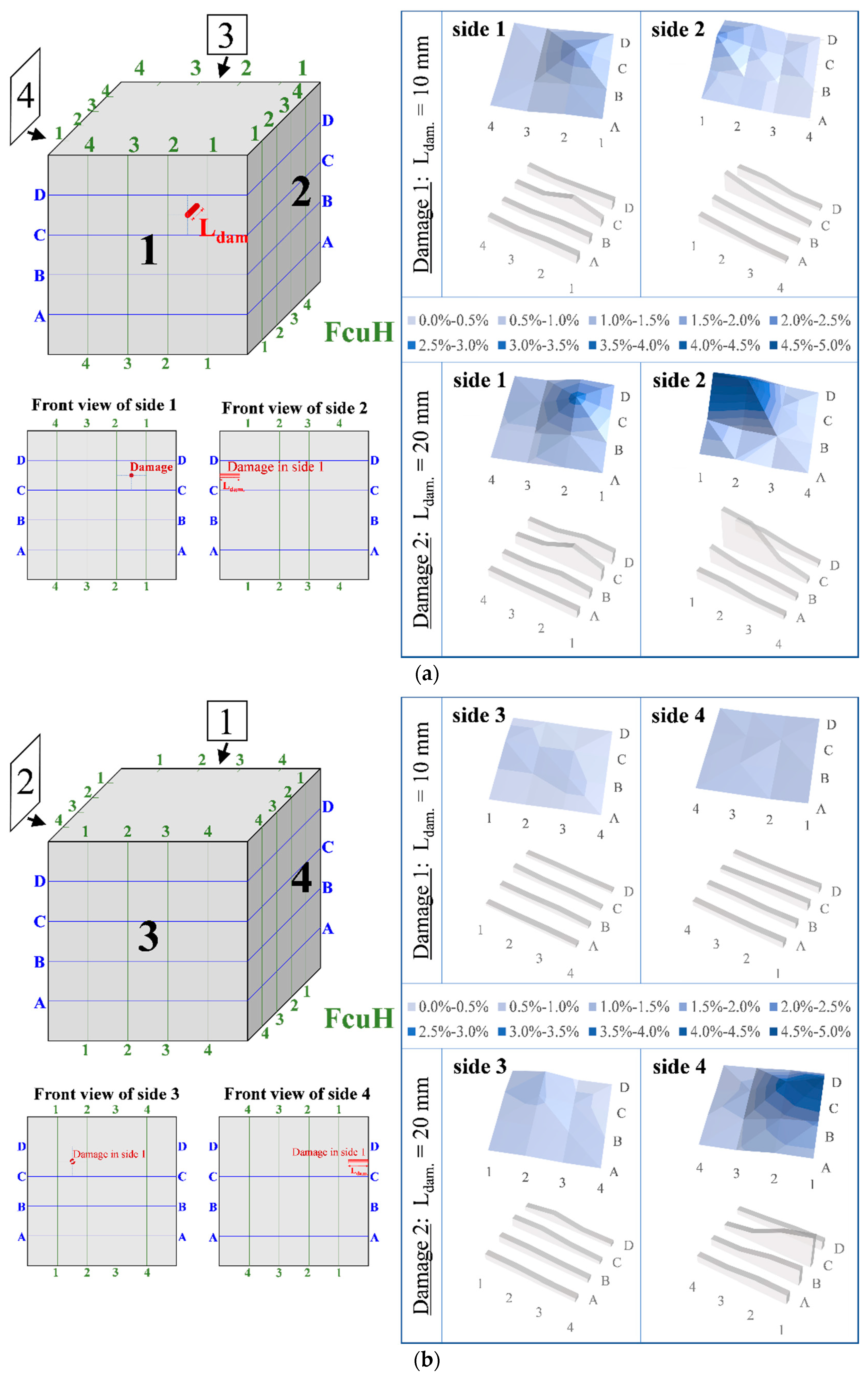
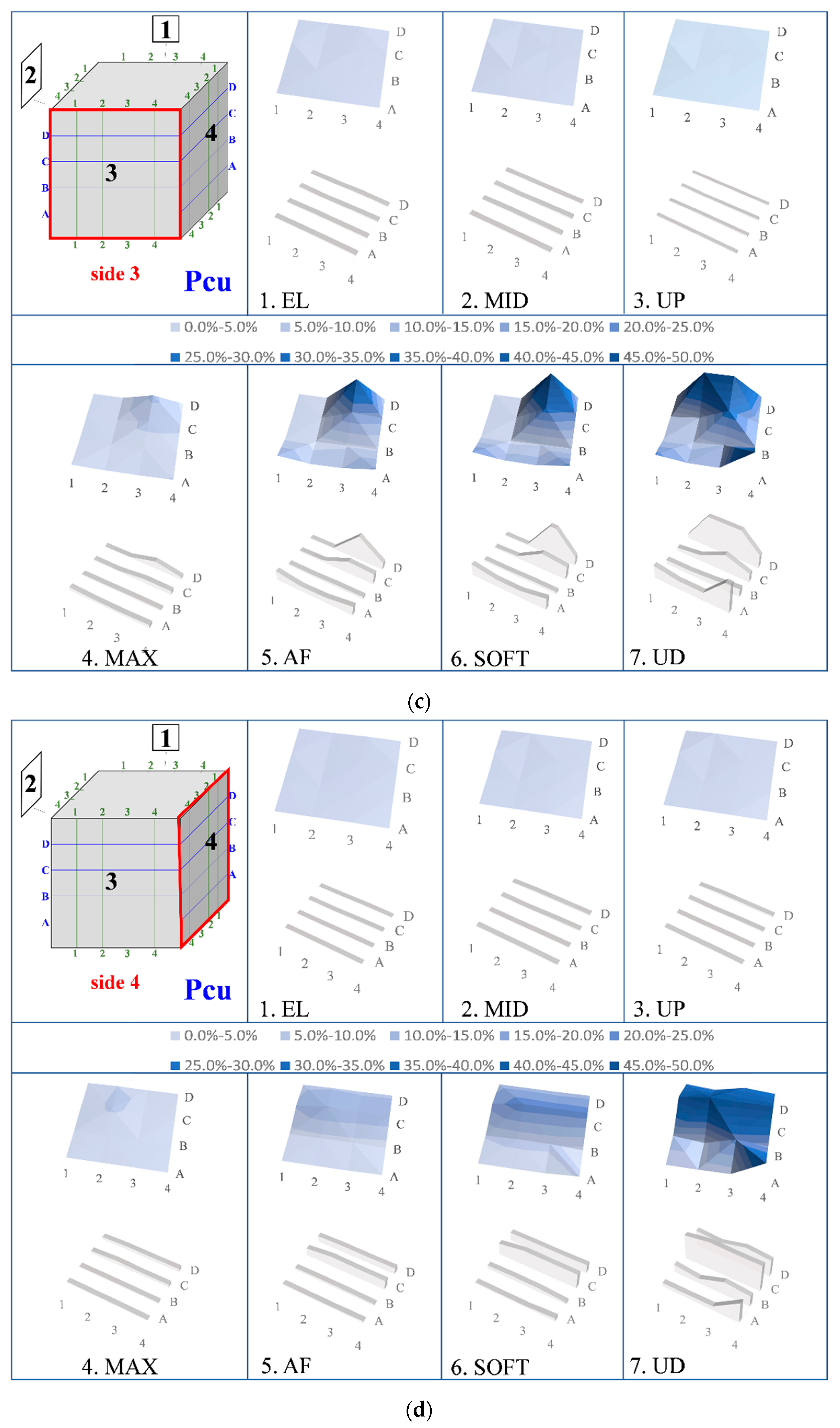
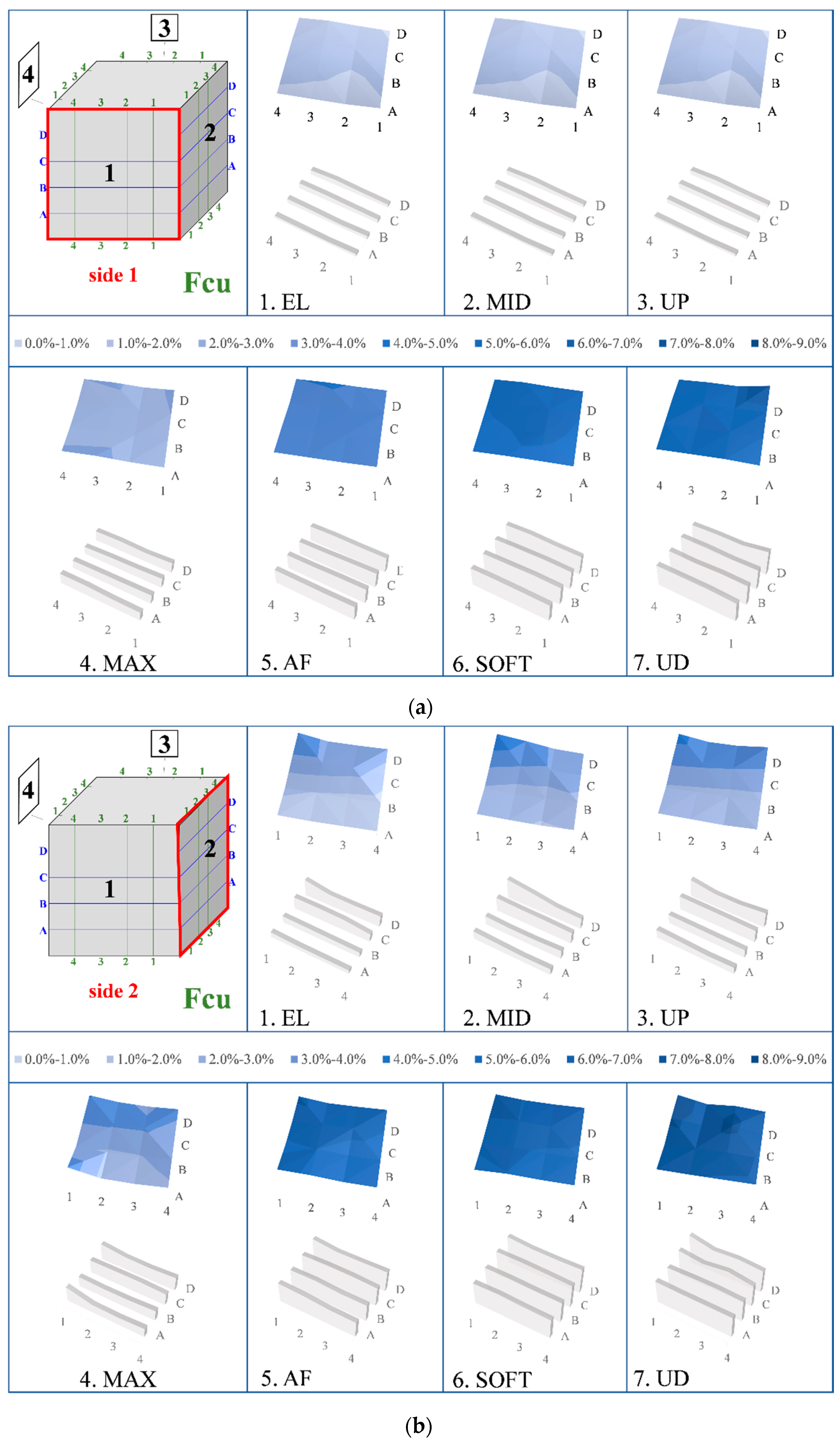
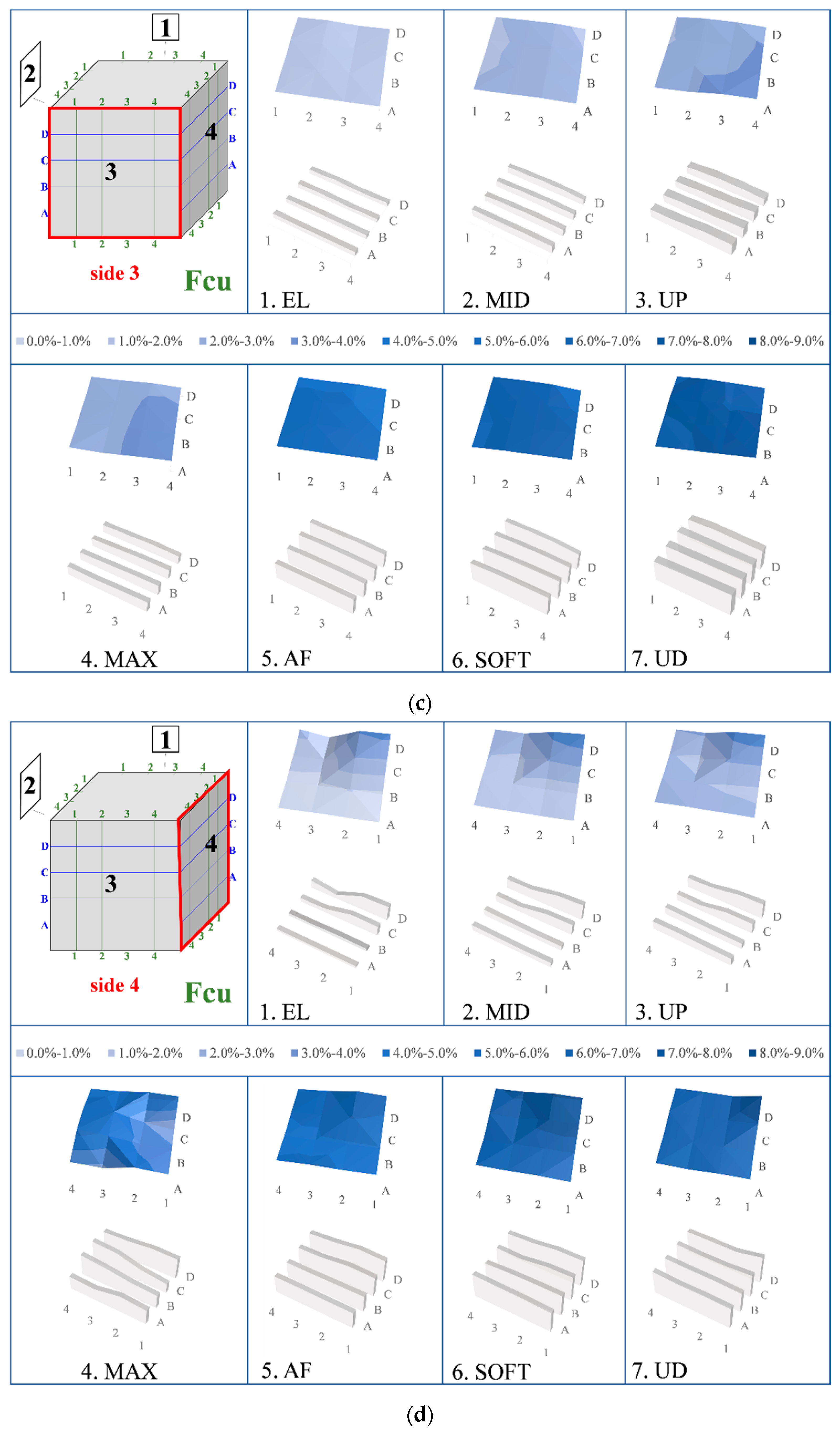
3.3. Damage Assessment of the Cubes Due to the Repeated Compressive Loading
4. Conclusions
- The effectiveness of the SHM system used to identify the location and severity level of damage was first verified using PC and FRC cubes with predefined and artificially induced damage in the form of drilled holes at two different depths.
- PZT transducers located at the transverse direction to the hole depth were more sensitive than the PZTs located at the longitudinal direction.
- The influence of distance-, direction-, and damage-level triggers changed in the measurements of the PZT transducers and the adopted RMSD index seemed to be a reliable statistical tool for structural damage assessment.
- The FRC cubes exhibited a rather slight increase (<10%) in compressive strength with respect to the PC cubes. A notable influence of the synthetic fibers on the improvement of the post-peak compressive behavior was observed, which indicates the ability of FRC to provide increased ductility.
- The illustrated 3D graphs clearly demonstrate that the RMSD index values increased gradually along with the progressive increase in the compressive load and the corresponding damage severity level of the tested cubes. Especially after concrete cracking at post-peak compressive response, the RMSD values of the PC cube were significantly higher than the corresponding RMSD values of the FRC cube. This is justified by the existence of the synthetic fibers, which provided ductile post-peak behavior with respect to the brittle response of the PC cube. This improvement was captured by the RMSD damage index with satisfactory accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caggiano, A.; Gambarelli, S.; Martinelli, E.; Nisticò, N.; Pepe, M. Experimental characterization of the post-cracking response in hybrid steel/polypropylene fiber-reinforced concrete. Constr. Build. Mater. 2016, 125, 1035–1043. [Google Scholar] [CrossRef]
- Smarzewski, P. Effect of curing period on properties of steel and polypropylene fiber reinforced ultra-high performance concrete. Mater. Sci. Eng. 2017, 245, 032059. [Google Scholar] [CrossRef]
- Guerini, V.; Conforti, A.; Plizzari, G.A.; Kawashima, S. Influence of steel and macro-synthetic fibers on concrete properties. Fibers 2018, 6, 47. [Google Scholar] [CrossRef] [Green Version]
- Rizzuti, L.; Bencardino, F. Effects of fiber volume fraction on the compressive and flexural experimental behavior of SFRC. Contemp. Eng. Sci. 2014, 7, 379–390. [Google Scholar] [CrossRef]
- Marcalikova, Z.; Cajka, R.; Bilek, V.; Bujdos, D.; Sucharda, O. Determination of mechanical characteristics for fiber-reinforced concrete with straight and hooked fibers. Crystals 2020, 10, 545. [Google Scholar] [CrossRef]
- Bencardino, F.; Rizzuti, L.; Spadea, G.; Swamy, R.N. Stress-strain behavior of steel fiber-reinforced concrete in compression. J. Mater. Civ. Eng. 2008, 20, 255–263. [Google Scholar] [CrossRef]
- Smarzewski, P. Hybrid fibres as shear reinforcement in high-performance concrete beams with and without openings. Appl. Sci. 2018, 8, 2070. [Google Scholar] [CrossRef] [Green Version]
- Gribniak, V.; Ng, P.-L.; Tamulenas, V.; Misiūnaitė, I.; Norkus, A.; Šapalas, A. Strengthening of fibre reinforced concrete elements: Synergy of the fibres and external sheet. Sustainability 2019, 11, 4456. [Google Scholar] [CrossRef] [Green Version]
- Karayannis, C.G.; Kosmidou, P.-M.K.; Chalioris, C.E. Reinforced concrete beams with carbon-fiber-reinforced polymer bars—Experimental study. Fibers 2018, 6, 99. [Google Scholar] [CrossRef] [Green Version]
- Gribniak, V.; Kaklauskas, G.; Torres, L.; Daniunas, A.; Timinskas, E.; Gudonis, E. Comparative analysis of deformations and tension-stiffening in concrete beams reinforced with GFRP or steel bars and fibers. Compos. Part B Eng. 2013, 50, 158–170. [Google Scholar] [CrossRef]
- Chalioris, C.E. Steel fibrous RC beams subjected to cyclic deformations under predominant shear. Eng. Struct. 2013, 49, 104–118. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G.; Elenas, A. Effect of steel fibers on the hysteretic performance of concrete beams with steel reinforcement—Tests and analysis. Materials 2020, 13, 2923. [Google Scholar] [CrossRef] [PubMed]
- Chalioris, C.E.; Kosmidou, P.-M.K.; Karayannis, C.G. Cyclic response of steel fiber reinforced concrete slender beams: An experimental study. Materials 2019, 12, 1398. [Google Scholar] [CrossRef] [Green Version]
- Tsonos, A.-D.; Kalogeropoulos, G.; Iakovidis, P.; Bezas, M.-Z.; Koumtzis, M. Seismic performance of RC beam–column joints designed according to older and modern codes: An attempt to reduce conventional reinforcement using steel fiber reinforced concrete. Fibers 2021, 9, 45. [Google Scholar] [CrossRef]
- Smarzewski, P. Study of toughness and macro/micro-crack development of fibre-reinforced ultra-high performance concrete after exposure to elevated temperature. Materials. 2019, 12, 1210. [Google Scholar] [CrossRef] [Green Version]
- Bencardino, F. Mechanical parameters and post-cracking behaviour of HPFRC according to three-point and four-point bending test. Adv. Civ. Eng. 2013, 2013, 179712. [Google Scholar] [CrossRef] [Green Version]
- Gribniak, V.; Kaklauskas, G.; Kwan, A.K.H.; Bacinskas, D.; Ulbinas, D. Deriving stress–strain relationships for steel fiber concrete in tension from tests of beams with ordinary reinforcement. Eng. Struct. 2012, 42, 387–395. [Google Scholar] [CrossRef]
- Bajpai, A.; Wetzel, B.; Klingler, A.; Friedrich, K. Mechanical properties and fracture behavior of high-performance epoxy nanocomposites modified with block polymer and core–shell rubber particles. J. Appl. Polym. Sci. 2019, 137, 48471. [Google Scholar] [CrossRef]
- Vougioukas, E.; Papadatou, M. A model for the prediction of the tensile strength of fiber-reinforced concrete members, before and after cracking. Fibers 2017, 5, 27. [Google Scholar] [CrossRef] [Green Version]
- Chalioris, C.E.; Panagiotopoulos, T.A. Flexural analysis of steel fiber-reinforced concrete members. Comput. Concr. 2018, 22, 11–25. [Google Scholar] [CrossRef]
- Hollý, I.; Bilčík, J. Effect of chloride-induced steel corrosion on working life of concrete structures. Solid State Phenom. 2018, 272, 226–231. [Google Scholar] [CrossRef]
- Almeida, F.; Cunha, V.M.C.F.; Miranda, T.; Cristelo, N. Indirect tensile behaviour of fibre reinforced alkali-activated composites. Fibers 2018, 6, 30. [Google Scholar] [CrossRef] [Green Version]
- El-Newihy, A.; Azarsa, P.; Gupta, R.; Biparva, A. Effect of polypropylene fibers on self-healing and dynamic modulus of elasticity recovery of fiber reinforced concrete. Fibers 2018, 6, 9. [Google Scholar] [CrossRef] [Green Version]
- Chalioris, C.E. Analytical approach for the evaluation of minimum fibre factor required for steel fibrous concrete beams under combined shear and flexure. Constr. Build. Mater. 2013, 43, 317–336. [Google Scholar] [CrossRef]
- Torres, J.A.; Lantsoght, E.O.L. Influence of fiber content on shear capacity of steel fiber-reinforced concrete beams. Fibers 2019, 7, 102. [Google Scholar] [CrossRef] [Green Version]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G. Analysis of residual flexural stiffness of steel fiber-reinforced concrete beams with steel reinforcement. Materials 2020, 13, 2698. [Google Scholar] [CrossRef]
- Abambres, M.; Lantsoght, E.O.L. ANN-based shear capacity of steel fiber-reinforced concrete beams without stirrups. Fibers 2019, 7, 88. [Google Scholar] [CrossRef] [Green Version]
- Kotecha, P.; Abolmaali, A. Macro synthetic fibers as reinforcement for deep beams with discontinuity regions: Experimental investigation. Eng. Struct. 2019, 200, 109672. [Google Scholar] [CrossRef]
- Mobasher, B.; Dey, V.; Bauchmoyer, J.; Mehere, H.; Schaef, S. Reinforcing efficiency of micro and macro continuous polypropylene fibers in cementitious composites. Appl. Sci. 2019, 9, 2189. [Google Scholar] [CrossRef] [Green Version]
- Bentur, A.; Mindess, S. Fiber Reinforced Cementitious Composites: Modern Concrete Technology Series, 2nd ed.; Taylor & Francis: New York, NY, USA, 2007; p. 624. [Google Scholar]
- Mindess, S.; Young, J.F.; Darwin, D. Concrete, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2003; p. 644. [Google Scholar]
- Carnovale, D.; Vecchio, F.J. Effect of fiber material and loading history on shear behavior of fiber-reinforced concrete. ACI Struct. J. 2014, 111, 1235–1244. [Google Scholar] [CrossRef]
- Hasan, M.J.; Afroz, M.; Mahmud, H.M.I. An experimental investigation on mechanical behavior of macro synthetic fiber reinforced concrete. Int. J. Civ. Environ. Eng. 2011, 11, 18–23. [Google Scholar]
- Roesler, J.R.; Altoubat, S.A.; Lange, D.A.; Rieder, K.A.; Ulreich, G.R. Effect of synthetic fibers on structural behavior of concrete slabs-on-ground. ACI Mater. J. 2006, 103, 3–10. [Google Scholar]
- Rainieri, C.; Fabbrocino, G.; Cosenza, E. Integrated seismic early warning and structural health monitoring of critical civil infrastructures in seismically prone areas. Struct. Health Monit. 2011, 10, 291–308. [Google Scholar] [CrossRef]
- Tsonos, A.-D.G. Ultra-high-performance fiber reinforced concrete: An innovative solution for strengthening old R/C structures and for improving the FRP strengthening method. WIT Trans. Eng. Sci. 2009, 64, 273–284. [Google Scholar] [CrossRef] [Green Version]
- Soh, C.K.; Tseng, K.K.-H.; Bhalla, S.; Gupta, A. Performance of smart piezoceramic patches in health monitoring of a RC bridge. Smart Mater. Struct. 2000, 9, 533–542. [Google Scholar] [CrossRef]
- Mei, H.; Haider, M.F.; Joseph, R.; Migot, A.; Giurgiutiu, V. Recent advances in piezoelectric wafer active sensors for structural health monitoring applications. Sensors 2019, 19, 383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Divsholi, B.S. Sub-frequency interval approach in electromechanical impedance technique for concrete structure health monitoring. Sensors 2010, 10, 11644–11661. [Google Scholar] [CrossRef] [Green Version]
- Talakokula, V.; Bhalla, S.; Gupta, A. Monitoring early hydration of reinforced concrete structures using structural parameters identified by piezo sensors via electromechanical impedance technique. Mech. Syst. Signal Process. 2018, 99, 129–141. [Google Scholar] [CrossRef]
- Huo, L.; Cheng, H.; Kong, Q.; Chen, X. Bond-slip monitoring of concrete structures using smart sensors—A review. Sensors 2019, 19, 1231. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Hu, Y.; Lu, Y. Sensitivity of PZT impedance sensors for damage detection of concrete structures. Sensors 2008, 8, 327–346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Providakis, C.P.; Angeli, G.M.; Favvata, M.J.; Papadopoulos, N.A.; Chalioris, C.E.; Karayannis, C.G. Detection of concrete reinforcement damage using piezoelectric materials—Analytical and experimental study. Int. J. Civil Archit. Struct. Constr. Eng. 2014, 8, 197–205. [Google Scholar] [CrossRef]
- Perera, R.; Torres, L.; Ruiz, A.; Barris, C.; Baena, M. An EMI-Based clustering for structural health monitoring of NSM FRP strengthening systems. Sensors 2019, 19, 3775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voutetaki, M.E.; Papadopoulos, N.A.; Angeli, G.M.; Providakis, C.P. Investigation of a new experimental method for damage assessment of RC beams failing in shear using piezoelectric transducers. Eng. Struct. 2016, 114, 226–240. [Google Scholar] [CrossRef]
- Bahl, S.; Nagar, H.; Singh, I.; Sehgal, S. Smart materials types, properties and applications: A review. Mater. Today Proc. 2020, 28, 1302–1306. [Google Scholar] [CrossRef]
- Sun, M.; Staszewski, W.J.; Swamy, R.N. Smart sensing technologies for structural health monitoring of civil engineering structures. Adv. Civ. Eng. 2010, 2010, 724962. [Google Scholar] [CrossRef] [Green Version]
- Chalioris, C.E.; Voutetaki, M.E.; Liolios, A.A. Structural health monitoring of seismically vulnerable RC frames under lateral cyclic loading. Earthq. Struct. 2020, 19, 29–44. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Providakis, C.P.; Favvata, M.J.; Papadopoulos, N.A.; Angeli, G.M.; Karayannis, C.G. Experimental application of a wireless earthquake damage monitoring system (WiAMS) using PZT transducers in reinforced concrete beams. WIT Trans. Built. Environ. 2015, 152, 233–243. [Google Scholar] [CrossRef] [Green Version]
- Chalioris, C.E.; Kytinou, V.K.; Voutetaki, M.E.; Karayannis, C.G. Flexural damage diagnosis in reinforced concrete beams using a wireless admittance monitoring system—Tests and finite element analysis. Sensors 2021, 21, 679. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, D.; Zheng, L.; Huo, L.; Song, G. Influence of axial load on electromechanical impedance (EMI) of embedded piezoceramic transducers in steel fiber concrete. Sensors 2018, 18, 1782. [Google Scholar] [CrossRef] [Green Version]
- CEN. EN 206:2013+A1:2016. Concrete—Specification, Performance, Production and Conformity; CEN: Brussels, Belgium, 2016. [Google Scholar]
- Providakis, C.P.; Liarakos, E.V. Web-based concrete strengthening monitoring using an innovative electromechanical impedance telemetric system and extreme values statistics. Struct. Control Health Monit. 2014, 21, 1252–1268. [Google Scholar] [CrossRef]
- Na, W.S.; Baek, J. A review of the piezoelectric electromechanical impedance based structural health monitoring technique for engineering structures. Sensors 2018, 18, 1307. [Google Scholar] [CrossRef] [PubMed] [Green Version]





| Cube | PC | FRC |
|---|---|---|
| 1 | 40.8 | 44.1 |
| 2 | 42.7 | 43.2 |
| 3 | 39.8 | 46.0 |
| 4 | 43.0 | 46.9 |
| 5 | 45.2 | 48.7 |
| 6 | 43.5 | 47.8 |
| Average | 42.5 | 46.1 |
| Standard deviation | 1.9 | 2.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voutetaki, M.E.; Naoum, M.C.; Papadopoulos, N.A.; Chalioris, C.E. Cracking Diagnosis in Fiber-Reinforced Concrete with Synthetic Fibers Using Piezoelectric Transducers. Fibers 2022, 10, 5. https://doi.org/10.3390/fib10010005
Voutetaki ME, Naoum MC, Papadopoulos NA, Chalioris CE. Cracking Diagnosis in Fiber-Reinforced Concrete with Synthetic Fibers Using Piezoelectric Transducers. Fibers. 2022; 10(1):5. https://doi.org/10.3390/fib10010005
Chicago/Turabian StyleVoutetaki, Maristella E., Maria C. Naoum, Nikos A. Papadopoulos, and Constantin E. Chalioris. 2022. "Cracking Diagnosis in Fiber-Reinforced Concrete with Synthetic Fibers Using Piezoelectric Transducers" Fibers 10, no. 1: 5. https://doi.org/10.3390/fib10010005
APA StyleVoutetaki, M. E., Naoum, M. C., Papadopoulos, N. A., & Chalioris, C. E. (2022). Cracking Diagnosis in Fiber-Reinforced Concrete with Synthetic Fibers Using Piezoelectric Transducers. Fibers, 10(1), 5. https://doi.org/10.3390/fib10010005









